Решения задач на теоремы Лапласа
На этой странице вы найдете решения типовых задач по теории вероятностей на использование теорем Лапласа (интегральной и локальной, еще их называют формулами Муавра-Лапласа) и их следствия.
Данные приближенные формулы применяются, когда мы по-прежнему решаем задачи схемы независимых испытаний Бернулли (примеры тут), но речь идет уже об очень большом числе испытаний (стандартные условия $n>100$, $np>20$). Непосредственные вычисления по формуле Бернулли трудоемки, и мы прибегаем к удобным и простым теоремам Муавра-Лапласа.
Формулы Муавра-Лапласа
Рассмотрим $n$ независимых испытаний, в каждом из которых событие может произойти с одной и той же вероятностью $p$. Тогда при больших $n$ вероятности можно вычислять по приближенным формулам Муавра-Лапласа.
Вероятность того, что событие наступит в точности $k$ раз, можно вычислить по формуле (локальная теорема Лапласа):
$$
P(X=k) approx frac{1}{sqrt{npq}} phi left( frac{k-np}{sqrt{npq}} right) .
$$
Значения функции $phi (x) =frac{1}{sqrt{2pi}} e^{-x^2/2}$ берутся из таблиц.
Вероятность того, что событие наступит от $k_1$ до $k_2$ раз, можно вычислить по формуле (интегральная теорема Лапласа):
$$
P(k_1 le X le k_2) approx Phi left( frac{k_2-np}{sqrt{npq}} right) – Phi left( frac{k_1-np}{sqrt{npq}} right)
$$
Здесь $Phi(x)$ — нормированная функция Лапласа (ее значения берутся из таблиц)
$$Phi (x)= frac{1}{sqrt{2pi}}int_0^x e^{-z^2/2}dz$$
Еще теорию по этой теме вы найдете в онлайн-учебнике.
Примеры решений
Локальная теорема Лапласа
Задача 1. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
Задача 2. Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна $р$. Найти вероятность, что за смену откажут $m$ элементов.
$р=0,024, m=6$.
Задача 3. На конвейер за смену поступает 300 изделий. Вероятность того, что поступившая на конвейер деталь стандартна, равна 0,75. Найти вероятность того, что стандартных деталей на конвейер за смену поступило ровно 240.
Задача 4. Вероятность поражения мишени стрелком при одном выстреле равна 0,8 Найти вероятность того, что при 100 выстрелах стрелок поразит мишень ровно 75 раз. Найти наивероятнейшее число попаданий в цель.
Задача 5. Игральную кость подбрасывают 500 раз. Какова вероятность того, что цифра 1 при этом выпадет 50 раз?
Интегральная теорема Лапласа
Задача 6. В жилом доме имеется $n$ ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между $m1$ и $m2$.
Найти наивероятнейшее число включенных ламп среди $n$ и его соответствующую вероятность.
$n = 6400, m1 = 3120, m2 = 3200$.
Задача 7. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.
Задача 8. Вероятность изготовления годной детали равна 0,8. Произведено 500 деталей. Какое число годных деталей вероятнее получить: а) менее 390; б) от 390 до 410?
Задача 9. Стоматологическая клиника распространяет рекламные листовки у входа в метро. Опыт показывает, что в одном случае из тысячи следует обращение в клинику. Найти вероятность того, что при распространении 50 тыс. листков число обращений будет:
А) равно 41,
Б) находиться в границах от 36 до 47.
Задача 10. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найти вероятность, что таких случаев будет не более 870.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятностей
Тысячи решенных и оформленных задач на формулу Лапласа и другие темы:
Локальная и интегральная теоремы Лапласа
При достаточно большом
формула Бернулли дает громоздкие
вычисления. Поэтому в таких случаях
применяют локальную теорему Лапласа.
Теорема (локальная теорема Лапласа).
Если вероятностьpпоявления
события А в каждом испытании постоянна
и отлична от 0 и 1, то вероятностьтого, что событие А появится вnнезависимых испытаниях ровноkраз, приближенно равна значению функции:
,
где
.
Имеются таблицы, в которых находятся
значения функции
,
для положительных значенийx.
Заметим, что функция
четна.
Итак, вероятность того, что событие А
появится в nиспытаниях
ровноkраз приближенно
равна
,
где.
Пример. На опытном поле посеяли 1500
семян. Найти вероятность того, что всходы
дадут 1200 семян, если вероятность того,
что зерно взойдет, равна 0,9.
Решение.
Интегральная теорема Лапласа
Вероятность того, что в nнезависимых испытаниях событие А
появится не менееk1 раз
и не болееk2 раз вычисляется
по интегральной теореме Лапласа.
Теорема (интегральная теорема
Лапласа). Если вероятность р наступления
события а в каждом испытании постоянна
и отлична от 0 и 1, то вероятность того,
что событие А вnиспытаниях
появится не менееk1раз
и не болееk2раз
приближенно равна значению определенного
интеграла:
,
где
.
Функция
называется интегральной функцией
Лапласа, она нечетна и ее значение
находятся по таблице для положительных
значенийx.
Пример.В лаборатории из партии
семян, имеющих всхожесть 90%, высеяно 600
семян, давших всходы, не менее 520 и не
более 570.
Решение.
Формула Пуассона
Пусть производится nнезависимых испытаний, вероятность
появления события А в каждом испытании
постоянна и равна р. Как мы уже говорили,
вероятность появления события А вnнезависимых испытаниях ровноkраз можно найти по формуле Бернулли.
При достаточно большомnиспользуют локальную теорему Лапласа.
Однако, эта формула непригодна, когда
вероятность появления события в каждом
испытании мала или близка к 1. А при р=0
или р=1 вообще не применима. В таких
случаях пользуются теоремой Пуассона.
Теорема (теорема Пуассона). Если
вероятность р наступления события А в
каждом испытании постоянна и близка к
0 или 1, а число испытаний достаточно
велико, то вероятность того, что вnнезависимых испытаниях событие А
появится ровноkраз
находится по формуле:
.
Пример. Рукопись объемом в тысячу
страниц машинописного текста содержит
тысячу опечаток. Найти вероятность
того, что наудачу взятая страница
содержит хотя бы одну опечатку.
Решение.
Вопросы для
самопроверки
-
Сформулируйте классическое определение
вероятности события. -
Сформулируйте теоремы сложения и
умножения вероятностей. -
Дайте определение полной группы событий.
-
Запишите формулу полной вероятности.
-
Запишите формулу Бейеса.
-
Запишите формулу Бернулли.
-
Запишите формулу Пуассона.
-
Запишите локальную формулу Лапласа.
-
Запишите интегральную формулу Лапласа.
Тема 13. Случайная величина и ее числовые характеристики
Литература: [2],[8],[9],[10],[18],[22].
Одним из основных понятий в теории
вероятностей является понятие случайной
величины. Так принято называть переменную
величину, которая принимает свои значения
в зависимости от случая. Различают два
вида случайных величин: дискретные и
непрерывные. Случайные величины принято
обозначать X,Y,Z.
Случайная величина Х называется
непрерывной (дискретной), если она может
принимать лишь конечное или счетное
число значений. Дискретная случайная
величина Х определена, если даны все ее
возможные значения х1, х2,
х3,…хn(число которых может
быть как конечным, так и бесконечным) и
соответствующие вероятности р1,
р2, р3,…рn.
Закон распределения дискретной случайной
величины Х обычно задается таблицей:
|
Х |
х1 |
х2 |
х3 |
… |
хn |
(1) |
|
Р |
р1 |
р2 |
р3 |
… |
рn |
Первая строка состоит из возможных
значений случайной величины Х, а во
второй строке указаны вероятности этих
значений. Сумма вероятностей, с которыми
случайная величина Х принимает все свои
значения, равна единице, то есть
р1+р2+ р3+…+рn=1.
Закон распределения дискретной случайной
величины Х можно изобразить графически.
Для этого в прямоугольной системе
координат строят точки М1(х1,р1),
М2(х2,р2), М3(х3,р3),…Мn(xn,pn)
и соединяют их отрезками прямых.
Полученную фигуру называют многоугольником
распределения случайной величины Х.
Пример. Дискретная величина Х задана
следующим законом распределения:
|
Х |
48 |
53 |
57 |
61 |
|
Р |
0,2 |
0,4 |
0,3 |
0,1 |
Требуется вычислить: а) математическое
ожидание М(Х), б) дисперсию D(X),
в) среднее квадратическое отклонение
σ.
Решение. а) Математическое ожидание
М(Х), дискретной случайной величины Х
называется сумма попарных произведений
всех возможных значений случайной
величины на соответствующие вероятности
этих возможных значений. Если дискретная
случайная величина Х задана с помощью
таблицы (1), то математическое ожидание
М(Х) вычисляется по формуле
М(Х)=х1∙р1+х2∙р2+х3∙р3+…+хn∙pn. (2)
Математическое ожидание М(Х) называют
также средним значением случайной
величины Х. Применяя (2), получим:
М(Х)=48∙0,2+53∙0,4+57∙0,3 +61∙0,1=54.
б) Если М(Х) есть математическое ожидание
случайной величины Х, то разность Х-М(Х)
называется отклонением случайной
величины Х от среднего значения. Эта
разность характеризует рассеяние
случайной величины.
Дисперсией (рассеянием) дискретной
случайной величины Х называется
математическое ожидание (среднее
значение) квадрата отклонения случайной
величины от ее математического ожидания.
Таким образом, по самому определению
имеем:
D(X)=M[X-M(X)]2. (3)
Вычислим все возможные значения квадрата
отклонения.
[x1-M(X)]2=(48-54)2=36
[x2-M(X)]2=(53-54)2=1
[x3-M(X)]2=(57-54)2=9
[x4-M(X)]2=(61-54)2=49
Чтобы вычислить дисперсию D(X),
составим закон распределения квадрата
отклонения и затем применим формулу
(2).
|
[x-M(X)]2 |
36 |
1 |
9 |
49 |
|
Р |
0,2 |
0,4 |
0,3 |
0,1 |
D(X)=
36∙0,2+1∙0,4+9∙0,3 +49∙0,1=15,2.
Следует отметить, что для вычисления
дисперсии часто используют следующее
свойство: дисперсия D(X)
равна разности между математическим
ожиданием квадрата случайной величины
Х и квадратом ее математического
ожидания, то есть
D(X)-M(X2)-[M(X)]2. (4)
Чтобы вычислить дисперсию по формуле
(4), составим закон распределения случайной
величины Х2:
|
Х2 |
482 |
532 |
572 |
612 |
|
Р |
0,2 |
0,4 |
0,3 |
0,1 |
Теперь найдем математическое ожидание
М(Х2).
М(Х2)= (48)2∙0,2+(53)2∙0,4+(57)2∙0,3
+(61)2∙0,1=
=460,8+1123,6+974,7+372,1=2931,2.
Применяя (4), получим:
D(X)=2931,2-(54)2=2931,2-2916=15,2.
Как видно, мы получили такой же результат.
в) Размерность дисперсии равна квадрату
размерности случайной величины. Поэтому
для характеристики рассеяния возможных
значений случайной величины вокруг ее
среднего значения более удобно
рассматривать величину, которая равна
арифметическому значению корня
квадратного из дисперсии, то есть
.
Эту величину называют средним
квадратическим отклонением случайной
величины Х и обозначают через σ. Таким
образом
σ=. (5)
Применяя (5), имеем: σ=.
Пример. Случайная величина Х
распределена по нормальному закону.
Математическое ожидание М(Х)=5; дисперсияD(X)=0,64. Найти
вероятность того, что в результате
испытания Х примет значение в интервале
(4;7).
Решение. Известно, что если
случайная величина Х задана дифференциальной
функциейf(x),
то вероятность того, что Х примет
значение, принадлежащее интервалу
(α,β), вычисляется по формуле
. (1)
Если величина Х распределена по
нормальному закону, то дифференциальная
функция

где а=М(Х) и σ=.
В этом случае получаем из (1)

Формулу (2) можно преобразовать, используя
функцию Лапласа.
Сделаем подстановку. Пусть
.
Тогдаилиdx=σ∙dt.
Следовательно

гдеt1иt2соответствующие пределы для переменнойt.
Сократив на σ, будем иметь
Из введенной подстановки
следует, что
и
.
Таким образом,
(3)
По условию задачи имеем: а=5; σ==0,8;
α=4; β=7. Подставив эти данные в (3), получим:
=Ф(2,5)-Ф(-1,25)=
=Ф(2,5)+Ф(1,25)=0,4938+0,3944=0,8882.
Пример. Считается, что отклонение
длины изготавливаемых деталей от
стандарта является случайной величиной,
распределенной по нормальному закону.
Стандартная длина (математическое
ожидание) а=40 см, среднее квадратическое
отклонение σ=0,4 см. Найти вероятность
того, что отклонение длины от стандартной
составит по абсолютной величине не
более 0,6 см.
Решение. Если Х – длина детали,
то по условию задачи эта величина должна
быть в интервале (а-δ,а+δ), где а=40 и δ=0,6.
Положив в формулу (3) α= а-δ и β= а+δ, получим
Итак,
. (4)
Подставив в (4) имеющиеся данные, получим:
Следовательно, вероятность того, что
изготавливаемые детали по длине будут
в пределах от 39,4 до 40,6 см, составляет
0,8664.
Пример. Диаметр деталей, изготавливаемых
заводом, является случайной величиной,
распределенной по нормальному закону.
Стандартная длина диаметраа=2,5см,
среднее квадратическое отклонение
σ=0,01. В каких границах можно практически
гарантировать длину диаметра этой
детали, если за достоверное принимается
событие, вероятность которого равна
0,9973?
Решение. По условию задачи имеем:
а=2,5; σ=0,01;
.
Применяя формулу (4), получаем равенство:
или
.
По таблице 2 находим, что такое значение
функция Лапласа имеет при х=3. Следовательно,
;
откуда σ=0,03.
Таким образом, можно гарантировать, что
длина диаметра будет изменяться в
пределах от 2,47 до 2,53 см.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Видеоурок: интегральная теорема Муавра-Лапласа
17 сентября 2015
- Таблица значений функции Лапласа
Данная теорема является дальнейшим развитием схемы Бернулли и позволяет работать с диапазонами: какова вероятность, что число успехов будет лежать в пределах указанного отрезка.
Интегральная теорема Муавра-Лапласа. Пусть число испытаний $n$ достаточно велико, а вероятность успеха $0 lt ,p, lt 1$. Пусть также$q=1-p$ — вероятность неудачного испытания. Тогда вероятность того, что число успехов будет лежать в пределах от ${{k}_{1}}$ до ${{k}_{2}}$, можно примерно посчитать по формуле:
[{{P}_{n}}left( {{k}_{1}};{{k}_{2}} right)approx Phi left( frac{{{k}_{2}}-np}{sqrt{npq}} right)-Phi left( frac{{{k}_{1}}-np}{sqrt{npq}} right)]
где
[Phi left( x right)=frac{1}{sqrt{2text{ }!!pi!!text{ }}}intlimits_{0}^{x}{{{e}^{-frac{{{t}^{2}}}{2}}}dt}]
Функция $Phi left( x right)$ называется функцией Лапласа и содержит в себе интеграл, который не считается напрямую. Как следствие, значения этой функции сведены в таблицу, которую можно загрузить прямо на этой странице.
Разумеется, в таблице приведены не все возможные значения. Для больших значений $x$ (скажем, для $x gt 6$ ) считают, что $Phi left( x right)approx 0,5$. Кроме того, функция Лапласа является нечётной, поэтому из неё можно выносить знак «минус»:
[Phi left( -x right)=-Phi left( x right)]
Это прямо следует из определения, в котором присутствует определённый интеграл.
Что такое “интегральная теорема Муавра-Лапласса”?
Сегодня мы разберем интегральную теорему Муавра-Лапласа. Это «старшая сестра» второй версии теоремы Муавра-Лапласа, разобранной в прошлом уроке. Во-первых, разберемся, зачем вообще нужна еще одна теорема — интегральная.
Допустим, у нас есть 1000 изделий, о которых известно, что там в среднем есть 10% брака. Однако это не означает, что в партии из 1000 изделий будет ровно 100 бракованных изделий, скорее всего, их будет 101-102 или 98, но не 100. Вероятность того, что будет ровно 100, легко считается при помощи более легкой теоремы Муавра-Лапласа, и вы можете сами убедиться, что она будет велика. В этом случае возникает вопрос: «Какова тогда вероятность, что деталей будет от 95 до 105, либо от 50 до 150?». Считать такую конструкцию при помощи первой версии теоремы Муавра-Лапласса крайне сложно, потому что нам придется отдельно посчитать, какова возможность того, что бракованных изделий будет 50, 51, 51 и так до 150, т.е. сто отдельных однотипных вычислений. Это очень трудоемко и бессмысленно. Вот именно в таких примерах нам на помощь приходит интегральная теорема Муавра-Лапласа. С назначением самой интегральной теоремы все ясно, теперь давайте разберемся с ее формулой.
Вероятность того, что при $n$-испытаниях количество успешных испытаний будет в пределах от ${{K}_{1}}$ до ${{K}_{2}}$ выражается следующей формулой:
[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]
Сама же функция $F$ называется функцией Муавра-Лапласа, и выглядит она следующим образом:
[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]
Сразу же скажу, что данный интеграл «красиво» не считается, поэтому вместо красивого интегрирования у вас всегда будет в распоряжении таблица значений функции Лапласа, и с помощью этой таблицы, а также некоторых способов, которые мы разберем чуть позже в этом уроке, мы и будем решать все примеры на данную интегральную теорему.
Разумеется, возникает вопрос «А что это за буквы такие — $n$, $q$, $p$?».
С $n$, я думаю, все понятно — это число испытаний.
$p$ — это вероятность успеха в каждом конкретном испытании.
$q$ — по аналогии с формулой Бернули это вероятность провала, т.е. неуспеха в каждом конкретносм испытании. Считатеся она по очень простой формуле:
[q=1-p]
Надеюсь, с буквами теперь понятно, поэтому перейдем к решению конкретных примеров.
Задача № 1
Начнем мы с довольно простой задачи, однако уже на ее примеры мы познакомимся с особенностями применения интегральной теоремы Муавра-Лапласса.
Известно, что в среднем 5% студентов носят очки. Какова вероятность того, что из 200 студентов, находящихся в аудитории, окажется не менее 10%, носящих очки?
В первую очередь, давайте запишем саму интегральную теорему Муавра-Лапласса:
[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]
При этом полезно помнить еще одну формулу:
[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]
Собственно, из-за этого интеграла, присутствуещего в функции Муавра-Лапласса, сама теорема и называется интегральной.
При первом взгляде на эту интегральную теорему многие ученики приходят в шок — уж больно много здесь разных конструкций, корней, вычислений и т.д. На самом деле, все очень просто, и сейчас вы сами в этом убедитесь.
Для начала давайте выпишем все значения. Итак, нам известно следующее:
- Всего студентов 200 — $n=200$;
- Вероятность попадания студента, который носит очки — $p=0,05$;
- Вероятность того, что студенты не носят очки будет равна $1-0,05=0,95$.
Далее мы можем найти $sqrt{npq}$:
[sqrt{npq}=sqrt{200cdot 0,05cdot 0,95}=sqrt{9,5}approx 3,08]
Разумеется, такие вычисления выполняются на калькуляторе.
Кроме того, в нашей формуле, в интегральной теореме Муавра-Лапласса, мы наблюдаем выражение $np$ — произведение количества испытаний на вероятность успеха:
[np=200cdot 0,05=10]
Давайте перепишем формулу с учетом всех фактов:
[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{200-10}{3,08} right)-Fleft( frac{20-10}{3,08} right)=]
[=Fleft( 61,7 right)-Fleft( 3,25 right)]
И вот здесь нас поджидает первая проблема: если мы посмотрим на таблицу значений, то значение $3,25$ здесь еще присутствует, но вот числа от $60$ и более здесь вообще не представлены. Для решения этого вопроса предлагаю взглянуть на исходную формулу Муавра-Лапласса:
[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]
При больших «иксах» ${{e}^{-frac{{{t}^{2}}}{2}}}$ будет очень маленьким числом, т.е. возрастание $x$ дает очень маленькую, стремящуюся к «нулю» добавку к вероятности. Поэтому для всех «иксов», начиная от шести и более примерно считается, что значение функции Лапласса равно $0,5$. $$ $$
Итак, продолжим наше решение:
[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx 0,5-0,49942=0,00058=5,8cdot {{10}^{-4}}]
Нюансы решения
Как видите, ничего сверхъестественного. Все применение интегральной теоремы Муавра-Лапласса сводится к следующему:
- Аккуратно выписать все значения: число испытаний, вероятность и «единицу» «минус» вероятность.
- Посчитать корни и величины.
- Пробежаться глазами по таблице и найти значение функции в тех точках, которые мы получили.
Однако, как вы понимаете, это была самая простая задача — существуют гораздо более сложные и навороченные. И один из самых «противных» типов заданий на применение интегральной теоремы Муавра-Лапласса состоит в том, что общая вероятность, которую мы обычно рассчитываем по формуле, нам известна, а необходимо найти либо ${{K}_{1}}$, либо ${{K}_{2}}$. Вот именно сейчас такую задачу мы и решим.
Самое обидное, что именно такие чаще всего и попадаются на всяких контрольных, зачетах и экзаменах. Они будут вам встречаться на исследованиях, где необходимо определить какую-нибудь статистическую величину. Поэтому именно сейчас мы попытаемся решить такую задачу.
Задача № 2
Театр, вмещающий 1000 человек, имеет два разных входа, каждым из которых любой зритель может воспользоваться с равной вероятностью. Около каждого входа имеется свой гардероб. Сколько мест должно быть в каждом гардеробе, чтобы с вероятностью в 0,99 любой зритель смог раздеться в том гардеробе, в который он обратился сразу после входа в театр.
Я думаю, очевидно, что в данной задаче общее количество испытаний, т.е. человек, которые придут в театр, не более 1000 — $n=1000$.
Всего входов два, при этом в каждый с одинаковой вероятностью входит один и тот же человек — $p=frac{1}{2}$.
Следовательно, $q=1-frac{1}{2}=frac{1}{2}$.
Кроме того, общая возможность того, что при 1000 испытаний количество успеха попадет в искомый нами диапазон, равно 0,99 — ${{P}_{1000}}left( {{K}_{1}};{{K}_{2}} right)=0,99$. Остается разобраться с числами ${{K}_{1}}$ и ${{K}_{2}}$, т.е. границами диапазона. ${{K}_{1}}$ — наименьшее количество людей, которые могут обратиться в данный гардероб. Очевидно, будет «ноль», потому что меньше нуля прийти не может — ${{K}_{1}}=0$. Остается вопрос: «Чему равно ${{K}_{2}}$?». Именно это нам и нужно найти по условию.
Опять запишем интегральную теорему Муавра-Лапласса:
[{{P}_{1000}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]
Посмотрим:
[np=1000cdot frac{1}{2}=500]
[sqrt{npq}=sqrt{1000cdot frac{1}{2}cdot frac{1}{2}}=sqrt{250}=5sqrt{10}=15,8]
Подставим все полученные числа в формулу, с учетом того, что ${{K}_{1}}=0$:
[{{P}_{1000}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-500}{15,8} right)-Fleft( frac{0-500}{15,8} right)=0,99]
Теперь внимательно посмотрим на эту формулу. Отдельно посчитаем значение функции Муавра-Лапласса в следующей точке:
[Fleft( frac{-500}{15,8} right)=-Fleft( 31,6 right)=0,5]
Итого переписывая, мы получаем:
[Fleft( frac{{{K}_{2}}-500}{15,8} right)+0,5=0,99]
[Fleft( frac{{{K}_{2}}-500}{15,8} right)=+0,49]
Единственный способ, при помощи которого можно решить этот пример — это взять таблицу значений функции Муавра-Лапласса и посмотреть, когда она равна $0,49$, при каком $x$. Проблема состоит в том, что точного значения мы не найдем. Однако есть значение функции Муавра-Лапласса в точках $2,32$ и $2,34$ :
[Fleft( 2,32 right)=0,48983]
[Fleft( 2,34 right)=0,49036]
Где-то между ними лежит наша искомая величина $0,49$. А между числами $2,32$ и $2,34$ лежит величина $2,33$. Так и запишем:
[frac{{{K}_{2}}-500}{15,8}=2,33]
Теперь нам осталось решить простейшее уравнение:
[{{K}_{2}}-500=2,33cdot 15,8]
[{{K}_{2}}-500=36,8]
[{{K}_{2}}approx 536,8=537]
Ответ: 537.
Каверзные вопросы
Подождите, есть несколько вопросов. Во-первых, почему мы так легко вынесли «минус» из функции Лапласса наружу, а во-вторых, почему мы постоянно пользуемся калькулятором?
Давайте для начала посмотрим на формулу функции Муавра-Лапласса:
[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]
Это, прежде всего, интеграл от «нуля» до $x$ в прелах четной функции, поэтому если перед $x$ внезапно появится «минус», мы можем поменять местами верхние и нижнее пределы интегрирования, при том перед самим интегралом также появится знак «минус», и больше никаких изменений не будет. Это одно из ключевых свойств определенного интеграла.
Кроме того, в таблице значений все аргументы функций приведены именно в виде десятичных дробей, поэтому считая значение функции, мы просто обязаны перевести то, что стоит у нас внутри скобок, в десятичную дробь, в том числе с помощью калькулятора.
В заключение посмотрим еще одну задачку, в которой мы не только еще раз отработаем использование стандартной формулы, но и вспомним, что такое вторая версия теоремы Муавра-Лапласса, отличная от интегральной, и в каких ситуациях она применяется.
Задача № 3
Радиотелеграфная станция передает цифровой текст. В силу наличия помех каждая цифра независимо от других может быть неправильно принята с вероятностью 0,01. Найдите вероятность того, что в принятом тексте, содержащем 1100 цифр, будет:
а) 15 ошибок;
б) менее 20 ошибок.
Решение пункта б)
Что касается б), то тут все вполне очевидно — это чистейшая теорема Муавра-Лапласса, причем интегральная. Так и запишем:
[n=1100]
[p=0,01]
[q=0,99]
[{{K}_{1}}=0]
[{{K}_{2}}=19]
Теперь запишем интегральную формулу Муавра-Лапласса:
[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]
Посчитаем:
[np=1100cdot 0,01=11]
[sqrt{npq}=sqrt{11cdot 0,99}=sqrt{frac{11cdot 11cdot 9}{100}}=sqrt{frac{{{11}^{2}}cdot {{3}^{2}}}{{{10}^{2}}}}=frac{11cdot 3}{10}=3,3]
Осталось подставить числа в формулу:
[{{P}_{1100}}left( 0;19 right)approx Fleft( frac{19-11}{3,3} right)-Fleft( frac{0-11}{3,3} right)=]
[=Fleft( 2,42 right)+Fleft( 3,33 right)=]
[=0,49224+0,49960=0,99184approx 0,99]
Ответ: 0,99
Решение пункта а)
А теперь давайте разберемся с пунктом а). В нем от нас требуется, чтобы при тех же исходных данных, вычислить, что в итоге появится ровно 15 ошибок.
Очевидно, что это идеальная задача для применения второй версии теоремы Муавра-Лапласса — не интегральной. Давайте я ее запишу:[]
[{{P}_{n}}left( K right)approx frac{1}{sqrt{npq}}cdot varphi left( frac{K-np}{sqrt{npq}} right)]
Выпишем известные данные:
[n=1100]
[p=0,01]
[q=0,99]
Решим:
[{{P}_{1100}}left( 15 right)approx frac{1}{3,3}cdot varphi left( frac{15-11}{3,3} right)approx 0,303cdot varphi left( 1,212 right)approx ]
[approx 0,303cdot 0,1919approx 0,058]
Ответ: 0,058.
Ключевые моменты
Вот и все, что я хотел вам рассказать об интегральной теореме Муавра-Лапласса, такой, на первый взгляд сложной, но очень простой на практике. Все, что вам необходимо — это
- Знать сами формулы для обеих теорем Муавра-Лапласса, в том числе, интегральной.
- Грамотно считать корни и элементы $np$, которые являются матожиданием.
В ближайшее время я размещу на своем сайте целый комплект задач, посвященный теоремам Муавра-Лапласса, в том числе, интегральной. Поэтому присоединяйтесь к нам на YouTube, ставьте лайки и пишите комментарии. До новых встреч!
Смотрите также:
- Локальная теорема Муавра — Лапласа
- Схема Бернулли. Примеры решения задач
- Основное тригонометрическое тождество
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Иррациональные неравенства. Часть 2
- Задача B4: обмен валют в трех различных банках
Применение локальной и интегральной теоремы Муавра-Лапласа
Содержание:
-
Локальная и интегральная теоремы Муавра-Лапласа
- Локальная теорема Лапласа
- Интегральная предельная теорема Муавра-Лапласа
- Таблица значений для вычисления определителей
- Пример решения задачи
Локальная и интегральная теоремы Муавра-Лапласа
В том случае, когда количество манипуляций достаточно большое, применять формулу Бернулли становится нецелесообразно. Упростить решение задачи или доказательство выражения можно с помощью локальной и интегральной теорем Лапласа. Данные закономерности позволяют получить результат испытаний, приближенный к итогам вычислений по формуле Бернулли, и характеризуются меньшими расчетами.
Рассматриваемые теоремы активно применяют в решении задач по данным большого количества экспериментов для нахождения приближенного значения вероятности. С помощью локальной теоремы можно вычислить определенное число явлений. Благодаря интегральной теореме Муавра-Лапласа, достаточно просто найти ответ при заданном диапазоне вероятного количества возникновения событий.
Локальная теорема Лапласа
В том случае, когда вероятность p возникновения явления A характеризуется постоянством, и (pne 0) и (pne 1), то вероятность (P_n ( k )) того, что событие A возникнет k раз в n экспериментах, равна приближенно (увеличивая n, получаем более точный результат испытаний и меньше погрешность) значению функции (y=frac { 1 } { sqrt { ncdot pcdot q } } cdot frac { 1 } { sqrt { 2pi } } cdot e^ { – { x^2 } / 2 } =frac { 1 } { sqrt { ncdot pcdot q } } cdot varphi ( x ))
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В данном случае( x=frac { k-ncdot p } { sqrt { ncdot pcdot q } })
Из выражения можно сделать вывод:
(label { eq2 } P_n ( k )approx frac { 1 } { sqrt { ncdot pcdot q } } cdot varphi ( x ))
где (x=frac { k-ncdot p } { sqrt { ncdot pcdot q } })
Следует отметить, что функция (varphi ( x )=varphi ( { -x } )) является четной.
Свойства представленной функции:
- функция является четной;
- если аргумент обладает значением больше, чем 4, то функция будет сколь угодно мала.
Интегральная предельная теорема Муавра-Лапласа
Вероятность P, что возникнет событие A, для каждого эксперимента по порядку обладает стабильным значением, и (pne 0) и (pne 1), тогда вероятность (P_n ( { k_1 ,k_2 } )) того, что явление A наступит от (k_ { 1 }) до (k_ { 2 }) раз в n опытах, равна (P_n ( { k_1 ,k_2 } )approx frac { 1 } { sqrt { 2cdot pi } } intlimits_ { x_1 } ^ { x_2 } { e^ { – { z^2 } / 2 } dz } =Phi ( { x_2 } )-Phi ( { x_1 } ))
В смысле данной формулировки,( x_1 =frac { k_1 -ncdot p } { sqrt { ncdot pcdot q } }) , (x_2 =frac { k_2 -ncdot p } { sqrt { ncdot pcdot q } })
Следует отметить, что (Phi ( x )=frac { 1 } { sqrt { 2cdot pi } } int { e^ { – { z^2 } / 2 } dz }) можно определить с помощью специальных табличных схем.
(Phi ( { -x } )=-Phi ( x )) является нечетной функцией.
Рассматриваемая функция обладает следующими основными свойствами:
- функция является нечетной;
- если аргумент больше, чем 5, то значение функции составляет 0,5.
Таблица значений для вычисления определителей
В случае применения локальной теории Лапласа целесообразно использовать специальные таблицы:
Таблица значений интегральной функции Лапласа имеет следующий вид:
Применительно к вероятностям распределения Пуассона сформирована таблица:
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Пример решения задачи
Задача № 1
Требуется определить, какова вероятность возникновения события А в течение 80 раз во время проведения 400 опытов. Следует учитывать вероятность появления данного события в каждом эксперименте составляет( р = 0,2.)
Решение:
В том случае, когда р = 0,2: q = 1 – p = 1 – 0,2 = 0,8
Таким образом:
(P_ { 400 } ( { 80 } )approx frac { 1 } { sqrt { ncdot pcdot q } } varphi ( x ),,,)
где (x=frac { k-ncdot p } { sqrt { ncdot pcdot q } })
В таком случае:
(begin{array} { l } x=frac { k-ncdot p } { sqrt { ncdot pcdot q } } =frac { 80-400cdot 0,2 } { sqrt { 400cdot 0,2cdot 0,8 } } =frac { 80-80 } { sqrt { 400cdot 0,16 } } =0 \ varphi ( 0 )=0,3989,,,P_ { 400 } ( { 80 } )approx frac { 0,3989 } { 20cdot 0,4 } =frac { 0,3989 } { 8 } =0,0498 \ end{array})
Ответ: вероятность равна 0,0498
Задача № 2
По условиям задания, в процессе контроля качества выявляют 10% брака от произведенных изделий. Для этой процедуры выбирают 625 изделий. Необходимо определить вероятность того, что в объеме отобранных изделий имеется не меньше 550 и не больше 575 качественных экземпляров.
Решение:
В том случае, когда брак составляет 10% от изделий, то качественные экземпляры должны определяться, как 90%. При таком условии:
(n=625, p=0,9, q=0,1, k_1 =550, k_2 =575)
Тогда:
(ncdot p=625cdot 0,9=562,5)
Исходя из полученного выражения, определим:
(begin{array} { l } P_ { 625 } (550,575)approx Phi ( { frac { 575-562,5 } { sqrt { 625cdot 0,9cdot 0,1 } } } )- Phi ( { frac { 550-562,5 } { sqrt { 626cdot 0,9cdot 0,1 } } } )approx Phi (1,67)- Phi (-1,67)=2 Phi (1,67)=0,9052 \ end{array})
Ответ: вероятность составит 0,9052
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Локальная теорема Лапласа
Пусть проводится $n$ испытаний Бернулли с вероятностью р появления события А в каждом из них. Пусть при этом $n$ достаточно большое число и $npq$ ≥ 10 ($n$ — большое, а $p$ — не очень маленькое) Тогда вероятность, того, что событие А произойдет ровно k раз может быть найдена по приближенной формуле:
Замечание
таблица значений функции $varphi$$(x)$обычно приводится в задачниках Теории вероятностей.
Свойства функции $varphi$$left(xright):$
- $varphi$$left(xright)>0$
- $varphi$$left(-xright)=$$varphi$$left(xright)$
- ${mathop{lim}_{nto infty } (x) }=0, (left(xright)
Пример 1
Какова вероятность, что из 100 новорожденных ровно 40 окажутся мальчики.
[left. begin{array}{c}
n=100 \
k=40 \
p=0,5 end{array}
right} x=frac{k-np}{sqrt{npq}}=frac{40-100cdot 0,5}{sqrt{100cdot 40cdot 0,5}}=-2]
[P_{100}left(40right)=frac{1}{sqrt{100cdot 0,5cdot 0,5}}varphi left(-2right)=frac{1}{5}varphi left(-2right)=frac{1}{5}varphi left(2right)=frac{1}{5}cdot 0,054=0,04]
Интегральная теорема Лапласа
В условиях локальной теоремы Лапласа вероятность того, что событие А произойдет от $k_1$ до $k_2$ раз $left(k_1le kle k_2right)$
[P_nleft(k_1;k_2right)=left(x”right)-left(x’right)]
[x”=frac{k_2-np}{sqrt{npq}} x’=frac{k_1-np}{sqrt{npq}}]
$Pleft(xright)=frac{1}{sqrt{2pi }}int{e^{frac{-t^2}{2}dt}}-$формула Лапласа
Замечание
Иногда функцией Лапласа называется выражение несколько отличающееся от написанного.
Свойство функции Лапласа:
- $left(-xright)=left(xright)$
- $left(xright)$ — монотонно возрастает
- $0,5
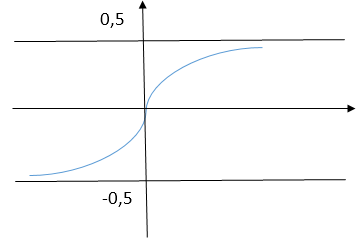
Замечание
Замечание: функция Лапласа $left(xright)$ связана с $left(xright): left(xright)=intnolimits^x_0{left(tright)dt}$
«Локальная и интегральная теоремы Лапласа» 👇
Пример 2
Схожесть семян составляет 90%. Какова вероятность, что из 100 семян взойдут от 84 до 96 семян.
[n=100]
[p=0,9]
[84le kle 96]
[k_1=84]
[k_2=96]
[x”=frac{k_2-np}{sqrt{npq}}=frac{96-100cdot 0,9}{sqrt{9}}=2]
[x’=frac{k_1-np}{sqrt{npq}}=frac{84-100cdot 0,9}{sqrt{9}}=-2]
[P_{100}left(84,96right)=left(x”right)-left(x’right)=left(2right)-left(-2right)=2left(2right)=0,95]
Замечание
Имеются таблицы, в которых помещены значения функции $left(xright)=frac{1}{sqrt{2}}e^{-frac{x^2}{2}},$ соответствующие положительным значениям аргумента x. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция $varphi $(x) является чётной.
Пример 3
В театре, который вмещает 1000 зрителей, есть два входа, каждый из которых имеет свой гардероб. Какое должно быть минимальное количество мест в каждом гардеробе, что б с вероятностью $Pge 0,99$ все зрители смогли раздеться в гардеробе того входа, через который они заходили? Примем во внимание, что зрители приходят парами и каждая пара независимо друг от друга выбирает один из входов с равным количеством вероятностей.
Пускай в каждом из двух гардеробов должно быть $2n$ мест. Через $2m$ обозначим число тех зрителей, которые воспользовались первым входом в театр, тогда вторым входом воспользовалось $1000-2m$ зрителей. В задаче необходимо что б выполнялось условие:
$Pleft{2mle 2n, 1000-2mle 2nright}ge 0,99$ или
[Pleft{1000-2nle 2mle 2nright}ge 0,99; ]
[Pleft{500-nle mle nright}ge 0,99]
Принимая во внимания, что $n=500,$ а $p=frac{1}{2},$ за формулой $P_nleft(k_1;;k_2right)=left(x^{”}right)-left(x’right), $получим
[Pleft{500-nle mle nright}=left(frac{n-500cdot frac{1}{2}}{sqrt{500cdot frac{1}{2}cdot frac{1}{2}}}right)-left(frac{500-n-500cdot frac{1}{2}}{sqrt{500cdot frac{1}{2}cdot frac{1}{2}}}right)=]
[=left(frac{n-250}{5sqrt{5}}right)-left(-frac{n+250}{5sqrt{5}}right)=left(frac{n-250}{5sqrt{5}}right)+left(frac{n-250}{5sqrt{5}}right)=]
[=2left(frac{n-250}{5sqrt{5}}right)ge 0,99.]
Искомое минимальное значение найдем с условия $left(frac{n-250}{5sqrt{5}}right)ge 0,495.$
За таблицей которая имеется почти во всех книгах теории вероятности найдем, что $frac{n-250}{5sqrt{5}}=2,68.$ Откуда $nge 279.$
Значит, в каждом из гардеробов должно быть не меньше $279cdot 2=558$ мест.
Пример 4
Вероятность того, что деталь не прошла контроль качества $p=0,2.$ Найти вероятность того, что среди 400 случайно выбранных деталей окажется непроверенными 70 деталей.
По условию задачи $p=0,2; q=1-0,2=0,8; n=400; k=70.$
Найдем
[x_{70}=frac{70-np}{sqrt{npq}}=frac{70-400cdot 0,2}{sqrt{400cdot 0,2cdot 0,8}}=-1,25.]
За локальной теоремой Лапласа, получим
[P_{400}left(70right)=frac{1}{sqrt{400cdot 0,2cdot 0,8}}cdot left(-1,25right).]
Значение $left(-1,25right)=left(1,25right)$ в таблице находим $left(1,25right)=0,8126.$ Тогда подставив это значение в предыдущую формулу получим $P_{400}left(70right)=frac{0,1826}{8}approx 0,023.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме





