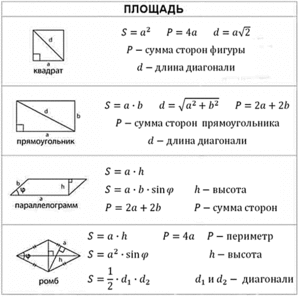
Чтобы найти площадь прямоугольника, надо его ширину умножить на длину.
Формула площади
S = a * b
Чтобы найти периметр прямоугольника, надо сложить все его стороны.
Формула периметра
Р = а * 2 + b * 2 или Р = (а + b ) * 2
Формулы площади и периметра для квадрата выглядят так:
S = a * a
Р = а * 4
Чтобы найти объем прямоугольного параллелепипеда, надо умножить его длину на ширину и высоту.
Формула объема
V = a * b * c
Формула объема для куба
V = a * a * a
Задачи
- Длина прямоугольника равна 5 см, а ширина – 4 см. Найдите площадь и периметр прямоугольника.
- Сторона квадрата равна 20 см. Найдите площадь и периметр квадрата.
- Вычислите периметр квадрата со стороной 6 дм.
- Вычислите площадь прямоугольника, длины сторон которого равны 12 мм и 8 мм.
- Длина прямоугольника равна 30 см, ширина – на 10 см меньше. Найдите Р и S этого прямоугольника.
- Длина одной стороны прямоугольника 4 см, а ширина в 2 раза больше. Найдите периметр и площадь прямоугольника.
- Сторона квадрата равна 10 дм. Чему равен периметр?
- Ширина прямоугольника 9 дм, а длина в 2 раз больше ширины. Найдите Р и S этого прямоугольника.
- Площадь прямоугольника 54 см², его длина 9 см. Чему равна ширина прямоугольника?
- Периметр квадрата равен 20 см. Найдите его площадь.
- Площадь прямоугольника равна 360 см², его длина 6 см. Найдите периметр этого прямоугольника.
- Периметр прямоугольника равен 40 дм. Ширина – 5 дм. Найдите его площадь?
- Сад около дома имеет ширину 20 м, а длину – 30 м. Какой длины надо поставить вокруг сада. Какова площадь сада?
- Прямоугольный параллелепипед имеет следующие грани – 6 см, 8 см, 10см. Найдите объем параллелепипеда.
- Высота комнаты 3 м, ширина 6 м, а длина 10 м. Сколько кубических метров воздуха находится в комнате? Найдите площадь пола, потолка, стен?
- Найдите объем бассейна, если его глубина 3 м, ширина 12м, длина 20 м.
- Длина аквариума 50 см, ширина – 30 см, высота 40 см. Сколько литров воды можно в него налить (до краев)?
- Найдите объем книги. Толщина – 2 см, ширина – 15 см, а длина – 20 см.
Также посмотрите дополнительные задания по темам:
Задания на таблицу умножения и деления.
Уравнения простые и составные, 3 класс.
Карточки для развития внимания на каждый день (примеры с несколькими действиями плюс упражнение на внимание).
Единицы времени.
Примеры на порядок действий (примеры с несколькими действиями).
Единицы длины и Единицы веса.
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.

S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
Как найти площадь четырехугольника 3 класс?
Что такое площадь для 3 класса?
Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. . Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Какая формула у площади квадрата?
S = a × a = a 2 , где S — площадь, a — сторона. Эту формулу проходят в 3 классе.
Что такое площадь как ее найти?
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина. Проверить полученный результат поможет онлайн-калькулятор площади прямоугольника.
Как найти площадь прямоугольного треугольника в 3 классе?
Вывод: чтобы найти площадь прямоугольного треугольника, нужно катеты перемножить и произведение разделить на 2.
.
закреплять материал, изученный на предыдущих уроках:
- нахождение части от числа и числа от части,
- нахождение площади прямоугольника,
- нахождение процентов.
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними

Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | диагональ и угол между ними |  |
|
| 2 | стороны и углы между этими сторонами |  |
|
| 3 | стороны (по Формуле Брахмагупты) |
 |
|
| 4 | стороны и радиус вписанной окружности |  |
|
| 5 | стороны и углы между ними |  |
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
 Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).

Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
[spoiler title=”источники:”]
http://doza.pro/art/math/geometry/area-tetragon
http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika
[/spoiler]
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе – это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь – это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник : 
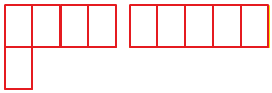
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
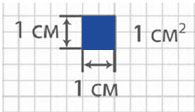
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
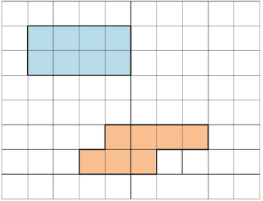
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
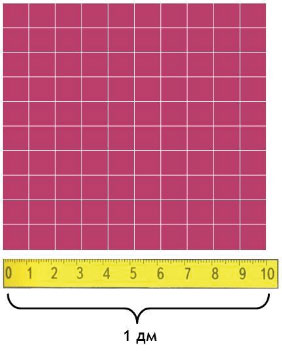
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
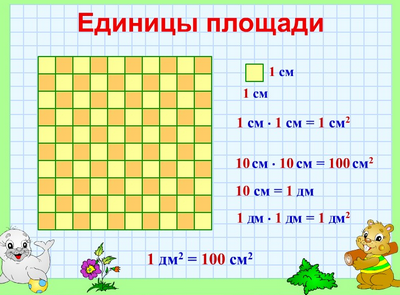
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
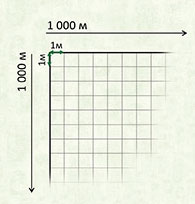
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
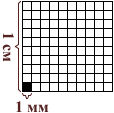
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
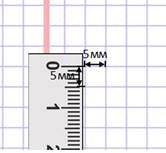
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар – это площадь квадрата со стороной 10 м.
Слово “ар” при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар – это площадь квадрата со стороной 100 м.
Слово “гектар” при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 43. Урок 17,
Петерсон, Учебник, часть 2
Страница 47. Урок 18,
Петерсон, Учебник, часть 2
Страница 81. Урок 33,
Петерсон, Учебник, часть 2
Страница 82. Урок 34,
Петерсон, Учебник, часть 2
Страница 88. Урок 37,
Петерсон, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 3
Страница 33. Урок 11,
Петерсон, Учебник, часть 3
Страница 40. Урок 14,
Петерсон, Учебник, часть 3
Страница 52. Урок 18,
Петерсон, Учебник, часть 3
Страница 56. Урок 20,
Петерсон, Учебник, часть 3
3 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 1
Страница 85. Урок 31,
Петерсон, Учебник, часть 1
Страница 18. Урок 7,
Петерсон, Учебник, часть 2
Страница 88. Урок 38,
Петерсон, Учебник, часть 2
Страница 42. Урок 19,
Петерсон, Учебник, часть 3
4 класс
Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 28. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 107,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 38,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 70,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 2
