Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
- стрелок ощущает отдачу при выстреле из ружья;
- рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
- шары сталкиваются на бильярдном столе.
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Замкнутая система – система тел, на которую со стороны других тел не действуют внешние силы.
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
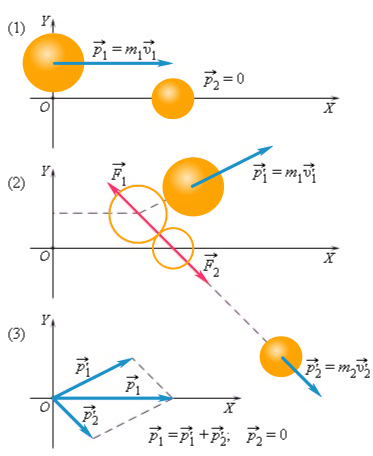
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F1→ и F2→ – это силы взаимодействия между телами. Третий закон Ньютона гласит, что F2→=-F1→. Пусть тела взаимодействуют во течение времени t. Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.
F2t→=-F1→t.
По второму закону Ньютона:
F1→t=m1v1’→-m1v1→; F2→t=m1v2’→-m1v2→
Здесь v1’→ и v2’→ – скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.
Из записанного выше следует соотношение:
m1v1→+m2v2→=m1v1’→+m2v2’→
Это равенство – математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
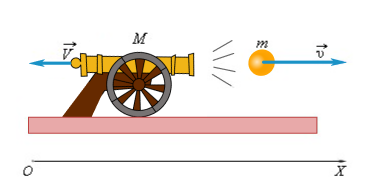
Рассмотрим снаряд, вылетающий из пушки.
В данном случае взаимодействующие тела – это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость v→ и летит вперед, а пушка откатывается назад со скоростью V→. Откатывание пушки называется отдачей от выстрела.
По закону сохранения импульса в проекции на ось OX можно записать:
mv-MV=0
V=mvM.
Реактивное движение
Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью u→. Пусть масса газов равна m, а масса ракеты после истечения газов – M. Рассматривая замкнутую систему “ракета-газы” и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты V после истечения газов.
V=muM
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
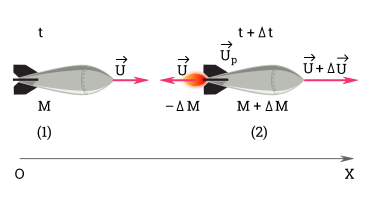
Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени t равна M, а сама ракета движется со скоростью v→. В течение малого промежутка времени ∆t из сопла ракеты выбрасывается порция газа с относительной скоростью u→. По истечении времени ∆t ракета будет двигаться со скоростью v+∆v, а масса ракеты станет равной M-∆M.
В момент t+∆t импульс ракеты равен:
M-∆M·v→+∆v→.
Импульс реактивных газов:
∆M·v→+u→.
По закону сохранения импульса:
Mv→=M-∆M·v→+∆v→+∆M·v→+u→.
Или
M∆v→=∆M·u→-∆M·∆v→.
Величиной ∆M·∆v→ можно пренебречь, так как ∆M намного меньше M.
Разделим последнее равенство на ∆t и перейдем к пределу ∆t→0.
M∆v→∆t=∆M·u→∆t (∆t→0)
Ma→=-μu→.
Здесь μ – расход топлива в единицу времени, а -μu→ – реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.
Формула Ma→=-μu→ выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:
Ma=μu.
Конечная скорость ракеты определяется по формуле:
v=ulnM0M.
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.
Для того, чтобы развить первую космическую скорость v=v1=7,9·103 мс при скорости истечения газов u=3·103 мс стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20k
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Зако́н сохране́ния и́мпульса (зако́н сохране́ния количества движения) — закон, утверждающий, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю[1].
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении системы в пустом пространстве импульс сохраняется во времени, а при наличии внешнего воздействия скорость изменения импульса определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной из фундаментальных симметрий, — однородностью пространства[2].
Закон сохранения импульса впервые был сформулирован Р. Декартом[3].
Вывод в механике Ньютона[править | править код]
Согласно второму закону Ньютона для системы из N частиц выполняется соотношение
где 
— импульс системы:
— импульс материальной точки, а 
— равнодействующая всех сил, приложенных к частицам системы:
Здесь 
— сила (или сумма сил, если таковых несколько), действующая на n-ю частицу со стороны m-ой, а 
— равнодействующая всех внешних сил, приложенных к k-й частице.
Согласно третьему закону Ньютона, силы вида и 
равны по абсолютному значению и противоположны по направлению, то есть 
. Поэтому вторая сумма в правой части выражения для будет равна нулю, внутренние силы исключаются, и получаем, что производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на систему:
Для системы из N частиц, в которой сумма всех внешних сил равна нулю:
и тем более для системы, на частицы которой не действуют внешние силы
(
для всех k от 1 до N), имеем
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
(постоянный вектор).
То есть суммарный импульс системы из N частиц является постоянной величиной. При N = 1 получаем выражение для случая одной частицы. Таким образом, следует вывод[1]:
Если векторная сумма всех внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, то есть не меняется со временем.
Закон сохранения импульса выполняется не только для систем, на которые не действуют внешние силы, он справедлив и в тех случаях, когда сумма всех внешних сил, действующих на систему, равна нулю. То есть отсутствие внешних сил, действующих на систему, достаточно, но не необходимо для выполнения закона сохранения импульса.
Если проекция суммы внешних сил на какое-либо направление или координатную ось равна нулю, то в этом случае говорят о законе сохранения проекции импульса на данное направление или координатную ось.
Связь с однородностью пространства[править | править код]
| Симметрия в физике | ||
|---|---|---|
| Преобразование | Соответствующая инвариантность |
Соответствующий закон сохранения |
| ↕ Трансляции времени | Однородность времени |
…энергии |
| ⊠ C, P, CP и T-симметрии | Изотропность времени |
…чётности |
| ↔ Трансляции пространства | Однородность пространства |
…импульса |
| ↺ Вращения пространства | Изотропность пространства |
…момента импульса |
| ⇆ Группа Лоренца (бусты) | Относительность Лоренц-ковариантность |
…движения центра масс |
| ~ Калибровочное преобразование | Калибровочная инвариантность | …заряда |
Согласно теореме Нётер каждому закону сохранения ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения импульса эквивалентен однородности пространства, то есть независимости всех законов, описывающих систему, от положения системы в пространстве. Простейший вывод этого утверждения основан на применении лагранжева подхода к описанию системы.
Вывод из закона сохранения энергии[править | править код]
Рассмотрим систему нескольких соударяющихся упругим образом (без превращения части механической энергии в другие формы) частиц с массами 
и скоростями 
до столкновений и 
после столкновений. Закон сохранения энергии имеет вид
Перейдём в систему отсчёта, равномерно и прямолинейно движущуюся со скоростью 
. Скорости частиц с точки зрения этой системы отсчёта будут 
до столкновений и 
после столкновений. Закон сохранения энергии с точки зрения этой системы имеет вид
- или
Следовательно 
, откуда следует 
. Поскольку скорость произвольна, то последнее равенство будет справедливым только в случае выполнения закона сохранения импульса
- [4]
Вывод из формализма Лагранжа[править | править код]
Рассмотрим функцию Лагранжа свободного тела 
зависящую от обобщённых координат 
обобщённых скоростей 
и времени 
. Здесь точка над 
обозначает дифференцирование по времени, 
Выберем для рассмотрения прямоугольную декартову систему координат, тогда 
для каждой 
-той частицы. Используя однородность пространства, мы можем дать всем радиус-векторам частиц одинаковое приращение, которое не будет влиять на уравнения движения: 
где 
В случае постоянства скорости функция Лагранжа изменится следующим образом:
где суммирование идет по всем частицам системы. Так как приращение не влияет на уравнения движения, вариация функции Лагранжа должна быть равной нулю: 
С учётом того, что вектор 
— произвольный, последнее требование выполняется при:
Воспользуемся уравнением Лагранжа 
Это означает, что сумма, стоящая под знаком дифференциала, — постоянная величина для рассматриваемой системы. Сама сумма и есть суммарный импульс системы:
Учитывая, что лагранжиан свободной частицы имеет вид: 
нетрудно видеть, что последнее выражение совпадает с выражением в ньютоновом формализме:
Для релятивистской свободной частицы лагранжиан имеет несколько другую форму: 
что приводит к релятивистскому определению импульса
В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
Закон сохранения импульса в квантовой механике[править | править код]
Закон сохранения импульса в изолированных системах выполняется и в квантовой механике[5][6]. В тех явлениях, когда проявляются корпускулярные свойства частиц, их импульс, как и в классической механике, равен 
, а когда проявляются волновые свойства частиц, их импульс равен 
, где 
– длина волны[7]. В квантовой механике закон сохранения импульса является следствием симметрии относительно сдвигов по координатам[8].
Закон сохранения импульса в теории относительности[править | править код]
Закон сохранения импульса выполняется и в теории относительности. Отличие от классической механики состоит лишь в том, что в теории относительности зависимость импульса от
скорости имеет вид
- [9][6]
В общей теории относительности, аналогично ситуации с законом сохранения энергии, при переходе к искривлённому пространству-времени закон сохранения импульса, выражаемый пространственными компонентами соотношения для тензора энергии-импульса
где точка с запятой выражает ковариантную производную, приводит лишь к локально сохраняющимся величинам. Это связано с отсутствием глобальной однородности пространства в пространстве-времени общего вида.
Можно придумать такие определения импульса гравитационного поля, что глобальный закон сохранения импульса будет выполняться при движении во времени системы тел и полей, но все такие определения содержат элемент произвола, так как вводимый импульс гравитационного поля не может быть тензорной величиной при произвольных преобразованиях координат.
См. также[править | править код]
- Закон сохранения момента импульса
- Теорема о движении центра масс системы
- Теорема об изменении количества движения системы
Ссылки[править | править код]
- Опыт с шарами по демонстрации закона сохранения импульса (видео)
Литература[править | править код]
- Кузнецов Б. Г. Принципы классической физики. — М.: АН СССР, 1958. — 321 с.
- Фейнман Р. Ф. Фейнмановские лекции по физике. Вып. 1 Современная наука о природе. Законы механики.. — М.: Едиториал УРСС, 2004. — 440 с. — ISBN 5-354-00699-6.
- Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — 670 с.
- Готт В. С. Философские вопросы современной физики. — М.: Высшая школа, 1972. — 416 с.
- Ферми Э. Квантовая механика. — М.: Мир, 1968. — 367 с.
Примечания[править | править код]
- ↑ 1 2 Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. — 4-е изд., испр. — М.: «Наука», 1988. — Т. I. Механика. — С. 26. — 215 с. — ISBN 5-02-013850-9.
- ↑ Готт, 1972, с. 222.
- ↑ Кузнецов, 1958, с. 135.
- ↑ Перкинс Д.[en] Введение в физику высоких энергий. — М., Мир, 1975. — c. 94
- ↑ 1 2 Широков, 1972, с. 276.
- ↑ Фейнман, 2004, с. 194.
- ↑ Ферми, 1968, с. 183.
- ↑ Фейнман, 2004, с. 193.
В этой статье будут проиллюстрированы подробности того, как найти закон сохранения импульса.
Линейный импульс (p) или импульс — это произведение массы (m) и линейной скорости (v) тела.
р=мв
Прежде чем приступить к математическому процессу нахождения сохранения импульса, сначала следует сформулировать закон сохранения импульса. Согласно закону сохранения импульса, если внешние силы отсутствуют, то полный импульс системы остается постоянным и не зависит от времени. Это означает, что импульс не меняется и остается неизменным независимо от времени. Если перейти к столкновениям, то можно сказать, что в отсутствие внешних сил, если полный импульс до столкновения и полный импульс после столкновения остаются одними и теми же, то импульс сохраняется.
Примером этого является выстрел из ружья. Прежде чем стрелять из пистолета и пули, оставайтесь в покое. Следовательно, полный начальный импульс остается равным нулю. После выстрела пуля (масса m) приобретает скорость (v) и движется вперед, тогда как пуля (масса M) получает скорость отдачи (V) и движется назад, что, в свою очередь, сохраняет общий конечный импульс также равным нулю. Так что импульс здесь сохраняется.
V=-м/м
Предположим, что тела A и B массами mA и mB движутся навстречу друг другу со скоростями uA и uB соответственно. После столкновения массы mA и mB начинают двигаться в противоположных направлениях друг относительно друга со скоростями vA и vB соответственно.
Тогда изменение импульса тела A массы mA равно:
pA= mA(vA-uA)………..(1) и масса тела B массы mB равна:
pB= mB(vB-uB)…………(2)
Теперь сохранение количества движения можно объяснить с помощью третьего закона движения Ньютона. Он утверждает, что каждое действие имеет равное и противоположное противодействие. Используя этот закон, можно сказать, что
fAB= -fBA ………….(3)
где fAB — сила, с которой тело A действует на тело B, а fBA — сила, с которой тело B действует на тело A.
fAB= pA/t= mA(vA-uA)/t [с использованием уравнения (1)] и
fBA=pB/t= mB(vB-uB)/t [с использованием уравнения (2)]
mA(vA-uA)/t = -mB(vB-uB)/t [используя уравнение (3)]
mA(vA-uA)=-mB(vB-uB)
mAvA+mBvB= mAuA+mBuB……………(4)
Пример:
В. Автомобиль массой (mA) 10 кг и грузовик массой (mB) 10 кг движутся навстречу друг другу с начальной скоростью 20 м/с (uA) и 50 м/с (uB) соответственно. После столкновения скорость автомобиля стала 30 м/с(vA), а скорость грузовика стала 40 м/с(vB). Сохраняется ли импульс при этом столкновении?
Здесь,
мА=10 кг
mB=10 кг
uA=20 м/с
uB=50 м/с
vA=30 м/с
vB=40 м/с
Общий финальный импульс=mAvA+mBvB
=10*30+10*40
= 300 + 400
=700 кг.м/с
Общий начальный импульс = mAuA+mBuB
=10*20+10*50
= 200 + 500
=700 кг.м/с
Следовательно,
Общий конечный импульс = общий начальный импульс
Следовательно, импульс сохраняется.
Как найти начальную скорость используя закон сохранения импульса?
Математическая формула сохранения импульса:
mAvA+mBvB=mAuA+mBuB [из уравнения (4)]
С помощью этой формулы можно найти начальные скорости сталкивающихся тел А и В. Если в вопросе даны значения масс mA и mB, значения конечных скоростей vA и vB и значение uA, то значение uB можно вычислить следующим образом:
uB=(mAvA+mBvB-mAuA)/mB……..(5)
Пример
В. Деревянный брусок (массой 5 кг=мА), двигавшийся со скоростью (uА) 10 м/с, столкнулся с другим бруском массой 10 кг(мВ). После удара брусок массой 5 кг начал двигаться со скоростью 5 м/с(vA), а брусок массой 10 кг начал двигаться со скоростью 7.5 м/с(vB). Какова была начальная скорость (uB) бруска массой 10 кг до столкновения?
мА=5кг
мб=10кг
uA=10 м/с
уб=?
ВА=5м/с
vB=7.5 м/с
uB=(5*5+10*7.5-5*10)/10
=(25+75-50)/10
=(100-50)/10
= 50 / 10
= 5 м / с
Таким же образом можно рассчитать uA по формуле, написанной ниже:
uA=(mAvA+mBvB-mBuB)/мА…………(6)
Как найти конечную скорость по импульсу?
Точно так же конечные скорости тел A и B также могут быть найдены с использованием математической формулы сохранения импульса. Если в вопросе указаны значения масс А и В, их начальные скорости и конечная скорость одного из двух, то значение конечной скорости другого можно вычислить по формуле
vA=(mAuA+mBuB-mBvB)/мА……….(7)
и vB=(mAuA+mBuB-mAvA)/mB…………(8)
Пример
Мяч массой (mA) 0.5 кг, движущийся со скоростью (uA) 20 м/с, ударяется о деревянный брусок (массой 5kg=mB), находящийся в состоянии покоя. После этого мяч двигался со скоростью (vA) 10 м/с. Какова была конечная скорость (vB) бруска после столкновения?
мА=0.5кг
мб=5кг
uA=20 м/с
uB=0
ВА=10м/с
ВБ=?
vB=(0.5*20+5*0-0.5*10)/5
=(10-5)/5
= 1 м / с
Как найти массу по закону сохранения импульса?
Используя обобщенную формулу сохранения импульса массы mA и mB также можно вычислить следующим образом:
mAvA+mBvB=mAuA+mBuB [из уравнения (4)]
mA(vA-uA)=mBuB-mBvB
мА=(mBuB-mBvB)/(vA-uA)…………(9)
Кроме того,
mB=(mAvA-mAuA)/(uB-vB)………….(10)
Пример:
Пуля массой (мА) 50 г выпущена из ружья со скоростью (vА) 400 м/с. Какова масса орудия (mB), если его скорость отдачи (vB) равна 10 м/с.
мА=50 г/м=0.05 кг
мБ=?
uA=0 (так как пуля перед выстрелом находилась в состоянии покоя)
uB=0 (т.к. перед выстрелом орудие находилось в состоянии покоя)
ВА=400м/с
vB=10 м/с
mB=(0.05*400-0.05*0)/(0-10)
=(20-0)/(-10)
=-2 кг
= 2 кг
Среди законов механики есть, казалось бы, простенький закон, который часто остается в тени. Мы постоянно встречаемся с ним как в нашей жизни, так и на страницах учебников. Часто получается, что разобраться с ним бывает даже сложнее, чем с законами Ньютона или законом сохранения механической энергии.
Речь идёт о законе сохранения импульса. Вопрос относится к теме #классическая механика .
Импульс – это довольно популярное слово в нашей разговорной речи. Оно означает что-то, что исходит от нас или из нас самих. Что-то, что является источником будущего движения или деятельности.
В физике же под импульсом понимается количество движения. Если проанализировать применение слова импульс в быту и жизни, то оно, в целом-то, будет соответствовать обозначенной выше логике и тоже будет подразумевать количество движения. Что это за такое количество движения?
Представьте себе, что вы кого-то ударили. Вполне понятно, что в процессе участвовали такие характеристики, как сила удара и сопротивление среды (пусть ветер). Но даже если мы рассчитали силу, с которой мы ударили человека по второму закону Ньютона и учли все внешние воздействия, мы не можем предсказать, сколько пролетит человек, не понимая в каком количестве мы его ударили. Мы передали ему какое-то количество движения, которое может и дальше перемещать этого человека и рассеиваться на сопротивление внешней среды. Абсолютное значение мы можем рассчитать по стандартным формулам типа F=ma, но есть что-то, что сохраняет это количество. Появляется такая характеристика, как инерция.
Интересно отметить, что никто до сих пор так и не может сказать, что именно является “носителем” этой инерции и что это такое. Часто инерцию связывают с гравитацией. Но пока мы изучаем классическую механику и отвлечемся от этих сложных рассуждений.
Для того, чтобы понять что такое импульс в механике, нужно обратиться, как бы это ни было странно, к истории. Изначально предполагалось, что для движения тела ему постоянно следует сообщать некоторую силу. Было резонно замечено, что если пнуть ногой лежащий камень, то он продолжает лететь даже при отсутствии взаимодействия с этой пнувшей его ногой. Не нужно пинать камень каждую миллисекунду и сохранять связь с ногой, чтобы движение камня продолжалось. Мы бы сказали, что такой камень продолжает движение по инерции.
Инерция – это способность тела оставаться в состоянии покоя или равномерного прямолинейно двигаться в отсутствие внешних воздействий, а также препятствовать изменению своей скорости.
Всё здорово, но как посчитать это количество инерции? Ведь где-то её больше, а где-то меньше?
Была выдвинута идея, что перемещающийся предмет обладает неким импетусом, который прямо пропорционален скорости. Кроме того, импетус сохраняется бесконечно, если на перемещающееся тело не воздействуют другие факторы типа ветра.
Но ближе всего к импульсу в нашем современном понимании подобрался Рене Декарт. Он доработал идею с импетусом и сказал, что есть величина “количество движения”. Мало того, что сохраняется количество движения одного тела, так ещё и сохраняется количество движения системы других взаимодействующих друг с другом тел, но изолированных от внешнего мира. По сути дела, речь идёт про вагон метро, который обладает количеством движения вне зависимости от взаимодействия пассажиров внутри него.
Далее представление Декарта об этом вопросе было дополнено “векторностью”. Логично было предположить, что направление вектора скорости соответствует направлению количества движения.
Ну а Ньютон довел эту идею до ума.
В итоге, было логично предположено, что количество движения зависит от массы тела, которое вступает во взаимодействие с другим телом и от скорости, с которой это взаимодействие происходит. Считается оно как произведение массы тела, на его скорость. Эту характеристику стали называть импульс тела. Если речь идёт про систему тел, то мы должны найти векторную сумму всех импульсов, входящих в эту систему.
Но ведь именно сила является причиной изменения импульса тела. Эту характеристику стали называть импульс силы. И равна она произведению силы, которая воздействовала на тело на время этого воздействия.
Импульс тела равен импульсу силы.
Это значит, что mV=Ft
Возвращаясь из теории на землю, мы бьем камень с силой два ньютона, взаимодействие ноги и камня длится пусть 0,01 часа. Полученный импульс от ноги – это произведение 0,01 часа на два ньютона. Этого импульса хватит, чтобы камень массой 1 кг полетел со скоростью 0,02 м/с.
Было установлено, что импульс не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Что относится к таким характеристикам? Ну в примере с ногой – это тип движения и его взаимодействия.
Получается, что импульс имеет свойство сохраняться. Тот же факт, что мы постоянно не перемещаемся в хаотическим движении связан с тем, что на нас воздействуют другие силы – сила трения, сила тяготения и т.п. и т.д. Мы подходим к закону сохранения импульса:
Закон сохранения импульса утверждает, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю.
Значит ли это, что закон сохранения импульса не работает на Земле в обычных условиях?
Ведь тут далеко не всегда векторная сумма всех сил, действующих на систему, равна нулю. Отнюдь нет! Он работает. Правда “рассеивается” в итоге и полученное количество движение не сохранится постоянно. Использовать же запись вполне допустимо.
Пушка стрельнула, рассчитали начальные скорости ядра по закону сохранения импульса, зная массу ядер, и исходим из того, что скорости эти рассеиваются на внешние воздействия.
Поэтому, закон сохранения импульса проще было бы сформулировать так:
Векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых взаимодействиях этих тел.
Зато вот в космосе вполне можно разгуляться.
Так, если ракета разок получит импульс от сгорающего топлива (которое в космосе не горит)…поэтому, правильнее сказать – от реактивного движения, то взаимодействием ракеты с другими телами можно пренебречь и принять, что весь импульс от топлива передался ракете и не будет рассеиваться.
Стоит помнить и о том, что закон сохранения импульса является следствием всеобщего закона сохранения энергии и был выведен из него.
