Давление
Известно, что человеку удобнее ходить по глубокому снегу на лыжах, так как при этом он меньше проваливается под снег. А разрезать предметы удобнее остро отточенным ножом. Причина этого – давление. В первом случае мы стремимся уменьшить давление на снег, а во втором случае, мы стараемся максимально увеличить давление.
Формула давления твердого тела
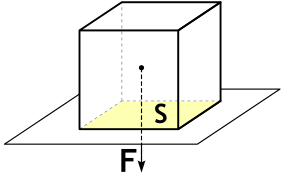
Рассмотрим твердое тело, например, кирпич. Пусть он лежит на горизонтальной поверхности и давит на нее своим весом (рис. 1).

Рис. 1. Твердое тело опирается на поверхность площадью S и давит на нее своим весом mg
На рисунке символом S обозначена нижнее основание тела – это площадь, на которую тело опирается (давит). Сила, с которой тело давит на поверхность – это сила тяжести mg.
Давление, которое твердое тело оказывает на поверхность, можно рассчитать так:
[ large boxed{ P = frac{F_{perp}}{S} }]
Примечание: Эта формула подходит для расчета давления твердых тел. Существует еще одна формула, с помощью которой рассчитывают давление жидкостей.
( P left( text{Па}right) ) – давление;
( F_{perp} left(H right) ) – сила, которая давит (сила давления). Эта сила располагается под прямым углом к поверхности;
( S left( text{м}^{2}right) ) – площадь, на которую давит сила.
Иногда в условии задачи указывают площадь в квадратных сантиметрах, или других единицах, отличающихся от основных единиц, принятых в СИ. Чтобы правильно рассчитать давление, нужно уметь переводить площадь в квадратные метры.
В системе СИ давление измеряется в Паскалях.
[ large 1 text{Па} = frac{1 H}{1 text{м}^{2}} ]
Поэтому, перед решением задач, нужно давление переводить в Паскали, если в условии встретятся другие единицы измерения давления.
В некоторых школьных задачах просят найти не давление, а силу давления. Нужно уметь их различать.
Сила давления, как и любая сила, измеряется в Ньютонах. Именно она давит на поверхность.
А давление — это дробь, в числителе расположена сила, которая давит, а в знаменателе — площадь поверхности, на которую давят. Давление измеряют в Паскалях.
Примечание: Давление – это сила, деленная на площадь. Сила должна располагаться перпендикулярно поверхности (рис. 2а).
Когда сила не перпендикулярна поверхности
Силу раскладываем на проекции, если она направлена к поверхности не под прямым углом (рис. 2б). Выберем часть силы, расположенную перпендикулярно поверхности. Именно эту часть силы и нужно подставлять в формулу для расчета давления.

Рис. 2. Если сила, которая давит на поверхность, направлена не под прямым углом к поверхности, раскладываем силу на проекции и выбираем часть, которая располагается к поверхности перпендикулярно
Оценка статьи:
![]() Загрузка…
Загрузка…

{p = dfrac{F}{S}}
Давление – физическая величина, равная отношении силы, приложенной перпендикулярно поверхности на площадь этой поверхности. Единица измерения давления – Паскаль (обозначается Па).
На странице приведены два варианта нахождения давления:
- если известно давление и площадь опоры
- если известна масса тела и площадь опоры
Содержание:
- калькулятор давления твердых тел
- формула давления твердых тел через силу и площадь опоры
- формула давления твердых тел через массу и площадь опоры
- примеры задач
Очевидно, что давление будет тем больше, чем больше сила и чем меньше площадь, на которую эта сила действует. Другими словами, человек, стоящий на одной ноге будет оказывать на землю бОльшее давление, чем когда он стоит на двух ногах (так как сила одна и та же, а площадь в первом случае меньше). Человек на лыжах будет оказывать на землю меньшее давление, чем человек без лыж.
Формула давления твердых тел через силу и площадь опоры
{p = dfrac{F}{S}}
p – давление
F – сила
S – площадь опоры
Если учесть, что на тело действует только сила тяжести, то формулу {p=dfrac{F}{S}} можно преобразовать, заменив силу на вес тела ({F=mcdot g}. Тогда мы получим зависимость давления от массы: {p=dfrac{m cdot g}{S}}.
Формула давления твердых тел через массу и площадь опоры
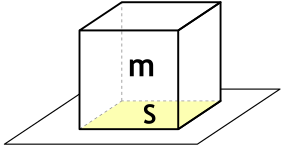
{p = dfrac{m cdot g}{S}}
p – давление
m – масса тела
g – ускорение свободного падения (9,80665 м/с²)
S – площадь опоры
Примеры задач на нахождение давления твердых тел
Задача 1
Гусеничный трактор ДТ-75М массой 6610 кг имеет опорную площадь обеих гусениц 1,4 м². Определите давление этого трактора на почву.
Решение
Так как в условии указана масса трактора, воспользуемся формулой давления через массу и площадь опоры. Подставим в нее значения массы и площади и произведем вычисления. Значение ускорения свободного падения примем равным 9.8 м/с².
p = dfrac{m cdot g}{S} = dfrac{6610 cdot 9.8}{1.4} = dfrac{6610 cdot 9.8}{1.4} = dfrac{64778}{1.4} = dfrac{64778}{1.4} = 46270 Па = 46.27 кПа
Ответ: 46.27 кПа
Получившийся результат просто проверить с помощью калькулятора .
Задача 2
Найдите давление которое оказывает тело массой 20 кг на пол, если площадь опоры 200 см².
Решение
Задача похожа на ту, которую мы решили выше. И процесс ее решения будет аналогичный. Значение g также будем считать равным 9.8 м/с². Площадь опоры дана в квадратных сантиметрах, ее необходимо преобразовать в квадратные метры: 200 см² = 0.02 м².
p = dfrac{m cdot g}{S} = dfrac{20 cdot 9.8}{0.02} = 1000 cdot 9.8 = 9800 Па = 9.8 кПа
Ответ: 9.8 кПа
Проверим ответ на калькуляторе .
Задача 3
Найдите давление которое оказывает тело массой 350 кг, если его длина 15 см а ширина 25 см.
Решение
Еще одна похожая задача, для решения которой мы будем использовать вторую формулу. Как видим, нам прямо не указана площадь опоры, но даны ее размеры. Из них понятно, что точка опоры имеет прямоугольную форму, а найти площадь прямоугольника не составит труда – достаточно умножить длину на ширину:
S = a cdot b = 15 cdot 25 = 375 см^2
Теперь необходимо перевести квадратные сантиметры в квадратные метры, разделив 375 см² на 10000:
375 см^2 = dfrac{375 см^2}{10000} = 0.0375 м^2
Осталось произвести расчет по формуле:
p = dfrac{m cdot g}{S} = dfrac{350 cdot 9.8}{0.0375} = 91 560 Па = 91.56 кПа
Ответ: 91.56 кПа
Проверка .
Давление – это физическая величина, которая играет особую роль в природе и жизни человека. Это незаметное глазу явление не только влияет на состояние окружающей среды, но и очень хорошо ощущается всеми. Давайте разберемся, что это такое, какие виды его существуют и как находить давление (формула) в разных средах.
Что называется давлением в физике и химии
Данным термином именуется важная термодинамическая величина, которая выражается в соотношении перпендикулярно оказываемой силы давления на площадь поверхности, на которую она воздействует. Это явление не зависит от размера системы, в которой действует, поэтому относится к интенсивным величинам.

В состоянии равновесия, по закону Паскаля, давление одинаково для всех точек системы.
В физике и химии оное обозначается с помощью буквы «Р», что является сокращением от латинского названия термина – pressūra.
Если речь идет об осмотическом давлении жидкости (равновесие между давлением внутри и снаружи клетки), используется буква «П».
Единицы давления
Согласно стандартам Международной системы СИ, рассматриваемое физическое явление измеряется в паскалях (кириллицей – Па, латиницей – Ра).
Исходя из формулы давления получается, что один Па равен одному Н (ньютон – единица измерения силы) разделенному на один квадратный метр (единица измерения площади).
Однако на практике применять паскали довольно сложно, поскольку эта единица очень мала. В связи с этим, помимо стандартов системы СИ, данная величина может измеряться по-другому.
Ниже приведены наиболее известные ее аналоги. Большинство из них широко используется на просторах бывшего СССР.
- Бары. Один бар равен 105 Па.
- Торры, или миллиметры ртутного столба. Приблизительно один торр соответствует 133, 3223684 Па.
- Миллиметры водяного столба.
- Метры водяного столба.
- Технические атмосферы.
- Физические атмосферы. Одна атм равна 101 325 Па и 1,033233 ат.
- Килограмм-силы на квадратный сантиметр. Также выделяются тонна-сила и грамм-сила. Помимо этого, есть аналог фунт-сила на квадратный дюйм.
Общая формула давления (физика 7-го класса)
Из определения данной физической величины можно определить способ ее нахождения. Выглядит он таким образом, как на фото ниже.
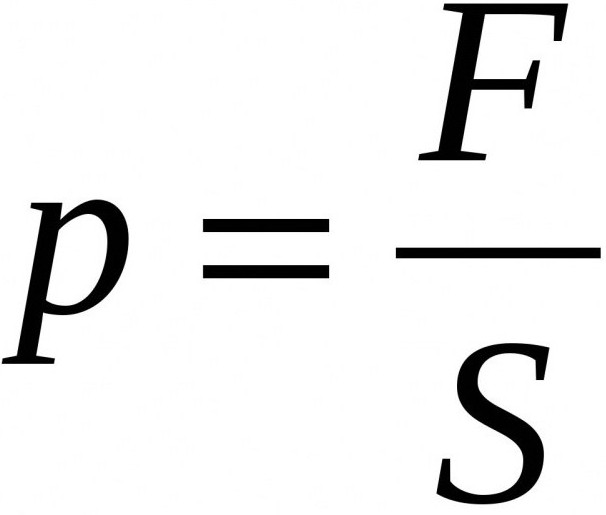
В нем F – это сила, а S – площадь. Иными словами, формула нахождения давления – это его сила, разделенная на площадь поверхности, на которую оно воздействует.
Также она может быть записана так: Р = mg / S или Р = pVg / S. Таким образом, эта физическая величина оказывается связанной с другими термодинамическими переменными: объемом и массой.
Для давления действует следующий принцип: чем меньше пространство, на которое влияет сила – тем большее количество давящей силы на него приходится. Если, же площадь увеличивается (при той же силе) – искомая величина уменьшается.
Формула гидростатического давления
Разные агрегатные состояния веществ, предусматривают наличие у них отличных друг от друга свойств. Исходя из этого, способы определения Р в них тоже будут другими.
К примеру, формула давления воды (гидростатического) выглядит вот так: Р = pgh. Также она применима и к газам. При этом ее нельзя использовать для вычисления атмосферного давления, из-за разности высот и плотностей воздуха.
В данной формуле р – плотность, g – ускорение свободного падения, а h – высота. Исходя из этого, чем глубже погружается предмет или объект, тем выше оказываемое на него давление внутри жидкости (газа).

Рассматриваемый вариант является адаптацией классической примера Р = F / S.
Если вспомнить, что сила равна производной массы на скорость свободного падения (F= mg), а масса жидкости – это производная объема на плотность (m = pV), то формулу давление можно записать как P = pVg / S. При этом объем – это площад, умноженная на высоту (V = Sh).
Если вставить эти данные, получится, что площадь в числителе и знаменателе можно сократить и на выходе – вышеупомянутая формула: Р = pgh.
Рассматривая давление в жидкостях, стоит помнить, что, в отличие от твердых тел, в них часто возможно искривление поверхностного слоя. А это, в свою очередь, способствует образованию дополнительного давления.
Для подобных ситуаций применяется несколько другая формула давления: Р = Р0 + 2QH. В данном случае Р0 – давление не искривленного слоя, а Q – поверхность натяжения жидкости. Н – это средняя кривизна поверхности, которую определяют по Закону Лапласа: Н = ½ (1/R1+ 1/R2). Составляющие R1 и R2 – это радиусы главной кривизны.
Парциальное давление и его формула
Хотя способ Р = pgh применим как для жидкостей, так и для газов, давление в последних лучше вычислять несколько другим путем.
Дело в том, что в природе, как правило, не очень часто встречаются абсолютно чистые вещества, ведь в ней преобладают смеси. И это касается не только жидкостей, но и газов. А как известно, каждый из таких компонентов осуществляет разное давление, называемое парциальным.
Определить его довольно просто. Оно равно сумме давления каждого компонента рассматриваемой смеси (идеальный газ).
Из этого следует, что формула парциального давления выглядит таким образом: Р = Р1+ Р2+ Р3… и так далее, согласно количеству составляющих компонентов.

Нередки случаи, когда необходимо определить давление воздуха. Однако некоторые по ошибке проводят вычисления только с кислородом по схеме Р = pgh. Вот только воздух – это смесь из разных газов. В нем встречаются азот, аргон, кислород и другие вещества. Исходя из сложившейся ситуации, формула давления воздуха – это сумма давлений всех его составляющих. А значит, следует приметь вышеупомянутую Р = Р1+ Р2+ Р3…
Наиболее распространенные приборы для измерения давления
Несмотря на то что высчитать рассматриваемую термодинамическую величину по вышеупомянутым формулам не сложно, проводить вычисление иногда попросту нет времени. Ведь нужно всегда учитывать многочисленные нюансы. Поэтому для удобства за несколько столетий был разработан ряд приборов, делающих это вместо людей.
Фактически почти все аппараты такого рода являются разновидностями манометра (помогает определять давление в газах и жидкостях). При этом они отличаются по конструкции, точности и сфере применения.
- Атмосферное давление измеряется с помощью манометра, именуемого барометром. Если необходимо определить разряжение (то есть давление ниже атмосферного) – применяются другая его разновидность, вакуумметр.
- Для того чтобы узнать артериальное давление у человека, в ход идет сфигмоманометр. Большинству он более известен под именем неинвазивного тонометра. Таких аппаратов существуют немало разновидностей: от ртутных механических до полностью автоматических цифровых. Их точность зависит от материалов, из которых они изготавливаются и места измерения.
- Перепады давления в окружающей среде (по-английски – pressure drop) определяются с помощью дифференциальных манометров или дифнамометров (не путать с динамометрами).
Виды давления
Рассматривая давление, формулу его нахождения и ее вариации для разных веществ, стоит узнать о разновидностях этой величины. Их пять.
- Абсолютное.
- Барометрическое
- Избыточное.
- Вакуумметрическое.
- Дифференциальное.
Абсолютное
Так называется полное давление, под которым находится вещество или объект, без учета влияния других газообразных составляющих атмосферы.
Измеряется оно в паскалях и являет собою сумму избыточного и атмосферного давлений. Также он является разностью барометрического и вакуумметрического видов.
Вычисляется оно по формуле Р = Р2 + Р3 или Р = Р2 – Р4.
За начало отсчета для абсолютного давления в условиях планеты Земля, берется давление внутри емкости, из которой удален воздух (то есть классический вакуум).
Только такой вид давления используется в большинстве термодинамических формул.
Барометрическое
Этим термином именуется давление атмосферы (гравитации) на все предметы и объекты, находящие в ней, включая непосредственно поверхность Земли. Большинству оно также известно под именем атмосферного.
Его причисляют к термодинамическим параметрам, а его величина меняется относительно места и времени измерения, а также погодных условий и нахождения над/ниже уровня моря .
Величина барометрического давления равна модулю силы атмосферы на площади единицу по нормали к ней.
В стабильной атмосфере величина данного физического явления равна весу столпа воздуха на основание с площадью, равной единице.
Норма барометрического давления – 101 325 Па (760 мм рт. ст. при 0 градусов Цельсия). При этом чем выше объект оказывается от поверхности Земли, тем более низким становится давление на него воздуха. Через каждый 8 км оно снижается на 100 Па.
Благодаря этому свойству в горах вода в чайниках закивает намного быстрее, чем дома на плите. Дело в том, что давление влияет на температуру кипения: с его снижением последняя уменьшается. И наоборот. На этом свойстве построена работа таких кухонных приборов , как скороварка и автоклав. Повышение давления внутри их способствуют формированию в посудинах более высоких температур, нежели в обычных кастрюлях на плите.

Используется для вычисления атмосферного давления формула барометрической высоты. Выглядит она таким образом, как на фото ниже.
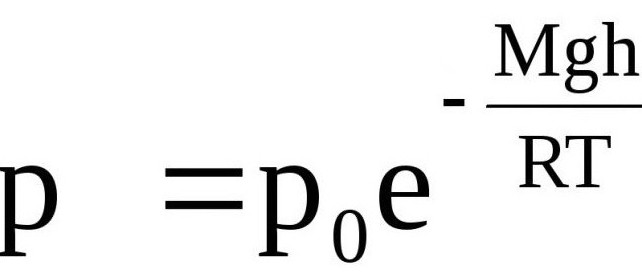
Р – это искомая величина на высоте, Р0 – плотность воздуха возле поверхности, g – свободного падения ускорение, h – высота над Землей, м – молярная масса газа, т – температура системы, r – универсальная газовая постоянная 8,3144598 Дж⁄(моль х К), а е – это число Эйклера, равное 2.71828.
Часто в представленной выше формуле давления атмосферного вместо R используется К – постоянная Больцмана. Через ее произведение на число Авогадро нередко выражается универсальная газовая постоянная. Она более удобна для расчетов, когда число частиц задано в молях.
При проведении вычислений всегда стоит брать во внимание возможность изменения температуры воздуха из-за смены метеорологической ситуации или при наборе высоты над уровнем моря, а также географическую широту.

Избыточное и вакуумметрическое
Разницу между атмосферным и измеренным давлением окружающей среды называют избыточным давлением. В зависимости от результата, меняется название величины.
Если она положительная, ее называют манометрическим давлением.
Если же полученный результат со знаком минус – его именуют вакуумметрическим. Стоит помнить, что он не может быть больше барометрического.
Дифференциальное
Данная величина является разницей давлений в различных точках измерения. Как правило, ее используют для определения падения давления на каком-либо оборудовании. Особенно это актуально в нефтедобывающей промышленности.
Разобравшись с тем, что за термодинамическая величина называется давлением и с помощью каких формул ее находят, можно сделать вывод, что это явление весьма важно, а потому знания о нем никогда не будут лишними.
Содержание:
Сила давления и единицы давления:
Вы уже знаете, что действие одного тела на другое характеризуют приложенной к нему силой. От чего зависит результат действия этой силы на тело?
Наблюдение 1. Из собственного опыта вы знаете, что очень тяжело идти по глубокому рыхлому снегу, поскольку ноги глубоко проваливаются в нём, а на лыжах передвигаться намного легче, так как проседание снеговой поверхности в этому случае значительно меньше. В обоих случаях вы действуете на снег с одинаковой силой, но площадь поверхности, на которую она распределяется в случае лыж значительно больше, чем в случае обуви, поэтому и деформация снега оказывается разной. Стоя на лыжах, выдавите на каждую единицу площади поверхности снега с силой, меньшей во столько раз, во сколько раз площадь поверхности лыж больше площади подошв обуви.
Наблюдение 2. Легковой автомобиль, в отличие от гусеничного трактора или болотохода, не может проехать по болотистой местности, хотя его вес намного меньше веса трактора. Рассмотрев колёса легкового автомобиля и гусеницы трактора, вы убеждаетесь в том, что площадь поверхности гусениц намного больше, чем колес.
Результат действия силы на поверхность зависит не , только от её значения, но и от площади той поверхности, перпендикулярно к которой она действует.
Убедимся в этом с помощью опытов.
Опыт 1. Заполним стеклянный сосуд песком. На песок поставим столик ножками вверх и на него — гирю массой 2 кг. Результат: столик почти не погрузился в песок (рис. 93, а). Поставим столик ножками на песок и на него — снова гирю массой 2 кг. Результат: ножки стола увязли в песке (рис. 93, б). Возьмём столик с острыми ножками. Поставим его ножками на песок, положив сверху ту же гирю массой 2 кг. Результат: заострённые ножки полностью погрузились в песок (рис. 93, в).

Опыт свидетельствует, что чем меньше площадь опоры столика, тем глубже он погружается в песок под действием одинаковой силы.
Опыт 2. Возьмём два столика. Площадь поверхности ножек одного столика вдвое больше, чем второго. Положим на столики груз, причем на столик с большей площадью поверхности ножек положим вдвое больший груз. Результат действия силы будет одинаковый.
В рассмотренных примерах имела значение сила, действующая перпендикулярно к поверхности тела. Такую силу называют силой давления.
Величину, которая определяется отношением значения силы давления к площади поверхности, на которую она действует, называют давлением.
Давление обозначают малой латинской буквой р. Итак, чтобы определить давление р, нужно силу F , действующую перпендикулярно к поверхности, поделить на площадь этой поверхности S, т. е.
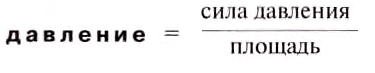
Единицей давления является один паскаль (1 Па), она названа в честь французского учёного Блеза Паскаля. Давление 1 Па создаёт сила давления 1 Н, действующая на поверхность площадью 1 м2, то есть 1 Па = 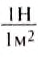 = 1
= 1 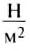 .
.
На практике ещё используют кратные единицы давления: гектопаскаль (гПа), килопаскаль (кПа): 
Зная давление, можно определить силу давления, действующую на поверхность тела. Давление показывает, какая сила давления действует на единицу площади, поэтому эта сила давления равна произведению давления и площади поверхности: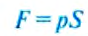 .
.
Всем хорошо известно, что во время шитья иглой швеи пользуются напёрстком. Иглу делают очень острой, чтобы умеренной силой пальцев создавать большое давление на ткань и прокалывать её. Но во время нажима пальца на иглу она с такой же силой давит на палец. Конец иглы со стороны ушка делают притуплённым, но во время работы давление на кожу пальца может быть очень большим, достаточным, чтобы ее поранить. Прочный металлический наперсток надежно защищает палец.
Почему подушка мягкая? Почему удобно лежать на перине или на надувном матрасе, а лежать на досках или твёрдой поверхности неудобно ? Оказывается, ощущение мягкости или твёрдости зависит не от свойства материала, а от значения давления на поверхность тела. Сделаем небольшие расчеты.
Будем считать, что масса взрослого человека составляет 60 кг, что равно весу приблизительно 600 Н, а поверхность тела — приблизительно 2 м2. Если человек лежит в кровати на перине, которая прогибается и будто охватывает тело, с ней соприкасается приблизительно четверть всей поверхности его тела, т. е. 0,5 м2 Расчёты по таким данным дают давление 1200 Па. А если человек ляжет на твердую поверхность, то площадь соприкосновения будет составлять около 0,01 м2. Это соответствует давлению 60 000 Па, т. е. давление тела на твёрдую поверхность увеличится в 50 раз, отсюда и неудобства.
В разных областях современной техники приходится решать задачи получения высоких давлений, снижения давления или сохранения его в заданных границах. Проблема давления играет важную роль в транспорте. Дороги и железнодорожные пути должны надежно выдерживать давление разных транспортных средств. Этого достигают, уменьшая вес транспортных средств и увеличивая их площадь опоры. Колеса легкового автомобиля производят на дорогую давление около 300 кПа. Чтобы уменьшить давление на дорогу грузовых автомобилей, их делают многоосными, с колёсами большого диаметра, используют гусеницы. Так, давление, производимое трактором Т-130, вес которого — сотни тысяч ньютонов, равен 27 кПа. Это в 1,5 раза больше давления, которое оказывает на дорогу человек весом 600 Н.
С помощью чрезвычайно тонкого инструмента – жала — оса создаёт давление, соизмеримое с давлением во время взрыва (33 000 000 000 Па).
Кстати:
В Арктике и Антарктике на научных станциях пользуются такими транспортными средствами, как снегоходы «Пингвин» и «Харьковчанка». Снегоход «Харьковчанка» имеет дизельный двигатель мощностью 736 кВт и запас горючего на 1500 км. При массе 35 т он имеет гусеницы шириной 1 м, что даёт ему возможность преодолевать снежную целину, ледовые торосы, крутые склоны. Снегоход имеет утеплённую кабину площадью 25 м2 с мощной отопительной системой, специальной герметичной обшивкой, позволяющей работать даже при морозах ниже – 70 0С. В кабине есть спальные места, радиорубка, рабочая комната, кухня, сушилка, гардероб, санузел. Размеры снегохода: длина – 8,5 м, ширина – 3,5 м, высота – 4,2 м.
Пример №1
С какой целью под головку болта и гайку подкладывают широкие металлические кольца — шайбы, особенно когда скрепляют деревянные детали (рис. 94)?

Ответ: во избежание повреждений деталей уменьшают на них давление за счёт увеличения площади контактной поверхности.
Пример №2
Взрослый человек, у которого площадь подошв обуви равна 450 см2, давит на пол с силой 700 Н. Определите давление человека на пол.
Дано:
F = 700 Н
S = 450 см2 = 0,0450 м2
р — ?
Решение:
Определим давление человека на пол по формуле:
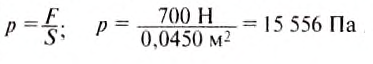
Ответ: давление человека на пол равно 15 556 Па.
Давление жидкостей и газов и закон Паскаля
Опыт 1. Возьмём три цилиндрических сосуда: в один положим деревянный брусок, в другой насыпем какой-либо крупы или песку, а в третий нальём воды (рис. 96).

Деревянный брусок вследствие действия на него силы тяжести будет давить лишь на дно сосуда. Горох будет давить не только на дно, а и на стенки сосуда во всех точках касания горошин. Каждая горошина внутри сжата со всех сторон соседними горошинами и вследствие действия сил упругости сама будет давить во все стороны на горошины. Эти силы давления будут тем больше, чем глубже лежит горошина, т. е. чем больший слой гороха давит на неё сверху.
Вода, налитая в сосуд, вследствие большой подвижности молекул будет давить на дно и стенки сосуда. Каждая частица внутри воды будет сжата со всех сторон соседними частицами и вследствие упругости будет с такой же силой давить на соседние частицы. Эти силы будут тем больше, чем глубже будет находиться частица.
На рис. 97, а изображён прибор, который называют шаром Паскаля. Он имеет в разных местах поверхности маленькие отверстия. К нему присоединена трубка-цилиндр, в которую вставлен поршень. Если набрать в шар воды и нажать на поршень, то увидим, что струйки воды сквозь отверстия бьют во все стороны с одинаковой силой. Это объясняется тем, что поршень давит на поверхность жидкости в трубке. Частицы воды передают давление поршня другим частицам, которые лежат глубже. Таким способом давление поршня передаётся на все частицы воды в шаре. Вследствие этого часть воды выталкивается из шара в виде струек, бьющих изо всех отверстий.
Если шар заполнить дымом, то из всех отверстий шара начнут выходить струи дыма (рис. 97, б).
Это подтверждает, что и газы передают давление, оказываемое на них, во все стороны одинаково.
Давление, оказываемое на жидкость или газ внешними силами, передаётся жидкостью или газом одинаково во всех направлениях.
Это утверждение называют законом Паскаля.
На законе Паскаля основывается действие шприца: давление пальца врача на поршень шприца передаётся без изменений жидкости, содержащейся в нём, и лекарство выходят через иглу шприца.
Опыт 2. В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой плёнкой, нальём воду (рис. 98, а). Дно трубки прогнётся. Значит, на дно действует сила давления воды. Чем больше наливаем воды, тем более прогибается плёнка. Но каждый раз после того, как резиновое дно прогнулось, вода в трубке находится в равновесии, так как кроме силы тяжести на воду действует сила упругости резиновой плёнки.
Опустим трубку с резиновым дном, в которую налита вода, в более широкий сосуд с водой. Видим, что по мере опускания трубки вниз резиновая плёнка постепенно распрямляется (рис. 98, б). Полное распрямление плёнки показывает, что давление на неё сверху и снизу одинаковое. Значит, в жидкости существует давление, направленное снизу вверх, и на этой глубине оно равно давлению, направленному сверху вниз.
Если выполнить опыт с трубкой, в которой резиновая плёнка закрывает боковое отверстие (рис. 99, а, б), то мы убедимся, что боковое давление жидкости на резиновую плёнку также будет одинаковым с обеих сторон.
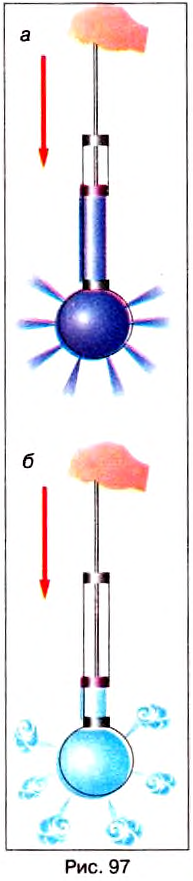
Опыт 3. Сосуд, дно которого может отпадать, опускаем в банку с водой (рис. 100, а). Дно при этом плотно прижимается к краям сосуда давлением воды снизу вверх. Потом в сосуд осторожно нальём воды. Когда уровень воды в ней совпадёт с уровнем воды в банке, дно оторвётся от сосуда (рис. 100, б). В момент отрывания на дно давит сверху столб жидкости в сосуде, а снизу – столб воды, находящейся в банке. Эти давления одинаковы по значениям, однако дно отрывается от сосуда под действием силы тяжести.
Согласно закону Паскаля давление внутри жидкости на одном уровне одинаково во всех направлениях. Давление увеличивается с глубиной.
Давление жидкостей, обусловленное силой тяжести, называют гидростатическим.
А как рассчитать давление жидкости на дно и стенки сосуда ?
Чтобы ответить на этот вопрос припомним, что для того, чтобы определить плотность вещества р, нужно массу тела m разделить на его объём V, т. е.: 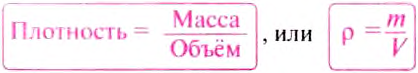
Единицей плотности в СИ является один килограмм на кубический метр 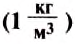 .
.
Из формулы для плотности можно определить массу тела. Для этого нужно плотность вещества р умножить на объем тела V, т. е.: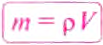
Теперь возвратимся к рис. 98 в опыте 2. Рассчитаем давление, которое создаёт столбик жидкости высотой h на дно цилиндрического сосуда. Мы уже знаем, что давление р равно отношению силы давления F к площади поверхности S, на которую она действует: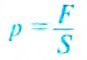
В нашей задаче сила давления равно весу жидкости Р : 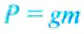
где m – масса жидкости, которую можем определить через плотность жидкости 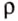 и объём жидкости V :
и объём жидкости V : 
Объём цилиндрического столба жидкости V равен произведению площади дна сосуда S и высоты уровня жидкости над дном h: 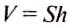 .
.
С учётом этих соотношений формула для давления приобретёт окончательный вид:

Видим, что гидростатическое давление на любой глубине внутри жидкости зависит только от ее плотности 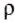 и высоты уровня h: оно равно произведению этих величин и постоянной
и высоты уровня h: оно равно произведению этих величин и постоянной 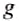 .
.
Гидростатическое давление жидкости не зависит ни от формы сосуда, ни от массы жидкости в сосуде, ни от площади его дна. Согласно закону Паскаля это давление на одном уровне жидкости одинаково действует и на дно, и на стенки сосуда.
Кстати:
В 1648 г. Блез Паскаль провёл интересный опыт. Он вставил в закрытую деревянную бочку, наполненную водой, тонкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кварту
( 0,9 дм3) воды. Из-за малой толщины трубки вода в ней поднялась на значительную высоту, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
0,9 дм3) воды. Из-за малой толщины трубки вода в ней поднялась на значительную высоту, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Пример №3
Чем объяснить, что вёдра в форме срезанного конуса очень распространены (рис. 101), хотя они менее устойчивы, и из них больше расплёскивается вода по сравнению с ведрами цилиндрической формы и такой же высоты? Кроме того, конусообразные ведра неудобно нести, так как приходится широко расставлять руки.

Ответ: оказывается, в большинстве случаев вёдра выходят из строя из-за того, что у них выпадает дно. Следовательно, прочность дна определяет долговечность ведра. В ведре конической формы площадь дна меньше, чем в ведре цилиндрической формы такой же вместимости, а потому сила давления на дно меньше. Это единственное преимущество конических ведер оправдывает все другие их недостатки.
Пример №4
Наибольшая глубина, на которой учёные с корабля «Витязь» выловили рыбу, составляет 7200 м. Какое давление создаёт вода на этой глубине?
Дано:
h = 7200м
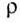 = 1030
= 1030 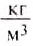
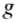 = 9,81
= 9,81 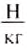
p = ?
Решение:
Давление создаваемое морской водой на глубине, определим по формуле: 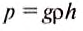 .
.
Подставив значения величин, получим: 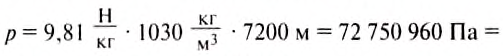
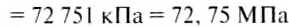 .
.
Ответ:  = 72, 75 МПа.
= 72, 75 МПа.
Давление и закон Архимеда
Почему жители севера для передвижения по снегу используют лыжи? Почему женщина, обутая летом в обувь на шпильках, оставляет на мягком асфальте заметные и глубокие следы? Зачем лезвия ножей время от времени натачивают? для чего у гвоздя есть острие? Попытаемся выяснить ответы на эти вопросы.
Давление твердых тел на поверхность и сила давления
Наблюдаем последствия действия силы: Одно из последствий действия силы — деформация тел, при этом чем большая сила действует на тело, тем больше будет деформация. Деформация зависит и от других факторов, в частности от площади поверхности, по которой распределяется действие силы.
В большинстве случаев чем больше площадь поверхности, на которую действует данная сила, тем меньше будет деформация. Проиллюстрируем это утверждение с помощью простого опыта: поставим деревянный брусок на снег сначала гранью меньшей площади, а затем — гранью большей площади (рис. 22.1).
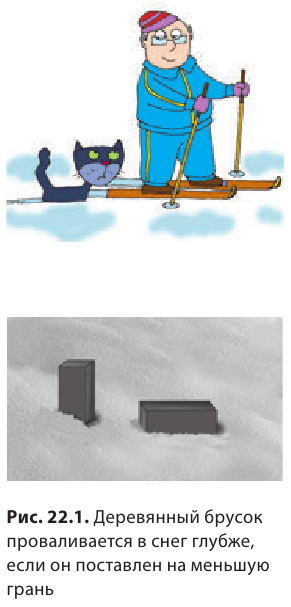
В первом случае снег деформируется сильнее (брусок глубже провалится в снег), хотя в обоих случаях сила, действующая на снег со стороны бруска (то есть вес бруска), одинакова. Можно провести еще один опыт: нажмите с одинаковой небольшой силой на поверхность песка сначала раскрытой ладонью, а затем пальцем — и вы увидите, в каком случае глубина следа будет больше (рис. 22.2).

Определение давления
Для характеристики зависимости результата действия силы от площади поверхности, на которую действует эта сила, используют такое понятие, как давление.
Давление — это физическая величина, которая характеризует результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: 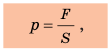 где p — давление; F — сила давления — сила, действующая на поверхность перпендикулярно этой поверхности; S — площадь поверхности. Единица давления в СИ — паскаль (Па); названа в честь французского ученого Блеза Паскаля (рис. 22.3): [p]=Па. 1 Па — это давление, которое создает сила 1 Н, действуя перпендикулярно поверхности площадью
где p — давление; F — сила давления — сила, действующая на поверхность перпендикулярно этой поверхности; S — площадь поверхности. Единица давления в СИ — паскаль (Па); названа в честь французского ученого Блеза Паскаля (рис. 22.3): [p]=Па. 1 Па — это давление, которое создает сила 1 Н, действуя перпендикулярно поверхности площадью 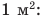
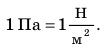 1 Па — небольшое давление (примерно такое давление оказывает на стол альбомный лист для рисования), поэтому чаще используют кратные единицы давления: гектопаскаль (1 гПа = 100 Па), килопаскаль (1 кПа = 1000 Па), мегапаскаль (1 МПа = 1 000 000 Па). Рассмотрите таблицу и подумайте, почему, например, гусеницы трактора оказывают на грунт намного меньшее давление, чем колеса легкового автомобиля.
1 Па — небольшое давление (примерно такое давление оказывает на стол альбомный лист для рисования), поэтому чаще используют кратные единицы давления: гектопаскаль (1 гПа = 100 Па), килопаскаль (1 кПа = 1000 Па), мегапаскаль (1 МПа = 1 000 000 Па). Рассмотрите таблицу и подумайте, почему, например, гусеницы трактора оказывают на грунт намного меньшее давление, чем колеса легкового автомобиля.

Как можно увеличить или уменьшить давление
Из определения давления 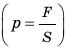 следует, что давление твердых тел можно изменить двумя способами. Первый способ: изменить силу, действующую на поверхность данной площади. С увеличением силы давление увеличивается; с уменьшением силы давление уменьшается. Второй способ: изменить площадь поверхности, на которую действует данная сила давления. Для увеличения давления площадь нужно уменьшить (именно поэтому натачивают инструменты — ножницы, ножи, шила и т. п.) (рис. 22.4). Для уменьшения давления площадь поверхности нужно увеличить. Рассмотрите рис. 22.5 и объясните, почему человек оказывает на снег большее давление, чем тяжелый вездеход.
следует, что давление твердых тел можно изменить двумя способами. Первый способ: изменить силу, действующую на поверхность данной площади. С увеличением силы давление увеличивается; с уменьшением силы давление уменьшается. Второй способ: изменить площадь поверхности, на которую действует данная сила давления. Для увеличения давления площадь нужно уменьшить (именно поэтому натачивают инструменты — ножницы, ножи, шила и т. п.) (рис. 22.4). Для уменьшения давления площадь поверхности нужно увеличить. Рассмотрите рис. 22.5 и объясните, почему человек оказывает на снег большее давление, чем тяжелый вездеход.


Пример №5
Сравните давления, которые оказывают на поверхность снега юные спортсмены — турист и лыжник. Масса каждого из них вместе со снаряжением равна 63 кг. Площадь подошвы ботинка туриста — приблизительно  , площадь лыжи — приблизительно
, площадь лыжи — приблизительно 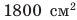 . Анализ физической проблемы. Давление, которое оказывает каждый спортсмен, определяется силой давления и площадью, на которую он опирается. В обоих случаях сила давления —это вес спортсмена; он распределяется на две подошвы или две лыжи. Будем считать, что на обе подошвы (лыжи) нагрузка распределяется равномерно. Задачу будем решать в единицах СИ.
. Анализ физической проблемы. Давление, которое оказывает каждый спортсмен, определяется силой давления и площадью, на которую он опирается. В обоих случаях сила давления —это вес спортсмена; он распределяется на две подошвы или две лыжи. Будем считать, что на обе подошвы (лыжи) нагрузка распределяется равномерно. Задачу будем решать в единицах СИ.
Дано:
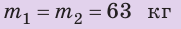 ,
,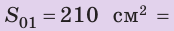
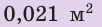 ,
,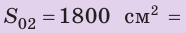
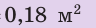 ,
,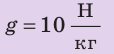
Найти:
 ,
,
Решение:
По определению давления: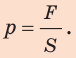
Здесь 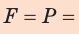
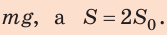 Подставив выражения для F и S в формулу давления, имеем:
Подставив выражения для F и S в формулу давления, имеем: 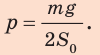 Проверим единицу, найдем значения искомых величин:
Проверим единицу, найдем значения искомых величин: 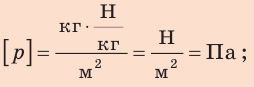 для туриста:
для туриста: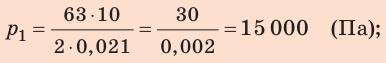
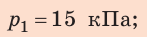
для лыжника:
Анализ результатов. Давление, создаваемое туристом, приблизительно в 8,6 раза больше давления, создаваемого лыжником. Это реальный результат, ведь при равных силах большее давление создает та сила, которая действует на меньшую площадь.
Ответ: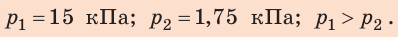
Итоги:
Давление p — это физическая величина, которая характеризует результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: 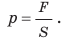 . Единица давления в СИ — паскаль
. Единица давления в СИ — паскаль 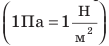 . Для увеличения давления следует уменьшить площадь поверхности, на которую действует сила давления, или увеличить силу давления. Для уменьшения давления нужно увеличить площадь поверхности, на которую действует сила давления, или уменьшить силу давления.
. Для увеличения давления следует уменьшить площадь поверхности, на которую действует сила давления, или увеличить силу давления. Для уменьшения давления нужно увеличить площадь поверхности, на которую действует сила давления, или уменьшить силу давления.
Давление газов и жидкостей. Закон паскаля
Почему при надувании резинового воздушного шарика увеличивается его объем? ответ понятен: в шарике становится больше воздуха. а можно ли увеличить объем шарика без того, чтобы его надувать? Почему налитая в сосуд жидкость создает давление не только на дно сосуда, но и на его боковые поверхности? Почему водитель, нажимая на тормоз, может остановить тяжелый автомобиль? Попробуем «разгадать» эти загадки.

Почему газы создают давление
Положим слегка надутый завязанный воздушный шарик под колокол воздушного насоса (рис. 23.1, а). Если из под колокола откачивать воздух, объем шарика будет увеличиваться (рис. 23.1, б). Почему это происходит?
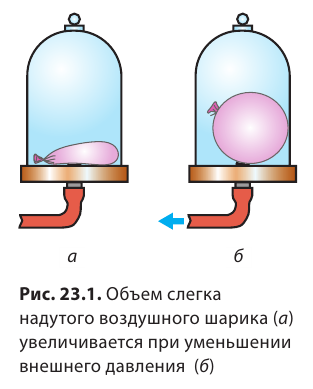
И снаружи шарика, и внутри него находится воздух (газ). Газ состоит из частиц (атомов и молекул), которые непрерывно движутся во всех направлениях и «бомбардируют» резиновую пленку, создавая на нее давление (рис. 23.2). Понятно, что сила удара одной частицы очень мала. Однако частиц в газе очень много — всего за 1 секунду количество их ударов по поверхности пленки таково, что для его записи требуется число с 23 нулями!
Поэтому общая сила, с которой ударяет такое огромное количество частиц, является значительной. Воздух внутри и снаружи шарика оказывает давление соответственно на внутреннюю и внешнюю поверхности резиновой пленки.
Если эти давления одинаковы, резиновая пленка не растягивается. А вот если давление внутри шарика становится больше внешнего давления, то шарик увеличивает свой объем. Надеемся, теперь вы сможете объяснить, почему воздушный шарик раздувается и тогда, когда мы его надуваем, и тогда, когда откачиваем воздух снаружи шарика.
- Заказать решение задач по физике
От чего зависит давление газов
Давление газа создается ударами его частиц, поэтому увеличение как количества ударов, так и силы ударов приводит к увеличению давления газа. Следовательно, давление газов можно увеличить двумя способами. Первый способ — увеличить плотность газа 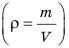 . Для этого можно добавить газ в сосуд (увеличить массу m газа), а можно уменьшить объем V самого сосуда (рис. 23.3)
. Для этого можно добавить газ в сосуд (увеличить массу m газа), а можно уменьшить объем V самого сосуда (рис. 23.3)
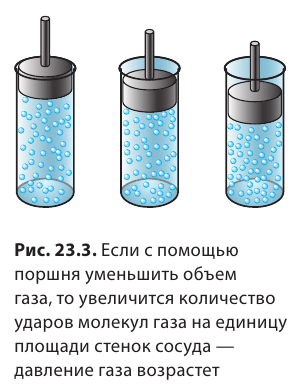
Второй способ — увеличить температуру газа. Чем выше температура газа, тем быстрее движутся его частицы. Удары частиц о стенки сосуда становятся чаще, сила их ударов возрастает, и в результате давление газа в сосуде увеличивается. Соответственно уменьшение давления газа будет происходить при уменьшении плотности или температуры газа.
Исследование давления жидкостей
В отличие от твердых тел жидкости легко изменяют свою форму — они приобретают форму того сосуда, в котором находятся, другими словами, жидкости текучи. Именно поэтому жидкости оказывают давление и на дно, и на боковые стенки сосуда, в котором находятся (в отличие от твердых тел, которые оказывают давление только на ту часть поверхности, на которую опираются). Если в боковой стенке сосуда, заполненного жидкостью, сделать отверстия, то жидкость польется через них (рис. 23.4).

Следствием текучести жидкостей является также то, что на любое погруженное в жидкость тело жидкость давит со всех сторон.
Закон Паскаля
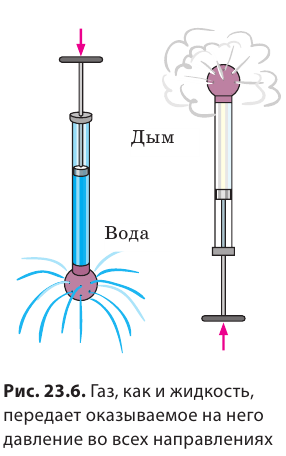
Благодаря своей текучести жидкость способна передавать давление по всему объему сосуда, в котором находится. Сделав иглой небольшие отверстия в полиэтиленовом пакете, наберем в пакет воду и завяжем. Нажмем на пакет — вода будет выливаться из всех отверстий (рис. 23.5).

Аналогичный эксперимент можно провести с воздухом или другим газом (рис. 23.6). Опираясь на подобные опыты, французский физик Б. Паскаль открыл закон, который сейчас называется закон Паскаля: давление, оказываемое на неподвижную жидкость, передается жидкостью одинаково во всех направлениях. То же самое можно сказать о газах.
Применяем закон Паскаля:
Свойство жидкостей и газов передавать давление во всех направлениях мы наблюдаем в повседневной жизни; это свойство широко используют в технике. Благодаря ему мы имеем возможность слышать, ведь воздух передает звук; работает наша сердечнососудистая система, ведь несмотря на то, что кровеносные сосуды имеют большое количество изгибов, давление, создаваемое сердцем, передается во все части тела. На законе Паскаля основана система торможения многих транспортных средств, действие домкратов, насосов и других гидравлических машин. Рассмотрим принцип действия гидравлических машин на примере гидравлического пресса, который применяют для прессования фанеры и картона, отжима растительных масел, изготовления деталей машин и механизмов и т. п.
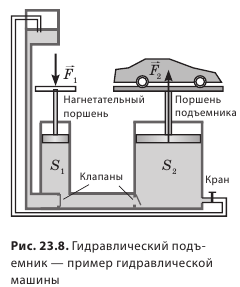
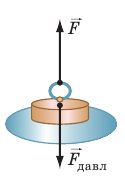
Гидравлический пресс — это простейшая гидравлическая машина, которую используют для создания больших сил давления. Гидравлический пресс состоит из двух соединенных между собой цилиндров разного диаметра, заполненных рабочей жидкостью (чаще машинным маслом) и закрытых подвижными поршнями (см. рис. 23.7). Если к поршню меньшего цилиндра приложить силу 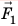 (см. рис. 23.7, б), то эта сила создаст на поверхность жидкости некоторое дополнительное давление p:
(см. рис. 23.7, б), то эта сила создаст на поверхность жидкости некоторое дополнительное давление p: 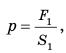 где
где 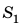 — площадь меньшего поршня. Согласно закону Паскаля это дополнительное давление будет передаваться во все точки жидкости, заполняющей сообщающиеся цилиндры. Следовательно, жидкость начнет давить на поршень большего цилиндра с некоторой силой
— площадь меньшего поршня. Согласно закону Паскаля это дополнительное давление будет передаваться во все точки жидкости, заполняющей сообщающиеся цилиндры. Следовательно, жидкость начнет давить на поршень большего цилиндра с некоторой силой 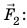
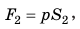 где
где 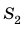 — площадь большего поршня; р — дополнительное давление.
— площадь большего поршня; р — дополнительное давление.
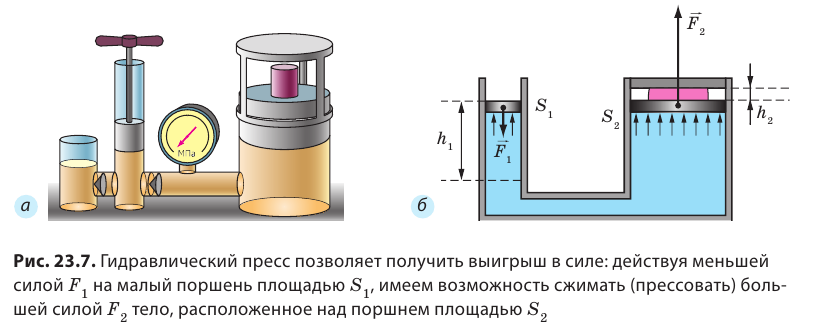
Поскольку 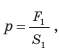 имеем:
имеем: 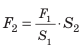 , то есть
, то есть 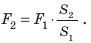 сила давления, которая действует со стороны жидкости на большой поршень, больше силы, которая действует на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого:
сила давления, которая действует со стороны жидкости на большой поршень, больше силы, которая действует на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого: 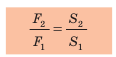 Отношение
Отношение 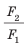 — это выигрыш в силе. Гидравлический пресс позволяет получить значительный выигрыш в силе: чем больше будут различаться между собой площади поршней, тем большим будет выигрыш в силе (рис. 23.7). По такому принципу работают и другие гидравлические инструменты и устройства. Так, гидравлический подъемник позволяет, приложив небольшую силу, поднять тяжелый автомобиль (рис. 23.8), гидравлический тормоз позволяет остановить автомобиль, приложив незначительную силу давления ноги, и т. д. Опираясь на рис. 23.8, попробуйте разобраться, как работает гидравлический подъемник.
— это выигрыш в силе. Гидравлический пресс позволяет получить значительный выигрыш в силе: чем больше будут различаться между собой площади поршней, тем большим будет выигрыш в силе (рис. 23.7). По такому принципу работают и другие гидравлические инструменты и устройства. Так, гидравлический подъемник позволяет, приложив небольшую силу, поднять тяжелый автомобиль (рис. 23.8), гидравлический тормоз позволяет остановить автомобиль, приложив незначительную силу давления ноги, и т. д. Опираясь на рис. 23.8, попробуйте разобраться, как работает гидравлический подъемник.
Итоги:
Газ оказывает давление на поверхность в результате многочисленных ударов об эту поверхность частиц газа. Давление газа возрастает при увеличении плотности или температуры газа и уменьшается при уменьшении плотности или температуры газа. Вследствие своей текучести жидкость оказывает давление на дно и боковые стенки сосуда, а также на любое тело, погруженное в данную жидкость. Давление, оказываемое на неподвижную жидкость, передается этой жидкостью одинаково во всех направлениях (закон Паскаля). Свойство жидкостей передавать давление одинаково во всех направлениях положено в основу действия гидравлических машин. Сила, действующая со стороны жидкости на большой поршень гидравлической машины, больше силы, действующей на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого: 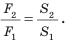
Гидростатическое давление
На рис. 24.1 изображен современник Блеза Паскаля, стоящий на кожаной подушке, заполненной водой. с подушкой соединена открытая сверху трубка — ее исследователь держит в руках. Почему доска, на которой стоит человек, не сжимает подушку полностью и не вытесняет через трубку всю воду наружу?
Получаем формулу для расчета:
Гидростатического давления Вы уже знаете, что в результате притяжения к Земле и благодаря собственной текучести жидкость оказывает давление как на дно, так и на стенки сосуда, в котором содержится. Жидкость оказывает давление и на любое погруженное в нее тело. Давление неподвижной жидкости называют гидростатическим давлением.

Определим гидростатическое давление на дно сосуда. Чтобы упростить расчеты, возьмем цилиндрический сосуд с площадью дна S. Пусть в сосуд налита жидкость плотностью ρ, а высота столба жидкости в сосуде — h (рис. 24.2).
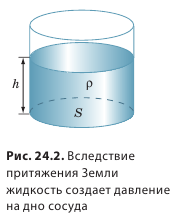
Чтобы вычислить давление, которое создает жидкость на дно сосуда, следует силу F, действующую на дно, разделить на площадь S дна: 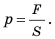 В данном случае сила F, создающая давление на дно сосуда, — это вес P жидкости. Поскольку жидкость в сосуде неподвижна, вес жидкости равен произведению массы m жидкости на ускорение свободного падения g:
В данном случае сила F, создающая давление на дно сосуда, — это вес P жидкости. Поскольку жидкость в сосуде неподвижна, вес жидкости равен произведению массы m жидкости на ускорение свободного падения g: 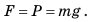 Массу жидкости найдем через объем и плотность жидкости: m=ρ ;V объем налитой в сосуд жидкости — через высоту h столба жидкости и площадь S дна сосуда: V= Sh. Следовательно, массу жидкости можно найти по формуле:
Массу жидкости найдем через объем и плотность жидкости: m=ρ ;V объем налитой в сосуд жидкости — через высоту h столба жидкости и площадь S дна сосуда: V= Sh. Следовательно, массу жидкости можно найти по формуле: 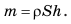 Подставив последовательно выражения для F и m в формулу давления, получим:
Подставив последовательно выражения для F и m в формулу давления, получим:  Итак, имеем формулу для расчета гидростатического давления — давления, которое создает неподвижная жидкость:
Итак, имеем формулу для расчета гидростатического давления — давления, которое создает неподвижная жидкость: 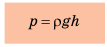 Как видим, гидростатическое давление зависит только от плотности жидкости и высоты столба жидкости в сосуде.
Как видим, гидростатическое давление зависит только от плотности жидкости и высоты столба жидкости в сосуде.
Проводим исследования и делаем выводы:
Зависимость гидростатического давления от высоты столба жидкости впервые продемонстрировал Блез Паскаль. Взяв бочку, до краев заполненную водой, исследователь герметично закрыл ее крышкой со вставленной длинной тонкой трубкой. Поднявшись на балкон второго этажа жилого дома, Паскаль вылил в трубку всего один стакан воды. Вода заполнила всю трубку и создала на стенки и дно бочки такое огромное давление, что в боковых стенках бочки появились щели (рис. 24.3).

Обратите внимание! Согласно закону Паскаля давление жидкости передается во всех направлениях, а значит, по формуле 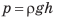 можно также определить давление, которое создает слой жидкости высотой h на любое тело, погруженное в эту жидкость на данную глубину, а также давление на стенки сосуда. Из закона Паскаля и формулы гидростатического давления также следует, что давление внутри неподвижной однородной жидкости на одном уровне* одинаково. Рассмотрите рис. 24.4. Казалось бы, давление воды на дне подводной пещеры меньше, чем на дне открытого моря. Однако, если бы это действительно было так, вследствие большего давления вода из моря хлынула бы в пещеру. Но этого не происходит.
можно также определить давление, которое создает слой жидкости высотой h на любое тело, погруженное в эту жидкость на данную глубину, а также давление на стенки сосуда. Из закона Паскаля и формулы гидростатического давления также следует, что давление внутри неподвижной однородной жидкости на одном уровне* одинаково. Рассмотрите рис. 24.4. Казалось бы, давление воды на дне подводной пещеры меньше, чем на дне открытого моря. Однако, если бы это действительно было так, вследствие большего давления вода из моря хлынула бы в пещеру. Но этого не происходит.

Пример №6
На дне бассейна расположено круглое отверстие, закрытое пробкой радиусом 5 см. Какую силу нужно приложить к пробке, чтобы вынуть ее из отверстия, если высота воды в бассейне 2 м? Массой пробки и силой трения между пробкой и отверстием пренебречь. Анализ физической проблемы. Вынуть пробку мешает сила давления воды в бассейне. Массу пробки и силу трения учитывать не нужно, поэтому сила, необходимая для того, чтобы вынуть пробку из отверстия, по значению должна быть не меньше, чем сила гидростатического давления воды на пробку:  (см. рисунок).
(см. рисунок).
Уровнем называют любую горизонтальную поверхность.
Дано:
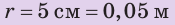 ,
,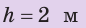 ,
,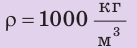 ,
,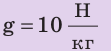
найти:

Решение:
По определению давления:
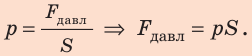
Здесь 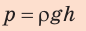 — гидростатическое давление;
— гидростатическое давление; 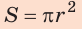 — площадь круга. Подставив выражения для p и S в формулу для
— площадь круга. Подставив выражения для p и S в формулу для 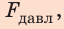 получим:
получим:
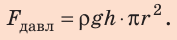
Так как 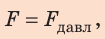 окончательно имеем:
окончательно имеем: 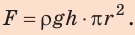 Проверим единицу, найдем значение искомой величины:
Проверим единицу, найдем значение искомой величины:
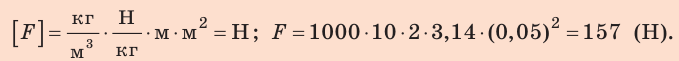
Ответ: следует приложить силу не менее чем 157 Н.
Итоги:
В результате притяжения к Земле жидкости создают давление на дно и стенки сосудов, а также на любое погруженное в них тело. Давление p неподвижной жидкости называют гидростатическим давлением — оно зависит только от плотности ρ жидкости и высоты h столба жидкости. Гидростатическое давление вычисляют по формуле 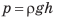 . Давление внутри неподвижной однородной жидкости на одном уровне одинаково.
. Давление внутри неподвижной однородной жидкости на одном уровне одинаково.
Атмосферное давление и его измерение. Барометры
Когда мы делаем глоток чая, то вряд ли размышляем над физикой этого процесса. При этом глотание, как и многие другие процессы, происходит благодаря давлению воздуха вокруг нас — атмосферному давлению. откроем для себя некоторые важные свойства атмосферного давления и научимся его измерять.
Что такое атмосфера
Вы хорошо знаете, что наша планета Земля окружена воздушной оболочкой, которую называют атмосферой (в переводе с греческого — «пар» и «сфера») (рис. 25.1). Почему же существует воздушная оболочка Земли? Воздух состоит из молекул и атомов. Молекулы и атомы имеют массу, поэтому они притягиваются к Земле благодаря действию силы тяжести. Все огромное количество молекул газов, составляющих атмосферу, находится в непрерывном хаотическом движении — они все время сталкиваются, отскакивают друг от друга, изменяют значение и направление скорости своего движения… Именно поэтому они не «падают» на Землю, а находятся в пространстве вблизи нее.

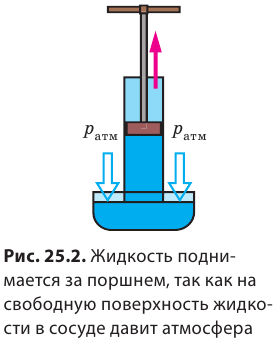
По подсчетам, атмосфера Земли имеет массу около 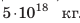 . Под действием силы тяжести верхние слои атмосферы давят на нижние, поэтому воздушный слой непосредственно у поверхности Земли сжат больше и, согласно закону Паскаля, создает давление на поверхность Земли и на все тела вблизи нее. Это и есть атмосферное давление p(атм .) Атмосферное давление обусловливает существование всасывания — поднятия жидкости за поршнем (в насосах, шприцах и т. п.) (рис. 25.2). Если поднимать поршень, то атмосферное давление, действуя на свободную поверхность жидкости в сосуде, будет нагнетать жидкость вверх, в пустоту под поршнем. Со стороны все выглядит так, будто жидкость поднимается за поршнем сама по себе.
. Под действием силы тяжести верхние слои атмосферы давят на нижние, поэтому воздушный слой непосредственно у поверхности Земли сжат больше и, согласно закону Паскаля, создает давление на поверхность Земли и на все тела вблизи нее. Это и есть атмосферное давление p(атм .) Атмосферное давление обусловливает существование всасывания — поднятия жидкости за поршнем (в насосах, шприцах и т. п.) (рис. 25.2). Если поднимать поршень, то атмосферное давление, действуя на свободную поверхность жидкости в сосуде, будет нагнетать жидкость вверх, в пустоту под поршнем. Со стороны все выглядит так, будто жидкость поднимается за поршнем сама по себе.
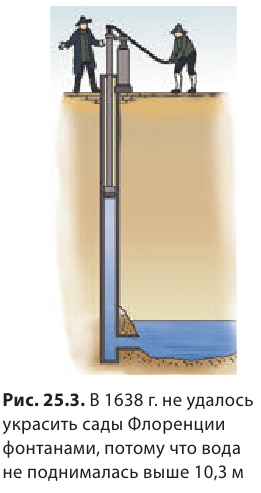
Кстати, долгое время поднятие жидкости за поршнем, движущимся вверх, приводилось как одно из доказательств известного принципа Аристотеля «Природа боится пустоты». Однако в середине XVII в. при строительстве фонтанов во Флоренции столкнулись с непонятным явлением: оказалось, что вода, которая всасывается насосами, не поднимается выше 10,3 м (рис. 25.3). Галилео Галилей предложил разобраться в этом своим ученикам — Эванджелисте Торричелли (1608–1647) и Винченцо Вивиани (1622–1703). Разбираясь с данной проблемой, Э. Торричелли впервые доказал существование атмосферного давления.
Измерение атмосферное давления
Для удобства проведения опытов Э. Торричелли догадался заменить воду жидкостью с намного большей плотностью. Стеклянную трубку длиной около метра, запаянную с одного конца, ученый доверху наполнил ртутью. Затем, плотно закрыв отверстие, он перевернул трубку, опустил ее в чашу с ртутью и открыл отверстие — часть жидкости из трубки вылилась в чашу. В трубке остался столб ртути высотой приблизительно 760 мм, а над ртутью образовалась пустота (рис. 25.4). Проведя множество опытов, Торричелли установил: высота столба ртути, остающейся в трубке (760 мм), не зависит ни от длины трубки, ни от ее диаметра, — эта высота немного изменяется только в зависимости от погоды.
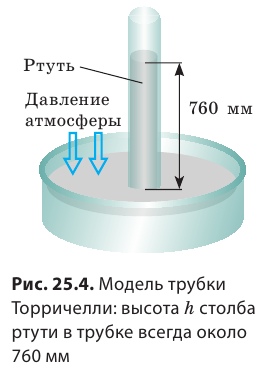
Торричелли сумел также объяснить, почему высота столба ртути имеет именно такую высоту. Однородная жидкость в трубке и чаше неподвижна. Значит, согласно закону Паскаля давление на поверхность ртути со стороны атмосферы и гидростатическое давление столба ртути в трубке одинаковы. То есть давление столба ртути высотой 760 мм равно атмосферному давлению.давление, которое создает столб ртути высотой 760 мм, называют нормальным атмосферным давлением: 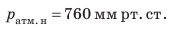 В данном случае в качестве единицы атмосферного давления взят один миллиметр ртутного столба (1 мм рт. ст.). Выразим нормальное атмосферное давление в единицах СИ — паскалях. Из материала 4 вы знаете, что гидростатическое давление вычисляют по формуле: p=ρ hg. Учитывая, что плотность ртути
В данном случае в качестве единицы атмосферного давления взят один миллиметр ртутного столба (1 мм рт. ст.). Выразим нормальное атмосферное давление в единицах СИ — паскалях. Из материала 4 вы знаете, что гидростатическое давление вычисляют по формуле: p=ρ hg. Учитывая, что плотность ртути 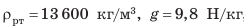 , а высота столба ртути h = 0,76 м, имеем:
, а высота столба ртути h = 0,76 м, имеем: 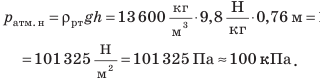 Обратите внимание: выражая атмосферное давление в паскалях, для расчетов следует брать
Обратите внимание: выражая атмосферное давление в паскалях, для расчетов следует брать 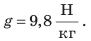 В физике и технике также используют внесистемную единицу атмосферного давления — физическую атмосферу (1 атм). Одна физическая атмосфера равна нормальному атмосферному давлению: 1атм ≈100кПа.
В физике и технике также используют внесистемную единицу атмосферного давления — физическую атмосферу (1 атм). Одна физическая атмосфера равна нормальному атмосферному давлению: 1атм ≈100кПа.
Конструкция барометра-анероида
Если к трубке Торричелли присоединить вертикальную шкалу (линейку), то получим простейший барометр — прибор для измерения атмосферного давления. Действие такого барометра основано на том, что столб жидкости прекращает подниматься (опускаться) как только гидростатическое давление столба жидкости становится равным атмосферному давлению. Барометр Торричелли — достаточно точный прибор, однако большой размер, ядовитые пары ртути и стеклянная трубка делают его неудобным для повседневного использования. Сейчас широко применяют барометры анероиды — приборы для измерения атмосферного давления, работающие без помощи жидкости (рис. 25.5). Главная часть барометраанероида — легкая и упругая пустая металлическая коробочка 1 с гофрированной (ребристой) поверхностью. Воздух в коробочке находится при сниженном давлении. К стенке коробочки прикреплена стрелка 2, насаженная на ось 3. Конец стрелки передвигается по шкале 4, размеченной в миллиметрах ртутного столба или паскалях. Все детали барометра размещены в корпусе, передняя часть которого закрыта стеклом. Изменение атмосферного давления вызывает изменение силы, сжимающей стенки коробочки. Соответственно изменяется изгиб стенок коробочки. Изгиб стенок передается стрелке и вызывает ее движение.
Барометры анероиды более удобны в использовании, чем ртутные приборы: они легкие, компактные и безопасные.
Определение зависимости атмосферного давления от погоды и высоты
Наблюдая за барометром, можно легко прогнозировать изменение погоды. Например, перед ненастьем атмосферное давление обычно падает. Показания барометра зависят не только от погоды, а и от высоты над уровнем моря. Чем выше место наблюдения над уровнем моря, тем меньше атмосферное давление. Вблизи поверхности Земли через каждые 11 м высоты атмосферное давление уменьшается приблизительно на 1 мм рт. ст. Поскольку атмосферное давление зависит от высоты, барометр можно проградуировать таким образом, чтобы по давлению воздуха определять высоту. Так был изобретен альтиметр — прибор для измерения высоты (рис. 25.6).

Итоги:
Воздух имеет массу. Из-за притяжения Земли верхние слои атмосферы (воздушной оболочки Земли) давят на нижние. Давление воздуха на поверхность Земли и на все тела вблизи нее называют атмосферным давлением. Точное измерение атмосферного давления обеспечивает ртутный барометр (барометр Торричелли). Давление столба ртути высотой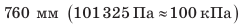 — это нормальное атмосферное давление. На практике используют барометры анероиды благодаря их удобству, небольшим размерам и безопасности. С помощью барометров можно прогнозировать изменение погоды и определять высоту: атмосферное давление уменьшается перед ненастьем, а также с высотой.
— это нормальное атмосферное давление. На практике используют барометры анероиды благодаря их удобству, небольшим размерам и безопасности. С помощью барометров можно прогнозировать изменение погоды и определять высоту: атмосферное давление уменьшается перед ненастьем, а также с высотой.
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
- Блоки в физике
- Вес тела в физике
- Закон всемирного тяготения
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
Содержание:
- Определение и формула давления
- Среднее давление
- Давление идеального газа
- Гидростатическое давление
- Единицы измерения давления
- Примеры решения задач
Определение и формула давления
Определение
Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$Delta S$ к размеру данной площади при
$Delta S rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:
$$p=lim _{Delta S rightarrow 0} frac{Delta F_{n}}{Delta S}=frac{d F_{n}}{d S}$$
Выражение (1) определяет давление в точке.
Среднее давление
Средним давлением на поверхность называют величину:
$$langle prangle=frac{F_{n}}{S}(2)$$
где Fn – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.
Давление идеального газа
Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:
$$p=n k T(3)$$
где $n=frac{N}{V}$– концентрация молекул газа
(N – число частиц), k=1,38•10-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа.
Гидростатическое давление
Гидростатическое давление – давление внутри столба жидкости или газа, находится по формуле:
$$p=p_{0}+rho g h(4)$$
где $rho$ – плотность вещества, g=9,8 м/с2 –
ускорение свободного падения, h- высота столба вещества. p0 – внешнее давление на газ или жидкость.
Искривление поверхностного слоя жидкости ведет к возникновению дополнительного давления на жидкость, тогда давление под искривленной
жидкостью определяется как:
$$p=p_{0}^{*}+2 sigma H(5)$$
где $mathrm{P}_{0}^{*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости,
H – средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:
$$H=frac{1}{2}left(frac{1}{R_{1}}+frac{1}{R_{2}}right)$$
R1, R2 – главные радиусы кривизны.
Единицы измерения давления
Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)
Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.
Па= Н/м2 и 1 бар=105 Па.
Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.
Примеры решения задач
Пример
Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно
p0=105 Па, плотность морской воды равна
$rho$=1,03•103 кг/м3
Решение. Основой для решения задачи служит выражение:
$$p=p_{0}+rho g h(1.1)$$
Все данные в задаче указаны в системе СИ, поэтому можно провести вычисления:
$p=10^{5}+1,03 cdot 10^{3} cdot 9,8 cdot 8,5=1,88 cdot 10^{5}$ (Па).
Ответ. $p=1,88 cdot 10^{5}$ (Па)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом
$alpha$ к нормали
плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.
Решение. Сделаем рисунок.
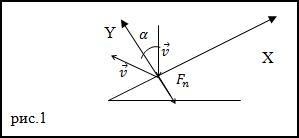
За время $Delta t$ о стенку ударяется масса воды равная:
$$m=l S rho=v Delta t S rho$$
где S – поперечное сечение струи, $rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:
$$F Delta t=m Delta v rightarrow F=frac{m Delta v}{Delta t}(2.2)$$
где F – сила, с которой вода действует на стенку.
Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:
$$Delta v=v_{2} cos alpha-left(-v_{1} cos alpharight)=v_{2} cos alpha+v_{1} cos alpha=2 v cos alpha(2.3)$$
Подставим $Delta v$ из (2.3) в выражение (2.2), учтем выражение (2.1) имеем:
$$F=frac{m 2 v cos alpha}{Delta t}=frac{v Delta t S rho 2 v cos alpha}{Delta t}=2 operatorname{Sov}^{2} cos alpha(2.4)$$
В таком случае искомое давление струи на стенку будет равно:
$$p=frac{F_{n}}{S}=2 rho v^{2}$$
Ответ. $p=2 rho v^{2}$
Читать дальше: Формула закона Ома.
