Сегодня мы говорим про окружность и круг, друзья мои. У многих шестиклассников, да и не только у них, возникают трудности с этой темой. А она-то как раз и есть ваш реальный шанс на получение хорошей отметки. Да, есть там одна заковырка. Вот она не нравится ребятам. Но я сейчас подробно всё расскажу. Давайте приступим)))
Сначала дам несколько определений. Они очень лёгкие, просто посмотрите:
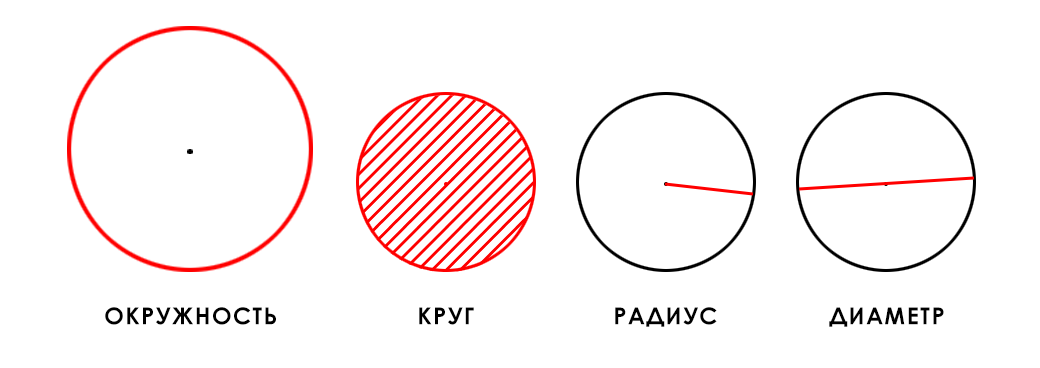
Есть окружность, а есть круг:
Определения, ребята, есть у вас в учебнике. Их надо знать наизусть, учителя это любят. Выучите их, пожалуйста. А я вам простыми словами расскажу, чтобы совсем понятно было.
- Окружность – это линия на бумаге или ещё где-нибудь. На асфальте мелом, например.
- Круг – это часть листа (плоскости).
Как отличить круг от окружности?
Круг я могу вырезать ножницами и у меня в руках будет круглый кусок бумаги. А линию я вам как вырежу?!
Окружность нельзя вырезать ножницами! Она же линия!
Дальше. У вас будут две формулы. Я знаю, что их три, на самом деле – две. Расскажу попозже. Сначала основные определения простыми словами дам:
А это диаметр. Присмотритесь: вам ничего не показалось?)))
Вы молодцы, если вам показалось, что один диаметр – это ДВА РАДИУСА! Так и есть!
Значит, вот эти две формулы одинаковые.
Запомните: один диаметр – это два радиуса! Один радиус – это половина диаметра! Если знаете диаметр – радиус тоже знаете!!! И наоборот!
Что такое C в этой формуле? Это длина окружности. Если я возьму окружность, мысленно её разрежу и разогну, то получится прямая. Тогда я смогу померить её длину. А можно и не разрезать. Возьмите сантиметровую ленту у бабушки или у мамы. Потом найдите чашку на кухне, отметьте точку (незаметно, чтобы потом смыть) и действуйте по схеме:
Есть ещё формула площади круга:
Тоже легко. В статье я уже не буду об этом писать. А вот видео, в нём я задачи разбираю для шестиклассников, именно на эту тему. Там про площадь круга рассказываю подробно. Для других классов тоже подойдёт, кто не понял, забыл или не успел)))
Подведём итог. Если вы будете знать наизусть определение диаметра и радиуса, если вы будете знать 2 формулы (а на самом деле одну!) длины окружности и одну формулу площади круга, то по этой теме у вас точно будет не ниже четвёрки, друзья мои школьники.
Если статья показалась вам полезной, поставьте, пожалуйста, оценку. Она поможет мне дальше помогать вам)))
Вот здесь кое-что про борьбу со списыванием с сайта ГДЗ
А вот здесь – как учить стихи
P. S.: Про число “ПИ” я ничего не говорила в этой статье. Но в видео я про него рассказываю. Это фантастическое, просто удивительное число!!!!! Но мне места не хватило, В другой раз…
Окружность, круг, сегмент, сектор. Формулы и свойства
- Окружность – определение
- Круг – определение
- Радиус и диаметр окружности
- Основные свойства окружности
- Формулы длины окружности и площади круга
- Уравнение окружности
- Касательная окружности и ее свойства
- Секущая окружности и ее свойства
- Хорда окружности и ее свойства
- Центральный угол, вписанный угол и их свойства
- Дуга, длина дуги, градусная мера дуги
- Полуокружность и полукруг
- Сектор, площадь сектора
- Сегмент, площадь сегмента
- Концентрические окружности
- Кольцо
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равен единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
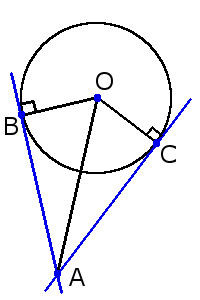
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
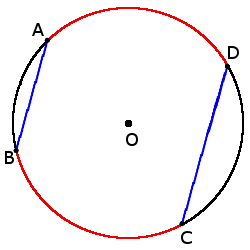
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
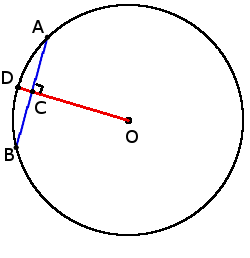
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
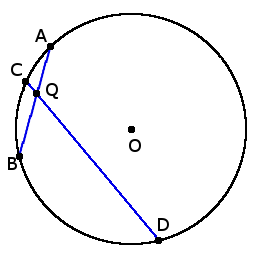
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
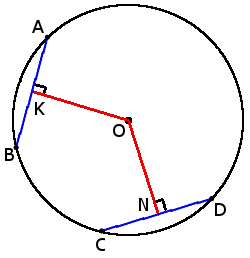
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
6. Чем больше хорда, тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
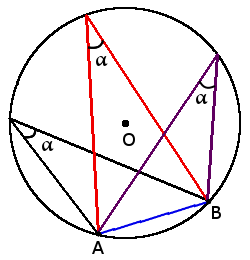
1. Все вписанные углы, которые опираются на одну дугу – равны.
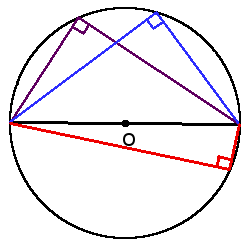
2. Вписанный угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
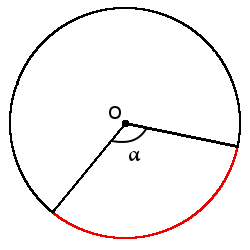
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
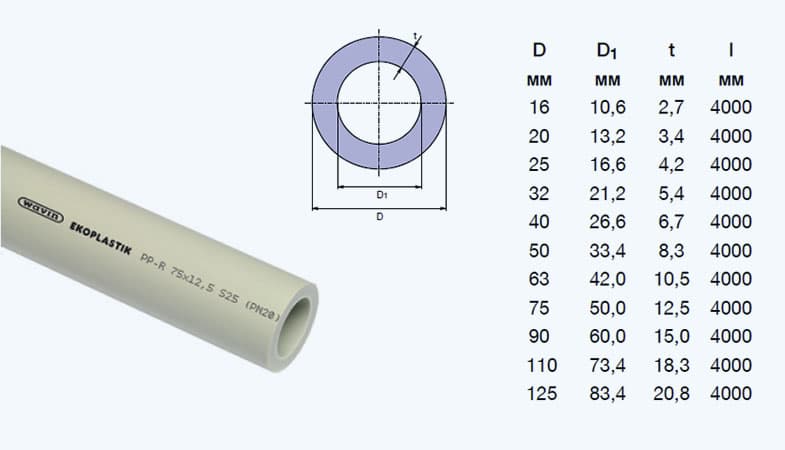
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.

Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Содержание
- Основные определения и свойства
- Чем круг отличается от окружности: объяснение
- Круг и окружность: примеры, фото
- Свойства окружности
- Свойство 1
- Свойство 2
- Свойство 3
- Формулы
- Формулы для площади круга и его частей
- Формулы для длины окружности и её дуг
- Формула длины окружности и площади круга: сравнение
- Площадь круга
- Длина окружности
- Как найти длину окружности через диаметр
- Как найти длину окружности через радиус
- Как вычислить длину окружности через площадь круга
- Как найти длину окружности через диагональ вписанного прямоугольника
- Как вычислить длину окружности через сторону описанного квадрата
- Как найти длину окружности через стороны и площадь вписанного треугольника
- Как найти длину окружности через площадь и полупериметр описанного треугольника
- Как вычислить длину окружности через сторону вписанного правильного многоугольника
- Длина дуги
- Площадь сектора
- Площадь сегмента
- Уравнение окружности
- Касательная окружности и ее свойства
- Основные свойства касательных к окружности
- Секущая окружности и ее свойства
- Основные свойства секущих
- Хорда окружности ее длина и свойства
- Длина хорды
- Основные свойства хорд
- Центральный угол, вписанный угол и их свойства
- Основные свойства углов
- Вписанная окружность
- Описанная окружность
- Теорема Птолемея
- Задачи для решения
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |  |
Часть окружности, расположенная между двумя точками окружности |
| Круг |  |
Конечная часть плоскости, ограниченная окружностью |
| Сектор |  |
Часть круга, ограниченная двумя радиусами |
| Сегмент |  |
Часть круга, ограниченная хордой |
| Правильный многоугольник |  |
Выпуклый многоугольник, у которого все стороны равны и все углы равны |
 |
Около любого правильного многоугольника можно описать окружность |
| Окружность |

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |

Часть окружности, расположенная между двумя точками окружности |
| Круг |

Конечная часть плоскости, ограниченная окружностью |
| Сектор |

Часть круга, ограниченная двумя радиусами |
| Сегмент |

Часть круга, ограниченная хордой |
| Правильный многоугольник |

Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность |
- Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
- Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
- Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Чем круг отличается от окружности: объяснение
Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:
- Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
- Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
- Сходство между окружностью и кругом: радиус и диаметр;
- У круга и окружности единый центр;
- В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
- У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.
Круг и окружность: примеры, фото
Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.

Сравнение между кругом и окружностью
Свойства окружности
Свойство 1
Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.
Свойство 2
Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.

Свойство 3
Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.
Формулы
- Диаметр окружности (d):
![]()
- Длина окружности (С):
![]()
- Радиус окружности (R):
![]()
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
,
где R – радиус круга, D – диаметр круга |
| Площадь сектора |  |
,
если величина угла α выражена в радианах |
| ,
если величина угла α выражена в градусах |
||
| Площадь сегмента |  |
,
если величина угла α выражена в радианах |
| ,
если величина угла α выражена в градусах |
| Площадь круга |

, где R – радиус круга, D – диаметр круга |
| Площадь сектора |

, если величина угла α выражена в радианах если величина угла α выражена в градусах |
| Площадь сегмента |

, если величина угла α выражена в радианах если величина угла α выражена в градусах |
Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула |
| Длина окружности |  |
C = 2πR = π D,
где R – радиус круга, D – диаметр круга |
| Длина дуги |  |
L(α) = αR,
если величина угла α выражена в радианах |
| ,
если величина угла α выражена в градусах |
| Длина окружности |

C = 2πR = π D, где R – радиус круга, D – диаметр круга |
| Длина дуги |

L(α) = αR, если величина угла α выражена в радианах , если величина угла α выражена в градусах |
Формула длины окружности и площади круга: сравнение
Формула длины окружности L=2 πR
Формула площади круга S= πR²
Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан – угольникnправильный (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1
равнаR, – угольника, вписанного в окружность радиуса nПлощадь правильного
, равна1 – угольника, вписанного в окружность радиуса nПлощадь правильного
Следовательно,
Поскольку π, стремится к 1 – угольника, вписанного в окружность радиуса n площадь правильного nпри увеличении , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим – угольникnправильный B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2
Поскольку – угольникаnплощадь B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
l=πd, где
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
l=2πr , где
π — число пи, равное 3,14
r — радиус окружности
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:

где:
- π — число пи, равное 3,14
- S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
l=πd, где
- π — число пи, равное 3,14
- d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
l=πa, где
- π — математическая константа, равная 3,14
- a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:
- π — математическая константа, она всегда равна 3,14
- a — первая сторона треугольника
- b — вторая сторона треугольника
- c — третья сторона треугольника
- S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:
- π — математическая константа, равная 3,14
- S — площадь треугольника
- p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:

где:
- π — математическая константа, равная 3,14
- a — сторона многоугольника
- N — количество сторон многоугольника
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

Рис.4
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Рис.5
Уравнение окружности
- Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
- Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x — a)2 + (y — b)2
- Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
- Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
- Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

- Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих

- Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

- Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды

- Длина хорды через центральный угол и радиус:
AB = 2r sin α2

- Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

- Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD

- Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC

- Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC

- Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC

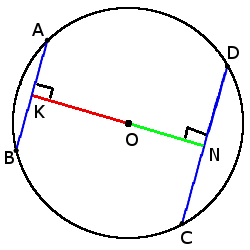
- Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK

- Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Центральный угол окружности — угол, вершиной которого есть центр окружности.
Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов

β = α2

- Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.Определение.Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла,который ограничивает эту дугу своими сторонами. 
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение.Полуокружность — дуга в которой концы соединены диаметром окружности.Определение.Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.Определение.Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Формула.Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.
Вписанная окружность
Окружность называетсявписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.
Площадь многоугольника, в который вписана окружность можно найти по формуле

,
здесь  — полупериметр многоугольника,
— полупериметр многоугольника,  — радиус вписанной окружности.
— радиус вписанной окружности.
Отсюда радиус вписанной окружности равен 
Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:


В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен 
. Здесь 
Описанная окружность
Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:
Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна
.

∠
+∠
=∠
+∠
Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:


Где  — длины сторон треугольника,
— длины сторон треугольника,  — его площадь.
— его площадь.
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:

Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
- Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
l=πd
Подставляем туда известные переменные и получается, что длина окружности равна
l=πd=3,14·5=15,7(см)
Ответ: 15,7 (см)
- Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Подставим туда наши переменные и получим 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Так и сделаем:
l=2πr=2·π·4≈2·3,14·4=25,12(дм)
Ответ: l=25,12(дм)
Окружность
Окружность – геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Центр окръжности
Радиус: расстояние от центра окружности до его границы. 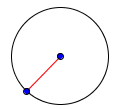
Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам. 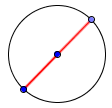
$d = 2cdot r$
Периметр (длина окружности): длина границы окружности. 
Длина окружности $= pi cdot$ диаметр $= 2 cdot pi cdot$ радиус
Длина окружности $= pi cdot d = 2 cdot pi cdot r$
$pi$ – pi: число, равное 3,141592. или $approx frac<22><7>$, то есть отношение $frac<text<длины окружности>><text<диаметр>>$ любого окружности. 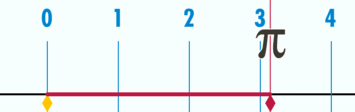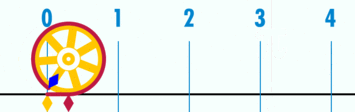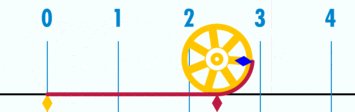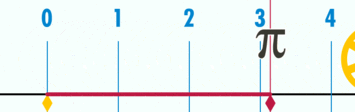
Дуга: изогнутая линия, которая является частью окружности. 
Дуги окружности измеряется в градусах или радианах.
Например: 90° или $frac<pi><2>$ – четверть круга,
180° или $pi$ – половина круга.
Сумма всех дуг окружности составляет 360° или $2pi$
Хорда: отрезок прямой, соединяющей две точки на окружности. 
Сектор: похож на часть пирога (клин). 
Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.
Формулы
Длина окружности $=pi cdot text <диаметр>= 2cdot pi cdot text<радиус>$
Площадь круга $= pi cdot$ радиус 2
Радиус обозначается как r , диаметр как d , длина окружности как P и площадь как S .
Площадь сектора круга
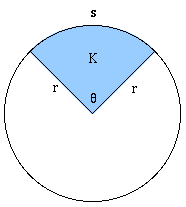
Площадь сектора круга K : (с центральным углом $theta$ и радиусом $r$).
Если угол $theta$ в градусах, тогда площадь = $frac<theta> <360>pi r^2$
Если угол $theta$ в радианах, тогда площадь, тогда площадь = $frac<theta> <2>r^2$
Центральный угол
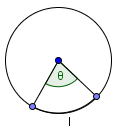
Если длина дуги составляет $theta$ градуов или радиан, то значение центрального угла также $theta$ (градусов или радиан).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах . ) вы можете найти значение её соответствующего центрального угла ($theta$) по формуле:
Вписанный угол
Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.
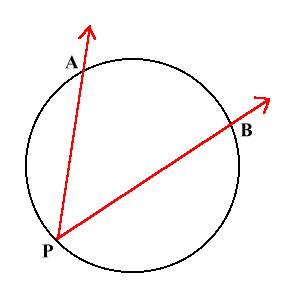
Пример:
$widehat = 84^circ$
$angle APB = frac<84> <2>= 42^circ$
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
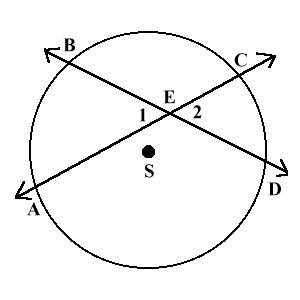
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $frac<1><2>(60^circ + 50^circ)=55^circ$
Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
$angle ABC =frac<1><2>(x – y)$
На рисунке дуга AB=80° и дуги CD=30°.
$angle ABC = frac<1><2>(80 – 30) = frac<1> <2>cdot 50 = 25^circ$
Хорды
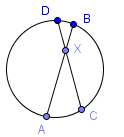
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
[spoiler title=”источники:”]
http://www.resolventa.ru/demo/diaggia6.htm
[/spoiler]







