Формулы как найти конечную скорость

Many formulae and equations in physics problems involve calculating an initial and final velocity. The difference between initial and final velocity in equations for conservation of momentum or equations of motion tell you the velocity of an object before and after something happens. This could be a force applied to the object, a collision or anything that could change its trajectory and motion.

The final velocity of an object is an instantaneous velocity at a certain time t at the end of an interval. It measures the final speed (with a directional component) after a given time.

To calculate final velocity for an object under uniform acceleration, you can use the corresponding equation of motion. These equations use combinations of distance, initial velocity, final velocity, acceleration and time to relate them to one another.

Final Velocity Formula

Determining changes in velocity relies on the acceleration of an object. Acceleration is the change in velocity over time. For example, the final velocity (v_f ) formula that uses initial velocity (‌v_i‌), acceleration (‌a‌) and time (‌t‌) is:

v_f = v_i + aDelta t

For a given initial velocity of an object, you can multiply the acceleration due to a force by the time the force is applied and add it to the initial velocity to get the final velocity. The “delta” Δ in front of the ‌t‌ means it’s a change in time that can be written as ‌t‌_f ‌− t‌_i.

This is ideal for a ball falling toward the ground due to gravity. In this example, the acceleration due to the force of gravity would be the gravitational acceleration constant ‌g‌ = 9.8 m/s². This acceleration constant tells you how fast any object accelerates when you drop it on Earth, no matter what the mass of the object is.

If you drop a ball from a given height and calculate how long it takes the ball to reach the ground, then you can determine the velocity just before it hits the ground as the final velocity. The initial velocity would be 0 if you dropped the ball without any external force. Using the equation above, you can determine the final velocity of the object ‌v_f‌.

Alternative Final Velocity Calculator Equations

You can always use the other kinematic equations for whichever situation you’re working with, as they are always logically and mathematically equivalent with one another. If you knew the distance an object traveled (Δ‌x‌), along with the initial velocity and time it took to travel that distance, you could calculate final velocity using the equation for final position after an elapsed time, based on the average velocity:

Delta x = bar{v} t = frac{1}{2}(v_f+v_i)t \ newline{} \ text{This can then be rearranged to solve for } v_f: \ newline{} \ v_f = frac{2Delta x}{t} – v_i

Make sure to use the correct units in these calculations.

A Rolling Cylinder

For a cylinder rolling down an inclined plane or a hill, you can calculate the final velocity using the formula for conservation of energy. This formula dictates that, if the cylinder starts from rest, the energy it has at its initial position should equal its energy after rolling down a certain distance.

At its initial position, the cylinder has no kinetic energy because it’s not moving. Instead, all of its energy is potential energy, meaning its energy can be written as:

E = mgh

with a mass ‌m‌, gravitational constant ‌g‌ = 9.8 m/s² and height ‌h‌. After the cylinder has rolled down a distance to a height of ‌h‌ = 0, its energy is only the sum of its translational kinetic energy and rotational kinetic energy. This gives you:

E = frac{1}{2}mv^2 + frac{1}{2}Iomega^2

for velocity ‌v‌, rotational inertia ‌I‌ and angular velocity “omega” ‌ω‌.

The rotational inertia ‌I‌ for a cylinder is ‌I‌ = ‌mr‌² / 2 and the angular velocity ‌ω‌ = v/r. By the law of conservation of energy, you can set the cylinder’s initial potential energy equal to the sum of the two kinetic energies. Solving for ‌v‌, we can find:

mgh = frac{1}{2}mv^2 + frac{1}{2}(frac{mr^2}{2})(frac{v^2}{r^2}) \ newline{} \ text{the mass and radius cancel leaving:} \ newline{} \ gh = frac{1}{2}v^2 + frac{1}{4}v^2 = frac{3}{4}v^2 \ newline{} \ text{solving for $v$, we get:} \ newline{} \ v = sqrt{frac{4}{3}gh}

This formula for the final velocity doesn’t depend on the weight or mass of the cylinder. If you knew the weight of the cylinder formula in kg (technically, the mass) for different cylindrical objects, you could compare different masses and find their final velocities are the same, because mass cancels out of the expression above.

Other Influences on Velocity

Anything that affects the acceleration of a moving object will affect the state of velocity (or constant acceleration). If a force is applied in the opposite direction of the velocity, then the acceleration is negative relative to the velocity, so the final velocity will be lower than the initial velocity.

A more complex scenario might be found with an object in free fall. If an object is falling under the force of gravity it will also experience the force of air resistance in the opposite direction. Eventually, in a complex relationship of velocities and forces, the object will actually reach a constant velocity known as the terminal velocity for a falling object.

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

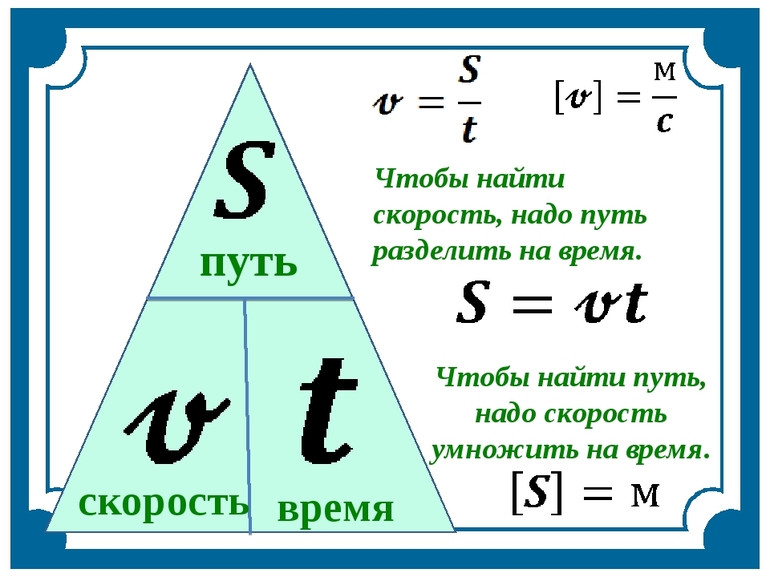
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

• S — расстояние (путь), пройденное материальной точкой или телом (м);
• T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

• неравномерную;
• среднюю;
• равномерно-переменную;
• поступательную;
• вращательную;
• ускоренную.

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

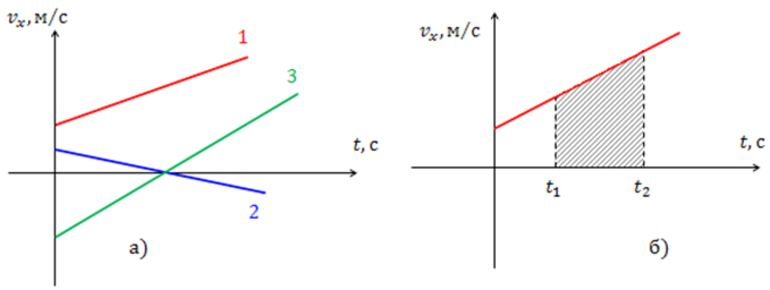
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

• V0 — начальная скорость;
• A — ускорение (имеет постоянное значение);
• t — время движения.

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r^-1(t). То есть, с математической точки зрения, это первая производная.

Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t²/2 = (V² — V²0) /2*A.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V²0 — 2* A * s)^½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)^½.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

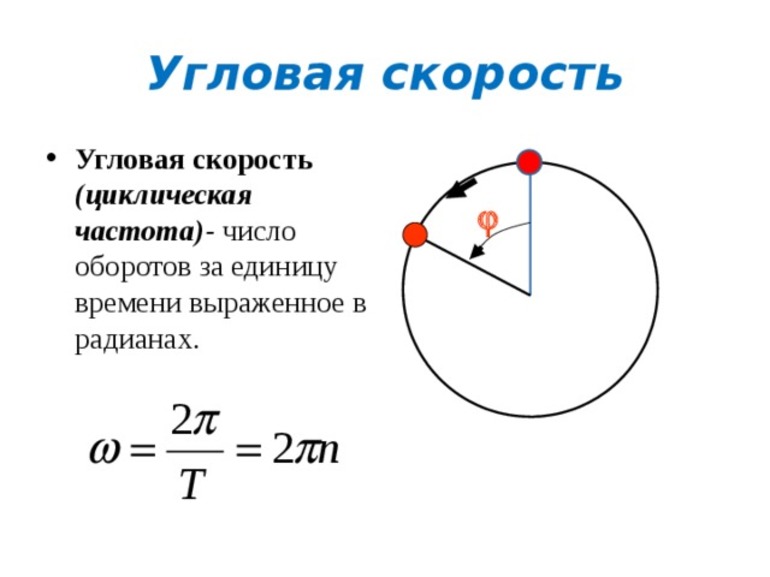
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

1. Справочный портал «Калькулятор».
2. Allcalc.
3. Fxyz.

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Второй закон Ньютона тут на фиг не нужен, потому что все тела, независимо от их массы, на высоте трёх метров нгаз землёй движутся с одним и тем же ускорением – g. Равным 9,81 м/с². То есть это задачка чисто кинематическая, а не на динамику.

Ну и учитывая уровень самой задачки, можно не заморачиваться “разложением скорости на составляющие”. Ясен пень, что направлена она по вертикали, причём совершенно по фигу, вверх или вниз, потому что даже если вверх, то потом при движении вниз ЭТУ точку тело пройдёт С ТОЙ ЖЕ скоростью. Поэтому ответ АлексаМ12, в котором приращение скорости рассматривается с точки зрения баланса энергий, по направлению мысли верный, но арифметически – с грубой ошибкой, потому что складвать скорости надо квадратично, а не “+ начальные 3 метра”.

Итак, будем считать, что скорость направлена вниз (раз по фигу куда). Тогда из закона сохранения энергии имеем gH+v_о²/2 = v_к²/2 (v_о – начальная скорость, v_к – конечная), откуда v_к = корень из (2gH+v_о²). И вся любовь.

Числа подставьте сами.

Разумеется, можно это решить и без привлечения закона сохранения энергии, а через квадратное уравнение S = gt²/2+v_ot, или же збавиться от времени, вспомнив, что v_о+gt = v_к, a S = 1/2 (v_о+v_к)t.