
При построении карты какой-либо площади изобразить реальные размеры достаточно сложно. Их уменьшают до необходимых размеров, сохраняя пропорции. Для этого применяется масштаб. Первое знакомство с этой категорией происходит в общеобразовательной школе, где на уроках учитель объясняет, что такое масштаб, какие существуют виды, как его правильно записывать и вычислять. Потом эти знания используются студентами колледжей, лицеев и вузов при выработке проектов, создании чертежей или в работе с географическими картами.
Содержание:
- Что такое масштаб
- Виды
- Где применяется масштаб
- В географии
- В математике
- В фотографии
- В черчении
- Как вычислить масштаб
Что такое масштаб
Термин «масштаб» пришел в русский язык из немецкого во времена петровского кораблестроения и означает «мерная палка». Это – отношение расстояния в существующих условиях к этому же отрезку на карте или плане. Эту научную категорию можно сравнить с проецированием. К примеру, в картографии, реальная местность проецируется на бумагу в виде карт.
Виды
Существует три вида отображения масштаба:
- Численный масштаб. Он записывается, как деление. Первая цифра – делитель. Она всегда представлена единицей, а вторая цифра, называемая в математической функции, делимым – число, показывающее, во сколько раз уменьшили размеры для изображения на карте. Например, 1:100 000 означает, что расстояния на плане местности уменьшены в 100 000 раз по сравнению с их реальной протяженностью. 1 см на карте – это 100 000 см или 1 км на местности. Чем меньше число в делителе, тем меньше увеличение объекта, и, следовательно, тем крупнее масштабируемая территория или объект. Увеличенное масштабирование допускается для относительно небольших объектов, и позволяет изобразить их крупными, а карту сделать более наглядной. Оно используется в составлении топографических карт для изображения небольших территорий, в проектировании строительных объектов, интерьерных или ландшафтных дизайнов.
- Именованный масштаб получил свое название потому, что он записывается словами и по сути расшифровывает значение первой записи. Именованный масштаб показывает, сколько метров или километров соответствует одному сантиметру на плане. Например, карта выполнена в масштабе: в 1 см – 300 м. Это означает, что расстояние 300 м на местности соответствует 1 см на карте.
| Масштаб | Как записывается |
| Численный | 1:10 000 |
| Именованный | В 1 см 10 000 см – 100 м |
- Графический масштаб. Этот вид масштабирования делится на два подвида: линейный и поперечный.
Линейный подтип изображается как линия, разделенная на равные отрезки. Эта часть называется основанием. Слева от нуля каждая часть делится на более мелкие отрезки для повышения точности измерений.
При чтении линейного масштаба используется пропорциональный циркуль. С его помощью измеряется на карте отрезок между нужными объектами, и переносится на линейный масштаб.
Второй вид графического масштаба – поперечный.

Он используется для составления более подробных топографических планов. Поперечный масштаб представляет собой сетку, в которой пересекаются горизонтальные, вертикальные и наклонные линии. При помощи циркуля определяют длину рек, горных хребтов и дорог.
Для более полного представления о размерах территории, изображенной на карте, на нее наносят все три варианта масштабирования.
| Вид | Как выглядит | Что показывает | Для чего применяется |
| Численный | В виде дроби | Величину | Для определения величины |
| Именованный | Слова | Во сколько раз уменьшены размеры | Для краткой записи |
| Линейный | Деления на отрезки | Расстояния на местности, соответствующие делениям | Для определения расстояния циркулем |
Масштаб карты указывается в ее углу, в легенде. Здесь под легендой подразумевается список используемых обозначений и их толкование.
Где применяется масштаб
Наибольшее распространение масштаб получил в таких сферах деятельности, как география, геодезия, картография. Он используется при составлении плана или карты местности, когда невозможно изобразить реальные размеры объектов. Масштабом пользуются также при изготовлении уменьшенных копий зданий (макетов), в проектировании.
Но масштабирование это не всегда означает уменьшение. К примеру, для изображения микромира необходимо, наоборот, увеличивать размеры для большей наглядности. Так увеличение применяется, чтобы показать, как устроен атом, живая клетка или как выглядят микроорганизмы. Масштабирование с целью увеличения записывается примерно так: 2:1; 5:1; 50:1; 100:1.
В географии
Впервые с понятием «масштаб» учащиеся сталкиваются на занятиях по географии, когда начинают знакомиться с картами.
В зависимости от изображаемых площадей все карты делятся на три вида:
- мелкомасштабные или обзорные (менее 1:1 000 000);
- среднемасштабные или обзорно-топографические (от 1:200 000 до 1:1 000 000);
- крупномасштабные или топографические (от 1:200 000 и более).
При составлении топографического плана используется масштаб до 1:5000.
В математике
На занятиях по математике учащиеся решают задачи по определению масштаба карты. Но перед этим учитель предлагает им вспомнить о том, что такое пропорции и отношения чисел. Эти знания пригодятся, так как масштаб представляет собой действие деления (или дробь), а его расчет выполняется через пропорцию.
Пример задачи 1: Расстояние между двумя населенными пунктами на карте равняется 6 см. Необходимо вычислить это расстояние на местности при условии, что масштаб равен 1:10 000.
Для решения составляется пропорция:
| На карте | На местности | |
| Масштаб, см | 1 | 10 000 |
| Расстояние, см | 6 | Х |
Х = 6 × 10 000 = 60 000 см = 600 м.
Ответ: 600 м.
Пример задачи 2: Расстояние между пунктом А и пунктом В составляет 600 км. Какой масштаб необходимо применить, чтобы на карте это расстояние равнялось 15 см?
Для начала переводим расстояние в см: 600 км = 60000000 см.
60000000 : 15 = 4000000
Ответ: масштаб 1:4000000.
В фотографии
Фотографы понимают под этим понятием отношение линейных размеров объекта к размерам его проекции на фотопленке или матрице. В фотосъемке используется широкий диапазон масштабов: от самых крупных до самых мелких.
Макрофотография – это съемка в размере 1 к 1 и крупнее. Но вследствие появления компактных цифровых фотоаппаратов, а также по причине совершенствования камер мобильных телефонов этот термин стал применяться по отношению к съемке объектов, расположенных на расстоянии менее 50 см от объектива.
Важную роль масштаб играет в композиции фотоизображения. Эта категория способна приукрасить произведение искусства, или, напротив, сделать его тяжелым для восприятия. Его необходимо правильно подобрать, избежать ошибок, и тогда сохранится целостность композиции и задумка автора.
Масштабность основывается на сравнении реальных размеров объекта с нашими представлениями о его величине. Например, велосипед, стоящий на дороге среди машин, кажется маленьким. Но если занести его в квартиру, то он будет восприниматься как большой объект.
В черчении
При проектировании и работе с чертежами применяются масштабы, утвержденные ГОСТом. В этой области выделяют 5 видов этой масштабирования:
- Натуральный (1:1). Он удобен в использовании и позволяет легко сориентироваться в размерах.
- Масштаб уменьшения (1:2, 1:25, 1:100 и др.). Применяется в тех случаях, когда необходимо изобразить большую деталь или производственный станок.
- Особый масштаб уменьшения. Он используется при проектировании крупных объектов (небоскребов, мостов). Такой тип масштаба вычисляют по формуле: 1:10n, 1:(2×10n), где n – целое число.
- Масштаб увеличения (2:1, 4:1, 10:1 и др.). Используется для наглядного изображения мелких деталей.
- Особый масштаб увеличения. Вычисляется по обратной формуле: (10× n):1, где n также является целым числом. Применяется для деталей самого маленького и даже микроскопического размера.
Эта величина обязательно прописывается на каждом чертеже в отведенном для этого разделе основной надписи. Если на одном листе изображены чертежи, выполненные в разных масштабах, то значение прописывается отдельно под каждым. Даже если проект выполняется в естественную величину, то есть 1 к 1, то масштаб все равно на чертеже должен быть указан.
Как вычислить масштаб
Масштаб выбирается в зависимости от конечной цели: составление плана местности или чертеж детали. В первом случае применяется уменьшающий масштаб, а во втором он может быть увеличивающим. При этом важно, чтобы карта или чертеж получился наглядным и подробным. В работе с масштабом и при решении задач используются пропорции.
Пример задачи: Первая карта выполнена в масштабе 1:20 000. Длина отрезка между двумя точками на ней составляет 4,8 см. На второй карте это же расстояние равняется 9,6 см. Рассчитайте масштаб второй карты.
Составляем пропорцию.
| На карте | На местности | |
| Масштаб, см | 1 | 20 000 |
| Расстояние, см | 4,8 | Х |
Х = 4,8 × 20 000 = 96 000 см = 960 м – это расстояние между точками на местности.
Чтобы вычислить масштаб второй карты необходимо 96 000 см : 9,6 см = 10 000 см.
Ответ: вторая карта выполнена в масштабе 1:10 000.
Узкие специалисты, работающие с географическими изображениями территорий, проектами и чертежами, должны уметь правильно вычислять масштаб без помощи калькулятора. Для остальных людей существуют специальные онлайн-калькуляторы, которые сделают это за них.
С понятием «масштаб» человек сталкивается во время путешествия или поиска на карте определенного места, заведения. Эта величина используется во многих сферах деятельности: проектировании, фотосъемке, моделировании. Поэтому каждому необходимо иметь представление о масштабе, понимать, что он показывает и каких видов бывает.
Как рассчитать масштаб пример?
Чтобы определить масштаб, нужно узнать, во сколько раз расстояние на карте меньше, чем на местности. Для этого нужно расстояние на местности привести к тем же единицам, что и на плане: 20 м = 20*100 см=2000 см.
Что такое масштаб и как его определить?
В математике масштаб определяется как отношение расстояния на карте к соответствующему расстоянию на реальной местности. Масштаб 1:100000 означает, что 1 см на карте соответствует 100000 см = 1000 м = 1 км на местности.
Как найти масштаб 4 класс?
Необходимо найти длину отрезка на местности. Обозначим длину отрезка на местности через Х и найдем отношение длины отрезка на карте к длине отрезка на местности, которое и будет равно масштабу карты.
Как понять масштаб 1 к 10000?
1:10000 = в один см вмещается 10 000 см или же сто метров.
Как рассчитать масштаб 6 класс?
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности. Рассмотрим пример: Длина отрезка на карте равна 8 см. Ответ: 800 м.
Как перевести в масштаб?
Численный масштаб можно перевести в именованный и наоборот. Например, в 1 см — 1 м; если мы хотим перевести именованный масштаб в численный, то мы должны перевести метры в сантиметры. Помним, что в одном метре 100 сантиметров, добавим два нуля и получим численный масштаб — 1 : 100.
Что такое масштаб 1 к 50?
Численный масштаб 1: 50 000 надо понимать так: одному см на плане или карте соответствует 50 000 см на местности. При переводе в именованный получаем следующий масштаб: В 1 см 500 м, или в 1 см 0,5 км. Масштаб помогает определять расстояния по планам и картам.
Как понять масштаб 1 к 1000?
Масштаб 1:1000 означает, что в 1 сантиметре на карте помещается 1000 сантиметров. Читается такой масштаб так: в одном сантиметре тысяча сантиметров. Переведём сантиметры в метры, и получим: в 1 см. 10 м.
Как научиться определять масштаб?
Масштаб — это отношение двух чисел, например 1 : 1000 или 1 : 100000. Отношение показывает, во сколько раз одно число больше другого. Масштаб 1 : 1000 означает, что изображение меньше изображаемого объекта в тысячу раз, а масштаб 1 : 100000 — в сто тысяч раз. Чем меньше число в правой части, тем крупнее масштаб.
Как быстро определить масштаб?
В этом случае надо измерить по карте линейкой расстояние в сантиметрах от одного населенного пункта до другого и подписанное количество километров разделить на расстояние в сантиметрах. Полученное число будет означать величину масштаба карты (число километров в одном сантиметре).
Как определить масштаб карты формула?
В этом случае надо измерить по карте линейкой расстояние в сантиметрах от одного населенного пункта до другого и подписанное количество километров разделить на расстояние в сантиметрах. Полученное число будет означать величину масштаба карты (число километров в одном сантиметре).
Сколько метров в 1 см в 500 масштабе?
Численный масштаб 1:500 означает, что один сантиметр на карте соответствует 500 сантиметрам в реальности. 500 сантиметров – это 5 метров (так как в 1 метре укладывается 100 сантиметров). Если записать этот масштаб в численном виде, то он будет выглядеть так: в 1 см. 5 м.
Как перевести числовой масштаб в именованный?
Чтобы перевести численный масштаб в именованный – убери 2 последние цифры, получатся метры. Например, 1:1000, в 1 см – 10 м местности.
Какие применяются масштабы чертежей?
уменьшения: 1:2; 1 : 2,5; 1:4; 1:5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000; увеличения: 2:1; 2,5: 1; 4:1; 5:1; 10 : I; 20 : 1; 40 : 1; 50 : 1; 100 : 1; натуральная величина 1:1.
Как определить масштаб формула?
Формулу для вычисления масштабов можно выразить следующим образом: М = l L = 1 m . Читаются численные масштабы так: в одной единице длины на пла- не, карте содержится m таких же единиц на местности.
Что значит в масштабе 1 к 100?
Масштаб 1:100 читается так – в одном сантиметре 100 сантиметров. Мы знаем, что 100 сантиметров равно одному метру. Таким образом, масштаб 1:100 означает, что 1 сантиметр на карте равен 1 метру на местности. Масштаб 1:1000 читается так: в одном сантиметре 1000 сантиметров, или в 1 сантиметре 10 метров.
Какой из масштабов является стандартным?
Масштабы (ЕСКД ГОСТ 2.302-68)
| Масштабы уменьшения | 1:2, 1:2,5; 1:4, 1:5, 1:10, 1:15, 1:20, 1:25, 1:40, 1:50, 1:75, 1:100, 1:200, 1:400, 1:500, 1:800, 1:1000 |
|---|---|
| Натуральная величина | 1:1 |
| Масштабы увеличения | 2:1, 2,5:1, 4:1, 5:1, 10:1, 20:1, 40:1, 50:1, 100:1 |
Определение расстояний и превышений по бумажной карте.
Определение расстояния.
Для определения горизонтального расстояния по обычной карте, следует измерить длину линии и пересчитать пропорционально масштабу. Прямую линию можно измерить линейкой или циркулем-измерителем, извилистую (например, при измерении длины дороги или реки) – курвиметром (прибором, который можно катать по карте, а “колесико” отчитывает сантиметры).
Пересчет измеренной длины ведется пропорционально масштабу:
например, измеренное расстояние 2,5 см, а масштаб карты 1:50000 (т.е. в 1 см – 500 метров), тогда
1 см = 500 м
2,5 см = x м
x = (2,5 см * 500 м) / 1 см = 1250 м (по свойству пропорции).
При определении расстояний по мелкомасштабной карте также можно опираться на следующие сведения:
длина дуги 1° экватора
≈ 111,3 км (длина экватора 40 075 км/ 360°);
длина дуги 1° параллели 15° ≈ 108 км, 30° ≈ 96 км, 45° ≈ 79 км, 60° ≈ 56 км, 75° ≈ 29 км
(длина дуги 1° экватора (111,3 км) * cos (угла широты параллели));
длина дуги 1° меридиана ≈ 111,1 км ≈ 111 км (длина меридиана 20 004 км/ 180°).
Определение превышений.
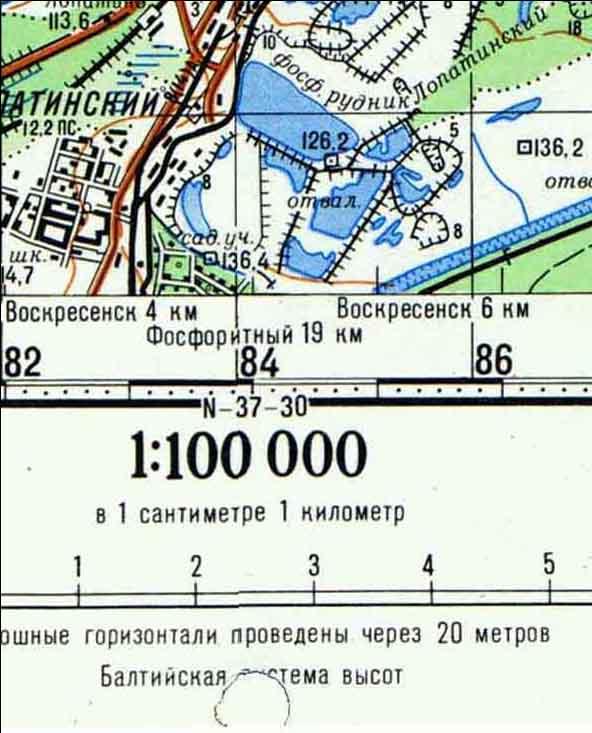
Превышения на топографической карте показывают горизонтали. Горизонтали – это изолинии, которые соединяют одинаковые уровни высот. Под масштабом указано через сколько метров проведены сплошные горизонтали (например, через каждые 10 метров, т.е. на уровнях 10м, 20м, 30 м и т.д.), пунктиром могут быть проведены полугоризонтали между основными (где необходимо подчеркнуть характер рельефа), каждая пятая горизонталь для улучшения восприятия утолщена, пики высот подписаны дополнительно. Подписи горизонталей принято размещать верхом текста в сторону повышения высот, а в сторону понижения склона размещаются черточки, прикреплённые перпендикулярно горизонталям – бергштрихи, указывающие куда со склона потечет вода.

На примере пунктирной линии превышение между ее концами примерно 73 метра. Правый край чуть выше 210 м (≈212 м), левый чуть ниже 140 м (≈139 м).
При построении профиля следует учесть, что чем ближе (чаще) расположены горизонтали друг к другу, тем круче спуск.
На мелкомасштабных физических картах вместо горизонталей используют цветовую высотную шкалу – зелеными тонами низины, коричневыми – горы.
Определение длины линии в трехмерном пространстве.
Если расстояние по горизонтали между точками 400 метров, а разница высот между этими точками 300 метров, то длина линии в трехмерном пространстве между точками будет составлять 500 метров (подсчёт аналогичен вычислению гипотенузы по теореме Пифагора).
Вести пересчёт имеет смысл только при построении маршрута в горном рельефе с резкими перепадами высот. При достаточно плоском равнинном рельефе или при измерениях по мелкомасштабным картам длина линии в трехмерном пространстве практически не будет отличаться от горизонтального расстояния, учитывать перепад высот в таких случаях не имеет смысла.
На заданиях ОГЭ/ЕГЭ и в школьных задачах под определением расстояния по прямой подразумевается расстояние по горизонтали, учитывать, что точки могут находиться на разных высотах и пересчитывать длину линии с учетом этого не нужно!Определение расстояний и превышений по электронной карте.
Большинство электронных карт имеют инструменты для измерения расстояний по прямой или по дорогам специальным функционалом, например, построением маршрута. При построении маршрута большинство электронных карт (например, Яндекс-карты) учитывают все изгибы дороги, но не пересчитывают расстояния с учетом перепада высот (к примеру, перейти через ущелье по подвесному мосту, или по кратчайшей прямой траектории, но без моста, спустившись вниз и затем поднявшись на другой берег – это разные расстояния). Некоторые приложения навигации (например Maps.me при переходе в режим пешеходной или велонавигации) просчитывают расстояния с учётом перепада высот и отображают превышения.
Vint
Гуру
(4417)
13 лет назад
Масштабом называется отношение длины линии на плане или карте к соответствующей проекции этой линии на местности.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м) , 0,1 мм — 100 см (1 м) .
цой оксана
Знаток
(392)
7 лет назад
Масштабом обзывается отношение длины линии на плане или карте к соответствующей проекции этой линии на местности Например, масштаб 1:100 показывает, что 1 см на плане соответствует 100 см на местности
Дон Кихот
Знаток
(382)
6 лет назад
Если касается предмета или вещи, модели и т.. д. то смело делим размер прототипа на требуемый масштаб,
например:
Фактические габариты Тяжёлого Танка Panzerkampfwagen VIII “Maus”
Длина 9030 мм
длина с пушкой 10200 мм
ширина 3670 мм
высота 3660 мм
В масштабе 1:38 размер модели будет составлять:
Длина 237 мм или 23 см 7 мм
длина с пушкой 268 мм или 26см 8 мм
ширина 96 мм или 9 см 6 мм
высота 96 мм или 9 см 6 мм
Ульяна Румак
Профи
(867)
4 года назад
Очень просто! Если, допустим, у вас стена идёт 3 метра в длину, то сначала надо метры перевести в сантиметры (!) Получается 300 см. Далее зависит от того, какого вам нужно масштаба. Если 1:20, то мы это число 300 см (длина стены в сантиметрах в натуральную величину) разделить на 20 (Если масштаб 1:15, то делить на 15 и т. д.). Вот мы разделили 300 на 20, и у нас получилось 15. Это длина стены в сантиметрах, которая должна быть в чертеже или на макете. Всё)
Лера БрылуноваЗнаток (389)
3 года назад
а вот смотрите мне нужен масштаб снимка.. радиус спутника равен 1820 км а на снимке диаметр равен 15см ..цифры получаются нереальные
План урока:
Отношение двух чисел
Определение пропорции
Масштаб
Отношение двух чисел
На уроке математики ребята выполняли самостоятельную работу. На решение самостоятельных заданий Наталья Ивановна выделила 15 минут, после чего попросила сдать тетради на проверку. Подумайте, какую часть урока заняла самостоятельная работа?

Чтобы дать ответ на данное задание, давайте вспомним, какую продолжительность имеет обычный урок? Всем известно, что стандартный урок длится 45 минут. Получается, из 45 минут только 15 дети решали самостоятельную работу. Следовательно, нужно выяснить, какая часть целого урока потрачена на самостоятельную работу. В арифметике для вычисления части от числа или определения во сколько раз одно число больше другого существует специальное понятие «Отношение чисел»:

Исходя из рассмотренного определения, необходимо составить отношение длительности самостоятельной работы к длительности целого урока. Таким образом, ответим на главный вопрос задачи. Запишем отношение (частное) двух чисел:
15/45 – данную дробь можно сократить, разделив числитель и знаменатель на 15.
15/45 = 1/3.
Выходит, что на самостоятельную работу класс потратил 1/3 всего урока.
Важно помнить, что числовое значение отношения чисел останется прежним, если каждый компонент отношения умножить или разделить на одно и то же число.
Например:
Давайте, составляющие отношения 6/7 умножим на 2, то есть на дробь 2/2.
6/7 × 2/2 (числитель умножаем на числитель, знаменатель на знаменатель);
Получаем:
6×2/7×2 = 12/14 – при сокращении на 2, получим исходную дробь.
Следовательно, числовое значение дроби не изменилось – 6/7 = 12/14.
При составлении отношений с использованием различных чисел и величин, важно помнить, что отношение будет верным, если все компоненты отношения выражены в одинаковых единицах измерения.
Разберем на примере.
В вазочке находился один килограмм конфет. Бабушка отсыпала 300 граммов сладостей в пакет. Определите, какую часть всех конфет отсыпала бабушка?

Чтобы ответить на главный вопрос задачи нужно составить отношение массы отсыпанных конфет к общей массе сладостей: 300 граммов/1 килограмм. Сразу определить числовое значение отношения не можем, составляющие имеют разные единицы измерения массы – грамм и килограмм. Выразим один килограмм в граммах:
1кг = 1000 грамм
Теперь определим, какую часть составили отсыпанные сладости:

Бабушка отсыпала 3/10 всех сладостей в пакет.
Запомни!
Если a и b числовые значения или значения, выраженные в одной и той же величине, тогда:
- отношение a/b, будет равно частному a и b;
- при условии, что a>b, отношение a/b говорит, во сколько раз a больше, чем b;
- при условии, что a<b, отношение a/b говорит, какую часть a составляет от b.
Определение пропорции
Руководитель детского хореографического кружка, для пошива костюмов своим воспитанникам, приобрел в магазине тканей 10 метров шелка, на сумму 420 рублей. Но купленной ткани не хватило. Какую сумму нужно потратить, чтобы купить еще 5 метров такого же материала?

Данную задачу можно решить двумя способами. Рассмотрим каждый из них подробно.
1 способ.
По условию нам известно, что 10 метров материала, стоит 420 рублей. Отсюда можно узнать цену одного метра. Для этого, общую сумму(420) необходимо разделить на количество приобретенной ткани(10):
420 : 10 = 42 рубля стоит один метр ткани.
Зная цену одного метра ткани, можно узнать стоимость пяти метров. Для этого стоимость одного метра (42), умножаем на количество таких метров (5):
42 × 5 = 210 рублей необходимо, для покупки 5 метров материала.
Этот способ известен еще из начальной школы. Но далеко не все задачи такого вида можно решить первым способом.
В этом случае используют второй способ решения задач такого вида.
2 способ.
Вначале, запишем краткое условие.
10м. – 420 р.
5м. – ? р.
Теперь нужно подумать. В нашем случае, количество материала уменьшается, следовательно,уменьшается стоимость покупки. Обозначим цену пяти метров материала – х.
Имеем,
10 – 420.
5 – х.
Для решения задач такого вида в математике существует специальное определение – «Пропорция»

Используя рассмотренное определение, подумаем, как составить пропорцию из чисел? Формировать пропорцию будем, опираясь на краткую запись условия задачи – десять относится к пяти как четыреста двадцать к иксу:
10/5 = 420/х.
Пропорция составлена и возникает вопрос, как вычислить неизвестный компонент?
Для вычисления неизвестной составляющей пропорции существует правило, которое называется «Основное свойство пропорции»:

Определим крайние и средние члены в составленном равенстве:
Крайними членами пропорции будут числа 10, х.
Средними членами пропорции будут числа 5, 420.
Запишем равенство произведений крайних и средних членов в составленной пропорции:
10/5 = 420/х;
10х = 5 × 420 – высчитываем произведение;
10х = 2100 – решаем как обычное уравнение;
х = 2100 : 10;
х = 210.
Выходит, 210 рублей необходимо для приобретения пяти метров материала.
Вот так на примере решения задачи мы разобрали новое определение. Запомните, пожалуйста, все правила и поиск неизвестного компонента в любых отношениях и пропорциях будет для вас только развлечением!
Продолжаем дальше знакомиться с пропорцией.
Прямая и обратная пропорциональная зависимость.
Рассмотрим ситуацию, в которой оказывается каждый, попадая в магазин.

Витя пришел в магазин за покупками. В кошельке ребенка лежало 300 рублей. Витя купил хлеб, молоко, масло, заплатил за товар. Денег у мальчика стало меньше. После посещения кондитерского отдела, где он купил карамель, пирожные, рулет денег стало совсем мало. Делаем вывод: чем больше покупок делает мальчик, тем меньше денег у него остается.

Значит, количество денег в нашем кошельке и количество покупок имеют обратно пропорциональную зависимость и являются обратно пропорциональными величинами.
А если взять ситуацию с оплатой за пользование водой и электроэнергией

Чем больше воды/электроэнергии мы используем, тем больше должны заплатить. В таком случае величины кубы воды/киловатты электроэнергии и денежные единицы называются прямо пропорциональными и имеют прямую пропорциональную зависимость.

Масштаб
Мама с Арсением решили нарисовать путь, который проходит мальчик, идя из дома в школу. Ребенок заволновался: «Как можно на листке бумаги нарисовать 450 метров пути?». Мама успокоила сына и рассказала, что именно для таких случаев и используется определение масштаба карты.

Рассмотрим решение задачи с использованием масштаба.
Расстояние на карте от Москвы до Киева составляет пять сантиметров. Вычислите, сколько километров от Москвы до Киева, если масштаб карты 1:15 000 000.

В первую очередь, нужно понимать, что масштаб 1:15 000 000 показывает, что 1 см карты содержит 15 000 000 сантиметров или 150 километров на местности.
Чтобы ответить на главный вопрос задачи,составим пропорцию. Для этого, расстояние на местности от Москвы до Киева примем за х:
1 : 150 = 5 : х.
Помним, произведение крайних членов пропорции равно произведению средних. Имеем:
х= 150 × 5;
х = 750.
Выходит, 750 километров – расстояние от Москвы до Киева.
Расчеты оказались верными. Вся справочная литература говорит о том, что расстояние Москва – Киев составляет примерно 755 км!
Теперь вы совершенно самостоятельно можете рассчитать абсолютно любое расстояние, имея под рукой линейку и карту!
Интересно!
С пропорциями мы сталкиваемся, ежедневно, ежеминутно. Все в нашем мире пропорционально. Любая вещь, предмет, техника, животные, растения – все имеет свои пропорции! Мы можем любоваться красивой архитектурой – благодаря пропорциям, наслаждаться цветками роз или ромашек – тоже не без участия пропорций. Природа создает все в строгой пропорциональности. В случае, когда пропорции отсутствуют, вещь или предмет нам кажутся неправильными. Ведь даже в нашем теле все имеет свои пропорции:
- длина ладони равна длине четырех пальцев, длина четырех ладошек(без учета пальцев) равна длине стопы, шесть ладоней – длина локтя, а четыре локтя в точности укажут на рост хозяина;
- длина человеческой ладони с пальцами составляет 1/10 роста человека;
- длина расставленных в стороны рук совпадает с длиной человеческого тела;
- стопа составляет 1/7 часть роста;
- длина от корней волос до кончика подбородка равна 1/10 роста.
