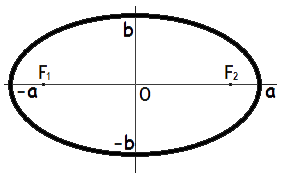1. Формула площади равнобедренной трапеции через стороны и угол
b – верхнее основание
a – нижнее основание
c – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m – средняя линия трапеции
c – боковая сторона
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b – верхнее основание
a – нижнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Содержание
- – Как найти длину и ширину периметра если известна площадь?
- – Как определить длину и ширину?
- – Как считается 1 квадратный метр?
- – Как найти площадь прямоугольника если известна длина и ширина?
- – Какая длина у прямоугольника?
- – Как найти длины сторон прямоугольника если известна площадь?
- – Как узнать длину периметра?
- – Как найти площадь стен по площади пола?
- – Как рассчитать размеры по площади?
- – Как определить размер комнаты по площади?
Как найти длину и ширину периметра если известна площадь?
P = 2 * (a + S : a), где a — сторона, S — площадь.
Как определить длину и ширину?
Длина всегда представляет собой направление наибольшего размера. Ширина – это протяженность между двумя точками плоскости, которые лежат, в отличие от длины, на наименьшем расстоянии друг от друга. То есть, длина – это наибольший размер предмета, а ширина – наименьшей.
Как считается 1 квадратный метр?
Чтобы узнать число квадратных метров, нужно умножить длину на высоту стены. Для пола – длину на ширину.
- Пример: ширина стены 3,6 м, высота – 2,9 м.
- Площадь такой стены будет 3,6 х 2,9 = 10,44 м2.
Как найти площадь прямоугольника если известна длина и ширина?
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина.
Какая длина у прямоугольника?
Длиной прямоугольника называют длину более длинной пары его сторон, а шириной — длину более короткой пары сторон. Величина площади прямоугольника равна произведению ширины прямоугольника на его длину. Периметр прямоугольника равен удвоенной сумме длин его ширины и длины.
Как найти длины сторон прямоугольника если известна площадь?
Площадь прямоугольника равна произведению его длины на ширину. У числа 65 есть 4 целых делителя: 1, 5, 13, 65. В этой задаче, думаю, нас интересуют только 5 и 13. Получаем, что длины сторон прямоугольника: 5 см и 13 см, периметр (5 +13) * 2 = 36 см.
Как узнать длину периметра?
Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно. P = 2 * (a + b), где a — ширина, b — высота.
Как найти площадь стен по площади пола?
Подставив длину, ширину и высоту комнаты в форму расчёта мы получим следующие значения: для комнаты 4*3*3 площадь стен составит 42 кв. метра; для комнаты 6*2*3 площадь стен будет равна 48 кв.
Как рассчитать размеры по площади?
В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.
Как определить размер комнаты по площади?
Формула расчета простая, S = a*b, где S – площадь, а и b – соответственно, длина и ширина комнаты. В нашем примере (рисунка с обмерами) вместо маленьких букв длина – А и ширина – Б., и противоположенных стен – Г и В.
Интересные материалы:
Сколько тонн в 1м3 опилок?
Сколько тонн в м3 бетона?
Сколько тонн в одном кубическом метре чернозема?
Сколько травы на квадратный метр?
Сколько травы съедает овца в день?
Сколько цемент застывает?
Сколько цемента добавлять в ПГС?
Сколько цемента надо на отмостку?
Сколько цемента в одном кубе керамзитобетона?
Сколько цветет Ито Пион?
Прямоугольник и тригонометрические функции
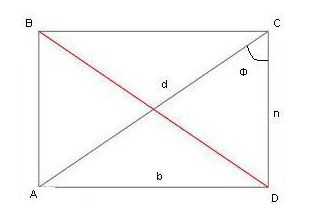
Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.
Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.
Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.
Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.
√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.
Периметр равен 2(17,3+10)=2*27,3=54,6 см.
Основные понятия
Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.
Рассмотрим пример:по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Рис. 1. Земельный участок формой прямоугольника.
Земельный участок имеет стороны длиной 2 м, 4 м, 2 м, 4 м. Поэтому чтобы узнать общую длину забора необходимо сложить длины всех его сторон:
2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.
Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют латинскую букву P.
Для вычисления периметра произвольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.
Периметр прямоугольника измеряется в различных единицах длины: мм, см, м, км и так далее. При необходимости, данные в задании, переводят в одинаковые единицы измерения.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, слово «периметр» пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или « измерять вокру г». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
О периметре квадрата.
- Формула периметра квадрата
- Как найти периметр квадрата. если известна сторона!?
- Как найти периметр квадрата. если известна площадь!?
Что такое периметр квадрата
Слово периметр пришло из древности и например древние-греческом обозначала окружность(περίμετρον).
Или если совсем по простому — периметр квадрата это — сумма всех границ.
Периметр квадрата это сумма всех сторон квадрата, поскольку их 4 одинаковых, то одну сторону, надо умножить на 4.
Формула периметра квадрата — периметр квадрата равен стороне умноженной на 4 -> P=4a
Где P — периметр квадрата,
a — длина одной из сторон.
Как мы уже говорили выше у нас есть формула нахождения периметра :
найдите периметр квадрата, если сторона квадрата равна 12 см.
Сторона квадрата это а, она равна 12см.
Подставляем 12 в формулу вместо буквы «а».
P = 4a -> P = 4 * 12-> P = 48см.
Если сторона квадрата равна 12 см, то периметр квадрата равен 48см.
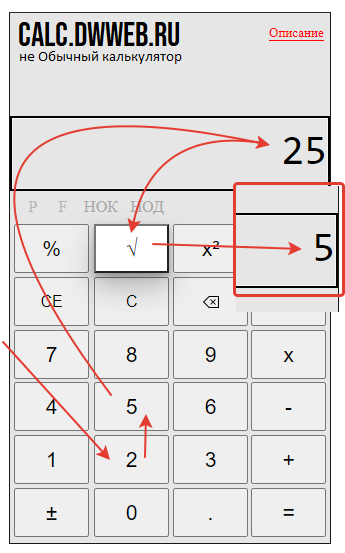
найдите периметр квадрата, если площадь квадрата равна 25см².
Опять вспоминаем формулу площади квадрата :
Из этой формулы нам требуется вывести сторону :
Далее берем формулу периметра квадрата и заменяем сторону на корень квадратный.
Извлекаем корень из 25 на калькуляторе
После этого умножаем на 4 :
Если площадь квадрата 25см², то периметр будет равен 20см.
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
Первый способ вычисления периметра квадрата
Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
где: P — периметр квадрата a — длина стороны квадрата
Второй способ вычисления периметра квадрата
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
где: P — периметр квадрата a — длина стороны квадрата d — длина диагонали квадрата
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
- Математика
- Информатика
- Финансы
- Жизнь
- Здоровье
- Работа с текстом
- Работа с цветом
- Конвертеры
- Графики
- Алгебра
- Геометрия
- Тригонометрия
- Физика
- Химия
- Литература
- Информатика
- Астрономия
- Законы
- Единицы измерений
- Таблицы
- Инструкции
- Знаменитые химики
- Знаменитые физики
- Знаменитые математики
- Знаменитые биологи
- Знаменитые психологи
- Знаменитые философы
- ЕГЭ
- Гаджеты
- Разное
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX. Поэтому для корректного отображения формул и выражений пожалуйста дождитесь полной загрузки страницы.
- Пользовательское соглашение
- Cookie
- О сайте
2021 Все калькуляторы online
Копирование материалов запрещено
Используя этот онлайн калькулятор, вы сможете найти периметр квадрата.
Воспользовавшись онлайн калькулятором для вычисления периметра квадрата, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
квадрата:
Периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Как найти периметр прямоугольника
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны .
Периметр в математике обозначается латинской буквой «Р» . И соответственно формула выглядит так:
С учетом равенства сторон, формулы можно существенно упростить :
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника
Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом , который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
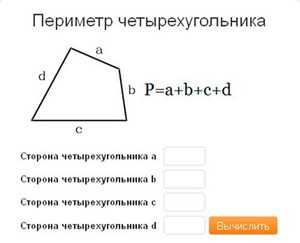
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона. Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет
Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Периметр круга (длина окружности)
Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:
L = 2πr
L= 2πd
L – длина окружности
π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.
π = 3.141 592 653 589 793 238 462 643 383 279 502
Для удобства вычислений обычно используют значение 3.14
R – это радиус окружности
D – Диаметр окружности
Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то
Например, перед нами круг с радиусом 3 см. Найдем его периметр.
L= 2*3,14*3
L=6π
L=6*3.14
L = 18.84 см
Pк= 18,84 см
Ответ: 18.84 см
Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Математика – 3 класс. Прямоугольники
Что такое прямоугольник и квадрат
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2. Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Определим PABCD.
Пример:
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см. Решение:
Нарисуем прямоугольник ABCD с исходными данными.
PABCD = 2 * (AB + BС)
Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
PABCD= 4 * AB
Пример:
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата. Решение:
Нарисуем квадрат ABCD с исходными данными.
PABCD = 4 * AB
Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.
Задачи на нахождение периметра прямоугольника
Измерь ширину и длину прямоугольников. Определи их периметр.
Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника. 3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора. 2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев. Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.). В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
- S AKMO = AK * KM
- S AKMO= AK * KM = 7 см * 2 см = 14 см2.
Пример:
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
Ответ: 14 см2.
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя. Пример:
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
- S AВСО = AB * BC = AB * AB
- S AKMО = AK * KM = 8 см * 8 см = 64 см2
Пример:
Определи площадь квадрата AKMO со стороной 8 см.
Ответ: 64 см2.
Задачи на нахождение площади прямоугольника и квадрата:
- Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
- Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Источник: https://mathematics-tests.com/matematika-3-klass-urok-perimetr-ploshad-pryamougolnika
Что такое периметр и площадь
Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».
Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).
Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.
Периметр и площадь квадрата
Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:
- P= a*4
- P= a+a+a+a
Например, перед нами квадрат со стороной 10 см:
- P= 10*4
- P=40
Ответ: 40 см
- P= 10+10+10+10
- P=40
Ответ: 40 см
Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.
Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:
- S= a*a
- S=a2
S – это площадь, а – сторона квадрата.
Например, в задаче указано, что длина стороны квадрата составляет 10см.
- S=10*10
- S= 100см2
Ответ: 100см2
Периметр и площадь прямоугольника
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:
- P= (a+b)*2
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два. Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см:
- P= (6+2) * 2
- P= 16
Ответ: 16 см
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
- S= a*b
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа:
- S= 5*2
- S=10см2
Ответ: 10 см2
Периметр круга (длина окружности)
Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:
- L = 2πr
- L= 2πd
L – длина окружности
π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.
π = 3.141 592 653 589 793 238 462 643 383 279 502
Для удобства вычислений обычно используют значение 3.14
R – это радиус окружности
D – Диаметр окружности
Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то
Например, перед нами круг с радиусом 3 см. Найдем его периметр:
- L= 2*3,14*3
- L=6π
- L=6*3.14
- L = 18.84 см
- Pк= 18,84 см
Ответ: 18.84 см
Отличие периметра от площади
Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ. Площадь всегда измеряется в квадратных единицах (см2, м2, мм2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.
Источник: https://topkin.ru/voprosy/nauka-voprosy/chto-takoe-perimetr-i-ploshhad/
Площадь прямоугольника
Площадь прямоугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.
Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.
Площадь прямоугольника через две стороны
a — сторона
b — сторона
a (или b) — сторона
P — периметр
a (или b) — сторона
d — диагональ
d — диагональ
α° — угол между диагоналями
a (или b) — сторона
R — радиус описанной окружности
a (или b) — сторона
D — диаметр описанной окружности
Прямоугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Источник: https://doza.pro/art/math/geometry/area-rectangle