Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
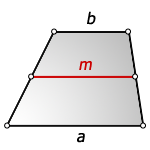
b – верхнее основание
a – нижнее основание
m– средняя линия
Формула средней линии, (m ):
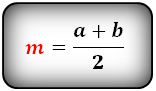
2. Формулы средней линии через основание, высоту и углы при нижнем основании
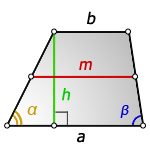
b – верхнее основание
a – нижнее основание
α, β – углы трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m):
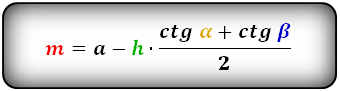
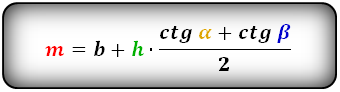
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
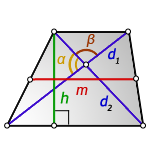
α, β – углы между диагоналями
d1 , d2 – диагонали трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
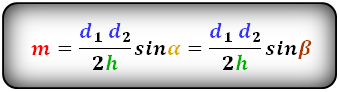
4. Формула средней линии трапеции через площадь и высоту
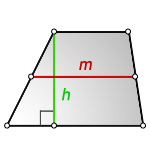
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m):
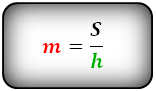
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 24 сентября 2013
-
Обновлено: 13 августа 2021
Средняя линия трапеции
Это отрезок, который соединяет середины 2 боковых сторон трапеции. Существует несколько способов (формул), позволяющих узнать, чему равна средняя линия.
Рассмотрим некоторые из них.
Как найти среднюю линию трапеции через основания
Если известно, чему равны основания трапеции, то среднюю линию найти совсем не сложно.
Она будет равна полусумме оснований.

EF = (AB + CD) / 2.
Например, если основание AB = 10 см, а основание CD = 6 см, то средняя линия равна (10 + 6) / 2 = 8 см.
Как найти среднюю линию трапеции через площадь и высоту
По классической формуле, площадь трапеции равна полусумме оснований умноженной на высоту. А полусумма оснований и есть средняя линия.

Поэтому, если площадь S = EF * DH, то средняя линия EF = S / DH.
Например, если площадь трапеции равна 30 кв. см, а высота – 6 см, то средняя линия = 30 / 6 = 5 см.
Как найти среднюю линию трапеции через высоту, диагонали и угол между ними
Если неизвестна площадь трапеции, но известны диагонали и угол между ними, то можно воспользоваться одной из формул нахождения площади.
А после этого подставить полученное значение в формулу, позволяющую найти среднюю линию через площадь и высоту.
Если даны диагонали d1 и d2, а также угол между ними (например, γ), то S = 0,5 * d1 *d2 * sinγ.
Подставим это в формулу нахождения средней линии: EF = S / DH = (0,5 * AC * BD * sinγ) / DH = AC * BD * sinγ / 2DH.
Например, высота = 6 см, диагонали – 8 и 10 см, угол между ними – 30 градусов.
EF = (8 * 10 * 0,5) / (2 * 6) = 40 / 12 = 3,33 см.
Средняя линия трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Мы снова затронем тему трапеций (что это?).
И расскажем о том, что такое средняя линия этой геометрической фигуры.
Средняя линия – это…
Вообще, этот термин в геометрии весьма распространен.
Средняя линия – это отрезок, проходящий через противоположные стороны, и который делит их ровно на две одинаковых части.
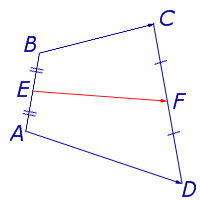
Средняя линия есть практически у каждой геометрической фигуры. Например, у четырехугольников она выглядит вот так:
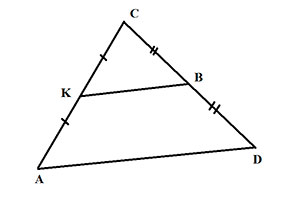
А вот так у треугольников:
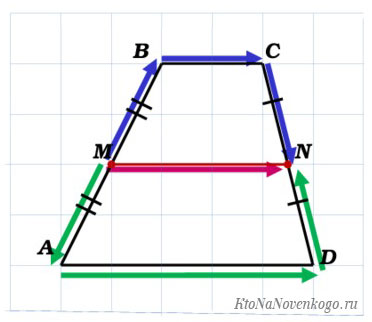
И наконец, в случае трапеции изображение средней линии будет вот таким:
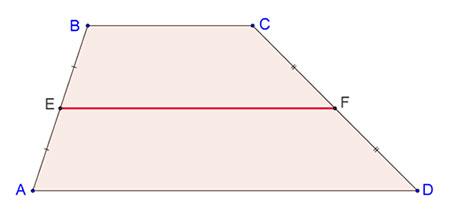
На данном рисунке показана трапеция ABCD. Если кто забыл, то у такой фигуры две противоположные грани расположены на параллельных прямых.
Они называются основаниями. А оставшиеся стороны, которые соответственно не параллельны друг другу, это боковые.
Так вот в нашем случае мы имеем среднюю линию EF, которая делит боковые стороны АВ и СD на две половинки. То есть:
AE = EB и СF = FD
Как найти среднюю линию трапеции (формула)
Есть одна главная формула, позволяющая рассчитать значение нашего отрезка.
Так, длина средней линии будет равна сумме оснований фигуры, поделенной на два. Или, другими словами, половине суммы оснований.
Возьмем для примера трапецию:
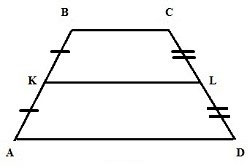
И тогда формула расчета будет выглядеть так:
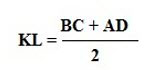
Если есть желание доказать правдивость этой формулы, нужно несколько дорисовать нашу изначальную фигуру. А именно провести линию через В и L, а также продлить сторону АD. И сделать так, чтобы эти две линии пересеклись.
В итоге получится вот что:
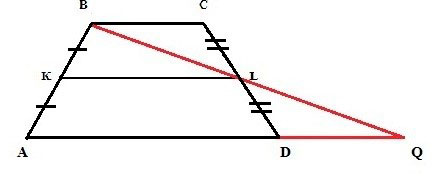
Далее нас будут интересовать оба треугольника, которые получились. Это BLC и DLQ. Необходимо доказать, что они имеют равные размеры.
И это просто, так как у них одинаковы углы:
- BLC и QLD – как вертикальные;
- BCL и QDL – как лежащие накрест при имеющихся параллельных прямых и секущей.
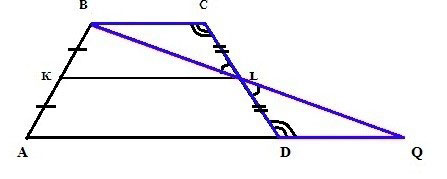
Соответственно, если равны в треугольниках углы и стороны между ними, то и сами фигуры одинаковы.
DLQ = BLC
А уже из этого следует, что ВL и LQ равны. А значит, КL является не только средней линией трапеции, но также и аналогичной линией для треугольника ABQ.
А дальше уже совсем просто, так как есть специальная формула для расчета средней линии треугольника. Она равна одной второй (половине) длины параллельной стороны:
KL = 1/2AQ
Длина стороны AQ у нас равна AD + DQ (или ВС). И таким образом мы и получаем ту самую формулу расчета средней линии трапеции:
KL = ½ AQ = ½ (AD + DQ) = ½ (AD + ВС)
Как принято говорить в таких случаях – что и требовалось доказать.
Свойства средней линии трапеции
У средней линии трапеции есть три главных свойства:
- Она параллельна основаниям трапеции;
- Она равна полусумме оснований (та самая формула, о которой мы только что рассказывали);
- Она разбивает исходную трапецию на две более маленькие по площади. Причем их площади имеют вполне конкретное соотношение друг к другу. А именно:
S1/S2 = (3BC + AD) / (BC + 3AD)
Эту формулу мы не будем доказывать. Просто поверьте, что так и есть на самом деле.
Вторая средняя линия
Внимательный читатель мог бы заметить, что мы рассказывали до этого только про одну среднюю линию. Ту, что лежит параллельно основаниям. Но ведь у этой геометрической фигуры, как и любого четырехугольника, таких отрезков должно быть два.
И действительно, у трапеции имеется вторая такая линия. И она уже делит на две равные части оба основания:
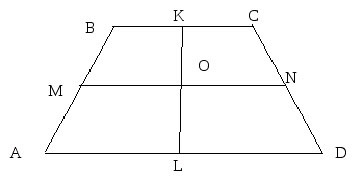
В нашем случае, это отрезок KL.
Интересно, что эту среднюю линию крайне мало изучают во время школьного обучения. И на экзаменах нет задач, с ней связанных. Хотя у нее есть несколько интересных свойств:
- Диагонали трапеции и эта средняя линия пересекаются в одной точке;
- Та прямая, частью которой эта линия является, пересекается в единой точке с теми прямыми, которые совпадают с боковыми сторонами;
- В равнобокой трапеции (у которой боковые стороны идут под одним углом) средняя линия пересекает основания под углом в 90 градусов;
- В точке, в которой пересекаются две средние линии, они делятся пополам…
Вот и все, что мы хотели рассказать о средних линиях в трапеции.
Как найти среднюю линию трапеции
Содержание:
- Средняя линия трапеции – что это?
- Свойства
-
Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Через площадь и высоту
- Примеры задач
Средняя линия трапеции – что это?
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон трапеции.
Свойства
- Параллельна обоим основаниям трапеции.
- Вычисляется как половина суммы оснований.
- Разбивает трапецию на две, площади которых соотносятся как (frac{S_1}{S_2}=frac{3,BC+AD}{BC+3,AD})
Как вычислить, основные формулы
Через основания
(m=frac{a+b}2)
Где (a) – нижнее основание, (b) – верхнее, (m) – средняя линия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Через основание, высоту и углы при нижнем основании
(m=a-htimesfrac{ctgalpha+ctgbeta}2)
(m=b+htimesfrac{ctgalpha+ctgbeta}2)
Где (a) – нижнее основание, (b) – верхнее, (m) – средняя линия, (h) – высота, (alpha,beta) – углы при нижнем основании.
Через диагонали, высоту и угол между диагоналями
(m=frac{d_1d_2}{2h}timessinalpha=frac{d_1d_2}{2h}timessinbeta)
Где (a) – нижнее основание, (b) – верхнее, (m) – средняя линия, (h) – высота, (alpha,beta) – углы между диагоналями, (d_1), (d_2) – диагонали трапеции.
Через площадь и высоту
(m=frac{{}_S}h)
Где (h) – высота трапеции, (m) – средняя линия, (S) – площадь.
Примеры задач
Задача 1
Найдите площадь трапеции, если большее основание равно 18, меньшее 6, боковая сторона равна 7. Угол между боковой стороной и одним из оснований 150 градусов.
(angle ABC) и (angle BAH) односторонние (Rightarrow angle ABC+angle BAH;=;180^circ Rightarrow angle BAH;=;30^circ)
Рассмотрим (angle ABH)
(BH=frac12AB=3,5)
(S_{ABCD}=frac{AD+BC}2times BH=frac{6+18}2times3,5=42)
Ответ: 42
Задача 2
Основания трапеции равны 4 и 10. Чему равен больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей?
Средняя линия трапеции ABCD так же является средней линией треугольников ABC и ACD т.к. проходит через середину одной стороны и параллельна основанию. Значит, из треугольника ACD x = 5.
Ответ: 5
Задача 3
ABCD – трапеция, BC = 2, AD = 3, PQ – средняя линия, BD и AC – диагонали. Найти MN.
(PQ=frac{BC+AD}2=2,5)
Отрезок MN лежит на средней линии трапеции. Докажем: PM и NQ средние линии треугольников ABC и BCD, значит M и N середины соответственно AC и BD. Из треугольника ABC находим длину PM = 1, из треугольника BCD находим NQ = 1, следовательно MN = 2,5 – 1 – 1 = 0,5
Ответ: 0,5
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
-
Определение средней линии трапеции
-
Свойства средней линии трапеции
- Свойство 1
- Свойство 2
- Свойство 3
- Признак средней линии трапеции
- Вторая средняя линия
-
Пример задачи
Определение средней линии трапеции
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.

- LM – средняя линия трапеции ABCD
- L – середина стороны AB, т.е. AL = LB
- M – середина стороны CD, т.е. CM = MD
Свойства средней линии трапеции
Свойство 1
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Для рисунка выше:
![]()
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.

Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
![]()
![]()
![]()
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.

Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.

Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Решение
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b)/2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b)/2.
Таким образом, S = m ⋅ h = 25 см ⋅ 7 см = 175 см2.
