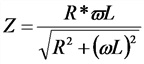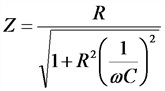Содержание:
Цепи переменного тока:
Основное применение в электротехнике и радиотехнике имеют переменные напряжения и токи, являющиеся периодическими функциями времени. Мгновенные значения периодических напряжений u и токов i повторяются через промежуток времени Т, называемый периодом:
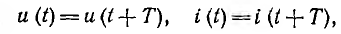
где t — время; число периодов в единицу времени 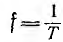
Электротехника сильных токов использует в основном низкие частоты. Промышленной частотой в СССР и Европе является 50 гц, в Америке 60 гц, в некоторых областях техники применяют частоты в сотни герц и выше. Техника проводной и радиосвязи использует широкий диапазон частот от долей герц до 1012 гц. Постоянные э.д. с. и токи можно рассматривать как частный случай переменных, частота которых равна нулю (f — 0).
Простейшими и широко применяемыми в электротехнических и радиотехнических устройствах являются периодические напряжения и токи, изменяющиеся по закону синуса. Для случая синусоидального закона изменения функций разработаны простые методы расчета цепей, подобные методам расчета цепей постоянного тока. Если закон изменения периодического напряжения u (t) или i (t) отличен от синусоиды, эти функции могут быть разложены в ряд Фурье, т. е. представлены в виде суммы синусоид, что позволит при расчетах линейных цепей применить метод наложения и свести расчеты к синусоидальным функциям.
Что такое цепь постоянного тока
Цепью постоянного тока называется такая цепь, в которой ЭДС, токи и напряжения остаются постоянными по величине и не зависят от времени.
Цепи делятся на два больших класса:
- линейные;
- нелинейные.
Электрические цепи, содержащие только элементы с линейными вольтамперными характеристиками, называются линейными цепями.
Генератор синусоидального напряжения
Для получения синусоидальных переменных токов в линейных цепях э. д. с. также должны изменяться по синусоиде. Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка, вращающаяся с постоянной угловой скоростью в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции (рис. 6.1). При этом пронизывающий катушку магнитный поток изменяется, и в ней по закону электромагнитной индукции индуктируется э. д. с. Цепь нагрузки подключается к генератору с помощью щеток, наложенных на два кольца, соединенных с катушкой.
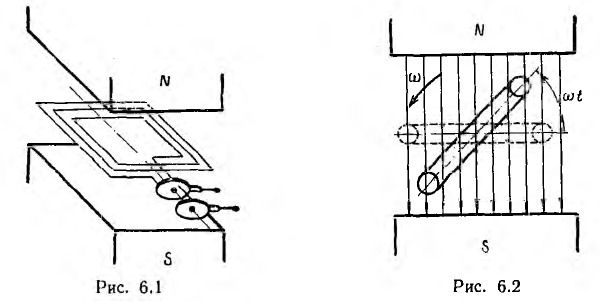
Пусть в начальный момент времени t=О плоскость катушки будет перпендикулярна магнитным линиям (пунктир на рис. 6.2). Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол ωt, и мгновенные значения ее потока и потокосцепления будут равны
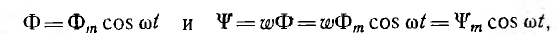
где 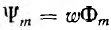 — максимальное значение потокосцепления.
— максимальное значение потокосцепления.
Тогда мгновенное значение э. д. с. катушки
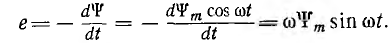
Величина 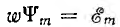 представляет собой максимальное значение
представляет собой максимальное значение
э. д. с., которое она получает, когда sinωt становится равным единице.
Следовательно, 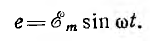
Временные диаграммы
Временная диаграмма магнитного потока и электродвижущей силы катушки показана на рис. 6.3, а. Максимальная э. д. с. индуктируется в моменты, когда поток, пронизывающий катушку, равен нулю, так как тогда скорость изменения потока достигает наибольшего значения. Э д. с. равна нулю в моменты, когда поток получает максимальное значение, так как при этом поток не меняет своей величины.
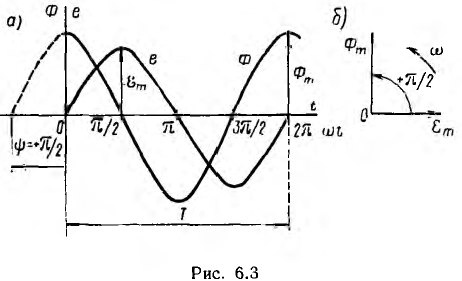
Как видно из рис. 6.3, а,
откуда 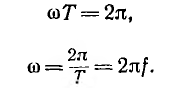
Величина ω, пропорциональная частоте f и равная в данном случае угловой скорости вращения катушки, называется угловой частотой.
Общее выражение для синусоидальной функции времени имеет вид:
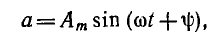
где а — мгновенное значение функции; Аm — ее максимальное значение (амплитуда); ω— угловая частота; угол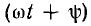 — фаза, а угол ψ — начальная фаза. Начальная фаза определяет значение функции для начального момента времени:
— фаза, а угол ψ — начальная фаза. Начальная фаза определяет значение функции для начального момента времени:
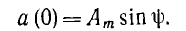
Так, для рассмотренного источника синусоидальной э. д. с.
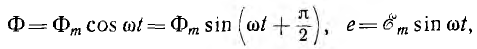
начальная фаза потока равна + π/2 , э. д. с. — нулю, т. е. магнитный поток и э. д. с. сдвинуты по фазе на π/2.
На временной диаграмме, как видно из рис. 6.3, а, положительная начальная фаза откладывается от начала координат влево, т. е. в сторону отрицательных значений ωt, а отрицательную начальную фазу следует откладывать в сторону положительных значений ωt.
Векторные диаграммы
Расчеты в цепях с синусоидальными напряжениями и токами весьма упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами.
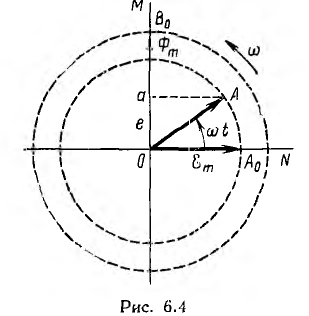
Пусть NOM является прямоугольной системой осей координат и пусть положительные углы откладываются против направления вращения стрелки часов (рис. 6.4). Если нужно найти, например, мгновенные значения синусоиды э. д. с. 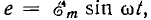 то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с.
то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с. 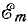 считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э. д. с. е
считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э. д. с. е
для этого момента времени будет равно проекции Оа вектора ОА на ось ОМ:
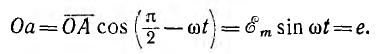
Проекция вектора ОА на ось ОМ для начального момента времени 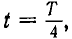
будет равна нулю, для момента времени, когда вектор повернется на угол π/2, проекция будет равна 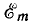 полный цикл изменений э. д. с. получится за один полный оборот вектора ОА.
полный цикл изменений э. д. с. получится за один полный оборот вектора ОА.
Таким же образом можно находить мгновенные значения потока 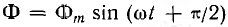 , с той разницей, что для начального момента
, с той разницей, что для начального момента
времени вектор ОВ0, изображающий в выбранном масштабе максимальное значение потока Фm, необходимо направить по оси ОМ, так как он должен образовать с осью ON угол + π/2, равный начальной фазе потока.
Таким образом, можно условиться изображать синусоидальную функцию вектором, длина которого определяется максимальным ее значением, а направление — ее начальной фазой, при этом положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получается векторная диаграмма, показанная для рассмотренного примера потока и э. д. с. на рис. 6.3, б.
Векторы, изображающие синусоидальные функции времени, имеют совсем другой смысл, чем векторы, изображающие, например, силы в механике. Вектор силы дает ее величину и направление в пространстве, вектор, изображающий синусоиду, является вращающимся вектором, дающим своей проекцией на неподвижную ось мгновенное значение синусоиды. Такой вектор чертится в начальном своем положении, которое дает начальную фазу синусоиды, но, конечно, не направление изображаемой величины впространстве. Подобным вектором можно изображать любую синусоидально изменяющуюся величину, в том числе скалярную — э. д. с., тон, поток и т. п.
Векторные диаграммы особенно удобны при сложении или вычитании синусоид одинаковой частоты. Как известно, результатом будет также синусоида той же частоты. При сложении нескольких синусоид нужно складывать их мгновенные значения, т. е. проекции векторов, изображающих эти синусоиды, но так как сумма проекций векторов на какую-либо ось равна проекции геометрической суммы этих векторов на ту же ось, то эга геометрическая сумма и будет вектором, изображающим результирующую синусоиду. Длина вектора даст амплитуду результирующей синусоиды, угол с горизонтальной осью — ее начальную фазу.
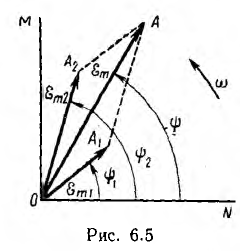
Так, например, для двух синусоид (рис. 6.5)
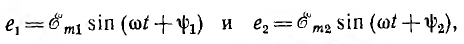
изображаемых векторами 0А1 и 0А2, вектор ОА, изображающий суммарную синусоиду
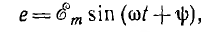
будет геометрической суммой векторов OA1 и ОА2. Он имеет величину 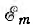 и составляет с осью ON угол ψ. Так как синусоиды е1 и е2 имеют одну и ту же частоту, изображающие их векторы вращаются с одинаковой угловой скоростью, углы между ними не изменяются, и результирующий вектор сохраняет постоянную длину, вращаясь с той же угловой скоростью.
и составляет с осью ON угол ψ. Так как синусоиды е1 и е2 имеют одну и ту же частоту, изображающие их векторы вращаются с одинаковой угловой скоростью, углы между ними не изменяются, и результирующий вектор сохраняет постоянную длину, вращаясь с той же угловой скоростью.
Аналогично, путем геометрического вычитания, может быть найден вектор, изображающий результирующую синусоиду разности двух синусоид. Следовательно, алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами.
Особенности цепей переменного тока
Для цепей переменного тока справедливы законы Ома, Кирхгофа и Джоуля — Ленца применительно к мгновенным значениям напряжений, токов и мощностей для одного и того же момента времени. Однако в отличие от пассивной цепи постоянного тока, в которой ток определяется приложенным к ней напряжением и ее сопротивлением, в пассивной цепи переменного тока возникают внутренние переменные э. д. с. самоиндукции и э. д. с. емкости, которые должны, быть учтены, кроме приложенного напряжения, при составлении уравнений по основным законам.
Так же, как и в цепях постоянного тока, при составлении уравнений по этим законам для цепей переменного тока необходимо задаться условным положительным направлением напряжений и токов, хотя действительные их направления периодически меняются. По аналогии с цепями постоянного тока удобно принять, что положительные направления напряжения и тока всей цепи и каждого из ее элементов — резистора, катушки индуктивности и конденсатора — совпадают. Тогда мгновенная мощность р = ui всей цепи и каждого из ее элементов будет положительной, когда действительные направления их напряжения и тока совпадают, т. е. когда цепь или ее элементы являются потребителями энергии, что принято характеризовать положительной мощностью.
Выбранные положительные направления для мгновенных значений напряжений и токов сохраняются при переходе к векторам— сумме (разности) мгновенных значений соответствует геометрическая сумма (разность) изображающих их векторов.
Физические и энергетические процессы на участках цепи с сопротивлением, с индуктивностью, с емкостью весьма различны, поэтому предварительно они рассматриваются раздельно до изучения цепей с их сочетанием.
Цепь с сопротивлением
Постоянный ток распределяется по всему сечению проводника равномерно, т. е. во всех точках его сечения плотность тока одинакова.
Плотность переменного тока возрастает от оси проводника к его поверхности. Это явление называется поверхностным эффектом, рассматриваемым в ч. IV. Приближенно можно считать, что переменный ток в проводнике использует только часть s’ его сечения s. Следовательно, сопротивление R постоянному току, называемое обычно омическим, будет меньше сопротивления r переменному току:
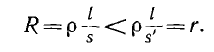
Сопротивление г получило название активного сопротивления проводника.
Поверхностный эффект проявляется тем сильней, чем больше частота, сечение, удельная проводимость и магнитная проницаемость проводника. При промышленной частоте (50 гц) и тонких медных или алюминиевых проводах поверхностным эффектом можно пренебречь и считать активное сопротивление равным омическому.
Пусть к активному сопротивлению (рис. 6.6, а) приложено синусоидальное напряжение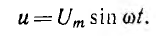
По закону Ома ток
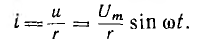
Ток получает максимальное значение 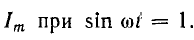 . Тогда
. Тогда
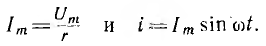
Следовательно, в цепи с сопротивлением r напряжение и ток совпадают по фазе (рис. 6.6, 6.) На векторной диаграмме вектор напряжении совпадает по направлению с вектором тока (рис. 6.6, в). Максимальные значения напряжения и тока также подчинены закону Ома.
Мгновенная мощность р равна произведению мгновенных значений напряжения и тока:
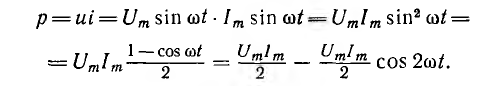
Как видно из этого выражения, мгновенная мощность имеет постоянную составляющую 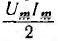 и переменную составляющую, изменяющуюся по косинусоиде двойной частоты
и переменную составляющую, изменяющуюся по косинусоиде двойной частоты 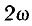 с амплитудой
с амплитудой 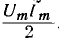
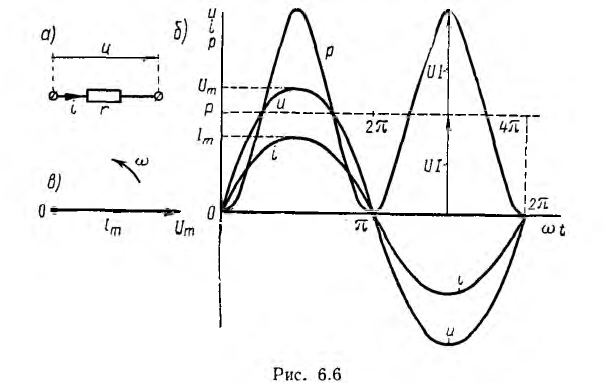
Кривая мощности также изображена на рис. 6.6, б. Мощность равна нулю при u = 0 и i = 0, всегда положительна и получает максимальное значение в те моменты, когда напряжение и ток также максимальны.
Среднее значение мощности за период — средняя мощность
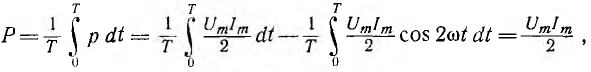
т. e. равна постоянной составляющей мгновенной мощности.
Пользуясь зависимостью между максимальными значениями напряжения и тока, выражение для средней мощности можно переписать следующим образом:
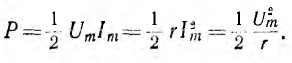
Обычно величина переменного тока характеризуется действующим значением. Так называется значение постоянного тока I, которое дает ту же мощность Р в том же сопротивлении r:
следовательно, 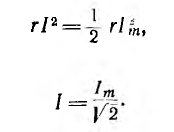
Аналогично, действующее значение напряжения
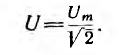
Следовательно, мгновенная мощность
средняя мощность 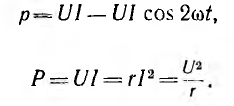
Энергия, поглощаемая активным сопротивлением,
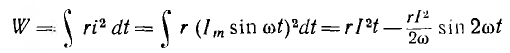
непрерывно растет. Эта энергия поставляется источником, питающим цепь.
Цепь с индуктивностью и цепь с емкостью
Цепь с индуктивностью и цепь с емкостью являются накопителями энергии соответственно электрического и магнитного поля. Чтобы подчеркнуть эту аналогию, цепь с индуктивностью и цепь с емкостью
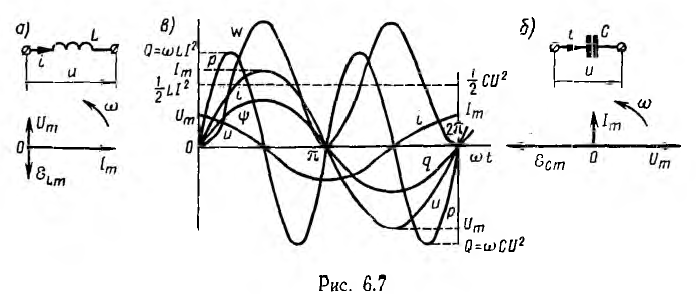
рассматриваются одновременно. Величины, определяющие процессы в них, — ток в цепи с индуктивностью и напряжение на цепи с емкостью — задаются с одинаковой фазой.
Пусть ток цепи с индуктивностью L (рис. 6.7, а)
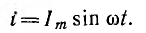
Тогда потокосцепление
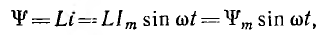
т. e. совпадает по фазе с током.
Пусть напряжение цепи с емкостью С (рис. 6.7, б)
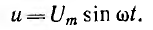
Тогда заряд
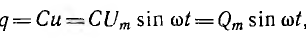
т. e. совпадает по фазе с напряжением.
Временная диаграмма этих и далее вычисляемых величин изображена на рис. 6.7, в, причем обозначения кривых показаны соответственно слева и справа.
Энергия, запасаемая в электрическом поле,
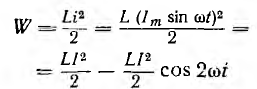
пульсирует с двойной частотой 2ω около среднего значения 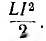 Увеличиваясь с ростом тока за счет энергии источника, энергия поля при уменьшении тока возвращается источнику.
Увеличиваясь с ростом тока за счет энергии источника, энергия поля при уменьшении тока возвращается источнику.
Энергия, запасаемая в магнитном поле,
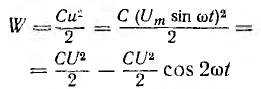
пульсирует с двойной частотой 2ω около среднего значенияя 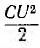 . Увеличиваясь с ростом напряжения за счет энергии источника, энергия поля при уменьшении напряжения возвращается источнику.
. Увеличиваясь с ростом напряжения за счет энергии источника, энергия поля при уменьшении напряжения возвращается источнику.
Мгновенная мощность, равная производной энергии по времени,

также изменяется с двойной частотой, будучи положительной, когда энергия поступает в приемник, и отрицательной, когда приемник возвращает энергию источнику.
Средняя мощность
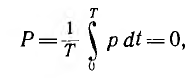
т. е. процесс колебаний энергии между источником и приемником не сопровождается потерями. Максимальное значение мощности
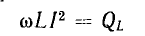 называется индуктивнои мощностью.
называется индуктивнои мощностью.
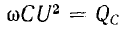 называется емкостной мощностью.
называется емкостной мощностью.
В системе СИ эти мощности измеряются в реактивных вольтамперах (вар).
Мгновенное значение напряжения
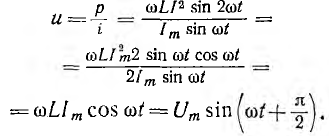
Векторная диаграмма цепи с L показана на рис. 6.7, а. Следовательно, в цепи с L ток отстает от напряжения пофазе на угол 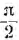 . Так как направление отсчета этого угла от вектора тока к вектору напряжения совпадает с направлением вращения векторов, этот угол считается положительным, т. е.
. Так как направление отсчета этого угла от вектора тока к вектору напряжения совпадает с направлением вращения векторов, этот угол считается положительным, т. е. 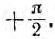
Максимальное значение напряжения
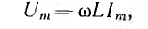 отсюда частные
отсюда частные 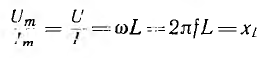
Мгновенное значение тока
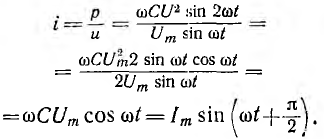
Векторная диаграмма цепи с С показана на рис. 6.7, б. Следовательно, в цепи с С ток опережает напряжение по фазе на угол 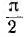 . Так как направление отсчета этого угла от вектора тока к вектору напряжения противоположно направлению вращения векторов, этот угол считается отрицательным, т. е. —
. Так как направление отсчета этого угла от вектора тока к вектору напряжения противоположно направлению вращения векторов, этот угол считается отрицательным, т. е. —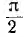 .
.
Максимальное значение тока
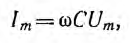 отсюда частные
отсюда частные 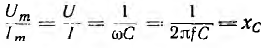
играют роль сопротивления применительно к максимальным и действующим значениям напряжения и тока. Они называются индуктивным сопротивлением емкостным сопротивлением и в системе единиц СИ измеряются в омах.
Емкостное сопротивление обратно пропорционально емкости и частоте; при постоянном напряжении оно равно бесконечности.
В цепи с емкостью величина
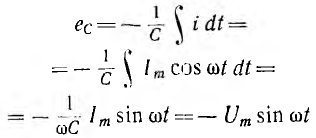
может быть названа э. д. с. емкости. Она равна и противоположна по фазе напряжению цепи.
Индуктивное сопротивление прямо пропорционально индуктивности и частоте; при постоянном токе оно равно нулю.
В цепи с индуктивностью возникает э. д. с. самоиндукции
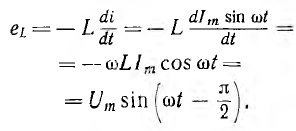
Она равна и противоположна по фазе напряжению цепи.
Отсюда видно, что применять индуктивное или емкостное сопротивления в соотношениях между мгновенными напряжениями и токами нельзя, так как

Соотношения u = —е, полученные в предположении их одинакового положительного направления, аналогичны соотношениям для напряжения U и э. д. с. 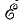 источника энергии без внутреннего сопротивления при выборе для них одинакового направления
источника энергии без внутреннего сопротивления при выборе для них одинакового направления 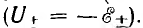
Итак, соотношения в цепи с индуктивностью и в цепи с емкостью аналогичны. От зависимостей в одной цепи к зависимостям в другой можно перейти, заменяя соответствующие величины по табл. 6.1.
Таблица 6.1
| Цепь с индуктивностью | L | ψ | u | i | ω | t | W | p |
| Цепь с емкостью | C | q | i | u | ω | t | W | p |
Измерения в цепях переменного тока
Для измерения переменного тока и напряжения могут быть применены амперметры и вольтметры электромагнитной и электродинамической систем, рассмотренные. При включении такого aмперметра в цепь переменного тока его мгновенный момент вращения mвр будет пропорционален квадрату мгновенного значения тока i, подвижная же часть прибора, очевидно, даст отклонение, пропорциональное среднему значению этого момента:
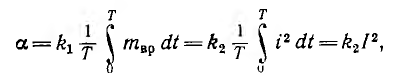
т. е. прибор измерит действующее значение тока. Аналогично, вольтметры этих двух систем измеряют действующее значение напряжения.
Для измерения мгновенных значений переменных токов и напряжений применяется осциллограф, основным элементом которого является вибратор — прибор магнитоэлектрической системы, подвижной частью которой является легкая петелька; ее момент вращения и угол отклонения пропорциональны измеряемой величине. Вместо стрелки на подвижной части укреплено зеркальце, отражающее луч света на движущуюся фотопленку, на которой записывается временная диаграмма тока или напряжения.
Для измерения средней мощности в цепях переменного тока применим ваттметр электродинамической системы. Как следует из , его мгновенный момент вращения mвр будет пропорционален мгновенной мощности р = ui. Тогда отклонение подвижней части пропорционально ее среднему значению:
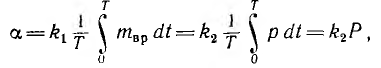
т. е. средней мощности.
Для получения положительного отклонения ваттметр следует включать по схеме рис. 2.9. В цепях только с индуктивностью и с емкостью ваттметр, очевидно, должен дать нулевое показание.
Анализ и расчет простых цепей переменного тока
Основной особенностью цепей переменного тока (по сравнению с цепями постоянного тока) является наличие в них реактивных элементов – емкостей и индуктивностей . Реактивные элементы, не рассеивая мощность электромагнитных колебаний, изменяют разность фаз между колебаниями электрического тока и напряжения на участке цепи. Вследствие этого амплитудные значения напряжения и силы тока достигаются не одновременно. При расчете электрической цепи переменного тока необходимо учитывать эту особенность, т.е. учитывать фазовые отношения между колебаниями токов и напряжений.
Цепь с последовательным соединением участков с сопротивлением, с индуктивностью и с емкостью
По закону Ома мгновенное значение тока в цепи с последовательно
включенными активным сопротивлением r, индуктивностью L и емкостью С (рис. 7.1, а) зависит не только от приложенного напряжения и, но и от возникающих в цепи э. д. с. индуктивности eL и э. д.с. емкости ес–
отсюда 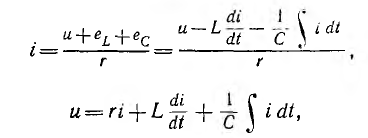
т. е. приложенное напряжение распадается на три напряжения, из которых первое Ua=ri преодолевает активное сопротивление цепи, второе 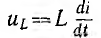
уравновешивает противоположную ему по знаку э. д. с. индуктивности eL и третье 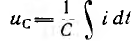 уравновешивает противоположную ему по знаку э. д.с емкости ес.
уравновешивает противоположную ему по знаку э. д.с емкости ес.
Задавшись током цепи
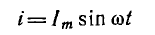
и подставив это выражение тока в уравнение напряжений:
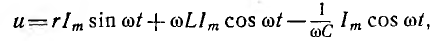
можно видеть, что отдельные составляющие напряжения представляют собой синусоиды и, следовательно, суммарное напряжение также будет синусоидой, вектор которой равен геометрической сумме векторов составляющих синусоид.
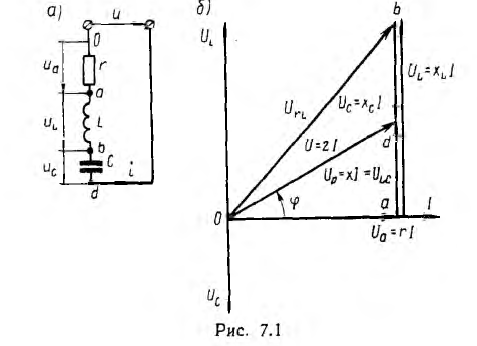
Это построение сделано на рис. 7.1, б для векторов, равных по величине действующим значениям. Вектор активного напряжения UB=rl совпадает по фазе с вектором тока I. Индуктивное напряжение
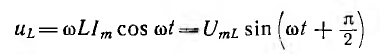
опережает ток на 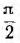 и, следовательно, вектор индуктивного напряжения
и, следовательно, вектор индуктивного напряжения
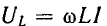 сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение
сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение
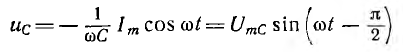
и его вектор 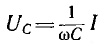 противоположен по фазе вектору UL. На рис. 7.1, б он отложен из конца вектора UL в противоположную сторону. Замыкающий вектор и есть вектор полного напряжения U. Необходимо отметить интересную особенность векторной диаграммы рис. 7.1, б.
противоположен по фазе вектору UL. На рис. 7.1, б он отложен из конца вектора UL в противоположную сторону. Замыкающий вектор и есть вектор полного напряжения U. Необходимо отметить интересную особенность векторной диаграммы рис. 7.1, б.
При ее построении векторы напряжений на участках цепи откладывались в той же последовательности, в какой эти участки включены в цепь рис. 7.1, а. Поэтому отдельным точкам векторной диаграммы (0, a, b, d) соответствуют одноименные точки цепи. Такая диаграмма может быть названа топографической. Она позволяет сразу найти векторы напряжений между любыми точками цепи, соединив их прямой линией. На рис. 7.1, б показаны векторы напряжений UrL и ULC на участках rL и LC.
В результате сложения векторов получается прямоугольный треугольник напряжений с гипотенузой, равной полному напряжению U, катетом, равным активному напряжению UB и катетом Up = UL — Uc; напряжение Up называется реактивным. На диаграмме рис. 7.1, б преобладает индуктивное напряжение (UL > Uс) и поэтому реактивное напряжение совпадает по фазе с индуктивным.
Из треугольника напряжений видно, что
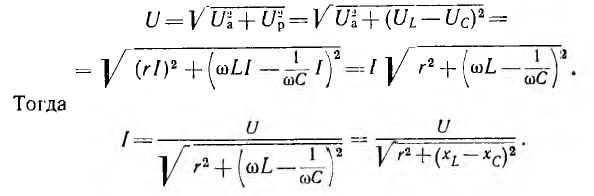
Сопротивление  называется реактивным и обозначается буквой х. Знаменатель выражения для тока
называется реактивным и обозначается буквой х. Знаменатель выражения для тока
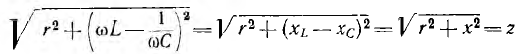
играет роль сопротивления и называется полным сопротивлением.
В системе единиц СИ z также измеряется в омах.
Следовательно,
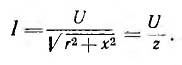
Полученные выражения могут рассматриваться как аналог закона Ома для переменного тока. Необходимо подчеркнуть, что закон Ома в таком виде справедлив только для максимальных и действующих значений переменного тока и напряжения. Для мгновенных значений но в таком виде неприменим; написать 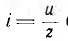 было бы грубой ошибкой, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
было бы грубой ошибкой, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
Здесь полезно сопоставить различные выражения закона Ома для этой цепи. Для мгновенных значений

для векторов, очевидно, можно было бы написать:

где 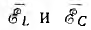 — векторы э. д. с. индуктивности и емкости, а для действующих значений аналог закона Ома:
— векторы э. д. с. индуктивности и емкости, а для действующих значений аналог закона Ома:

Отсюда видно, что физически существующие э. д. с. индуктивности и емкости, входящие в выражения (7.1) и (7.2), в выражении (7.3) формально учитываются через реактивные сопротивления xL и хс.
Вектор тока сдвинут по фазе относительно вектора напряжения на острый угол 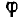 ; на диаграмме рис. 7.1, б вектор тока отстает от век тора напряжения. Угол
; на диаграмме рис. 7.1, б вектор тока отстает от век тора напряжения. Угол 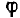 может быть определен из треугольника напряжений:
может быть определен из треугольника напряжений:
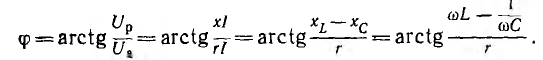
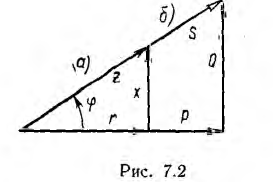
Если разделить все стороны треугольника напряжений на общий множитель I, получится подобный ему треугольник сопротивлений с гипотенузой z и
катетами r и х (рис. 7.2, а), откуда
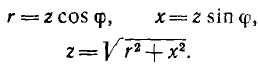
Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:
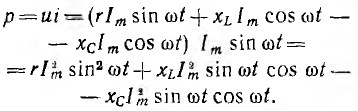
После подстановки значений 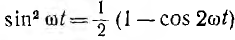 и
и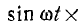
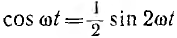
выражение для мгновенной мощности получает вид
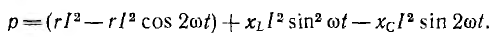
Первый член правой части есть мгновенная мощность активного сопротивления
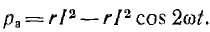
После подстановки соотношений из треугольника напряжений
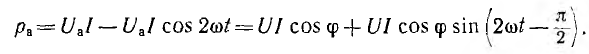
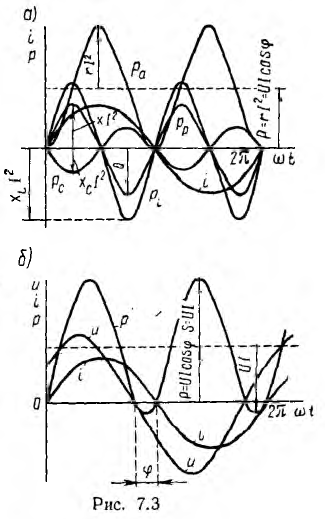
Эта мощность (рис. 7.3, a) имеет постоянную составляющую
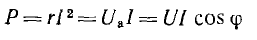
переменную — синусоиду двойной частоты с такой же амплитудой.
Величина Р является, очевидно, средней мощностью за период. Она называется активной мощностью. В системе СИ мгновенная и активная мощности измеряются в ваттах (вт).
Второй и третий член дают мгновенную мощность индуктивности и емкости (см. рис. 7.3, а):
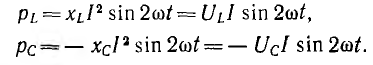
Эти мощности изменяются по синусоидам двойной частоты противоположным по фазе, т. е. когда индуктивность отдает энергию, емкость ее получает, и наоборот. Среднее значение pL и рс равно нулю. В сумме они дают мгновенную мощность реактивных участков цепи:
Амплитуда синусоиды этой мощности
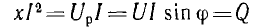
называется реактивной мощностью. В системе СИ реактивная мощность измеряется в реактивных вольт-амперах (вар).
Теперь выражение для мгновенной мощности всей цепи может быть
преобразовано:
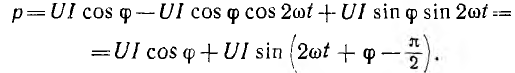
Таким образом, мгновенная мощность р всей цепи имеет постоянную составляющую UI cos ф и переменную составляющую — синусоиду с амплитудой UI (рис. 7.3, б); р равно нулю когда u = 0 или i = 0.
Так как амплитуда переменной части UI больше постоянной составля
ющей UI cosϕ, мощность в определенные промежутки времени становится отрицательной. Когда мощность положительна, цепь получает энергию от источника; когда мощность отрицательна, цепь отдает энергию источнику. Очевидно, возврат энергии источнику получается за счет энергии поля того из реактивных участков цепи, мощность которого больше (для рис. 7.3, б за счет индуктивности). Отдавая запасенную в своем поле энергию, индуктивность снабжает энергией емкость, отдает часть своей энергии безвозвратно активному сопротивлению, а остаток возвращает источнику. Промежутки времени, в течение которых мощность положительна, больше, чем те, при которых мощность отрицательна.
Амплитуда переменной части мгновенной мощности всей цепи
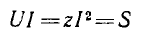
называется полной мощностью и измеряется в системе СИ в вольт-амперах (ва).
Если умножить все стороны треугольника сопротивлений на общий множитель I2, получается подобный ему прямоугольный треугольник мощностей (см. рис. 7.2, б) с углом у вершины, равным ϕ, гипотенузой, равной полной мощности 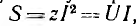 катетом равным активной мощности
катетом равным активной мощности 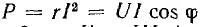 и другим катетом равным реактивной мощности
и другим катетом равным реактивной мощности 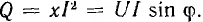 Из треугольник; мощностей видно, что
Из треугольник; мощностей видно, что
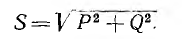
Полная мощность S является характерной величиной для всякой электрической установки, любой электрической машины, аппарата, линии передачи и т. п. Сечение их проводов рассчитывается на ток I таким образом, чтобы провода не перегревались от выделяемого в них тепла. Изоляция рассчитывается на напряжение U; сердечник и н. с. обмотки электромагнитных механизмов рассчитываются на магнитный поток, который также пропорционален напряжению (см., например, формулу для 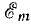 ). Другими словами, любая электрическая установка рассчитывается на напряжение и на ток, т. е. на полную мощность UI, средняя же мощность
). Другими словами, любая электрическая установка рассчитывается на напряжение и на ток, т. е. на полную мощность UI, средняя же мощность
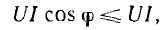
так как 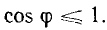 . Следовательно, полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого cosϕ, называемого коэффициентом мощности.
. Следовательно, полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого cosϕ, называемого коэффициентом мощности.
В общем случае напряжение и и ток i цепи записываются так:
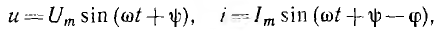
где ψ — начальная фаза напряжения;
ϕ — разность фаз напряжения и тока.
Если в рассмотренной цепи 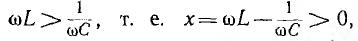 то
то 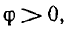 и ток отстает по фазе от напряжения. Если
и ток отстает по фазе от напряжения. Если 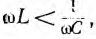 т.е.
т.е. 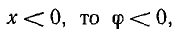 и ток опережает напряжение.
и ток опережает напряжение.
Для цепи с последовательным соединением сопротивления r и индуктивности L аналог закона Ома и сдвиг по фазе могут быть получены 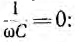
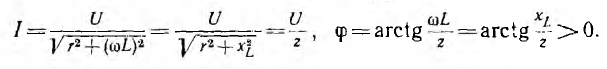
Аналогично, для цепи с последовательным соединением сопротивления r и емкости С, положив 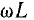 = 0:
= 0:
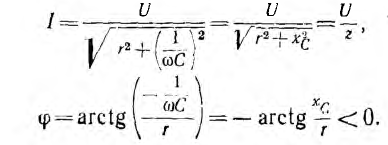
Резонанс напряжений
В электрических цепях, содержащих индуктивности и емкости, возможно явление резонанса, при котором напряжение и ток цепи совпадают по фазе. В цепи с последовательным соединением сопротивления, индуктивности и емкости (см. рис. 7.1, а) будет резонанс напряжений, когда
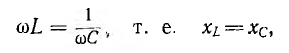
так как в этом случае ток и разность фаз напряжения и тока
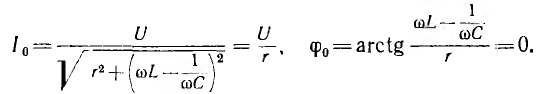
Напряжения на участках цепи при резонансе
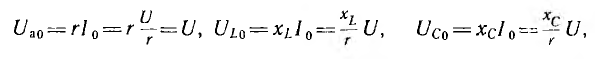
т. е. активное напряжение равно полному, а индуктивное напряжение — емкостному напряжению, так как индуктивное сопротивление xL равно емкостному хс. Если
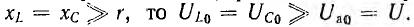
При резонансе, ограниченный лишь активным сопротивлением, при малом r также может получить большое значение.
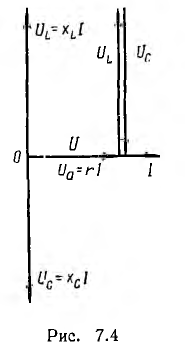
На рис. 7.4 показана векторная диаграмма для случая резонанса. Как видно из этой диаграммы и приведенных соотношений, при резонансе цепь, несмотря на наличие в ней индуктивности и емкости, ведет себя как активное сопротивление. Ток совпадает по фазе с напряжением и получает наибольшее значение. Реактивное напряжение
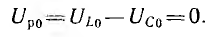
Так как условием резонанса является равенство 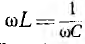 то для данных двух величин из трех (L, С, ω) резонанс может быть получен подбором третьей. Итак, резонанс будет при
то для данных двух величин из трех (L, С, ω) резонанс может быть получен подбором третьей. Итак, резонанс будет при
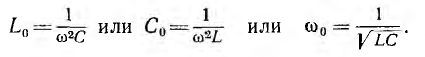
Индуктивное и емкостное сопротивления при резонансе
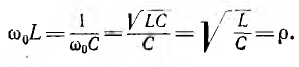
Величина р называется характеристическим сопротивлением цепи, а ее отношение к активному сопротивлению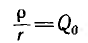 называется добротностью цепи (контура). Добротность равна также отношению индуктивного или емкостного напряжения при резонансе к напряжению всей цепи. Обратная величина
называется добротностью цепи (контура). Добротность равна также отношению индуктивного или емкостного напряжения при резонансе к напряжению всей цепи. Обратная величина
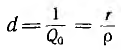
называется затуханием цепи. Чем меньше r, а следовательно, и d, тем при резонансе больше активная (средняя) мощность
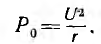
Мгновенные мощности индуктивности и емкости при резонансе равны по величине и обратны по знаку (рис. 7.5):
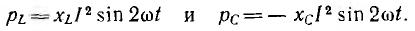
Индуктивная QL = xLP2 и емкостная Qc = ХсР2 мощности также равны друг другу. Следовательно, при резонансе мгновенная мощность рр и реактивная мощность Q всей цепи будут
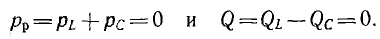
Этого следовало ожидать, так как при резонансе, как показано, цепь ведет себя как активное сопротивление.
Максимальное значение энергии индуктивности
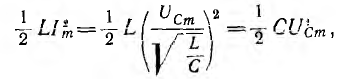
т. е. равно максимальному значению энергии емкости. Тогда, если
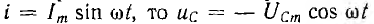 и мгновенное значение суммарной энергии индуктивности и емкости равно:
и мгновенное значение суммарной энергии индуктивности и емкости равно:
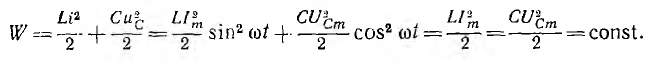
Отсюда видно, что при резонансе суммарная энергия, запасенная реактивными элементами цепи, постоянна и равна максимальной энергии индуктивности, равной, в свою очередь, максимальной энергии емкости. Колебания энергии индуктивности и емкости противоположны по фазе и в цепи происходит полный обмен энергиями между ними.
Источник не участвует в этом обмене и доставляет лишь энергию активному сопротивлению цепи.
Таким образом, при резонансе происходит взаимная компенсация индуктивных и емкостных сопротивлений, напряжений и мощностей.
Далее рассмотрен режим, когда напряжение на зажимах цепи постоянно, а частота изменяется от 0 до .
.
Ток I = 0 при ω = 0 и ω =  и максимален при резонансе, когда ω = ω0.
и максимален при резонансе, когда ω = ω0.
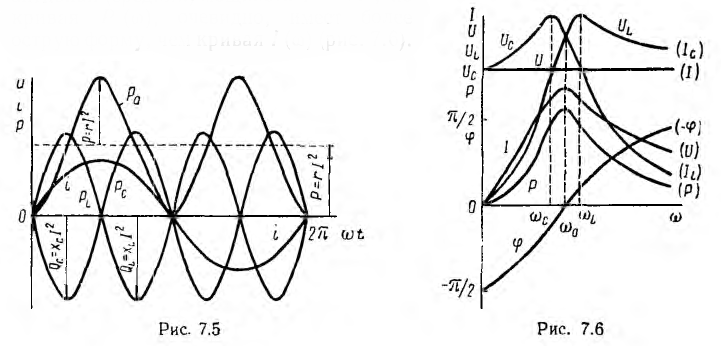
Аналогично изменяется активное напряжение Uа = rl и активная (средняя) мощность Р = rI2, но кривая Р (ω), очевидно, имеет более острую форму, чем кривая I(ω) (рис. 7.6). Индуктивное напряжение UL = 0 при ω = 0. При ω = UL = U, при резонансе
UL = U, при резонансе 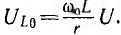 . Для определения частоты
. Для определения частоты 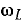 , при которой UL максимально, вместо исследования на максимум величины
, при которой UL максимально, вместо исследования на максимум величины
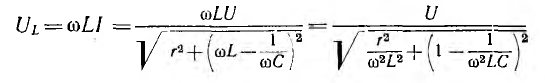
проще исследовать подрадикальное выражение на минимум, взяв его
производную по ω и приравняв нулю:
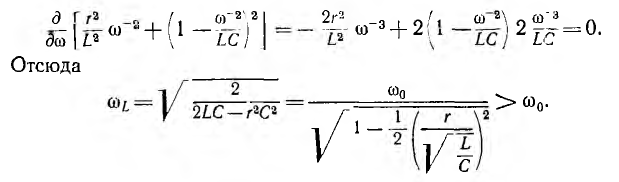
Значение ULmax получится после подстановки значения 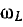 в общее выражение для UL:
в общее выражение для UL:
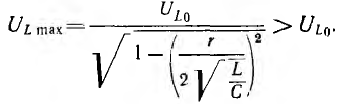
Емкостное напряжение Uc = U при ω=0, U=0 при ω= 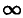 при резонансе
при резонансе 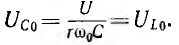
Определение частоты 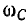 , при которой Uc проходит через максимум, и значение Ucmax можно провести аналогично предыдущему:
, при которой Uc проходит через максимум, и значение Ucmax можно провести аналогично предыдущему:
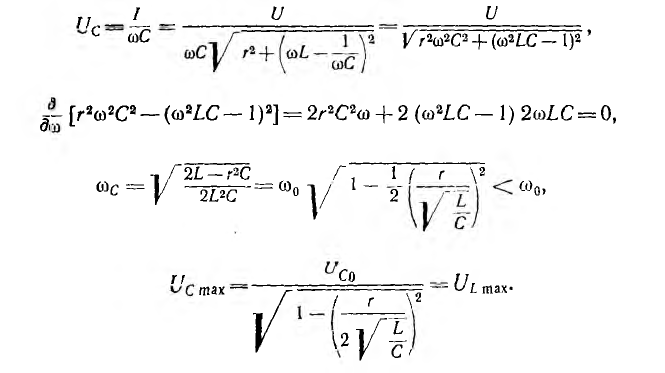
Таким образом, наибольшие значения напряжений на индуктивности и емкости равны между собой.
Графики зависимостей 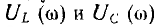 показаны также на рис. 7.6.
показаны также на рис. 7.6.
При увеличении активного сопротивления r цепи 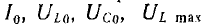
и Ucmax уменьшаются, а частоты ωL и ωс удаляются от резонансной частоты
ω0; при 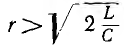 максимумов нет.
максимумов нет.
Кривые на рис. 7.6 называются резонансными кривыми или частотными характеристиками цепи.
Явление резонанса имеет широкое применение в радиотехнике.
Например, в ряде устройств используется зависимость режима работы
цепи с последовательным соединением L и С от частоты и повышение тока этой цепи при резонансе.
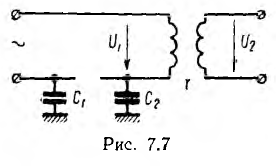
В электротехнике резонанс напряжений часто является аварийным режимом; так при обрыве линии передачи, питающей отключенный со вторичной стороны трансформатор Т (рис. 7.7), может наступить резонанс между емкостью
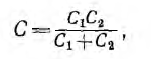
(С1 и С2 — емкости на землю двух участков линии передачи) и индуктивностью L первичной обмотки трансформатора, что вызовет недопустимое для изоляции и безопасности установки повышение напряжения U1 в первичной и, следовательно, U2 во вторичной обмотках трансформатора.
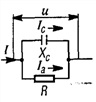
Цепь с параллельным соединением участков с сопротивлением, с индуктивностью и с емкостью. Резонанс токов
Основные соотношения:
При параллельном соединении сопротивления r, индуктивности L и емкости С (рис. 7.8, а) мгновенное значение тока i всей цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников:
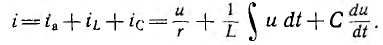
После подстановки в это выражение напряжения 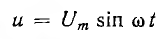 ток всей цепи представляется суммой ‘синусоид:
ток всей цепи представляется суммой ‘синусоид:
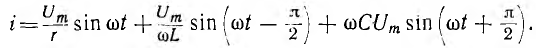
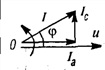
Следовательно, ток всей цепи также будет синусоидой, вектор которой может быть найден как геометрическая сумма векторов слагающих синусоид. Векторная диаграмма для действующих значений дана на рис. 7.8, б.
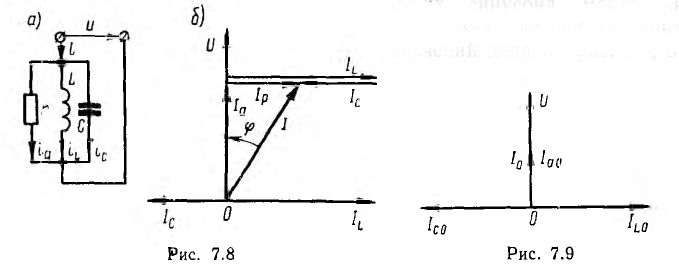
Активный ток 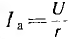 совпадает по фазе с напряжением U, индуктивный ток
совпадает по фазе с напряжением U, индуктивный ток 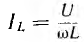 отстает отнапряжения на
отстает отнапряжения на 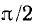 емкостный ток Iс = ωCU опережает напряжение на
емкостный ток Iс = ωCU опережает напряжение на 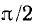 , реактивный ток
, реактивный ток 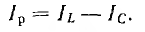
Тогда действующее значение тока всей цепи а разность фаз напряжения и тока
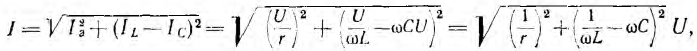
а разность фаз напряжения и тока
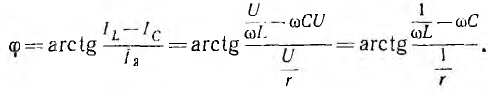
Резонанс токов наступит при
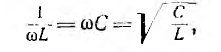
т. е. при условии, аналогичном условию резонанса напряжений.
Тогда
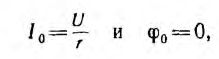
т. е. цепь будет вести себя как активное сопротивление.
Токи ветвей цепи при резонансе:
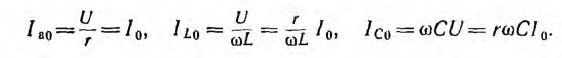
Векторная диаграмма для случая резонанса изображена на рис. 7.9.
Так как векторы 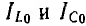 равны между собой и направлены противоположно, сумма их — реактивный ток — равна нулю. Ток цепи I0 равен активному току Iа0 и совпадает по фазе с напряжением.
равны между собой и направлены противоположно, сумма их — реактивный ток — равна нулю. Ток цепи I0 равен активному току Iа0 и совпадает по фазе с напряжением.
При 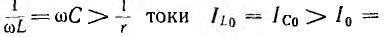 Ia0 т. е. токи в индуктивности и в
Ia0 т. е. токи в индуктивности и в
емкости будут больше тока всей цепи, равного току в активном сопротивлении.
Энергетическая сторона процесса здесь такая же, как и при резонансе напряжений: суммарная энергия, запасенная в полях цепи, постоянна и равна максимальной энергии емкости, равной в свою очередь максимальной индуктивности. Колебания энергии емкости и индуктивности противоположны по фазе, и в цепи происходит полный обмен энергиями между ними. Источник не участвует в этом обмене, он доставляет лишь энергию активному сопротивлению.
Если в рассматриваемой цепи поддерживать неизменным напряжение U и увеличивать частоту ω, активный ток 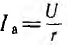 и активная мощность
и активная мощность 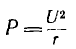 останутся неизменными, индуктивныи ток
останутся неизменными, индуктивныи ток 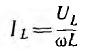 будет убывать, а емкостный ток
будет убывать, а емкостный ток 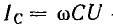 — возрастать; при резонансе
— возрастать; при резонансе 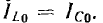 Частотные характеристики цепи показаны на рис 7.10.
Частотные характеристики цепи показаны на рис 7.10.
Ток всей цепи
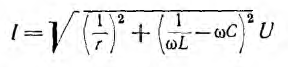
получает при резонансе, когда 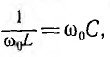 , минимальное значение
, минимальное значение 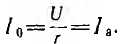 Фазный сдвиг
Фазный сдвиг  положителен при ω< ω0, равен нулю при ω = ω0 и отрицателен при ω > ω0.
положителен при ω< ω0, равен нулю при ω = ω0 и отрицателен при ω > ω0.
В высокочастотных генераторах, усилителях и других радиотехнических устройствах используется зависимость режимов работы от частоты в цепи с параллельным соединением L и С и повышение напряжения этой цепи при резонансе токов.
Дуальные цепи
При сравнении уравнения, написанного для цепи с параллельным соединением r, L и С (см. рис. 7.8, а) на основе первого закона Кирхгофа,
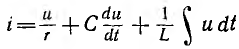
с уравнением для цепи с последовательным соединением r, L и С (см. рис. 7.1, а), написанного на основе второго закона Кирхгофа,
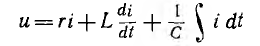
видно, что оба уравнения имеют в качестве независимой переменной время t и совершенно аналогичны, причем одно получается из другого при взаимной замене схемы и величин по табл. 7.1.
Таблица 7.1
| Парaллельное соединение | i | u | 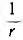 |
L | C |
| Последовательное соединение | u | i | r | C | L |
Две цепи, в которых напряжения первой цепи ведут себя, как токи второй и, наоборот, токи первой ведут себя, как напряжения второй, называются дуальными. Цепь с L и цепь с С, как видно, дуальны. Дуальными являются также цепи с последовательным и параллельным соединениями r, L и С, и все выводы, сделанные для последовательной схемы, можно перенести на параллельную, если заменить величины так, как указано в приведенной таблице. Взаимная замена напряжения и тока должна, очевидно, производиться
и для их действующих значений U и I, а частота ш для обеих схем должна быть одинакова.
Так, например, результаты исследования последовательной схемы при U = const и ω = var, изображенные на рис. 7.6, могут быть целиком перенесены на параллельную схему, работающую при I = const и ω= var, причем кривая, изображающая изменение тока I цепи, будет изображать кривую изменения напряжения U, кривая UL — кривую Iс и кривая Uc — кривую IL. Зависимость активной (средней) мощности 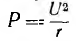 от частоты будет такой же, зависимость
от частоты будет такой же, зависимость  будет отличаться только знаком (рис. 7.6, обозначения кривых даны
будет отличаться только знаком (рис. 7.6, обозначения кривых даны
справа в скобках). Дуальными будут и векторные диаграммы, что можно видеть, например, из сравнения рис. 7.1, б и 7.3, б.
Общему выражению для емкостного напряжения последовательной схемы будет соответствовать общее выражение для индуктивного тока параллельной схемы:
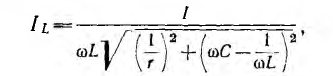
выражению для максимумов напряжений UL и Uc будет соответствовать выражение для максимумов токов Iс и IL:
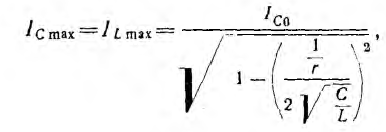
выражению для частоты 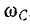 , при которой Uc проходит через максимум, будет соответствовать выражение
, при которой Uc проходит через максимум, будет соответствовать выражение 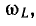 , при которой IL проходит через максимум:
, при которой IL проходит через максимум:
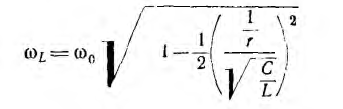
Совершенно аналогичны между собой и режимы работы параллельной цепи при ω = var и U = const (см. рис. 7.10) и последовательной — при ω = var и 1=const, если произвести указанную замену величин (обозначения кривых даны справа в скобках). Интересно отметить,что при неизменном токе напряжение U последовательной цепи при резонансе, когда 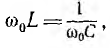 получает минимальное значение.
получает минимальное значение.
Повышение коэффициента мощности
Схема, в которой возможен резонанс токов, используется в электротехнике для повышения коэффициента мощности. Обычно приемники электрической энергии имеют активно-индуктивный характер, т. е. работают со сдвигом фаз 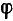 >0 между напряжением и током. Так, электрический двигатель переменного тока может быть представлен в виде схемы с параллельным соединением r и XL (рис. 7.11, а), где активная мощность Р, расходуемая в сопротивлении г, равна сумме полезной мощности двигателя и всех потерь в нем, а реактивная мощность Q индуктивного сопротивления XL равна индуктивной мощности двигателя, связанной с его магнитным полем.
>0 между напряжением и током. Так, электрический двигатель переменного тока может быть представлен в виде схемы с параллельным соединением r и XL (рис. 7.11, а), где активная мощность Р, расходуемая в сопротивлении г, равна сумме полезной мощности двигателя и всех потерь в нем, а реактивная мощность Q индуктивного сопротивления XL равна индуктивной мощности двигателя, связанной с его магнитным полем.
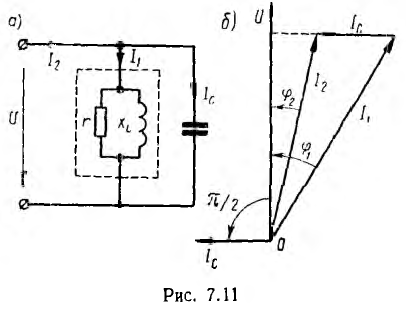
Источник энергии, питающий такой приемник, а также линия передачи должны быть рассчитаны на полную мощность S = UI, превышающую среднюю мощность приемника Р = UI cosϕ. Для меньшения полной мощности источника и линии передачи путем повышения коэффициента мощности часто применяется параллельное пюдключение к приемнику батареи конденсаторов, т. е. схема, в которой возможен резонанс токов.
На рис. 7.11, б показана векторная диаграмма этой цепи. Здесь r1 — ток нагрузки, ϕ1 — фазный сдвиг, / с — ток батареи конденсаторов, который при пренебрежении потерями в них опережает напряжение U по фазе на угол 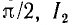 — ток источника, ϕ2 — новый фазный сдвиг. На основании этой диаграммы можно вычислить емкость С батареи конденсаторов, необходимой для уменьшения фазного сдвига ϕ1 до величины ϕ2:
— ток источника, ϕ2 — новый фазный сдвиг. На основании этой диаграммы можно вычислить емкость С батареи конденсаторов, необходимой для уменьшения фазного сдвига ϕ1 до величины ϕ2:
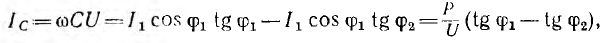
где Р — средняя мощность приемника.
Отсюда
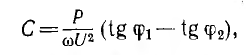
при ϕ2 = 0 емкость
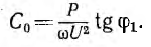
Элементарные методы расчета простых цепей переменного тока
Эквивалентные схемы:
При расчете цепи любой приемник может быть заменен эквивалентной схемой с сосредоточенными параметрами, имеющей равные ток и фазный сдвиг при том же напряжении и той же частоте. Если приемник (рис. 7.12, а) при напряжении U и частоте f потребляет ток I с фазным сдвигом 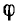 (рис. 7.12, б), то полное сопротивление r и полная мощность S этого приемника и его эквивалентной схемы будут:
(рис. 7.12, б), то полное сопротивление r и полная мощность S этого приемника и его эквивалентной схемы будут:
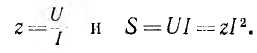
Первой простейшей эквивалентной схемой является последовательное соединение активного г и реактивного х сопротивлени, (рис. 7.12, в для случая преобладания индуктивного сопротивления)
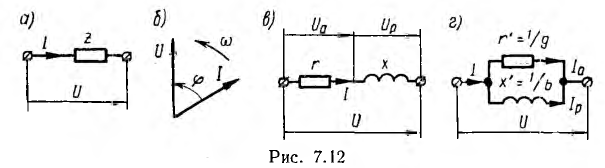
Тогда активные и реактивные сопротивления, напряжения и мощности этой эквивалентной схемы соответственно равны:
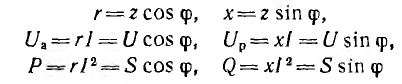
и могут быть представлены катетами подобных прямоугольных треугольников, гипотенузы которых равны полным величинам:
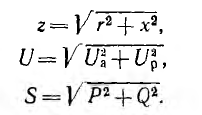
Треугольники сопротивлений, напряжений и мощностей изображены на рис. 7.13, а.
Второй простейшей эквивалентной схемой того же приемника является параллельное соединение активного r’ и реактивного x’ сопротивлений (рис. 7.12, г), не равных r и х эквивалентной ей последовательной схемы. Параллельную схему удобней характеризовать проводимостями: активной 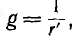 реактивной
реактивной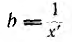 и полной у. Полная проводимость и полная мощность приемника и его параллельной эквивалентной схемы соответственно равны:
и полной у. Полная проводимость и полная мощность приемника и его параллельной эквивалентной схемы соответственно равны:
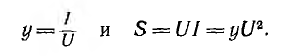
Токи ветвей параллельной эквивалентной схемы, называемые активным и реактивным:
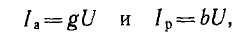
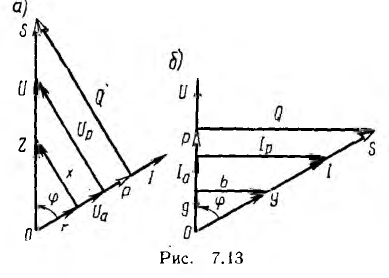
изображены на векторной диаграмме рис. 7.13, б. Так как они сдвинуты между собой по фазе на угол π/2, полный ток
откуда 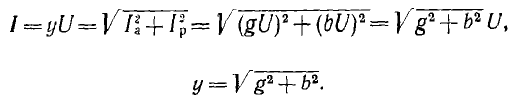
На рис. 7.13, б прямоугольный треугольник токов совмещен стреугольником проводимостей, а также с треугольником мощностей, гипотенуза которого равна полной мощности S, а катеты —активной и реактивной мощностям:

Все эти треугольники имеют у вершины угол 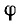 и подобны.
и подобны.
Сопротивления и проводимости часто называют параметрами приемников. Это определение полностью справедливо для и у, величины же r, х и g, b правильней называть параметрам и эквивалентных схем.
Так как последовательная и параллельная схемы эквивалентны между собой, активные, реактивные и полные мощности их должны быть также между собой равны:
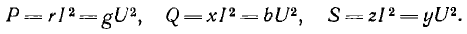
Отсюда могут быть получены переходные формулы зт сопротивлений последовательной схемы к проводимостям параллельной схемы:
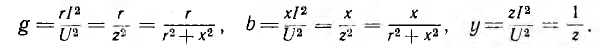
Аналогичным образом могут быть получены переходные формулы от проводимостей параллельной схемы к сопротивлениям последовательной:
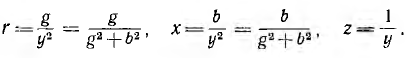
Таким образом, обратными друг другу являются только полные сопротивление г и проводимость у, активные и реактивные сопротивления и проводимости находятся в более сложной зависимости.
При анализе поведения какого-либо приемника при переменной частоте необходимо заменять его эквивалентной схемой, близкой физической сущности этого приемника, т. е. схемой, в которой сопротивления, индуктивности и емкости ее элементов могут быть приняты пастояинными. Так, в некотором диапазоне частот можно пренебречь поверхностным эффектом, и, например, для кольцевого соленоида считать сопротивление r и индуктивность L независящими от частоты, определяя их по формулам:
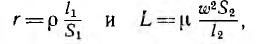
где l1 и l2 — соответственно длины провода обмотки и сердечника, S1, и S2 — их сечения. Пренебрегая током через межвитковые емкости соленоида, что допустимо только при низких частотах, следует представить соленоид в виде последовательной эквивалентной схемы постоянными параметрами r и L (см. рис. 7.12, в). Тогда при постоянном токе (ω = 0) соленоид и его эквивалентная схема будут иметь сопротивление r, а с ростом частоты ω его сопротивление z = 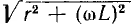 будет возрастать, что соответствует действительности, cопротивление параллельной схемы с постоянными параметрами r’ и L’ (см. рис. 7.12, г) при ω = 0 было бы равно нулю, при ω=
будет возрастать, что соответствует действительности, cопротивление параллельной схемы с постоянными параметрами r’ и L’ (см. рис. 7.12, г) при ω = 0 было бы равно нулю, при ω= 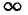 стало бы равным активному сопротивлению, что не соответствует действительности. Поэтому параметры г’ и L’ параллельной эквивалентно схемы должны изменяться с частотой.
стало бы равным активному сопротивлению, что не соответствует действительности. Поэтому параметры г’ и L’ параллельной эквивалентно схемы должны изменяться с частотой.
Цепи с последовательным и параллельным соединением приемников
При последовательном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из последовательного соединения активного г и реактивного х сопротивлений.
Ток всех приемников такой цепи одинаков, а мгновенное значение напряжения, согласие второму закону Кирхгофа, равно алгебраической сумме мгновенных значений напряжений отдельных приемников. При переходе к векторам алгебраическая сумма заменяется геометрической.
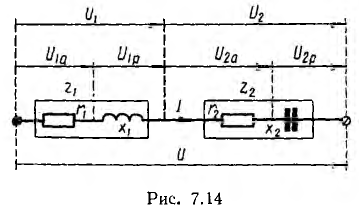
В качестве примера на рис. 7.15, а показана векторная диаграмма для цепи рис. 7.14, состоящей из последовательного соединения двух приемников —одного с индуктивным характером нагрузки и другого с емкостным. Векторы напряжения приемников и всей цени разлагаются на составляющие: активные Uа — по вектору тока и реактивные Uр — перпендикулярно вектору тока. Если разделить все напряжения (стороны треугольников напряжений: 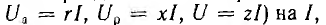 получится подобный рис. 7.15, а многоугольник сопротивлений (рис. 7.15, б). При умножении напряжений на I получится подобный рис. 7.15, а многоугольник мощностей со сторонами
получится подобный рис. 7.15, а многоугольник сопротивлений (рис. 7.15, б). При умножении напряжений на I получится подобный рис. 7.15, а многоугольник мощностей со сторонами 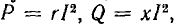
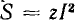 (рис. 7.15, в).
(рис. 7.15, в).
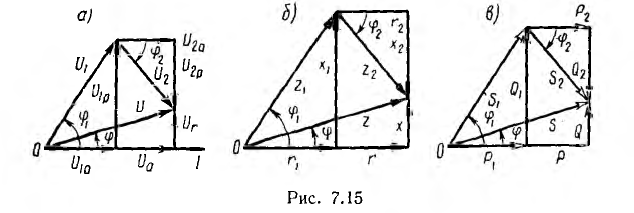
При параллельном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из параллельного соединения активной g и реактивной b проводимостей. Напряжение всех приемников такой цепи одинаково, а мгновенное значение тока цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников. При пере ходе к векторам алгебраическая сумма заменяется геометрической.
В качестве примера на рис. 7.17 дана векторная диаграмма для цепи, состоящей из параллельного соединения приемника с индуктивным характером нагрузки и приемника с емкостной нагрузкой (рис. 7.16). Векторы тока приемников и всей цепи разлагаются на составляющие:
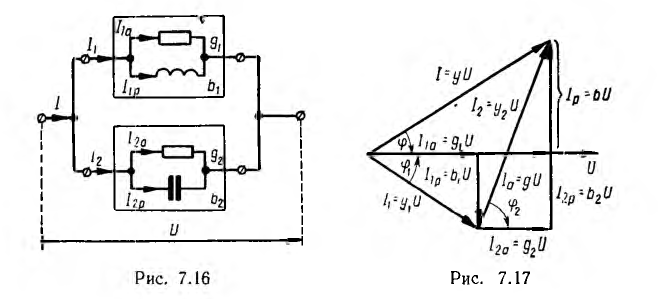
активные Iа по вектору напряжения U и реактивные Iр — перпендикулярно вектору напряжения. Если разделить все токи (стороны треугольников токов: 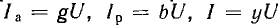 ) на U, получится подобный рис. 7.17 многоугольник проводимостей (g, b, у), а при умножении токов на U — подобный многоугольник мощностей (Р = gU2 , Q = bU2, , S = yU2).
) на U, получится подобный рис. 7.17 многоугольник проводимостей (g, b, у), а при умножении токов на U — подобный многоугольник мощностей (Р = gU2 , Q = bU2, , S = yU2).
Из многоугольников рис. 7.15 и 7.17 видно, что при последовательном соединении складываются сопротивления, напряжения и мощности, а при параллельном — проводимости, токи и тоже мощности. Активные величины складываются арифметически, реактивные — алгебраически, а полные — геометрически.
Расчет цепей со смешанным соединением приемников методами преобразования и пропорционального пересчета
При смешанном (параллельно-последовательном) соединении приемников с заданными параметрами, питаемых одним источником энергии, токи, напряжения и мощности ветвей цепи могут быть определены аналитически методом преобразования, заключающимся в постепенной замене сложной цепи более простой, ей эквивалентной. Ход решения подобной задачи показан на рис. 7.18.
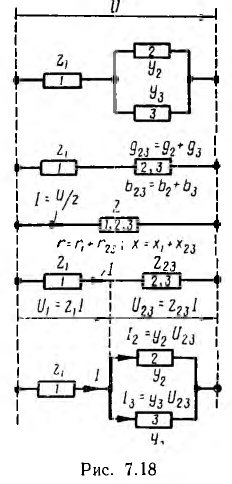
Группа приемников, соединенных параллельно, заменяется одним, активная проводимость которого равна арифметической сумме активных проводимостей приемников, а реактивная—алгебраической сумме реактивных. Группа приемников, соединенных последовательно, заменяется одним, активное сопротивление которого равно арифметической сумме активных сопротивлений отдельных приемников, а реактивное — алгебраической сумме. После замены всей цени одним приемником определяется ток при заданном напряжении или напряжение при заданном токе и сдвиг фаз между ними. Затем схема разворачивается в первоначальную цепь с постепенным определением напряжений, токов и фазных сдвигов в отдельных приемниках.
В процессе решения этой задачи несколько раз приходится при менять переходные формулы от сопротивлений к проводимостях и от проводимостей к сопротивлениям.
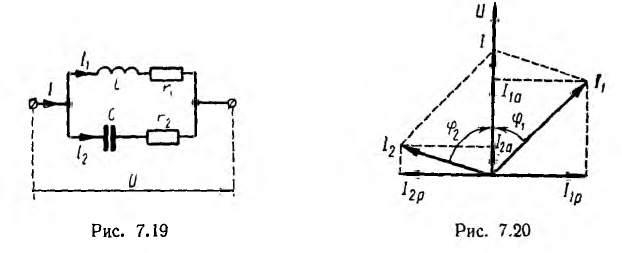
В качестве примера далее решается важная для электротехники задача определения частоты ω, при которой в схеме рис. 7.19 наступит резонанс токов, т. е. напряжение и ток всей цепи будут совпадать по фазе. Для этого, очевидно, реактивная проводимость всей цепи должна быть равна нулю:
откуда 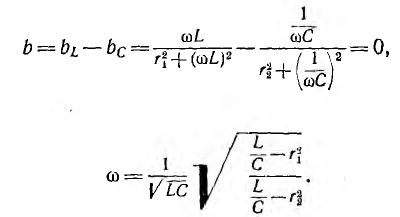
Таким образом, в общем случае, когда 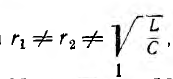 частота ω резонанса в этой цепи отличается от частоты
частота ω резонанса в этой цепи отличается от частоты 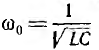 резонанс; при последовательном или параллельном соединении L и С. Векторная диаграмма для резонанса в цепи рис. 7.19 изображена на рис. 7.2G Реактивные составляющие токов ветвей в сумме дают нуль, и ток все цепи равен сумме активных составляющих.
резонанс; при последовательном или параллельном соединении L и С. Векторная диаграмма для резонанса в цепи рис. 7.19 изображена на рис. 7.2G Реактивные составляющие токов ветвей в сумме дают нуль, и ток все цепи равен сумме активных составляющих.
Так как в общем случае токи ветвей сдвинуты по фазе не на π/2, их мгновенные мощности, изменяющиеся с двойной частотой, будут сдвинуты по фазе на угол, отличный от π, т. е. они не находятся в противофазе. Это значит, что в общем случае резонанса полного обмена энергиями между индуктивной и емкостной ветвями не происходит.
Интересно отметить частные случаи:
1) при 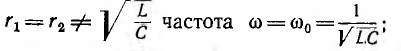
2) при 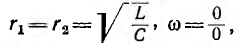 т. е. резонанс будет при любой частоте;
т. е. резонанс будет при любой частоте;
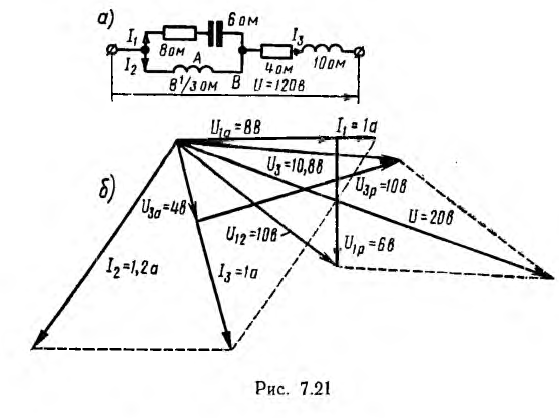
3) при  резонансная частота будет мнимым числом, а это значит, что резонанс в этой цепи невозможен.
резонансная частота будет мнимым числом, а это значит, что резонанс в этой цепи невозможен.
Расчет подобных цепей может быть произведен также графоаналитически — методом пропорционального пересчета. Он основан на том, что в линейной цепи токи пропорциональны напряжениям, следовательно, векторная диаграмма напряжений и токов, рассчитанная или построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении этого напряжения, и лишь масштабы для напряжения и тока изменятся во столько же раз.
Например, для цепи рис. 7.21, а, решая задачу графоаналитически, целесообразно строить векторную диаграмму, задавшись током первой ветви l1, = 1а. Затем последовательно вычисляются и в выбранном масштабе наносятся на диаграмму векторы в соответствии со своей фазой, после чего они складываются графически (рис. 7.21, б):
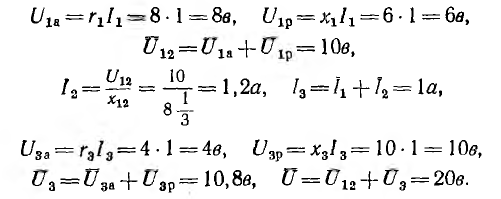
Таким образом, напряжение всей цепи оказалось равным 20 б вместо заданных 120 в. Следовательно, векторная диаграмма рис. 7.21, б остается действительной и для заданного напряжения, если увеличить масштабы для напряжений и токов в 120/20 = 6 раз.
Элементы и параметры электрических цепей переменного тока
Все реальные электротехнические устройства обладают электрическим сопротивлением R, индуктивностью L и емкостью С, которые являются параметрами электрической цепи переменного тока. Однако влияние каждого из параметров на ток в цепи различно, поэтому в некоторых случаях из расчетной схемы исключаются те, влияние которых незначительно.
Таким образом схема электрической цепи переменного тока характеризуется одним из указанных параметров R, L, C или комбинацией их при различных способах соединения элементов.
Цепь с активным сопротивлением
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
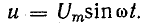
Требуется определить ток и мощность цепи.
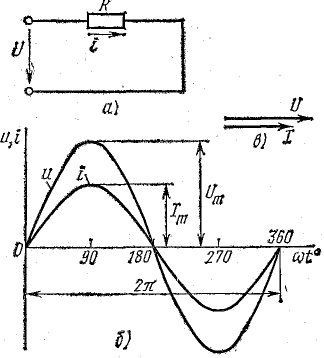
Рис. 13.1. К вопросу о цепи с активным сопротивлением
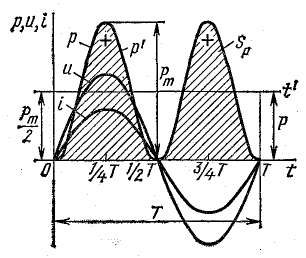
Рис. 13.2. График мгновенной мощности в цепи с активным сопротивлением
Ток в цепи
Выражение для мгновенного тока найдем по закону Ома:
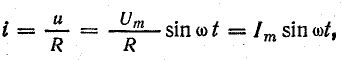
где 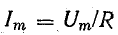 — амплитуда тока.
— амплитуда тока.
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, в).
Действующий ток найдем, разделив амплитуду на 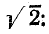
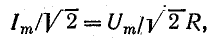
отсюда
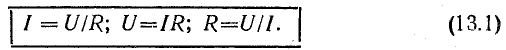
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы (2.6) для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока:
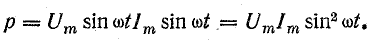
Из тригонометрии найдем
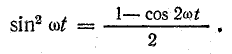
Учитывая это, запишем
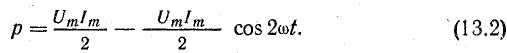
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2).
Если ось времени t поднять по чертежу на величину р = Рm/2 = UmIm/2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
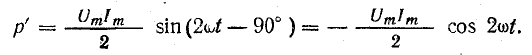
Таким образом, в первоначальной системе координат мгновенная мощность равна сумме постоянной величины 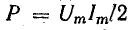 и переменной р’:
и переменной р’: 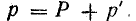
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2.
Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sр выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Рm.
В этом случае часть площади Sр, находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
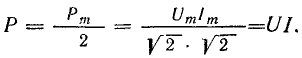
Активная мощность цепи с сопротивлением равна произведению действующих величин напряжения и тока:
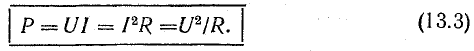
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности р(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
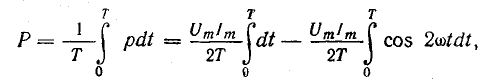
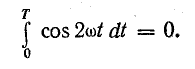
Поэтому
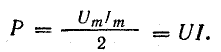
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Цепь с индуктивностью
Исследуемая далее цепь, содержащая только индуктивность, является искусственной, так как катушки, линии электропередачи и другие устройства кроме индуктивности L имеют и активное сопротивление.
Однако рассмотрение идеальной катушки (при R = 0) необходимо для уяснения физических процессов в реальных цепях.
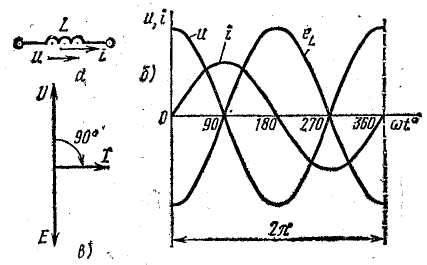
Рис. 13.4. К вопросу о цепи с индуктивностью
Это тем более важно, что в отдельных случаях активным сопротивлением и емкостью можно пренебречь из-за их малости. Например, ненагруженный трансформатор в схеме замещения в ряде случаев может быть представлен только своей индуктивностью.
Допустим, что для цепи (рис. 13.4, а) известны индуктивность L и ток, изменяющийся по закону

Требуется определить напряжение и мощность цепи.
Индуктивное напряжение
Переменный ток в катушке вызывает э. д. с. самоиндукции. При отсутствии активного сопротивления приложенное к катушке напряжение уравновешивается только э. д. с. самоиндукции, поэтому в соответствии со вторым законом Кирхгофа в любой момент времени 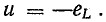
Э. д. с. самоиндукции пропорциональна скорости изменения тока [см. формулу (10.10)]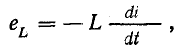
а напряжение
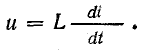
Уравнение приложенного напряжения можно найти, рассматривая векторную диаграмму на рис. 13.5, где ток изображен вектором Im, который предполагается вращающимся с угловой скоростью, равной угловой частоте ω. В начальном положении (при t = 0) вектор Im направлен по горизонтальной оси вправо. Это соответствует уравнению тока (13.4), если мгновенные величины i определять проекцией вращающегося вектора Im на вертикальную ось.
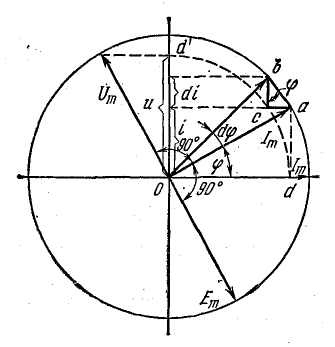
Рис. 13.5. Векторная диаграмма цепи с индуктивностью
Рассмотрим промежуточные положения вектора Im, отстоящие от начального на угол 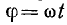 и
и 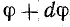 , где dφ — элементарный угол, на который вектор Im поворачивается за малый промежуток времени dt. За время dt ток изменился на di. Приращение тока выражается катетом прямоугольного треугольника abc, гипотенуза которого ab при весьма малом угле dφ может быть приравнена дуге окружности между точками а и b, а угол при вершине b равен φ. Поэтому отрезок ab в масштабе тока имеет значение
, где dφ — элементарный угол, на который вектор Im поворачивается за малый промежуток времени dt. За время dt ток изменился на di. Приращение тока выражается катетом прямоугольного треугольника abc, гипотенуза которого ab при весьма малом угле dφ может быть приравнена дуге окружности между точками а и b, а угол при вершине b равен φ. Поэтому отрезок ab в масштабе тока имеет значение 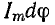 и
и 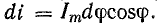
Уравнение напряжения
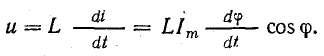
Но
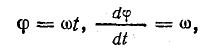
поэтому
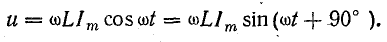
Это уравнение можно получить, дифференцируя уравнение тока:
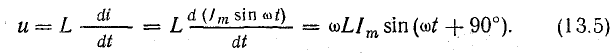
Индуктивное сопротивление
Действующая величина напряжения определяется из уравнения (13.5), где 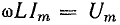 — амплитуда напряжения.
— амплитуда напряжения.
Разделив это выражение на 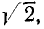 получим
получим
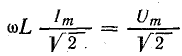
Отсюда
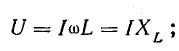

Коэффициент пропорциональности между действующими величинами напряжения и тока, равный произведению индуктивности и угловой частоты ωL, обозначают XL и называют реактивным сопротивлением индуктивности или индуктивным сопротивление е м.
Индуктивное сопротивление выражается в омах:
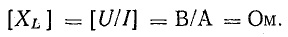
Действующая величина тока в цепи с индуктивностью равна отношению действующей величины напряжения к индуктивному сопротивлению.
Формула (13.6) похожа на формулу Ома. Это позволяет ток в цепи с индуктивностью определять так же, как ток в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения ничего общего с обычным сопротивлением не имеет. Понятие об индуктивном сопротивлении, введенное для облегчения расчета, заменяет в расчете фактическое влияние э. д. с. самоиндукции на ток в цени, т. е. отражает инерционные свойства электрической цепи.
Векторная диаграмма цепи
Сопоставление уравнений тока (13.4) и напряжения (13.5) показывает, что в цепи с индуктивностью ток отстает от напряжения по фазе на четверть периода, или в угловой мере на π/2. Это видно также на рис. 13.5. Мгновенное напряжение выражается отрезком о-d в масштабе, отличающемся от масштаба тока в ωL раз. Перенесем этот отрезок на вертикальную ось (отрезок о-d’), где откладываются мгновенные величины тока. Этому мгновенному напряжению и соответствует вектор Um, опережающий вектор Im по ходу вращения на угол 90°. Э.д.с. самоиндукции, направленная против приложенного напряжения, имеет уравнение
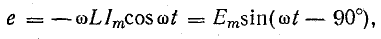
а на рис. 13.5 изображена вектором Еm, отстающим от вектора тока Im на 90°. На рис. 13.4 это показано отдельно на графике и векторной диаграмме (на векторной диаграмме отложены действующие величины).
Мгновенная и реактивная мощности
Мгновенная мощность 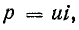 или
или
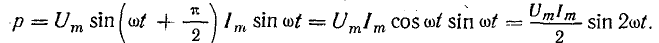
График изменения мощности (рис. 13.6) представляет собой синусоиду двойной частоты с амплитудой
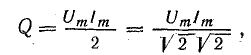
или

Наибольшая величина мощности в цепи с индуктивностью равна произведению действующих напряжения и тока.
Для выяснения физического смысла энергетических процессов обратим еще раз внимание на график мощности. Из него видно, что мгновенная мощность в течение периода четыре раза меняет знак (в моменты времени Т/4; Т/2; 3/4Т; Т). Изменение знака мощности означает, что направление потока энергии меняется.
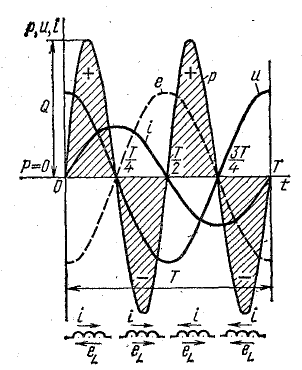
Рис. 13.6. График мгновенной мощности в цепи с индуктивностью
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии, ток направлен против э. д. с. самоиндукции. Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику).
Направления э. д. с. самоиндукции и тока в катушке совпадают — катушка является источником энергии. В следующую половину периода процесс повторяется. Нетрудно заметить, что количество энергии, накапливаемой в катушке за одну четверть периода (заштрихованная площадь «+»), точно равно количеству энергии, возвращаемой обратно в следующую четверть периода (заштрихованная площадь «—»).
Средняя (активная) мощность за период в цепи с индуктивностью равна нулю (Р = 0), так как в цепи с индуктивностью преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Скорость накопления и убыли энергии магнитного поля меняется по гармоническому закону. Амплитуда кривой мгновенной мощности Q является характеристикой этого процесса и называется реактивной мощностью.
Единицу мощности в этом случае называют вар — вольт-ампер реактивный — в отличие от единицы активной мощности — ватта.
Задача 13.4.
Катушка имеет индуктивность L = 15,9 мГн, активное сопротивление R = 0. Начертить график зависимости индуктивного сопротивления и тока в катушке от частоты приложенного напряжения, если действующее напряжение U = 100 В остается неизменным.
Решение. Нужно задаться несколькими величинами частоты, определить соответствующие индуктивные сопротивления, а затем величины тока.
Для частоты f = 50 Гц
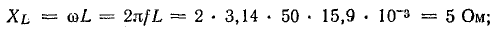
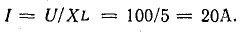
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте в прямоугольной системе координат графики согласно условию задачи.
Цепь с емкостью
В конденсаторе с идеальным диэлектриком предполагается полное отсутствие тока проводимости и потерь энергии. Изменение напряжения между обкладками конденсатора сопровождается электрическим током смешения, величина которого зависит от емкости С. При напряжении на конденсаторе (рис. 13.7, а) 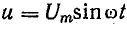 определим ток и мощность.
определим ток и мощность.
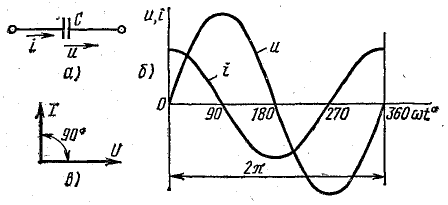
Рис. 13.7, К вопросу о цепи с емкостью
Электрический ток смещения
Внешнее электрическое поле вызывает поляризацию диэлектрика.
При всяком изменении электрического поля изменяется поляризованность диэлектрика, причем связанные заряженные частицы, входящие в состав атомов и молекул вещества, перемещаются, образуя электрический ток.
Явление движения связанных заряженных частиц в диэлектрике при изменении поляризации диэлектрика называют электрическим током поляризации.
Ток поляризации, согласно формуле (2.2),
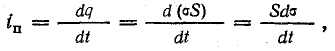
где σ —плотность электрического смещения заряда; отсюда
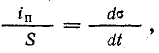
где 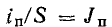 — плотность тока поляризации.
— плотность тока поляризации.
Учитывая формулу (7.20), найдем, что плотность тока поляризации равна скорости изменения поляризованности:
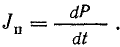
При изменении электрического поля меняется не только вектор поляризации Р, но и вектор электрического смещения в вакууме D0.Из выражений (7.22) и (7.24) следует
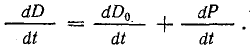
Второе слагаемое в правой части этого уравнения есть плотность тока поляризации, связанного с движением заряженных частиц диэлектрика. Первое слагаемое также имеет размерность плотности тока, но характеризует физический процесс в самом электрическом поле при его изменении во времени.
Величину 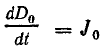 называют плотностью электрического смещения в вакууме. Плотность полного электрического тока смещения
называют плотностью электрического смещения в вакууме. Плотность полного электрического тока смещения
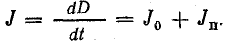
Введение понятия о токе смещения позволяет рассматривать электрическую цепь с конденсатором непрерывной: на участках из проводников имеется ток проводимости, а в диэлектрике — равный ему ток смещения.
Ток в цепи с емкостью
Заряд конденсатора пропорционален напряжению между его обкладками [см. формулу (7.28)], поэтому изменение напряжения сопровождается изменением заряда:
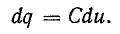
Скорость изменения заряда пропорциональна скорости изменения напряжения:
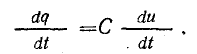
Но скорость изменения заряда равна электрическому току [см. формулу (2.2)]:

При этом во внешнем по отношению к конденсатору участке цепи происходит движение электронов (ток проводимости) через источник. Одновременно при увеличении напряжения совершается поляризация диэлектрика в конденсаторе и возникает ток смещения. При уменьшении напряжения диэлектрик деполяризуется.
Таким образом, ток в цепи с конденсатором пропорционален скорости изменения напряжения на его обкладках.
Уравнение (13.8) по форме подобно уравнению (13.5). Поэтому характер изменения тока при синусоидальном напряжении можно проследить на векторной диаграмме аналогично тому, как это сделано при рассмотрении цепи с индуктивностью (см. рис. 13.5), отнеся рассуждения к скорости изменения напряжения.
На диаграмме векторы тока и напряжения следует поменять местами . В связи с этим уравнение тока для цепи с емкостью можно записать аналогично уравнению для напряжения в цепи с индуктивностью:
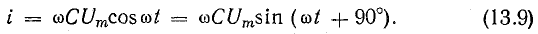
Уравнение тока можно получить, дифференцируя уравнение напряжения:
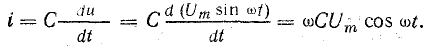
Емкостное сопротивление
Величина 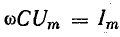 есть амплитуда тока. Разделив это выражение на
есть амплитуда тока. Разделив это выражение на 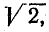 получим
получим

Величину 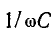 обозначают ХС и называют реактивным сопротивлением емкости или емкостным сопротивлением. Емкостное сопротивление — величина, обратная произведению емкости и угловой частоты.
обозначают ХС и называют реактивным сопротивлением емкости или емкостным сопротивлением. Емкостное сопротивление — величина, обратная произведению емкости и угловой частоты.
Действующий ток в цепи с емкостью равен отношению действующего напряжения к емкостному сопротивлению.
Формула (13.10) по форме совпадает с формулой Ома. Однако емкостное сопротивление физически ничего общего с обычным сопротивлением R не имеет.
Понятие о емкостном сопротивлении, введенное для облегчения расчетов, отражает в расчете противодействие заряженного конденсатора току в цепи.
Сопоставление уравнений напряжения и тока показывает, что в цепи с емкостью напряжение отстает от тока по фазе на четверть периода, или в угловой мере на π/2. На рис. 13.7, б, в это показано на графике и векторной диаграмме.
Мощность в цепи
Построение графика мгновенной мощности (рис. 13.8) выполняется точно так же, как и для цепи с индуктивностью, если иметь в виду, что мгновенная мощность выражается таким же произведением:
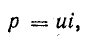
или
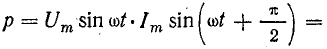
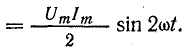
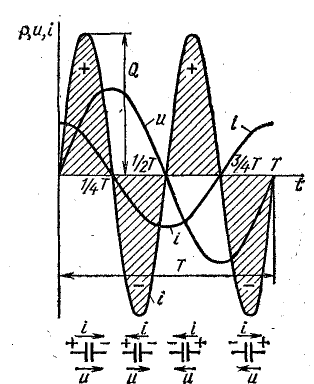
Рис. 13.8. График мгновенной мощности в цепи с емкостью
Из графика видно, что мгновенная мощность, как и в цепи с индуктивностью, четыре раза в течение периода меняет знак. В первую четверть периода, когда напряжение на конденсаторе увеличивается, энергия накапливается в электрическом поле конденсатора за счет работы источника. Конденсатор в это время заряжается, т. е. является приемником энергии: направления тока и приложенного напряжения совпадают. Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть (к источнику), ток в цепи направлен против напряжения сети, т. е. конденсатор является источником энергии (разряжается).
Проведя рассуждения, аналогичные тем, какие были вделаны для цепи с индуктивностью, найдем, что активная мощность в цепи с емкостью равна нулю (Р = 0), а реактивная мощность равна произведению действующих величин напряжения и тока:

Таким образом, в цепи с емкостью, так же как и в цепи с индуктивностью, преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Задача 13.7. Конденсатор имеет емкость С = 637 мкФ. Начертить график зависимости емкостного сопротивления и тока в конденсаторе от частоты приложенного напряжения, действующее значение которого U = 100 В остается неизменным.
Решение. Для решения задачи нужно задаться несколькими значениями частоты. Определить соответствующие величины емкостного сопротивления, а затем тока.
Для частоты 50 Гц

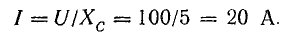
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте и прямоугольной системе координат графики согласно условию задачи.
Цепь с реальной катушкой индуктивности
Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р , а изменение энергии в магнитном поле — реактивной мощностью Q .
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.
Деление реальной катушки на два элемента искусственно, так как конструктивно оба элемента неразделимы. Однако такой же схемой замещения можно представить реальную цепь из двух конструктивно не совмещенных элементов, один из которых характеризуется только активной мощностью Р(Q = 0), а другой — реактивной (индуктивной) мощностью Q (Р = 0).
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
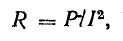
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением 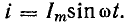 Требуется определить напряжение в цепи и мощность.
Требуется определить напряжение в цепи и мощность.
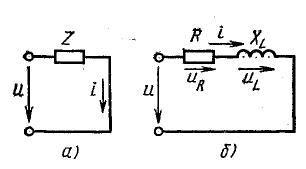
Рис. 13.9. Схема замещения реальной катушки индуктивности (цепь R, L)
При переменном токе в катушке возникает э. д. с. самоиндукции еL, поэтому ток зависит от действия приложенного напряжения и э. д. с. еL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид
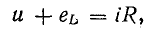
или
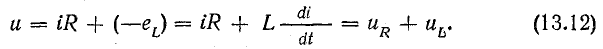
Приложенное к катушке напряжение состоит из двух слагаемых, одно из которых uR равно падению напряжения в активном сопротивлении, а другое 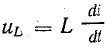 уравновешивает э. д. с. самоиндукции.
уравновешивает э. д. с. самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам, полученным, uR совпадает по фазе с током, а uL опережает ток на 90°.
Поэтому
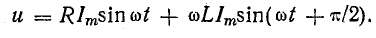
Векторная диаграмма напряжений. Полное сопротивление катушки
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
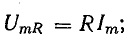
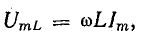
а действующие величины
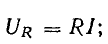
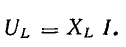
Вектор общего напряжения
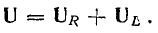
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Мi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока ψi = 0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ > 0, но <90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL:

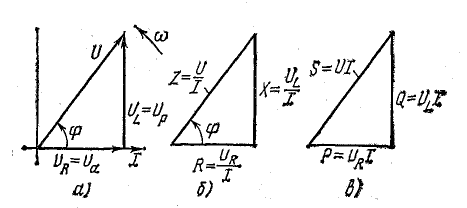
Рис. 13.10. Векторная диаграмма цепи, треугольники сопротивлений и мощностей
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Uа = UR

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Uр. Для катушки Up = UL

При токе 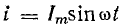 уравнение напряжения можно записать на основании векторной диаграммы в виде
уравнение напряжения можно записать на основании векторной диаграммы в виде
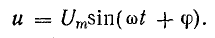
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное 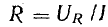 и индуктивное
и индуктивное 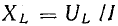 сопротивления, а гипотенузой — величина
сопротивления, а гипотенузой — величина 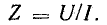
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома (2.6):
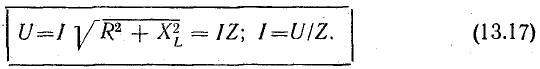
Из треугольников напряжений и сопротивлений определяются
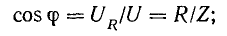
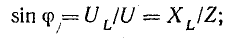
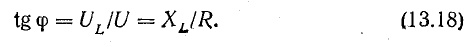
Мощность катушки
Мгновенная мощность катушки
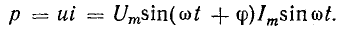
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенной мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
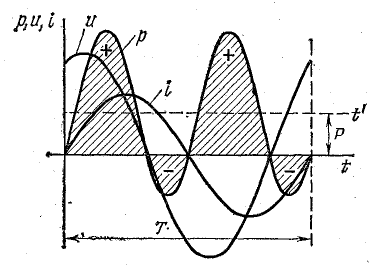
Рис. 13.11. График мгновенной мощности цепи
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
На основании выводов, в активном сопротивлении 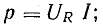
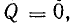 а в индуктивном
а в индуктивном 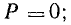
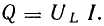
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении ХL . Подставляя значения 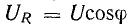 и
и 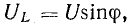 определяемые из треугольника напряжений по формулам (13.18), получим:
определяемые из треугольника напряжений по формулам (13.18), получим:


Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи:

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
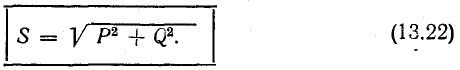
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток.
Из треугольника мощностей можно определить
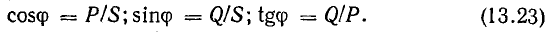
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В • А).
Активная мощность Р меньше или равна полной мощности цепи. Отношение активной мощности цепи к ее полной мощности 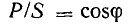 называют коэффициентом мощности.
называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование ее в другие виды энергии. Поэтому колебания энергии в цепи не только бесполезны, но и вредны, так как при этом в приемнике не совершается полного преобразования электрической энергии в работу или тепло, а в соединительных проводах она теряется.
Схема замещения катушки с параллельным соединением элементов
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной ВL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

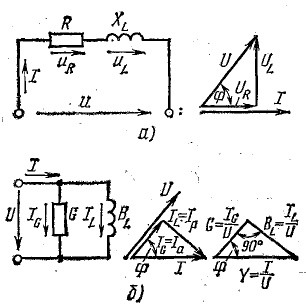
Рис. 13.12. Варианты схемы замещения катушки индуктивности
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG — ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и ILобразуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, 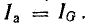
Составляющая тока в реактивном элементе

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная 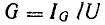 и индуктивная
и индуктивная 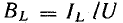 проводимости, а гипотенузой — величина
проводимости, а гипотенузой — величина 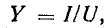 называемая полной проводимостью цепи.
называемая полной проводимостью цепи.
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим
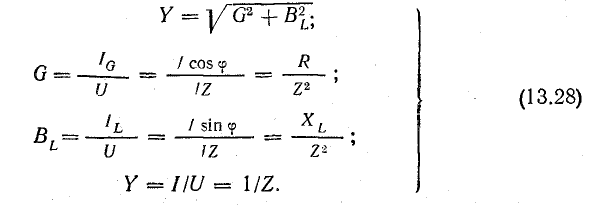
Кроме того,
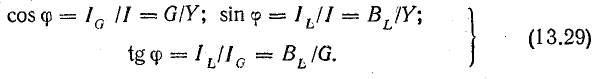
Задача 13.10.
Для определения параметров катушки R и L ее включили сначала в цепь постоянного тока, а затем в цепь переменного тока с частотой f = 50 Гц по схемам рис. 13.13, а, б.
При постоянном токе I1 = 4 А вольтметр показал U1 = 12 В, а при переменном I2 = 5А — U2 = 25 В. Определить активное сопротивление и индуктивность катушки и при переменном токе активную, реактивную и полную мощности. Построить векторную диаграмму и треугольник сопротивлений.
Решение. При постоянном токе э. д. с. самоиндукции в катушке не возникает. Поэтому индуктивное сопротивление ХL = 0. Ток определяется приложенным напряжением и активным сопротивлением.
По формуле Ома,
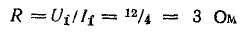
При переменном токе отношение напряжения к току даст величину полного сопротивления
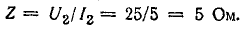
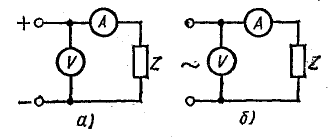
Рис. 13.13. к задаче 13.10
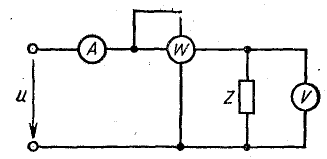
Рис. 13.14. К задачам 13.12, 13.13
Индуктивное сопротивление
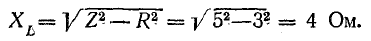
Индуктивность
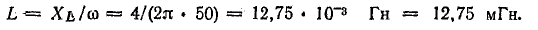
При разборе решения данной задачи на отдельном листе миллиметровой бумаги рекомендуется построить векторную диаграмму цепи и треугольники сопротивлений и мощностей, предварительно определив необходимые величины.
Задача 13.12.
В цепи переменного тока с активным сопротивлением и индуктивностью (рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают: амперметр — 10 А, вольтметр — 200 В, ваттметр — 1600 Вт. Определить параметры схем замещения цепи с последовательным (R, XL) и параллельным (G, ВL) соединением элементов; реактивную и полную мощности цепи. Построить векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с последовательным соединением элементов).
Сопротивления:
активное
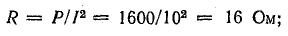
полное
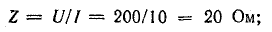
индуктивное
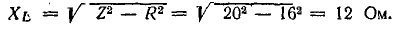
Мощности цепи:
реактивная
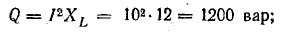
полная
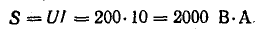
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие напряжения:
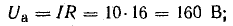
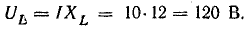
Векторная диаграмма показана на рис. 13.10, а.
Цепь с реальным конденсатором
При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток). Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.
Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(Р = 0).
Схема замещения конденсатора с параллельным соединением элементов
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Вс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе 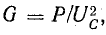 а емкость — конструкцией конденсатора .
а емкость — конструкцией конденсатора .
Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение 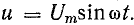
Требуется определить токи в цепи и мощность.
Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них также синусоидальны.
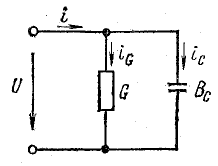
Рис. 13.15. Схема замещения реального конденсатора
При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:

Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:
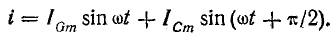
Так как
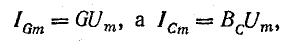
то
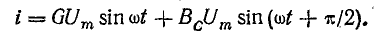
Векторная диаграмма токов
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
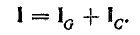
Действующие величины составляющих тока:


Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения 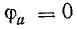 ).
).
Вектор IG совпадает по направлению с вектором U, а вектор Iс направлен перпендикулярно вектору U с положительным углом.
Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90′.
Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC:
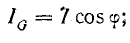
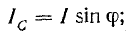
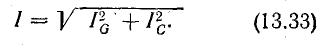
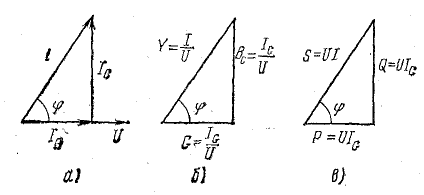
Рис. 13.16. Треугольники токов, проводимостей, мощностей
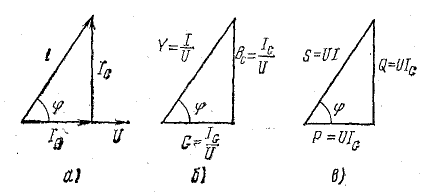
Рис. 13.17. График мгновенной мощности цепи
При напряжении 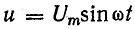 в соответствии с векторной диаграммой уравнение тока
в соответствии с векторной диаграммой уравнение тока
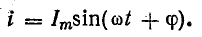
Треугольник проводимостей
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная 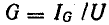 и емкостная
и емкостная 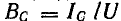 проводимости, а гипотенузой — полная проводимость цепи
проводимости, а гипотенузой — полная проводимость цепи 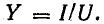
Из треугольника проводимостей

Связь между действующими величинами напряжения и тока выражается формулами
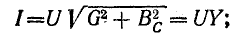
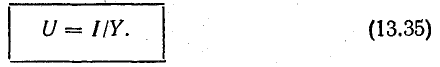
Из треугольников токов и проводимостей определяют величины
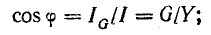
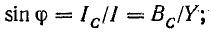
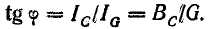
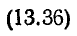
Мощность
Выражение мгновенной мощности реального конденсатора
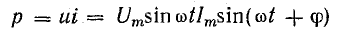
совпадает с выражением мгновенной мощности катушки.
Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17.
Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19)— (13.22)].
Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U.
В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности:
активная
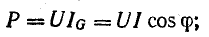
реактивная
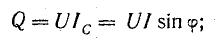
полная
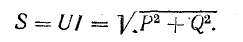
Схема замещения конденсатора с последовательным соединением элементов
Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями.
На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13.18, б). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным.
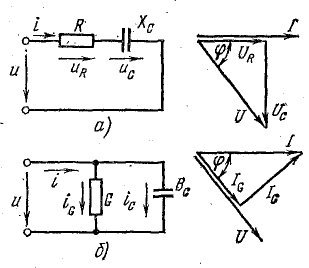
Рис. 13.18. Варианты схемы замещения реального конденсатора
Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью 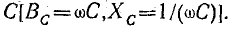
Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а.
Задача 13.13.
В цепи переменного тока с активным сопротивлением и емкостью (см. рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают. амперметр — 6 А, вольтметр — 180 В, ваттметр — 360 Вт. Определите параметры схем замещения цепи с параллельным (G, ВL) и последовательным (R, ХC) соединением элементов: реактивную и полную мощности цепи. Постройте векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с параллельным соединением элементов). Проводимости:
активная
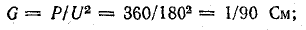
полная
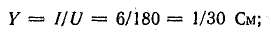
емкостная
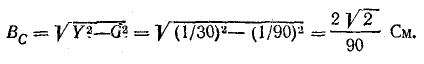
Мощности цепи
реактивная
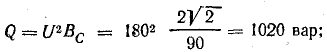
полная
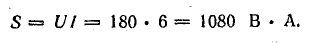
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие тока:
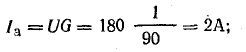
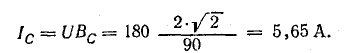
Векторная диаграмма показана на рис. 13.16, а.
Решить задачу для схемы с последовательным соединением элементов.
Расчет электрических цепей переменного тока с помощью векторных диаграмм
В данной главе будут рассмотрены электрические цепи переменного тока, содержащие три параметра R, L, С при последовательном, параллельном соединении резисторов, катушек и конденсаторов.
Расчет таких цепей можно вести на основе векторных диаграмм, из которых получаются расчетные формулы.
Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
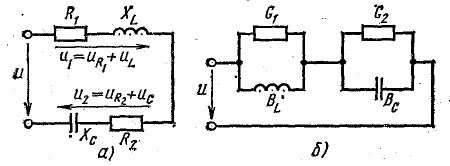
Рис. 14.1. Схемы замещения катушки и конденсатора при последовательном соединении
Предположим известными параметры катушки R1, L и конденсатора R2С; ток в цепи 
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цепи
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
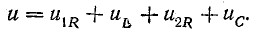
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
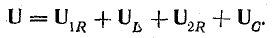
Для построения векторной диаграммы находим:
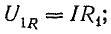
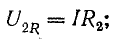
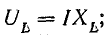
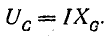
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая.
1.  . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
. Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
Векторная сумма напряжений 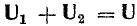 дает общее напряжение в цепи. Вместе с тем вектор UI является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения, цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются:
дает общее напряжение в цепи. Вместе с тем вектор UI является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения, цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: 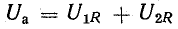 .
.
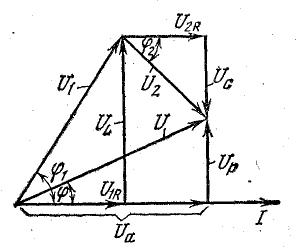
Рис. 14.2. Векторная диаграмма при ХL > ХC
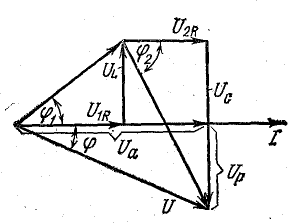
Рис. 14.3. Векторная диаграмма при ХL < X
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: 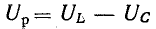
При одинаковом токе во всех элементах цепи 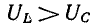 . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
. Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
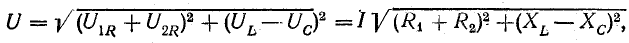
или
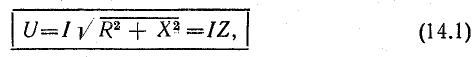
где 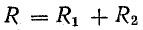 и
и 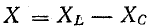 — общее активное и реактивное сопротивления цепи;
— общее активное и реактивное сопротивления цепи; 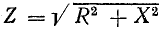 — полное сопротивление цепи.
— полное сопротивление цепи.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
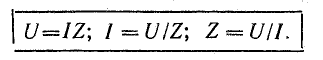
Из треугольников напряжения и сопротивлений определяют следующие величины:
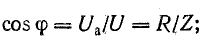
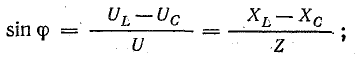
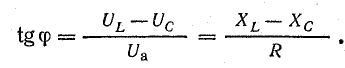
Угол сдвига по фазе между напряжением и током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2.  . Векторная диаграмма изображена на рис. 14.3, где UL < UC, поэтому общее напряжение отстает от тока на угол φ < 0.
. Векторная диаграмма изображена на рис. 14.3, где UL < UC, поэтому общее напряжение отстает от тока на угол φ < 0.
Реактивное сопротивление цепи носит емкостный характер. Расчетные формулы для первого случая остаются без изменения и для второго случая.
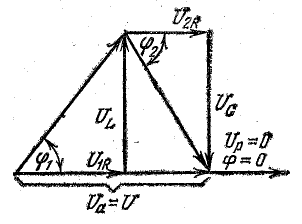
Рис. 14.4. Векторная диаграмма при XL = XC
3. 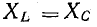 . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы:
. В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: 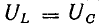 (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R. Общее напряжение совпадает по фазе с током и равно по величине активной составляющей напряжения.
(рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R. Общее напряжение совпадает по фазе с током и равно по величине активной составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
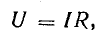 или
или 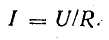
В случае ХL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи
Из треугольника напряжений легко получить треугольник мощностей, из которого следуют уже известные формулы:
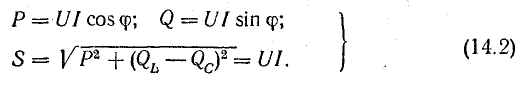
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ > 0 Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом угле, так как 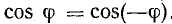
Полная мощность также всегда положительна.
На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии 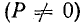 и обменный процесс между генератором и приемником
и обменный процесс между генератором и приемником 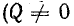 при
при 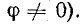
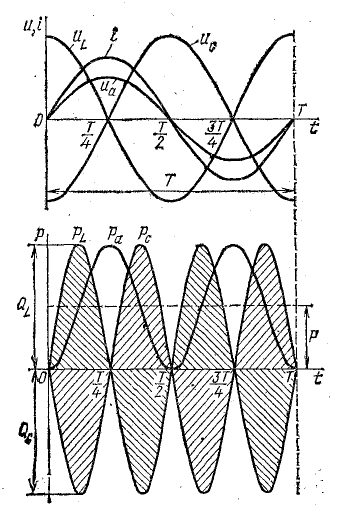
14.5. Графики u, i, p при XL = XC
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при 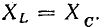
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задача 14.1.
Конденсатор емкостью С = 3,4 мкФ и катушка с активным сопротивлением R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к генератору с напряжением U = 200 В (рис. 14.6). Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и трех значениях частоты: 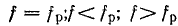 где fр — резонансная частота.
где fр — резонансная частота.
Решение. Для примера далее приведен расчет при частоте f = 250 Гц.
Реактивное сопротивление индуктивности
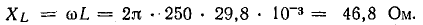
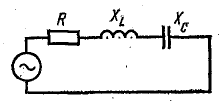
Рис. 14.6. К задаче 14.1
Реактивное сопротивление емкости
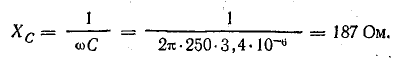
Полное сопротивление
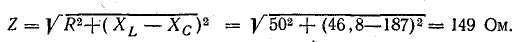
Ток в цепи
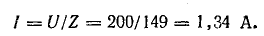
Угол сдвига фаз между током и напряжением
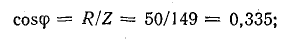

Активная мощность
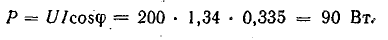
Реактивная мощность индуктивности
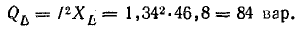
Реактивная мощность емкости
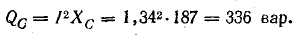
Реактивная мощность цепи
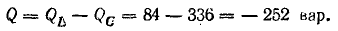
Сделать аналогичный подсчет для частот: f = fр; f < fр; f > fр.
Расчет неразветвленных цепей переменного тока
Порядок расчета, установленный для цепи при последовательном соединении катушки и конденсатора, можно применить и для цепи, содержащей произвольное число катушек и конденсаторов, соединенных последовательно.
На рис. 14.7, а для примера дана схема неразветвленной цепи, состоящей из пяти участков: конденсатора (R1, Х1) и катушки (R2, Х2), представленных активными и реактивными сопротивлениями; резистора R3; идеальных конденсатора Х4 и катушки Х5.
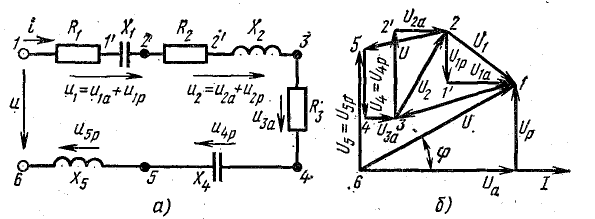
Рис. 14.7. Расчетная схема неразветвленной цепи и ее векторная диаграмма
Предположим, что кроме сопротивлений известен ток в цепи i = Imsinωt.
Требуется найти напряжения на участках, общее напряжение в цепи и мощность.
Векторная диаграмма
Выберем условно-положительное направление тока i, как указано на схеме. Для мгновенных величин в соответствии со вторым законом Кирхгофа уравнение напряжений
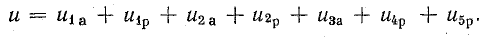
Переходя к действующим величинам напряжений, нужно написать векторную сумму:
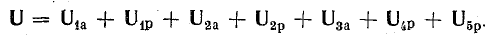
Численно векторы напряжений определяются произведением тока и сопротивления соответствующего участка.
На рис. 14.7, б построена векторная диаграмма, соответствующая этому уравнению. За исходный, как обычно при расчете неразветвленных цепей, принят вектор тока, а затем проведены векторы падения напряжения на каждом участке схемы, причем направления их относительно вектора тока выбраны в соответствии с характером сопротивления участков.
При построении диаграммы напряжений начальной точкой выбрана точка 6, совпадающая с началом вектора тока I. Из этой точки проведен вектор U5р реактивного напряжения индуктивности (по фазе опережает ток на 90°) между точками 5 и 6 цепи. Из конца его проведен вектор U4р реактивного напряжения емкости (по фазе отстает от тока на 90°) между точками 4 и 5 цепи. Затем отложен вектор U3a активного напряжения на резисторе (совпадает по фазе с током) между точками 3 и 4 цепи и т. д., если следовать по цепи против направления тока. Точки векторной диаграммы, где сходятся начало следующего вектора с концом предыдущего, обозначены теми же номерами, какими на схеме обозначены точки, отделяющие один элемент от другого.
При таком, построении напряжение между любыми двумя точками цепи можно найти по величине и фазе, проведя вектор на диаграмме между точками с теми же номерами. Например, напряжение U5.2 между точками 5 и 2 выражается вектором, проведенным из точки 2 в точку 5 (вектор U5.2 направлен в обратную сторону); напряжение U3.1 между точками 3 и 1 выражается вектором, проведенным из точки 1 в точку 3.
Векторная диаграмма, построенная в соответствии с чередованием элементов цепи, называется топографической, так как точки, отделяющие векторы друг от друга, соответствуют точкам, разделяющим элементы схемы.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов напряжений направлены одинаково — параллельно вектору тока, поэтому векторное сложение их можно заменить арифметическим и найти активную составляющую напряжения цепи: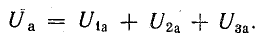
Реактивные составляющие векторов напряжений перпендикулярны вектору тока, причем индуктивные напряжения направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая напряжения цепи Uр определяется их алгебраической суммой, в которой индуктивные напряжения считаются положительными, а емкостные — отрицательными: 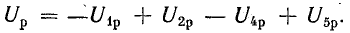
Векторы активного, реактивного и полного напряжений цепи образуют прямоугольный треугольник, из которого следует

Подставив падения напряжения, выраженные через ток и соответствующие сопротивления, получим:
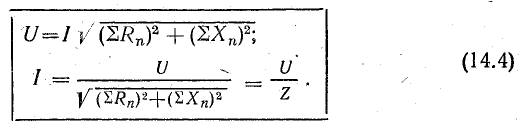
Таким образом снова получена знакомая уже формула, связывающая ток, напряжение и полное сопротивление цепи [ср. (14.4) и (14.1)].
В этой формуле 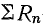 — общее активное сопротивление, равно арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь;
— общее активное сопротивление, равно арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь; 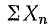 — общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные —отрицательными. Полное сопротивление неразветвленной цепи
— общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные —отрицательными. Полное сопротивление неразветвленной цепи
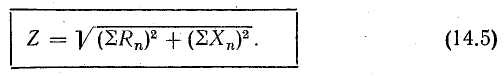
В общем случае полное сопротивление цепи определяется как гипотенуза прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активное и реактивное сопротивления всей цепи. Из треугольника сопротивлений следует:
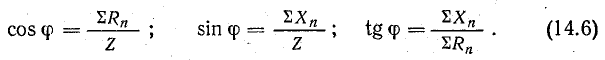
От треугольника напряжений можно перейти также к треугольнику мощностей и получить уже известные формулы для определения мощностей в цепи:
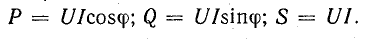
Вместе с тем активную мощность цепи можно представить как арифметическую сумму активных мощностей в элементах с активным сопротивлением. Реактивная мощность цепи равна алгебраической сумме мощностей реактивных элементов.
В этой сумме мощность индуктивных элементов считается положительной, а емкостных — отрицательной:
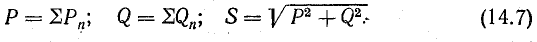
Формулы (14.2)—(14.7) являются общими; из них можно получить конкретное выражение для любой неразветвленной цепи.
Задача 14.3.
Определить ток и составить баланс мощностей для цепи, схема которой изображена на рис. 14.8. Построить топографическую диаграмму и по ней определить напряжение U8.5 между точками 8 и 5 и U6.1 между точками 6 и 1.
Дано:
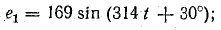
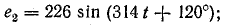
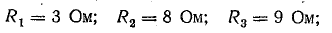
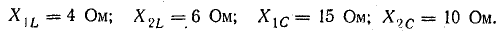
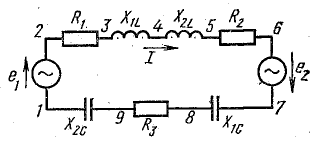
Рис. 14.8. К задаче 14.3
Решение. Согласно второму закону Кирхгофа, составим уравнение напряжений в векторной форме, предварительно выбрав условно-положительные направления э. д. с. и тока в схеме (их целесообразно выбрать одинаковыми независимо от того, в каком режиме работает источник э. д. с., так как фазовый угол сдвига, полученный в результате расчета, укажет истинный режим его работы):
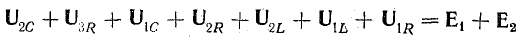
или
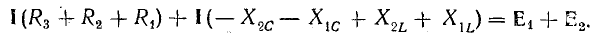
Общее активное сопротивление
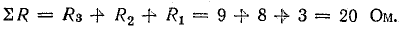
Общее реактивное сопротивление
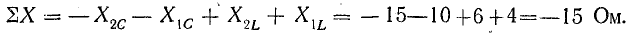
Как видно, общее реактивное сопротивление имеет емкостный характер. Полное сопротивление цепи
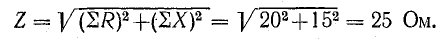
Действующие величины э. д. с.:
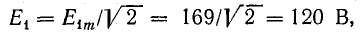
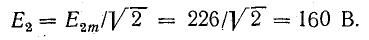
Для определения действующей величины суммы двух э. д. с. ( Е1 + Е2) построим векторную диаграмму (рис. 14.9, а) (рекомендуется построить на отдельном листе миллиметровой бумаги в масштабе Ми = 40 В/см).
Измерение вектора Е показывает, что величина суммарной э. д. с. Е = 200 В. Э. д. с. можно найти, учитывая, что ее составляющие взаимно перпендикулярны. В этом случае
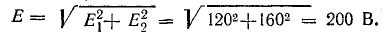
Ток
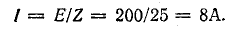
Напряжения на отдельных участках схемы:
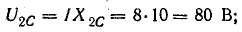
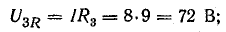
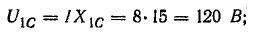
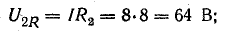
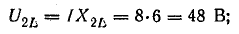
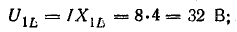
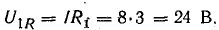
Для построения векторной топографической диаграммы (рис. 14.9, б) выберите масштабы Мi = 2 А/см; Ми = 40 В/см (рекомендуется построить на отдельном листе миллиметровой бумаги).
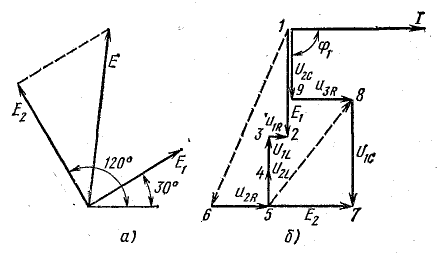
Рис. 14.9. К задаче 14.3
По векторной диаграмме найдены углы сдвига фаз между током и э. д. с. Е1 и Е2: φ1 = –90°, φ2 = 0.
Мощности участков приемника:
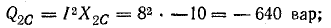
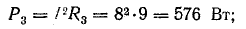
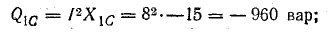
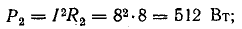
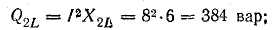
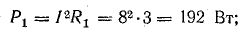
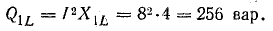
Мощности источников:
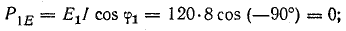
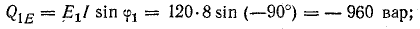
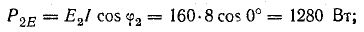
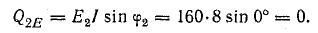
Баланс мощностей:
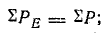
1280 = 192 + 576 + 512 = 1280;
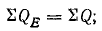
— 960 = — 640— 960 + 384 + 256 = — 960.
Реактивные мощности емкостного характера Q2С, Q1С и Q1E и отрицательны, так как между векторами напряжений и токов, определяющими их, углы отрицательны.
Для определения напряжений U8.5 и U6.1, проведем векторы между соответствующими точками топографической диаграммы. Вектор направляется к точке, стоящей первой в обозначении напряжения. Например, вектор U8.5 направлен в точку 8 из точки 5. Измерение векторов U8.5 и U6.1 дает:
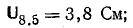
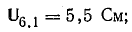
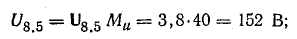
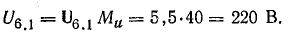
Параллельное соединение катушки и конденсатора
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
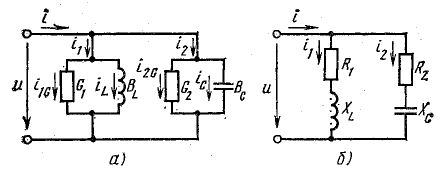
Рис. 14.11. Схемы замещения катушки и конденсатора при параллельном соединении
На схеме рис. 14.11, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, ВL и конденсатора G2, Вс, а также напряжение 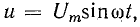 , определим токи в цепи и ее мощность.
, определим токи в цепи и ее мощность.
Векторная диаграмма цепи. Полная проводимость цепи
Согласно первому закону Кирхгофа, мгновенная величина общего тока равна сумме мгновенных токов отдельных ветвей:
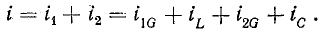
Имея в виду несовпадение по фазе активных и реактивных токов, величину общего тока найдем векторным сложением:
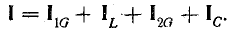
Для построения векторной диаграммы находим:
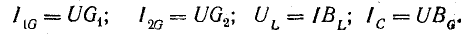
В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три случая.
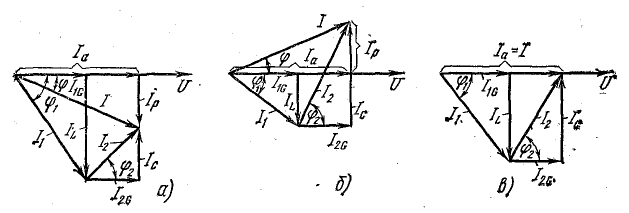
Рис. 14.12. Векторные диаграммы:
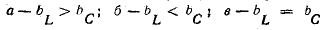
1. 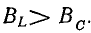 Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
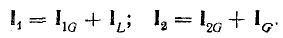
Векторная сумма токов 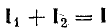 дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
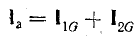 — активная составляющая;
— активная составляющая;
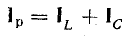 — реактивная составляющая.
— реактивная составляющая.
Векторы активных составляющих токов направлены в одну сторону, поэтому их численные значения складываются. Векторы реактивных составляющих токов направлены перпендикулярно вектору напряжения в противоположные стороны, поэтому им даются разные знаки: индуктивные токи считаются положительными, а емкостные — отрицательными. При одинаковом напряжении на всех элементах цепи  Общий ток отстает от общего напряжения по фазе на угол φ. Из треугольника токов следует
Общий ток отстает от общего напряжения по фазе на угол φ. Из треугольника токов следует
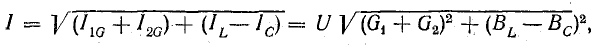
или
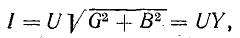
где 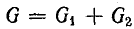 и
и 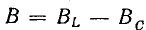 — общие активная и реактивная проводимости цепи;
— общие активная и реактивная проводимости цепи; 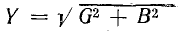 — полная проводимость цепи.
— полная проводимость цепи.
Эти три проводимости графически можно изобразить сторонами прямоугольного треугольника проводимостей, который получается уже известным способом из треугольника токов.
Полная проводимость цепи У является коэффициентом пропорциональности между действующими величинами общего тока и напряжения цепи:
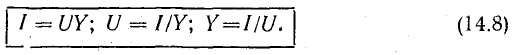
Из треугольников токов и проводимостей определяются величины:
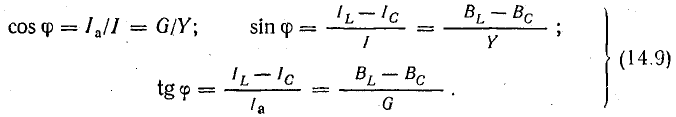
Угол сдвига по фазе между напряжением и общим током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2. 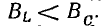 Векторная диаграмма изображена на рис. 14.12, б. Так как
Векторная диаграмма изображена на рис. 14.12, б. Так как 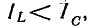 то напряжение отстает от общего тока на угол φ < 0.
то напряжение отстает от общего тока на угол φ < 0.
Реактивная проводимость цепи имеет емкостный характер. Расчетные формулы, полученные для случая 1, действительны и для этого случая.
3. 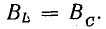 В этом случае реактивные составляющие токов катушки и конденсатора равны по величине:
В этом случае реактивные составляющие токов катушки и конденсатора равны по величине:  Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол φ сдвига фаз между общим током и напряжением равен нулю.
Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол φ сдвига фаз между общим током и напряжением равен нулю.
Общий ток в цепи и напряжение связаны формулой
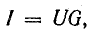 , или
, или 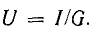
В случае 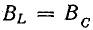 в цепи имеет место резонанс токов.
в цепи имеет место резонанс токов.
Энергетический процесс в цепи
Из векторной диаграммы токов легко получить треугольник мощностей, из которого следуют те же формулы (14.2), которые были получены для последовательного соединения катушки и конденсатора.
Реактивные мощности индуктивности и емкости входят в расчет с разными знаками: реактивная мощность индуктивности положительна, а реактивная мощность емкости отрицательна. В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует из формул (14.2).
Если φ > 0, то Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом значении угла. Полная мощность тоже всегда положительна.
В рассматриваемой цепи активная мощность имеет определенную величину 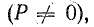 следовательно, имеет место преобразование электрической энергии в другой вид. Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор
следовательно, имеет место преобразование электрической энергии в другой вид. Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор 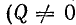 при
при 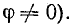 Обмен энергией совершается также между катушкой и конденсатором.
Обмен энергией совершается также между катушкой и конденсатором.
Задача 14.5.
В цепи, схема которой изображена на рис. 14.13, определить ток, активную, реактивную и полную мощность катушки, конденсатора и всей цепи при неизменном напряжении U = 200 В и частоте источника f = 100 Гц. Параметры цепи: R1 = 10 Ом, L = 55,2 мГн, С = 138 мкФ, R2 = 0.
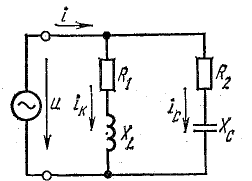
Рис. 14.13. К задаче 14.5
Решение. При частоте f = 100 Гц индуктивное сопротивление первой ветви
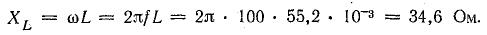
Проводимости:
активная
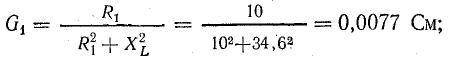
реактивная
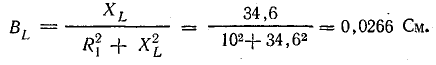
Полная проводимость катушки
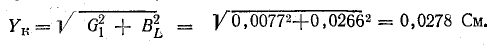
Проводимости второй ветви:
активная

реактивная
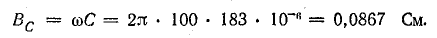
Полная проводимость цепи
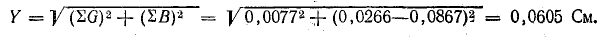
Токи:
в неразветвленной части цепи
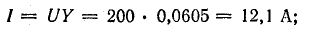
в конденсаторе
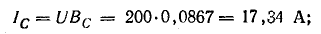
в катушке
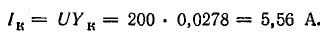
Коэффициент мощности цепи
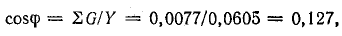
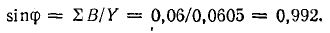
Реактивные мощности:
катушки
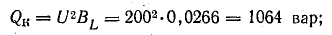
конденсатора
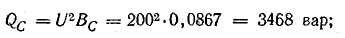
цепи
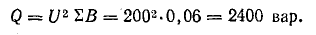
Активная мощность цепи
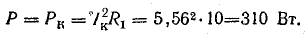
Полные мощности:
катушки
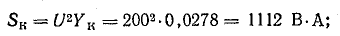
конденсатора
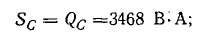
цепи
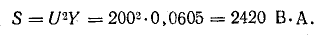
Задача 14.6.
Для схемы рис. 14.13 по данным условия задачи 14.5 найти резонансную частоту fр. Выполнить расчет цепи в порядке, изложенном при решении задачи 14.4, для двух значений частоты источника: 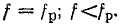
Решение. При резонансе 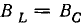 , т. е.
, т. е.
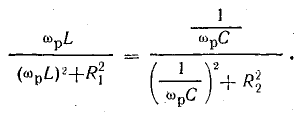
Решая относительно резонансной частоты, можно получить формулу
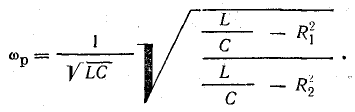
Учитывая, что R2 = 0, и подставляя другие данные, получим:
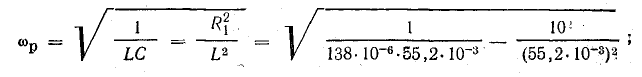
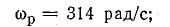
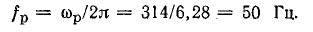
Далее расчет цепи по условию задачи выполните самостоятельно.
Расчет цепей с параллельным соединением ветвей
Расчет электрической цепи, рассмотренный в предыдущем параграфе, можно распространить на цепи, содержащие произвольное число приемников, соединенных параллельно.
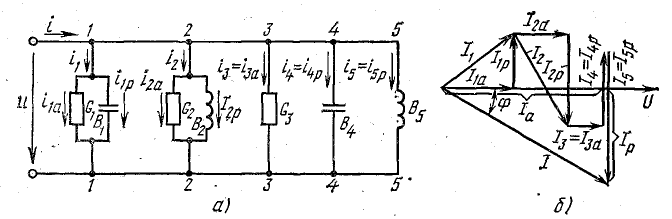
Рис. 14.14. Расчетная схема разветвленной цепи с двумя узлами и ее векторная диаграмма
На рис. 14.14, а параллельно соединены те же элементы цепи, были рассмотрены при последовательном соединении (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение 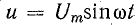 и параметры элементов цепи R, L, C. Требуется найти токи в цепи и мощность.
и параметры элементов цепи R, L, C. Требуется найти токи в цепи и мощность.
Векторная диаграмма
Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов
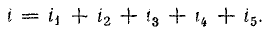
Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим
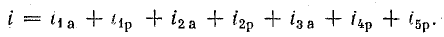
Для действующих токов нужно написать векторное уравнение
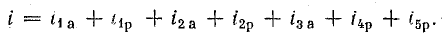
Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.
На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным соединением ветвей, вектор напряжения U, а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения . Из этой точки проведен вектор I1а активного тока ветви I-I (по фазе совпадает с напряжением), а из конца его проведен вектор I1p реактивного тока той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора I1 тока первой ветви. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость ветви 3-3 активная, поэтому реактивная составляющая тока в этой ветви равна нулю. В ветвях 4-4 и 5-5 проводимости реактивные, поэтому в составе этих токов нет активных составляющих.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока: 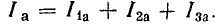
Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными: 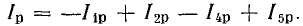
Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует

Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим
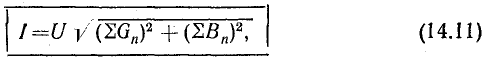
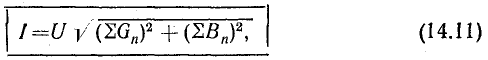
где 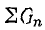 — общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей;
— общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей; 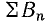 — общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
— общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
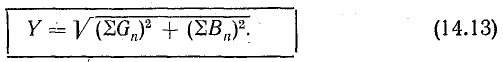
Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].
Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.
Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:
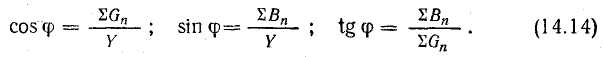
От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы
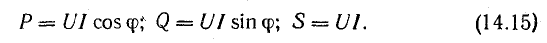
Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.
Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:
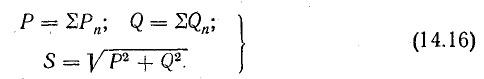
Расчет цепи без определения проводимостей ветвей
Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).
Определяют токи в ветвях по формуле (14.4):
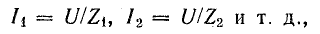
где Z1, Z2 и т. д. — полные сопротивления ветвей.
Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).
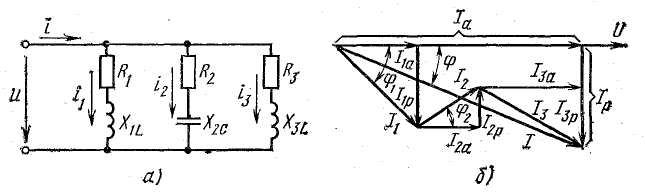
Рис. 14.15. Схема электрической цепи и ее векторная диаграмма
Для построения векторной диаграммы токов (рис. 14.15, б) можно определить активную и реактивную составляющие тока каждой ветви по формулам
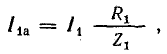
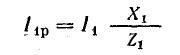
и т. д. для всех ветрей.
В этом случае отпадает необходимость определения углов φ1, φ2 и построения их на чертеже.
Ток в неразветвленной части цепи
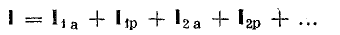
Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее [см. формулы (14.10), (14.15), (14.16)].
Задача 14.7.
Определить ток в неразветвленной части цепи (рис. 14.16, а), активную, реактивную и полную мощности всей цепи. Построить векторную диаграмму токов и напряжений. Дано: R1 = 6 Ом, L1 = 25,5 мГн, R2 = 20 Ом, R2 = 15 Ом; L3 = 47,9 мГн, С3 = 159 мкФ, и 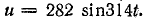
Решение. Реактивные сопротивления ветвей:
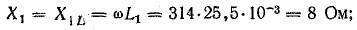
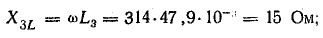
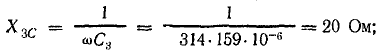
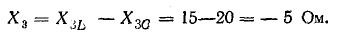
Полные сопротивления ветвей:
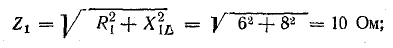
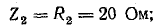
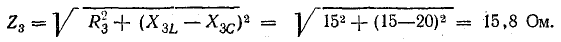
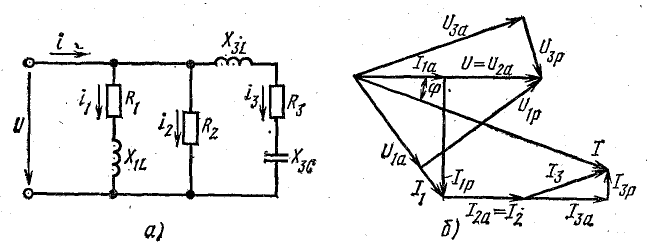
Рис. 14.16. к задаче 14.7
Действующее, напряжение
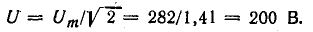
Токи в ветвях:
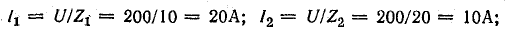
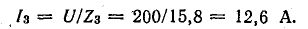
Составляющие токов ветвей:
активные
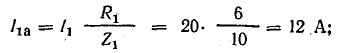
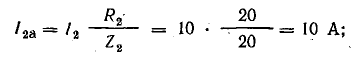
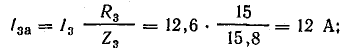
реактивные
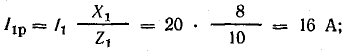
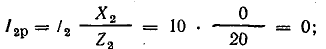
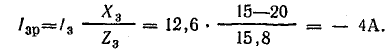
Общий ток:
активный
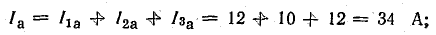
реактивный
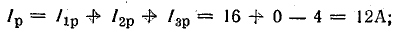
в неразветвленной части цепи
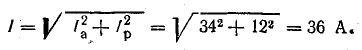
Активные мощности:
ветвей
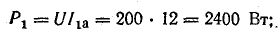
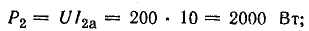
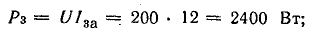
всей цепи
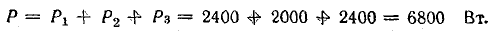
Реактивные мощности:
ветвей
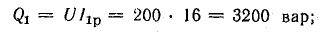
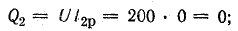
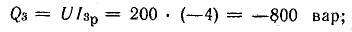
всей цепи
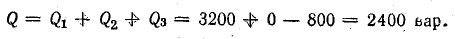
Полная мощность цепи
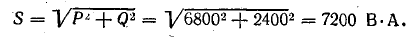
Проверка правильности подсчета мощности:
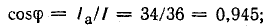
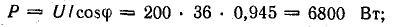
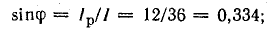
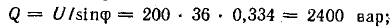
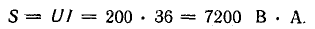
Для построения векторной диаграммы дополнительно определим активные и реактивные напряжения ветвей:
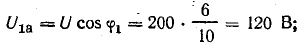
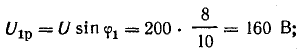
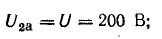
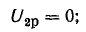
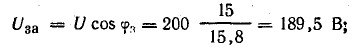
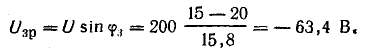
Векторная диаграмма показана на рис. 14.16, б.
- Символический метод расчета цепей
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Энергия в электрических цепях
- Линейные электрические цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
Содержание:
- Переменный ток
- Получение переменного тока
- Генератор переменного тока
- Величина переменного тока. Действующее (эффективное) значение тока и напряжения
- Индуктивность и ёмкость цепи переменного тока
- Трёхфазный ток
- Соединение звездой
- Соединение треугольником
- Асинхронный двигатель
- Двухэлектродная электронная лампа
- Устройство выпрямителей переменного тока
- Генератор постоянного тока
- Передача электрической энергии
- Трансформатор
- Электрификация
- Мощность в цепи переменного тока
- Вращение рамки в однородном магнитном поле. Период и частота переменного тока
- Понятие об устройстве индукционных генераторов
- Действующие значения ЭДС, напряжения и силы переменного тока
- Индуктивность и емкость в цепи переменного тока
- Преобразование переменного тока. Трансформатор
- Индукционная катушка
- Трехфазный ток
- Получение, передача и распределение электрической энергии в народном хозяйстве
Переменный ток – это направленное движение заряженных частиц, направление движения которых меняется на противоположное через равные промежутки времени.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Переменный ток
Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Получение переменного тока
Поместим в постоянное и однородное магнитное поле виток проволоки abсd (рис. 178).
При равномерном вращении этого витка вокруг оси ОО магнитный поток, пронизывающий его площадь, будет непрерывно меняться как по величине, так и по направлению.
Вследствие этого, согласно закону электромагнитной индукции, в витке возникает переменная по величине и направлению э. д. с. индукции.

Когда плоскость вращающегося витка становится перпендикулярна силовым линиям магнитного поля (рис. 178,а), пронизывающий её магнитный поток наибольший  , скорость же изменения его равна нулю
, скорость же изменения его равна нулю  , так как при прохождении через это положение проводники витка ab и cd скользят вдоль силовых линий поля, не пересекая их. Следовательно, э. д. с. индукции, возникающая в витке, которая пропорциональна скорости изменения потока, будет равна нулю (Е = 0).
, так как при прохождении через это положение проводники витка ab и cd скользят вдоль силовых линий поля, не пересекая их. Следовательно, э. д. с. индукции, возникающая в витке, которая пропорциональна скорости изменения потока, будет равна нулю (Е = 0).
Когда же плоскость витка параллельна силовым линиям поля (рис. 178,б), поток, пронизывающий её, равен нулю (Ф = 0), скорость же изменения его при прохождении через это положение наибольшая  так как проводники витка ab и cd движутся перпендикулярно к силовым линиям поля.
так как проводники витка ab и cd движутся перпендикулярно к силовым линиям поля.
Э. д. е., возникшая в этом случае в витке, имеет наибольшее значение  В части ab витка э. д. с. будет направлена от чертежа к наблюдателю, а в части cd, наоборот,— от наблюдателя за чертёж. При дальнейшем повороте витка э. д. е., сохраняя неизменным направление, будет уменьшаться, и в положении, изображённом на рисунке 178, в, величина э. д. с. станет опять равной нулю (Е= 0), так как в этом положении при наибольшей величине магнитного потока, пронизывающего плоскость витка, скорость изменения его наименьшая.
В части ab витка э. д. с. будет направлена от чертежа к наблюдателю, а в части cd, наоборот,— от наблюдателя за чертёж. При дальнейшем повороте витка э. д. е., сохраняя неизменным направление, будет уменьшаться, и в положении, изображённом на рисунке 178, в, величина э. д. с. станет опять равной нулю (Е= 0), так как в этом положении при наибольшей величине магнитного потока, пронизывающего плоскость витка, скорость изменения его наименьшая.
При дальнейшем вращении витка скорость изменения потока, пронизывающего виток, будет увеличиваться; следовательно, э. д. с. по абсолютной величине будет возрастать от 0 до  (рис. 178, г). Но так как виток движется теперь навстречу магнитным силовым линиям другой стороной плоскости, то направление э. д. с. в нём изменяется на противоположное: в части ab э. д. с. направлена от наблюдателя за чертёж, а в части cd, наоборот,— от чертежа к наблюдателю. Это направление э. д. с. сохранится и при дальнейшем движении витка, при этом абсолютная величина её будет убывать до нуля (рис. 178, а).
(рис. 178, г). Но так как виток движется теперь навстречу магнитным силовым линиям другой стороной плоскости, то направление э. д. с. в нём изменяется на противоположное: в части ab э. д. с. направлена от наблюдателя за чертёж, а в части cd, наоборот,— от чертежа к наблюдателю. Это направление э. д. с. сохранится и при дальнейшем движении витка, при этом абсолютная величина её будет убывать до нуля (рис. 178, а).
При последующих оборотах витка все эти явления будут повторяться вновь.
Таким образом, величина э. д. с. индукции во вращающемся витке за один его оборот изменяется 
Разомкнём виток abсd и присоединим концы его к осциллографу (рис. 179, а). При вращении витка в магнитном поле В осциллограф запишет все изменения тока, по которым можно будет судить и об изменении э. д. с. индукции в витке. На рисунке 179, б показан график изменения э. д. с. в витке за время одного оборота. Вверху показаны последовательные положения витка в магнитном поле, против них (внизу)—значения э. д. с. индукции в витке. Направление силовых линий магнитного потока, пронизывающего виток, показано стрелками. Кружочки изображают сечение витка плоскостью чертежа с указанием направления тока в нём.
Ток, возникающий в витке при равномерном вращении его в однородном магнитном поле, как показывает осциллограмма, изображённая на рисунке 179, а, изменяется синусоидально. Такой ток называется переменным синусоидальным током.
Промежуток времени, в течение которого э. д. с. совершает одно полное колебание, называется периодом переменного тока.


Период колебания обозначают буквой Т. Число полных колебаний за 1 сек называется частотой тока и обозначается буквой f. Единица частоты называется герц (гц):

или

Если значение э. д. с. в некоторый произвольный момент времени мы обозначим через е (мгновенное значение э. д. е.), а наибольшее значение её (амплитудное значение) — через Ем, то закон, выражающий зависимость е от времени, в случае синусоидального тока можно записать в виде следующего выражения:

В Советском Союзе и в большинстве других стран в промышленности и в быту применяют переменный ток частотой в 50 гц. продолжительность периода такого тока 0,02 секунды.
Генератор переменного тока
Машины, превращающие механическую энергию в энергию электрического тока, называются генераторами. Действие их основано на явлении электромагнитной индукции.
Простейшей схемой генератора может служить проводник в виде рамки, вращающейся вокруг оси ОО в магнитном поле постоянного магнита или электромагнита (рис. 180). При вращении рамки в ней возникает переменная э. д. с.
Если рамку соединить с внешней частью цепи, то в цепи появится переменный ток. Для соединения рамки с внешней цепью используются кольца, укреплённые на той же оси, на которой укреплена и вращающаяся рамка. К кольцам присоединяются концы рамки, а над каждым кольцом устанавливаются неподвижные скользящие контакты — щётки. При вращении рамки за один оборот полярность щёток меняется два раза.

Мы рассмотрели на схеме принцип работы генератора переменного тока. Устройство генератора переменного тока значительно сложнее. С клемм генератора должно сниматься достаточно высокое напряжение; поэтому вместо одного витка приходится брать значительное их число и соответствующим образом соединять их между собой.
Однако такой тип генератора переменного тока с неподвижной магнитной системой (индуктором) и вращающимися витками (якорем), в которых возбуждается э. д. е., строится сравнительно редко. Это вызвано тем, что при помощи подвижных контактов практически невозможно отводить от генератора ток высокого напряжения из-за сильного искрения в подвижных контактах.
Поэтому почти во всех генераторах переменного тока обмотку (якорь), в которой индуктируется э.д.е., устанавливают неподвижно, а вращаться заставляют магнитную систему (индуктор).
Неподвижная часть машины получила название статора, а подвижная — ротора.
Статор генератора переменного тока собирается из листовой стали (для борьбы с вихревыми токами). В пазах, сделанных во внутренней полости статора, укладываются проводники, в которых индуктируется э. д. с. (рис. 181, а). Вращающаяся электромагнитная система — ротор — имеет вид, показанный на рисунке 181, б. На магнитные полюсы ротора надеты обмотки, по которым пропускается постоянный ток. Этот ток подводится к обмотке через щётки и кольца от постороннего источника постоянного тока.


На рисунке 181, в показана полная схема генератора переменного тока, где отчётливо видно, что если ротор вращать какой-либо внешней механической силой, то вместе с ним будет вращаться и создаваемое им магнитное иоле. При этом силовые линии поля будут пересекать проводники, вложенные в пазы статора, и индуктировать в них э. д. с. Величина суммарной э. д. с. генератора будет зависеть от размера и типа обмотки статора, величины магнитного поля ротора и скорости его вращения.
На рисунке 182 изображён внешний вид мощного гидрогенератора Днепрогэса имени В. И. Ленина. Ротор генератора питается постоянным током, даваемым небольшой машиной постоянного тока, находящейся на одном валу с генератором.
Генератор, ротор которого вращается на общем валу с паровой турбиной, называется турбогенератором.
Величина переменного тока. Действующее (эффективное) значение тока и напряжения
Переменная э. д. с. вызывает в цепи переменный по величине и направлению ток.
Если цепь индуктивностью и ёмкостью не обладает, то ток в ней изменяется в соответствии с изменением э. д. с.
Наибольшему значению э. д. с. соответствует и наибольшее значение тока; и наоборот, когда э. д. с. равна нулю, ток также равен нулю. В этом случае принято говорить, что изменения э. д. с. и тока совпадают по фазе.
Разделив, согласно закону Ома, значение э. д. с.  на сопротивление цепи R,
на сопротивление цепи R,
мы получим выражение тока в зависимости от времени:

или

где  представляет собой мгновенное значение тока, а величина
представляет собой мгновенное значение тока, а величина  — его амплитудное (наибольшее) значение.
— его амплитудное (наибольшее) значение.

На рисунке 183 изображены две синусоиды: одна из них изображает изменение э. д. е., другая — тока. Обе эти кривые совпадают по фазе.
Сопротивление проводника, в котором напряжение и ток совпадают по фазе, называется активным сопротивлением. В проводнике с активным сопротивлением энергия тока необратимо превращается в другие виды энергии (в механическую, во внутреннюю и др.).
Мгновенное значение переменного тока всё время изменяется, колеблясь между нулём  и некоторым наибольшим значением его
и некоторым наибольшим значением его  . Тем не менее мы измеряем переменный ток, как и постоянный, в амперах. Так, например, мы говорим, что по лампочке идёт ток в 0,5 а, а по спиральке нагревательного прибора — ток в 5 а и т. д. О каком же значении переменного тока идёт здесь речь?
. Тем не менее мы измеряем переменный ток, как и постоянный, в амперах. Так, например, мы говорим, что по лампочке идёт ток в 0,5 а, а по спиральке нагревательного прибора — ток в 5 а и т. д. О каком же значении переменного тока идёт здесь речь?
Очевидно, что средняя величина тока за полный период его изменения равна нулю, независимо от того, какие большие значения она принимает в различные моменты времени. Следовательно, ею нельзя оценивать величину переменного тока. Может быть, можно характеризовать переменный ток по его наибольшему (амплитудному) значению? Принципиально это возможно, но практически трудно построить прибор, непосредственно измеряющий эту величину тока.
При установлении значения величины переменного тока обычно исходят из таких его действий, которые не зависят от направления тока и могут быть вызваны также постоянным током. К ним относятся, например, тепловые действия тока. Действительно, если через проводник, обладающий некоторым сопротивлением, проходит ток I, то выделяемое в проводнике количество теплоты пропорционально  , т. е. не зависит от направления тока.
, т. е. не зависит от направления тока.
Пусть переменный ток проходит по проводнику данного сопротивления и в каждую секунду выделяет в нём некоторое количество теплоты. Очевидно, можно пропустить по этому проводнику такой постоянный ток, чтобы в секунду выделялось такое же количество теплоты, как и в случае переменного тока.
Значение постоянного тока, выделяющего в проводнике такое же количество теплоты, что и переменный ток (за одно и то же время), называется действующим (эффективным) значением переменного тока.
Для синусоидального переменного тока действующее значение его (I) меньше амплитудного ( ) в
) в  раза, т. е.
раза, т. е.

Точно так же действующее значение э. д. с. и напряжения меньше амплитудного их значения в  раза:
раза:

Рассмотренные нами в § 83 амперметры и вольтметры магнитоэлектрической системы (рис. 145), очевидно, не пригодны для измерений в цепях переменного тока, так как при каждом изменении направления тока в катушке меняется и направление вращающего момента, поворачивающего стрелку прибора. Вследствие же большой инерции катушки и стрелки такой прибор не будет реагировать на переменный ток.
Для измерений тока и напряжения в цепях переменного тока применяются приборы, показания которых не зависят от направления тока. Для этой цели пригодны, например, тепловые приборы. В них поворот стрелки вызывается удлинением нити, которая нагревается током.
Пригодны для измерений в цепях переменного тока технической частоты (f=50 гц) и приборы электромагнитной системы (рис. 148). Подвижной частью приборов этой системы является небольшой железный диск, который, перемагничиваясь, всё время втягивается внутрь катушки, по которой идёт переменный ток.
Индуктивность и ёмкость цепи переменного тока
В предыдущем параграфе мы рассмотрели тепловое действие переменного тока, которым в равной степени обладает и постоянный ток. Однако быстрое изменение величины и направления тока обусловливает ряд особенностей переменного тока, отличающих его действия от действий постоянного тока.
Переменный ток, например, не годится для зарядки аккумулятора, его нельзя использовать и для технических применений электролиза.
Величина переменного тока зависит не только от напряжения и сопротивления цепи, но и от индуктивности проводников, включённых в цепь. В этом можно убедиться на следующем опыте. Включим в цепь постоянного тока катушку из многих витков медной проволоки и амперметр. Заметим по амперметру величину тока. Вдвинем теперь в катушку железный сердечник, ток при этом не изменится. Если включить теперь катушку в цепь переменного тока с действующим напряжением, равным напряжению постоянного тока, то ток в катушке окажется меньшим. Введение же в катушку железного сердечника приведёт к ещё большему ослаблению тока (рис. 184).

Таким образом, индуктивность цепи переменного тока уменьшает величину тока.
Так как сопротивление цепи измеряется отношением напряжения к току, проходящему по ней, то можно сказать, что наличие в цепи катушки индуктивности увеличивает сопротивление цепи.
Причиной этого является возникающая в цепях переменного тока э. д. с. самоиндукции, которая препятствует нарастанию тока. Вследствие э. д. с. самоиндукции в момент, когда напряжение в цепи достигает максимума, ток не успевает достигнуть той величины, которую он достиг бы в отсутствие самоиндукции.
Рассмотрим следующий пример.
Одна из обмоток трансформатора, который часто можно встретить в школьных физических кабинетах, имеет 600 витков медной проволоки диаметром 1 мм. На эту катушку пошло 150 м медной проволоки, сопротивление которой

Если измерить сопротивление этой катушки в цепи переменного тока частотой 50гц, то окажется, что сопротивление её около 20 ом.
Итак, индуктивность в цепи переменного тока действует в отношении величины тока так же, как сопротивление проводника цепи. С увеличением индуктивности растёт и сопротивление цепи. Сопротивление, которым обладает цепь вследствие наличия в ней индуктивности, называется индуктивным сопротивлением.

Величина индуктивного сопротивления зависит от индуктивности цепи L и частоты тока f. Рассчитывается индуктивное сопротивление по формуле:

Если в цепь постоянного тока мы включим батарею конденсаторов, то никакого тока не обнаружим, что вполне понятно, так как пластины конденсатора отделены друг от друга изолятором. Через конденсатор постоянный ток течь не может.
Если же включить батарею конденсаторов в цепь переменного тока, то в цепи будет ток; электрическая лампочка, включённая в эту цепь, будет гореть (рис. 185).
В цепи переменного тока электроны совершают колебательное движение; это приводит к тому, что обкладки конденсаторов попеременно заряжаются то положительно, то отрицательно; электроны же в проводах цепи движутся то в одном, то в другом направлении. Если выключить конденсатор из цепи, то лампочка будет гореть ярче. Следовательно, наличие конденсатора в цепи переменного тока увеличивает сопротивление цепи.
Опыт показывает, что, чем больше ёмкость конденсатора, включённого в цепь, тем меньшее сопротивление он оказывает переменному току.
Сопротивление, которым обладает цепь вследствие наличия в ней ёмкости, называется ёмкостным сопротивлением. Величина ёмкостного сопротивления зависит от ёмкости цепи и частоты тока. Рассчитывается ёмкостное сопротивление по формуле: 
Наличие в цепи переменного тока индуктивности или ёмкости приводит к сдвигу фаз между током и напряжением. При индуктивном сопротивлении, вследствие появления в цепи э. д. с. самоиндукции, ток отстаёт по фазе от приложенного напряжения, а при ёмкостном сопротивлении ток по фазе опережает напряжение.
Если изменение напряжения в цепи происходит по закону  то в случае наличия в этой цепи активного и индуктивного сопротивления изменение тока в ней выразится формулой:
то в случае наличия в этой цепи активного и индуктивного сопротивления изменение тока в ней выразится формулой:  где
где  сдвиг фаз между напряжением и током. Графики напряжения и тока в этом случае будут иметь вид, изображённый на рисунке 185а.
сдвиг фаз между напряжением и током. Графики напряжения и тока в этом случае будут иметь вид, изображённый на рисунке 185а.

При наличии в цепи активного и ёмкостного сопротивления изменение тока в цепи выразится формулой  На рисунке 185б показаны графики напряжения и тока в этом случае.
На рисунке 185б показаны графики напряжения и тока в этом случае.
Трёхфазный ток
Рассмотренный нами в §96 переменный ток создавался одной э. д. е., возникшей в генераторе. Такой ток называется однофазным переменным током. Однако основной системой тока, принятой в настоящее время повсеместно, является система трёхфазного тока, обладающая, как мы увидим далее (§101), рядом преимуществ перед однофазной системой.
Трёхфазным током называется система трёх однофазных токов, создаваемых тремя э. д. с., имеющими одинаковые амплитуды и частоту, но сдвинутыми одна относительно другой по фазе на  или по времени на
или по времени на  периода.
периода.
Каждая отдельная цепь трёхфазной системы сокращённо называется фазой.
Трёхфазную систему токов принципиально можно получить от трёх одинаковых генераторов переменного однофазного тока, роторы которых, находясь в одном и том же положении, жёстко связаны между собой и не меняют своего относительного положения при вращении. Статорные же обмотки генераторов повёрнуты относительно друг друга на 120° в сторону вращения ротора, как это показано на рисунке 186 (концы их обозначены буквами Н и К). При этих условиях вполне очевидно, что э. д. с. второго генератора  будет запаздывать в своих изменениях относительно э. д. с. первого генератора
будет запаздывать в своих изменениях относительно э. д. с. первого генератора  на 120°, т. е. максимальное значение э. д. с. того же направления во втором генераторе наступит после того, как все роторы генераторов повернутся на 120°. Э. д. с. третьего генератора
на 120°, т. е. максимальное значение э. д. с. того же направления во втором генераторе наступит после того, как все роторы генераторов повернутся на 120°. Э. д. с. третьего генератора  также будет запаздывать относительно э. д. с. второго генератора на 120°.
также будет запаздывать относительно э. д. с. второго генератора на 120°.


Но такой способ получения трёхфазного тока оказывается технически сложным и экономически невыгодным. Гораздо проще все три статорные обмотки совместить в одном корпусе статора, что и представлено на рисунке 187. Начала обмоток на этом рисунке обозначены буквами Н, концы — буквами К. Такой генератор называется генератором трёхфазного тока.
Таким образом, статор генератора трёхфазного тока имеет три обмотки (называемые фазами генератора), смещённые на 120° своими началами (или концами) одна относительно другой.
Ротор же генератора трёхфазного тока конструктивно одинаков с ротором генератора однофазного тока.
При вращении ротора во всех обмотках будут создаваться одинаковые по частоте и амплитуде э. д. е., но только они будут не одновременно достигать своих максимумов. Считая, что максимальная э. д. с. создаётся в момент прохождения центра северного полюса ротора под началом обмотки, нетрудно видеть, что максимум э. д. с. того же направления во второй обмотке наступит после поворота ротора на 120е, а максимум э. д. с. того же направления в третьей обмотке наступит после поворота ротора на 240° относительно первой.
Соединяя каждую фазу генератора с внешней цепью, мы получим три цепи однофазного тока, не имеющие между собой никаких электрических соединений, причём токи в каждой отдельной цепи при одинаковом их сопротивлении будут равны по амплитуде, но сдвинуты по фазе друг относительно друга так же, как и э. д. е., на 120°.
График трёхфазного тока, записанный осциллографом, будет иметь вид, изображённый на рисунке 188.

Для соединения такого генератора с внешней цепью потребуется шесть проводов. С целью уменьшения числа проводов, идущих во внешнюю цепь, обмотки генератора и приёмников соединяют между собой, образуя электрически связанную трёхфазную систему. Такое соединение можно выполнить двумя способами: звездой и треугольником.
Оба эти соединения позволяют сэкономить материал на проводку при передаче заданной мощности в сравнении с расходом его при передаче той же мощности от трёх независимых однофазных генераторов.
Соединение звездой
Генератор трёхфазного тока на схемах принято рисовать в виде трёх статорных обмоток, расположенных под углом 120° друг к другу. Буквами Н и К обозначаются начала и концы соответствующих обмоток.
Если три конца статорных обмоток соединить в одну общую точку, называемую нулевой точкой О генератора, то получим такое соединение статорных обмоток, которое называется соединением звездой. К началам
соединить в одну общую точку, называемую нулевой точкой О генератора, то получим такое соединение статорных обмоток, которое называется соединением звездой. К началам  тех же обмоток подключаются провода линии, называемые линейными проводами (рис. 189,а). Аналогично могут соединяться и приёмники (рис. 189,б). Провод, соединяющий нулевую точку генератора О с нулевой точкой приёмников О, называется нулевым проводом.
тех же обмоток подключаются провода линии, называемые линейными проводами (рис. 189,а). Аналогично могут соединяться и приёмники (рис. 189,б). Провод, соединяющий нулевую точку генератора О с нулевой точкой приёмников О, называется нулевым проводом.
Такая четырёхпроводная система трёхфазного тока имеет два разных напряжения. Напряжение между линейным и нулевым проводами, или, что то же самое, напряжение между началом и концом какой-нибудь обмотки статора называется фазным напряжением 
Напряжение, измеряемое между двумя линейными проводами или между началами статорных обмоток, называется линейным напряжением  .
.
Линейное напряжение в  раза больше фазного:
раза больше фазного:


Пример. Напряжение между линейными проводами трёхфазной системы, соединённой на звезду, 220 в. Чему равно фазное напряжение?
Решение;

Пример. Фазное напряжение трёхфазной системы, соединённой на звезду, 220 в. Чему равно напряжение между линейными проводами?
Решение:

В настоящее время во все новые жилые дома вводится трёхфазный ток с линейным напряжением в 220 в (например, в Москве, в черте города) и 380 в (в загородных линиях Москвы). Электрические же лампочки включают (на звезду) между линейными проводами и нулевым проводом (нулевой провод обязательно должен быть) соответственно на напряжение.

При одинаковой нагрузке фаз ток в нулевом проводе равен нулю  и этот провод становится излишним. С таким случаем мы встречаемся, например, при включении в цепь электродвигателя трёхфазного тока.
и этот провод становится излишним. С таким случаем мы встречаемся, например, при включении в цепь электродвигателя трёхфазного тока.
Соединение треугольником
Соединение треугольником называется такое соединение, при котором конец первой фазы генератора  соединяется с началом второй его фазы
соединяется с началом второй его фазы  , конец второй фазы
, конец второй фазы  — с началом третьей фазы
— с началом третьей фазы  и, наконец, конец третьей
и, наконец, конец третьей  — с началом первой фазы
— с началом первой фазы  ; к вершинам полученного треугольника присоединяются провода линии (рис. 190, а). Аналогично соединяются и потребители (рис. 190, б).
; к вершинам полученного треугольника присоединяются провода линии (рис. 190, а). Аналогично соединяются и потребители (рис. 190, б).
Из рассмотрения рисунка 190 нетрудно заключить, что при соединении треугольником линейное и фазное напряжения одинаковы 

Асинхронный двигатель
Введение в технику трёхфазного тока позволило создать простой по устройству и удобный в эксплуатации электродвигатель, который получил название асинхронного двигателя. Устройство асинхронного двигателя основано на использовании вращающегося магнитного поля. В простейшем случае такое иоле можно получить, вращая подковообразный магнит. Магнитная стрелка, установленная на оси и расположенная вблизи магнита (рис. 191), начнёт при этом вращаться в ту же сторону, что и магнит, и с той же скоростью.
Если во вращающееся магнитное поле поместить замкнутый проводник, укреплённый на оси (рис. 192), то магнитное поле, при своём вращении пересекая стороны контура проводника, будет индуктировать в них э. д. с. индукции, создающую в этом замкнутом контуре индукционный ток. Этот ток, взаимодействуя с магнитным полем вращающегося магнита, приведёт виток во вращение. Направление вращения витка определяется правилом левой руки.
Вращение витка будет направлено в сторону вращения магнитного поля. Однако к разбору этого явления гораздо лучше подойти не с точки зрения формальных правил правой и левой руки, а на основе закона Ленца, вскрывающего физическую сущность этого явления.
Причиной появления индукционного тока в витке является вращение магнитного поля относительно витка. Следовательно, индукционный ток, согласно закону Ленца, будет противодействовать этому вращению поля. Но замедлить вращение магнитного поля он не может, так как оно определяется внешней механической силой, поэтому виток сам будет вращаться в сторону вращающегося магнитного поля. При этом относительная скорость пересечения магнитным полем сторон витка будет уменьшаться.
Если допустить, что виток достиг скорости вращения поля, то э. д. е., а следовательно, и ток в нём будут равны нулю и электромагнитная сила, создающая люмен г вращения, исчезнет.

Поэтому виток, всегда находящийся под действием момента сил сопротивления (например, трения), начнёт останавливаться. Вследствие уменьшения скорости вращения витка его стороны снова будут пересекаться магнитным полем и снова возникнет вращающий момент, который при равномерном вращении всегда будет равен моменту силы сопротивления. Скорость вращения витка во вращающемся магнитном поле всегда меньше скорости вращения поля; поэтому принято говорить, что вращение витка относительно поля является асинхронным (неодновременным).
Трёхфазные асинхронные двигатели состоят из двух основных частей: неподвижной части — статора и вращающейся части — ротора.
Вращающееся магнитное поле создается в двигателе не путём механического вращения магнитных полюсов, а при обтекании переменным трёхфазным током неподвижных обмоток статора.
Если во вращающееся магнитное поле статора поместить на оси железный цилиндр (ротор), то в его теле, пронизываемом вращающимся полем, будут возникать индукционные токи. Эти токи, взаимодействуя с вращающимся полем, по закону Ленца, вызовут вращение ротора в сторону поля со скоростью, меньшей скорости вращения поля.
Чтобы увеличить вращающий момент двигателя и уменьшить потери энергии на нагревание двигателя, необходимо, чтобы токи индуктировались не во всей толще ротора, а только на его поверхности. Для этого тело ротора делается не в виде сплошного цилиндра, а из отдельных стальных пластин толщиной 0,3—0,5 мм (рис. 193, а), изолированных друг от друга лаком или очень тонкой бумагой.

 В выштампованных пазах этих пластин укладываются медные или алюминиевые стержни. Эти стержни с обоих концов по торцам впаиваются в кольца (рис. 193, б), вследствие чего сам ротор называется короткозамкнутым (рис. 193, в), и так как его обмотка, взятая отдельно от тела ротора, имеет вид беличьего колеса (рис. 193, б), то этот простейший вид роторной обмотки называется «беличьим колесом».
В выштампованных пазах этих пластин укладываются медные или алюминиевые стержни. Эти стержни с обоих концов по торцам впаиваются в кольца (рис. 193, б), вследствие чего сам ротор называется короткозамкнутым (рис. 193, в), и так как его обмотка, взятая отдельно от тела ротора, имеет вид беличьего колеса (рис. 193, б), то этот простейший вид роторной обмотки называется «беличьим колесом».
На рисунке 194а показана схема включения трёхфазного асинхронного электродвигателя в сеть.
Следует помнить, что токи в роторе носят индукционный характер.
Асинхронный короткозамкнутый двигатель является очень простым и надёжным двигателем; он лишён коллектора или скользящих контактов; этим обусловлено его широкое распространение в промышленности и сельском хозяйстве. Изменение направления вращения двигателя достигается простым переключением двух каких-либо проводов, соединяющих обмотки статора с линией.
Асинхронный двигатель в разобранном виде показан на рисунке 1946.

Система трёхфазного тока была разработана одним из выдающихся электротехников XIX и начала XX в.— русским инженером М. О. Доливо-Добровольским (1862—1919). Эта система открыла широчайшие возможности промышленного использования электрической энергии. Отметим два важнейших преимущества трёхфазной системы перед обычной однофазной системой переменного тока: 1) экономия в проводах линии, соединяющей станцию с потребителем; 2) возможность получения вращающегося магнитного поля, применяющегося в асинхронных электродвигателях.
Двухэлектродная электронная лампа
Электронными лампами называют обширный класс приборов, действие которых основано на явлении испускания электронов накалёнными металлами.
Область применения их чрезвычайно широка и разнообразна. Достаточно сказать, что радиотехника (радиовещание, радиолокация и телевидение), автоматика и телемеханика целиком базируются на работе этих приборов. В дальнейшем мы познакомимся с некоторыми практическими применениями электронных ламп.
На рисунке 195 показаны внешний вид и схема устройства простейшей двухэлектродной электронной лампы. Анод в этой лампе представляет собой металлический цилиндр, по оси которого устанавливается нить накала — катод.
При накаливании нити током из неё вылетают электроны. Если напряжение между нитью и анодом равно нулю, то вылетевшие из нити электроны образуют вокруг неё своего рода «электронное облачко» (рис. 196). Оно удерживается около нити, которая из-за потери электронов заряжается положительно. Положительно заряженная нить не только удерживает вылетающие из неё электроны, но и втягивает их обратно. В конечном итоге между этими двумя процессами наступит подвижное равновесие, аналогичное тому, которое имеет место между насыщающим паром и жидкостью (при неизменной температуре). При таком равновесии среднее число электронов в облачке остаётся неизменным.

Если создать теперь в лампе электрическое поле, сделав нить К катодом, а пластинку А анодом, включив для этого в анодную цепь батарею на 80—100 в, то электроны из облачка устремятся к аноду: по анодной цепи лампы пойдёт ток.
Если при данном накале катода увеличивать напряжение между нитью и анодом, то всё большее и большее число электронов будет двигаться к аноду и, следовательно, всё меньшее число их будет возвращаться в нить. Ток в анодной цепи при этом будет возрастать.
При некотором напряжении между катодом и анодом все выбрасываемые нитью электроны будут увлекаться к аноду.
Если после этого ещё повышать напряжение, то ток уже не будет возрастать, так как нить при данной её температуре может выделять ежесекундно только определённое число электронов, которое и определяет наибольший ток. Такой ток называется током насыщения. График зависимости тока в анодной цепи от напряжения между анодом и нитью показан на рисунке 197. Этот график называется анодной характеристикой л а м п ы.
Важным свойством электронной лампы является её односторонняя проводимость: электроны в ней движутся от нити к аноду, что соответствует направлению тока от анода к нити. Обратное направление тока невозможно, так как для обратного направления тока нужно было бы соединить электрод А с отрицательным полюсом источника тока, а в этом случае электрическое поле будет отталкивать вылетающие из нити электроны.
Благодаря своей односторонней проводимости электронная лампа используется для выпрямления переменного тока, т. е. для преобразования переменного тока в постоянный.
Устройство выпрямителей переменного тока
Выпрямителями переменного тока называются приборы, дающие возможность превращать переменный ток в ток прерывистый, пульсирующий, постоянного направления, который с помощью специальных устройств (фильтров) может быть сделан не только постоянным по направлению, но и по величине.
Большинство выпрямителей основано на применении приборов, обладающих односторонней проводимостью. Через эти приборы свободно проходит ток одного направления и почти не проходит ток противоположного направления.

Для выпрямления переменного тока широко используется двух-электродная электронная лампа. На рисунке 198 изображена схема включения электронной лампы в цепь переменного тока. Источник переменного тока может быть включен в анодную цепь лампы непосредственно (рис. 198, а) или же через трансформатор (рис. 198, б).
Каждый раз, когда анод имеет положительный потенциал по отношению к катоду, через лампу и участок цепи с сопротивлением R проходит ток. Когда же анод имеет потенциал отрицательный, ток отсутствует. Таким образом, через проводник с сопротивлением R ток проходит только в течение каждого положительного полупериода напряжения, приложенного к выпрямителю.
Ток, протекающий через проводник с сопротивлением R, представляет собой пульсирующий ток постоянного направления. На рисунке 199 верхняя кривая изображает переменный ток, а нижняя — выпрямленный пульсирующий ток.
Для использования обоих полупериодов переменного тока применяются схемы двухполупериодного выпрямления. На рисунке 200 изображена такая схема с двумя лампами, а на рисунке 201 показана кривая пульсирующего тока, проходящего через проводник R. Когда верхний вывод А вторичной обмотки трансформатора имеет положительный потенциал, а нижний вывод В — отрицательный, работает верхняя лампа. В следующий полупериод, когда знаки потенциалов на этих обмотках

изменяются, работает нижняя лампа. Через проводник с сопротивлением R ток в течение любого полупериода проходит в одном и том же направлении. Таким образом, используются оба полупериода подводимого к лампе переменного напряжения.

Двухэлектродная лампа, служащая для выпрямления переменного тока, называется кенотроном.
Кенотрон обладает идеальной односторонней проводимостью, однако сопротивление его очень велико, поэтому кенотронные выпрямители применяются главным образом для питания радиоустановок, не требующих значительных по величине токов.
Широкое применение в практике получили полупроводниковые выпрямители. Выпрямляющее действие полупроводникового выпрямителя основано на том, что сопротивление его различно в зависимости от направления (полярности) приложенного напряжения.
На рисунке 202 показана схема устройства и включения в цепь полупроводникового выпрямителя. Выпрямитель такого типа состоит из металла М и полупроводника Р, разделённых весьма тонким слоем Z особого вещества (толщиной порядка  ). Этот слой называется запирающим слоем. Металлическая пластина К служит для образования контакта с полупроводником.
). Этот слой называется запирающим слоем. Металлическая пластина К служит для образования контакта с полупроводником.

Процессы, происходящие в запирающем слое при прохождении через него переменного тока, рассмотрены в приложении. Его особенностью является односторонняя проводимость. При положительном потенциале на полупроводнике Р электрический ток проходит через выпрямитель, при отрицательном же потенциале ток не проходит.
В практике применяются меднозакисные (купроксные) выпрямители с запирающим слоем, образующимся при создании закиси меди на медной пластинке, между закисью меди и медью. В последнее время стали широко применяться селеновые выпрямители с запирающим слоем, образующимся при специальной обработке между селеном и нанесённым на него металлом.
Мы рассмотрели типы выпрямителей, которые часто можно встретить в физических кабинетах школ. Мощность их сравнительно невелика. В технике применяются выпрямители, позволяющие выпрямлять переменные токи высоких напряжений и больших мощностей.
Генератор постоянного тока
Постоянный ток может быть получен также от специального генератора постоянного тока.
Мы видели (§ 96), что э. д. с. в витке, вращающемся в магнитном поле, дважды меняет своё, направление за один оборот витка. Для получения во внешней цепи постоянного по направлению тока применяют особое механическое переключающее устройство — коллектор.
В простейшем случае коллектор представляет собой два изолированных друг от друга полукольца, к которым прикрепляются концы витка. Полукольца укрепляются на оси и вращаются вместе с витком, касаясь при этом неподвижных щёток (рис. 203).

В те моменты, когда ток в витке меняет направление, полукольца меняют щётки. Поэтому во внешней цепи ток будет иметь всё время одно и то же направление, но он будет меняться по величине. График изменения тока во внешней цепи, соединённой с генератором, изображён на рисунке 204. Пунктирной синусоидой изображён ток в витке; сплошной линией изображён ток во внешней цепи.
Применяя вместо одного большее число витков, можно получить постоянный ток, график которого будет представлять собой почти прямую, параллельную оси времени. Коллектор в этом случае будет состоять из многих изолированных друг от друга пластин.
Обмотка якоря современного генератора постоянного тока представляет собой очень сложную замкнутую систему, состоящую из большого числа секций с отпайками к коллекторным пластинам от каждой секции.

Тело якоря имеет вид цилиндра, укреплённого на оси и собранного из отдельных стальных пластин толщиной 0,3—0,5 мм, изолированных друг от друга тонкой бумагой или лаком. В вы-штампованных пазах укладывается обмотка якоря. Якорь без обмотки представлен на рисунке 205, а якорь в собранном виде изображен на рисунке 206.

Станина генератора постоянного тока изготовляется из литой стали или чугуна. На внутренней её части укрепляются полюсные сердечники, сделанные из листовой стали (рис.207). На полюсные сердечники надеваются обмотки возбуждения, создающие магнитный поток в машине, который проходит по станине и телу якоря. Вся эта система образует индуктор. Ток в обмотки возбуждения поступает из якоря машины. При вращении якоря проводники, уложенные в его пазах, пересекают силовые линии магнитного поля, создаваемого обмотками возбуждения, и в них возникает э. д. с. а при наличии внешней замкнутой цепи — индукционный ток.
По закону Ленца, индукционный ток противодействует причине, его вызывающей. Такой причиной является движение якоря; следовательно, индукционный ток в якоре противодействует вращению якоря. На преодоление этого противодействия и расходуется механическая энергия теплового или гидравлического двигателя.

Если обмотку возбуждения и якорь генератора постоянного тока приключить к постороннему источнику постоянного напряжения, то якорь придёт во вращение. Генератор превратится в электродвигатель. Это свойство генератора постоянного тока называется обратимостью.
Двигатели постоянного тока находят широкое применение на транспорте. Электрифицированные железные дороги, метро, трамвай, троллейбусы работают на двигателях постоянного тока.
Передача электрической энергии
Преимущество электрической энергии перед другими видами энергии заключается главным образом в том, что передачу её можно осуществлять с относительно малыми потерями на большие расстояния. Шатурская станция, например, передаёт электрическую энергию в Москву по линии длиной 130 км; линия передачи Свирской электростанции, посылающей энергию в Ленинград, имеет протяжение около 250 км; для использования в Москве энергии Волжских гидроэлектростанций имени В. И. Ленина и имени XXII съезда КПСС приходится передавать электрический ток на значительно большие расстояния.
При передаче электроэнергии на расстояние неизбежны потери энергии в линии передачи, так как ток, проходя по проводам линии, нагревает их. Энергия тока, идущая на нагревание проводов линии передачи, является потерянной энергией.
Чтобы передача электрической энергии была экономически выгодной, необходимо потери на нагревание проводов сделать возможно малыми. Как это осуществить?
Закон Джоуля — Ленца указывает два различных пути решения этой задачи. Один путь — уменьшить сопротивление проводов линии передачи, что можно сделать/взяв провода с большим сечением. Выясним на примере, осуществимо ли это практически.
Пусть на электростанции установлен генератор постоянного тока мощностью 200 квт. создающий напряжение 120 в. Требуется передать вырабатываемую генератором энергию на расстояние 10 км от станции. Какого сечения нужно взять провода, чтобы потери в линии передачи не превышали 10% от передаваемой мощности?
Ток, протекающий в линии передачи, определится из равенства:

Потеря мощности в линии  По потере мощности находим сопротивление линии:
По потере мощности находим сопротивление линии:

По формуле  найдём площадь сечения проводов:
найдём площадь сечения проводов:

Один метр такого провода весит 435 кГ, а вес провода для всем линии составил бы 8700 Т. Практически это значит, что такой способ передачи энергии невозможен.
Другой путь, везущий к уменьшению потерь энергии в линии передачи, заключается в уменьшении тока в линии передачи.
Но при данной мощности уменьшение тока возможно лишь при увеличении напряжения.
Пусть теперь та же мощность в 200 квт передастся при напряжении 12000 в.
Ток в линии передачи определится из равенства:

Так как величина тока уменьшилась в 100 раз, то при тех же потерях мощности в линии передачи, рассчитываемой по формуле  сопротивление линии передачи увеличится в
сопротивление линии передачи увеличится в  раз.
раз.
Сечение же проводов линии в  раз уменьшится и станет равным:
раз уменьшится и станет равным:

В  раз уменьшится и вес меди, идущей на изготовление провода. Передача энергии станет практически возможной.
раз уменьшится и вес меди, идущей на изготовление провода. Передача энергии станет практически возможной.
Таким образом, при передаче электроэнергии на большие расстояния необходимо пользоваться высоким напряжением.
На практике при передаче энергии на большие расстояния пользуются напряжениями в 3300, 6600, 110 000, 160 000, 220 000 в.
Чем длиннее линия передачи, тем более высокое напряжение используется в ней.

Днепровская гидроэлектростанция передаёт ток под напряжением 160 000 в, Свирская станция —220 000 в. Передача электроэнергии новых мощных гидроэлектростанций проектируется под ещё большим напряжением — 400 000 в и выше.
Генераторы переменного тока обычно строят на 2200, 6600, 11 000, 13 200 в. Постройка генераторов на более высокие напряжения затруднительна; в этих случаях потребовалось бы особо высокое качество изоляции всех частей генератора, находящихся под током, выполнение этого связано с большими техническими трудностями и экономически невыгодно.
Поэтому при передаче энергии на большие расстояния приходится повышать напряжение тока, получаемого от генераторов, что осуществляется при помощи трансформаторов.
Трансформатор
В основе работы трансформатора лежит явление электромагнитной индукции. Сердечник технического трансформатора состоит из отдельных стальных пластин, собранных в замкнутую раму той или иной формы (рис. 208). На сердечнике помещены две обмотки  с числом витков
с числом витков  Обмотки обладают незначительным сопротивлением и большой индуктивностью.
Обмотки обладают незначительным сопротивлением и большой индуктивностью.
Приложим к концам обмотки  которую будем называть первичной, переменное напряжение
которую будем называть первичной, переменное напряжение  (от сети или генератора). По обмотке пойдёт переменный ток I, который намагнитит сталь сердечника, создав в нём переменный магнитный поток.
(от сети или генератора). По обмотке пойдёт переменный ток I, который намагнитит сталь сердечника, создав в нём переменный магнитный поток.
Намагничивающее действие тока пропорционально числу ампер-витков 
По мере нарастания тока будет расти и магнитный поток в сердечнике, изменение которого возбудит в витках катушки э. д. с. самоиндукции. Как только э. д. с. самоиндукции достигнет величины приложенного напряжения, рост тока в первичной цепи прекратится. Таким образом, в цепи первичной обмотки трансформатора будут действовать приложенное напряжение  и э. д. с. самоиндукции
и э. д. с. самоиндукции  При этом напряжение
При этом напряжение  больше
больше  на величину падения напряжения в обмотке, которое очень мало. Следовательно, приближённо можно написать:
на величину падения напряжения в обмотке, которое очень мало. Следовательно, приближённо можно написать:

Переменный магнитный поток, возникающий в сердечнике трансформатора, пронизывает и витки вторичной обмотки трансформатора, возбуждая в каждом витке этой обмотки такую же по величине э. д. е., как и в каждом витке первичной обмотки.
Так как число витков в первичной обмотке  , а во вторичной обмотке
, а во вторичной обмотке  , то индуктированные в них э. д. с. будут соответственно равны:
, то индуктированные в них э. д. с. будут соответственно равны:

где e — э. д. е., возникающая в одном витке.
Напряжение же  на концах разомкнутой вторичной обмотки равно э. д. с. в ней, т. е.
на концах разомкнутой вторичной обмотки равно э. д. с. в ней, т. е.

Из равенств (1), (2) и (3) следует, что величина напряжения на концах первичной обмотки трансформатора так относится к величине напряжения на концах вторичной обмотки, как число витков первичной обмотки относится к числу витков вторичной обмотки:

Постоянная величина k называется коэффициентом’ трансформации трансформатора.
В том случае, когда нужно повысить напряжение, вторичная обмотка устраивается с большим числом витков (повышающий трансформатор); в случае же, когда надо понизить напряжение, вторичная обмотка трансформатора берётся с меньшим числом витков (понижающий трансформатор).
Пока вторичная обмотка разомкнута (тока в ней нет), трансформатор работает вхолостую. При холостом ходе он потребляет небольшую энергию, так как ток, намагничивающий стальной сердечник вследствие большой индуктивности катушки, очень мал. Передача энергии из первичной цепи во вторичную при холостом ходе отсутствует.

Нагрузим наш трансформатор, замкнув через реостат цепь вторичной обмотки его (рис. 208). По ней теперь пойдёт индукционный ток, обозначим его буквой  . Этот ток, согласно закону Ленца, вызовет уменьшение магнитного потока в сердечнике. Но ослабление магнитного потока в сердечнике приведёт к уменьшению э. д. с. самоиндукции в первичной обмотке и к нарушению равновесия между напряжением
. Этот ток, согласно закону Ленца, вызовет уменьшение магнитного потока в сердечнике. Но ослабление магнитного потока в сердечнике приведёт к уменьшению э. д. с. самоиндукции в первичной обмотке и к нарушению равновесия между напряжением  , даваемым генератором на первичную обмотку, и э. д. с. самоиндукции
, даваемым генератором на первичную обмотку, и э. д. с. самоиндукции  . В результате этого в первичной обмотке ток увеличится на какую-то величину
. В результате этого в первичной обмотке ток увеличится на какую-то величину  и станет равным
и станет равным  . Вследствие увеличения тока магнитный поток в сердечнике трансформатора возрастёт до прежней величины и нарушенное равновесие между
. Вследствие увеличения тока магнитный поток в сердечнике трансформатора возрастёт до прежней величины и нарушенное равновесие между  снова восстановится. Таким образом, появление вторичного тока
снова восстановится. Таким образом, появление вторичного тока  вызывает увеличение тока в первичной обмотке на величину
вызывает увеличение тока в первичной обмотке на величину  , которая определит нагрузочный ток первичной обмотки трансформатора. Так как намагничивающее действие тока пропорционально числу ампер-витков
, которая определит нагрузочный ток первичной обмотки трансформатора. Так как намагничивающее действие тока пропорционально числу ампер-витков  , то соотношение между нагрузочными токами
, то соотношение между нагрузочными токами  определится из равенства:
определится из равенства:

т.е. нагрузочные токи в первичной и вторичной обмотках трансформатора обратно пропорциональны числам витков в них.
При нагрузке трансформатора происходит непрерывная передача энергии из первичной цепи во вторичную. Согласно закону сохранения и превращения энергии, мощность тока во вторичной цепи равна мощности в первичной цепи; следовательно, должно было бы иметь место равенство:



В действительности это равенство не соблюдается, так как при работе трансформатора имеются потери на нагревание обмоток трансформатора, на вихревые токи в сердечнике и на перемагничивание сердечника; однако потери эти невелики.
Трансформатор принадлежит к числу наиболее совершенных преобразователей энергии. Коэффициент полезного действия современных мощных трансформаторов достигает значений 94—99%. На рисунке 210 изображён трансформатор на небольшую мощность. На рисунке 211 показана трансформаторная подстанция Днепровской гидроэлектростанции.
В линиях трёхфазного тока используются или обычные однофазные трансформаторы, включаемые в каждую из трёх фаз линии, или же специальные трёхфазные трансформаторы, имеющие три пары обмоток.
Идея трансформатора впервые родилась в России и принадлежит изобретателю «русского света» П. Н. Яблочкову. Разрабатывая эту идею дальше, ассистент Московского университета И. Ф. Усагин сконструировал первый трансформатор, который он демонстрировал в 1882 г. на промышленной выставке в Москве.
Электрификация
Громадное значение электрификации СССР придавал создатель Советского государства В. И. Ленин. В речи на III съезде комсомола он говорил:
«Мы знаем, что коммунистического общества нельзя построить, если не возродить промышленности и земледелия, причем надо возродить их не по-старому. Надо возродить их на современной, по последнему слову науки построенной, основе. Вы знаете, что этой основой является электричество, что только, когда произойдёт электрификация всей страны, всех отраслей промышленности и земледелия, когда вы эту задачу освоите, только тогда вы для себя сможете построить то коммунистическое общество, которое не сможет построить старое поколение».
В феврале 1920 г. по инициативе Ленина была создана Государственная комиссия по электрификации России (сокращённо: ГОЭЛРО).
По плану ГОЭЛРО намечалось за 10—15 лет построить 30 районных электростанций общей мощностью в 1,75 млн. киловатт. При жизни Ленина были построены две первые мощные электростанции: Шатурская тепловая электростанция (в 130 км от Москвы) мощностью свыше 100 000 квт и Волховская гидроэлектростанция мощностью 80 000 квт.
Но уже в 1932 г. мощность районных электростанций составляла 2,9 млн. квт.
За годы второй пятилетки мощность электростанций выросла до 8,1 млн. квт.
В 1946 г. СССР располагал электростанциями общей мощностью 10,7 млн. квт. За пятилетие с 1946 по 1950 г. по государственному плану восстановления и развития народного хозяйства СССР мощность действующих в СССР электростанций должна была увеличиться на 11,7 млн. квт. План этот перевыполнен.
Ещё более грандиозным будет рост электроэнергетической базы СССР в результате осуществления строительства гидроэлектростанций на Волге, Каме, Днепре, Ангаре, Иртыше и других больших реках нашей Родины, а также многих тепловых электростанций.
Сооружение крупнейших в мире Волжской имени В. И. Ленина (мощностью 2 млн. 300 тыс. квт), Волжской имени XXII съезда КПСС (мощностью 2 млн. 530 тыс. квт) и Братской (на 3 500 000 квт) гидроэлектростанций играет огромную роль в деле снабжения промышленных предприятий и сельского хозяйства электроэнергией, позволяет в ещё большей степени электрифицировать железные дороги.

Создание судоходного Волго-Донского канала имени В. И. Ленина позволило объединить все моря Европейской части Союза в единую водную систему. Сооружение гидростанции при плотине Цимлянского гидроузла мощностью 160 тыс. квт обеспечило дешёвую электроэнергию для промышленности и земледелия орошаемых полупустынных и засушливых земель Ростовской и Волгоградской областей. Энергию наших рек мы заставляем служить развитию промышленности и сельского хозяйства, увеличению их продуктивности, облегчению труда советских людей, улучшению материального благосостояния народа, строящего коммунизм.
Большую роль в деле электрификации имеет также строительство теплоэлектроцентралей и ветроэлектростанций.

В некоторых районах нашей страны нет крупных рек для строительства гидроэлектростанций, но имеются большие запасы горючих ископаемых: торфа, горючих сланцев, каменного угля. В этих районах строятся теплоэлектроцентрали; в них энергия, полученная при сжигании топлива, превращается в электрическую энергию, которая затем передаётся по проводам к потребителям.
Кроме того, важным источником электрической энергии служит ветер — «голубой уголь». В ветроэлекгростанциях энергия движущегося воздуха превращается в электрическую энергию. Эти станции особенно выгодно строить в тех районах, где постоянно дуют ветры.
В связи со строительством гигантских электростанций наши учёные разрабатывают проблемы передачи электроэнергии на сверхдальние расстояния с наименьшими потерями. Самой важной из этих проблем является изыскание возможностей максимального повышения напряжения в линиях передачи. В настоящее время построены линии электропередач от крупнейших гидроэлектростанций— Волжских имени В. И. Ленина и имени XXII съезда КПСС — на напряжение в 400 000 в.
Для передачи энергии от мощных сибирских электростанций будут использовать ещё более высокие напряжения (800 кв).
В настоящее время в Советском Союзе ведутся экспериментальные работы по передаче электрической энергии постоянным током. Удачное решение этой проблемы позволит ещё выше поднять к. п. д. линий передачи. Объясняется это тем, что одна и та же линия передачи оказывает меньшее сопротивление постоянному току, чем переменному, при одной и той же величине тока. Но генераторы постоянного тока не могут быть построены на необходимые для линий передач высокие напряжения. Поэтому напряжение от генераторов переменного тока необходимо сначала повысить до требуемого значения с помощью трансформаторов, а затем преобразовать в специальных высоковольтных выпрямителях в постоянное напряжение, которое и передавать в линию электропередачи. В пункте потребления постоянное напряжение надо преобразовать в переменное (в инвертерах), затем понизить до нужного значения с помощью трансформаторов.
Мощность в цепи переменного тока
В цепи постоянного тока мощность на каком-нибудь участке характеризует величину энергии электрического тока, которая превращается на этом участке в другие виды энергии за время, равное одной секунде. Величина этой мощности измеряется произведением напряжения на ток:

То же самое можно сказать и о мощности на каком-нибудь участке цепи переменного тока, если эта цепь не обладает ни индуктивностью, ни ёмкостью. Мощность на участке цепи переменного тока, обладающей активным сопротивлением, называется активной мощностью. Активная мощность характеризует величину энергии переменного тока, которая необратимо превращается за 1 секунду в другие виды энергии (во внутреннюю, механическую и др.). Единицей активной мощности является ватт (вт) или киловатт (квт).
Обратимся к опыту. В цепь переменного тока включим проводник с активным сопротивлением. Напряжение при этом будем измерять вольтметром, ток — амперметром, а мощность — ваттметром (рис. 28,а).
Сравнивая показания ваттметра Р с произведением  , убеждаемся, что
, убеждаемся, что  . Следовательно, активную мощность можно измерять непосредственно ваттметром или вычислять по показаниям вольтметра и амперметра.
. Следовательно, активную мощность можно измерять непосредственно ваттметром или вычислять по показаниям вольтметра и амперметра.
Значительно сложнее решается вопрос о мощности в цепи переменного тока, если, кроме активного сопротивления, эта цепь обладает ещё индуктивным или ёмкостным сопротивлением.
Включим в цепь переменного тока последовательно с активным сопротивлением катушку индуктивности (рис. 28,б). Показания ваттметра, соответствующие активной мощности в цепи, в этом случае оказываются меньше, чем произведение .
.

Можно записать, что  , где
, где  —некоторый коэффициент, получивший название коэффициента мощности. Как показывают теоретические расчёты, коэффициент мощности
—некоторый коэффициент, получивший название коэффициента мощности. Как показывают теоретические расчёты, коэффициент мощности  равен
равен  —сдвиг фаз между током и напряжением в цепи переменного тока. Введём значение k в формулу мощности (1), получим:
—сдвиг фаз между током и напряжением в цепи переменного тока. Введём значение k в формулу мощности (1), получим:

Величина UI=S получила название полной мощности. Полная мощность в цепи переменного тока измеряется вольтамперами (сокращённо ва) или киловольтамперами (ква). Итак, активная мощность в цепи переменного тока равна полной мощности, умноженной на 

В общем случае (при наличии как активного, так и реактивного сопротивлений) в цепи переменного тока активная мощность меньше полной мощности, поэтому коэффициент мощности  . При активной нагрузке
. При активной нагрузке  ; при чисто индуктивной или ёмкостной нагрузке цепи
; при чисто индуктивной или ёмкостной нагрузке цепи 
Чем выше коэффициент мощности, тем лучше используется генератор и сеть. Поэтому необходимо стремиться увеличить коэффициент мощности цепей, питаемых переменным током.
Необходимость увеличения  потребителя энергии видно на следующем примере.
потребителя энергии видно на следующем примере.
Допустим, что на электростанции установлен генератор переменного тока мощностью 240 ква. Напряжение на зажимах генератора 1200 в. Ток, который может установиться в сети, будет равен:

Если к генератору подключить нагрузку, имеющую только активное сопротивление (например, электрические лампы накаливания и электронагревательные приборы), то  и активная мощность
и активная мощность  В этом случае энергия генератора используется полностью.
В этом случае энергия генератора используется полностью.
Если же подключить к этому генератору нагрузку, имеющую  (включить потребители с активным и индуктивным сопротивлением), то активная мощность в сети будет:
(включить потребители с активным и индуктивным сопротивлением), то активная мощность в сети будет:  Следовательно, хотя по обмоткам генератора и подводящим к потребителю проводам будет проходить прежний ток, но активная мощность уменьшится. Низкий коэффициент мощности приводит к уменьшению к. п. д. генераторов.
Следовательно, хотя по обмоткам генератора и подводящим к потребителю проводам будет проходить прежний ток, но активная мощность уменьшится. Низкий коэффициент мощности приводит к уменьшению к. п. д. генераторов.
Увеличение  в цепях, потребляющих переменный ток, представляет собой важную и довольно сложную задачу энергетики.
в цепях, потребляющих переменный ток, представляет собой важную и довольно сложную задачу энергетики.
Вращение рамки в однородном магнитном поле. Период и частота переменного тока
В сети переменного тока э. д, с. и напряжение должны изменяться по гармоническому закону, т. е. должны быть синусоидальными (§ 24.6). Отклонение от синусоидальной формы напряжения в сети переменного тока приводит к дополнительным потерям энергии.
Рассмотрим получение синусоидального переменного тока при равномерном вращении рамки в однородном магнитном поле. Пусть рамка ABCD, концы которой присоединены к металлическим кольцам, находится в однородном магнитном поле с индукцией В (рис. 26.1, а). К кольцам прижаты щетки a и b, соединенные с потребителем электрической энергии л. Если рамку привести во вращение вокруг оси ОO1 по часовой стрелке с постоянной угловой скоростью  то в отрезках провода АВ и CD возникнут э. д. с. индукции e1 и е2, равные по величине и противоположные по направлению.
то в отрезках провода АВ и CD возникнут э. д. с. индукции e1 и е2, равные по величине и противоположные по направлению.

Рис. 26.1.
Движение проводов АВ и CD будет происходить по окружности диаметром d=AD и с линейной скоростью  Если отсчет времени и углов вести от положения 1 рамки на рис. 26.1, б, то угол поворота рамки
Если отсчет времени и углов вести от положения 1 рамки на рис. 26.1, б, то угол поворота рамки выразится формулой
выразится формулой
 или
или  (26.1)
(26.1)
где Т — время одного полного оборота рамки. Поскольку угол  равен углу между векторами В и
равен углу между векторами В и  для э. д. с. индукции в отрезке АВ или CD имеем формулу (§ 23.3)
для э. д. с. индукции в отрезке АВ или CD имеем формулу (§ 23.3)

где l — длина проводника АВ или CD. Заметим, что такие проводники называют активными, так как при вращении контура только в них наводится э. д. с. Общая э. д. с. в рамке при этом
 или
или 
Таким образом, при равномерном вращении рамки в однородном магнитном поле в ней наводится э. д. с., определяемая формулой
 или
или  (26.2)
(26.2)
Поскольку  и В постоянны, их произведение можно обозначить одной буквой
и В постоянны, их произведение можно обозначить одной буквой  т. е.
т. е.  Тогда
Тогда
 или
или  (26.3)
(26.3)
Вспомним, что максимальное значение синуса равно единице. Следовательно,  в формуле (26.3) обозначает максимальную э. д. с., возникающую в рамке при ее вращении; называют еще амплитудой э. д. с. График синусоидально изменяющейся э. д. с. изображен на рис. 26.2. Заметим, что мгновенные значения величин для переменного тока принято обозначать строчными буквами, а максимальные, амплитудные значения — заглавными буквами. Например, для мгновенного значения силы тока применяют обозначение i, а для амплитудного — Iм. Напряжения соответственно обозначают u и Uм.
в формуле (26.3) обозначает максимальную э. д. с., возникающую в рамке при ее вращении; называют еще амплитудой э. д. с. График синусоидально изменяющейся э. д. с. изображен на рис. 26.2. Заметим, что мгновенные значения величин для переменного тока принято обозначать строчными буквами, а максимальные, амплитудные значения — заглавными буквами. Например, для мгновенного значения силы тока применяют обозначение i, а для амплитудного — Iм. Напряжения соответственно обозначают u и Uм.

Рис. 26.2.

Рис. 26.3.
В рассматриваемом примере круговая (циклическая) частота переменного тока со в формулах (26.2) и (26.3) совпадает с угловой скоростью вращения рамки в магнитном поле, а период изменения переменного тока Т совпадает с периодом вращения рамки. Скорость повторяемости изменений переменного тока характеризуется частотой 

Поэтому формулу (26.3) можно записать так:
 Рис. 26.2.
Рис. 26.2.
Если число оборотов рамки в минуту обозначить через n, то
 (26.4)
(26.4)
Стандартная техническая частота переменного тока составляет 50 Гц. Это означает, что э. д. с. и ток меняют свое направление в цепи 100 раз в секунду. Такой ток относят к токам низкой частоты. Для специальных целей применяются токи, частота которых достигает миллионов герц. Их называют токами высокой частоты.
Понятие об устройстве индукционных генераторов
Электрические машины, в которых механическая энергия превращается в электрическую с помощью явления электромагнитной индукции, называют индукционными генераторами.
Основные элементы индукционного генератора переменного тока показаны на рис. 26.1, а: 1 — индуктор, создающий магнитное поле; 2 — якорь (проводник, в котором наводится э. д . с.); 3 — металлические кольца и 4 — щетки, соединяющие неподвижные проводники с вращающимися проводниками.
Для получения э. д. с. индукции важно относительное перемещение проводника и магнитного поля, поэтому на практике индуктор делают вращающимся и называют его ротором, а якорь делают неподвижным и называют его статором. Это целесообразно, так как ротором является электромагнит, для питания которого нужен сравнительно слабый постоянный ток. При такой конструкции ток в ротор передается с. помощью скользящего контакта, который хорошо работает при слабом токе, а потребитель соединяется с генератором неподвижными проводами.
Ротор и статор делают из стали и между ними оставляют очень маленький зазор, поэтому вектор индукции В в зазоре везде перпендикулярен к поверхности статора. Следовательно, вектор В все время перпендикулярен к вектору линейной скорости точек поверхности ротора, т. е. к вектору скорости относительного движения магнитного поля и проводников якоря.
Это означает, что в выражении для э. д. с.  угол
угол  все время равен
все время равен  и
и  Поэтому, чтобы в проводниках наводилась синусоидально изменяющаяся э. д. с., магнитным полюсам ротора придают специальную форму, обеспечивающую синусоидальное изменение величины вектора В вдоль окружности ротора (рис. 26.3).
Поэтому, чтобы в проводниках наводилась синусоидально изменяющаяся э. д. с., магнитным полюсам ротора придают специальную форму, обеспечивающую синусоидальное изменение величины вектора В вдоль окружности ротора (рис. 26.3).
Когда у ротора имеется одна пара магнитных полюсов, то частота вращения ротора совпадает с частотой переменного тока. При двух парах полюсов частота изменения магнитного поля в зазоре вдвое больше частоты вращения ротора, поэтому для получения стандартной частоты переменного тока такой ротор должен делать не 50, а 25 об/с. Одну пару полюсов делают у турбогенераторов; роторы которых приводятся во вращение паровой турбиной, а тихоходные многополюсные генераторы устанавливаются на гидростанциях.
Схема устройства индукционного генератора постоянного тока показана на рис. 26.4. Она отличается от схемы генератора переменного тока (рис. 26.1, а) только тем, что здесь вместо колец используется коллектор (3 на рис. 26.4), представляющий собой кольцо, разрезанное на секторы, изолированные друг от друга. Коллектор создает у потребителя ток, постоянный по направлению. Это обеспечивается тем, что левая щетка (см. рис. 26.4) всегда соединена с поднимающейся стороной витка, а правая — с опускающейся стороной. Ясно, что у генераторов постоянного тока якорь делать неподвижным нельзя. График изменения э. д. с. такого генератора показан на рис. 26.5.

Рис. 26.4.

Рис. 26.5.
Для сравнения на рисунке пунктиром показано изменение э. д. с. в случае сплошных колец.
На практике обмотку якоря разбивают на ряд секций, соединенных с отдельными секторами коллектора. Это ослабляет пульсации напряжения на полюсах машины, т. е. делает его постоянным по величине.
При работе генератора на проводники якоря действует сила Ампера (§ 22.9), препятствующая вращению якоря, которая тем больше, чем сильнее ток, протекающий через обмотку якоря. Следовательно, при увеличении тока, потребляемого от генератора, для вращения его якоря приходится затрачивать все больше энергии. Это относится и к генератору переменного тока.
Отметим еще, что электрические машины постоянного тока обладают обратимостью, т. е. могут работать и как генератор и как электродвигатель.
Действующие значения ЭДС, напряжения и силы переменного тока
При синусоидальном переменном токе средние значения напряжения и тока за период равны нулю и не могут служить его характеристиками. Однако среднее значение квадрата силы тока за период отлично от нуля. Следовательно, при включении в цепь переменного тока измерительного прибора, отклонение стрелки которого пропорционально квадрату силы тока, стрелка отклонится и установится на определенном делении шкалы. Каков смысл этого показания?
Вспомним, что количество выделенного в проводнике тепла изменяется пропорционально квадрату силы тока. Представим себе, что в цепь переменного тока включен тепловой амперметр, действие которого основано на выделении тепла электрическим током. Поскольку шкала такого амперметра градуируется на амперы для постоянного тока, можно заключить, что переменный ток по своему тепловому эффекту эквивалентен постоянному току, силу которого указывает на шкале прибора стрелка. Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.
Все амперметры, предназначенные для переменного тока, показывают эффективное значение силы тока. В курсе электротехники доказывается, что оно в  раз меньше амплитудного значения силы тока Iм, т. е.
раз меньше амплитудного значения силы тока Iм, т. е.
 (26.5)
(26.5)
Так как деления на шкале вольтметра соответствуют произведению  где при переменном токе
где при переменном токе  — эффективное значение тока, протекающего через вольтметр, а
— эффективное значение тока, протекающего через вольтметр, а  — сопротивление вольтметра, то
— сопротивление вольтметра, то  называют эффективным напряжением переменного тока, которое в
называют эффективным напряжением переменного тока, которое в  раз меньше
раз меньше  т. е.
т. е.
 (26.6)
(26.6)
Аналогично эффективное значение э. д. с. переменного тока  в
в  раз меньше его амплитудного значения
раз меньше его амплитудного значения 
 (26.7)
(26.7)
Все вольтметры, предназначенные для переменного тока, показывают эффективные значения э. д. с. и напряжения.
Индуктивность и емкость в цепи переменного тока
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения  и
и  При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:
При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:
 (26.8)
(26.8)
 (26.9)
(26.9)
 (26.10)
(26.10)
Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле (16.18):

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е.  Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цени и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока 
 (26.11)
(26.11)
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Рис. 26.6.
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.
Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте 
 (26.12)
(26.12)
Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Хс отстает по фазе от тока.
Индуктивное ХL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:
 (26.13)
(26.13)
и имеет индуктивный характер при  и емкостный характер при
и емкостный характер при 
В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой
 (26.14)
(26.14)
Мощность, затрачиваемая только на тепловое действие тока, выражается формулой
 (26.15)
(26.15)
Из (26. 14) видно, что для увеличения активной мощности переменного тока нужно повышать  (Объясните, почему наибольшее значение
(Объясните, почему наибольшее значение  имеет при
имеет при 
Преобразование переменного тока. Трансформатор
Одно из важных преимуществ переменного тока перед постоянным заключается в том, что напряжение переменного тока относительно легко поддается изменению с помощью электромагнитной индукции, а способы преобразования постоянного тока сложны.
Прибор для преобразования напряжения и силы переменного тока при неизменной частоте называют трансформатором (рис. 26.7, а). Он был изобретен П. Н. Яблочковым в 1876 г. Трансформатор состоит из замкнутого сердечника, сделанного из мягкой стали или феррита, на котором имеются две изолированные друг от друга катушки (их называют обмотками) с разным числом витков. Первичная обмотка включается в сеть переменного тока, а вторичная — соединяется с потребителем. Ток в первичной обмотке создает в сердечнике переменный магнитный поток (рис. 26.7, б), который наводит одинаковую э. д. с. индукции в каждом витке обеих обмоток. Если первичная обмотка имеет w1, витков, а вторичная w2, то э. д. с. индукции в обмотках прямо пропорциональны числу витков в них:
 (26.16)
(26.16)

Рис. 26.7.
При разомкнутой цепи вторичной обмотки (холостой ход трансформатора) напряжение U2 на ее зажимах равно э. д. с.  В первичной обмотке при этом течет слабый ток I0, который называют током холостого хода. Так как падение напряжения U1 на сопротивлении обмотки очень мало, то напряжение Ut немного больше э. д. с.
В первичной обмотке при этом течет слабый ток I0, который называют током холостого хода. Так как падение напряжения U1 на сопротивлении обмотки очень мало, то напряжение Ut немного больше э. д. с.  но практически
но практически 
Таким образом, при холостом ходе трансформатора напряжения на обмотках прямо пропорциональны числу витков обмоток:
 (26.17)
(26.17)
Если число витков во вторичной обмотке w2 больше, чем в первичной w1, то трансформатор называют повышающим, а если w2 меньше, чем — понижающим. Отношение числа витков первичной обмотки к числу витков вторичной обмотки называют коэффициентом трансформации n:
 (26.18)
(26.18)
Итак, у понижающего трансформатора n больше единицы, а у повышающего — меньше единицы.
Когда цепь вторичной обмотки замыкается (к трансформатору подключается нагрузка), ток вторичной обмотки I2 создает в сердечнике магнитный поток, направленный навстречу потоку первичной обмотки. Ослабление потока в сердечнике уменьшает э. д. с.  в первичной обмотке. Поэтому ток в ней возрастает до такого значения I1, при котором ее магнитный поток скомпенсирует встречный поток вторичной катушки и результирующий поток в сердечнике останется прежним.
в первичной обмотке. Поэтому ток в ней возрастает до такого значения I1, при котором ее магнитный поток скомпенсирует встречный поток вторичной катушки и результирующий поток в сердечнике останется прежним.
Поскольку магнитный поток катушки пропорционален числу ее витков и току, то можно приближенно считать, что  (на самом деле
(на самом деле  немного больше
немного больше  ). Отсюда
). Отсюда
 (26.19)
(26.19)
т. е. сила тока в обмотках обратно пропорциональна числу витков.
Падения напряжения на сопротивлениях обмоток невелики, поэтому можно считать  и
и  т. е. выражение (26.17) приближенно справедливо и для трансформатора под нагрузкой.
т. е. выражение (26.17) приближенно справедливо и для трансформатора под нагрузкой.
Из (26.17) и (26.19) следует, что  Это означает, что мощности тока в первичной цепи Р1 и во вторичной цепи Р2 приближенно равны *). (На рис. 26.7 б справа — условное изображение трансформатора.)
Это означает, что мощности тока в первичной цепи Р1 и во вторичной цепи Р2 приближенно равны *). (На рис. 26.7 б справа — условное изображение трансформатора.)
*) Углы сдвига фаз в обеих обмотках мало отличаются друг от друга.
Индукционная катушка
Для получения в лаборатории переменного тока высокого напряжения за счет энергии постоянного тока применяют индукционную катушку Румкорфа, которая представляет собой трансформатор оригинальной конструкции (рис. 26.8).

Рис. 26.8.
При замыкании ключа К ток от батареи Б проходит через стойку, винт В, стальной молоточек М, первичную катушку А с сердечником из ферромагнетика и возвращается к батарее Б. Так как сердечник при этом намагничивается, то молоточек М притягивается к нему, и цепь размыкается. Тогда сердечник размагничивается, молоточек выпрямляется и снова замыкает цепь через винт В. Затем весь описанный процесс повторяется снова.
Таким образом, вокруг первичной катушки создается переменное магнитное поле, которое наводит э. д. с. индукции  во вторичной катушке, имеющей большое число витков. Ее концы показаны наверху.
во вторичной катушке, имеющей большое число витков. Ее концы показаны наверху.
При размыкании цепи между молоточком М и винтом В возникает искра, которая замедляет изменение поля, т. е. снижает напряжение между концами вторичной катушки. Для ослабления искры параллельно искровому промежутку присоединяют конденсатор С. Индукционная катушка позволяет получить между концами вторичной катушки напряжение порядка 10 000 В.
Трехфазный ток
В настоящее время очень широкое применение получила трехфазная система переменного тока, изобретенная в конце прошлого века русским электротехником М. О. Доливо-Добровольским. Выясним, как получается трехфазный ток.
Генератор трехфазного тока отличается от индукционного генератора, рассмотренного в §§ 26.1 и 26.2, тем что на его статоре вместо одной обмотки якоря размещены три одинаковые обмотки (рис. 26.9), смещенные относительно друг друга на 1/3 окружности (120°). Начала обмоток обозначены буквами А, В и С, а концы — соответственно X, Y и Z.

Рис. 26.9.
Ротор (индуктор) представляет собой постоянный электромагнит со скользящими контактами, создающий в воздушном зазоре генератора магнитное поле с синусоидальным распределением индукции по окружности (рис. 26.3). При вращении ротора в каждой из трех обмоток индуцируется синусоидальная э. д. с. Период изменения этих э. д. с. равен периоду вращения ротора, а круговая частота  совпадает с круговой скоростью вращения.
совпадает с круговой скоростью вращения.
Поскольку обмотки смещены на 1/3 окружности, то э. д. с. в каждой из них запаздывает по отношению к предыдущей по ходу вращения ротора на 1/3 периода. Так, если в момент времени, изображенный на рис. 26.9, э. д. с. еА в обмотке А—X имеет максимальное значение, то, когда ротор повернется на 1/3 оборота (т. е. через 1/3 периода), он займет такое же положение относительно следующей обмотки В—Y, и ее э. д. с. еВ будет иметь максимальное значение; еще через 1/3 периода будет максимальна э. д. с. еВ в третьей обмотке С—Z, затем снова в первой (еА) и т. д. Таким образом, получается, что э. д. с. еВ отстает по фазе от еА, а еC в свою очередь отстает от еВ на 1/3 периода, т. е. на угол  или 120° (рис. 26.10, а). Этот сдвиг фаз э. д. с. еА, еВ и еC удобно выразить (подобно тому как это делалось для механических колебаний в § 24.7) с помощью векторов
или 120° (рис. 26.10, а). Этот сдвиг фаз э. д. с. еА, еВ и еC удобно выразить (подобно тому как это делалось для механических колебаний в § 24.7) с помощью векторов  и
и  равных по величине амплитудному значению э. д. с.
равных по величине амплитудному значению э. д. с.  и составляющих друг с другом углы 120° (рис. 26.10, б). При вращении этих векторов с круговой скоростью
и составляющих друг с другом углы 120° (рис. 26.10, б). При вращении этих векторов с круговой скоростью  против часовой стрелки их проекции на вертикальную ось дадут мгновенные значения соответствующих э. д. с. еА, еВ и еC.
против часовой стрелки их проекции на вертикальную ось дадут мгновенные значения соответствующих э. д. с. еА, еВ и еC.

Рис. 26.10.
Система, состоящая из трех электрических цепей, в которых действуют переменные э. д. с. одной и той же частоты, сдвинутые по фазе друг относительно друга на 1/3 периода (т. е. на  или 120°, называется трехфазной системой. Каждая из этих трех цепей называется фазой, а система переменных токов в таких цепях называется трехфазным током. Трехфазный ток обладает важными преимуществами перед обычным переменным током, поэтому почти на всех электростанциях установлены генераторы трехфазного тока.
или 120°, называется трехфазной системой. Каждая из этих трех цепей называется фазой, а система переменных токов в таких цепях называется трехфазным током. Трехфазный ток обладает важными преимуществами перед обычным переменным током, поэтому почти на всех электростанциях установлены генераторы трехфазного тока.
Каждую из трех фаз генератора в принципе можно было бы соединить отдельными проводами с потребителями и использовать в виде отдельных источников переменного тока. Однако это нецелесообразно, и фазы всегда соединяют между собой.
На рис. 26.11 показан один из способов соединения генератора с потребителями. Концы фаз генератора X, У и Z соединены в одни узел О, который называют нейтральной точкой или нейтралью. Такой способ соединения фаз называют соединением звездой. На рис. 26.11 аналогично включены потребители, разбитые на три группы, которые называют фазами нагрузки. От генератора к потребителям идут четыре провода: провода АА’, ВВ’, СС’ называют линейными, а OO’ — нейтральным проводом.

Рис. 26.11.
Напряжения между началом каждой фазы А, В, С и нулевой точкой О называют фазными напряжениями и обозначают UA, UB и UC или в общем случае Uф. Поскольку падение напряжения внутри обмоток генератора мало, то напряжения на фазах генератора равны соответствующим э. д. с. (см. рис. 26.10) и также изображаются симметричной звездой векторов UA, UB, UC (рис. 26.12, а), составляющих между собой углы 120°.
Напряжения между началами обмоток, т. е. между линейными проводами (рис. 26.11),называются линейными напряжениями и обозначаются UAB, UBC, UCA или Uл. Линейные напряжения равны разности соответствующих фазных напряжений. Например, линейное напряжение Uл—UAB —UA—UB и на рис. 26.12, а изображается вектором UAB, замыкающим концы векторов UA и UB (направленным из конца вычитаемого вектора в конец уменьшаемого). Аналогично определяются напряжения UBC и UCA.
Проведем в равнобедренном треугольнике, образованном векторами двух фазных и одного линейного напряжений, высоту из точки О (рис. 26.12, а). Тогда получим  Таким образом, присоединении звездой линейное напряжение в
Таким образом, присоединении звездой линейное напряжение в  раз больше фазного:
раз больше фазного:
 (26.20)
(26.20)
Так, если фазное напряжение равно 127 В, то линейное составляет 
Токи, текущие в фазах, называют фазными токами (обозначают Iф), а токи в линейных проводах — линейными токами (IЛ). Из рис. 26.11 видно, что для этой схемы соединений токи в фазах генератора IA, IB, IC равны соответствующим линейным токам и токам в фазах нагрузки  т. е.
т. е.
 (26.21)
(26.21)
Величина этих токов определяется фазными напряжениями и сопротивлениями фаз нагрузки. Заметим, что при чисто активной нагрузке токи совпадают по фазе с соответствующими фазными напряжениями; если же нагрузка имеет индуктивный или емкостной характер, то токи отстают или опережают напряжения на некоторый угол 

Рис. 26.12.
Ток в нейтральном проводе I0 равен сумме фазных токов. Поэтому на векторной диаграмме он должен быть равен геометрической сумме векторов IА, IB, IC. При одинаковой нагрузке фаз токи IА, IB, IC получаются одинаковыми по величине и образуют симметричную звезду векторов (рис. 26.12, б). Нетрудно понять, что в этом случае ток в нейтральном проводе получается равным нулю. Поэтому при одинаковой нагрузке фаз нейтральный провод можно отключить, и в системе ничего не изменится.
Рассмотрим другой способ соединения фаз генератора; начало каждой фазы соединяется с концом предыдущей фазы так, что фазы образуют замкнутый треугольник (рис. 26.13). Такое соединение фаз называется соединением треугольником. Поскольку фазы генератора подключены непосредственно к линейным проводам, то при соединении треугольником линейные напряжения равны фазным:
 (26.22)
(26.22)
Из сравнения (26.20) и (26.22) видно, что при переключении фаз генератора со звезды на треугольник линейные напряжения уменьшаются в  раз.
раз.
Для каждого узла соединения (рис. 26.13) сумма втекающих токов равна сумме вытекающих токов. Поэтому получается, что токи в линейных проводах равны разности соответствующих фазных токов (рис. 26.14). При одинаковой нагрузке фаз из рис. 26.14 получается соотношение
 (26.23)
(26.23)

Рис. 26.13.

Рис. 26.14.
Потребители также можно соединить треугольником, подключив их прямо к линейным проводам (рис. 26.15). Ясно, что при этом для напряжений выполняется соотношение (26.22). Токи в фазах нагрузки  определяются их сопротивлениями; при одинаковых сопротивлениях фаз выполняется соотношение (26.23).
определяются их сопротивлениями; при одинаковых сопротивлениях фаз выполняется соотношение (26.23).

Рис. 26.15.
Генератор может быть соединен звездой, а потребители — треугольником, и наоборот. Следует помнить, что при соединении фаз (генератора или нагрузки) звездой выполняются соотношения (26.20) и (26.21), а при соединении фаз треугольником — (26.22) и (26.23). В зависимости от того, какое напряжение надо получить на потребителе, применяется та или иная схема соединений фаз генератора и нагрузки. (Покажите, что при одном и том же фазном напряжении генератора  можно, применяя различные варианты соединений, получить на нагрузке напряжения 127, 220, 380 В.)
можно, применяя различные варианты соединений, получить на нагрузке напряжения 127, 220, 380 В.)
Общая активная мощность трехфазной системы равна сумме активных мощностей трех фаз (см. (26.14)). При одинаковой нагрузке фаз
 (26.24)
(26.24)
(Напомним, что при чисто активной нагрузке  )
)
Выразив Uф и Iф через Uл и Iл с помощью соотношений (26.20) и (26.21) при соединении фаз звездой или (26.22) и (26.23) при соединении треугольником, получим для обоих случаев
 (26.25)
(26.25)
Из этого соотношения видно, что линия передачи трехфазного тока экономичнее двухпроводной линии передачи: при одних и тех же напряжениях и токах в линиях передач в трехфазной линии общая длина проводов в 1,5 раза больше, чем в двухпроводной линии, а передаваемая мощность больше в  раза.
раза.
Важнейшим достоинством трехфазной системы является простота, надежность и экономичность трехфазных электродвигателей. В основе их устройства лежит вращающееся магнитное поле. Выясним, как оно образуется.
Статор трехфазного двигателя по устройству аналогичен статору генератора (рис. 26.9). На внутренней поверхности статора размещаются три катушки — фазы двигателя. Они соединяются звездой или треугольником и подключаются к трехфазной линии.
Поскольку катушки (фазы) одинаковые, то токи в них получаются одинаковыми по величине, но сдвинутыми по фазе друг относительно друга на угол  или 120°, и в любой момент времени могут быть представлены как проекции на вертикальную ось векторов IА, IB и IC,вращающихся с круговой скоростью
или 120°, и в любой момент времени могут быть представлены как проекции на вертикальную ось векторов IА, IB и IC,вращающихся с круговой скоростью  На рис. 26.16, а показаны положения этих векторов через промежутки времени
На рис. 26.16, а показаны положения этих векторов через промежутки времени  что соответствует их повороту на угол
что соответствует их повороту на угол  или 30°.
или 30°.

Рис. 26.16.
Ток в каждой катушке создает магнитное поле, синусоидально изменяющееся вдоль оси, перпендикулярной плоскости катушки. Напряженности полей НА, НB и НC катушек в каждый момент времени (рис. 26.16, б) пропорциональны токам катушек (§ 22.14).
Напряженность результирующего поля всех трех катушек Н равна геометрической сумме напряженностей НА, НB и НC. Из рис. 26.16,б видно, что вектор Н получается одинаковым по величине и поворачивается на тот же угол  что и векторы IA, IB, IC, т. е. вращается в статоре с той же круговой скоростью
что и векторы IA, IB, IC, т. е. вращается в статоре с той же круговой скоростью 
Таким образом, при наложении трех синусоидальных магнитных полей, направленных под углом  (120°) друг к другу и сдвинутых по фазе на такой же угол, получается вращающееся магнитное поле с постоянной по величине напряженностью.
(120°) друг к другу и сдвинутых по фазе на такой же угол, получается вращающееся магнитное поле с постоянной по величине напряженностью.
Представим себе, что внутрь статора помещен ротор, представляющий собой постоянный электромагнит со скользящими контактами. Северный и южный полюсы вращающегося магнитного поля будут притягивать к себе противоположные полюсы ротора, и ротор будет вращаться с той же скоростью, с какой вращается поле статора. Поэтому такой двигатель называют синхронным. Он имеет такое же устройство, как и генератор (рис. 26.9).
В конструкции трехфазного двигателя другого типа вдоль поверхности ротора в пазы укладываются проводники (рис. 26.17, а), которые замыкаются по торцам кольцами. Такой ротор называется короткозамкнутым; его обмотка, снятая с ротора, напоминает беличье колесо (рис. 26.17, б). Отметим, что скользящие контакты для такого ротора не нужны.

Рис. 26.17.
Линии индукции вращающегося магнитного поля, пересекая проводники ротора, наводят в них индукционные токи, которые замыкаются через торцевые кольца. Направление этих токов можно определить по правилу правой руки (§ 23.3), учитывая, что отогнутый большой палец должен показывать направление движения проводника относительно поля (в двигателе, изображенном на рис. 26.17, а, поле вращается по часовой стрелке). Эти токи в свою очередь взаимодействуют с магнитным полем, в результате чего возникают силы Ампера (§ 22.9), действующие на проводники в сторону вращения поля (в соответствии с правилом левой руки). Эти силы увлекают ротор вслед за вращающимся полем.
Однако ротор вращается со скоростью несколько меньшей, чем поле (на несколько процентов), так как при его синхронном вращении с полем прекратилось бы относительное движение проводников и поля, исчезли бы индукционные токи и силы, действующие на проводники. Такой трехфазный двигатель называют асинхронным. Он очень прост по устройству и применяется очень широко.
Получение, передача и распределение электрической энергии в народном хозяйстве
Развитие народного хозяйствав первую очередь определяется развитием энергетики. Поскольку главными источниками энергии для промышленности являются электростанции, в уделяется большое внимание строительству новых и увеличению мощности уже работающих электростанций. Общая мощность электростанций в в 1974 г. превысила 200•106 кВт, а в 1980 г. возросла примерно в 1,4 раза.
Наша страна обладает огромными запасами гидроэнергии. Построены такие гиганты, как Братская ГЭС мощностью 4,5•106 кВт, крупнейшая в мире Красноярская ГЭС мощностью 6•106 кВт, на которой установлены и самые мощные в мире гидроагрегаты — по 0,5•106 кВт. Строится Саяно-Шушенская ГЭС мощностью 6,4•106 кВт. Продолжается строительство каскада ГЭС на Ангаре, общая мощность которого будет составлять (12—15)•106 кВт.
Большая часть электроэнергии в нашей стране в настоящее время вырабатывается на тепловых станциях, работающих на дешевом топливе. Мощность крупнейшей в мире Криворожской станции составляет 3•106 кВт. Строятся еще более крупные станции, каждая мощностью по (4—5)•106 кВт. На них устанавливаются турбогенераторы мощностью до 1,2•106 кВт.
Наиболее быстрыми темпами идет строительство атомных электростанций, которые в недалеком будущем займут первое место по производству электроэнергии.
Для получения электроэнергии используются и другие источники — солнечные электростанции, геотермальные, ветровые и т. д. В будущем предполагается использовать энергию морских приливов; проектируется, например, мощная приливная электростанция на Белом море.
Эффективное использование электроэнергии можно осуществить только с помощью передачи ее на большие расстояния с минимальными потерями. Для этого энергию нужно передавать при высоком напряжении. Уже имеются линии передачи, работающие при напряжениях 500, 750 кВ, разрабатываются передачи на напряжение более миллиона вольт.
Высоковольтные линии передачи объединяют электростанции обширных районов страны, образуя энергетическую систему. Созданы энергосистемы Сибири, Средней Азии, Европейской части. Объединение этих энергосистем завершает создание Единой энергетической системы. Она связывает густонаселенные районы европейской части страны и Средней Азии с мощными источниками энергии Сибири. Кроме того, при большой разнице во времени между восточными и западными районами нашей страны это позволяет сэкономить до 40•106 кВт мощности, т. е. вместо строительства электростанции такой мощности можно обходиться переброской электроэнергии в ту зону, где потребление в данный момент максимально. Большие выгоды дает и объединение энергоресурсов соседних социалистических стран.
Упрощенная схема передачи электроэнергии на большие расстояния показана на рис. 26.18. При высоких напряжениях на линиях передач, применяемых в настоящее время, выгодно осуществлять передачу на постоянном токе. Разрабатываются такие передачи на напряжение 1,5•106 В.

Рис. 26.18.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.
Расчет цепей переменного тока. В таблице ниже представлены основные расчетные формулы цепей переменного тока. Формулы для переменного тока.
|
Вид нагрузки |
Схема |
Векторная диаграмма |
Полное сопротивление цепи |
|
Активное сопротивление |
|
|
|
|
Индуктивное сопротивление |
|
|
|
|
Емкостное сопротивление |
|
|
|
|
Последовательное соединение |
|||
|
Активное и индуктивное сопротивления |
|
|
|
|
Активное и емкостное сопротивления |
|
|
|
|
Активное, индуктивное и емкостное сопротивление |
|
|
|
|
Параллельное соединение |
|||
|
Активное и индуктивное сопротивления |
|
|
|
|
Активное и емкостное сопротивления |
|
|
|
Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.

Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I2R, откуда
![]()
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.

Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:

Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.

Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.

Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.
При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.
Мультиметром
Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.
Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.
Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.
Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.
Задача 1.
На участке цепи имеются три параллельно включенных резистора (см. рис. 5). Значения сопротивлений резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и на всём участке, если на нем поддерживается постоянное напряжение 100 В.

Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
- I1 = U/R1 =100/5 = 20 А;
- I2 = U/R2 =100/25 ≈ 4 А;
- I3 = U/R3 =100/50 = 2 А.
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:
![]()
Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
Ответ:
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Задача 2.
Мощность электрочайника 2 кВт. Чайник работает от городской сети под напряжением 220 В. Сколько электричества потребляет этот электроприбор?
Решение:
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Задача 3.
Вычислить силу тока в цепи, если известно, что сопротивление составляет 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление составляет 1 Ом.
Решение.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
I = 6 В / (5 Ом + 1 Ом) = 1 А.
Ответ: сила тока 1 А.
Задача 4.
Сколько энергии потребляет электроплита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?
Решение:
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U2/R)*t или
A = ((220 В)2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.
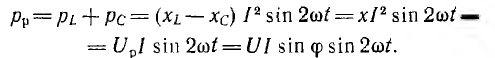
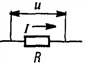
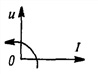
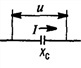
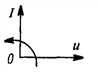
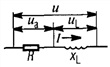
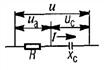
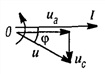
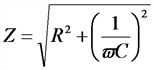
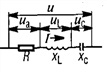
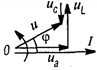
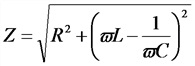
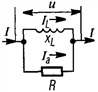
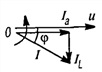
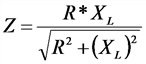 или
или