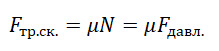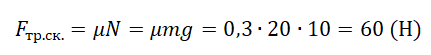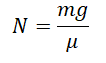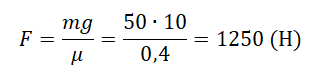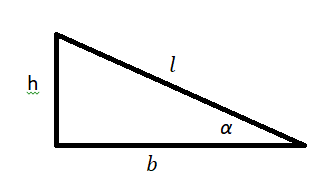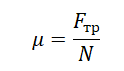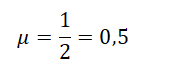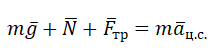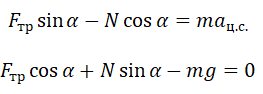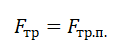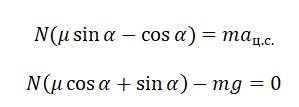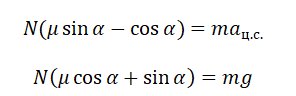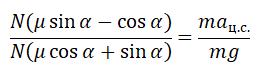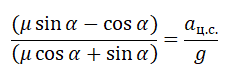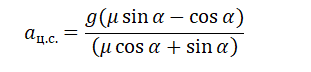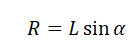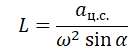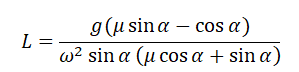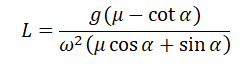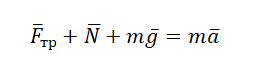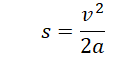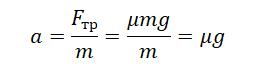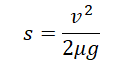{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
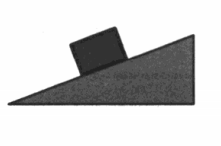
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 августа 2022 года; проверки требует 1 правка.
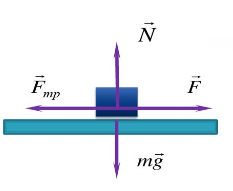
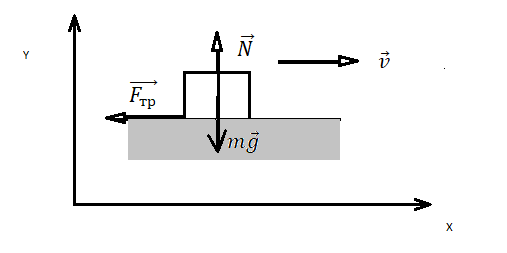
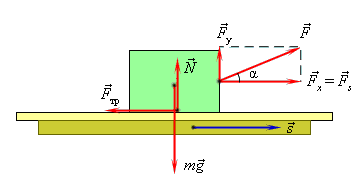
Изображения сил, действующих на скользящее тело.
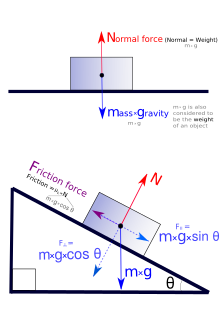
Изображения сил, действующих на тело, находящееся на ровной и наклонной плоскости.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения, от площади соприкосновения[1].
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения и обозначается обычно латинской буквой 
или греческой буквой 
. Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то можно считать постоянным. В первом приближении величина силы трения скольжения может быть рассчитана по формуле[1]:
— коэффициент трения скольжения,
— сила нормальной реакции опоры.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда в большей или меньшей степени происходит преобразование механического движения в другие формы движения материи — чаще всего в тепловую форму движения, и происходит нагревание взаимодействующих тел.
Независимость от площади[править | править код]
Так как никакое тело не является абсолютно ровным, сила трения не зависит от площади соприкосновения, и истинная площадь соприкосновения гораздо меньше наблюдаемой. На самом деле, площадь соприкосновения, казалось бы, ровных поверхностей может находиться в пределах 
от всей мнимой площади соприкосновения.[2] А в случае поверхностей максимально гладких начинает возникать межмолекулярное притяжение.
Обычно это демонстрируется примером:
Два цилиндра из мягких металлов соединяют плоскими частями, а затем с легкостью отрывают. После этого два цилиндра соединяют и немного двигают относительно друг друга. При этом все неровности поверхности притираются друг к другу, образуя максимальную площадь соприкосновения: появляются силы межмолекулярного притяжения. А после разъединить эти два цилиндра становится очень сложно.
Типы трения скольжения[править | править код]
Если между телами отсутствует жидкая или газообразная прослойка (смазочный материал), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
По физике взаимодействия трение скольжения принято разделять на:
- Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазочными материалами — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя;
- Сухое с сухой смазкой (графитовым порошком);
- Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазочного материала) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
- Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
- Граничное, когда в области контакта могут содержаться слои и участки различной природы (оксидные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения;
Также можно классифицировать трение по его области. Силы трения, возникающие при относительном перемещении различных тел, называются силами внешнего трения. Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
Измерение[править | править код]
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики. Поэтому нет точной формулы для коэффициента трения. Его оценка производится на основе эмпирических данных: так как по первому закону Ньютона тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения, то для измерения действующей на тело силы трения достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Таблица коэффициентов трения скольжения[править | править код]
Значения таблицы взяты из справочника по физике[3]
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,99 | 0,20 |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лёд по льду | 0,028 | |
| Металл по асботекстолиту | 0,35-0,50 | |
| Металл по дереву (в среднем) | 0,60 | 0,40 |
| Металл по камню (в среднем) | 0,42-0,50 | |
| Металл по металлу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь (коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примечания[править | править код]
- ↑ 1 2 Билимович Б. Ф. Законы механики в технике. – М., Просвещение, 1975. – Тираж 80000 экз. – с. 58
- ↑ Сила трения. ЗФТШ, МФТИ. Дата обращения: 14 февраля 2019. Архивировано 13 февраля 2019 года.
- ↑ Енохович А. С. Справочник по физике. — Просвещение, 1978. — С. 85. — 416 с.
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
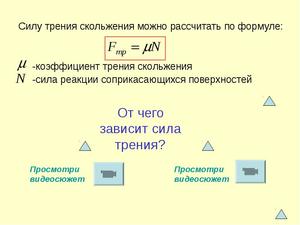
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
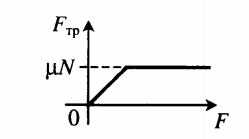
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
 |
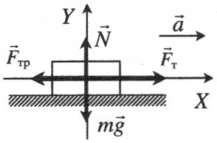Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
 |
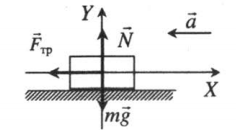Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
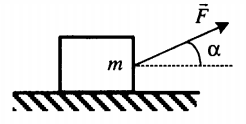
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
 |
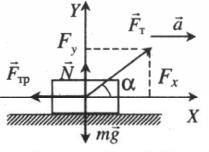Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
 |
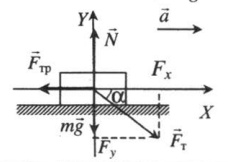Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
 |
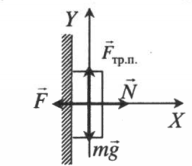Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
 |
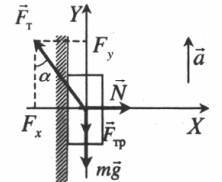Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
Движение тела по наклонной плоскости
Движение вниз без трения |
|
 |
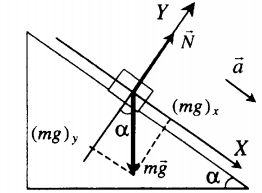Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
 |
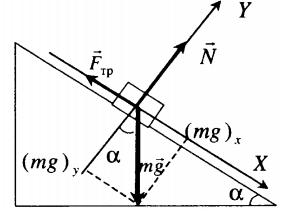Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
 |
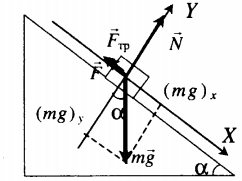Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
 |
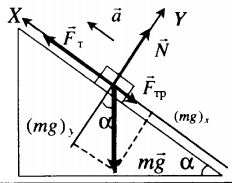Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
 |
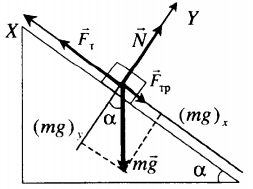Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
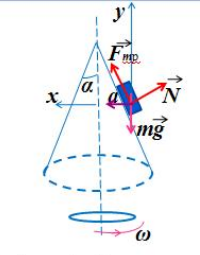
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.4k
Коэффициент трения скольжения — отношение силы трения к силе нормальной реакции опоры.
Коэффициент трения скольжения выводится из формулы силы трения скольжения: Ft=μ·N
Так как сила реакции опоры N, это масса умножить на ускорение свободного падения, то формула коэффициента получается:
Ниже приведена таблица коэффициентов трения скольжения для некоторых материалов:
Обозначения:
μ — коэффициент трения скольжения
Ft — сила трения скольжения
N — сила нормальной реакции опоры
m — масса тела
g — ускорение свободного падения
Одной из наиболее интересных тем школьной программы по физике является «сила трения». Она достаточно доступна в понимании учащихся и быстро поддается осмыслению, так как её наличие можно проверить, не отходя от парты.
Стоит начать с определения самого понятия. Сила трения — есть итог сопротивления движению физических тел. Иными словами, она появляется, когда происходит относительное перемещение между взаимодействующими телами.
Различают по его области:
- Внешнее — зарождается при непосредственном движении действующих друг на друга тел,
- Внутреннее — возникает между частями одного предмета.
Основная формула силы трения
Ввиду отсутствия в природе абсолютно твердых тел сила трения существует постоянно, и его наличие разъясняют действием даже микроскопически шероховатых поверхностей между собой. Результат при умножении силы реакции опоры на коэффициент трения есть:
F тр.= N * k
В СИ (международная система единиц) измеряется F тр. в Ньютонах (Н).
Нужно знать, что противоположно ходу движения направлена F тр., а N против силы тяжести и перпендикулярно поверхности. Безразмерная величина k не зависит от площади соприкасания тел, а зависит от степени шероховатости и типа материалов трущихся тел.
Необходимо иметь полное представление о физических величинах, участвующих в основной формуле. В первую очередь, F тр. это векторная величина, то есть она имеет направление. Следовательно, нужно знать направление и точку ее приложения. Приложена она в области соприкосновения поверхностей, а направлена против движения объекта.
Из названия нормальной реакции опоры понятно, что она показывает реакцию самой опоры, а возникает на молекулярном уровне. Направлена против силы, с которой предмет давит на поверхность.
Коэффициент пропорциональности k является связующим звеном между F тр. и силой нормальной реакции. Если k соответствует наибольшей F тр. пок., то в большинстве своих случаев он больше коэффициента скольжения.
Коротко о типах трения
Отличают такие разновидности, как:
- покоя,
- скольжения,
- качения.
Прилагая минимум F тр. пок., объект начнет свое движение. Она не определяется достаточно точно и зависит от приложенного усилия. Поразительно, но именно оно разгоняет тела. F тр. пок. не исчезает бесследно, после того, как привела в движение предмет, она превращается в F тр. , а, следовательно, не может бесконечно увеличиваться — есть верхний максимальный предел, равный по величине F тр. скольжения.
В названии «сила трения качения» скрыта суть самого явления. Она намного меньше трения скольжения и возникает во время качения одного тела по-другому, скорости их соприкосновения в точках касания одинаковы по направлению и значению.
Типы трения скольжения различают по физике взаимодействия:
- Вязкое. Появляется, когда взаимодействующие тела разделены между собой слоем жидкости, газа или иного смазочного материала различного размера. F тр. пок. отсутствует. Абсолютная величина этой силы сопротивления зависит от скорости: прямо пропорциональна скорости при малых скоростях движение и прямо пропорциональна ее квадрату при больших.
- Сухое. Дополнительным смазочным материалом соприкасающиеся тела не разделены. Может возникать даже при отсутствии относительного движения предметов. Особый пример — F тр. покоя . Существует вид сухого взаимодействия с сухой смазкой, как пример, со слоем графитового порошка.
- Граничное. Одновременное содержание и слоев, и частей отличных по природе.
- Смешанное. Имеются участки частичной смазки.
Формула выглядит следующим образом:
F тр. скольж. = μN .
Использовались такие физические величины, как, μ — коэффициент трения скольжения, N — сила реакции опоры.
Также можно вывести формулу через массу:
F <> μmg,
где N = mg, g — свободного падения.
Формула коэффициента пропорциональности μ
В формуле, описывающей процесс приложения F тр. к любому телу, принимает участие коэффициент пропорциональности. Он выражается исключительно числами и почти при любых обстоятельствах меньше единицы. Это величина, зависящая от материала взаимодействующих объектов и от степени обработки их поверхностей.
μ =FN .
Данную формулу можно вывести через массу и ускорение свободного падения:
μ =Fmg, где замена N происходит ранее описанным способом.
Трение повинуется третьему закону Ньютона, так как является разновидностью взаимодействия. А конкретно, если F тр. действует на один из объектов, то такая же в точности сила по модулю, но устремленная противоположно оказывает воздействие и на второе тело. Все силы противодействия возникают как результат молекулярного и атомного взаимодействия трущихся тел.
В заключение приведены слова Шарля Гийом (1861−1938): «Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиною с каменную глыбу или малы, как песчинка, никогда не удержатся одно на другом: все будет скользить и катиться, пока не окажется на одном уровне. Не будь трения, Земля представляла бы шар без неровностей, подобно жидкому».
Видео
Это видео поможет вам понять, что такое сила трения.
