Задача о гамильтоновом пути и задача о гамильтоновом цикле — это задачи определения, существует ли гамильтонов путь или гамильтонов цикл в заданном графе (ориентированном или неориентированном). Обе задачи NP-полны[1].
Связь задач о гамильтоновом пути и гамильтоновом цикле[править | править код]
Существует простое отношение между задачами нахождения гамильтонова пути и нахождения гамильтонова цикла. В одном направлении задача о гамильтоновом пути для графа эквивалентна задаче о гамильтоновом цикле в графе H, полученного из графа G путём добавления новой вершины и соединения её со всеми вершинами графа G. Таким образом, поиск гамильтонова пути не может быть существенно медленнее (в худшем случае, как функция числа вершин), чем поиск гамильтонова цикла.
В обратном направлении задача о гамильтоновом цикле для графа G эквивалентна задаче о гамильтоновом пути в графе H, полученном копированием одной вершины v графа G (в v’), то есть вершина v’ будет иметь ту же окрестность, что и v, и добавлением двух вспомогательных вершин степени один, одна из которых соединена с v, а другая с v’[2].
Задача о гамильтоновом цикле является также частным случаем задачи коммивояжёра, полученной установкой всех расстояний между двумя пунктами в единицу, если они смежны, и двум в противном случае. После решения задачи коммивояжёра следует проверить, что полное расстояние равно n (если так, маршрут является гамильтоновым циклом, если же гамильтонова цикла нет, кратчайший путь будет длиннее этой величины).
Алгоритмы[править | править код]
Есть n! различных последовательностей вершин, которые могут быть гамильтоновыми путями в заданном графе с n вершинами (и их столько в полном графе), так что алгоритм полного перебора, который перебирает все возможные последовательности, был бы очень медленным.
Ранний точный алгоритм нахождения гамильтонова цикла в ориентированном графе был алгоритмом перебора (алгоритм Мартелло)[3].
Процедура поиска Франка Рубина[4] разбивает рёбра графа на три класса — те, которые должны быть на пути, те, которые пути принадлежать не могут, и рёбра, для которых решение не принято. В процессе поиска набор правил принятия решений классифицирует рёбра, для которых решение не принято, и определяет, остановиться или продолжить поиск. Алгоритм разбивает граф на компоненты, которые могут быть обработаны отдельно.
Для решения задачи за время 

Андреас Бьёрклунд даёт альтернативный подход, использующий принцип включения/исключения для сокращения числа перебираемых гамильтоновых циклов и задача подсчёта циклов может быть решена путём вычисления определителя некоторой матрицы.
Используя этот метод, он показал, как решить задачу о гамильтоновом цикле для произвольных графов с n вершинами с помощью алгоритма Монте-Карло за время 

Для графов с максимальной степенью три аккуратный поиск с возвратом может найти гамильтонов цикл (если таковой существует) за время 
Гамильтоновы пути и циклы можно найти с помощью SAT решателя.
Ввиду сложности решения задач о гамильтоновом пути и цикле на обычных компьютерах, они изучались для нестандартных моделей вычислений. Например, Леонард Адлеман показал, что задачи о гамильтоновом пути могут быть решены с помощью ДНК-компьютера. Используя параллелелизм, свойственный химическим реакциям, задача может быть решена с помощью нескольких шагов химических реакций, линейно зависящих от числа вершин графа. Однако это требует факториальное число молекул ДНК, участвующих в реакции[9].
Оптическое решение гамильтоновой задачи предложил Ольтеан[10]. Идея заключается в создании подобной графу структуры из оптических кабелей и расщепителей луча, через которую прогоняется луч в порядке решения задачи. Слабым моментом этого подхода является экспоненциальный рост требуемой энергии от числа узлов.
Сложность[править | править код]
Задача нахождения гамильтонова цикла или пути имеет сложность FNP[en]. Аналогичная задача разрешимости — проверить, существует ли гамильтонов цикл или путь. Ориентированные и неориентированные задачи о гамильтоновом цикле являлись двумя из 21 NP-полных задач Карпа. Они остаются NP-полными даже для неориентированных планарных графов максимальной степени три[11], для ориентированных планарных графов с полустепенью входа и выхода, не превосходящими двух[12], для неориентированных планарных 3-регулярных двудольных графов без мостов, для 3-связных 3-регулярных двудольных графов[13], подграфов квадратной решётки[14] и для кубических подграфов квадратной решётки[15].
Однако 4-связные планарные графы всегда гамильтоновы, согласно результату Татта, а задача нахождения гамильтонова цикла в этих графах может быть выполнена за линейное время[16] путём вычисления так называемого пути Татта. Татт доказал этот результат, показав, что любой 2-связный планарный граф содержит путь Татта. Пути Татта, в свою очередь, можно вычислить за квадратичное время даже для 2-связных планарных графов[17], что может быть использовано для поиска гамильтоновых циклов и длинных циклов в обобщённых планарных графах.
Складывая всё вместе, остаётся открытой задача, всегда ли 3-связные 3-регулярные двудольные планарные графы должны содержать гамильтонов цикл и если должны, задача, ограниченная этими графами, не будет NP-полной (см. статью «Гипотеза Барнетта»).
В графах в которых все вершины имеют нечётную степень, довод, связанный с леммой о рукопожатиях, показывает, что число гамильтоновых циклов через фиксированное ребро всегда чётно, так что если дан один гамильтонов цикл, то и другой должен существовать[18]. Однако поиск этого второго цикла не выглядит как простая вычислительная задача. Пападимитриу определил класс сложности PPA[en], чтобы собрать вместе задачи, подобные этой[19].
Примечания[править | править код]
- ↑ Garey, Johnson, 1979, с. 199—200, A1.3: GT37 – 39.
- ↑ graph theory – Reduction from Hamiltonian cycle to Hamiltonian path – Mathematics Stack Exchange. Дата обращения: 18 февраля 2019. Архивировано 23 апреля 2019 года.
- ↑ Martello, 1983, с. 131–138.
- ↑ Rubin, 1974, с. 576–80.
- ↑ Bellman, 1962, с. 61–63.
- ↑ Held, Karp, 1962, с. 196–210.
- ↑ Björklund, 2010, с. 173–182.
- ↑ Iwama, Nakashima, 2007, с. 108–117.
- ↑ Adleman, 1994, с. 1021–1024.
- ↑ Oltean, 2006, с. 217–227.
- ↑ Garey, Johnson, Stockmeyer, 1974, с. 47–63.
- ↑ Plesńik, 1979, с. 199–201.
- ↑ Akiyama, Nishizeki, Saito, 1980–1981, с. 73–76.
- ↑ Itai, Papadimitriou, Szwarcfiter, 1982, с. 676–686.
- ↑ Buro, 2000, с. 250–261.
- ↑ Chiba, Nishizeki, 1989, с. 187–211.
- ↑ Schmid, Schmidt, 2018.
- ↑ Thomason, 1978, с. 259–268.
- ↑ Papadimitriou, 1994, с. 498–532.
Литература[править | править код]
- Michael R. Garey, David S. Johnson. [Computers and Intractability: A Guide to the Theory of NP-Completeness Computers and Intractability: A Guide to the Theory of NP-Completeness]. — W.H. Freeman, 1979. — ISBN 978-0-7167-1045-5.
- Silvano Martello. An Enumerative Algorithm for Finding Hamiltonian Circuits in a Directed Graph // ACM Transactions on Mathematical Software. — 1983. — Т. 9, вып. 1. — С. 131–138. — doi:10.1145/356022.356030.
- Frank Rubin. A Search Procedure for Hamilton Paths and Circuits // Journal of the ACM. — 1974. — Т. 21, вып. 4. — С. 576–80. — doi:10.1145/321850.321854.
- Richard Bellman. Dynamic programming treatment of the travelling salesman problem // Journal of the ACM. — 1962. — Т. 9. — С. 61–63. — doi:10.1145/321105.321111.
- Held, Karp. A dynamic programming approach to sequencing problems // J. SIAM. — 1962. — Т. 10, вып. 1. — С. 196–210. — doi:10.1137/0110015.
- Andreas Björklund. Determinant sums for undirected Hamiltonicity // Proc. 51st IEEE Symposium on Foundations of Computer Science (FOCS ’10). — 2010. — С. 173–182. — ISBN 978-1-4244-8525-3. — doi:10.1109/FOCS.2010.24.
- Kazuo Iwama, Takuya Nakashima. An improved exact algorithm for cubic graph TSP // Proc. 13th Annual International Conference on Computing and Combinatorics (COCOON 2007). — 2007. — Т. 4598. — С. 108–117. — (Lecture Notes in Computer Science). — ISBN 978-3-540-73544-1. — doi:10.1007/978-3-540-73545-8_13.
- Leonard Adleman. Molecular computation of solutions to combinatorial problems // Science. — 1994. — Ноябрь (т. 266, вып. 5187). — С. 1021–1024. — doi:10.1126/science.7973651. — Bibcode: 1994Sci…266.1021A. — PMID 7973651. — JSTOR 2885489.
- Mihai Oltean. A light-based device for solving the Hamiltonian path problem // Unconventional Computing. — Springer LNCS 4135, 2006. — doi:10.1007/11839132_18.
- Michael Garey, David S. Johnson, Larry Stockmeyer. Some simplified NP-complete problems // Proc. 6th ACM Symposium on Theory of Computing (STOC ’74). — 1974. — С. 47–63. — doi:10.1145/800119.803884.
- Plesńik J. The NP-completeness of the Hamiltonian cycle problem in planar digraphs with degree bound two // Information Processing Letters. — 1979. — Т. 8, вып. 4. — С. 199–201. — doi:10.1016/0020-0190(79)90023-1.
- Takanori Akiyama, Takao Nishizeki, Nobuji Saito. NP-completeness of the Hamiltonian cycle problem for bipartite graphs // Journal of Information Processing. — 1980–1981. — Т. 3, вып. 2. — С. 73–76.
- Alon Itai, Christos Papadimitriou, Jayme Szwarcfiter. Hamilton Paths in Grid Graphs // SIAM Journal on Computing. — 1982. — Т. 4, вып. 11. — С. 676–686. — doi:10.1137/0211056.
- Michael Buro. Simple Amazons endgames and their connection to Hamilton circuits in cubic subgrid graphs // Conference on Computers and Games. — 2000. — Т. 2063. — С. 250–261. — (Lecture Notes in Computer Science). — ISBN 978-3-540-43080-3. — doi:10.1007/3-540-45579-5_17.
- Norishige Chiba, Takao Nishizeki. The Hamiltonian cycle problem is linear-time solvable for 4-connected planar graphs // Journal of Algorithms. — 1989. — Т. 10, вып. 2. — С. 187–211. — doi:10.1016/0196-6774(89)90012-6.
- Andreas Schmid, Jens M. Schmidt. Computing Tutte Paths // Proceedings of the 45th International Colloquium on Automata, Languages and Programming (ICALP’18), to appear.. — 2018.
- Thomason A. G. Hamiltonian cycles and uniquely edge colourable graphs // Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). — 1978. — Т. 3. — С. 259–268. — (Annals of Discrete Mathematics). — ISBN 9780720408430. — doi:10.1016/S0167-5060(08)70511-9.
- Christos H. Papadimitriou. On the complexity of the parity argument and other inefficient proofs of existence // Journal of Computer and System Sciences. — 1994. — Т. 48, вып. 3. — С. 498–532. — doi:10.1016/S0022-0000(05)80063-7.
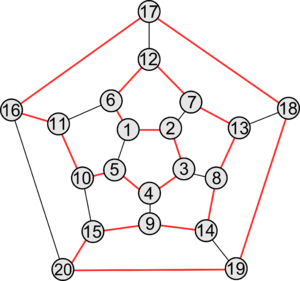
Граф додекаэдра с выделенным циклом Гамильтона
Содержание
- 1 Основные определения
- 2 Достаточные условия гамильтоновости графа
- 2.1 Теорема Дирака
- 2.2 Теорема Оре
- 2.3 Теорема Поша
- 2.4 Теорема Редеи-Камиона
- 2.5 Теорема Гуйя-Ури
- 2.6 Теорема Хватала
- 3 Задача о коммивояжере
- 3.1 Описание задачи
- 3.2 Варианты решения
- 3.2.1 Перебор перестановок
- 3.2.2 Динамическое программирование по подмножествам (по маскам)
- 3.2.3 Поиск любого гамильтонова пути методом динамического программирования
- 3.3 Псевдокод
- 3.4 Алгоритм нахождения гамильтонова цикла
- 3.5 Алгоритм нахождения гамильтонова пути
- 4 См. также
- 5 Источники информации
Основные определения
| Определение: |
| Гамильтоновым путём (англ. Hamiltonian path) называется простой путь, проходящий через каждую вершину графа ровно один раз. |
| Определение: |
| Гамильтоновым циклом (англ. Hamiltonian cycle) называют замкнутый гамильтонов путь. |
| Определение: |
| Граф называется полугамильтоновым (англ. Semihamiltonian graph), если он содержит гамильтонов путь. |
| Определение: |
| Граф называется гамильтоновым (англ. Hamiltonian graph), если он содержит гамильтонов цикл. |
Очевидно, что любой гамильтонов граф также и полугамильтонов.
Достаточные условия гамильтоновости графа
Теорема Дирака
| Теорема: |
|
Если и для любой вершины неориентированного графа , то — гамильтонов граф. |
Теорема Оре
| Теорема: |
|
Если и для любых двух различных несмежных вершин и неориентированного графа , то — гамильтонов граф. |
Теорема Поша
| Теорема (Поша): |
|
Пусть граф имеет вершин и выполнены следующие два условия:
тогда — гамильтонов граф. |
Теорема Редеи-Камиона
| Теорема: |
|
Любой сильносвязный турнир — гамильтонов. |
Теорема Гуйя-Ури
| Теорема (Ghouila-Houri): |
|
Пусть — сильносвязный ориентированный граф. |
Теорема Хватала
| Теорема (Хватал): |
|
Пусть:
Тогда если верна импликация: то граф гамильтонов. |
Задача о коммивояжере
Рассмотрим алгоритм нахождения гамильтонова цикла на примере задачи о коммивояжёре.
Описание задачи
| Задача: |
| Задача о коммивояжере (англ. Travelling salesman problem, TSP) — задача, в которой коммивояжер должен посетить городов, побывав в каждом из них ровно по одному разу и завершив путешествие в том городе, с которого он начал. В какой последовательности ему нужно обходить города, чтобы общая длина его пути была наименьшей? |
Варианты решения
Задача о коммивояжере относится к классу NP-полных задач. Рассмотрим два варианта решения с экспоненциальным временем работы.
Перебор перестановок
Можно решить задачу перебором всевозможных перестановок. Для этого нужно сгенерировать все всевозможных перестановок вершин исходного графа, подсчитать для каждой перестановки длину маршрута и выбрать минимальный из них. Но тогда задача оказывается неосуществимой даже для достаточно небольших . Сложность алгоритма .
Динамическое программирование по подмножествам (по маскам)
Задача о коммивояжере представляет собой поиск кратчайшего гамильтонова цикла в графе.
Зафиксируем начальную вершину и будем искать гамильтонов цикл наименьшей стоимости — путь от до , проходящий по всем вершинам (кроме первоначальной) один раз. Т.к. искомый цикл проходит через каждую вершину, то выбор не имеет значения. Поэтому будем считать .
Подмножества вершин будем кодировать битовыми векторами, обозначим значение -ого бита в векторе .
Обозначим как наименьшую стоимость пути из вершины в вершину , проходящую (не считая вершины ) единожды по всем тем и только тем вершинам , для которых (т.е. уже найденный оптимальный путь от -ой вершины до -ой, проходящий через те вершины, где . Если ,то эти вершины еще не посещены).
Алгоритм поиска цикла будет выглядеть следующим образом:
- Начальное состояние — когда находимся в -й вершине, ни одна вершина не посещена, а пройденный путь равен (т.е. и ).
- Для остальных состояний ( или ) перебираем все возможные переходы в -ую вершину из любой посещенной ранее и выбираем минимальный результат.
- Если возможные переходы отсутствуют, решения для данной подзадачи не существует (обозначим ответ для такой подзадачи как ).
Стоимостью минимального гамильтонова цикла в исходном графе будет значение — стоимость пути из -й вершины в -ю, при необходимости посетить все вершины. Данное решение требует памяти и времени.
Для того, чтобы восстановить сам путь, воспользуемся соотношением , которое выполняется для всех ребер, входящих в минимальный цикл . Начнем с состояния , , найдем вершину , для которой выполняется указанное соотношение, добавим в ответ, пересчитаем текущее состояние как , . Процесс заканчивается в состоянии , .
Поиск любого гамильтонова пути методом динамического программирования
Пусть содержит булево значение — существует ли в подмножестве гамильтонов путь, заканчивающийся в вершине .
Сама динамика будет такая:
Это решение требует памяти и времени. Эту оценку можно улучшить, если изменить динамику следующим образом.
Пусть теперь хранит маску подмножества всех вершин, для которых существует гамильтонов путь в подмножестве , заканчивающихся в этой вершине. Другими словами, сожмем предыдущую динамику: будет равно . Для графа выпишем масок , для каждой вершины задающие множество вершин, которые связаны ребром с данной вершиной. То есть .
Тогда динамика перепишется следующим образом:
Особое внимание следует уделить выражению . Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве без вершины , а вторая — подмножество вершин, связанных с ребром. Если эти множества пересекаются хотя бы по одной вершине (их не равен ), то, как нетрудно понять, в существует гамильтонов путь, заканчивающийся в вершине .
Окончательная проверка состоит в сравнении c .
Это решение использует памяти и имеет асимптотику .
Псевдокод
Прежде чем писать код, скажем пару слов о порядке обхода состояний. Обозначим за количество единиц в маске (иначе говоря количество пройденных вершин не считая текущей). Тогда, поскольку при рассмотрении состояния мы смотрим на состояния
, и , то состояния с большим должны быть посещены позже, чтобы к моменту вычисления текущего состояния были вычислены все те, которые используются для его подсчёта.
Однако если использовать рекурсию, об этом можно не беспокоиться (и сэкономить немало кода, времени и памяти).
// все переменные используются из описания алгоритма, = бесконечность
function findCheapest(i, mask):
if d[i][mask] !=
return d[i][mask]
for j = 0 .. n - 1
if w(i, j) существует and j-ый бит mask == 1
d[i][mask] = min(d[i][mask], findCheapest(j, mask - ) + w(i, j))
return d[i][mask]
function start():
for i = 0 .. n - 1
for mask = 0 .. - 1
d[i][mask] =
d[0][0] = 0
ans = findCheapest(0, - 1)
return ans
Дальше ищем сам цикл:
function findWay():
i = 0
mask = - 1
path.push(0)
while mask != 0
for j = 0 .. n - 1
if w(i, j) существует and j-ый бит mask == 1 and d[i][mask] == d[j][mask - ] + w(i, j)
path.push(j)
i = j
mask = mask -
continue
Алгоритм нахождения гамильтонова цикла
Алгоритм нахождения гамильтонова цикла легко получить слегка изменив алгоритм нахождения минимального гамильтонова цикла.
В массиве мы хранили расстояния, но сейчас нас не интересует какой длины будет это расстояние, так как главной задачей является нахождение цикла. В этом массиве мы теперь просто храним посещение вершин. И каждый раз, когда при запуске находим непосещенную вершину, то запускаем функцию рекурсивно от нее. Если она возвращает , то есть до вершины можно добраться, то записываем, что мы можем посетить вершину. Проходы так же осуществляются по рёбрам.
Алгоритм нахождения гамильтонова пути
Алгоритм нахождения гамильтонова пути легко получить, используя алгоритм нахождения гамильтонова цикла. Нужно добавить в граф еще одну вершину и ребра от нее до всех остальных вершин и из всех остальных вершин до неё. И далее запустить алгоритм поиска цикла от новой вершины. В восстановлении пути учтем, что эта вершина лишняя, и не будем записывать её в путь.
См. также
- Кратчайший путь в ациклическом графе
- Задача о наибольшей общей подпоследовательности
- Задача о наибольшей возрастающей подпоследовательности
- Задача о рюкзаке
- Алгоритм нахождения Гамильтонова цикла в условиях теорем Дирака и Оре
Источники информации
- Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом “ЛИБРОКОМ”, 2009. — 60 с.
- Седжвик Р. Фундаментальные алгоритмы на C++. Алгоритмы на графах. — СПб: ООО «ДиаСофтЮП», 2002.
- Гамильтонов граф
- Задача коммивояжера в русской википедии
- Задача коммивояжера в немецкой википедии
- Романовский И. В. Дискретный анализ. СПб.: Невский Диалект; БХВ-Петербург, 2003. ISBN 5-7940-0114-3
- Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом “Вильямс”, 2005. ISBN 5-8459-0857-4
From Wikipedia, the free encyclopedia
This article is about the nature of Hamiltonian paths. For the question of the existence of a Hamiltonian path or cycle in a given graph, see Hamiltonian path problem.

A Hamiltonian cycle around a network of six vertices
In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs (the Hamiltonian path problem and Hamiltonian cycle problem) are NP-complete.
Hamiltonian paths and cycles are named after William Rowan Hamilton who invented the icosian game, now also known as Hamilton’s puzzle, which involves finding a Hamiltonian cycle in the edge graph of the dodecahedron. Hamilton solved this problem using the icosian calculus, an algebraic structure based on roots of unity with many similarities to the quaternions (also invented by Hamilton). This solution does not generalize to arbitrary graphs.
Despite being named after Hamilton, Hamiltonian cycles in polyhedra had also been studied a year earlier by Thomas Kirkman, who, in particular, gave an example of a polyhedron without Hamiltonian cycles.[1] Even earlier, Hamiltonian cycles and paths in the knight’s graph of the chessboard, the knight’s tour, had been studied in the 9th century in Indian mathematics by Rudrata, and around the same time in Islamic mathematics by al-Adli ar-Rumi. In 18th century Europe, knight’s tours were published by Abraham de Moivre and Leonhard Euler.[2]
Definitions[edit]
A Hamiltonian path or traceable path is a path that visits each vertex of the graph exactly once. A graph that contains a Hamiltonian path is called a traceable graph. A graph is Hamiltonian-connected if for every pair of vertices there is a Hamiltonian path between the two vertices.
A Hamiltonian cycle, Hamiltonian circuit, vertex tour or graph cycle is a cycle that visits each vertex exactly once. A graph that contains a Hamiltonian cycle is called a Hamiltonian graph.
Similar notions may be defined for directed graphs, where each edge (arc) of a path or cycle can only be traced in a single direction (i.e., the vertices are connected with arrows and the edges traced “tail-to-head”).
A Hamiltonian decomposition is an edge decomposition of a graph into Hamiltonian circuits.
A Hamilton maze is a type of logic puzzle in which the goal is to find the unique Hamiltonian cycle in a given graph.[3][4]
Examples[edit]

Orthographic projections and Schlegel diagrams with Hamiltonian cycles of the vertices of the five platonic solids – only the octahedron has an Eulerian path or cycle, by extending its path with the dotted one
- v
- t
- e
- A complete graph with more than two vertices is Hamiltonian
- Every cycle graph is Hamiltonian
- Every tournament has an odd number of Hamiltonian paths (Rédei 1934)
- Every platonic solid, considered as a graph, is Hamiltonian[5]
- The Cayley graph of a finite Coxeter group is Hamiltonian (For more information on Hamiltonian paths in Cayley graphs, see the Lovász conjecture.)
- Cayley graphs on nilpotent groups with cyclic commutator subgroup are Hamiltonian.[6]
- The flip graph of a convex polygon or equivalently, the rotation graph of binary trees, is Hamiltonian.[7][8]
Properties[edit]

Any Hamiltonian cycle can be converted to a Hamiltonian path by removing one of its edges, but a Hamiltonian path can be extended to Hamiltonian cycle only if its endpoints are adjacent.
All Hamiltonian graphs are biconnected, but a biconnected graph need not be Hamiltonian (see, for example, the Petersen graph).[9]
An Eulerian graph G (a connected graph in which every vertex has even degree) necessarily has an Euler tour, a closed walk passing through each edge of G exactly once. This tour corresponds to a Hamiltonian cycle in the line graph L(G), so the line graph of every Eulerian graph is Hamiltonian. Line graphs may have other Hamiltonian cycles that do not correspond to Euler tours, and in particular the line graph L(G) of every Hamiltonian graph G is itself Hamiltonian, regardless of whether the graph G is Eulerian.[10]
A tournament (with more than two vertices) is Hamiltonian if and only if it is strongly connected.
The number of different Hamiltonian cycles in a complete undirected graph on n vertices is (n – 1)!/2 and in a complete directed graph on n vertices is (n – 1)!. These counts assume that cycles that are the same apart from their starting point are not counted separately.
Bondy–Chvátal theorem[edit]
The best vertex degree characterization of Hamiltonian graphs was provided in 1972 by the Bondy–Chvátal theorem, which generalizes earlier results by G. A. Dirac (1952) and Øystein Ore. Both Dirac’s and Ore’s theorems can also be derived from Pósa’s theorem (1962). Hamiltonicity has been widely studied with relation to various parameters such as graph density, toughness, forbidden subgraphs and distance among other parameters.[11] Dirac and Ore’s theorems basically state that a graph is Hamiltonian if it has enough edges.
The Bondy–Chvátal theorem operates on the closure cl(G) of a graph G with n vertices, obtained by repeatedly adding a new edge uv connecting a nonadjacent pair of vertices u and v with deg(v) + deg(u) ≥ n until no more pairs with this property can be found.
Bondy–Chvátal Theorem (1976) — A graph is Hamiltonian if and only if its closure is Hamiltonian.
As complete graphs are Hamiltonian, all graphs whose closure is complete are Hamiltonian, which is the content of the following earlier theorems by Dirac and Ore.
Dirac’s Theorem (1952) — A simple graph with n vertices (

Ore’s Theorem (1960) — A simple graph with n vertices (
The following theorems can be regarded as directed versions:
Ghouila–Houiri (1960) — A strongly connected simple directed graph with n vertices is Hamiltonian if every vertex has a full degree greater than or equal to n.
Meyniel (1973) — A strongly connected simple directed graph with n vertices is Hamiltonian if the sum of full degrees of every pair of distinct non-adjacent vertices is greater than or equal to 
The number of vertices must be doubled because each undirected edge corresponds to two directed arcs and thus the degree of a vertex in the directed graph is twice the degree in the undirected graph.
Rahman–Kaykobad (2005) — A simple graph with n vertices has a Hamiltonian path if, for every non-adjacent vertex pairs the sum of their degrees and their shortest path length is greater than n.[12]
The above theorem can only recognize the existence of a Hamiltonian path in a graph and not a Hamiltonian Cycle.
Many of these results have analogues for balanced bipartite graphs, in which the vertex degrees are compared to the number of vertices on a single side of the bipartition rather than the number of vertices in the whole graph.[13]
Existence of Hamiltonian cycles in planar graphs[edit]
Theorem — A 4-connected planar triangulation has a Hamiltonian cycle.[14]
Theorem — A 4-connected planar graph has a Hamiltonian cycle.[15]
The Hamiltonian cycle polynomial[edit]
An algebraic representation of the Hamiltonian cycles of a given weighted digraph (whose arcs are assigned weights from a certain ground field) is the Hamiltonian cycle polynomial of its weighted adjacency matrix defined as the sum of the products of the arc weights of the digraph’s Hamiltonian cycles. This polynomial is not identically zero as a function in the arc weights if and only if the digraph is Hamiltonian. The relationship between the computational complexities of computing it and computing the permanent was shown by Grigoriy Kogan.[16]
See also[edit]
- Barnette’s conjecture, an open problem on Hamiltonicity of cubic bipartite polyhedral graphs
- Eulerian path, a path through all edges in a graph
- Fleischner’s theorem, on Hamiltonian squares of graphs
- Gray code
- Grinberg’s theorem giving a necessary condition for planar graphs to have a Hamiltonian cycle
- Hamiltonian path problem, the computational problem of finding Hamiltonian paths
- Hypohamiltonian graph, a non-Hamiltonian graph in which every vertex-deleted subgraph is Hamiltonian
- Knight’s tour, a Hamiltonian cycle in the knight’s graph
- LCF notation for Hamiltonian cubic graphs.
- Lovász conjecture that vertex-transitive graphs are Hamiltonian
- Pancyclic graph, graphs with cycles of all lengths including a Hamiltonian cycle
- Seven Bridges of Königsberg
- Shortness exponent, a numerical measure of how far from Hamiltonian the graphs in a family can be
- Snake-in-the-box, the longest induced path in a hypercube
- Steinhaus–Johnson–Trotter algorithm for finding a Hamiltonian path in a permutohedron
- Subhamiltonian graph, a subgraph of a planar Hamiltonian graph
- Tait’s conjecture (now known false) that 3-regular polyhedral graphs are Hamiltonian
- Travelling salesman problem
Notes[edit]
- ^ Biggs, N. L. (1981), “T. P. Kirkman, mathematician”, The Bulletin of the London Mathematical Society, 13 (2): 97–120, doi:10.1112/blms/13.2.97, MR 0608093.
- ^ Watkins, John J. (2004), “Chapter 2: Knight’s Tours”, Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, pp. 25–38, ISBN 978-0-691-15498-5.
- ^ de Ruiter, Johan (2017). Hamilton Mazes – The Beginner’s Guide.
- ^ Friedman, Erich (2009). “Hamiltonian Mazes”. Erich’s Puzzle Palace. Archived from the original on 16 April 2016. Retrieved 27 May 2017.
- ^ Gardner, M. “Mathematical Games: About the Remarkable Similarity between the Icosian Game and the Towers of Hanoi.” Sci. Amer. 196, 150–156, May 1957
- ^ Ghaderpour, E.; Morris, D. W. (2014). “Cayley graphs on nilpotent groups with cyclic commutator subgroup are Hamiltonian”. Ars Mathematica Contemporanea. 7 (1): 55–72. arXiv:1111.6216. doi:10.26493/1855-3974.280.8d3. S2CID 57575227.
- ^ Lucas, Joan M. (1987), “The rotation graph of binary trees is Hamiltonian”, Journal of Algorithms, 8 (4): 503–535, doi:10.1016/0196-6774(87)90048-4
- ^ Hurtado, Ferran; Noy, Marc (1999), “Graph of triangulations of a convex polygon and tree of triangulations”, Computational Geometry, 13 (3): 179–188, doi:10.1016/S0925-7721(99)00016-4
- ^ Eric Weinstein. “Biconnected Graph”. Wolfram MathWorld.
- ^ Balakrishnan, R.; Ranganathan, K. (2012), “Corollary 6.5.5”, A Textbook of Graph Theory, Springer, p. 134, ISBN 9781461445296.
- ^ Gould, Ronald J. (July 8, 2002). “Advances on the Hamiltonian Problem – A Survey” (PDF). Emory University. Retrieved 2012-12-10.
- ^ Rahman, M. S.; Kaykobad, M. (April 2005). “On Hamiltonian cycles and Hamiltonian paths”. Information Processing Letters. 94: 37–41. doi:10.1016/j.ipl.2004.12.002.
- ^ Moon, J.; Moser, L. (1963), “On Hamiltonian bipartite graphs”, Israel Journal of Mathematics, 1 (3): 163–165, doi:10.1007/BF02759704, MR 0161332, S2CID 119358798
- ^ Whitney, Hassler (1931), “A theorem on graphs”, Annals of Mathematics, Second Series, 32 (2): 378–390, doi:10.2307/1968197, JSTOR 1968197, MR 1503003
- ^ Tutte, W. T. (1956), “A theorem on planar graphs”, Trans. Amer. Math. Soc., 82: 99–116, doi:10.1090/s0002-9947-1956-0081471-8
- ^ Kogan, Grigoriy (1996), “Computing permanents over fields of characteristic 3: where and why it becomes difficult”, 37th Annual Symposium on Foundations of Computer Science (FOCS ’96): 108–114, doi:10.1109/SFCS.1996.548469, ISBN 0-8186-7594-2, S2CID 39024286
References[edit]
- Berge, Claude; Ghouila-Houiri, A. (1962), Programming, games and transportation networks, New York: Sons, Inc.
- DeLeon, Melissa (2000), “A study of sufficient conditions for Hamiltonian cycles” (PDF), Rose-Hulman Undergraduate Math Journal, 1 (1), archived from the original (PDF) on 2012-12-22, retrieved 2005-11-28.
- Dirac, G. A. (1952), “Some theorems on abstract graphs”, Proceedings of the London Mathematical Society, 3rd Ser., 2: 69–81, doi:10.1112/plms/s3-2.1.69, MR 0047308.
- Hamilton, William Rowan (1856), “Memorandum respecting a new system of roots of unity”, Philosophical Magazine, 12: 446.
- Hamilton, William Rowan (1858), “Account of the Icosian Calculus”, Proceedings of the Royal Irish Academy, 6: 415–416.
- Meyniel, M. (1973), “Une condition suffisante d’existence d’un circuit hamiltonien dans un graphe orienté”, Journal of Combinatorial Theory, Series B, 14 (2): 137–147, doi:10.1016/0095-8956(73)90057-9, MR 0317997.
- Ore, Øystein (1960), “Note on Hamilton circuits”, The American Mathematical Monthly, 67 (1): 55, doi:10.2307/2308928, JSTOR 2308928, MR 0118683.
- Pósa, L. (1962), “A theorem concerning Hamilton lines”, Magyar Tud. Akad. Mat. Kutató Int. Közl., 7: 225–226, MR 0184876.
External links[edit]
- Weisstein, Eric W. “Hamiltonian Cycle”. MathWorld.
- Euler tour and Hamilton cycles
1. Введение
В данной статье представлен вариант применения квантового алгоритма Гровера для решения задачи поиска гамильтоновых циклов в графе.
Сразу отмечу, что данный вариант решения задачи является учебным. Он не даст так называемого «квантового превосходства», поскольку при росте числа вершин в графе, нам потребуется большее число кубит, циклов Гровера и запусков самого алгоритма. Однако, считаю, что данный вариант заслуживает внимания, возможно он вдохновит кого-либо на поиск более оптимального решения.
2. Постановка задачи
Представим, что существует граф, состоящий из пяти вершин O, A, B, C, D, и восьми ребер. Вершину O мы будем считать исходной точкой.
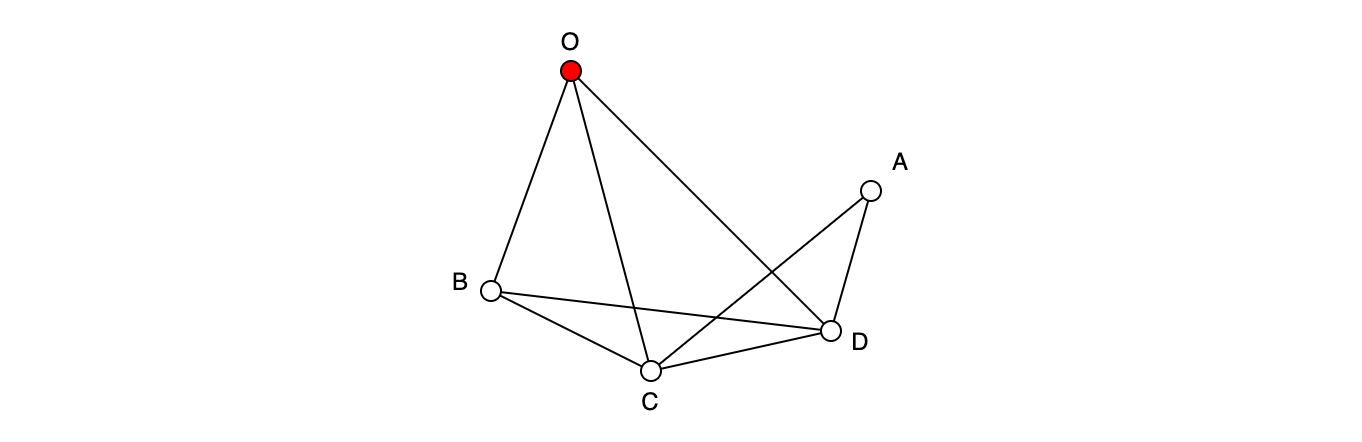
Некий путник, который находится в точке O, хочет пройти через все вершины графа, зайти в каждую из них только один раз и вернуться снова в исходную точку O. Необходимо найти все возможные маршруты путника, удовлетворяющие условиям задачи.
Решение этой задачи легко найти самостоятельно. Всего существуют 4 варианта такого пути, при том, что два из них являются обратными последовательностями двух других:
-
OCADBO и OBDACO
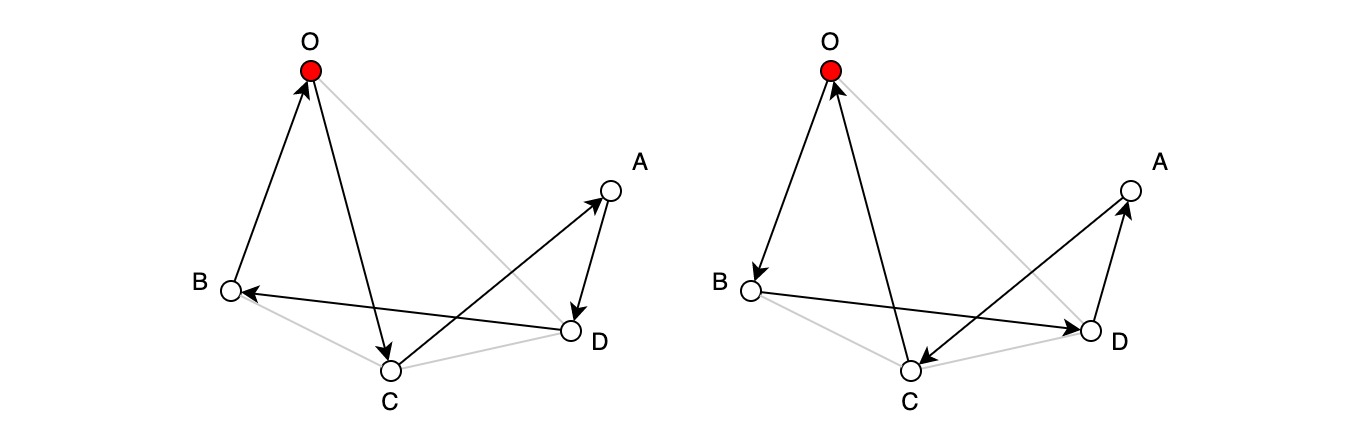
-
ODACBO и OBCADO

Путнику, находящемуся в исходной точке O, необходимо совершить 5 шагов. На каждом из шагов путник переходит по связывающему ребру из одной вершины в другую. Все посещенные вершины должны быть уникальны для маршрута, кроме точки O, в ней путник оказывается дважды, поскольку последний 5-ый шаг должен привести его на исходную позицию.
Маршрутом мы будем называть последовательность вершин, через которые должен пройти путник, например: OBCADO. Каким бы ни был маршрут (последовательность вершин), он должна удовлетворять следующим правилам:
-
вершины маршрута должны быть уникальны, путник дважды не заходит в один и тот же пункт;
-
переход на любом шаге маршрута возможен только в ту вершину, которая связана с текущей:
-
A соединяется с C и D
-
B соединяется с O, C и D
-
C соединяется с O, A, B, C, D
-
D соединяется с O, A, B, C, D
-
-
маршрут начинается и заканчивается в точке O, поэтому для простоты мы исключим ее из маршрута, оставим только изменяющуюся часть — 4 вершины.
Как будем решать?
Решить данную задачу можно в лоб, методом перебора. Итак, мы будем перебирать 4 * 4 * 4 * 4 = 256 комбинации вершин:
При переборе нам необходимо определить, удовлетворяет ли рассматриваемый в конкретный момент маршрут условиям задачи. Рассмотрим несколько примеров.
Допустим, мы рассматриваем маршрут ADCB. Он невозможен для путника, поскольку первый шаг должен быть из точки O в одну из вершин, соединенных с этой точкой. Вершина A не соединяется с точкой O, такой маршрут мы должны отбросить.
Другой пример, маршрут CAAB — его также необходимо отбросить, поскольку в нем путнику придется дважды зайти в вершину A.
Еще пример, маршрут BACD, тоже отбрасываем, путник никак не может попасть из вершины B сразу в вершину A (второй шаг), так как эти вершины не связаны.
Итак, нам необходимо перебрать 256 комбинаций, из которых следует отбрасывать те, в которых:
-
повторяется хотя бы одна из вершин
-
любые две соседние вершины в комбинации не связаны ребром
-
первая в комбинации вершина не связана с исходной точкой O
-
последняя в комбинации вершина не связана с исходной точкой O
Решить данную задачу можно в цикле на обычном ПК, однако, мы преследуем учебные цели и хотим разработать решение для квантового компьютера. Для этого будем использовать квантовый алгоритм Гровера.
Выразим маршрут и вершины на языке кубит.
Возьмем 8 кубит, разобьем их условно на 4 пары. Первая пара соответствует первой вершине пути, вторая пара — второй вершине, и т.д. В каждой паре кубит возможна одна из 4-х комбинаций кубит: 00, 01, 10, 11. Положим, что каждой из этих комбинаций соответствует одна из возможных вершин: A, B, C, D:
Рассмотренные ранее комбинации ADCB, CAAB и BACD будут соответствовать следующим комбинациям кубит: 00111001, 10000001 и 01001011 соответственно.
Если мы применим к этим восьми кубитам оператор Адамара, то получим суперпозицию из всех возможных вариантов движения путника, то есть все 256 комбинаций. Далее в оракуле нам необходимо реализовать процедуры, которые будут проверять эти комбинации на соответствие условиям задачи.
Однако, еще до реализации оракула мы можем воспользоваться одной хитростью, которая позволит нам сократить число комбинаций почти в два раза.
3. Суперпозиция
Самым первым шагом большинства квантовых алгоритмов является создание суперпозиции всех входных кубитов. Однако, мы можем тут отойти от традиции и применить небольшую хитрость, которую применили авторы этой статьи. Суть хитрости заключается в следующем: если нам известны невозможные комбинации кубит, мы можем их заранее исключить из суперпозиции.
Поскольку 1-ый шаг совершается из точки O, и первая вершина должна быть связана с этой точкой, значит это не может быть вершина A, это могут быть только вершины B, C или D. Аналогично, последний 5-ый шаг совершается из 4-ой вершины в точку O, и она должна быть связана с точкой O, значит это не может быть вершина A.
Раз первая вершина в маршруте может быть только вершиной B, C или D, то и первая пара кубит, соответствующая первой вершине в маршруте путника, может принимать только следующие значения: 01, 10 и 11. Это же справедливо и для последней пары кубит, соответствующей четвертой вершине маршрута.
Таким образом, мы исключим из суперпозиции ненужную комбинацию 00 (вершину A) для первой и четвертой вершины и, благодаря этому нам уже не потребуется в оракуле проводить проверку на связь этих вершин с точкой O, и мы сократим число комбинаций до 3 * 4 * 4 * 3 = 144.
Итак, рассмотрим, как работает этот прием для пары кубит.
Начальное состояние системы из двух кубит запишем следующим образом:
Выполним ряд преобразований.
Шаг 1. Подействуем на первый кубит оператором
с таким углом , при котором матрица оператора принимает следующий вид:
Не будем для угла искать «красивое» значение, положим его равным:
Посмотрим, как этот оператор подействует на первый кубит :
После действия оператора на первый кубит пары мы получим следующую суперпозицию 2-х кубит:
Шаг 2. Подействуем на второй кубит контролируемым вентилем Адамара
Контролируемый вентиль Адамара изменяет второй кубит только тогда, когда первый кубит равен
Шаг 3. Подействуем на второй кубит вентилем NOT
Ко второму кубиту применим вентиль NOT:
Итак, мы получили суперпозицию, в которой отсутствует комбинация 00.
После того, как мы подробно разобрали теоретическую часть, приступим к написанию соответствующей процедуры. Библиотека qiskit имеет в своем арсенале все вентили, приведенные в теоретической части:
-
Однокубитный вентиль
— QuantumCirquit.ry(theta, target_qubit)
-
theta — угол
-
target_qubit — кубит, на который воздействует вентиль
-
-
Контролируемый вентиль Адамара — QuantumCirquit.ch(control_qubit, target_qubit)
-
control_qubit — контролирующий кубит
-
target_qubit — кубит, на который воздействует вентиль
-
-
Однокубитный вентиль NOT— QuantumCirquit.x(target_qubit)
-
target_qubit — кубит, на который воздействует вентиль
-
Напишем процедуру, которая на вход будет получать пару кубит и применять к ним последовательно все перечисленные в теоретической части операторы:
import numpy as np
theta = 2 * np.arccos(1 / np.sqrt(3))
def exclude_00(qc, pair, reverse=False):
if not reverse:
qc.ry(theta, pair[0])
qc.ch(pair[0], pair[1])
qc.x(pair[1])
else:
qc.x(pair[1])
qc.ch(pair[0], pair[1])
qc.ry(-theta, pair[0])Отмечу сразу, должна быть возможность выполнить данную процедуру в обратном порядке, поэтому мы ввели дополнительный аргумент reverse. О необходимости в этом подробнее расскажу позже.
Исключать возможность получить вариант A мы будем из первой и четвертой вершины маршрута. Вторая и третья вершины должны иметь все возможные варианты в суперпозиции, поэтому на них будем действовать классически — вентилем Адамара.
4. Оракул
В алгоритме Гровера оракул должен инвертировать фазу «хорошей» комбинации входящих кубит. Если комбинация удовлетворяет условиям уникальности и требованию по связанности вершин, то у такой комбинации оракул должен изменить фазу. В противном случае, если хотя бы одно из условий будет нарушено, оракул оставляет фазу неизменной.
Инверсия фазы равносильна простой инверсии результирующего кубита из в
, который не является частью входных кубит маршрута. Оракул должен быть построен таким образом, чтобы для «хорошей» комбинации результирующий кубит изменял свое состояние
на состояние
.
По умолчанию комбинация объявляется «хорошей». Однако, если будет найдено хотя бы одного совпадение вершин или один несвязанный переход между ними, маршрут будет признан «плохим» и инверсии результирующего кубита не произойдет.
На рисунке условно изображена схема алгоритма для решения нашей задачи.
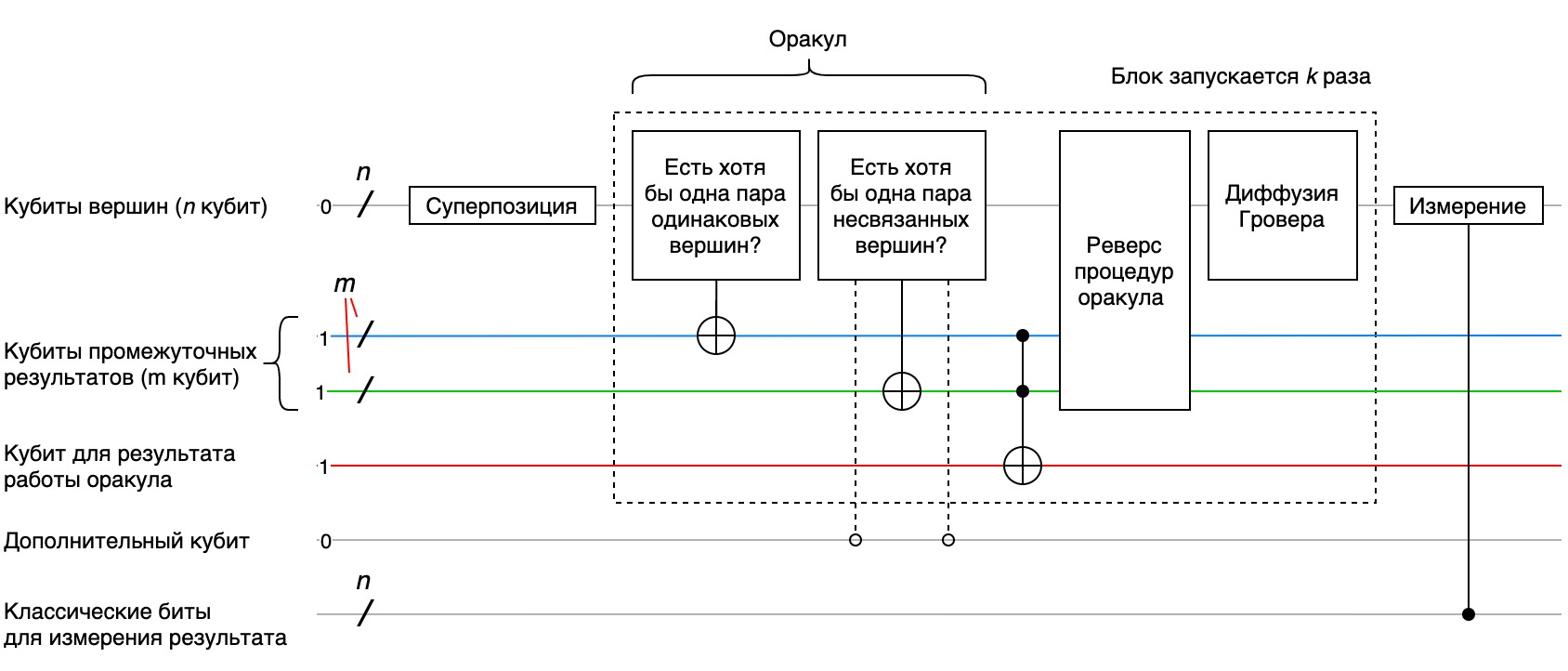
Рассмотрим детально содержание проверок на уникальность и на связанность вершин.
4.1. Контроль совпадения вершин
Задача данного блока состоит в том, чтобы не дать оракулу инвертировать результирующий кубит, если вдруг в комбинации встретятся хотя бы две одинаковых вершины.
Чтобы проверить, нет ли совпадающих вершин в комбинации, нам необходимо последовательно проверить все возможные пары вершин на равенство. Для каждой пары вершин будем проверять, не являются ли они обе одновременно либо вершинами A, либо B, либо C, либо D.

Представим, что на вход подаются две вершины A, тогда все четыре входных кубита равны 0. После применения ко всем четырем кубитам вентиля NOT они становятся равны 1. Множественный вентиль Тоффоли инвертирует результирующий кубит. Дальше в схеме кубиты будут подвержены преобразованию для проверки одновременного равенства вершинам B, C и D. Эти проверки будут неудачными и не изменят результирующий кубит, его значение останется инвертированным.
Если на вход подаются несовпадающие вершины, результирующий кубит на всех этапах схемы останется нетронутым.
Процедура проверки совпадения вершин
Напишем простую процедуру, на вход которой будем подавать две пары кубит, соответствующие двум вершинам маршрута, а также кубит, в который функция будет передавать результат проверки.
Eсли в качестве пар переданы одинаковые вершины, то процедура изменяет результирующий кубит на обратный, сигнализирует о совпадение вершин.
def find_equality(qc, pair_1, pair_2, result_qubit):
qc.x(pair_1 + pair_2)
qc.mct(pair_1 + pair_2, result_qubit)
qc.x([pair_1[1], pair_2[1]])
qc.mct(pair_1 + pair_2, result_qubit)
qc.x(pair_1 + pair_2)
qc.mct(pair_1 + pair_2, result_qubit)
qc.x([pair_1[1], pair_2[1]])
qc.mct(pair_1 + pair_2, result_qubit)Полная схема «детектора совпадений» будет выглядеть примерно так:
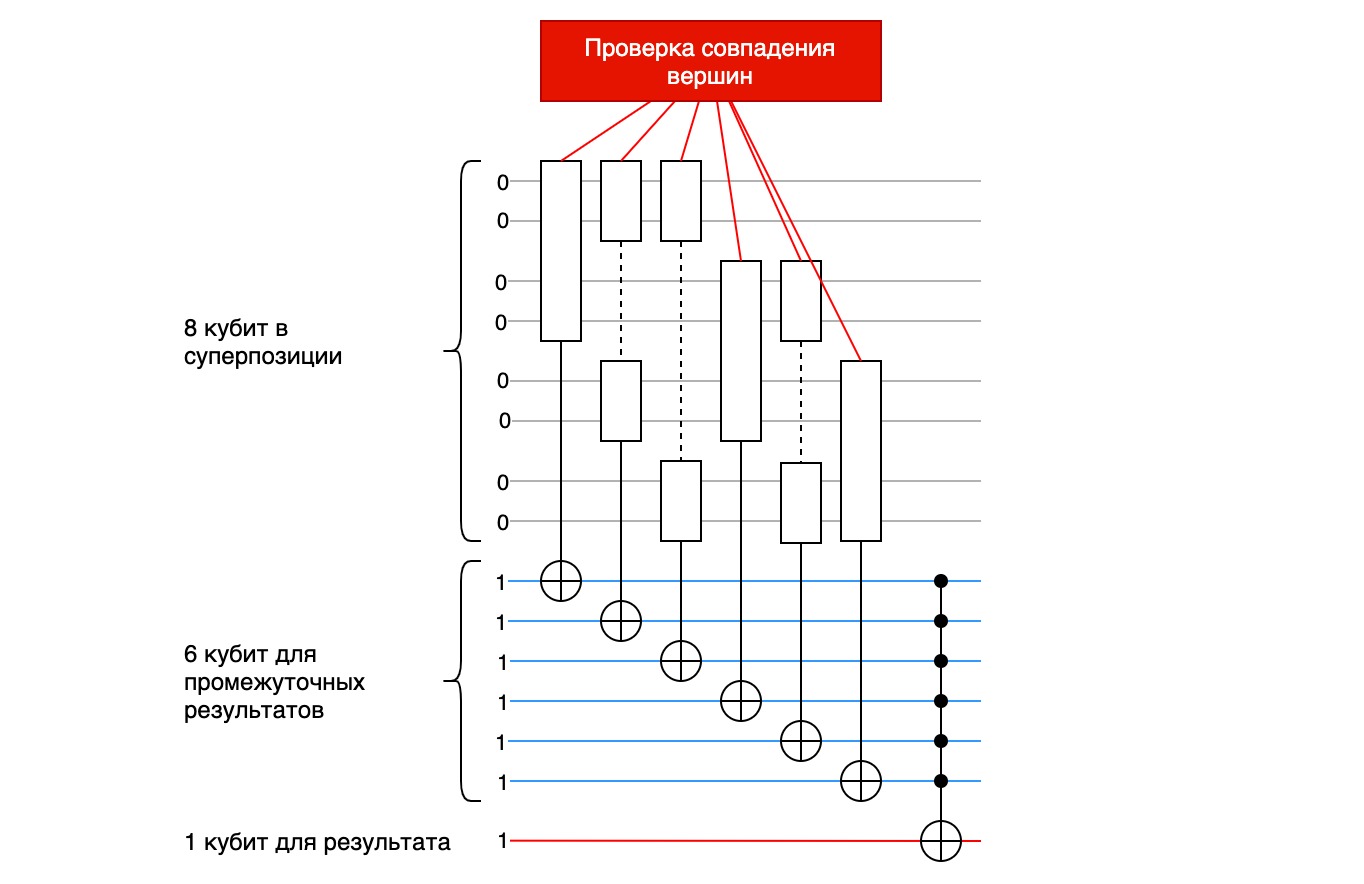
В оракуле нам потребуется применить эту процедуру ко всем парам вершин, а поскольку у нас 4 вершины, то процедуру придется запустить 6 раз — это число сочетаний из 4-х по 2:
При восьми вершинах нам уже потребуется запустить данную функцию для 28 пар вершин. Именно эта часть алгоритма и является узким местом.
4.2. Проверка связи вершин
Задача данного блока оракула состоит в том, чтобы для всех трех пар рядом стоящих вершин определить, существует ли связывающее их ребро. Если хотя бы у одной такой пары нет связи, то процедура не позволяет оракулу, объявить комбинацию «хорошей» и изменить результирующий кубит. Изменив результирующий кубит на 0, процедура не даст оракулу объявить такой маршрут «хорошим».
Суммарная логика должна быть такая: результирующий кубит проверки на связанность вершин должен измениться (1 → 0) если хотя бы одна пара рядом стоящих вершин не будет связана ребром.
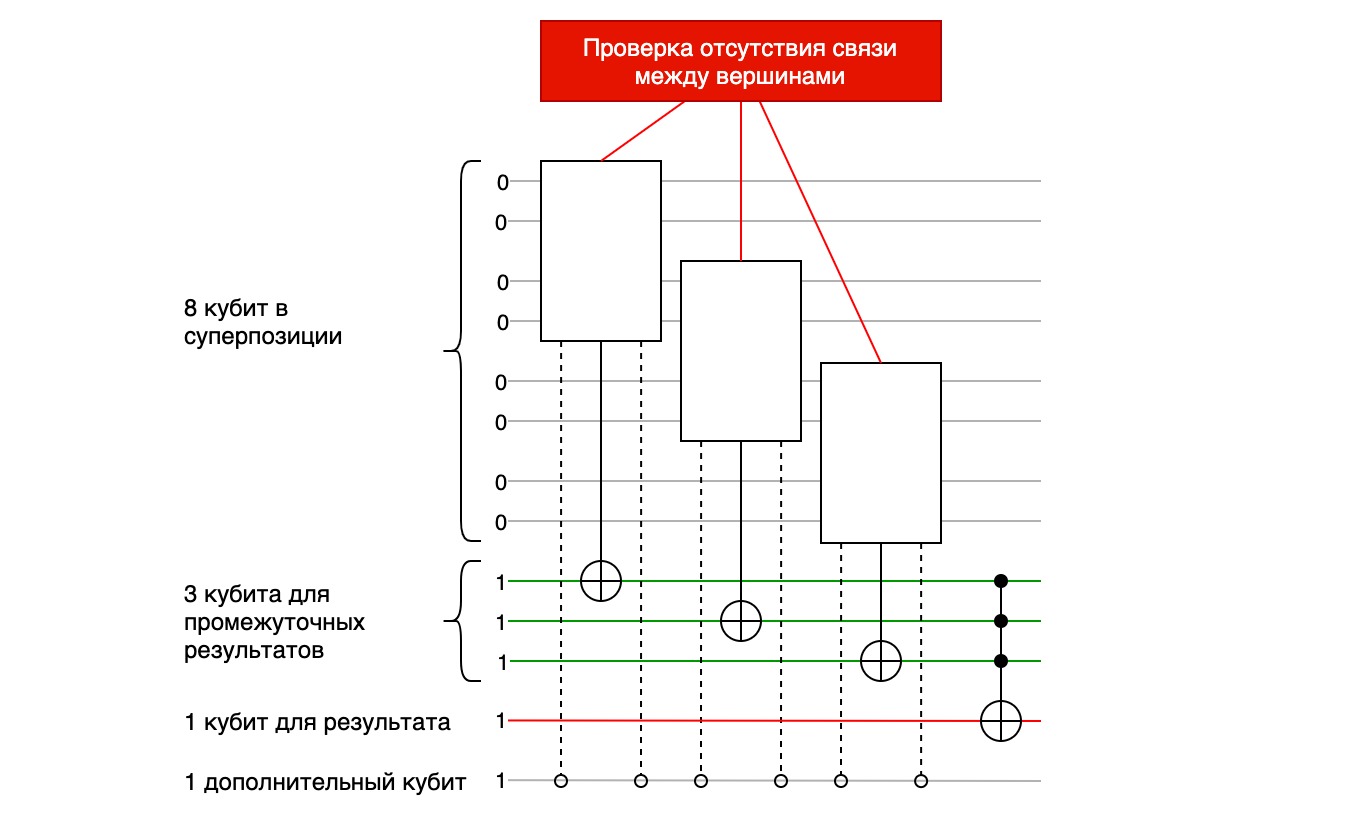
Как мы будем решать эту задачу?
Допустим мы проверяем 3-ю и 4-ю вершины маршрута. И допустим, 3-я вершина есть вершина A. Но мы знаем, что из вершины A можно попасть только в вершины C и D. Следовательно, сначала нужно проверить, выпала ли на 3-ем шаге вершина A, и если это так, то проверить, какая вершина следующая. Нам необходимо выявить именно негативные случаи, когда следующая 4-ая вершина не является ни вершиной C, ни D, и только в этом случае объявить комбинацию неудачной. Проверить это мы сможем от обратного, если 4-ая вершина является вершиной A или B (логически эквивалентно «ни C, ни D»), то считаем текущую комбинацию неудачной. Такая «обратная» форма для нас проще в реализации и позволит сократить число дополнительных кубит.
Не забываем про то, что нам необходимо провести аналогичные проверки для всех остальных случаев, когда третья вершина есть B, C или D. А также для всех возможных пар рядом стоящих вершин в маршруте.
Приступим к реализации данной процедуры. На вход ей будем подавать один кубит для результата и две пары кубит двух вершин. Первую будем называть основной, вторую — соседней.
Мы будем последовательно проверять, какой вершиной (A, B, C или D) является основная вершина. Для этого нам потребуется вентиль Тоффоли. Далее для каждой из возможных ситуаций будем проверять соседнюю вершину на предмет того, является ли она связанной с основной вершиной.
Логика работы процедуры следующая:
-
Проверяем, является ли основная вершина вершиной A, если верно, то проверяем:
-
Является ли соседняя вершина вершиной A или B, если верно, то инвертируем результирующий кубит.
-
-
Проверяем, является ли основная вершина вершиной B, если верно, то проверяем:
-
Является ли соседняя вершина вершиной A или B, если верно, то инвертируем результирующий кубит.
-
-
Проверяем, является ли основная вершина вершиной C, если верно, то проверяем:
-
Является ли соседняя вершина любой, то инвертируем результирующий кубит (условие всегда выполняется).
-
-
Проверяем, является ли основная вершина вершиной D, если верно, то далее логика аналогична логике с вершиной C.
Давайте детально рассмотрим алгоритм описанных выше проверок.
Сначала проверяем, является ли основная вершина вершиной A.
Но каким образом мы можем это проверить? Вершина A в виде кубит имеет представление 00, мы можем к обоим кубитам применить вентиль NOT, тогда пара станет равной 11. Далее мы направляем эту пару в вентиль Тоффоли в качестве контролирующих кубит, он инвертирует дополнительный кубит (0 → 1). Если основная вершина не является вершиной A, то дополнительный кубит останется неизменным. Если же равна — то дополнительный кубит будет инвертированным.

Далее, нам необходимо проверить соседнюю вершину на предмет равенства вершине A или B. Для этого мы вводим дополнительный кубит для сохранения промежуточного результата проверки, применяем множественный вентиль Тоффоли к двум кубитам проверяемой вершины, но также в качестве контрольного кубита подаем в вентиль дополнительный кубит с результатом проверки на равенство основной вершины вершине A. В случае успеха вентиль Тоффоли инвертирует кубит промежуточного результата проверки.
С теоретической частью закончили, приступаем к написанию процедуры.
Сначала составим общий список вершин, заодно зафиксируем для вершин представления в кубитах:
vertex_names = {
'A': '00',
'B': '01',
'C': '10',
'D': '11',
}Зафиксируем все связи вершин (кроме точки O).
connections = {
'A': ['C','D'],
'B': ['C','D'],
'C': ['A','B','D'],
'D': ['A','B','C'],
}Создадим справочник функций, который при подаче на вход вершины, соответствующей ключу в словаре, на выходе выдаст пару кубит 11. Вместе с вентилем Тоффоли этот справочник можно использовать как условный оператор.
vertex_to_11 = {
'A': lambda qc, pair: qc.x(pair),
'B': lambda qc, pair: qc.x(pair[0]),
'C': lambda qc, pair: qc.x(pair[1]),
'D': lambda qc, pair: None,
}Далее, создадим процедуру, которая в качестве аргументов получает две пары кубит, основной и соседней вершины, и проверяет наличие связи между ними. Также в процедуру передаем результирующий кубит, который заранее подготовлен в состоянии .
def find_disconnection(qc, pair_1, pair_2, ancilla_qubit, result_qubit):
for letter_1 in connections.keys():
vertex_to_find = [x for x in vertex_names.keys() if x not in connections[letter_1]]
if len(vertex_to_find) > 0:
vertex_to_11[letter_1](qc, pair_1)
qc.toffoli(*pair_1, ancilla_qubit)
for letter_2 in vertex_to_find:
vertex_to_11[letter_2](qc, pair_2)
qc.mct([*pair_2, ancilla_qubit], result_qubit)
vertex_to_11[letter_2](qc, pair_2)
qc.toffoli(*pair_1, ancilla_qubit)
vertex_to_11[letter_1](qc, pair_1)Эта процедура проверяет одну пару рядом стоящих вершин на предмет существования связи между ними. Если подобной связи нет, то она инвертирует результирующий кубит (1 → 0) процедуры, что не позволит оракулу объявить данную комбинацию «хорошей».
5. Оператор диффузии
Оператор диффузии Гровера в матричном выражении представляет собой обычную единичную матрицу, все диагональные элементы которой равны -1 за исключением самого левого верхнего элемента, который равен 1. Оператор инвертирует фазу любого вектора, кроме вектора .
Пример действия оператора на вектор :
Пример действия оператора на любой другой вектор:
«Сочинять» конфигурацию вентилей для оператора диффузии нет необходимости, он уже разработан. Для набора из n кубит оператор будет выглядеть следующим образом:

Теперь напишем функцию, которая выражает оператор диффузии Гровера. Функцию сделаем универсальной, она на вход будет принимать любое количество кубит.
def diffusion(qc, qubits):
qc.h(qubits)
qc.x(qubits)
qc.h(qubits[-1])
length = len(qubits)
if length > 3:
qc.mct(qubits[0:-1], qubits[-1])
elif length == 3:
qc.toffoli(qubits[0:-1], qubits[2])
elif length == 2:
qc.cx(qubits[0], qubits[1])
qc.h(qubits[-1])
qc.x(qubits)
qc.h(qubits)В качестве центрального элемента оператора используется один из трех вентилей:
-
когда на вход поступают всего 2 кубита — простой вентиль CNOT
-
когда 3 кубита — вентиль Тоффоли
-
когда 4 и более кубита — вентиль Тоффоли для многих кубит
Доработка оператора диффузии Гровера
Поскольку для создания начальной суперпозиции входных кубит мы не везде использовали однокубитный вентиль Адамара, нам потребуется видоизменить оператор диффузии.
В первоначальном виде оператор диффузии Гровера на входе применяет ко всем входным кубитам вентиль Адамара, тем самым как бы возвращая кубиты из суперпозиции в обычное несвязанное состояние. На выходе оператор снова применяет вентили Адамара для создания суперпозиции.
Однако, на шаге создания суперпозиции мы применили специальные операторы для исключения ненужных комбинаций из первой и четвертой пары кубит, а вентиль Адамара применили только ко второй и третьей.
Соответственно, для нашего алгоритма мы отключим в операторе диффузии Гровера входные и выходные вентили Адамара:
def diffusion(qc, qubits):
# qc.h(qubits)
qc.x(qubits)
qc.h(qubits[-1])
length = len(qubits)
if length > 3:
qc.mct(qubits[0:-1], qubits[-1])
elif length == 3:
qc.toffoli(qubits[0:-1], qubits[2])
elif length == 2:
qc.cx(qubits[0], qubits[1])
qc.h(qubits[-1])
qc.x(qubits)
# qc.h(qubits)Теперь он выглядит так:

А перед вызовом оператора будем применять преобразование, обратное созданию суперпозиции, после оператора — снова создание суперпозиции:
exclude_00(qc, qr[0:2], reverse=True)
qc.h(qr[2:6])
exclude_00(qc, qr[6:8], reverse=True)
diffusion(qc, qr[0:8])
exclude_00(qc, qr[0:2])
qc.h(qr[2:6])
exclude_00(qc, qr[6:8])Тут нам и пригодилась инверсная версия процедуры исключения комбинации 00 из суперпозиции.
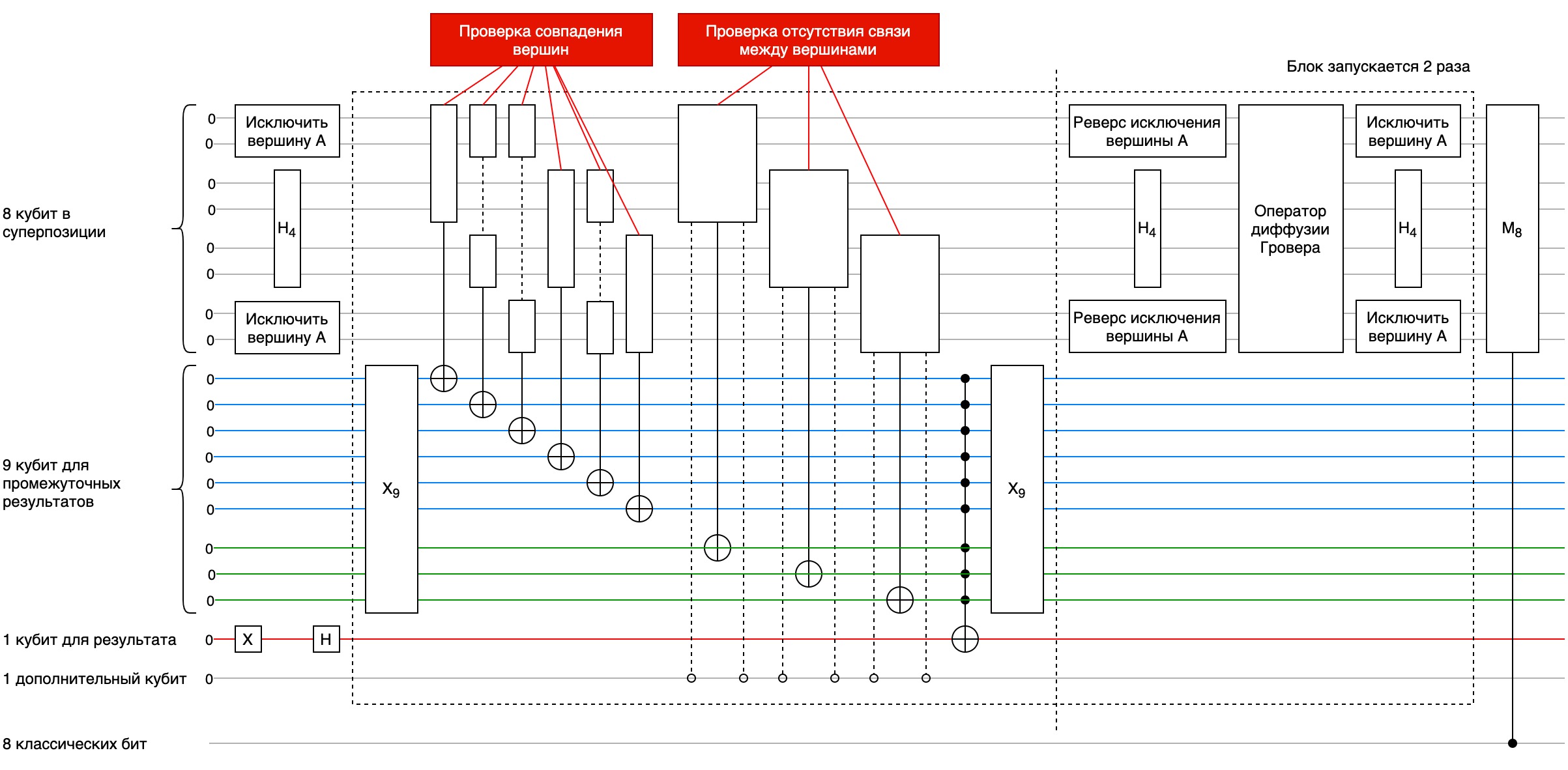
5. Собираем все вместе
Мы не будем подробно рассматривать принципы работы алгоритма Гровера с его учебными примерами, а сразу приступим к его реализации. Рассчитаем число итераций, пусть n — число входных кубит для оракула, в нашем случае оно равно 8, тогда количество итераций алгоритма Гровера должно быть следующим:
То есть, нам потребуется всего 2 итерации алгоритма для получения отчетливого результата.
5.1. Общая схема
Все составляющие алгоритма мы рассмотрели, начинаем сборку элементов в единую рабочую цепь. Общая схема выглядит следующим образом:
Скачиваем и устанавливаем библиотеки Qiskit, NumPy и Matplotlib для Python.
> pip3 install qiskit numpy matplotlibИмпортируем необходимые библиотеки.
import numpy as np
from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit, Aer, executeЗаранее подготовим процедуру поиска совпадений вершин.
def find_equality(...):
# См. код процедуры вышеЗаводим необходимые для работы переменные и вспомогательные функции:
vertex_names = {
'A': '00',
'B': '01',
'C': '10',
'D': '11',
}
connections = {
'A': ['C','D'],
'B': ['C','D'],
'C': ['A','B','D'],
'D': ['A','B','C'],
}
vertex_to_11 = {
'A': lambda qc, pair: qc.x(pair),
'B': lambda qc, pair: qc.x(pair[0]),
'C': lambda qc, pair: qc.x(pair[1]),
'D': lambda qc, pair: None,
}Готовим процедуру поиска несвязанных вершин и оператор диффузии.
def find_disconnection(...):
# См. код процедуры find_disconnection выше
def diffusion(...):
# См. код процедуры diffusion вышеПодготавливаем процедуру для исключения ненужных вершин из суперпозиции:
theta = 2 * np.arccos(1 / np.sqrt(3))
def exclude_00(qc, pair, reverse=False):
# См. код процедуры exclude_00Теперь необходимо решить, сколько нам всего потребуется кубит:
|
Индексы |
Число кубит |
Назначение |
|
0-7 |
8 |
Комбинации вершин в маршруте |
|
8-13 |
6 |
Промежуточные результаты поиска совпадающих вершин |
|
14-16 |
3 |
Промежуточные результаты поиска несвязанных вершин |
|
17 |
1 |
Результирующий кубит |
|
18 |
1 |
Дополнительный кубит для процедуры поиска несвязанных вершин |
Итого, нам потребуются 19 кубит. Для измерения результата также необходимо зарезервировать 8 обычных бит.
Создаем квантовую цепь:
qr = QuantumRegister(19)
cr = ClassicalRegister(8)
qc = QuantumCircuit(qr, cr)Создаем суперпозицию:
exclude_00(qc, qr[0:2])
qc.h(qr[2:6])
exclude_00(qc, qr[6:8])Подготавливаем результирующий кубит:
qc.x(17)
qc.h(17)Пишем цикл, который дважды запускает оракул и оператор диффузии Гровера.
pairs = [
[[qr[0],qr[1]], [qr[2],qr[3]]],
[[qr[0],qr[1]], [qr[4],qr[5]]],
[[qr[0],qr[1]], [qr[6],qr[7]]],
[[qr[2],qr[3]], [qr[4],qr[5]]],
[[qr[2],qr[3]], [qr[6],qr[7]]],
[[qr[4],qr[5]], [qr[6],qr[7]]],
]
for i in range(2):
# Oracle
qc.x(qr[8:17])
for i, pair in enumerate(pairs):
find_equality(qc, pair[0], pair[1], qr[8 + i])
find_disconnection(qc, pair_1=qr[2:4], pair_2=qr[0:2], ancilla_qubit=qr[18], result_qubit=qr[14])
find_disconnection(qc, pair_1=qr[4:6], pair_2=qr[2:4], ancilla_qubit=qr[18], result_qubit=qr[15])
find_disconnection(qc, pair_1=qr[6:8], pair_2=qr[4:6], ancilla_qubit=qr[18], result_qubit=qr[16])
# Store result
qc.mct(qr[8:17], qr[17])
# Oracle (reverse)
find_disconnection(qc, pair_1=qr[6:8], pair_2=qr[4:6], ancilla_qubit=qr[18], result_qubit=qr[16])
find_disconnection(qc, pair_1=qr[4:6], pair_2=qr[2:4], ancilla_qubit=qr[18], result_qubit=qr[15])
find_disconnection(qc, pair_1=qr[2:4], pair_2=qr[0:2], ancilla_qubit=qr[18], result_qubit=qr[14])
for i, pair in enumerate(pairs):
find_equality(qc, pair[0], pair[1], qr[8 + i])
qc.x(qr[8:17])
# Diffuser
exclude_00(qc, qr[0:2], reverse=True)
qc.h(qr[2:6])
exclude_00(qc, qr[6:8], reverse=True)
diffusion(qc, qr[0:8])
exclude_00(qc, qr[0:2])
qc.h(qr[2:6])
exclude_00(qc, qr[6:8])При запуске нескольких итераций необходимо «подчищать» дополнительные кубиты для экономии. Поэтому после сохранения результата работы оракула необходимо выполнить обратные процедуры, чтобы вернуть к исходному состоянию 1 все кубиты промежуточных результатов и состоянию 0 все дополнительные кубиты, иначе вторая итерация будет выполнена некорректно. Обратная процедура иногда бывает эквивалентна исходной, а иногда в ней требуется выполнить все шаги в обратном порядке. Все зависит от конфигурации вентилей, если повторное применение в обратном порядке возвращает систему в первоначальное состояние, то нет необходимости для процедуры писать инверсный вариант.
Измерение результата:
qc.measure(qr[0:8], cr)Итак, схема готова, теперь необходимо ее запустить.
Поскольку всего комбинаций 144, из них удачных только 4, то нам потребуется запустить алгоритм «приличное» число раз, чтобы отчетливо увидеть распределение вероятности удачных и неудачных маршрутов.
Запускаем алгоритм на симуляторе.
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend = simulator, shots = 1000).result()
counts = result.get_counts()
print(counts)Получаем результат.
{'10011001': 1, ..., '11000110': 146, ..., '01100010': 4}Метод measure класса QuantumCirquit возвращает ответ в виде массива с ключами, где каждый ключ соответствует комбинации кубит, а значение есть частота появления этой комбинации среди всех запусков алгоритма. Ключ представляет кубиты с 0-го по n-й справа налево, как принято при записи двоичных и десятичных чисел. Например:
Кроме того, этот массив не отсортирован, и найти в нем наиболее вероятные варианты тяжело. Напишем небольшое выражение, которое придаст результату «человекопонятный» вид.
answers = {''.join(dict(zip(map(lambda x: x[::-1], vertex_names.values()), vertex_names.keys()))[k[i*2:i*2+2]]
for i in range(len(k)//2)): v
for k, v in {item[0]: item[1]
for item in sorted(counts.items(), key=lambda x:x[1], reverse=True)}.items()}
print(answers)Получаем результат.
{'CADB': 161, 'BDAC': 135, 'DACB': 130, 'BCAD': 127, 'DCAC': 8, ... }Теперь мы видим, что наибольшую частоту имеют маршруты:
{
'CADB': 161,
'BDAC': 135,
'DACB': 130,
'BCAD': 127
}Частота остальны значительно ниже. Для наглядности построим гистограмму распределения вероятностей ответов:
from qiskit.visualization import plot_histogram
plot_histogram(counts)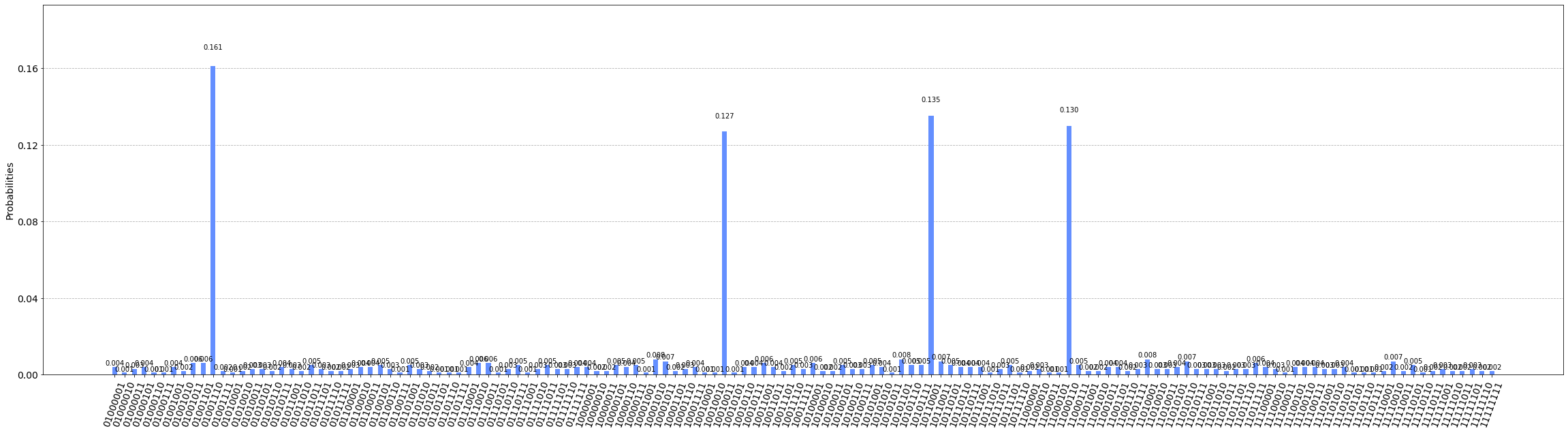
6. Выводы
Используя квантовый алгоритм Гровера мы с вами нашли гамильтоновы пути в графе с 5-ю вершинами. Практическое применение алгоритма Гровера требует учета ряда особенностей:
-
Характер суперпозиции влияет на оператор диффузии.
-
При запуске нескольких итераций необходимо применять инверсию оракула для экономии дополнительных кубит.
-
Оракул должен готовиться особым образом, входящие в него процедуры должны обнаруживать «нарушения условий», оракул инвертирует фазу комбинации только когда нет ни одного «нарушения».
Решение не универсальное, его невозможно применить к другой конфигурации ребер в графе, не говоря уже о большем числе вершин. Для создания универсального инструмента необходимо учесть следующие аспекты:
-
Решения вообще может не быть, тогда вероятность всех маршрутов будет примерно одинаковая.
-
Заранее неизвестно количество ответов. Зная это число, можно значительно сократить объем вычислений, необходимо применить к задаче алгоритмы поиска числа решений.
-
Решение не подходит для числа вершин, отличного от 5-ти как в большую так и в меньшую сторону. Потребуется значительная переработка для адаптации.
-
Рост числа вершин значительно увеличивает число кубит для обнаружения неуникальных вершин.
Надеюсь, статья будет кому-либо полезной:)
Ссылка на код алгоритма в репозитории GitHub
Гамильтоновы графы. Гамильтонов путь. Алгоритм нахождения гамильтоновых циклов в графе.
В 1859 г. известный
математик сэр Уильям Гамильтон придумал
игру, в которой требуется обойти замкнутый
контур всех ребер додекаэдра, минуя
каждую вершину лишь один раз.
Гамильтонов
путь в
графе G
– это путь, содержащий все вершины графа
G.
Гамильтоновым
циклом в
графе G
называется цикл, содержащий все вершины
графа G.
Граф G
называется гамильтоновым, если он имеет
гамильтонов цикл.

а )
)
б)
а) Гамильтонов
путь в графе.
б) Граф, в котором
не существует гамильтонова пути.
а
 )
)
б)
а) Гамильтонов
граф.
б) Негамильтонов
граф, имеющий гамильтонов путь.
Рассмотрим задачу
нахождения гамильтонова пути, т.е. пути,
проходящего только один раз через каждую
вершину, а не каждое ребро графа. В
отличие от эйлеровых путей не известно
ни одного простого необходимого и
достаточного условия для существования
гамильтоновых путей и это несмотря на
то, что эта задача – одна из центральных
в теории графов. Не известен также
алгоритм, который проверял бы существование
гамильтонова пути в произвольном графе,
используя число шагов, ограниченное
многочленом от переменной n
(числа вершин в графе). Проблема
существования гамильтонова пути
принадлежит к классу так называемых NP
– полных задач.
Очевидный алгоритм,
который мы можем применить, это “полный
перебор всех возможностей”. Генерируем
все n!
различных последовательностей вершин
и для каждой из них проверяем, определяет
ли она гамильтонов путь. Такие действия
требуют по меньшей мере n!n
шагов, но функция подобного вида растет
быстрее, чем произвольная экспоненциальная
функция an.
Опишем общий метод,
позволяющий значительно сократить
число шагов в алгоритмах типа полного
перебора всех возможностей.
Алгоритмы с возвратом
Общим методом
организации исчерпывающего поиска и
позволяющим значительно сократить
число шагов в алгоритмах типа полного
перебора всех возможностей является
так называемый возвратный ход по
упорядоченному множеству частичных
возможных решений. Этот метод – метод
поиска с возвращением – основан на том,
что мы многократно пытаемся расширить
текущее частичное решение, или, что то
же самое сузить множество тех возможных
полных решений, которые не противоречат
текущему частичному решению. Если
расширение невозможно на текущем шаге
поиска, то происходит возврат к предыдущему
более короткому частичному решению и
делается попытка его расширения, но уже
другим способом.
Чтобы применить
этот метод, искомое решение должно иметь
вид последовательности <x1,
x2,
…, xn>.
В качестве начального частичного решения
берется пустая последовательность
( ) (длины 0). Имея данное частичное решение
<x1,
x2,
…, xi>,
мы стараемся найти такое допустимое
значение xi+1,
относительно которого мы не можем сразу
заключить, что <x1,
x2,
…, xi,
xi+1>
можно расширить до некоторого решения,
либо <x1,
x2,
…, xi,
xi+1>
уже является решением. Если такое
предполагаемое, но еще не использованное
значение xi+1
существует,
то мы добавляем его к нашему частичному
решению и продолжаем процесс для
последовательности <x1,
x2,
…, xi,
xi+1>.
Если его не существует, то мы возвращаемся
к нашему частичному решению <x1,
x2,
…, xi,
xi-1>
и продолжаем наш процесс, отыскивая
новое, еще не использованное допустимое
значение xi‘
– отсюда название “алгоритм с возвратом”
(backtracking).
Мы предполагаем,
что для каждого k
> 0 существует некоторое множество Ak,
из которого мы будем выбирать кандидатов
для k-ой
координаты частичного решения. В общем
случае ограничения, описывающие решения,
говорят о том из какого подмножества
Sk
множества
Ak
выбираются кандидаты для расширения
частичного решения от <x1,
x2,
…, xk-1>
до <x1,
x2,
…, xk>.
Если частичное
решение <x1,
x2,
…, xk-1>
не предоставляет других возможностей
для выбора нового xk,
т.е. у частичного решения <x1,
x2,
…, xk-1>
либо нет кандидатов для расширения,
либо все кандидаты к данному моменту
уже использованы, то происходит возврат
и осуществляется выбор нового элемента
xk-1
из подмножества Sk-1.
Если новый элемент xk-1
выбрать
нельзя, т.е. к данному моменту множество
Sk-1
уже пусто, то происходит еще один возврат
и делается попытка выбрать новый элемент
xk-2
и т.д.
Мы предполагаем,
что существует некоторая простая
функция, которая произвольному частичному
решению <x1,
x2,
…, xi>
ставит в соответствие значение P(x1,
x2,
…, xi)
(истина
либо ложь)
таким образом, что если P(x1,
x2,
…, xi)
= ложь,
то последовательность <x1,
x2,
…, xi>
нельзя расширить до решения. Если P(x1,
x2,
…, xi)
= истина,
то мы говорим, что значение xi
допустимо
(для частичного решения <x1,
x2,
…, xi-1>),
но это отнюдь не означает, что <x1,
x2,
…, xi-1>
обязательно расширяется до полного
решения.
Общую схему
алгоритма, осуществляющего поиск с
возвратом для нахождения всех решений,
можно представить в следующем виде:
begin
k:=1;
while
k>0
do
if
существует еще неиспользованный элемент
y
Ak,
такой что
P(x[1],
…, x[k-1],
y)
then
begin
x[k]:=y;
/* элемент y
использован и удален из Sk
*/
if
< x[1],
…, x[k]>
является целочисленным решением
then
write
(x[1],
…, x[k]);
/* записать это решение */
k:=k
+ 1
end
else
k:=k
– 1 /* возврат на более короткое
частичное решение, все элементы множества
Ak
вновь становятся неиспользованными
*/
end.
/* все решения
найдены */
Этот алгоритм
находит все решения в предположении,
что множества Ak
конечные и все решения имеют длину
меньше n.
Более коротко
общую процедуру поиска с возвращением
можно записать в рекурсивной форме.
Procedure
AP
(k);
/* генерирование
всех решений, являющихся расширением
последовательности x[1],
…, x[k-1];
массив x
– глобальный */
begin
for
y
Ak
такого, что P(x[1],
…, x[k-1],
y)
является решением do
begin
x[k]:=y;
/* элемент y
использован и удален из Sk
*/
if
< x[1],
…, x[k]>
является целочисленным решением
then
write
(x[1],
…, x[k]);
/* записать это решение */
AP
(k
+ 1)
end
end.
Генерирование
всех целочисленных решений можно
произвести вызовом AP
(1), причем все возвраты скрыты в механизме,
регулирующем рекурсию, т.е. в рекурсивном
варианте “возврат” не появляются
в явном виде, будучи частью реализации
механизма рекурсии. Поэтому изучение
алгоритма с возвратом мы начали с
несколько более сложного нерекурсивного
варианта.
Применим теперь
алгоритм с возвратом для нахождения
гамильтонова цикла в графе G=<V,
E>.
Каждый такой цикл можно представить
последовательностью <x1,
x2,
…, xn+1>,
причем x1
= xn+1
= V0,
где V0
– некоторая фиксированная вершина графа,
{xi,
xi+1}
для 1
i
n
и xi
xj
для 1
i
< j
n..
Согласно этим
условиям можно задать:
Ak
= V – множество вершин,
P( x1,
…, xk-1,
y)
y
rec
[xk-1]
y
{ x1,
…, xk-1}.
– логическое
“и”.
– “тогда и
только тогда”.
Соседние файлы в папке алгоритмы
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
