Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие свойства площади фигуры вы знаете?
- Равные фигуры имеют равные площади.
- Площадь фигуры равна сумме площадей фигур, из которых она состоит.
2. Какой квадрат называют единичным?
Единичный квадрат — это квадрат, стороны которого равны единичному отрезку.
3. Какие единицы измерения площади вы знаете?
- мм² — квадратный миллиметр
- см² — квадратный сантиметр
- м² — квадратный метр
- км² — квадратный километр
4. Что означает измерить площадь фигуры?
Измерить площадь фигуры — это значит подсчитать, сколько единичных квадратов в ней помещается.
5. Чему равна площадь прямоугольника?
Площадь прямоугольника равна произведению длин его соседних сторон:
S = ab
6. По какой формуле вычисляют площадь квадрата?
S = a²
7. Сколько квадратных метров содержит 1 ар? 1 гектар?
1 ар = 100 м²
1 га = 10 000 м²
Решаем устно
1. Сколько сантиметров содержится в:
- 1 дм = 10 см
- 1 м 3 дм = 130 см
- 5 м 2 дм = 520 см
- 12 дм 5 см = 125 см
- 40 мм = 4 см
2. Лодка за 5 ч прошла 40 км. За сколько часов она пройдёт с той же скоростью 24 км?

1) 40 : 5 = 8 (км/ч) — скорость лодки.
2) 24 : 8 = 3 (ч) — потребуется дл преодоления 24 км.
Ответ: 3 часа.
3. Сколько литров воды может перекачать насос за 8 мин, если пять таких насосов за 6 мин перекачивают 450 л воды?

1) 450 : 6 = 75 (л/мин) — скорость работы пяти насосов.
2) 75 : 5 = 15 (л/мин) — скорость работы одного насоса.
3) 15 • 8 = 120 (литров) — воды перекачает один насос за 8 минут.
Ответ: 120 литров воды.
4. Какую цифру надо поставить вместо звёздочек, чтобы запись 1* + 3* + 5* = 111 стала верным равенством?
Вспомним таблицу умножения на 3 и подберём число, которое при умножении на 3 дает число, оканчивающееся на 1. Это число 7 (7 • 3 = 21).
Подставим цифру 7 в равенство:
17 + 37 + 57 = 111 — равенство верно.
Ответ: цифра 7.
Упражнения
564. 1) Сколько квадратных сантиметров содержит 1 дм²? 1 м²?
1 дм² = 10 см • 10 см = 100 см²
1 м²= 100 см • 100 см = 10 000 см²
2) Сколько квадратных метров содержит 1 км²?
1 км²= 1 000 м • 1 000 м = 1 000 000 м²
565. Вычислите площадь прямоугольника, соседние стороны которого равны 14 см и 8 см.
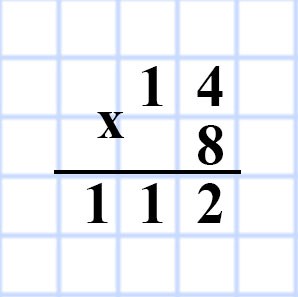
a = 14 см
b = 8 см
S = ?
S = ab
S = 14 • 8 = 112 (см²)
Ответ: S = 112 см²
566. Вычислите площадь квадрата со стороной 7 дм.
a = 7 дм
S = ?
S = a²
S = 7 • 7 = 49 (дм²)
Ответ: S = 49 дм²
567. Одна сторона прямоугольника равна 16 см, а соседняя сторона — на 6 см длиннее. Вычислите площадь прямоугольника.
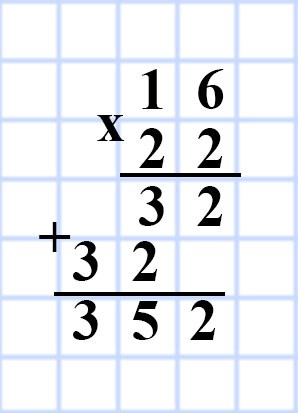
a = 16 см
b = (a + 6) см
S = ?
S = ab
S = 16 • (16 + 6) = 16 • 22 = 352 (см²)
Ответ: S = 352 см²
568. Одна сторона прямоугольника равна 48 см, а соседняя сторона — в 8 раз меньше. Вычислите площадь прямоугольника.
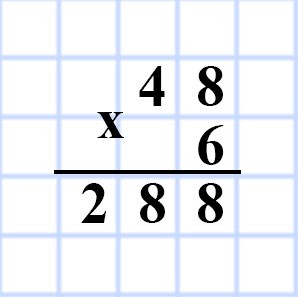
a = 48 см
b = (a : 8) см
S = ?
S = ab
S = 48 • (48 : 8) = 48 • 6 = 288 (см²)
Ответ: S = 288 см²
Внимание! Следующие 5 задач решены двумя способами!
569. Периметр прямоугольника равен 162 дм, а одна из сторон — 47 дм. Найдите площадь прямоугольника.

Способ 1:
a = 47 дм
P = 162 дм
S = ?
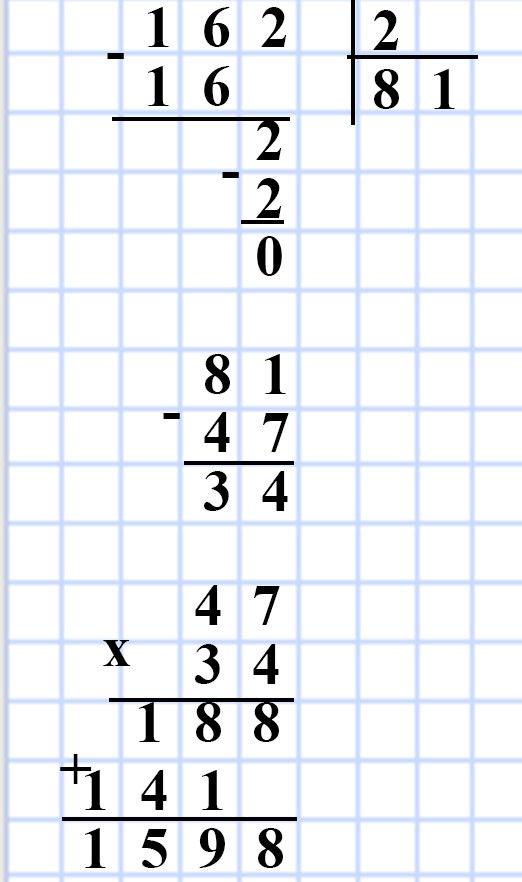
P = (a + b) • 2
b = P : 2 — a
b = 162 : 2 — 47 = 81 — 47 = 34 (дм) — длина стороны b.
S = ab
S = 47 • 34 = 1 598 (дм²) — площадь прямоугольника.
Ответ: S = 1598 дм².
Способ 2:
1) 162 : 2 = 81 (дм) — сумма двух соседних сторон прямоугольника.
2) 81 — 47 = 34 (дм) — длина второй стороны прямоугольника.
3) 47 • 34 = 1 598 (дм²) — площадь прямоугольника.
Ответ: S = 1598 дм².
570. Периметр прямоугольника равен 96 м, и он в 8 раз больше одной из сторон прямоугольника. Найдите площадь прямоугольника.
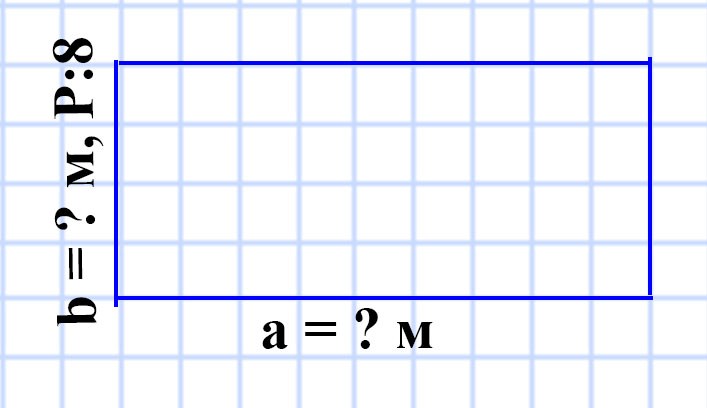
Способ 1:
P = 96 м
a = (P : 8) м
S = ?

a = P : 8
a = 96 : 8 = 12 (м) — длина стороны a прямоугольника.
P = (a + b) • 2
b = P : 2 — a
b = 96 : 2 — 12 = 48 — 12 = 36 (м) — длина стороны b.
S = ab
S = 36 • 12 = 432 (м²) — площадь прямоугольника.
Ответ: S = 432 м².
Способ 2:
1) 96 : 8 = 12 (м) — длина одной стороны прямоугольника.
2) 96 : 2 = 48 (м) — сумма длин соседних сторон прямоугольника.
3) 48 — 12 = 36 (м) — длина второй стороны прямоугольника.
4) 36 • 12 = 432 (м²) — площадь прямоугольника.
Ответ: S = 432 м².
571. Найдите площадь квадрата, периметр которого равен 96 см.
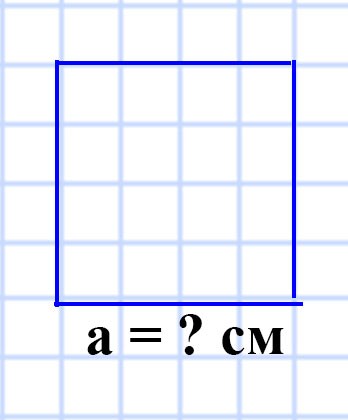
Способ 1:
P = 96 см
a = ? см
S = ?

a = P : 4
a = 96 : 4 = 24 (см) — длина стороны квадрата.
S = a²
S = 24 • 24 = 576 (см²) — площадь прямоугольника.
Ответ: S = 576 см².
Способ 2:
1) 96 : 4 = 24 (см) — длина стороны квадрата.
2) 24² = 24 • 24 = 576 (см²) — площадь прямоугольника.
Ответ: S = 576 см².
572. Периметр прямоугольника равен 4 м 8 дм, одна из его сторон в 5 раз больше соседней стороны. Найдите площадь прямоугольника.
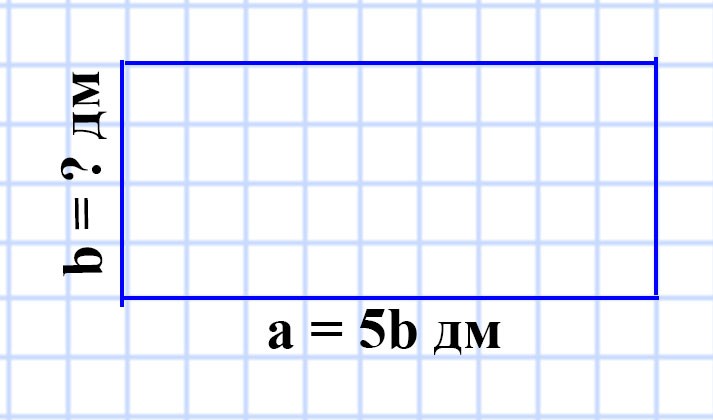
Способ 1:
P = 4 м 8 дм
a = 5b
S = ?
4 м 8 дм = 48 дм
P = (a + b) • 2 и a = 5b. Составим уравнение:
48 = (5b + b) • 2
5b + b = 48 : 2
6b = 24
b = 24 : 6
b = 4 (дм) — длина стороны b прямоугольника
a = 5b = 5 • 4 = 20 (дм) — длина стороны a прямоугольника
S = ab
S = 20 • 4 = 80 (дм²) — площадь прямоугольника.
Ответ: S = 80 дм².
Способ 2:
4 м 8 дм = 48 дм
1) 48 : 2 = 24 (дм) — сумма длин соседних сторон прямоугольника.
2) 24 : 6 = 4 (дм) — длина одной стороны прямоугольника.
3) 4 • 5 = 20 (дм) — длина другой стороны прямоугольника.
4) 20 • 4 = 80 (дм²) — площадь прямоугольника.
Ответ: S = 80 дм².
573. Периметр прямоугольника равен 6 дм 8 см, одна из его сторон на 1 дм 6 см меньше соседней стороны. Найдите площадь прямоугольника.
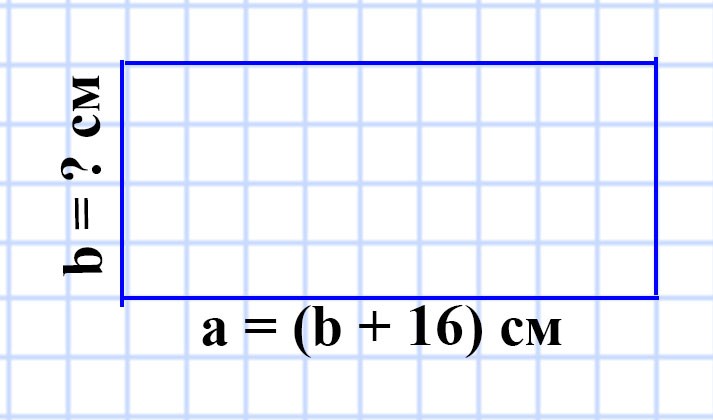
Способ 1
P = 6 дм 8 см
a = b + 1 дм 6 см
S = ?
6 дм 8 см = 68 см
1 дм 6 см = 16 см
P = (a + b) • 2 и a = b + 16 см. Составим уравнение:
68 = (b + 16 + b) • 2
b + 16 + b = 68 : 2
2b + 16 = 34
2b = 34 — 16
2b = 18
b = 18 : 2
b = 9 (см) — длина стороны b прямоугольника
a = b + 16 = 9 + 16 = 25 (см) — длина стороны a прямоугольника
S = ab
S = 25 • 9 = 225 (см²) — площадь прямоугольника.
Ответ: S = 225 см².
Способ 2:
6 дм 8 см = 68 см
1 дм 6 см = 16 см
1) 68 : 2 = 34 (см) — сумма длин двух соседних сторон прямоугольника.
2) 34 — 16 = 18 (см) — сумма длин двух коротких сторон прямоугольника.
3) 18 : 2 = 9 (см) — длина короткой стороны прямоугольника.
4) 34 — 9 = 25 (см) — длина длинной стороны прямоугольника.
5) 25 • 9 = 225 (см²) — площадь прямоугольника.
Ответ: S = 225 см².
574. Выразите:
1) в арах:
- 12 га = 1 200 а
- 45 га = 4 500 а
- 6 га 28 а = 600 а + 28 а = 628 а
- 14 га 68 а = 1 400 а + 68 а = 1468 а
- 32 400 м² = 324 а
- 123 800 м² = 1 238 а
- 2 км² 14 га 5 а = 20 000 а + 1 400 а + 5 а = 21 405 а
- 4 км² 72 га 16 а = 40 000 а + 7 200 а + 16 а = 47216 а
2) в квадратных метрах:
- 5 а = 500 м²
- 17 а = 1 700 м²
- 8 га = 80 000 м²
- 63 га = 630 000 м²
- 5 га 72 а = 50 000 м² + 7 200 м² = 57 200 м²
- 14 га 43 а = 140 000 м² + 4 300 м² = 144 300 м²
3) в гектарах и арах:
- 530 а = 5 га 30 а
- 1 204 а = 12 га 4 а
- 16 300 м² = 10 000 м² + 6 300 м² = 1 га 63 а
- 85 200 м² = 80 000 м² + 5 200 м² = 8 га 52 а
575. Выразите:
1) в квадратных сантиметрах:
- 8 дм² = 800 см²
- 16 дм² = 1 600 см²
- 4 м² = 40 000 см²
- 38 м² = 380 000 см²
- 16 м² 19 дм² = 160 000 см² + 1 900 см² = 161 900 см²
- 74 м² 3 дм² = 740 000 см² + 300 см² = 740 300 см²
2) в гектарах:
- 340 000 м² = 34 га
- 5 830 000 м² = 583 га
- 53 км² = 5 300 га
- 14 км² = 1 400 га
- 5 км² 18 га = 500 га + 18 га = 518 га
- 24 км² 6 га = 2 400 га + 6 га = 2 406 га
576. Поле прямоугольной формы имеет площадь 56 а, его длина — 80 м. Вычислите периметр поля.
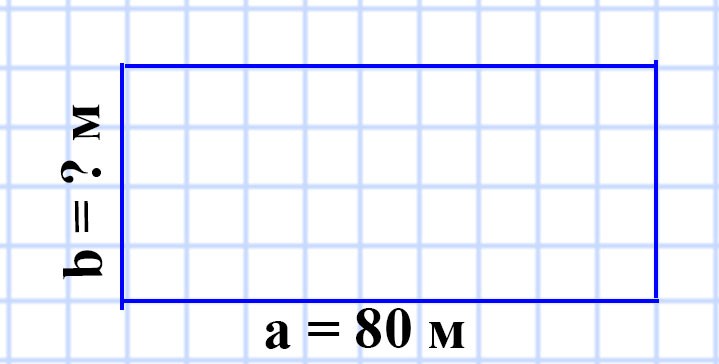
a = 80 м
S = 56 а
P = ? м
56 а = 5 600 м²
S = ab
b = S : a = 5 600 : 80 = 70 (м) — ширина поля.
P = (a + b) • 2 = (70 + 80) • 2 = 150 • 2 = 300 (м) — периметр поля
Ответ: P = 300 м.
577. Поле прямоугольной формы имеет площадь 48 а, его ширина — 150 м. Вычислите периметр поля.
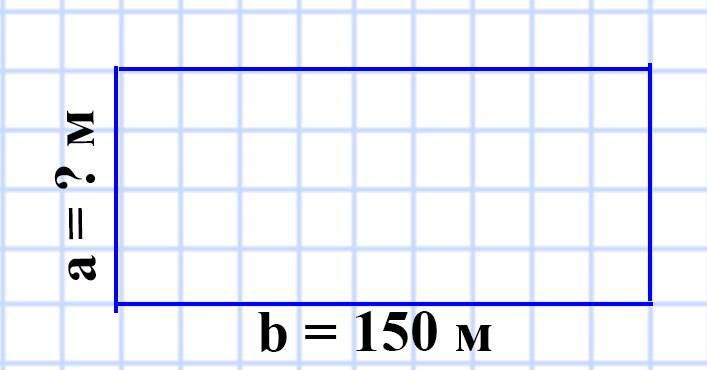
b = 150 м
S = 48 а
P = ? м
48 а = 4 800 м²
S = ab
a = S : b = 4 800 : 150 = 32 (м) — длина поля.
P = (a + b) • 2 = (32 + 150) • 2 = 182 • 2 = 364 (м) — периметр поля
Ответ: P = 364 м.
578. Вычислите периметр и площадь фигуры, изображённой на рисунке 149 (размеры даны в сантиметрах).
а)

1) Проведём вспомогательную линию и разделим фигуру на два прямоугольника.
2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:
- 15 — 5 = 10 (см) — длина части большого прямоугольника, не обозначенная на схеме и не равная стороне этого прямоугольника.
P = 15 + 18 + 10 + 8 + 5 + 8 + 18 = 82 (см) — периметр всей фигуры.
3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Найдём площадь маленького прямоугольника: S = ab = 8 • 5 = 40 (см²).
- Найдём площадь большого прямоугольника: S = ab = 18 • 15 = 270 (см²).
Значит площадь всей фигуры: S = S (маленького прямоугольника) + S (большого прямоугольника) = 40 + 270 = 310 (см²).
Ответ: P = 82см, S = 310 см².
б)
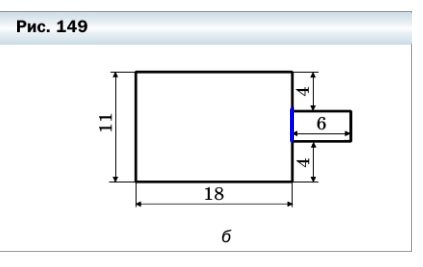
1) Проведём вспомогательную линию и разделим фигуру на два прямоугольника.
2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:
- 11 — (4 + 4) = 3 (см) — ширина маленького прямоугольника.
P = 18 + 4 + 6 + 3 + 6 + 4 + 18 + 11 = 70 (см) — периметр всей фигуры.
3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Найдём площадь маленького прямоугольника: S = ab = 6 • 3 = 18 (см²).
- Найдём площадь большого прямоугольника: S = ab = 18 • 11 = 198 (см²).
Значит площадь всей фигуры: S = S (маленького прямоугольника) + S (большого прямоугольника) = 18 + 198 = 216 (см²).
Ответ: P = 70 см, S = 216 см².
579. Вычислите периметр и площадь фигуры, изображённой на рисунке 150 (размеры даны в сантиметрах).

1) Проведём вспомогательную линию(синюю) и разделим фигуру на три прямоугольника.
2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:
- 12 + 6 + 12 = 30 (см) — длина большого прямоугольника.
- 18 — 4 = 14 (см) — ширина большого прямоугольника.
P = 12 + 4 + 6 + 4 + 12 + 18 + 30 + 18 = 104 (см) — периметр всей фигуры.
3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Найдём площадь первого маленького прямоугольника: S = ab = 12 • 4 = 48 (см²).
- Найдём площадь второго маленького прямоугольника: S = ab = 12 • 4 = 48 (см²).
- Найдём площадь большого прямоугольника: S = ab = 30 • 12 = 420 (см²).
Значит площадь всей фигуры: S = S (маленького первого прямоугольника) + S (маленького второго прямоугольника) + S (большого прямоугольника) = 48 + 48 + 420 = 516 (см²).
Ответ: P = 104 см, S = 516 см².
Комментарий: Площадь данной фигуры удобнее находить другим способом. Для этого надо провести вторую вспомогательную линию (красную) и из площади получившегося в результате построения большого прямоугольника вычесть площадь маленького прямоугольника:
- Найдём площадь большого прямоугольника: S = ab = 30 • 18 = 540 (см²).
- Найдём площадь маленького прямоугольника: S = ab = 6 • 4 = 24 (см²).
Значит площадь всей фигуры: S = S (большого прямоугольника) — S (маленького прямоугольника) = 540 — 24 = 516 (см²).
580. Хватит ли 5 т гороха, чтобы засеять им поле, имеющее форму прямоугольника со сторонами 500 м и 400 м, если на 1 га земли надо высеять 260 кг гороха?

5 т = 5 000 кг
1) 500 • 400 = 200 000 м² = 20 га — площадь поля.
2) 260 • 20 = 5 200 (кг) — гороха потребуется для засеивания поля.
3) 5 200 кг >5 000 кг — значит 5т гороха не хватит для засеивания поля.
Ответ: Нет, не хватит.
581. Отец решил облицевать кафелем стену кухни, длина которой равна 4 м 50 см, а высота — 3 м. Хватит ли ему 20 ящиков кафеля, если одна плитка имеет форму квадрата со стороной 15 см, а в одном ящике находится 30 плиток?

- 4м 50 см = 450 см — длина стены
- 3 м = 300 см — высота стены
1) 15 • 15 = 225 (см²) — площадь 1 плитки.
2) 450 • 300 = 135 000 (см²) — площадь стены.
3) 135 000 : 225 = 600 (шт) — плиток потребуется на облицовку стены.
4) 30 • 20 = 600 (шт) — плиток находится в 20 ящиках.
5) 600 шт = 600 шт — значит 20 ящиков плитки хватит для облицовки стены.
Ответ: Да, хватит.
582. Фермер Пётр Трудолюб посадил в теплице огурцы. Длина теплицы равна 16 м 50 см, а ширина — 12 м. Сколько килограммов огурцов соберёт фермер в своей теплице, если с 1 м² собирают 30 кг огурцов?

- 16 м 50 см = 1 650 см
- 12 м = 1 200 см
1) 1 650 • 1 200 = 1 980 000 см² = 198 м² — площадь теплицы.
2) 198 • 30 = 5 940 (кг) — огурцов соберёт фермер.
Ответ: 5 940 кг огурцов.
583. Расход эмалевой краски на однослойное покрытие составляет 180 г на 1 м². Хватит ли 3 кг эмали, чтобы покрасить стену длиной 6 м и высотой 3 м?

3 кг = 3 000 г
1) 6 • 3 = 18 (м²) — площадь стены.
2) 18 • 180 = 3 240 (г) — краски потребуется на однослойное покрытие стены.
3) 3 240 г > 3 000 г — значит 3 кг краски не хватит на окраску данной стены.
Ответ: Нет, не хватит.
584. Квадрат со стороной 12 см и прямоугольник, длина которого равна 18 см, являются равновеликими. Найдите периметр прямоугольника.

1) 12 • 12 = 144 (см²) — площадь квадрата = площадь прямоугольника.
2) 144 : 18 = 8 (см) — длина стороны b прямоугольника.
3) (18 + 8) • 2 = 26 • 2 = 52 (см) — периметр прямоугольника.
Ответ: 52 см.
585. Квадрат и прямоугольник являются равновеликими, соседние стороны прямоугольника равны 3 см и 12 см. Найдите периметр квадрата.

1) 12 • 2 = 36 (см²) — площадь прямоугольника = площадь квадрата.
2) Подберём число, квадрат которого равен 36. Это число 6 (6 • 6 = 36). Значит сторона квадрата равна 6 см.
3) 6 • 4 = 24 (см) — периметр квадрата.
Ответ: 24 см.
586. Ширина прямоугольника равна 26 см. На сколько квадратных сантиметров увеличится площадь этого прямоугольника, если его длину увеличить на 4 см?
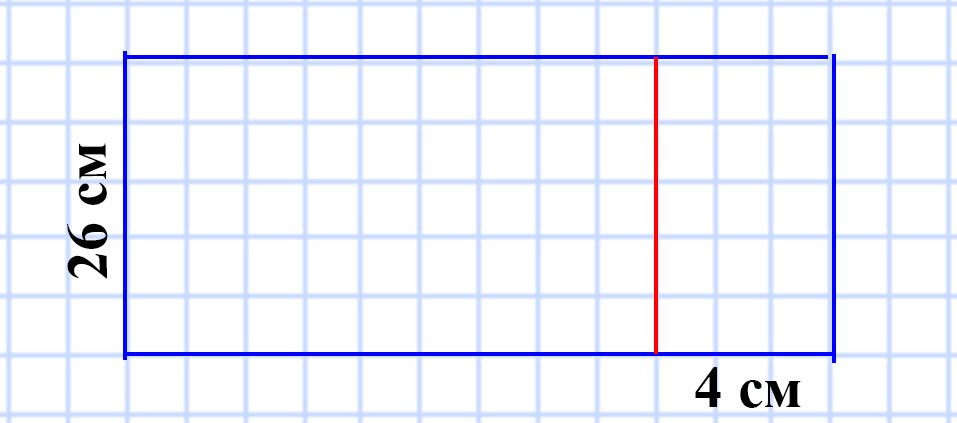
Для того, чтобы узнать на сколько квадратных сантиметров увеличится площадь этого прямоугольника, надо найти площадь маленького прямоугольника, полученного в результате увеличения длины на 4 см.
Мы знаем, что противоположные стороны прямоугольника равны.
26 • 4 = 104 (см²) — площадь, на которую увеличиться площадь исходного прямоугольника.
Ответ: на 104 см².
587. Во сколько раз увеличатся периметр и площадь прямоугольника, если каждую его сторону увеличить в 4 раза?
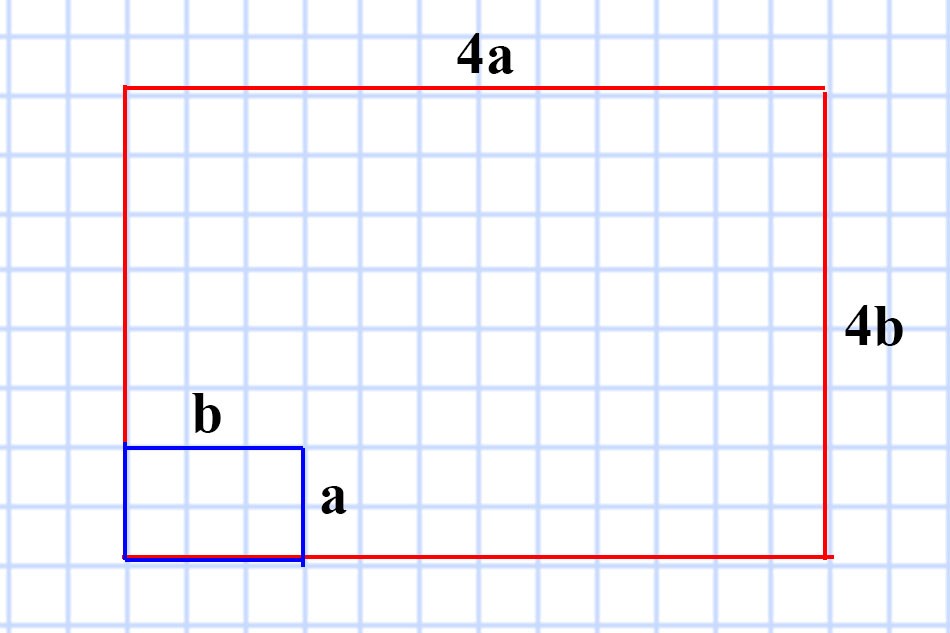
Посчитаем, во сколько раз увеличится периметр прямоугольника, если каждую его сторону увеличить в 4 раза.
- P (исходного прямоугольника) = (a + b) • 2 = 2(a + b)
- P (увеличенного прямоугольника) = (4a + 4b) • 2 = 8(a + b)
8(a + b) : 2(a + b) = 4 (раза) — увеличился периметр прямоугольника.
Посчитаем, во сколько раз увеличится площадь прямоугольника, если каждую его сторону увеличить в 4 раза.
- S (исходного прямоугольника) = ab
- S (увеличенного прямоугольника) = 4a • 4b = 16ab
16ab : ab = 16 (раз) — увеличится площадь прямоугольника.
Ответ: Периметр увеличится в 4 раза, а площадь увеличится в 16 раз.
588. Длина прямоугольника равна 32 см. На сколько квадратных сантиметров уменьшится площадь этого прямоугольника, если его ширину уменьшить на 5 см?
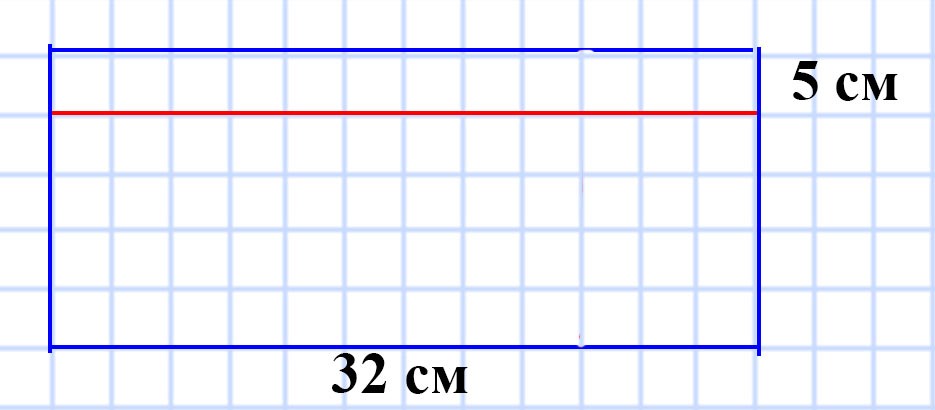
Для того, чтобы узнать на сколько квадратных сантиметров увеличится площадь этого прямоугольника, надо найти площадь маленького прямоугольника, полученного в результате увеличения ширины на 5 см.
Мы знаем, что противоположные стороны прямоугольника равны.
32 • 5 = 160 (см²) — площадь, на которую увеличиться площадь исходного прямоугольника.
Ответ: на 160 см².
589. Площадь квадрата ABCD равна 16 см² (рис. 151). Чему равна площадь прямоугольника ACFE?
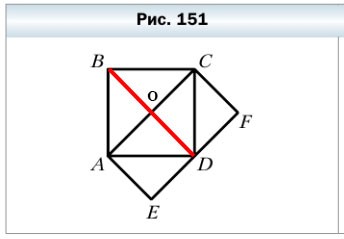
1) Проведём в квадрате ABCD ещё одну диагональ BD. Каждая из диагоналей делит квадрат ABCD на 2 равные части, а две диагонали AC и BD делят квадрат ABCD на 4 равных треугольника. Значит:
SAOB = SBOC = SCOD = SAOD = 16 : 4 = 4 см²
2) AODE — квадрат, так как две его соседние стороны AO и OD равны. Диагональ AD делит квадрат AODE на 2 равных треугольника. Значит:
SADE = SAOD = 4 см²
2) OCFD — квадрат, так как две его соседние стороны OD и OC равны. Диагональ CD делит квадрат OCFD на 2 равных треугольника. Значит:
SCFD = SOCD = 4 см²
3) SACFE = SAOD + SADE + SOCD + SCFD = 4 + 4 + 4 + 4 = 16 см².
Ответ: площадь прямоугольника ACFE равна 16 см².
590. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 12 см². Сколько квадратов площадью 4 см² можно вырезать из этого прямоугольника?
1) Если площадь листа равна 12 см², то лист может быть следующих форматов:
- 1 см х 12 см
- 2 см х 6 см
- 3 см х 4 см
2) Если площадь квадрата равна 4 см², то его сторона может быть равна только 2 см, так как 2 • 2 = 4 см².
3) Из листа со сторонами 1 см х 12 см невозможно вырезать ни одного квадрата со стороной 2 см.
4) Из листа со сторонами 2 см х 6 см можно вырезать 3 квадрата со стороной 2 см, так как:
- по длине 6 : 2 = 3
- по ширине 2 : 2 = 1
- 3 • 1 = 3
5) Из листа со сторонами 3 см х 4 см можно вырезать 2 квадрата со стороной 2 см, так как:
- по длине 4 : 2 = 2
- по ширине 3 : 2 = 1 (остаток 1).
- 2 • 1 = 2
Ответ: из листа площадью 12 см² можно вырезать 3 квадрата площадью 4 см², если стороны листа равны 2 и 6 см, либо 2 квадрата площадью 4 см², если стороны листа равны 3 и 4 см.
591. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 18 см². Сколько квадратов со стороной 3 см можно вырезать из этого листа?
1) Если площадь листа равна 18 см², то лист может быть следующих форматов:
- 1 см х 18 см
- 2 см х 9 см
- 3 см х 6 см
2) Из листа со сторонами 1 см х 18 см невозможно вырезать ни одного квадрата со стороной 3 см.
3) Из листа со сторонами 2 см х 9 см невозможно вырезать ни одного квадрата со стороной 3 см.
4) Из листа со сторонами 3 см х 6 см можно вырезать 2 квадрата со стороной 2 см, так как:
- по длине 6 : 3 = 2
- по ширине 3 : 3 = 1.
- 2 • 1 = 2
Ответ: из листа площадью 18 см² можно вырезать 2 квадрата со стороной 3 см, если стороны листа равны 3 и 6 см.
592. Внутри прямоугольника ABCD (рис. 152) вырезали отверстие прямоугольной формы. Как одним прямолинейным разрезом разделить полученную фигуру на две фигуры с равными площадями?
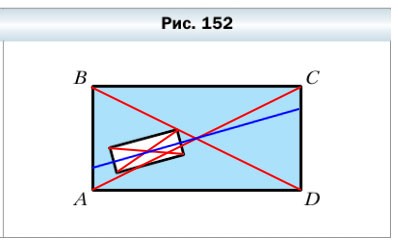
- Проведём две вспомогательные линии (красные) и найдём точку пересечения диагоналей малого прямоугольника.
- Проведём две вспомогательные линии (красные) и найдём точку пересечения диагоналей большого прямоугольника.
- Проведём прямую (синяя) через две точки:
- точку пересечения диагоналей малого прямоугольника
- точку пересечения диагоналей большого прямоугольника.
- Вдоль данной прямой выполним разрез и получим две фигуры с равными площадями.
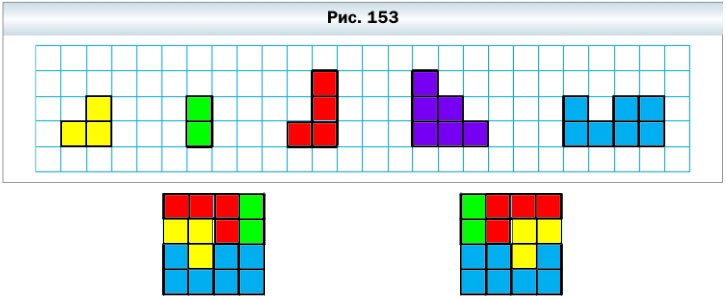
593. Используя четыре из пяти изображённых на рисунке 153 фигур, составьте квадрат.
594. Можно ли разрезать квадрат на несколько частей так, чтобы потом из них можно было составить два квадрата, длины сторон которых выражаются целым числом сантиметров, если сторона данного квадрата равна:
1) 5 см
Да, можно, так как площадь квадрата со стороной 5 см равна 5² = 25 см, а число 25 можно выразить суммой двух квадратов целых чисел: 25 = 4² + 3².
Например, можно разрезать квадрат со стороной 5 см на 4 квадрата со стороной по 2 см и 9 квадратов со стороной 1 см, а затем сложить из них одни квадрат со стороной 4 см и один квадрат со стороной 3 см.

2) 6 см
Нет, такие квадраты составить нельзя, так как число площадь квадрата со стороной 6 см равна 6² = 36 см, а число 36 нельзя выразить суммой двух квадратов целых чисел.
Упражнения для повторения
595. Из вершины прямого угла ABC (рис. 154) провели лучи BD и BE так, что угол АВЕ оказался больше угла DBE на 34º, а угол CBD больше угла DBE на 23º. Какова градусная мера угла DBE?
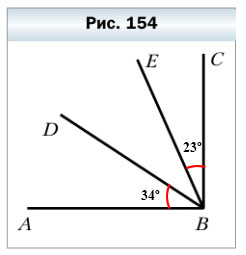
∠ABC= 90º — прямой
∠АВЕ — ∠DBE = 34º
∠CBD — ∠DBE = 23º
∠DBE = ?
1) ∠ABD = ∠АВЕ — ∠DBE = 34º
2) ∠EBC ∠CBD — ∠DBE = 23º
3) ∠DBE = ∠ABC — ∠ABD — ∠EBC = 90º — 34º — 23º = 33º
Ответ:∠DBE = 33º
596. Выполните действия:

Задача от мудрой совы
597. Расстояние между городами А и В равно 30 км. Из города А в город В выехал велосипедист и двигался со скоростью 15 км/ч. Одновременно из города В в направлении города А вылетела птица со скоростью 30 км/ч. Встретившись с велосипедистом, птица развернулась и полетела назад. Прилетев в город В, она снова развернулась и полетела навстречу велосипедисту. Встретившись с ним, птица развернулась и полетела назад в город В и т. д. Сколько километров пролетела птица за то время, пока велосипедист ехал из города А в город В?

1) 30 : 15 = 2 (часа) — потребуется велосипедисту, чтобы доехать из города А в город В.
Птица летала до места встречи с велосипедистом и обратно несколько раз все эти два часа, причём скорость полёта птицы была неизменна — 30 км/ч.
2) 30 • 2 = 60 (км) — пролетела птица в то время, пока велосипедист ехал из города А в город В.
Ответ: 60 км.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
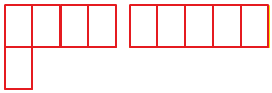
Вычисли площадь фигуры разными способами.


reshalka.com
ГДЗ учебник по математике 2 класс (часть 2) Рудницкая. Нахождение нескольких частей числа. Номер №17
Решение
1 способ:

Фигура состоит из 18 квадратов
Площадью 1 квадрата −
1
с
м
2
. Следовательно, площадь фигура −
18
с
м
2
.
1 * 18 = 18
с
м
2
Ответ: 18
с
м
2
.
2 способ:

Разделим фигуру двумя вертикальными линиями на 3 части: левый прямоугольник, центральный прямоугольник и правый прямоугольник. Получится 3 равных прямоугольника.
Площадь 1 прямоугольника − 6
с
м
2
3 * 2 = 6
с
м
2
Площадь фигуры:
6 * 3 = 18
с
м
2
Ответ: 18
с
м
2
.
3 способ:

Два квадрата из нижней части фигуры нужно переставить в верхнюю часть (в углубление). Таким образом, получится прямоугольник со сторонами 6 см и 3 см.
6 * 3 = 18
с
м
2
Ответ: 18
с
м
2
.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе – это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь – это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник : 
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
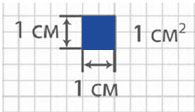
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
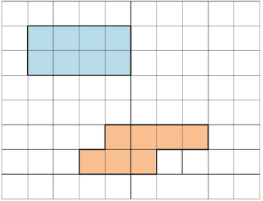
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
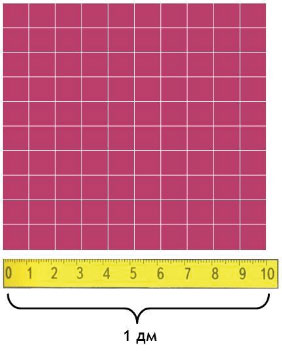
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
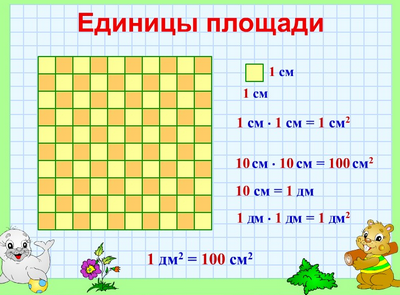
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
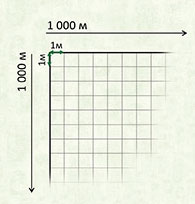
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
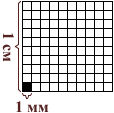
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
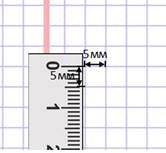
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар – это площадь квадрата со стороной 10 м.
Слово “ар” при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар – это площадь квадрата со стороной 100 м.
Слово “гектар” при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 47. Урок 18,
Петерсон, Учебник, часть 2
Страница 50. Урок 19,
Петерсон, Учебник, часть 2
Страница 65. Урок 26,
Петерсон, Учебник, часть 2
Страница 79. Урок 32,
Петерсон, Учебник, часть 2
Страница 81. Урок 33,
Петерсон, Учебник, часть 2
Страница 88. Урок 37,
Петерсон, Учебник, часть 2
Страница 40. Урок 14,
Петерсон, Учебник, часть 3
Страница 49. Урок 17,
Петерсон, Учебник, часть 3
Страница 90. Урок 35,
Петерсон, Учебник, часть 3
3 класс
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94. Урок 35,
Петерсон, Учебник, часть 1
Страница 87. Урок 38,
Петерсон, Учебник, часть 2
Страница 88. Урок 38,
Петерсон, Учебник, часть 2
Страница 51. Урок 23,
Петерсон, Учебник, часть 3
Страница 70. Повторение,
Петерсон, Учебник, часть 3
Страница 75. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 6,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 107,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
ГДЗ по Математике 5 класс Мерзляк А.Г. § 21. Площадь. Площадь прямоугольника
Вопросы к параграфу
1. Какие свойства площади фигуры вы знаете?
2. Какой квадрат называют единичным?
3. Какие единицы измерения площади вы знаете?
4. Что означает измерить площадь фигуры?
5. Чему равна площадь прямоугольника?
6. По какой формуле вычисляют площадь квадрата?
7. Сколько квадратных метров содержит 1 ар? 1 гектар?
Решаем устно
1. Сколько сантиметров содержится в:
2. Лодка за 5 ч прошла 40 км. За сколько часов она пройдёт с той же скоростью 24 км?
3. Сколько литров воды может перекачать насос за 8 мин, если пять таких насосов за 6 мин перекачивают 450 л воды?
4. Какую цифру надо поставить вместо звёздочек, чтобы запись 1* + 3* + 5* = 111 стала верным равенством?
Упражнения
564. 1) Сколько квадратных сантиметров содержит 1 дм?? 1 м?? 2) Сколько квадратных метров содержит 1 км??
565. Вычислите площадь прямоугольника, соседние стороны которого равны 14 см и 8 см.
566. Вычислите площадь квадрата со стороной 7 дм.
567. Одна сторона прямоугольника равна 16 см, а соседняя сторона — на 6 см длиннее. Вычислите площадь прямоугольника.
568. Одна сторона прямоугольника равна 48 см, а соседняя сторона — в 8 раз меньше. Вычислите площадь прямоугольника.
569. Периметр прямоугольника равен 162 дм, а одна из сторон — 47 дм. Найдите площадь прямоугольника.
570. Периметр прямоугольника равен 96 м, и он в 8 раз больше одной из сторон прямоугольника. Найдите площадь прямоугольника.
571. Найдите площадь квадрата, периметр которого равен 96 см.
572. Периметр прямоугольника равен 4 м 8 дм, одна из его сторон в 5 раз больше соседней стороны. Найдите площадь прямоугольника.
573. Периметр прямоугольника равен 6 дм 8 см, одна из его сторон на 1 дм 6 см меньше соседней стороны. Найдите площадь прямоугольника.
574. Выразите: 1) в арах:
575. Выразите: в квадратных сантиметрах:
576. Поле прямоугольной формы имеет площадь 56 а, его длина — 80 м. Вычислите периметр поля.
577. Поле прямоугольной формы имеет площадь 48 а, его ширина — 150 м. Вычислите периметр поля.
578. Вычислите периметр и площадь фигуры, изображённой на рисунке 149 (размеры даны в сантиметрах).
579. Вычислите периметр и площадь фигуры, изображённой на рисунке 150 (размеры даны в сантиметрах).
580. Хватит ли 5 т гороха, чтобы засеять им поле, имеющее форму прямоугольника со сторонами 500 м и 400 м, если на 1 га земли надо высеять 260 кг гороха?
581. Отец решил облицевать кафелем стену кухни, длина которой равна 4 м 50 см, а высота — 3 м. Хватит ли ему 20 ящиков кафеля, если одна плитка имеет форму квадрата со стороной 15 см, а в одном ящике находится 30 плиток?
582. Фермер Пётр Трудолюб посадил в теплице огурцы. Длина теплицы равна 16 м 50 см, а ширина — 12 м. Сколько килограммов огурцов соберёт фермер в своей теплице, если с 1 м? собирают 30 кг огурцов?
583. Расход эмалевой краски на однослойное покрытие составляет 180 г на 1 м?. Хватит ли 3 кг эмали, чтобы покрасить стену длиной 6 м и высотой 3 м?
584. Квадрат со стороной 12 см и прямоугольник, длина которого равна 18 см, являются равновеликими. Найдите периметр прямоугольника.
585. Квадрат и прямоугольник являются равновеликими, соседние стороны прямоугольника равны 3 см и 12 см. Найдите периметр квадрата.
586. Ширина прямоугольника равна 26 см. На сколько квадратных сантиметров увеличится площадь этого прямоугольника, если его длину увеличить на 4 см?
587. Во сколько раз увеличатся периметр и площадь прямоугольника, если каждую его сторону увеличить в 4 раза?
588. Длина прямоугольника равна 32 см. На сколько квадратных сантиметров уменьшится площадь этого прямоугольника, если его ширину уменьшить на 5 см?
589. Площадь квадрата ABCD равна 16 см? (рис. 151). Чему равна площадь прямоугольника ACFE?
590. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 12 см?. Сколько квадратов площадью 4 см? можно вырезать из этого прямоугольника?
591. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 18 см?. Сколько квадратов со стороной 3 см можно вырезать из этого листа?
592. Внутри прямоугольника ABCD (рис. 152) вырезали отверстие прямоугольной формы. Как одним прямолинейным разрезом разделить полученную фигуру на две фигуры с равными площадями?
593. Используя четыре из пяти изображённых на рисунке 153 фигур, составьте квадрат.
594. Можно ли разрезать квадрат на несколько частей так, чтобы потом из них можно было составить два квадрата, длины сторон которых выражаются целым числом сантиметров, если сторона данного квадрата равна:
Упражнения для повторения
595. Из вершины прямого угла ABC (рис. 154) провели лучи BD и BE так, что угол АВЕ оказался больше угла DBE на 34?, а угол CBD больше угла DBE на 23?. Какова градусная мера угла DBE?
596. Выполните действия:
Задача от мудрой совы
597. Расстояние между городами А и В равно 30 км. Из города А в город В выехал велосипедист и двигался со скоростью 15 км/ч. Одновременно из города В в направлении города А вылетела птица со скоростью 30 км/ч. Встретившись с велосипедистом, птица развернулась и полетела назад. Прилетев в город В, она снова развернулась и полетела навстречу велосипедисту. Встретившись с ним, птица развернулась и полетела назад в город В и т. д. Сколько километров пролетела птица за то время, пока велосипедист ехал из города А в город В?
