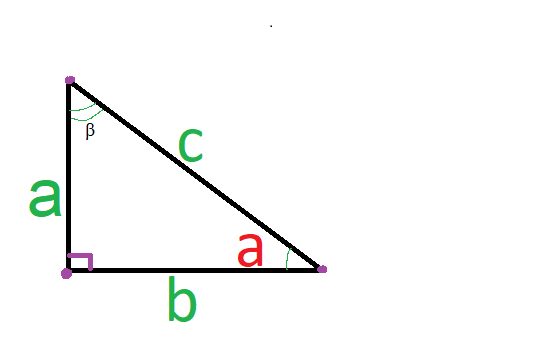Геометрическая мера как найти

Геометрическая теория меры занимается изученим геометрических свойств множеств (как правило, в евклидовом пространстве) с помощью теории меры.

История[править | править код]

Геометрическая теория меры родилась как подход к решению задачи Плато о существовании поверхности наименьшей площади при данной границе. 

 Основные понятия[править | править код]

• Спрямляемое множество
• Поток
• Формула коплощади
• Изопериметрическая задача

Примеры[править | править код]

• Неравенство Брунна — Минковского

Ссылки[править | править код]

• Федерер Г. Геометрическая теория меры. — 1987. — 760 с.

• Federer, Herbert & Fleming, Wendell H., Normal and integral currents, Annals of Mathematics, II Т. 72 (4): 458–520, DOI 10.2307/1970227. Первая работа Федерера и Флеминга, иллюстрирующая их подход к теории периметров (theory of perimeters), основанной на теории гомологических токов (theory of currents).

• Federer, H. (1978), Colloquium lectures on geometric measure theory, Bull. Amer. Math. Soc. Т. 84 (3): 291–338, doi:10.1090/S0002-9904-1978-14462-0, <http://www.ams.org/bull/1978-84-03/S0002-9904-1978-14462-0/>
• Fomenko, Anatoly T. (1990), Variational Principles in Topology (Multidimensional Minimal Surface Theory), Mathematics and its Applications (Book 42), Springer, Kluwer Academic Publishers, ISBN 978-0792302308
• Gardner, Richard J. (2002), The Brunn-Minkowski inequality, Bull. Amer. Math. Soc. (N.S.) Т. 39 (3): 355–405 (electronic), ISSN 0273-0979, doi:10.1090/S0273-0979-02-00941-2, <http://www.ams.org/bull/2002-39-03/S0273-0979-02-00941-2/>
• Mattila, Pertti (1999), Geometry of Sets and Measures in Euclidean Spaces, London: Cambridge University Press, с. 356, ISBN 978-0-521-65595-8
• Morgan, Frank (2009), Geometric measure theory: A beginner’s guide (Fourth ed.), San Diego, California: Academic Press Inc., с. viii+249, ISBN 978-0-12-374444-9
• Taylor, Jean E. (1976), The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces, Annals of Mathematics. Second Series Т. 103 (3): 489–539.
• O’Neil, T.C. (2001), «G/g130040» (недоступная ссылка), in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Определение
количества информации геометрическим
методом сводится к измерению длины
линии, площади или объема геометрической
модели данного информационного комплекса
в количестве дискретных единиц –
определенных выше квантов. Геометрическим
методом определяется потенциальное,т.е. максимально возможное количество
информации в заданных структурных
габаритах. Это количество будем называтьинформационной
емкостьюисследуемой части
информационной системы. Информационная
емкость вычисляется как сумма дискретных
значений по всем измерениям.

Информационная
емкость может быть представлена числом,
показывающим, какое количество квантов
содержится в полном массиве информации.

Геометрическую
меру можно применить не только для
оценки информационной емкости, но и для
оценки количества информации, содержащейся
в отдельном сообщении. Если о величине,
отображаемой сообщением, известно, что
она имеет максимальное значение из того
ряда значений, которые она уже принимала
ранее, то можно считать, что количество
информации, содержащееся как в этом,
так и в любых более ранних сообщениях,
определяется числом квантов, содержащихся
в максимальном значении.

Пусть
информация отражается полным комплексом
XTN.

Если
дискретные отсчеты осуществляются по
осям X,TиNсоответственно через интервалы_X,_Tи_N,
то непрерывные координаты распадаются
на элементы (кванты), количество которых
составляет:

m_X
= X/_X
; m_T =
T/_T
; m_N =
N/_N
. (3)

Тогда
количество информации, в квантах, в
полном комплексе XTN,
определенное геометрическим методом,
равно:

M=m_Xm_Tm_N.

Может
иметь место неравномерная (по осям) и
нестационарная (изменяющая свой характер
во времени) дискретизация. Тогда
количество информации определяется по
более сложным формулам, вытекающим из
переменных характеристик дискретизации.

2.1.2. Комбинаторная мера

К
комбинаторной мере целесообразно
прибегать тогда, когда требуется оценить
возможность передачи информации при
помощи различных комбинаций информационных
элементов. Образование комбинаций есть
одна из форм кодирования информации.

Количество
информации в комбинаторной мере
вычисляется как количество комбинаций
элементов. Таким образом, оценке
подвергается комбинаторное свойство
потенциального структурного разнообразия
информационных комплексов.

Комбинирование
возможно в комплексах с неодинаковыми
элементами, переменными связями или
разнообразными позициями. Элементы
неодинаковы, если они отличаются один
от другого любым признаком – размером,
формой, цветом и т.п.

Одинаковые
по всем своим признакам элементы могут
стать неодинаковыми, если учесть их
положение, позицию. Тогда местоположение
элементов оказывает влияние на целое
(позиционные системы счисления,
формирование образов). Примером проявления
влиятельности элементов может служить
перенос знаков в позиционной системе
представления двоичных чисел: 11110 и
01111 или 00001 и 10000. В первом случае меняет
положение нуль, во втором случае –
единица. В первом случае число меняется
с 30 на 15, во втором – единица превращается
в16.

Еще
более выразителен пример переноса точки
при образовании фигур и изображений,
когда одна безличная точка коренным
образом меняет изображение и его
смысловое содержание.

В
комбинаторике рассматриваются различные
виды соединения элементов.

Сочетания
изhэлементов поlразличаются составом элементов. Их
возможное число равно:

Сочетание
с повторениями также различается
составом элементов, но элементы в них
могут повторяться до lраз. Число различных сочетаний с
повторениями изhэлементов
поlравно:

Перестановкиhэлементов различаются
их порядком. Число возможных перестановокhэлементов

Соседние файлы в папке конспект ТИ

• #

  23.02.20151.26 Mб514.doc

• #
• #
• #

Среднее геометрическое значение чаще всего используется для усреднения темпов изменения во времени или для расчета скорости роста переменной.

В инвестициях мы часто используем среднее геометрическое для усреднения временного ряда ставок доходности актива или портфеля или для расчета темпов роста финансового показателя, такого как прибыль или выручка.

Например, в разделе, посвященному временной стоимости денег, мы вычислили темп роста продаж компании Hyundai Steel. Этот темп роста был средним геометрическим значением.

Из-за важности этой концепции в следующем разделе мы вернемся к использованию среднего геометрического и рассмотрим практические перспективы его использования. Среднее геометрическое определяется по следующей формуле.

Формула среднего геометрического.

Среднее геометрическое значение G (англ. ‘geometric mean’) множества наблюдений ( X_1, X_2, ldots, X_n ) равно:

Уравнение Формулы 5 имеет решение, и геометрическое среднее существует, только если произведение под знаком корня неотрицательно. Мы налагаем это ограничение таким образом, чтобы все наблюдения ( X_i ) в Формуле 5 были больше или равны нулю.

Мы можем найти геометрическое среднее, используя Формулу 5, напрямую, при помощи любого калькуляторс с клавишей возведения в степень (у большинства финансовых калькуляторов это клавиша ( y^x)).

---

Мы также можем найти среднее геометрическое, используя натуральные логарифмы.

Формулу 5 также можно представить в следующем виде:

(large dst
ln{G} = frac{1}{n} ln{(X_1 X_2 X_3dots X_n)}
)

или как

(large dst
ln{G} = {dsum_{i=1}^{n} ln{X_i} over n}
)

Если мы вычислили ( ln{G} ), то ( G=e^{ln{G}} ) (на большинстве калькуляторов клавишей для этого шага является (e^x)).

---

Рискованные активы могут иметь отрицательную доходность до -100% (если их цена падает до нуля), поэтому мы должны позаботиться об определении соответствующих переменных для усреднения при вычислении среднего геометрического.

Мы не можем просто рассчитать произведение ставок доходности выборки и затем взять (n)-ный корень, потому что доходность за любой период может быть отрицательной.

Мы должны пересмотреть результат расчета так, чтобы произведение ставок доходности под знаком корня было положительным. Мы делаем это, добавляя 1.0 к ставкам доходности, выраженным в десятичных числах.

Выражение ( 1 + R_t ) означает доход на конец года относительно начальной суммы инвестиций на начало года. Если мы используем выражение ( 1 + R_t ), наблюдения никогда не будут отрицательными, потому что отрицательный доход не может составлять менее -100% (т.е. менее -1).

Результатом будет среднее геометрическое ( 1 + R_t ); затем вычитая 1.0 из этого результата, мы получаем среднее геометрическое для отдельных ставок доходности ( R_t ).

---

Например, доходность Индексного фонда RBC за период 2008-2012 гг. из Таблицы 13 можно представить в десятичной форме как:

-0.331, 0.341, 0.168, -0.092, и 0.064.

Добавление 1.0 к этим ставкам дает:

0.669, 1.341, 1.168, 0.908 и 1.064.

Используя Формулу 5, мы получим:

( begin{align}
& sqrt[5]{(0.669)(1.341)(1.168)(0.908)(1.064)} = \
& sqrt[5]{51.012337} = 1.002455
end{align} )

Полученное число равно 1 плюс среднее геометрическое ставки доходности. Вычитая 1.0 из этого результата, мы получаем 1.002455 – 1.0 = 0.002455 или примерно 0.25%.

Среднегеометрическая доходность Канадского индексного фонда RBC за период 2008-2012 годов составила 0,25 процента.

---

Уравнение, которое суммирует вычисление среднего геометрического доходности (или геометрической ставки доходности), ( R_G ), является слегка измененной версией Формулы 5, в которой ( X_i ) представляет собой выражение: «1 + ставка доходности в десятичной форме».

Поскольку среднее геометрическое доходности использует временные ряды, мы используем подстрочный индекс (t) для обозначения временного периода.

( begin{align}
& 1+R_G = sqrt[T]{(1+R_1)(1+R_2)dots (1+R_T)} \
& 1+R_G = left[ prod_{t=1}^{T} (1+R_t) right]^frac{1}{T}
end{align} )

Это приводит к следующей формуле.

Формула среднегеометрической доходности.

Для данного временного ряда ставок доходности ( R_t, t = 1, 2, ldots, T ) среднегеометрическая доходность (или геометрическая ставка доходности, от англ. ‘geometric mean return’ или ‘time-weighted return’) за период времени, охватывающий ставки доходности от ( R_1 ) до ( R_T ), равна:

(large displaystyle
R_G = left[ prod_{t=1}^{T} (1+R_t) right]^frac{1}{T} ) (Формула 6)

Мы можем использовать Формулу 6 для расчета среднегеометрической доходности любого ряда ставок. Среднегеометрическая доходность также называется накапливаемой [сложной] доходностью (от англ. ‘compound return’).

Например, если усредненные результаты в Формуле 6 имеют месячную периодичность, мы можем назвать полученную ставку накапливаемой или сложной месячной доходностью.

Следующий пример иллюстрирует вычисление среднего геометрического, а также сравнение среднего геометрического и среднего арифметического.

Пример (1) расчета и сравнения среднегеометрической и среднеарифметической доходности.

Как аналитик взаимных фондов, вы изучаете совокупную доходность двух инвестиционных фондов за последние 5 лет, по состоянию на начало 2013 года.

Таблица 15. Совокупная доходность двух взаимных фондов, 2008-2012 гг.

Год	Фонд Selected American Shares (SLASX)	Фонд T. Rowe Price Equity Income (PRFDX)
2008	-39.44%	-35.75%
2009	31.64	25.62
2010	12.53	15.15
2011	-4.35	-0.72
2012	12.82	17.25

Источник: performance.morningstar.com.

Основываясь на данных из Таблицы 15, сделайте следующее:

1. Рассчитайте среднегеометрическую доходность SLASX.
2. Рассчитайте среднее арифметическое доходности SLASX и сопоставьте ее со среднегеометрической доходностью фонда.
3. Рассчитайте среднегеометрическую доходность PRFDX.
4. Рассчитайте среднее арифметическое доходности PRFDX и сопоставьте ее со среднегеометрической доходностью фонда.

---

Решение для части 1:

Сначала преобразуем ставки доходности SLASX в десятичную форму и добавим 1.0 к каждой ставке: 0,6056, 1,3164, 1,1253, 0,9565 и 1,1282.

Используем Формулу 6, чтобы найти среднегеометрическую доходность SLASX:

(begin{align}
R_G &= sqrt[5]{(0.6056)(1.3164)(1.1253)(0.9565)(1.1282)} – 1 \
&=  sqrt[5]{0.968084} – 1 = 0.993534 – 1 = -0.006466 \
&= -0.65% end{align} )

---

Решение для части 2:

Для SLASX,

(begin{align}
overline R &= (-39.44 + 31.64 + 12.53 – 4.35 +12.82) / 5 \
&= 13.20/5 = 2.64%
end{align} )

Среднее арифметическое доходности SLASX превышает среднегеометрическую доходность на 2.64 – (-0.65) = 3.29% или 329 базисных пунктов.

---

Решение для части 3:

Преобразовав ставки доходности PRFDX в десятичную форму и прибавив 1.0 к каждой из них, мы получим: 0.6425, 1.2562, 1.1515, 0.9928 и 1.1725.

Используем Формулу 6, чтобы найти среднее геометрическое значение доходности PRFDX:

(begin{align}
R_G &= sqrt[5]{(0.6425)(1.2562)1.1515)(0.9928)(1.1725)} – 1 \
&=  sqrt[5]{1.081859} – 1 = 1.015861 – 1 = 0.015861 = 1.59%
end{align} )

---

Решение для части 4:

Для PRFDX,

( begin{align}
overline R &= (-35.75 + 25.62 + 15.15 – 0.72 + 17.25)/5 \
&= 21.55/5 = 4.31%
end{align} )

Среднее арифметическое для PRFDX превышает среднегеометрическую доходность на 4.31 – 1.59 = 2.72% или 272 базисных пункта.

---

В таблице ниже обобщены полученные результаты.

Таблица 16. Итоги расчета среднеарифметической и среднегеометрической доходности для взаимных фондов.

Фонд	Среднее арифметическое (%)	Среднее геометрическое (%)
SLASX	2.64	-0.65
PRFDX	4.31	1.59

В приведенном примере для обоих взаимных фондов среднегеометрическая доходность была меньше среднеарифметической доходности. Фактически, геометрическое среднее всегда меньше или равно среднему арифметическому.

Неравенство Йенсена.

Это утверждение может быть доказано с помощью неравенства Йенсена (англ. ‘Jensen’s inequality’), которое означает, что среднее значение функции меньше или равно функции, вычисленной в среднем, если функция выпуклая вниз – в случае для ( ln {X}).

Единственный момент, когда два средних значения будут равны, – это когда нет изменчивости в наблюдениях, то есть, когда все наблюдения совокупности одинаковы.

Например, предположим, что доходность за каждый год в течение 3-х лет составляет 10%. Среднее арифметическое составляет 10%. Чтобы найти среднее геометрическое, мы сначала выражаем результаты как ( 1 + R_t ), а затем находим среднее геометрическое:

( bigl[(1.10)(1.10)(1.10)bigr]^{1/3} – 1.0 = 10% ).

Два средних значения одинаковы.

В приведенном выше примере наблюдалась изменчивость в доходности фондов; таким образом, для обоих фондов среднее геометрическое должно быть непременно меньше среднего арифметического.

В целом, разница между арифметическим и геометрическим средним возрастает вместе с изменчивостью наблюдений от периода к периоду.

В следующих разделах мы рассмотрим стандартное отклонение как меру изменчивости. При постоянной средней арифметической доходности средняя геометрическая доходность уменьшается на размер увеличения стандартного отклонения.

---

Эта взаимосвязь также иллюстрируется в рассмотренном выше примере. Случайная проверка показывает, что доходность SLASX несколько более изменчива, чем доходность PRFDX, и, следовательно, разброс между средней арифметической и геометрической доходностью больше для SLASX (329 базисных пунктов), чем для PRFDX (272 базисных пункта).

Мы введем формальные меры изменчивости позже. Но обратите внимание, например, на 71.08% в доходности между 2008 и 2009 годами для SLASX против 61.37% для PRFDX. Аналогичным образом, обратите внимание на колебание процентной ставки в 19.11% в период между 2009 и 2010 годами для SLASX против 10.47% для PRFDX.

Значения средней арифметической и среднегеометрической доходности не всегда должны ранжировать фонды одинаково, однако в этом примере PRFDX имеет как более высокую арифметическую, так и более высокую среднюю геометрическую доходность, чем SLASX.

Однако разница между средней геометрической доходностью двух фондов (2.24%) больше, чем разница между средней арифметической доходностью (1.67%).

Как финансовый аналитик должен интерпретировать эти результаты?

Среднегеометрическая доходность представляет собой темп роста или сложную норму прибыли от инвестиций. Один доллар, вложенный в SLASX в начале 2008 года, вырос бы (или, в данном случае, снизился бы) до (0.6056)(1.3164)(1.1253)(0.9565)(1.1282) = $0.9681, что равно 1 плюс средняя геометрическая доходность, начисленная по сложной ставке процента в течение 5 периодов:

( bigl[1 + (-0.006466)bigr]^5 = (0.993534)^5 = $0.9681 )

Это подтверждает, что среднее геометрическое является сложной процентной ставкой доходности.

Для PRFDX один доллар вырос бы до большей суммы (0.6425)(1.2562)(1.1515)(0.9928)(1.1725) = $1.0819, что равно (1.015861)⁵.

Приведенный ниже пример подчеркивает эти моменты в простом контексте.

Пример (2) средней геометрической и арифметической доходности.

Гипотетическая инвестиция в 1 акцию изначально составляет €100. Год спустя акции торгуются на уровне €200. В конце второго года цена акций опускается до первоначальной цены покупки в €100. В течение 2-летнего периода дивиденды не выплачиваются.

Рассчитайте арифметическую и геометрическую среднегодовую доходность.

---

Решение:

Во-первых, нам нужно найти годовую доходность за год 1 и год 2 по Формуле 1.

Доходность за год 1 = 200/100 – 1 = 100%
Доходность за год 2 = 100/200 – 1 = -50%

Среднее арифметическое годовой доходности составляет:

(100% – 50%)/2 = 25%

Прежде чем мы найдем среднее геометрическое, мы должны преобразовать процентные ставки доходности в ( 1 + R_t ). После этой корректировки среднее геометрическое по Формуле 6 составляет:

( sqrt{2.0 times 0.50} -1 = 0% )

Средняя геометрическая доходность 0% точно отражает то, что конечная стоимость инвестиций в год 2 равна начальной стоимости в год 1. Сложная норма прибыли на инвестиции составляет 0%. Средняя арифметическая доходность отражает среднее значение за 1 год.

Была ли эта статья полезной?

При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:

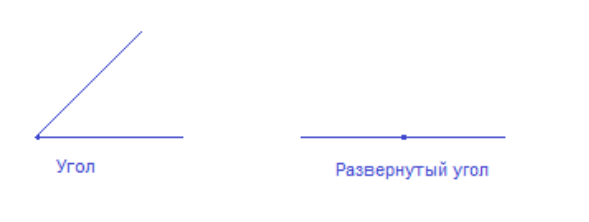
• Угол.
• Развернутый угол, неразвернутый угол.
• Градус, секунда и минута.
• Градусная мера.
• Острый, прямой или тупой.

Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.

Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.

Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.

Чему равна градусная мера угла

Транспортир используется следующим образом:

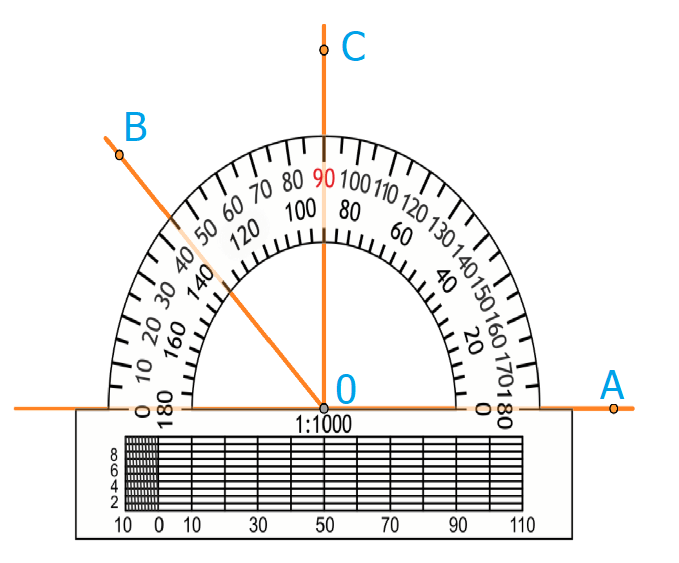
• Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
• Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.

Как найти градусную меру угла

На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.

Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].

Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.

• Минута – 1/60 часть градуса. Обозначается знаком ‘
• Секунда – 1/60 часть минуты. Обозначают знаком»

Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.

Градусная мера вписанного угла

Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.

Вписанный угол равняется половине градусной меры дуги, на которую он опирается.

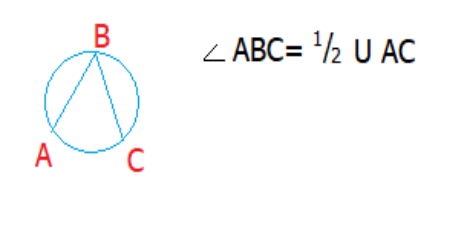
АВ-хорда

ВС-хорда

В-точка окружности.

Углы также различаются несколькими типами:

• Прямыми
• Острыми
• Тупыми

---

Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.

Существует еще такое понятие, как, биссектриса.

Пример 1. Задача с биссектрисой и развернутым углом.

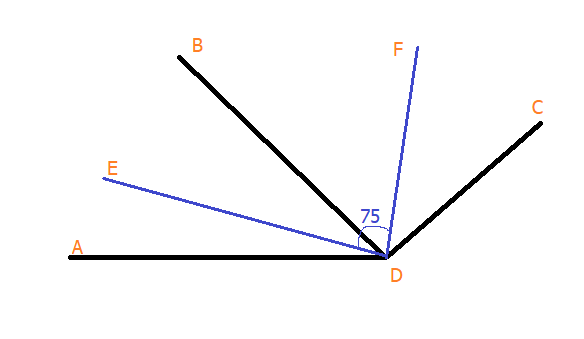
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.

Теперь нужно найти угол ADC, при этом угол EDF = 75°

Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.

Ответ: 150°

---

Пример 2. Задача с биссектрисой и прямым углом.

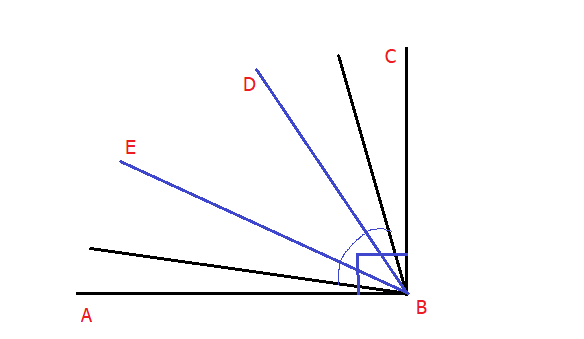
Рисунок 4.  По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.

Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.

Решение: 60°

Градусная мера углов треугольника

У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.

Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:

[angle a=90^{circ}-angle beta]

У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.

Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.

Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример —  рисунок 5.