Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Геометрические величины
Длина отрезка.
Расстояние между двумя точками. Расстояние
от точки до прямой. Расстояние между
параллельными прямыми.
Длина ломаной.
Периметр многоугольника.
Длина окружности
и ее дуги.
Площадь круга и
его сектора.
Измерения центральных
и вписанных углов.
Площадь фигуры.
Площадь треугольника, параллелограмма,
прямоугольника, ромба, квадрата,
трапеции.
Расстояние от
точки до плоскости. Расстояние между
параллельными прямыми. Расстояние между
параллельными прямой и плоскостью.
Расстояние между параллельными
плоскостями.
Угол между прямыми.
Угол между прямой и плоскостью. Мера
двугранного угла. Угол между
плоскостями.
Площади боковой
и полной поверхностей призмы.
Площади боковой
и полной поверхностей пирамиды.
Объем тела. Объем
призмы. Объем пирамиды.
Площадь сферы.
Площади боковой
и полной поверхностей цилиндра.
Площади боковой
и полной поверхностей конуса.
Объем цилиндра.
Объем конуса. Объем шара.
Геометрические построения
Построение прямого
угла с помощью угольника.
Построение угла
с данной градусной мерой с помощью
транспортира.
Круговые диаграммы.
Построение с
помощью циркуля и линейки серединного
перпендикуляра к отрезку; угла,
равного данному; биссектрисы угла.
Деление отрезка
на пропорциональные части.
Построение
правильного треугольника, четырехугольника
и шестиугольника.
Сечения многогранников
плоскостями.
II. Требования к подготовке абитуриентов Числа и вычисления
Уметь проводить
вычисления, обеспечивающие практические
потребности: складывать, вычитать,
умножать, делить действительные числа;
находить значения степени числа с
натуральным и целым показателем;
выполнять действия над числами,
записанными в стандартном виде.
Уметь определять
порядок выполнения действий в числовых
выражениях и находить их значение;
находить значение выражения с переменными
при данных значениях переменных;
сравнивать значения выражений.
Уметь представлять
бесконечную десятичную периодическую
дробь обыкновенной дробью.
Уметь округлять
числа и результаты вычислений с заданной
точностью.
Уметь контролировать
вычисления оценкой результата на
правдоподобие, прикидкой, повторным
вычислением, решением одной из обратных
задач.
Знать основные
числовые множества и их обозначения;
знать, как обозначаются числовые
промежутки, и уметь пользоваться этими
обозначениями при решении задач.
Выражения и их преобразования
Уметь находить
область определения выражения с
переменной.
Уметь выполнять
тождественные преобразования рациональных,
иррациональных, степенных, показательных,
логарифмических и тригонометрических
выражений.
Уравнения и неравенства
Знать и правильно
использовать термины: уравнения;
равносильные неравенства; следствие
уравнения; следствие неравенства.
Уметь решать
линейные, квадратные уравнения и
простейшие рациональные уравнения,
сводящиеся к ним.
Уметь решать
иррациональные уравнения и уравнения,
сводящиеся к ним.
Уметь решать
системы уравнений с одной переменной
первой и второй степени, уравнения и
системы, сводящиеся к ним.
Уметь решать
системы уравнений с двумя переменными
(системы линейных уравнений и системы,
в которых одно уравнение линейное, а
второе — квадратное).
Уметь решать
неравенства, системы неравенств первой
и второй степени с одной переменной,
неравенства и системы, сводящиеся к
ним.
Уметь решать
простейшие тригонометрические уравнения
и уравнения, сводящиеся к ним.
Уметь решать
показательные, логарифмические уравнения
и уравнения, сводящиеся к ним.
Уметь решать
рациональные, показательные, логарифмические
неравенства и неравенства, сводящиеся
к ним.
Уметь решать
уравнения и неравенства, которые содержат
переменную под знаком модуля.
Понимать графическую
интерпретацию решения уравнений и
систем уравнений, неравенств.
Уметь решать
текстовые задачи с помощью уравнений,
неравенств и их систем.
Координаты
и функции
Уметь строить
графики элементарных функций.
Уметь использовать
свойства функций для решения задач.
Знать особенности
графиков четной, нечетной, периодической
функций.
Уметь использовать
геометрические представления для
решения и исследования уравнений,
неравенств, систем.
Геометрические
фигуры и их свойства
Уметь применять
свойства плоских фигур и основные
отношения планиметрии.
Уметь применять
свойства пространственных фигур и
основные отношения стереометрии.
Уметь применять
различные методы для решения геометрических
задач.
Уметь решать задачи
на доказательство и на вычисления.
Уметь решать задачи
на комбинации призм и пирамид, призм и
пирамид с телами вращения.
Геометрические
величины
Уметь вычислять
значения геометрических величин.
Уметь находить
расстояние от точки до плоскости,
расстояние между параллельными прямыми,
расстояние между параллельными прямой
и плоскостью, расстояние между
параллельными плоскостями.
Уметь находить
угол между прямыми, угол между прямой
и плоскостью, угол между плоскостями.
Геометрические
построения
Уметь решать
основные задачи на построение с помощью
циркуля и линейки.
Уметь изображать
геометрические фигуры.
Уметь строить
сечения пространственных геометрических
фигур плоскостью.
Образовательный портал www.adu.by
/ Национальный институт образования
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.
Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым – разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция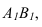
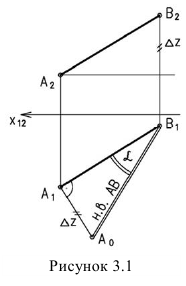
Если необходимо определить угол наклона отрезка АВ к плоскости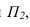 то построение прямоугольного треугольника ведется на фронтальной проекции.
то построение прямоугольного треугольника ведется на фронтальной проекции.
Решение метрических задач методами преобразовании проекций
Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций
Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.
Приведем некоторые из них.
1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).
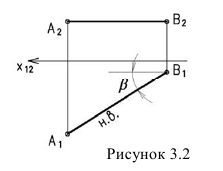
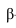 – угол наклона к плоскости
– угол наклона к плоскости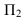
2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).
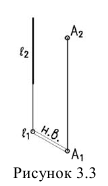
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).
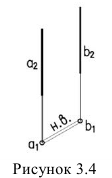
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).
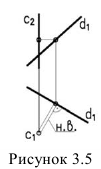
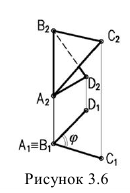
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7) 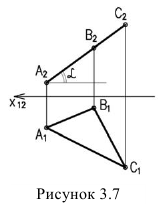
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)
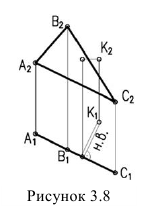
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)
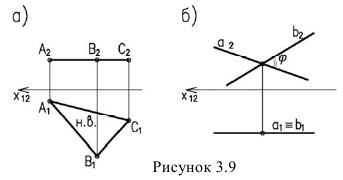
Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.
Для такого перехода и служат способы преобразования проекций.
Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.
Четыре основных задачи преобразовании проекций
Этими способами решаются четыре основные задачи:
- Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
- Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
- Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
- Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)
Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций
Способ вращения
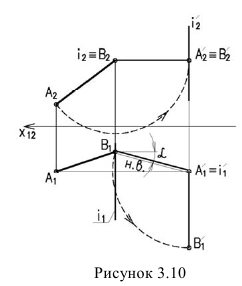
Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая – но прямой параллельной оси проекций.
На рисунке 3.10 вокруг оси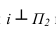 вращаем отрезок ЛВ до положения параллельного плоскости
вращаем отрезок ЛВ до положения параллельного плоскости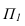 (1 задача). Далее вращением вокруг оси
(1 задача). Далее вращением вокруг оси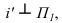 полученный отрезок до положения перпендикулярного плоскости
полученный отрезок до положения перпендикулярного плоскости 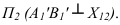 На
На 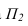 отрезок с проецируется в точку
отрезок с проецируется в точку 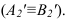
Способ плоскопараллельного перемещения
Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом 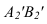 должно быть равно по величина
должно быть равно по величина 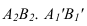 находим в пересечении вертикальных линий связи и линий
находим в пересечении вертикальных линий связи и линий 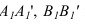 параллельных оси
параллельных оси 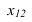 (1 задача). Далее отрезок
(1 задача). Далее отрезок 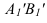 перемещаем до положения перпендикулярного оси
перемещаем до положения перпендикулярного оси 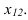 При этом
При этом 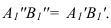 На фронтальной проекции отрезок с проецируется в точку
На фронтальной проекции отрезок с проецируется в точку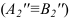 (2 задача).
(2 задача).
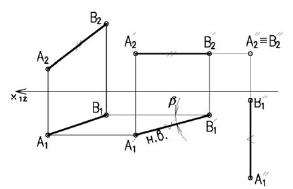
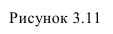
Способ замены плоскостей проекций
Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.
На рисунке 3.12 произведена первая замена плоскость 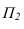 заменена на новую фронтальную плоскость
заменена на новую фронтальную плоскость 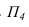 параллельную прямой АВ. При этом новая ось
параллельную прямой АВ. При этом новая ось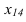 проводится параллельно проекции
проводится параллельно проекции 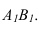 Линии связи проводятся перпендикулярно оси
Линии связи проводятся перпендикулярно оси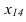 и на них от
и на них от 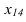 откладываются координаты z точек А и В (1 задача).
откладываются координаты z точек А и В (1 задача).
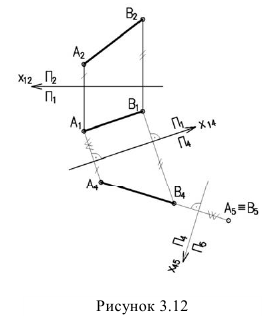
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось 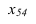 перпендикулярно проекции
перпендикулярно проекции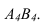 . Т.к.
. Т.к. 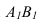 параллельна оси
параллельна оси 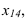 , расстояние до проекций
, расстояние до проекций 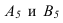 будет одинаковое и прямая спроецируется в точку
будет одинаковое и прямая спроецируется в точку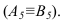 (2 задача)
(2 задача)
Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций
Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.
Способ плоскопараллельного перемещения
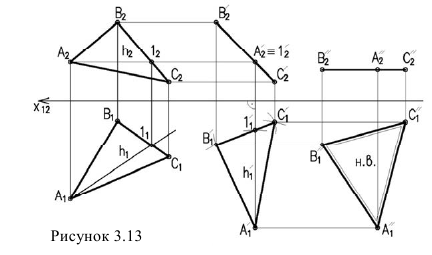
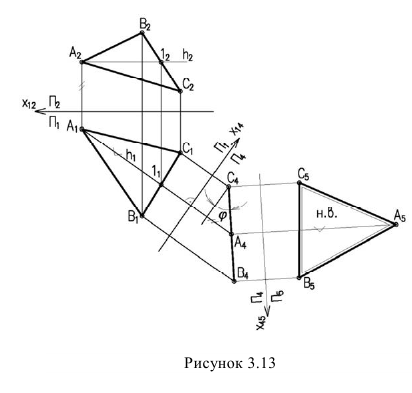
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь 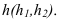 Далее
Далее 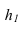 располагаем перпендикулярно оси
располагаем перпендикулярно оси 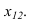 Откладываем на ней отрезок
Откладываем на ней отрезок 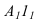 и циркулем строим треугольник
и циркулем строим треугольник 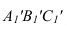 равный по величине
равный по величине 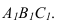 На фронтальной проекции треугольник проецируется в линию (3 задача).
На фронтальной проекции треугольник проецируется в линию (3 задача).
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию 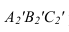 расположить параллельно оси
расположить параллельно оси 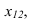 при этом на горизонтальной проекции треугольник проецируется в натуральную величину (4-я задача)
при этом на горизонтальной проекции треугольник проецируется в натуральную величину (4-я задача)
Способ замены плоскостей проекций
При решении задачи методом замены (рисунок 3.14) новую ось 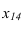 проводим перпендикулярно горизонтали
проводим перпендикулярно горизонтали 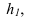 тогда на новую фронтальную плоскость
тогда на новую фронтальную плоскость 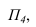 треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось
треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось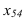 провести параллельно плоскости
провести параллельно плоскости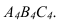 На новую плоскость
На новую плоскость 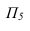 треугольник спроецируется в натуральную величину.
треугольник спроецируется в натуральную величину.
Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.
Метрические задачи
Метрические задачи – это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.
Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.
Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:
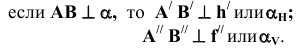
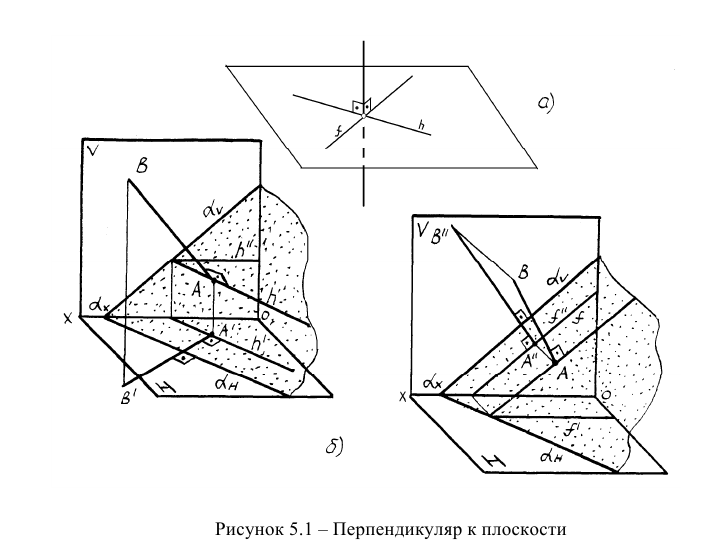
Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой – обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.
На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.
Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) – через точку К проведена плоскость перпендикулярно прямой АВ. 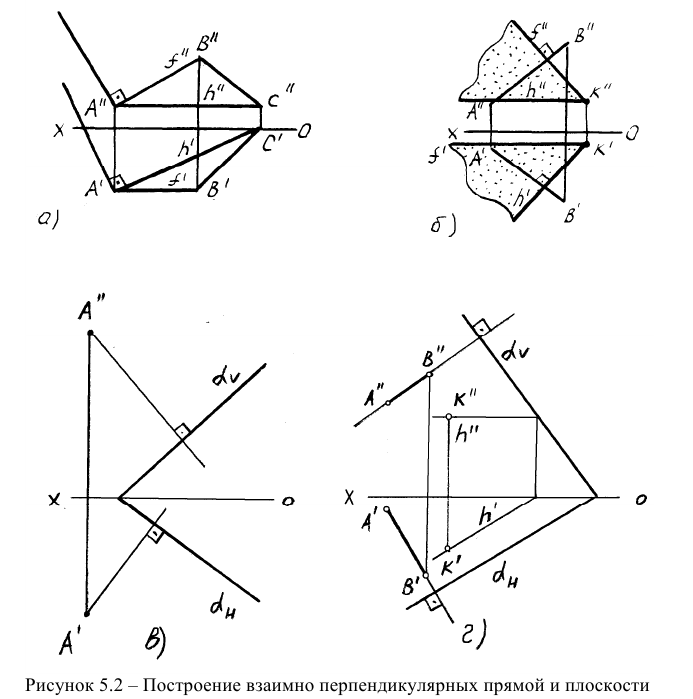
Определение расстояний между геометрическими объектами
Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.
Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:
- Из точки опустить перпендикуляр на заданную плоскость;
- Найти точку встречи перпендикуляра с плоскостью;
- Определить НВ расстояния между заданной и найденной точками.
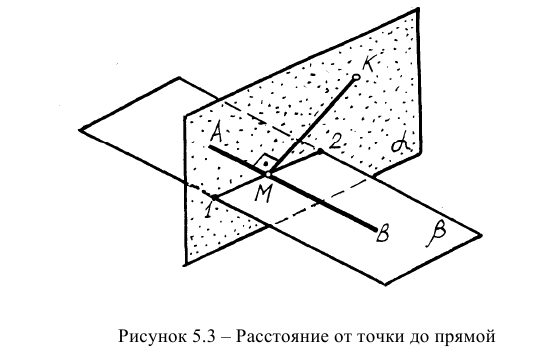
Задача на определение расстояния от точки до прямой решается по следующему плану:
- Через точку к провести плоскость, перпендикулярную заданной прямой;
- Найти точку встречи М заданной прямой с проведенной плоскостью;
- Соединить полученные точки (это будет перпендикуляр из точки на прямую);
- Определить НВ перпендикуляра.
Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.
Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.
Перпендикулярность плоскостей
Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.
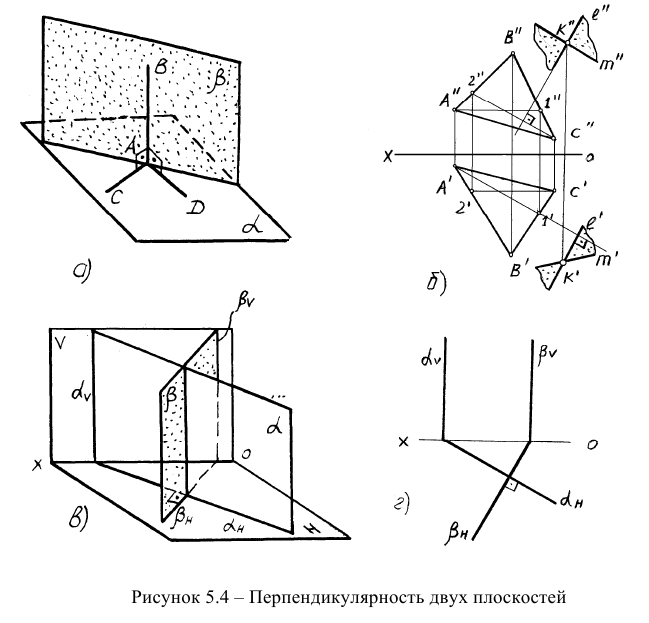
Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).
Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.
Определение углов между прямой и плоскостью и между двумя плоскостями
Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:
- Определить точку встречи прямой АВ с плоскостью а;
- Из точки В построить перпендикуляр на плоскость;
- Найти точку встречи перпендикуляра с плоскостью;
- Точки К и N соединить и определить НВ угла BKN.
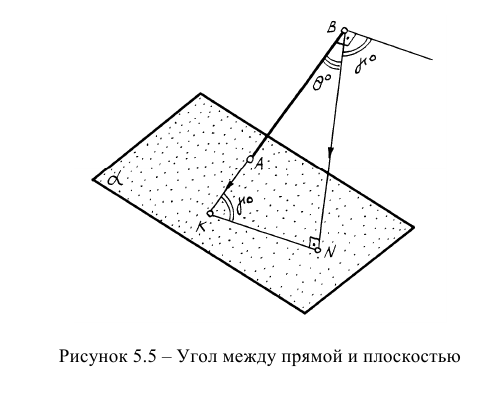
Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через 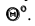 Из приведенного рисунка видно, что, если из точки В прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла
Из приведенного рисунка видно, что, если из точки В прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла 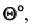 то искомый угол определится по формуле:
то искомый угол определится по формуле:
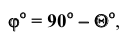
которую можно решить графически, достроив угол  до 90°.
до 90°.
То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.
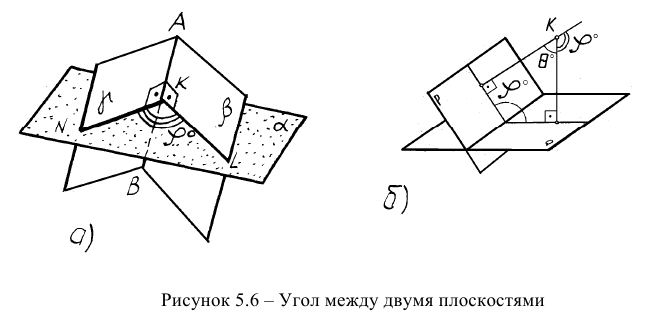
С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол 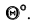 Далее определяют НВ дополнительного угла и дополняют его (графически) до 180 градусов, исходя из формулы:
Далее определяют НВ дополнительного угла и дополняют его (графически) до 180 градусов, исходя из формулы:
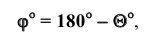
Дополненный угол будет искомым.
Натуральную величину дополнительного угла в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.
в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.
Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.
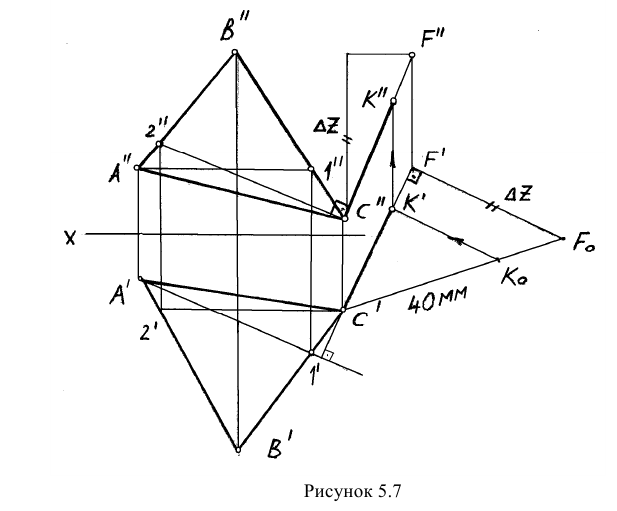
Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).
Пример: Найти расстояние от точки А до плоскости, заданной следами
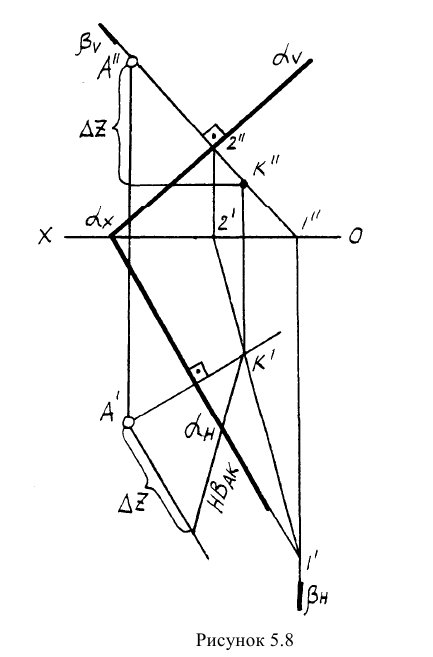
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости 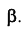 Находим линию пересечения плоскостей
Находим линию пересечения плоскостей 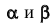 (линия 1-2) и точку встречи
(линия 1-2) и точку встречи 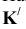 в месте пересечения горизонтальной проекции перпендикуляра с линией 1-2. Методом прямоугольного треугольника определяем НВ расстояния АК (рисунок 5.8).
в месте пересечения горизонтальной проекции перпендикуляра с линией 1-2. Методом прямоугольного треугольника определяем НВ расстояния АК (рисунок 5.8).
Пример: Определить расстояние от точки К до прямой AВ.
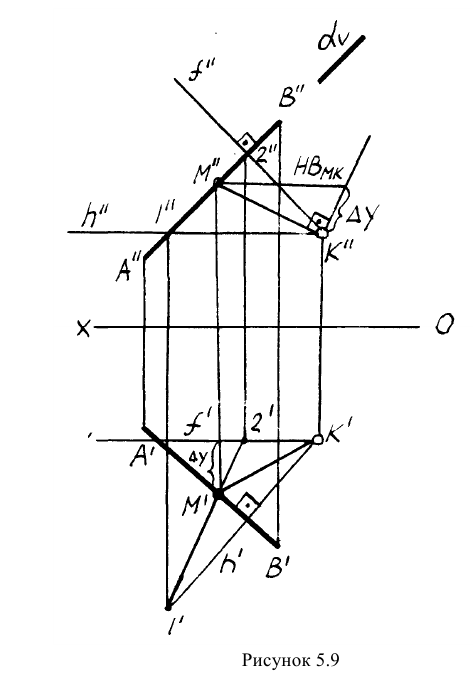
Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).
Примеры метрических задач
Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.
Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.
Теорема о проекциях прямого угла
Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).
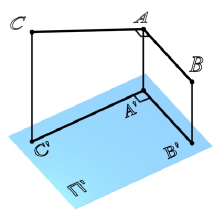
Рис. 10.1. Теорема о проекциях прямого угла
Дано : BAC = 90°; AB || П’
BAC = 90°; AB || П’
Доказать, что C’A’ A’B’
A’B’
Доказательство: если AB||П’, то A’B’||AB, но AA’ П’^AA’
П’^AA’ A’B’ значит AB
A’B’ значит AB AA,AB
AA,AB  плоскости CAA’C’, тогда и A’B’
плоскости CAA’C’, тогда и A’B’ CAA’C’. Следовательно,CA’
CAA’C’. Следовательно,CA’ A’B’.
A’B’.
На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П1 в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П2 – если одна из них фронталь (рис. 10.2,а).
Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.
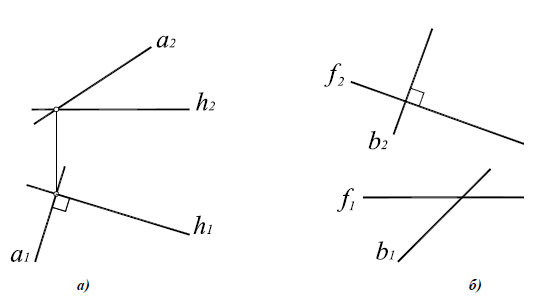
Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a1  h1
h1 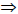 a
a  h ;
h ;
б -скрещивающиеся b2 
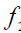 2
2 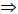 b
b 

Линии наибольшего наклона плоскости
Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали – линией наибольшего наклона к фронтальной плоскости проекций.
Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).
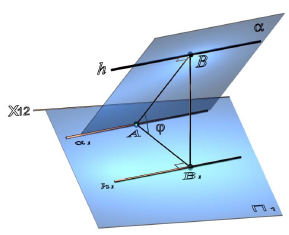
Рис. 10.3. Линия наибольшего наклона плоскости а к П1:
а – плоскость общего положения; h ∈α – горизонталь плоскости а; AB  h – линия наибольшего наклона;
h – линия наибольшего наклона;
φ = 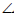 AB, AB 1 – угол наклона плоскости а к П1
AB, AB 1 – угол наклона плоскости а к П1
Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.
Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня – горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h× ), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция – фронтальной проекции фронтали плоскости.
), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция – фронтальной проекции фронтали плоскости.
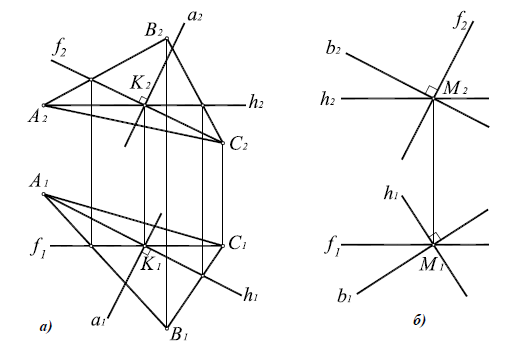
Рис. 10.4. Перпендикулярность прямой и плоскости:
а -построение прямой, перпендикулярной плоскости: 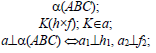
б -построение плоскости, перпендикулярной прямой: 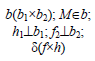
Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)
Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.
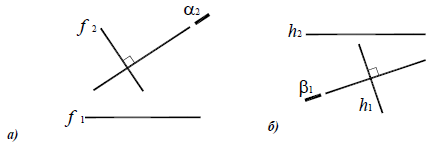
Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой
Взаимная перпендикулярность плоскостей
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a( × h) (рис. 10.6), достаточно построить прямую n,перпендикулярную плоскости α(
× h) (рис. 10.6), достаточно построить прямую n,перпендикулярную плоскости α( ×h): n1
×h): n1 h1; n2
h1; n2
 2. Вторая прямая m, определяющая искомую плоскость, может быть задана произвольно – как пересекающая прямую n или параллельная ей.
2. Вторая прямая m, определяющая искомую плоскость, может быть задана произвольно – как пересекающая прямую n или параллельная ей.
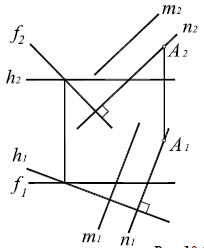
Рис. 10.6. Перпендикулярность двух плоскостей
Дано: α(h ×  ) ; A (A1, A2).
) ; A (A1, A2).
Построить: A ∈ β  α .
α .
Решение:
A ∈ n;
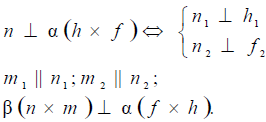
Определение метрических задач
Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.
Определение длины отрезка
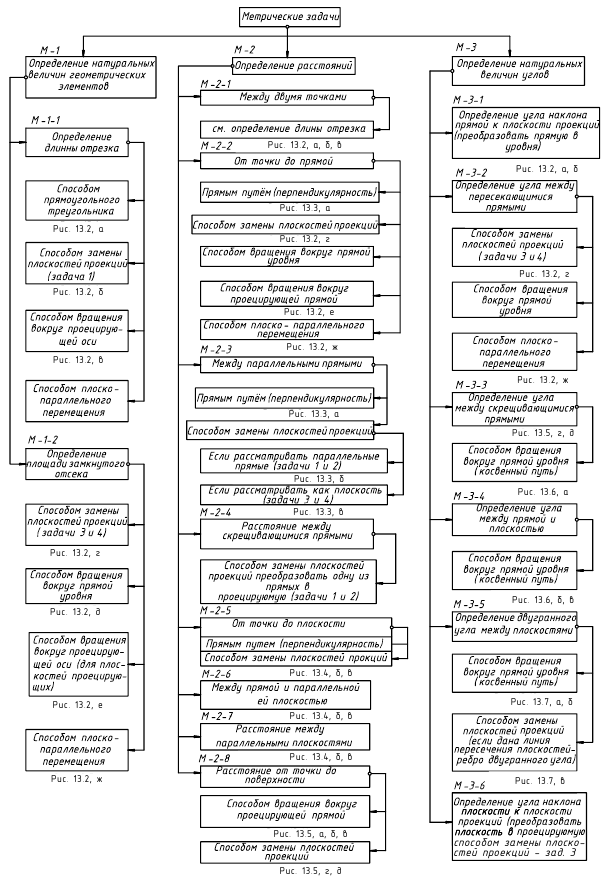
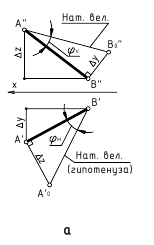
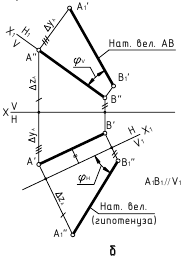
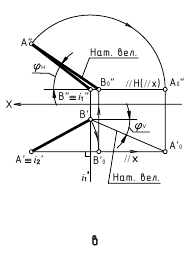
Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).
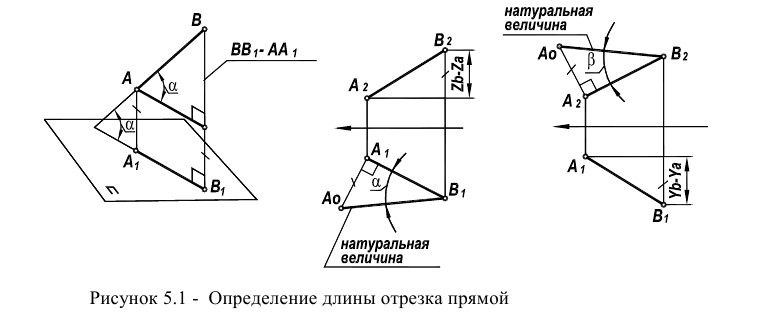
Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции 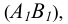 а второй катет -разница координат
а второй катет -разница координат 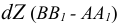 концов отрезка для оси, отсутствующей в рассматриваемой плоскости проекции (ортогональное дополнение). Угол между проекцией и гипотенузой этого треугольника (а) определяет наклон прямой к соответствующей плоскости проекции.
концов отрезка для оси, отсутствующей в рассматриваемой плоскости проекции (ортогональное дополнение). Угол между проекцией и гипотенузой этого треугольника (а) определяет наклон прямой к соответствующей плоскости проекции.
На комплексном чертеже возможно решение как на плоскости 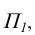 так и на плоскости
так и на плоскости 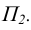 При правильных построениях
При правильных построениях 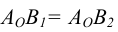 . Углы а и
. Углы а и 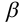 -углы наклона отрезка прямой АВ к плоскости
-углы наклона отрезка прямой АВ к плоскости 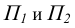 соответственно.
соответственно.
Определение площади треугольника
Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.
Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон 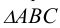 (в соответствии с рисунком 5.2), а затем на свободном месте построить треугольник по трем сторонам.
(в соответствии с рисунком 5.2), а затем на свободном месте построить треугольник по трем сторонам.
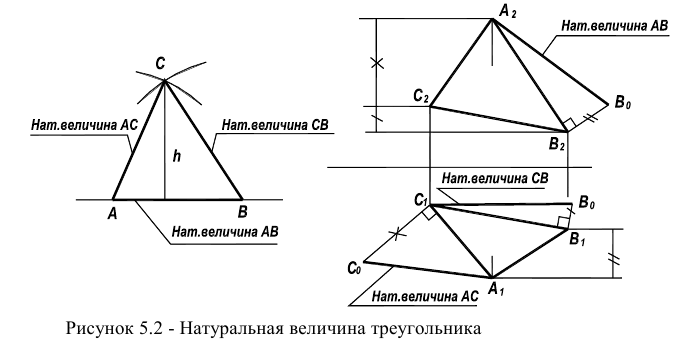
Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.
Проецирование прямого угла
Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.
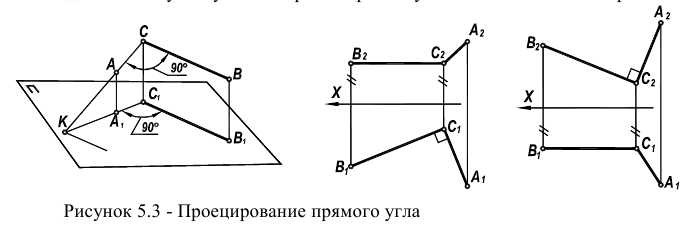
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на
соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая – ей не перпендикулярна.
- Заказать чертежи
Перпендикулярность прямых и плоскостей
Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.
Перпендикулярность прямой и плоскости
Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.
При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).
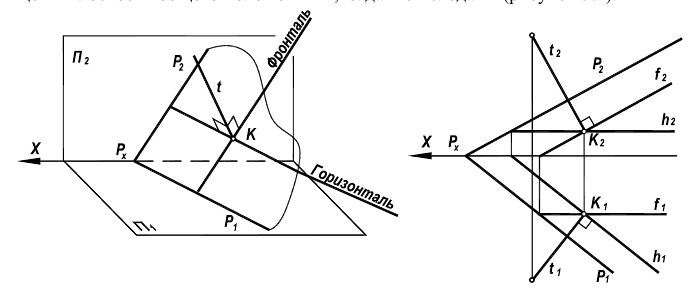
Рисунок 5.4 – Перпендикулярность прямой и плоскости
В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня 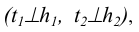 в соответствии с теоремой о проецировании прямого угла и данным выше определением, могут быть приняты за проекции прямой
в соответствии с теоремой о проецировании прямого угла и данным выше определением, могут быть приняты за проекции прямой 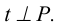 .
.
В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).
Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:
а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости 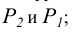
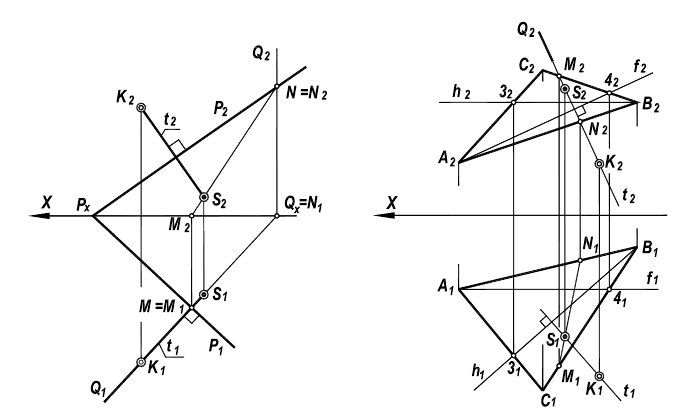
Рисунок 5.5 – Перпендикуляр к плоскости
б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые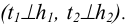 – Линия t принимается за перпендикуляр, опущенный из точки К к плоскости Р;
– Линия t принимается за перпендикуляр, опущенный из точки К к плоскости Р;
в) определяется точка S пересечения этого перпендикуляра t и плоскости.
Расстояние от точки до плоскости
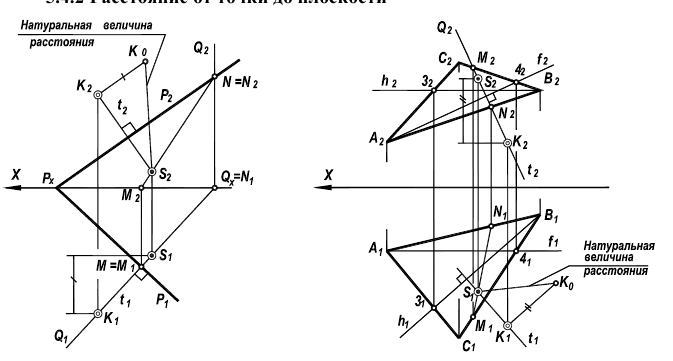
Рисунок 5.6 – Расстояние от точки до плоскости
Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)
Перпендикулярность плоскостей
Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.
Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.
При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).
Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии 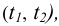 перпендикулярные соответствующим проекциям линий уровня (следам), определят перпендикуляр t к плоскости Р.
перпендикулярные соответствующим проекциям линий уровня (следам), определят перпендикуляр t к плоскости Р.
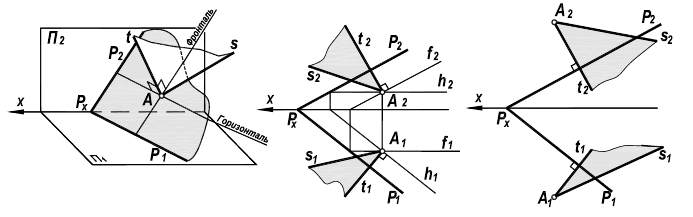
Рисунок 5.7 – Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.
Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.
Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).
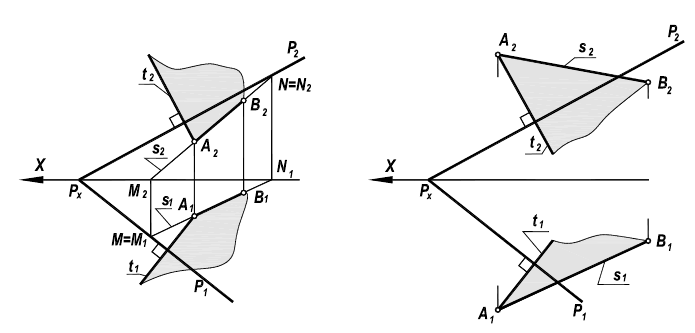
Рисунок 5.8 – Перпендикулярность плоскостей
Определение натуральных величин геометрических элементов
1. Определить натуральную величину отрезка общего положения:
- способом прямоугольного треугольника;
- способом замены плоскостей проекций преобразовать в прямую уровня;
- способом вращения вокруг проецирующей оси преобразовать в прямую уровня.
2. Определить натуральную величину плоскости общего положения (замкнутого отсека):
- способом замены плоскостей проекций преобразовать в плоскость уровня;
- способом вращения вокруг линии уровня преобразовать в плоскость уровня;
- способом плоскопараллельного перемещения преобразовать в плоскость уровня.
Определение расстояния между геометрическими элементами (образами)
1. Определить расстояние от точки до прямой общего положения:
- способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
- способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
- способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
- способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
- способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.
2. Определить расстояние между параллельными прямыми:
- способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
- способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
- способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
- способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
- способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.
3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).
4. Определить расстояние от точки до плоскости:
- по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
- способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.
5. Определить расстояние от точки до поверхности вращения:
- способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
- способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.
Определение углов наклона геометрических элементов к плоскостям проекций H и V
1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:
- способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
- способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
- способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.
2. Определить угол наклона прямой к заданной плоскости общего положения:
- из любой точки прямой опустить перпендикуляр к плоскости;
- способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
- искомый угол будет дополнять построенный угол до 90°.
3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):
- способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).
4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):
- задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
- эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
- искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).
Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).
Метрические задачи:
Определение натуральной величины геометрических элементов:
1. Определение длины отрезка
Способ прямоугольного треугольника
Способ замены плоскостей проекций (задача 1)
Способ вращения вокруг проецирующей оси
2. Определение площади замкнутого отсека
Способ замены плоскостей проекций (задачи 3 и 4)
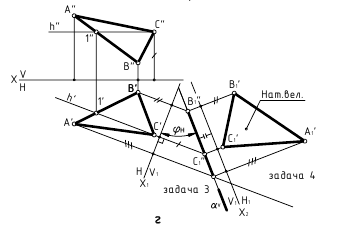
Способ вращения вокруг прямой уровня (горизонтали)
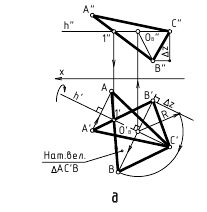
Способ вращения вокруг проецирующей оси i(i  V)
V)
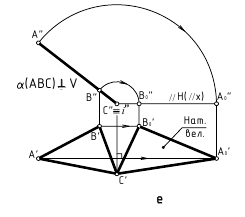
Способ плоско-параллельного перемещения (переноса)
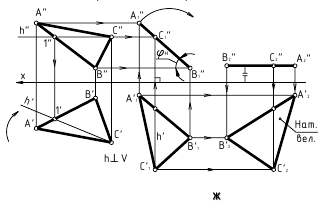
Определение расстояний:
1. Расстояние между точками – определяется величиной отрезка, соединяющего эти точки
См. рис. 13.2, а, б, в
2. Расстояние от точки до прямой – определяется величиной перпендикуляра, опущенного из точки к прямой
а. Прямой путь (перпендикулярность)
б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)
в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)
г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)
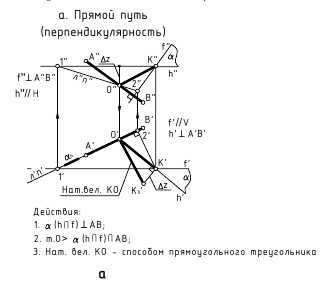
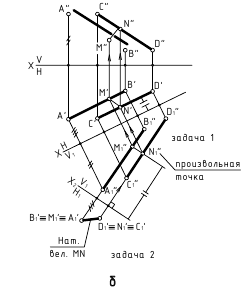
3. Расстояние между параллельными прямыми – определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой
а. Способ замены плоскостей проекции (рассматриваем две прямые) – задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)
б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) – задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))
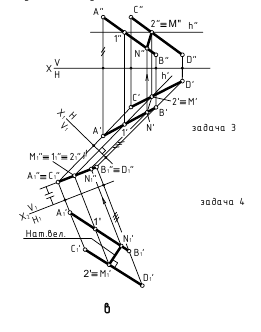
4. Расстояние между скрещивающимися прямыми – определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).
Способ замены плоскостей проекций – задачи 1 и 2
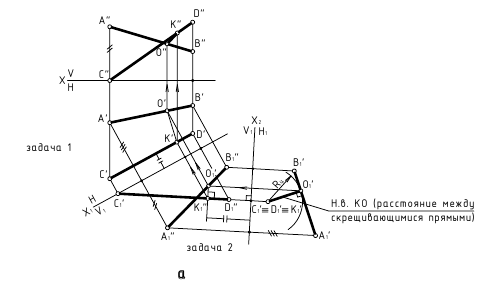
5. Расстояние от точки до плоскости – определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.
а. Прямой путь (перпендикулярность)
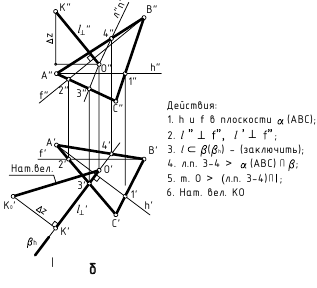
б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую – задача 3)
6. Расстояние между прямой и параллельной ей плоскостью – определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.
См. рис. 13.4, б, в
7. Расстояние между параллельными плоскостями – определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).
См. рис. 13.4, б, в
8. Расстояние от точки до поверхности
a. Cпособ вращения вокруг проецирующей оси
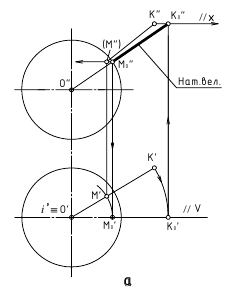
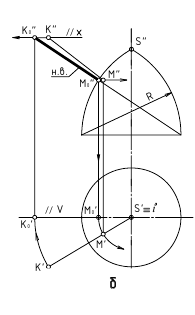
б. Способ замены плоскостей проекции
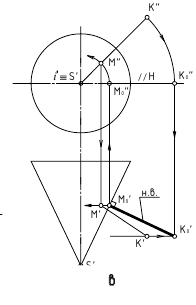
Определение величин углов:
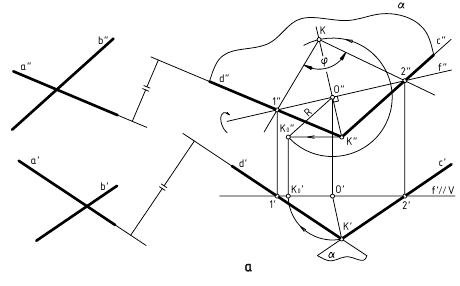
1. Угол φ между скрещивающимися прямыми – определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)
Способ вращения вокруг линии уровня
Дано:
а и b – скрещивающиеся прямые
Требуется:
∠φ – ?
Решение:
1. 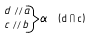
2. ∠φ – вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)
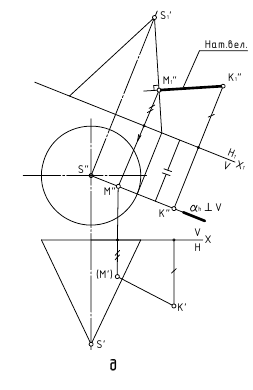
2. Угол φ между прямой и плоскостью – определяется углом между прямой и её проекцией на эту плоскость.
Дано:
α(h ∩ f);
AB – прямая общего положения
Требуется:
∠φ – ?
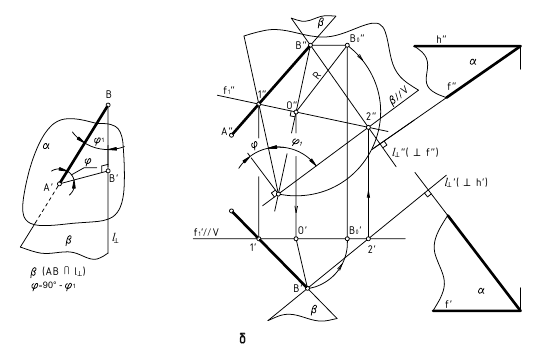
Решение:
1. l  α(h ∩ f);
α(h ∩ f);
l ”
”  f”;
f”;
l ‘
‘  h’;
h’;
2. ∠φ – вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)
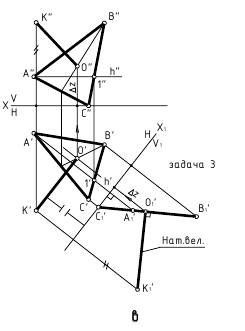
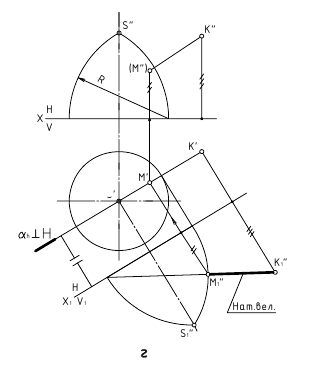
3. Угол φ между плоскостями α и β – определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).
а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) – угол φ определяется способом вращения вокруг линии уровня (рис. а)
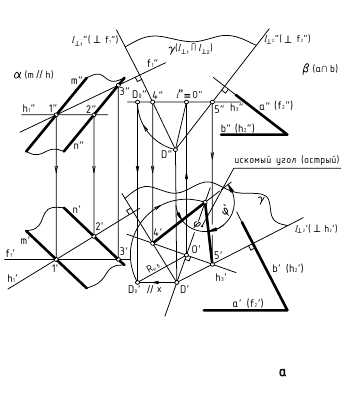
Дано:
(m // h); (а ∩ b).
Требуется:
∠φ – ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;
2. из произвольной точки пространства D (D’, D”) провести перпендикуляры l1 и l2 к заданными плоскостям, которые определяют плоскость γ(l1 ∩ l2);
3. ∠φ – вращением вокруг горизонтали h3, проведённой в построенной плоскости γ(l1 ∩ l2).
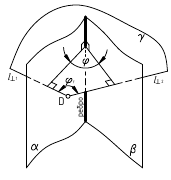
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) – угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)
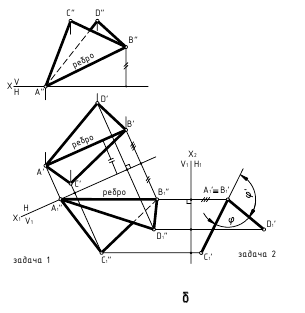
Решение:
ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.
- Тени в ортогональных проекциях
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Пересечение поверхности плоскостью и прямой
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
Справочник ОГЭ по математике. Раздел 7.5. Измерения геометрических величин
ОГЛАВЛЕНИЕ Перейти в другие разделы: 7.4 … 7.6
7.5. Измерения геометрических величин
7.5.1. Длина отрезка, длина ломаной, периметр многоугольника.
Расстояние от точки до прямой.

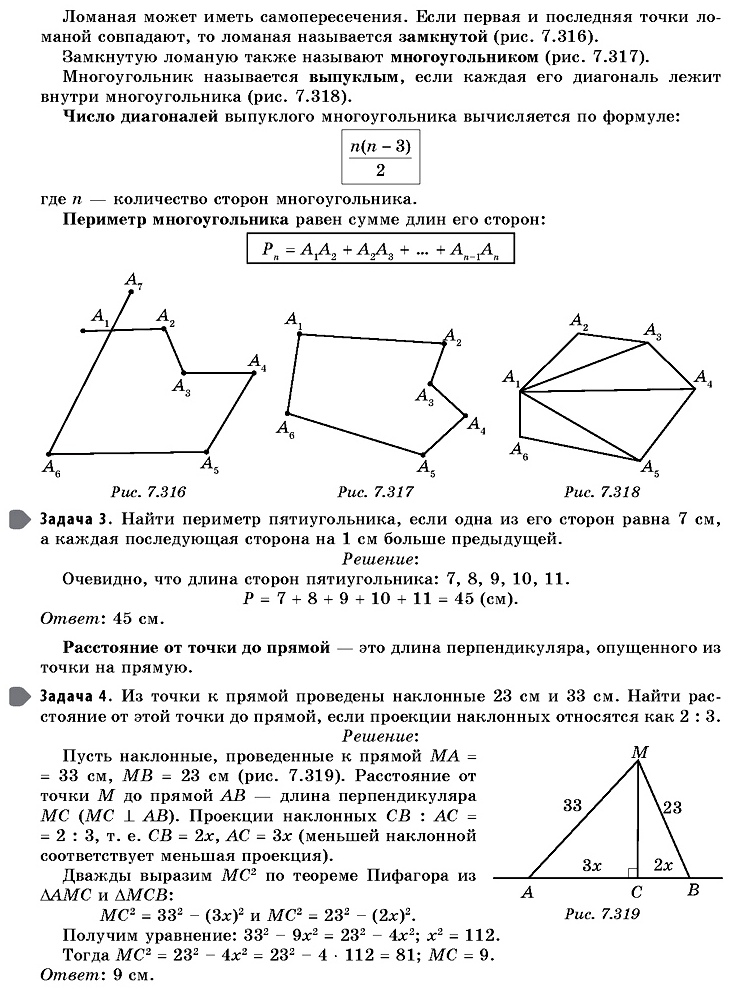
7.5.2. Длина окружности.


7.5.3. Градусная мера угла,
соответствие между величиной угла
и длиной дуги окружности.
7.5.4. Площадь и ее свойства.
Площадь прямоугольника.


7.5.5. Площадь параллелограмма.


7.5.6. Площадь трапеции.
7.5.7. Площадь треугольника.
7.5.8. Площадь круга. Площадь сектора.


7.5.9. Формулы объема прямоугольного
параллелепипеда, куба, шара.
Вы смотрели конспект по математике «7.5. Измерения геометрических величин (справочник ОГЭ)»:
- 7.5.1. Длина отрезка, длина ломаной, периметр многоугольника. Расстояние от точки до прямой.
- 7.5.2. Длина окружности.
- 7.5.3. Градусная мера угла, соответствие между величиной угла и длиной дуги окружности.
- 7.5.4. Площадь и ее свойства. Площадь прямоугольника.
- 7.5.5. Площадь параллелограмма.
- 7.5.6. Площадь трапеции.
- 7.5.7. Площадь треугольника.
- 7.5.8. Площадь круга. Площадь сектора.
- 7.5.9. Формулы объема прямоугольного параллелепипеда, куба, шара.
Выберите дальнейшее действие:
-
Перейти в Кодификатор ОГЭ по математике
-
Перейти к Оглавлению Справочника ОГЭ по математике (Третьяк И.В.)
-
Купить Справочник ОГЭ по математике (Третьяк И.В.)
Обновлено: 16.05.2023
В определении объема сказано, что объем тела — это величина (точнее было бы сказать, скалярная величина, так как бывают и векторные величины — о них пойдет речь в главе 5). Что же такое величина? На этот вопрос кратко можно ответить так: величина — это то, что можно измерить. Или более подробно: величина — это такое свойство предмета или явления, которое может быть в каком-то смысле больше или меньше и которое можно точно оценить.
Точная оценка величины называется ее измерением. Измерение происходит в результате процесса сравнения величины с некоторой величиной того же рода, принятой за единицу. Процесс сравнения зависит от рода рассматриваемых величин: для расстояний он один, для объемов — другой, для масс — третий и т.д. В результате измерения
величина получает определенное численное значение при данной единице измерения.
Величины играют большую роль в науке, особенно в физике. Почти все законы физики выражают связи между теми или иными величинами. Сила, масса, скорость, температура и т.д. — вот примеры физических величин.
Геометрические величины — это свойства геометрических фигур, характеризующие их форму и размеры; это длина, площадь, объем, величина угла.
Длины, площади, объемы — все это примеры неотрицательных скалярных величин. Скалярные величины вполне определяются своими численными значениями при данной единице измерения. Для скалярных величин определяются отношения сравнения (“равно”, “больше”, “меньше”), сложение и умножение на действительные числа. При этом действия со скалярными величинами и их отношения равносильны таким же действиям и отношениям с их численными значениями. Никаких других свойств у скалярных величин не предполагается.
При этом надо иметь в виду следующее: так как для величин данного рода определены действия сложения и умножения на число, то определить можно не отдельную величину, а множество всех величин (любого) данного рода. Так приходим к следующему определению.
Множеством неотрицательных скалярных величин (некоторого рода) называется множество, для элементов которого выполняются следующие условия (аксиомы величины):
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
2 класс. ПНШ. Методическая разработка урока по математике. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
2 класс. ПНШ. Методическая разработка урока по математике. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
Сергеева Татьяна Владимировна , учитель начальных классов
Урок
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ.Величины
Цели: повторить названия геометрических фигур; учить сравнивать геометрические фигуры, называть их свойства и признаки; совершенствовать навык построения геометрических фигур; развивать наблюдательность, мышление.
I. Организационный момент.
– Какие фигуры вы видите на рисунке? Назовите их.

– Сегодня на уроке вспомним свойства изученных геометрических фигур.
III. Устный счет.
1. Продолжите закономерность: 1, 5, 9, 13, … (17, 21).
2. Геометрическая сказка.
Жили-были два брата: треугольник с квадратом.
Старший – квадратный, добродушный, приятный.
Младший – треугольный, вечно недовольный.
Тот кричит ему: «Смотри, ты полней меня и шире.
Но настала ночь, и к брату, натыкаясь на столы,
Младший лезет воровать срезать младшему углы.
Уходя, сказал: «Приятных я тебе желаю снов!
Но наутро младший брат страшной мести был не рад.
Поглядел он – нет квадрата. Онемел… Стоял без слов…
Вот так месть! Теперь у брата сколько новеньких углов? (8.)
3. Геометрические фигуры.

– Посмотрите внимательно на фигуры и распределите их на две группы. Укажите признак, по которому вы распределили фигуры по группам.
4. Выполните вычисления:
IV. Работа по теме урока.
– Назовите признаки отрезка.
– Что общего между прямой, отрезком и лучом? Чем эти фигуры отличаются друг от друга?
– Какие предметы в нашей повседневной жизни напоминают нам прямую (линейка, указка и т. д.), луч (гвоздь, молоток, т. п.), отрезок (дверная ручка и т. п.)?
– Прочитайте задачу 6.
– Что известно? Что требуется узнать?

Решение: 12 – 8 = 4 (см).
Ответ: на 4 см первый отрезок длиннее второго.
– Какая фигура изображена в учебнике? (Прямоугольник.)
– Назовите признаки прямоугольника.
– Измерьте и запишите длины сторон прямоугольника. Нужно ли измерять все стороны прямоугольника?
Вывод: у прямоугольника противоположные стороны равны.

Физкультминутка
– Какие линии называются кривыми?
– Проведите две кривые линии, которые пересекаются в трех точках.

– Какой угол называют прямым?
– С помощью какого инструмента можно построить прямой угол? (Угольника.)
– Начертите две прямые, пересекающиеся под прямым углом.

– Сколько прямых углов на чертеже? (Четыре.)
– Назовите геометрические фигуры, изображенные на чертеже.
– Сколько кругов на чертеже?
V. Работа по карточкам.
1. Распределите линии в три группы.

– Назовите признаки, по которым вы образовали группы.
(1-я группа – 1, 4, 5 – прямые линии; 2-я группа – 2, 3 – кривые линии; 3-я группа – 6, 7 – ломаные линии.)
2. Продолжите закономерность.
![]()
3. Разделите квадрат на четыре равные части. Найдите как можно больше решений.

VI. Итог урока.
– Что нового узнали на уроке?
– Назовите свойство сторон прямоугольника.
Домашнее задание: начертить ломаную линию, состоящую из пяти звеньев.
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 933 человека из 80 регионов

Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 24 человека из 17 регионов
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Дистанционные курсы для педагогов
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 609 048 материалов в базе
Материал подходит для УМК
Геометрические фигуры и геометрические величины
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
Свидетельство и скидка на обучение каждому участнику
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
- 29.02.2020 1256
- DOCX 49.4 кбайт
- 24 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Сергеева Татьяна Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
40%
- Подготовка к ЕГЭ/ОГЭ и ВПР
- Для учеников 1-11 классов
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ
Время чтения: 1 минута
Время чтения: 2 минуты
Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие
Время чтения: 15 минут
Отчисленные за рубежом студенты смогут бесплатно учиться в России
Время чтения: 1 минута
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Время чтения: 1 минута
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Через понятие величины происходит познание окружающей действительности; знакомство с зависимостями между величинами помогает создать целостные представления об окружающем мире. Изучение процесса измерения величин способствует приобретению практических умений и навыков необходимых человеку в его повседневной деятельности. Курс математики в начальной школе имеет ярко выраженный
интегративный характер. В нём заложена содержательная основа для широкой реализации межпредметных связей всех дисциплин начальной школы. Содержание курса имеет концентрическое строение. Важная особенность – включение элементов алгебраической пропедевтики. Предметное содержание программы направлено на последовательное формирование и отработку УУД.
•Освоение математического содержания создает условия для повышения логической культуры и совершенствования коммуникативной деятельности учащихся.
•Формирование умений использовать полученные знания для самостоятельного поиска новых знаний.
•Формирование знаний и представлений необходимых для целостного восприятия объектов и явлений природы, памятников культуры и искусства.
•Обеспечивает развитие творческих способностей, формирует интерес к математическим знаниям и потребность в их расширении.

УМК “Перспективная начальная школа”, урок математики с применением технологий развивающего обучения.
Содержимое разработки
Технологическая карта урока математики
Цель для учителя:
Цель для обучающихся:
Планируемые результаты:
Критерий оценки:
Формирование умений узнавать, сравнивать геометрические фигуры, называть их свойства и признаки; находить геометрические величины фигур.
Знать свойства и признаки геометрических фигур.
Уметь находить периметр геометрических фигур.
Уметь находить периметр геометрических фигур, зная их свойства.
Актуализация знаний о свойствах и признаках геометрических фигур.
Организовать деятельность по выявлению специфики нахождения периметра геометрических фигур.
Организовать контрольно-оценочную деятельность обучающихся на уроке.
Вспомнить, что знаем о свойствах и признаках геометрических фигур.
Упражняться в вычислении периметра.
Оценить свою деятельность.
Характеристика этапов
Этапы урока
Содержание учебного материала
Деятельность учителя
Деятельность обучающихся
Организационно-мотивационный
Организовать рабочее место обучающихся, настрой на урок.
Организует класс на работу.
Проверяют организацию рабочего места.
Личностные: формирование положительного смысла учения. Коммуникативные: слушать и понимать речь другого. Познавательные:контроль.
Актуализация знаний
Работа в парах. Вычислить периметр многоугольника (по шаблонам)
Создает ситуацию, в которой обучающиеся повторяют ранее изученный материал.
Личностные: внимательно случать учителя и отвечать на вопросы. Познавательные:выделение необходимой информации. Регулятивные:осознание уровня и качества осознания материала. Коммуникативные: умение находить решение.
Определение темы
Определение темы по учебнику.
Выполняют задание, участвуют в диалоге.
Личностные: слыслообразование, формирование интереса. Познавательные:анализ объектов, поиск и выделение необходимой информации. Регулятивные:выделение и формулирование цели и задач в совместной с учителем деятельности. Коммуникативные: диалогические высказывания детей, планирование.
Целеполагание
Планирование деятельности по достижению цели
Сформулировать цель урока на основе темы. Определить пути ее достижения.
Формулируют цель и определяют этапы урока
Организует и контролирует выполнение упражнений.
Открытие новых знаний
Конструирование геометрических фигур.
Характеристика свойств геометрических фигур (треугольник, прямоугольник квадрат).
Организует работу для изучения нового материала. Создает учебные ситуации, в которых обучающие открывают новые знания.
Личностные: развитие познавательных интересов, учебных мотивов.
Познавательные: информационные:
поиск, фиксация, извлечение , представление информации, анализ. Регулятивные:удержание целей и задач урока.
Коммуникативные:умение выражать свои мысли в соответствии с задачами урока, взаимодействие.
Формирование первичных умений на основе самоконтроля
Работа в группе
На карточках задание: дочертить геометрическую фигуру. Найти периметр.
Самостоятельная работа в печатных тетрадях.
Организует и контролирует выполнение задания.
Оказывает индивидуальную помощь.
Выполняют прогнозирование, отмечают уровень усвоения материала.
Рефлексивно-оценочный
Осознание обучающимися своего эмоционального состояния во время урока.
+ Я все понял и могу рассказать другому!
? У меня есть вопросы!
– Я ничего не понял!
Регулятивные: целеполагание, осуществление самоконтроля и оценка своих умений.
Личностные: способность к самооценке на основе критерия успешности учебной деятельности.
Читайте также:
- Конспект по математике 6 класс параллельные прямые
- Переместительный закон сложения 1 класс конспект
- Внешняя политика николая первого крымская война конспект
- Решение задач с помощью систем уравнений 7 класс конспект урока
- Кодирование текстовой информации 8 класс угринович конспект урока
