Проекции точек на поверхностях геометрических тел
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
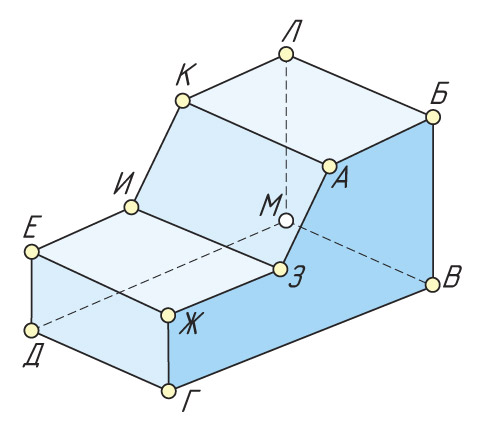
![]() Укажите количество вершин, ребер и граней изображенного предмета.
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
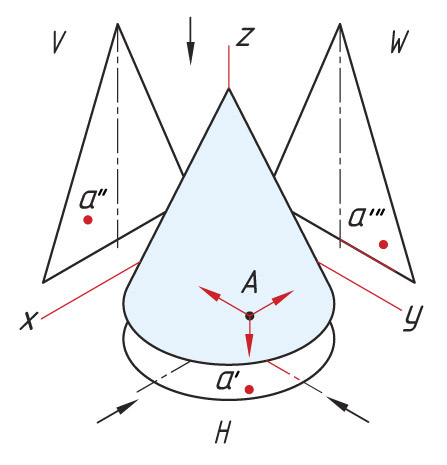
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
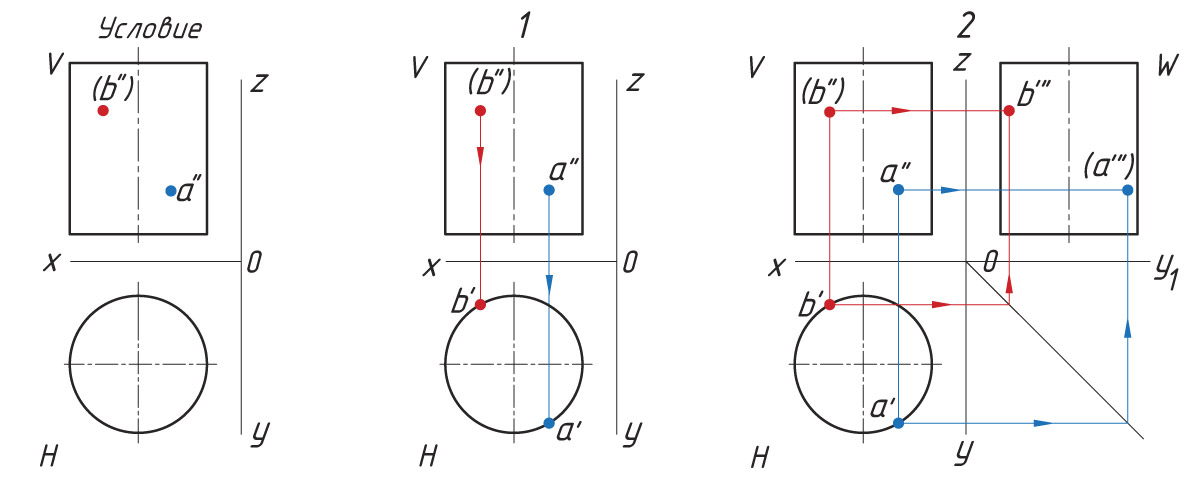
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
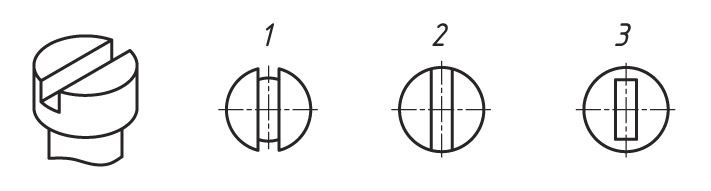
![]() Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
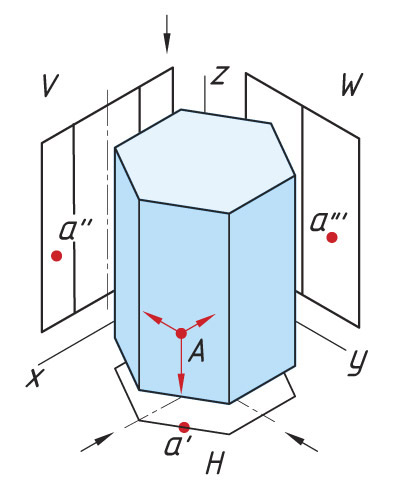
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
 |
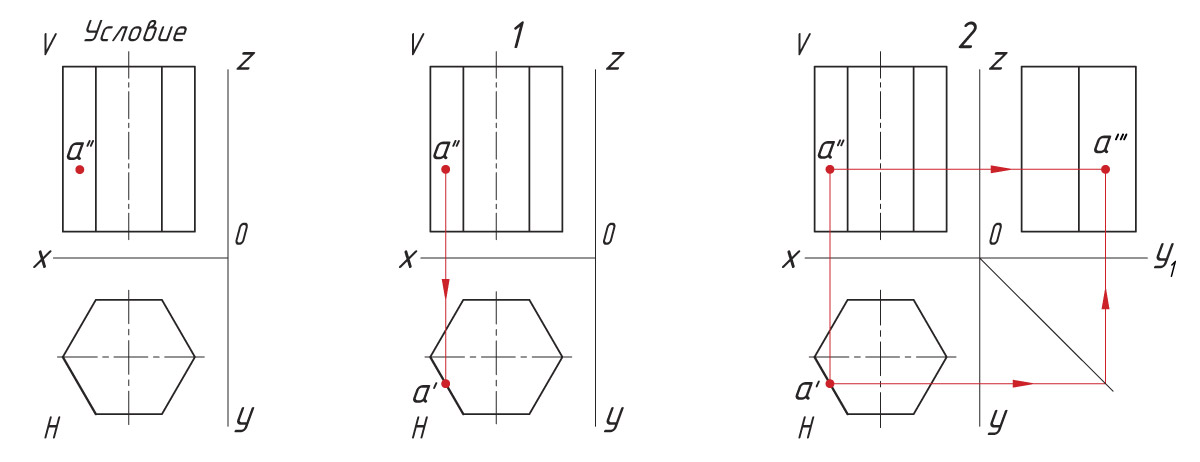
![]()
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
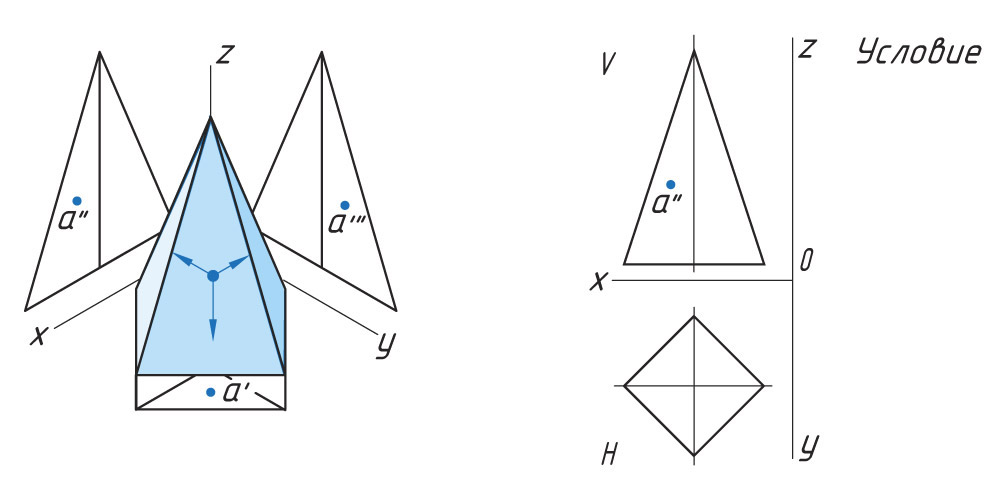
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

![]() Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
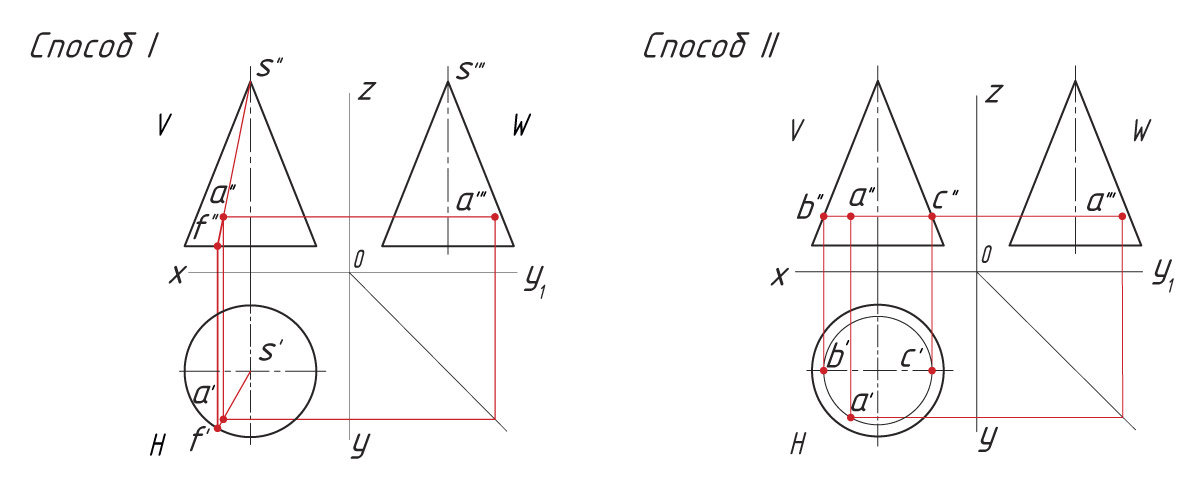
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
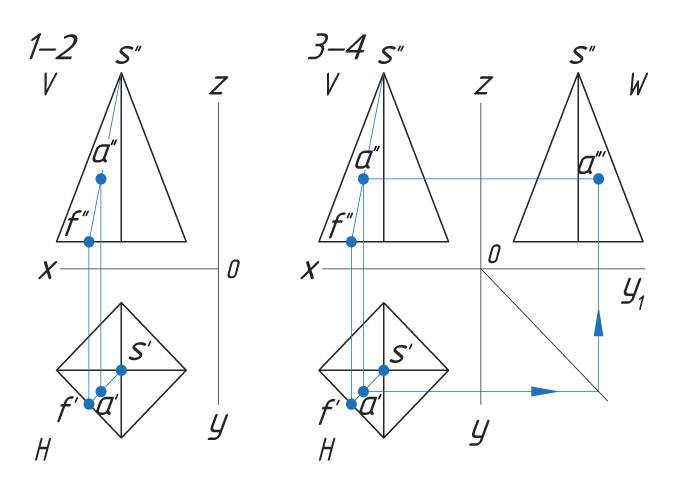 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
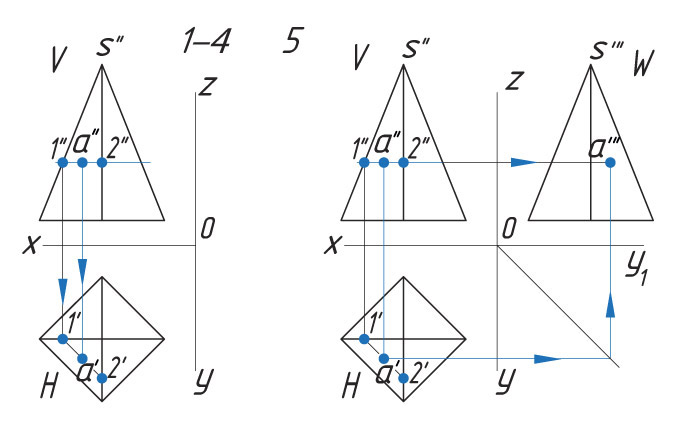 |
![]() На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
 |
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
7.1. Поверхности. Образование и задание поверхности на чертеже
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).
Подвижную линию принято называть образующей (li), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим.
Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.
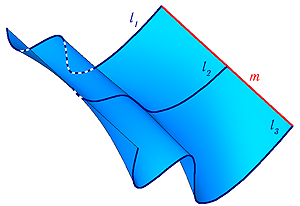
Рисунок 7.1 — Кинематическая поверхность
По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.
Линейчатые поверхности в свою очередь разделяют на развертывающиеся, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).
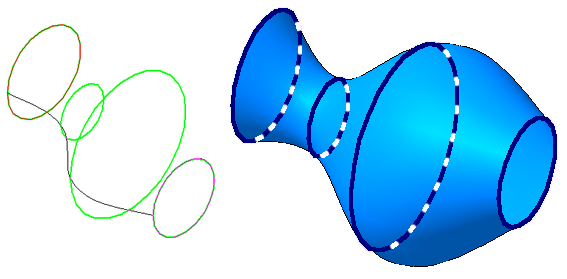
Рисунок 7.2 — Циклическая поверхность
Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:
- поверхности вращения;
- винтовые поверхности;
- поверхности с плоскостью параллелизма;
- поверхности параллельного переноса.
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Для графического изображения поверхности на чертеже используется её каркас.
Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.
Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.
Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.
Различают две части определителя: геометрическую и алгоритмическую.
Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.
Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:
- Геометрическая часть определителя: три направляющих l, m, n.
- Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение
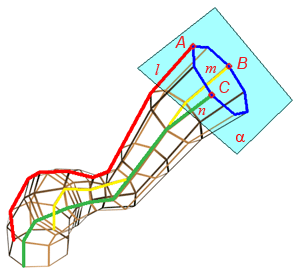
Рисунок 7.3 –Образование циклической поверхности
7.2. Поверхности вращения
Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).
Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.
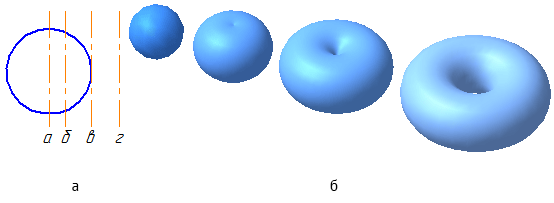
Рисунок 7.4 – Образование поверхностей вращения
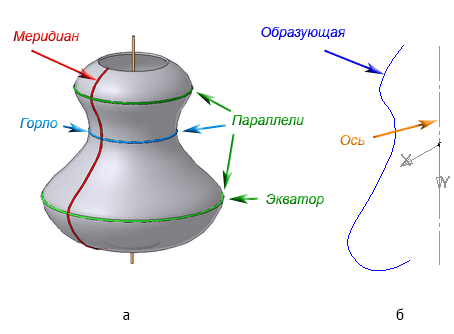
Рисунок 7.5 – Элементы поверхности вращения
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).
Наименьшая параллель называется горлом, наибольшая – экватором.
Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом.
Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом.
7.3. Цилиндрическая поверхность
Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).
Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.
Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра.
Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой.
Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным.
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.
Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).
Рисунок 7.6 – Проецирование цилиндра на плоскости проекций
Горизонтальная и профильная проекции точки F будут видимы.
При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.
Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.
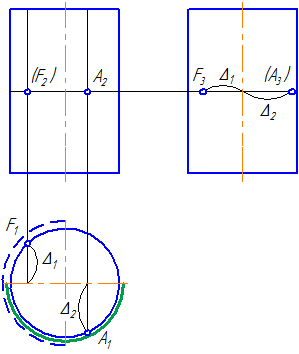
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек
7.4. Пересечение прямой с поверхностью прямого кругового цилиндра
Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.
Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.
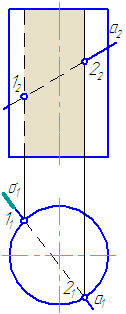
Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра
Упражнение
Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π1 и прямая а общего положения (Рисунок 7.8).
Построить точки пересечения прямой а с поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
- Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
- Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π2 условно заштрихован).
- Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);
Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.
Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π2 будет ещё невидим участок прямой от точки 1 до левой крайней образующей.
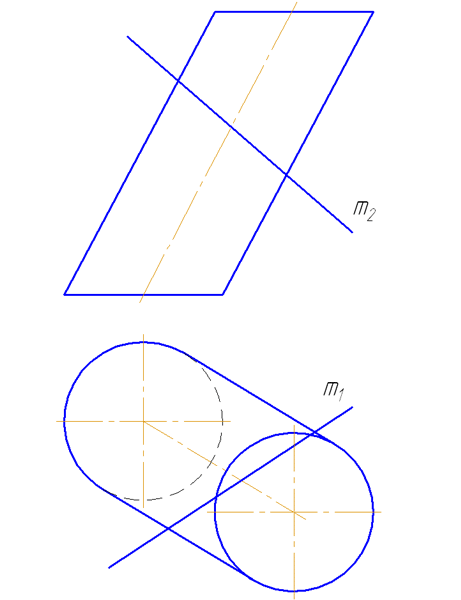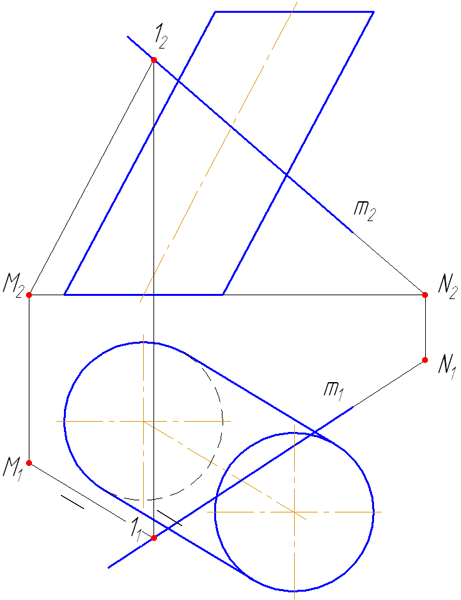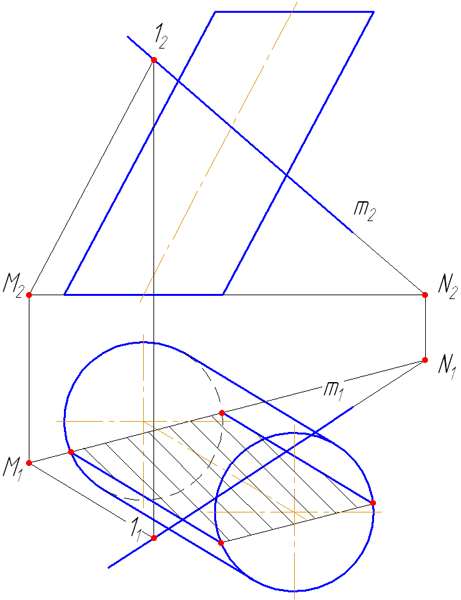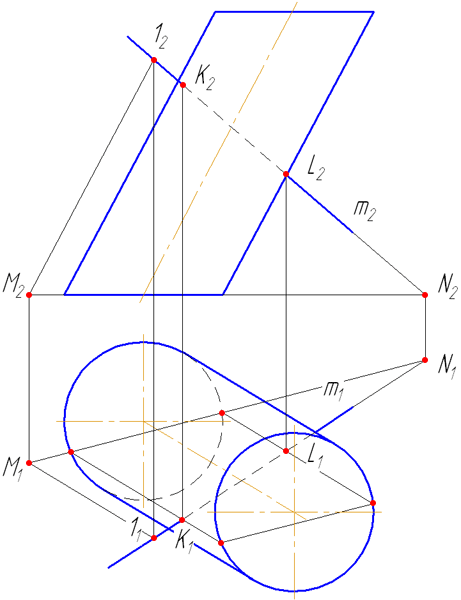
7.5. Пересечение прямой с поверхностью наклонного цилиндра
Упражнение
Заданы: наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π1 и прямая mобщего положения (Рисунок 7.9).
Построить точки пересечения прямой mс поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
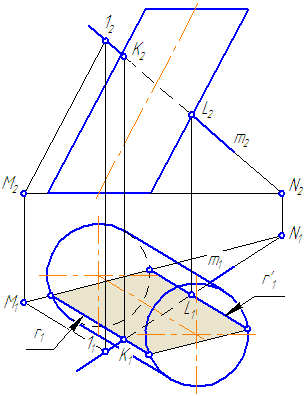
Рисунок 7.9 – Пересечение прямой с наклонным цилиндром
- Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
- Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π1) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π1 (основания)) – (MN);
- Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:
На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.
7.6. Сферическая поверхность
Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.
Шаром называется тело, ограниченное сферической поверхностью.
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).
Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.
Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.
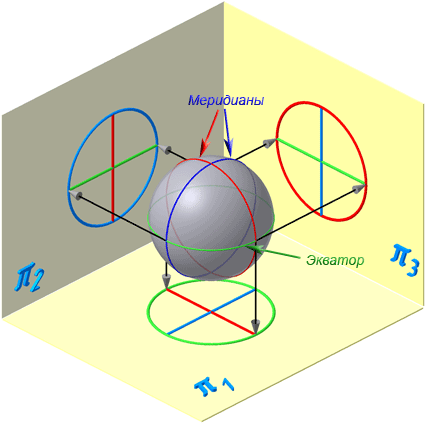
Рисунок 7.10 – Проецирование сферической поверхности
Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.
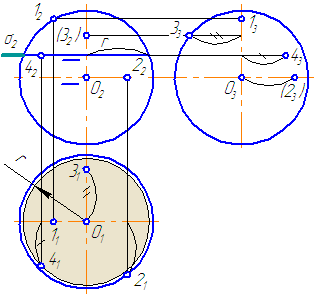
Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
Упражнение
Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.
Необходимо построить горизонтальные и профильные проекции заданных точек.
Решение.
- Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
- Точка 1 принадлежит главному меридиану (очерковой окружности на π2), проекция которого на π1 совпадает с проекцией горизонтальной оси, на π3 – с проекцией вертикальной оси.
- Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
- Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π1), проекции которого на π2 и π3 совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О3 вправо. Профильная проекция точки 2 невидима.
- Точка 3 принадлежит очерковой окружности на π3, которая также является меридианом, проекции которого на π2 и π1 совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π3 двумя засечками, отложить на π1 вверх от точки О1. Горизонтальная и профильная проекции точки 3 видимы.
- Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π1 и σ⊥π2). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π1 строим данное сечение и по линии проекционной связи находим 41. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π3 вправо от оси. Все проекции точки 4 видимы.
7.7. Пересечение прямой с поверхностью сферы
Упражнение
Заданы: сфера и прямая общего положения АВ.
Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).
Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:
- Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
- Построить фигуру пересечения сферы вспомогательной плоскостью;
- Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).
Решение
- Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:
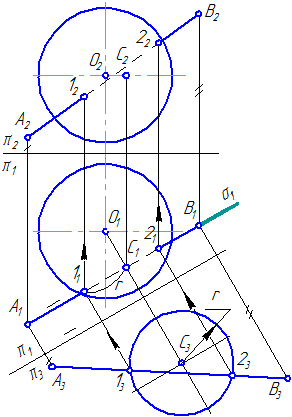
Рисунок 7.12 – Пересечение прямой с поверхностью сферы
- Введём π3⊥π1 и π3//σ1. Построим проекцию окружности сечения на π3 и проекцию А3В3.
- Находим точки их пересечения 12 и 23.
- Определим видимость участков прямой.
- На π1 точки 1 и 2 находятся на переднем полушарии, следовательно, на π2 они видимы.
7.8. Коническая поверхность
Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).
Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом.
Плоская фигура, ограниченная конической поверхностью, называется основанием конуса.
Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса.
Если основание конуса является кругом, то конус называется круговым.
Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым.
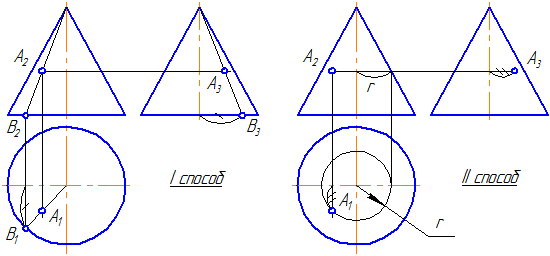
Перемещая точку A» — можно изменять диаметр основания конуса;
перемещая точку O’ — можно менять положение точки на поверхности конуса.
Рисунок 7.13 – Принадлежность точки конической поверхности
Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).
1 способ. Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.
2 способ. Точка А лежит на параллели конуса радиусом r. На π1 строим проекцию окружности (параллели) и по линии проекционной связи находим А1. По двум проекциям точки строим третью.
7.9. Пересечение прямой с поверхностью конуса
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.
- Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
- Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.
Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).
- Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
- Построим горизонтальные проекции этих объектов.
- Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.
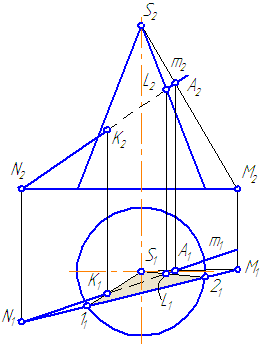
Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса
- Построим её горизонтальную проекцию.
- Соединим точки M1N1, на пересечении с окружностью основания получим точки 1 и 2.
- Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
- На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
- Определим видимость прямой относительно поверхности конуса.
На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.
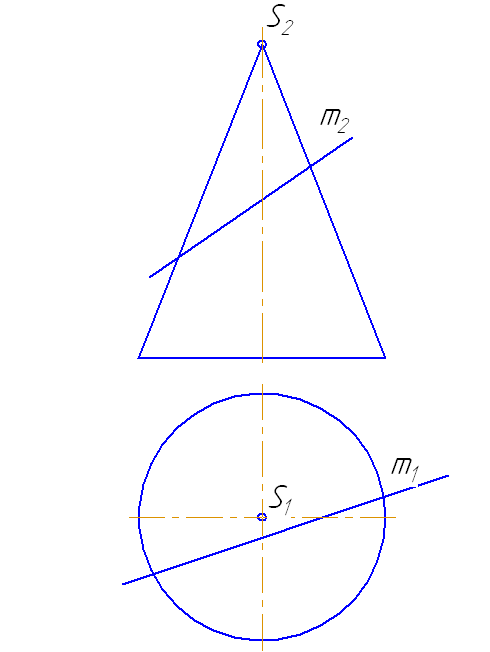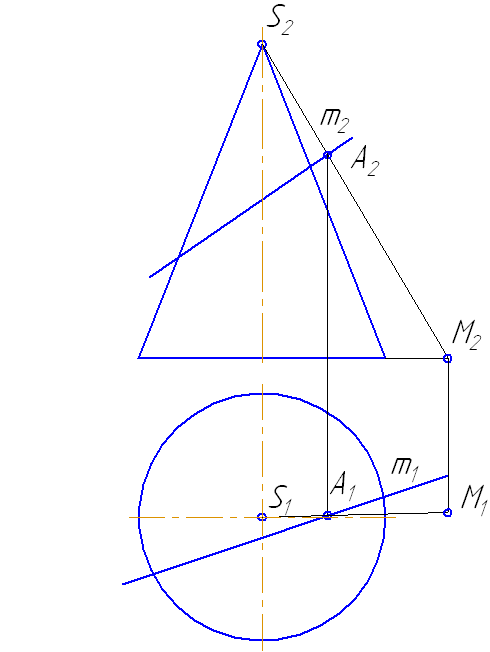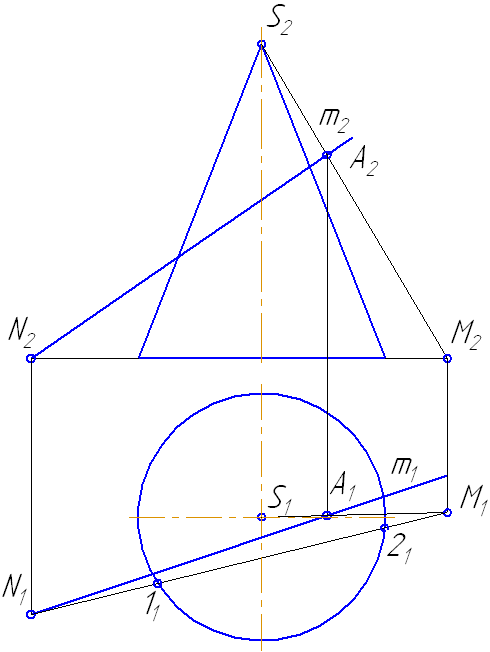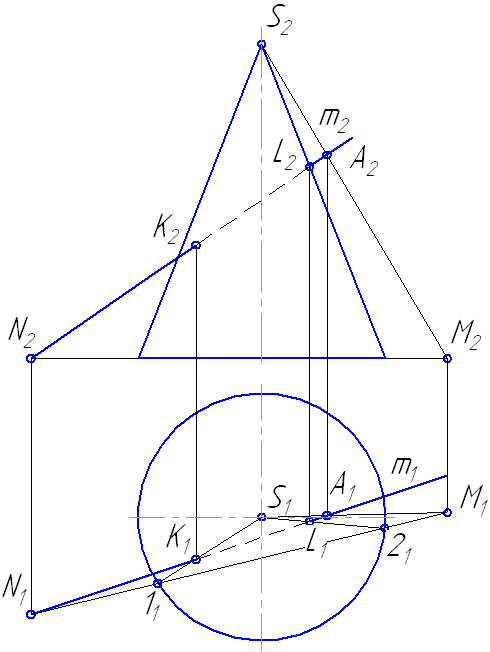
7.10. Пересечение цилиндра плоскостью
Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).
- Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
- Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
- Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.
Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):
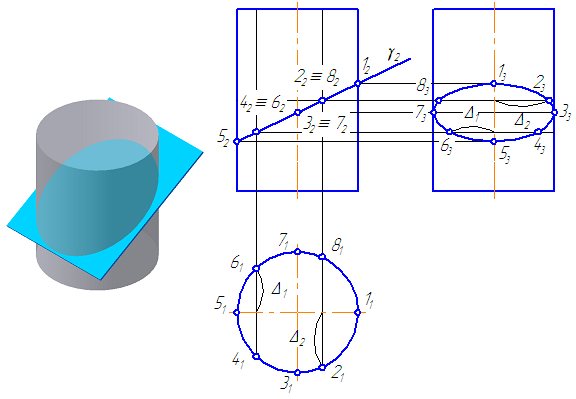
Рисунок 7.15 – пересечение цилиндра плоскостью
- Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
- Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π1 произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
- Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π3. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ1 и откладываем его по соответствующей линии связи на π3. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.
7.11. Пересечение сферы плоскостью
Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).
7.12. Пересечение конуса плоскостью
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π2 (Рисунок 7.16).
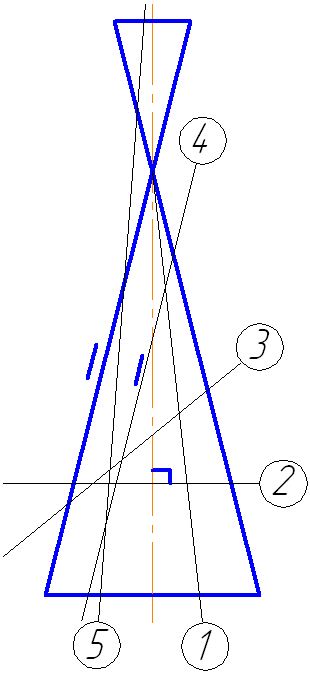
Рисунок 7.16
- Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
- Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
- Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
- Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
- Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.
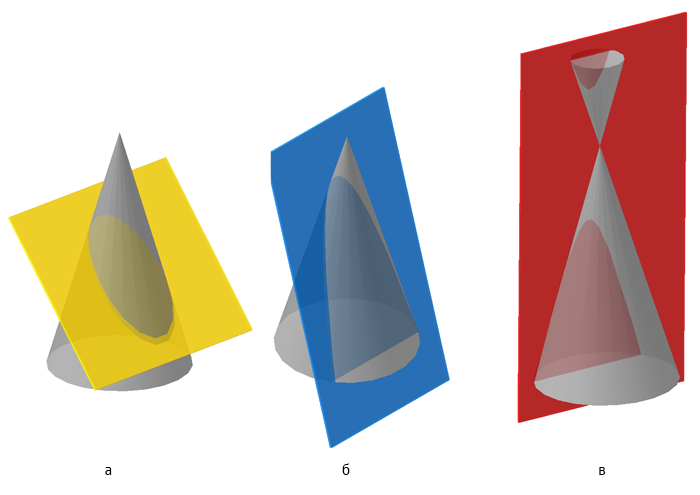
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)
Рассмотрим пример построения сечения конической поверхности плоскостью.
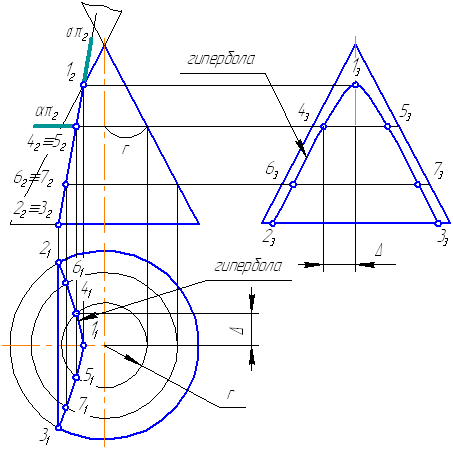
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью
Пусть задана секущая проецирующая плоскость σ⊥π2 (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.
- Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
- Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π2 и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π1. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π1 и π3 совпадают с линиями проекционной связи.
- На пересечении этих двух сечений на плоскости проекций π1 строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
- Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
- Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.
На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.
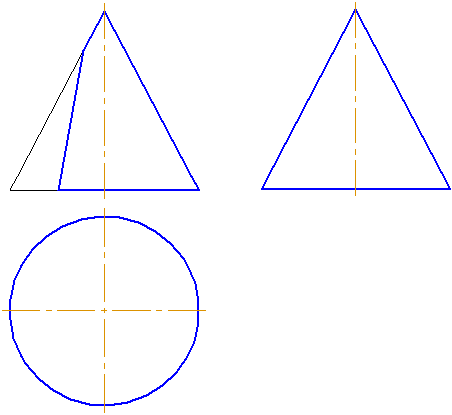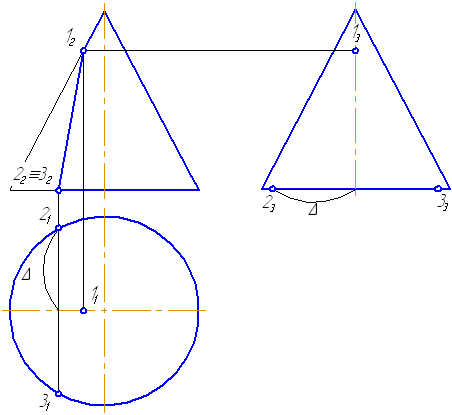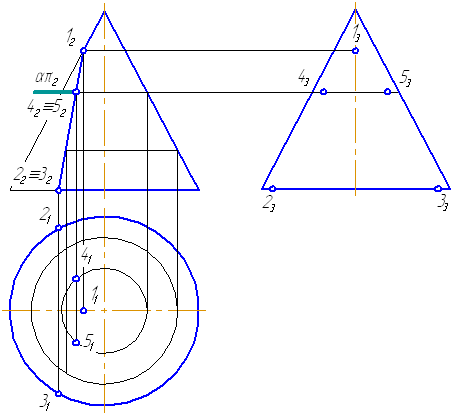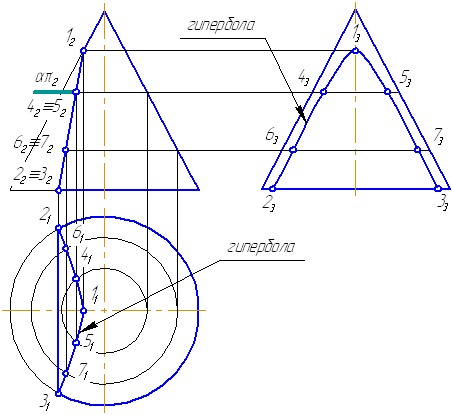
7.13. Задачи для самостоятельной работы
1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).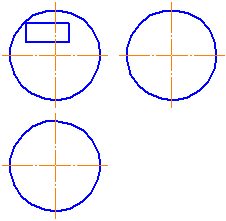
Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).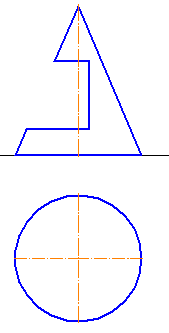
Рисунок 7.21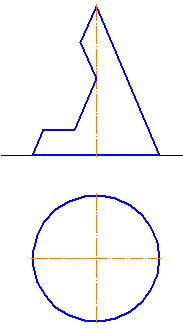
Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).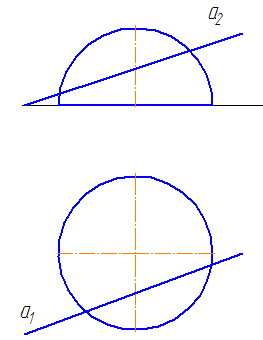
Рисунок 7.23
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Лекция № 2. Точка
1. Проекции точки на две плоскости проекций
Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.
Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а́ на фронтальную плоскость называют фронтальной проекцией.

Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху а́, b́, с́…
Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций — арабскими цифрами 1, 2… и 1́, 2́…
При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.

Через перпендикулярные прямые Аа и Аа́ проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аах, а фронтальную плоскость — по прямой а́ах. Прямые аах и а́ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха́ является прямоугольником.
При совмещении горизонтальной и фронтальной плоскостей проекции а и а́ будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аах и а́ах не нарушится.
Получаем, что на эпюре проекции а и а́ некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.
Две проекции а и а́ некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а́ к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.
Рассмотрим прямоугольник Aaaха́ (рис. 5), для которого справедливы следующие утверждения:
1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.
Аа́ = аах;
2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а́ от оси пересечения плоскостей, т. е.
Аа = а́ах.
Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).
Ось пересечения плоскостей делит горизонтальную плоскость на две четверти — переднюю и заднюю, а фронтальную плоскость — на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.

При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости — с верхней частью фронтальной плоскости.

На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В — во второй, точка С — в третьей и точка D — в четвертой.

При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.

Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция — ниже оси пересечения плоскостей.
Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.
В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.
В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная ḱ показывает фактическое местонахождение этой точки.

Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.
Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.
Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.
2. Отсутствие оси проекций
Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.
Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.
При построениях на эпюре всегда следует располагать проекции а и а́ точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа́.

Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа́ ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а́ до их пересечения, можно получить точку А. При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.
3. Проекции точки на три плоскости проекций
Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.
Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной.
В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х, общую прямую горизонтальной и профильной плоскостей — осью у, а общую прямую фронтальной и профильной плоскостей — осью z. Точка О, которая принадлежит всем трем плоскостям, называется точкой начала координат.

На рисунке 15а показана точка А
Конец ознакомительного фрагмента.
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ БУРЯТИЯ
Государственное
бюджетное профессиональное образовательное учреждение
«Авиационный
техникум»
ОП.01.
Инженерная графика
программы
подготовки специалистов среднего звена (ППССЗ)
по
специальности
15.02.08
Технология машиностроения (базовой подготовки)
Практическая
работа №8:
Тема «Проекции
точек»
Улан-Удэ,
2019 г.
Тема «Проекции
точек»
Практическая
работа №8:
Учебная цель: Построение
комплексного чертежа простейших геометрических тел (призма, конус, цилиндр,
пирамида и т.д.), вычертить аксонометрии группы тел, научиться находить
проекции точек.
Образовательные
результаты, заявленные во ФГОС:
Студент должен
уметь:
–
выполнять чертежи технических деталей в
ручной графике;
–
читать чертежи;
–
оформлять конструкторскую документацию в
соответствии с технической документацией;
знать:
–
законы, методы, приемы проекционного
черчения;
–
правила выполнения и чтения
конструкторской и технологической документации;
–
правила оформления чертежей,
геометрические построения и правила вычерчивания технических деталей;
–
требования стандартов Единой системы
конструкторской документации (далее – ЕСКД) и Единой системы технологической
документации (далее – ЕСТД) к оформлению и составлению чертежей и схем
Задачи
практической работы:
1. На формате
А4 (4шт.) выполнить четыре тела согласно варианту, найти проекции точек.
2. На формате
А4 выполнить аксонометрию группы тел согласно варианту.
3. Ответить
на вопросы теста.
4. Сделать
вывод от проделанной работы.



Рисунок
1 Образец готовой работы
Обеспеченность
занятия:
1. Учебно-методическая
литература:
–
Боголюбов
С.К. Индивидуальные задания по курсу черчения: Учебное пособие для средних
специальных заведений. 3-е изд., стереотипное. Перепечатка со второго издания
1994г.-М.: ООО ИД «Альянс», 2007.-368с.
–
В.П.Куликов,
А.В.Кузин: учебник. Инженерная графика -3-е изд., испр.-М.: ФОРУМ, 2009.-368с.
2. Технические
средства обучения:
–
мультимедиа-проектор;
3. Экран.
3.
4. Практическое
оборудование и инструменты:
–
Стол
ученический;
–
Стул
ученический;
–
Бумага
для черчения ф.А4;
–
Карандаш
чернографитный твердость М;
–
Карандаш
чернографитный твердость Т;
–
Ластик;
–
Циркуль;
–
Точилка
для карандашей механическая;
–
Линейка
металлическая 30см.
5. Рабочая папка
формата А4.
6. Практическая
работа №8 в электронном или бумажном варианте.
Краткие теоретические и
учебно-методические материалы по теме практической работы.

Рисунок
2 Комплексный чертеж цилиндра его
аксонометрическое изображение.
Практическая
работа предусматривает построение проекции простейших геометрических тел (призмы,
пирамиды, цилиндра, конуса), а так же аксонометрию группы геометрических тел.
В данном задании используются правила и
приемы проецирования точек, линий и плоскостей.
Для построения недостающих проекций точки
поверхности геометрического тела, заданной на одной из его проекций,
рекомендуется сначала найти все проекции поверхности, на которой расположена
заданная точка, затем найти остальные проекции этой точки.
На рис. 2 а,б в качестве примера
показано выполнение проекций цилиндра и заданных на его поверхности точек, а
так же изображена построенная по ним аксонометрическая проекция.
На рис. 3 а,б,в приведены примеры
нахождения недостающей проекции точки, заданной на поверхности конуса.

Рисунок
3 Комплексный чертеж конуса его
аксонометрическое изображение.

Рисунок
4 Комплексный чертеж пирамиды его аксонометрическое
изображение.
На рис.4 даны проекции
правильной четырехугольной пирамиды и точек, расположенных на ее поверхностях.
В задании принята
следующая система обозначения проекций точек. А – точка в пространстве, так ее
обозначают на технических рисунках в аксонометрических проекциях;
а–
проекция точки А на горизонтальной плоскости проекций (на виде сверху)
а’–
проекция точки А на фронтальной плоскости проекций (на виде спереди)
а”–
проекции точки А на профильной плоскости проекций (на виде слева)
Если точка видимая и
лежит на поверхности спроецированной в линию, то она указывается буквой без
скобок.
Если точка невидимая,
т.е. закрыта от глаз наблюдателя какой- либо поверхностью, то она указывается
буквой, взятой в скобки.
Например, а–
видимая проекция точки на горизонтальной плоскости; (а)– невидимая проекция
точки на горизонтальной плоскости.
Вопросы
для закрепления теоретического материала
к
практической работе:
1.
Сколько видов (как они называются) вы
использовали при построении каждой фигуры? Как располагаются приведенные выше
виды по отношению друг к другу?
2.
Что называется «комплексным чертежом»?
3.
Какие линии чертежа вы применили при выполнении
задания?
4.
Какой государственный стандарт
предусматривает построение прямоугольных проекций и взаимосвязь на чертеже
между видами?
5.
Назовите фигуры, изображенные вами на
чертеже.
Инструкция
по выполнению практической работы
1. На формате
А4 (4шт.) вычертить основную надпись.
2. Выполнить
комплексные чертежи четырех тел согласно варианту, найти проекции точек.
3. На пятом
листе ф.А4 вычертить основную надпись и выполнить аксонометрию группы тел
согласно схеме варианта.
4. Заполнить
основные надписи шрифтом ГОСТ 2.304-81 «шрифты чертежные» тип А.
5. Ответить
на вопросы теста.
6. Сделать
вывод от проделанной работы.










Критерии оценки
Если чертеж выполнен верно и аккуратно –
отлично
Если выполнен верно, есть незначительные
помарки и замечания преподавателя – хорошо
Если менее пяти не верных размера – удовлетворительно.
Если чертеж содержит более пяти грубых
ошибок – неудовлетворительно.
Тест: « Проекции точек на геометрических
телах».
Найти проекции точек на
двух недостающих плоскостях.
При определении проекций
точек используйте линии проекционной связи, которые сохраняйте на чертеже для
удобства контроля.
При построении проекций
точек, принадлежащих поверхности пирамиды и конуса, следует применять способ,
дающий наибольшую точность : либо «способ образующей», либо «способ секущих
плоскостей».
Пример выполнения задания
указан на рисунке 1.


Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
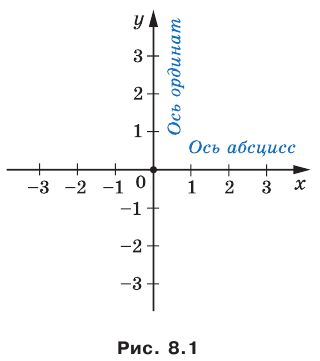
Договорились координатную плоскость с осью 
Координаты точки на плоскости  называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
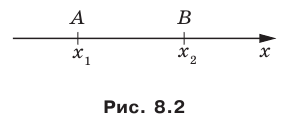
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 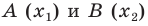 (рис. 8.2) имеем:
(рис. 8.2) имеем:
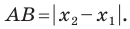
Научимся находить расстояние между точками 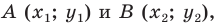 заданными на плоскости
заданными на плоскости 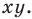
Рассмотрим случай, когда отрезок 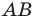 не перпендикулярен ни одной из координатных осей (рис. 8.3).
не перпендикулярен ни одной из координатных осей (рис. 8.3).
Через точки 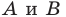 проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник
проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник 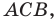 в котором
в котором 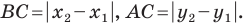 Отсюда
Отсюда 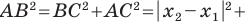
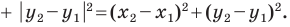
Тогда формулу расстояния между точками 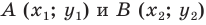 можно записать так:
можно записать так:

Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 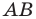 перпендикулярен одной из осей координат.
перпендикулярен одной из осей координат.
Пусть 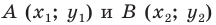 — точки плоскости
— точки плоскости 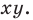 Найдем координаты
Найдем координаты 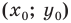 точки
точки 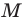 — середины отрезка
— середины отрезка 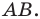
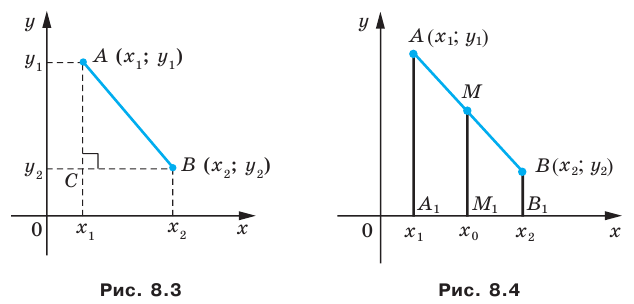
Рассмотрим случай, когда отрезок  не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что
не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что  (случай, когда
(случай, когда 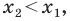 рассматривается аналогично). Через точки
рассматривается аналогично). Через точки 
 проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках
проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках 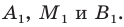 По теореме Фалеса
По теореме Фалеса 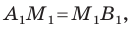 тогда
тогда 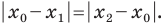 Поскольку
Поскольку 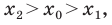 то можем записать:
то можем записать: 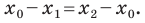 Отсюда
Отсюда  Аналогично можно показать что
Аналогично можно показать что 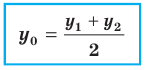
Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок  перпендикулярен одной из осей координат. Докажите это самостоятельно.
перпендикулярен одной из осей координат. Докажите это самостоятельно.
Пример №1
Докажите, что треугольник с вершинами в точках 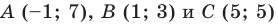 является равнобедренным прямоугольным.
является равнобедренным прямоугольным.
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
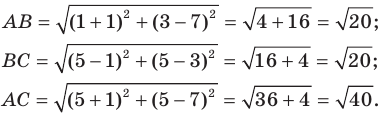
Следовательно, 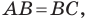 то есть треугольник
то есть треугольник 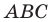 равнобедренный.
равнобедренный.
Поскольку 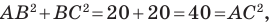 то треугольник
то треугольник 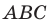 прямоугольный.
прямоугольный. 
Пример №2
Точка 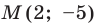 — середина отрезка
— середина отрезка 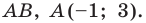 Найдите координаты точки
Найдите координаты точки 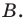
Решение:
Обозначим 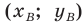 — координаты точки
— координаты точки 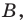
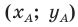 — координаты точки
— координаты точки 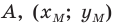 — координаты точки
— координаты точки 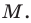
Поскольку 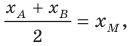 то получаем:
то получаем: 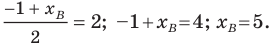
Аналогично 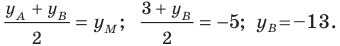
Ответ: 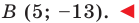
Пример №3
Докажите, что четырехугольник 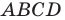 с вершинами в точках
с вершинами в точках 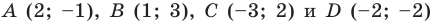 является прямоугольником.
является прямоугольником.
Решение:
Пусть точка  — середина диагонали
— середина диагонали 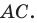 Тогда
Тогда
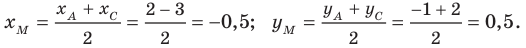
Следовательно, 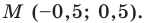
Пусть точка 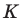 — середина диагонали
— середина диагонали 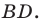 Тогда
Тогда
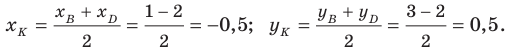
Следовательно, 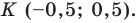
Таким образом, точки 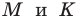 совпадают, то есть диагонали четырехугольника
совпадают, то есть диагонали четырехугольника 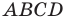 имеют общую середину. Отсюда следует, что четырехугольник
имеют общую середину. Отсюда следует, что четырехугольник 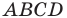 — параллелограмм.
— параллелограмм.
Найдем диагонали параллелограмма:
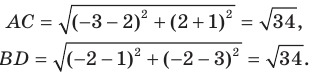
Следовательно, диагонали параллелограмма 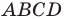 равны. Отсюда следует, что этот параллелограмм является прямоугольником.
равны. Отсюда следует, что этот параллелограмм является прямоугольником. 
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
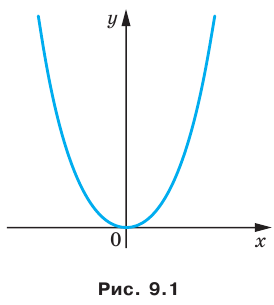
Координаты  каждой точки параболы, изображенной на рисунке 9.1, являются решением уравнения
каждой точки параболы, изображенной на рисунке 9.1, являются решением уравнения 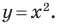 И наоборот, каждое решение уравнения с двумя переменными
И наоборот, каждое решение уравнения с двумя переменными 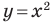 является координатами точки, лежащей на этой параболе. В этом случае говорят, что уравнение параболы, изображенной на рисунке 9.1, имеет вид
является координатами точки, лежащей на этой параболе. В этом случае говорят, что уравнение параболы, изображенной на рисунке 9.1, имеет вид 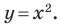
Определение. Уравнением фигуры  заданной на плоскости
заданной на плоскости 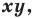 называют уравнение с двумя переменными
называют уравнение с двумя переменными 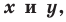 обладающее следующими свойствами:
обладающее следующими свойствами:
- если точка принадлежит фигуре
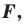 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения; - любое решение
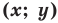 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 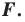
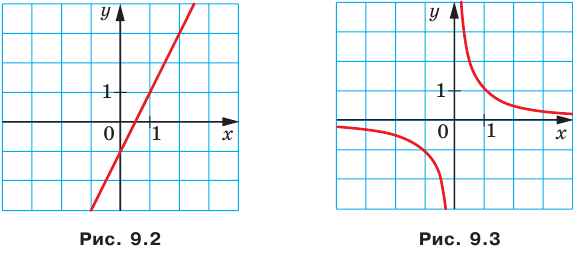
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 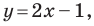 а уравнение гиперболы, изображенной на рисунке 9.3, имеет вид
а уравнение гиперболы, изображенной на рисунке 9.3, имеет вид 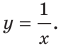 Принято говорить, что, например, уравнения
Принято говорить, что, например, уравнения 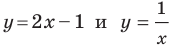 задают прямую и гиперболу соответственно.
задают прямую и гиперболу соответственно.
Если данное уравнение является уравнением фигуры 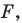 то эту фигуру можно рассматривать как геометрическое место точек (ГМТ), координаты которых удовлетворяют данному уравнению.
то эту фигуру можно рассматривать как геометрическое место точек (ГМТ), координаты которых удовлетворяют данному уравнению.
Пользуясь этими соображениями, выведем уравнение окружности радиуса  с центром в точке
с центром в точке 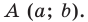
Пусть 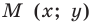 — произвольная точка данной окружности (рис. 9.4). Тогда
— произвольная точка данной окружности (рис. 9.4). Тогда 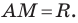 Используя формулу расстояния между точками, получим:
Используя формулу расстояния между точками, получим:
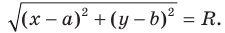
Отсюда
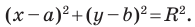
Мы показали, что координаты 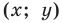 произвольной точки
произвольной точки 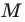 данной окружности являются решением уравнения
данной окружности являются решением уравнения 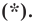 Теперь покажем, что любое решение уравнения
Теперь покажем, что любое решение уравнения 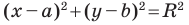 является координатами точки, принадлежащей данной окружности.
является координатами точки, принадлежащей данной окружности.
Пусть пара чисел 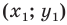 — произвольное решение уравнения
— произвольное решение уравнения 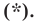
Тогда 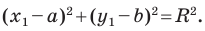 Отсюда
Отсюда 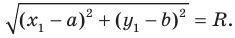
Это равенство показывает, что точка 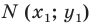 удалена от центра окружности
удалена от центра окружности 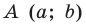 на расстояние, равное радиусу окружности, а следовательно, точка
на расстояние, равное радиусу окружности, а следовательно, точка 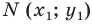 принадлежит данной окружности.
принадлежит данной окружности.
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса  с центром в точке
с центром в точке 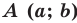 имеет вид
имеет вид
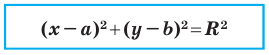
Верно и такое утверждение: любое уравнение вида 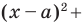 где
где 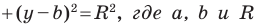 некоторые числа, причем
некоторые числа, причем 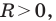 является уравнением окружности радиуса
является уравнением окружности радиуса 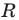 с центром в точке с координатами
с центром в точке с координатами 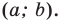
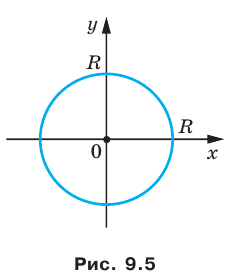
Если центром окружности является начало координат (рис. 9.5), то 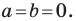 В этом случае уравнение окружности имеет вид
В этом случае уравнение окружности имеет вид 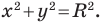
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок  если
если 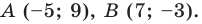
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 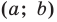 центра
центра  окружности:
окружности:
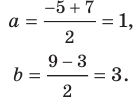
Следовательно, 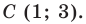
Радиус окружности 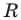 равен отрезку
равен отрезку 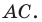 Тогда
Тогда
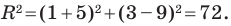
Следовательно, искомое уравнение имеет вид
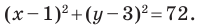
Ответ: 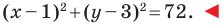
Пример №5
Докажите, что уравнение 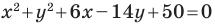 задает окружность. Найдите координаты центра и радиус этой окружности.
задает окружность. Найдите координаты центра и радиус этой окружности.
Решение:
Представим данное уравнение в виде 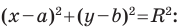
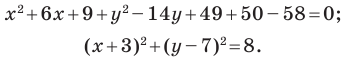
Следовательно, данное уравнение является уравнением окружности с центром в точке 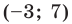 и радиусом
и радиусом 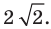
Ответ: 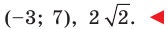
Пример №6
Докажите, что треугольник с вершинами в точках 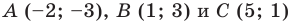 является прямоугольным, и составьте уравнение окружности, описанной около треугольника
является прямоугольным, и составьте уравнение окружности, описанной около треугольника 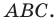
Решение:
Найдем квадраты сторон данного треугольника:
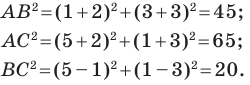
Поскольку 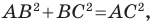 то данный треугольник является прямоугольным с прямым углом при вершине
то данный треугольник является прямоугольным с прямым углом при вершине 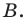 Центром описанной окружности является середина гипотенузы
Центром описанной окружности является середина гипотенузы 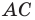 — точка
— точка 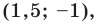 радиус окружности
радиус окружности 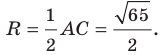 Следовательно, искомое уравнение имеет вид
Следовательно, искомое уравнение имеет вид
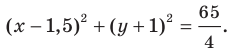
Ответ: 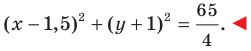
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 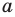 — данная прямая. Выберем две точки
— данная прямая. Выберем две точки  и
и 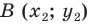 так, чтобы прямая
так, чтобы прямая 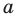 была серединным перпендикуляром отрезка
была серединным перпендикуляром отрезка 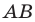 (рис. 10.1).
(рис. 10.1).
Пусть 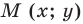 — произвольная точка прямой
— произвольная точка прямой 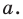 Тогда по свойству серединного перпендикуляра отрезка выполняется равенство
Тогда по свойству серединного перпендикуляра отрезка выполняется равенство 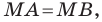 то есть
то есть
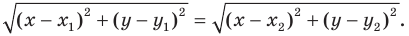
Мы показали, что координаты  произвольной точки
произвольной точки 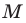 прямой
прямой 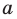 являются решением уравнения
являются решением уравнения 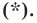
Теперь покажем, что любое решение уравнения 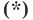 является координатами точки, принадлежащей данной прямой
является координатами точки, принадлежащей данной прямой 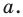
Пусть 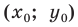 — произвольное решение уравнения
— произвольное решение уравнения 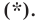 Тогда
Тогда 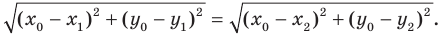 Это равенство означает, что точка
Это равенство означает, что точка 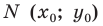 равноудалена от точек
равноудалена от точек 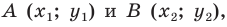 следовательно, точка
следовательно, точка 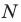 принадлежит серединному перпендикуляру отрезка
принадлежит серединному перпендикуляру отрезка 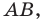 то есть прямой
то есть прямой 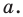
Итак, мы доказали, что уравнение 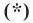 является уравнением данной прямой
является уравнением данной прямой 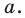
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 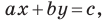 где
где 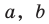 и
и 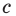 — некоторые числа, причем
— некоторые числа, причем 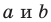 не равны нулю одновременно. Покажем, что уравнение
не равны нулю одновременно. Покажем, что уравнение  можно преобразовать к такому виду. Возведем обе части уравнения
можно преобразовать к такому виду. Возведем обе части уравнения 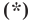 в квадрат. Имеем:
в квадрат. Имеем:
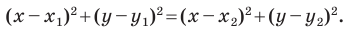
Раскроем скобки и приведем подобные слагаемые. Получим:
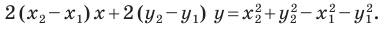
Обозначив 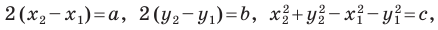 получим уравнение
получим уравнение 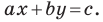
Поскольку точки 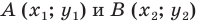 различны, то хотя бы одна из разностей
различны, то хотя бы одна из разностей 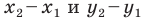 не равна нулю. Следовательно, числа
не равна нулю. Следовательно, числа 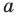 и
и 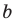 не равны нулю одновременно.
не равны нулю одновременно.
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
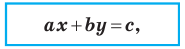
где 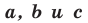 — некоторые числа, причем
— некоторые числа, причем 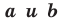 не равны нулю одновременно.
не равны нулю одновременно.
Верно и такое утверждение: любое уравнение вида 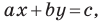 где
где 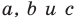 — некоторые числа, причем
— некоторые числа, причем 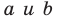 не равны нулю одновременно, является уравнением прямой.
не равны нулю одновременно, является уравнением прямой.
Если 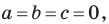 то графиком уравнения
то графиком уравнения 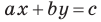 является вся плоскость
является вся плоскость 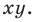 Если
Если 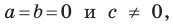 то уравнение не имеет решений.
то уравнение не имеет решений.
Из курса алгебры 7 класса вы знаете, что уравнение вида 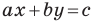 называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
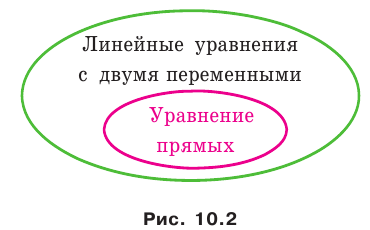
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 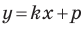 является прямая. Сейчас мы можем это доказать.
является прямая. Сейчас мы можем это доказать.
Перепишем уравнение 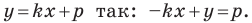 Мы получили уравнение вида
Мы получили уравнение вида  для случая, когда
для случая, когда 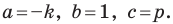 Поскольку в этом уравнении
Поскольку в этом уравнении 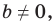 то мы получили уравнение прямой.
то мы получили уравнение прямой.
А любую ли прямую на плоскости можно задать уравнением вида 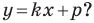 Ответ на этот вопрос отрицательный.
Ответ на этот вопрос отрицательный.
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида 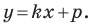
Вместе с тем, если в уравнении прямой 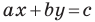 принять
принять 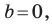 то его можно переписать так:
то его можно переписать так: 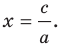 Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Если 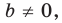 то уравнение прямой
то уравнение прямой 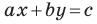 можно записать так:
можно записать так:
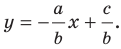 Обозначив
Обозначив 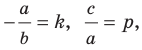 получим уравнение
получим уравнение 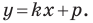
Следовательно, если 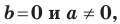 то уравнение прямой
то уравнение прямой 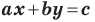 задает вертикальную прямую; если
задает вертикальную прямую; если 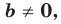 то это уравнение задает невертикальную прямую.
то это уравнение задает невертикальную прямую.
Уравнение невертикальной прямой удобно записывать в виде 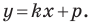
Данная таблица подытоживает материал, рассмотренный в этом пункте.

Пример №7
Составьте уравнение прямой, проходящей через точки:

Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 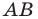 является вертикальной. Ее уравнение имеет вид
является вертикальной. Ее уравнение имеет вид 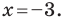
2) Поскольку данные точки имеют разные абсциссы, то прямая 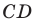 не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде
не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде 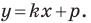
Подставив координаты точек 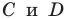 в уравнение
в уравнение 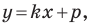 получаем систему уравнений:
получаем систему уравнений:
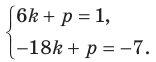
Решив эту систему уравнений, находим, что 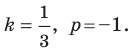
Ответ: 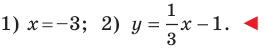
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 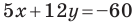 и осями координат.
и осями координат.
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 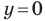 получаем
получаем 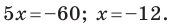
С осью ординат: при 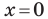 получаем
получаем 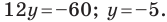
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 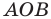 (рис. 10.3) с вершинами
(рис. 10.3) с вершинами 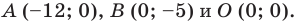 Найдем стороны треугольника:
Найдем стороны треугольника: 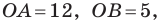
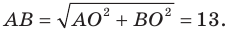 Тогда искомые периметр и площадь соответственно равны
Тогда искомые периметр и площадь соответственно равны 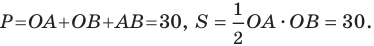
Ответ: 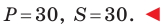
Угловой коэффициент прямой
Рассмотрим уравнение 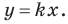 Оно задает невертикальную прямую, проходящую через начало координат.
Оно задает невертикальную прямую, проходящую через начало координат.
Покажем, что прямые 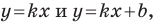 где
где 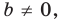 параллельны.
параллельны.
Точки 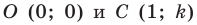 принадлежат прямой
принадлежат прямой 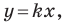 а точки
а точки 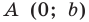 и
и 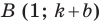 принадлежат прямой
принадлежат прямой 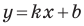 (рис. 11.1). Легко убедиться (сделайте это самостоятельно), что середины диагоналей
(рис. 11.1). Легко убедиться (сделайте это самостоятельно), что середины диагоналей  четырехугольника
четырехугольника  совпадают. Следовательно, четырехугольник
совпадают. Следовательно, четырехугольник  — параллелограмм. Отсюда
— параллелограмм. Отсюда 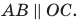
Теперь мы можем сделать такой вывод: если 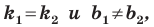 то прямые
то прямые 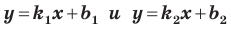 параллельны (1).
параллельны (1).
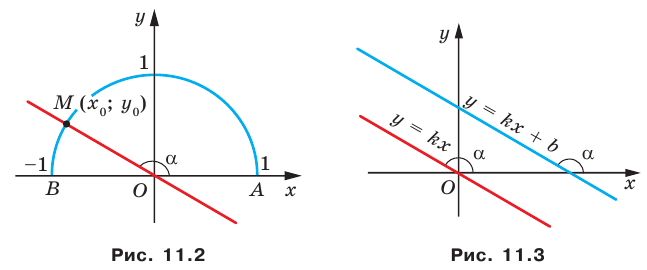
Пусть прямая 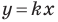 пересекает единичную полуокружность в точке
пересекает единичную полуокружность в точке 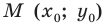 (рис. 11.2). Угол
(рис. 11.2). Угол 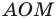 называют углом между данной прямой и положительным направлением оси абсцисс.
называют углом между данной прямой и положительным направлением оси абсцисс.
Если прямая 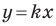 совпадает с осью абсцисс, то угол между этой прямой и положительным направлением оси абсцисс считают равным
совпадает с осью абсцисс, то угол между этой прямой и положительным направлением оси абсцисс считают равным 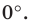
 Если прямая
Если прямая 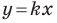 образует с положительным направлением оси абсцисс угол
образует с положительным направлением оси абсцисс угол  то считают, что и прямая
то считают, что и прямая  параллельная прямой
параллельная прямой 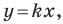 также образует угол
также образует угол 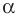 с положительным направлением оси абсцисс (рис. 11.3).
с положительным направлением оси абсцисс (рис. 11.3).
Рассмотрим прямую 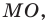 уравнение которой имеет вид
уравнение которой имеет вид 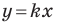 (рис. 11.2). Если
(рис. 11.2). Если 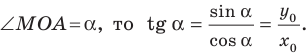 Поскольку точка
Поскольку точка 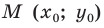 принадлежит прямой
принадлежит прямой 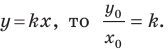 Отсюда
Отсюда 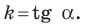 Таким образом, для прямой
Таким образом, для прямой 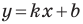 получаем, что
получаем, что
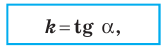
где 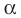 — угол, который образует эта прямая с положительным направлением оси абсцисс. Поэтому коэффициент
— угол, который образует эта прямая с положительным направлением оси абсцисс. Поэтому коэффициент 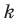 называют угловым коэффициентом этой прямой.
называют угловым коэффициентом этой прямой.
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 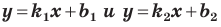 параллельны, то
параллельны, то 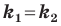 (2).
(2).
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 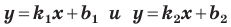 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 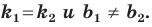
Пример №9
Составьте уравнение прямой, которая проходит через точку 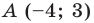 и параллельна прямой
и параллельна прямой 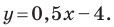
Решение:
Пусть уравнение искомой прямой 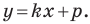 Поскольку эта прямая и прямая
Поскольку эта прямая и прямая 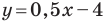 параллельны, то их угловые коэффициенты равны, то есть
параллельны, то их угловые коэффициенты равны, то есть 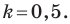
Следовательно, искомое уравнение имеет вид 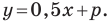 Учитывая, что данная прямая проходит через точку
Учитывая, что данная прямая проходит через точку 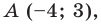 получаем:
получаем: 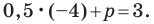 Отсюда
Отсюда 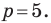
Искомое уравнение имеет вид 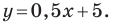
Ответ: 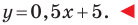
Метод координат
Мы часто говорим: прямая 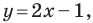 парабола
парабола 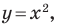 окружность
окружность 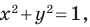 тем самым отождествляя фигуру с ее уравнением. Такой подход позволяет сводить задачу о поиске свойств фигуры к задаче об исследовании ее уравнения. В этом и состоит суть метода координат.
тем самым отождествляя фигуру с ее уравнением. Такой подход позволяет сводить задачу о поиске свойств фигуры к задаче об исследовании ее уравнения. В этом и состоит суть метода координат.
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
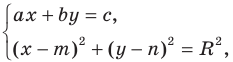
где числа 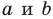 одновременно не равны нулю и
одновременно не равны нулю и 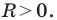
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 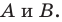 Вы хорошо знаете, какой фигурой является геометрическое место точек
Вы хорошо знаете, какой фигурой является геометрическое место точек  таких, что
таких, что 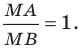
Это серединный перпендикуляр отрезка 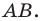 Интересно выяснить, какую фигуру образуют все точки
Интересно выяснить, какую фигуру образуют все точки 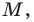 для которых
для которых 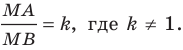 Решим эту задачу для
Решим эту задачу для 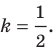
Плоскость, на которой отмечены точки 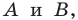 «превратим» в координатную. Сделаем это так: в качестве начала координат выберем точку
«превратим» в координатную. Сделаем это так: в качестве начала координат выберем точку 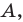 в качестве единичного отрезка — отрезок
в качестве единичного отрезка — отрезок 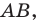 ось абсцисс проведем так, чтобы точка
ось абсцисс проведем так, чтобы точка 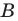 имела координаты
имела координаты 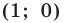 (рис. 11.6).
(рис. 11.6).
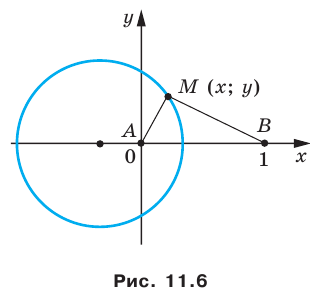
Пусть  — произвольная точка искомой фигуры
— произвольная точка искомой фигуры  Тогда
Тогда 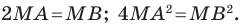 Отсюда
Отсюда
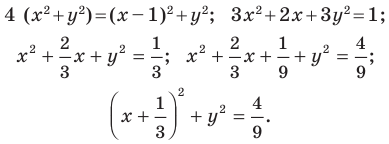
Следовательно, если точка 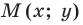 принадлежит фигуре
принадлежит фигуре  то ее координаты являются решением уравнения
то ее координаты являются решением уравнения 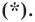
Пусть 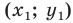 — некоторое решение уравнения
— некоторое решение уравнения 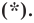 Тогда легко показать, что
Тогда легко показать, что 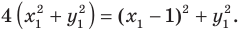 А это означает, что точка
А это означает, что точка 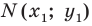 такова, что
такова, что 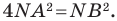 Тогда
Тогда 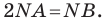 Следовательно, точка
Следовательно, точка 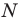 принадлежит фигуре
принадлежит фигуре 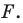
Таким образом, уравнением фигуры 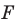 является уравнение
является уравнение 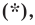 то есть фигура
то есть фигура 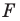 — это окружность с центром в точке
— это окружность с центром в точке 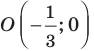 и радиусом
и радиусом 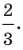
Мы решили задачу для частного случая, когда 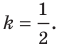 Можно показать, что искомой фигурой для любого положительного
Можно показать, что искомой фигурой для любого положительного 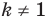 будет окружность. Эту окружность называют окружностью Аполлония
будет окружность. Эту окружность называют окружностью Аполлония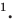
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 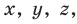 а коэффициенты — первыми:
а коэффициенты — первыми: 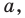
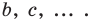 Привычные нам обозначения степеней
Привычные нам обозначения степеней 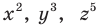 и т. д. также ввел Р. Декарт.
и т. д. также ввел Р. Декарт.

Справочный материал
Расстояние между двумя точками
Расстояние между точками 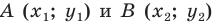 можно найти по формуле
можно найти по формуле 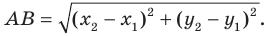
Координаты середины отрезка
Координаты 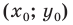 середины отрезка с концами
середины отрезка с концами 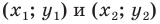 можно найти по формулам:
можно найти по формулам:
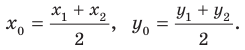
Уравнение фигуры
Уравнением фигуры 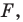 заданной на плоскости
заданной на плоскости  называют уравнение с двумя переменными
называют уравнение с двумя переменными 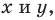 обладающее следующими свойствами:
обладающее следующими свойствами:
1) если точка принадлежит фигуре 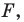 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;
2) любое решение 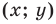 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 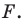
Уравнение окружности
Уравнение окружности радиуса 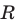 с центром в точке
с центром в точке 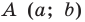 имеет вид
имеет вид 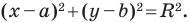
Любое уравнение вида 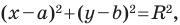 где
где 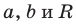 — некоторые числа, причем
— некоторые числа, причем 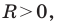 является уравнением окружности радиуса
является уравнением окружности радиуса 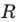 с центром в точке с координатами
с центром в точке с координатами 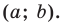
Уравнение прямой
Уравнение прямой имеет вид 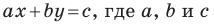 — некоторые числа, причем
— некоторые числа, причем 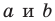 не равны нулю одновременно. Любое уравнение вида
не равны нулю одновременно. Любое уравнение вида 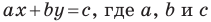 — некоторые числа, причем
— некоторые числа, причем 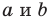 не равны нулю одновременно, является уравнением прямой.
не равны нулю одновременно, является уравнением прямой.
Если 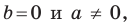 то уравнение прямой
то уравнение прямой 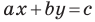 задает вертикальную прямую; если
задает вертикальную прямую; если 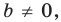 то это уравнение задает невертикальную прямую.
то это уравнение задает невертикальную прямую.
Угловой коэффициент прямой
Коэффициент 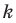 в уравнении прямой
в уравнении прямой 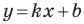 называют угловым коэффициентом прямой, и он равен тангенсу угла, который образует эта прямая с положительным направлением оси абсцисс.
называют угловым коэффициентом прямой, и он равен тангенсу угла, который образует эта прямая с положительным направлением оси абсцисс.
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 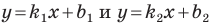 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 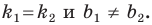
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
