Геометрия 7 класс как найти доказательства

Как правило, у большинства учеников самый нелюбимый блок в экзаменах — геометрия, потому что он тяжело даётся. А кто-то и вовсе его не понимает. А в геометрии есть самый нелюбимый тип заданий — это задачи на доказательство. Почему так происходит и как помочь ученику научиться их решать?

Что такое задача на доказательство

Задача на доказательство — это утверждение, которое нужно доказать, используя различные теоремы, аксиомы, следствия и признаки геометрии. Другими словами, нам нужно решить задачу и получить то же самое, что написано в условии, тогда задание будет выполнено. Поэтому задачи на доказательство на самом деле несильно отличаются от задач на нахождение чего-либо — просто то, что нужно найти, уже известно заранее. Звучит даже легче, не правда ли? Так почему же многие школьники всё равно намеренно пропускают эти задания и не решают их?

Всё дело в том, что задачи на доказательство очень похожи на то, как доказываются теоремы. А доказательство теорем начинается в 7 классе, когда происходит деление на Алгебру и Геометрию как отдельные предметы в школах. Однако обычно доказательство теорем выглядит следующим образом:

1. учитель доказывает теорему у доски,
2. ученики переписывают себе всё в тетрадь, иногда даже не понимая, что они пишут,
3. дальше звучит знакомая всем фраза «Выучите доказательство, потом ответите его на оценку»,
4. а дальше зачастую происходит зубрёжка переписанной теоремы.

Даже человек без педагогического образования догадается, что к пониманию, как осуществляется доказательство, это не приведёт. Да и зачем, если ни на одном экзамене не просят доказывать теоремы? Наоборот, нужно просто использовать уже готовые и доказанные формулировки. Но навык это очень полезный, и вот почему.

Где мы встречаемся с доказательствами

Умение доказывать геометрические задачи проверяют 2 главных школьных экзамена по математике — ОГЭ и ЕГЭ.

• В ОГЭ доказательство находится в № 24 как самостоятельная задача, которая приносит 2 балла максимум,
• в ЕГЭ доказательства встречаются в пунктах а) в № 13 (стереометрическая задача) и № 16 (планиметрическая задача), которые сами по себе приносят по 1 баллу, но без корректных доказательств практически невозможно перейти к пункту б) с решением, что в совокупности приносит по 3 балла за каждую задачу.

Как вы можете заметить, доказательства достаточно важны и приносят неплохие баллы сдающим экзамены. Но это не единственная их польза. Все задания на доказательство помогают ученикам выстраивать логические цепочки и учат рассуждать, а это пригодится не только на экзаменах, но и в жизни.

Так как помочь школьникам научиться их решать?

Как научить школьника решать задачи на доказательство

Доказательство, как я уже говорила, несильно отличается от решения всех геометрических задач. Алгоритм в обоих случаях такой:

1. построить чертеж,
2. отметить на чертеже, что дано,
3. отметить на чертеже, что нужно найти,
4. построить логическую цепочку от того, что нужно найти до того, что дано,
5. записать шаги доказательства.

Кроме того, в ходе решения или доказательства нужно не забывать выносить всю теорию на чертёж, а также строить чертеж, причем как можно большего размера — так будет лучше видно детали.

Но вернёмся к объяснению задач на доказательство ученикам. Самое главное — объяснить, как должно строиться доказательство, потому что именно здесь у учеников возникают проблемы. Обычно они двух видов:

• слабые ученики просто не берутся за доказательство, потому что не понимают, что делать,
• а сильные в ходе доказательства могут опускать и не расписывать некоторые важные пункты, потому что для них они кажутся очевидными, что приводит к нарушению логики и потере баллов.

Удобная аналогия для решения задач на доказательство

А секрет прост. Доказательство должно быть похоже на заплетание косички:

• три пряди, на которые мы делим все волосы — это то, что нам дано,
• готовая косичка — то, что должно получиться или то, что нужно доказать,
• процесс вплетания прядей — построение логической связи.

Заметили сходство с алгоритмом выше?

Если вы сможете донести это до учеников, то проблема с пропуском важных этапов решится. Ведь мы не можем пропустить прядь, пока плетём косичку? Тогда она у нас просто не получится.

Если пример с косичкой не поможет, то можно провести аналогию с объяснением доказательства очень-очень слабому ученику. Нужно посоветовать ему представить, что, записывая доказательство, он объясняет его другу, который ничего не понимает и всегда задаёт один и тот же вопрос «Почему?». Тогда «отвечая» каждый раз на «Почему?», ученик автоматически будет всё подробно расписывать, а у эксперта при проверке такого вопроса не возникнет.

Давайте объединим все вышеуказанные приёмы и алгоритм и разберём несложную задачу на доказательство. Я буду писать объяснение от первого лица, которое вы можете использовать на уроке, и к нему иногда добавлять поясняющие комментарии.

Разбор задачи на доказательство

Шаг 1. Понять, что нам дано

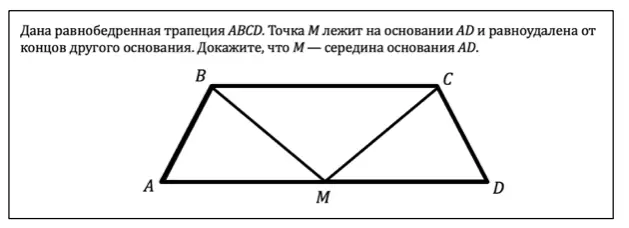
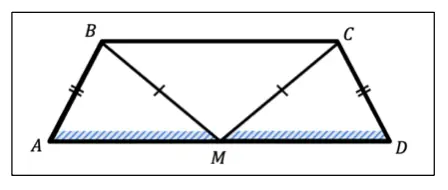
К счастью, первый пункт алгоритма можно опустить, потому что чертёж нам уже дан. Далее нужно вынести на чертёж всё что дано, а именно:

• АВ = CD, так как по условию трапеция равнобедренная, а значит её боковые стороны равны,
• ВМ = СМ, так как точка М равноудалена концов основания ВС.

Шаг 2. Понять, что нужно доказать

Теперь отмечаем то, что нужно доказать:

• нужно доказать, что М — середина AD, а значит отрезки АМ и MD должны быть равны.

Итак, получается следующая картина:

А теперь нужно построить логическую цепочку от того, что нужно найти, до того, что дано.

Я не оговорилась, нужно идти от вопроса к тому, что есть. Скажите ученикам, чтобы они представили, будто раскручивают клубок с рассуждениями, а когда дойдут до точки начала, будут закручивать его обратно и записывать всё по порядку. Кстати, вот вам ещё один приём, который поможет научить учеников доказывать задачи.

Шаг 3. Выстроить логическую цепочку

• Итак, как мы можем доказать, что AM = MD? Верно, из треугольников ABM и MCD, ведь если мы докажем, что данные треугольники равны, то и все их элементы тоже будут равны. Сейчас мы раскрутили первый виток нашего клубочка.
• Как нам доказать, что треугольники ABM и MCD равны? Правильно, у нас уже есть две равные стороны, осталось доказать, что углы ABM DCM равны. Ещё виток раскрутили!
• А как доказать, что углы ABM DCM равны? Конечно, можно воспользоваться свойством равнобедренной трапеции, а также получившимся равнобедренным треугольником ВМС. Вот мы и раскрутили клубок! А теперь будем его закручивать, подробно всё расписывая.

Не забывайте про ученика-почемучку, которому вы как будто объясняете доказательство. А также не забудьте в решение выписать всё то, что вы уже вынесли на чертёж, начинать нужно именно с этого.

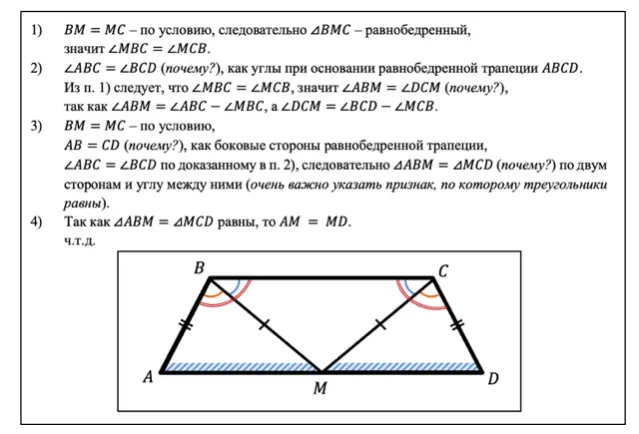
1. ВМ = МС по условию, следовательно треугольник BMC — равнобедренный, значит углы МВС и МСВ равны.
2. Углы АВС и BCD равны (почему?), как углы при основании равнобедренной трапеции ABCD.
   Из п. 1) следует, что углы МВС и МСВ равны, значит углы АВM и DCM равны (почему?), так как АВM = АВС — МВС, а DCM = BCD — МСВ.
3. ВМ = МС по условию,
   АВ = CD (почему?), как боковые стороны равнобедренной трапеции,
   углы АВС и BCD равны по доказанному в п. 2), следовательно треугольники ABM и MCD равны (почему?) по двум сторонам и углу между ними (очень важно указать признак, по которому треугольники равны).
4. Так как треугольники ABM и MCD равны, то AM = MD.
   Что и требовалось доказать.

Вот так легко мы доказали задачу, используя:

• алгоритм решения геометрической задачи,
• косичку,
• ученика-почемучку
• и клубочек.

Теперь вы знаете, как объяснить доказательство самому слабому ученику, а также как подсказать сильному, чтобы он не упускал важные факты. И пусть мы разобрали задачу уровня ОГЭ, в ЕГЭ на более сложных примерах все эти принципы работают с таким же успехом.

Добрый день, дорогие друзья! Сегодня мы с вами поговорим про задачи на доказательства по геометрии 7 класса.
В геометрии, в отличии от алгебры,  есть очень много задач на доказательство тех или иных тем.
В таких задачах, как правило, очень мало вычислительного материала, зато очень много логических рассуждений, связанных между собой цепочкой доказательств.
Здесь важно выделить конец доказательства, а затем, идя к началу, раскручивать его.
Как это происходит,  мы сегодня разберём.

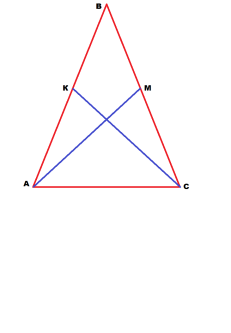
Задача 1. Докажите, что медианы, проведённые к боковым сторонам равнобедренного треугольника, равны.
Доказательство. Предположим, что мы доказали равенство медиан.
Смотрим, в каких фигурах эти медианы находятся, и что можно сказать об этих фигурах.
Итак, медианы АМ и СК находятся в треугольниках АМС и АКС или в треугольниках АВМ и СВК. Для доказательства равенства медиан надо доказать равенство треугольников.
Выбираем первую пару.  Треугольники АМС и СКА. Поскольку треугольник АВС равнобедренный, то АВ=ВС.
Но медиана делит противоположную сторону треугольника пополам. Отсюда АК=КВ=СМ=ВМ. Или АК=СМ.
Углы при основании равнобедренного треугольника равны. Получается ∠А=∠С.  Теперь вернёмся опять к треугольникам АМС и СКА. У них АК=СМ.
Угол МСА равен углу КАС, а сторона АС — общая.
Получается, треугольники равны по первому признаку равенства треугольников.
А в равных треугольниках против равных углов лежат равные стороны.
Против угла  МСА в треугольнике АМС лежит сторона АМ, а против угла КАС в треугольнике СКА лежит сторона КС. Значит, эти стороны равны.
Медианы, проведённые к боковым сторонам равнобедренного треугольника, равны.

Задача 2. Докажите, что диагональ параллелограмма разбивает его на 2 равных треугольника.
Доказательство. И опять, как в задаче 1. Предположим, что треугольники  АВД и ВСД равны.
Диагональ параллелограмма принадлежит обоим треугольникам. Т.е. у них одна сторона общая.
Осталось найти либо 2 пары равных углов, либо  равные стороны и два равных угла, либо по две равных стороны.
У параллелограмма, как мы знаем, противоположные стороны равны.
Имеем АД=ВС, АВ=СД.  Получается, что треугольники равны по трем сторонам.
Можно доказать по другому, согласно 2 признаку равенства треугольников.
В треугольниках АВД и ВСД углы
СВД и ВДА равны, как накрест лежащие
при параллельных прямых   ВС и АД и секущей ВД.
Углы ВДС и АВД равны, как накрест лежащие при параллельных прямых АВ и СД и секущей ВД.
Получается, что треугольники равны по стороне и двум прилежащим к ней углам.

 

Задача 3. Докажите, что отрезки касательных, проведённых к окружности из одной точки, равны.
Доказательство. Нам дано, что из точки С проведены 2 касательных АС и ВС  к окружности.
Для того, чтобы провести доказательство равенства сторон, сделаем дополнительные построения.
Проведём радиусы ОА и ОВ, а также прямую ОС. Доказав равенство треугольников ОАС и ОВС, мы сможем доказать равенство сторон АС и ВС.
Мы знаем, что радиусы, проведённые в точку касания перпендикулярны касательной. Поэтому, углы ОАС и ОВС — прямые.
Отсюда, треугольники САО и СВО — прямоугольные.
Эти треугольники равны, т.к. катеты ОА и ОВ равны, а гипотенуза ОС у них общая. Прямоугольные треугольники равны по катету и гипотенузе.
А в равных треугольниках против равных сторон лежат равные углы. Против стороны ОА лежит угол АСО, а против стороны ОВ — угол ВСО.
Эти углы равны. А если 2 угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы у них равны.
Значит, углы ВОС и АОС равны.
А в равных треугольниках против равных углов лежат равные стороны.
Против угла АОС лежит сторона АС, а против угла ВОС — сторона ВС.
Углы равны, значит и стороны АС и ВС равны.

На сегодня, пожалуй, достаточно. Ведь скоро Новый Год, все мысли о нём,
так что геометрию ненадолго отложим в сторону.
Спасибо всем и с НОВЫМ ГОДОМ!

«Если две стороны и угол между
ними одного треугольника равны двум сторонам и углу между ними другого
треугольника, то эти треугольники равны.»

Сокращенно его называют равенство «по
двум сторонам и углу между ними».

Прежде чем перейти к доказательству теоремы необходимо
вспомнить, что называют треугольником и в каком случае можно утверждать, что
два треугольника равны.

Что такое
треугольник и когда они считаются равными?

Треугольник –
это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии,
что они не лежат на одной прямой. Эти точки считаются вершинами треугольника.
А соединяющие их отрезки – сторонами).

На рисунке 1 представлен треугольник ABС. Который имеет три
вершины (А, В и С). И стороны – АВ, АС и ВС.

Рисунок
1

Треугольники считаются равными, когда все их стороны и углы
соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны,
треугольники называются подобными).
Таким образом очевидно, что равные треугольники можно наложить друг на друга –
и они полностью совпадут.

Дано:

Два
треугольника: ABC и DEF (рисунок 2).

Рисунок 2

По условию
теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ =
EF). Углы между отрезками также равны (т.е. ∠АСВ
= ∠EFD).

Доказать,
что треугольник ABC равен треугольнику DEF.

Доказательство:

1.               
Поскольку имеется равенство углов (∠АСВ
= ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина
С совпадала с вершиной F.

2.               
При этом отрезки СА и СВ наложатся на отрезки FE и FD.

3.               
А поскольку отрезки двух треугольников равны между собой (АС = FD
и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.

4.               
Это в свою очередь даст совмещение вершин А и D, В и Е.

5.               
Следовательно, треугольники полностью совместятся, а значит, они
равны.

Теорема
доказана.

Второй
признак равенства треугольников

Если
сторона и два прилежащих к ней угла одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого треугольника, то такие
треугольники равны.

MN=PR∡N=∡R∡M=∡P

Как
и в доказательстве первого признака, нужно убедиться, достаточно ли этого
для равенства треугольников, можно ли их полностью совместить?

1. Так какMN=PR, то эти отрезки совмещаются, если совместить их конечные точки.

2.
Так как∡N=∡R и∡M=∡P, то лучи MK и NK наложатся соответственно на лучи PT и RT.

3. Если
совпадают лучи, то совпадают точки их пересечения K и T.

4. Совмещены
все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит они
равны.

Третий
признак равенства треугольников

Если три
стороны одного треугольника соответственно равны трём сторонам другого треугольника,
то такие треугольники равны.

MN=PRKN=TRMK=PT

Опять
попробуем совместить треугольникиΔMNK и ΔPRT наложением и убедится, что
соответственно равные стороны гарантирует и равенство соответственных углов
этих треугольников и они полностью совпадут.

Совместим,
например, одинаковые отрезки MK иPT. Допустим, что точки N и R при этом не совмещаются.

Пусть O — середина отрезка NR.
Соответственно данной информацииMN=PR, KN=TR. Треугольники MNR и KNR равнобедренные с общим основанием NR.

Поэтому
их медианы MO и KO являются
высотами, значит перпендикулярны NR.
Прямые MO и KO не
совпадают, так как точки M, K, O не
лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы
пришли к противоречию.

Доказано,
что должны совместиться и вершины N и R.
  

Третий
признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда
говорят, что треугольник — жёсткая фигура.
Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника
такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.

Теорема
4.6. Из любой точки, не лежащей на данной прямой, можно опустить на эту
прямую перпендикуляр, и только один.

Доказательство.
Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через
какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через
точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как
прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна
и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к
прямой а.

Докажем
единственность перпендикуляра АВ. Допустим,

существует
другой перпендикуляр АС. Тогда у треугольника ABC будут два прямых угла. А это,
как мы знаем, невозможно. Теорема доказана.

Медианы,
биссектрисы и высоты треугольника

Медиана треугольника —
это отрезок, соединяющий вершину треугольника с серединой противолежащей
стороны.

Поэтому
для построения медианы необходимо выполнить следующие действия:
1. Найти середину стороны;
2. Соединить точку, являющуюся серединой стороны треугольника, с противолежащей
вершиной отрезком — это и будет медиана.

У
треугольника три стороны, следовательно, можно построить три медианы.

Все
медианы пересекаются в одной точке.

Биссектриса треугольника —
это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на
противоположной стороне.

Поэтому,
для построения биссектрисы необходимо выполнить следующие действия:
1. Построить биссектрису какого-либо угла треугольника (биссектриса
угла — это луч, выходящий из вершины угла и делящий его на две равные
части);
2. Найти точку пересечения биссектрисы угла треугольника с противоположной
стороной;
3. Соединить вершину треугольника с точкой пересечения на противоположной
стороне отрезком — это и будет биссектриса треугольника.

У
треугольника три угла и три биссектрисы.

Все
биссектрисы пересекаются в одной точке.

Высота треугольника —
это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей
противоположную сторону.

Поэтому,
для построения высоты необходимо выполнить следующие действия:
1. Провести прямую, содержащую одну из сторон треугольника (в
случае, если проводится высота из вершины острого угла в тупоугольном
треугольнике);
2. Из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к
ней (перпендикуляр — это отрезок, проведённый из точки к прямой,
составляющей с ней угол 90°) —
это и будет высота.

Также
как медианы и биссектрисы, треугольник имеет три высоты.

Высоты треугольника
пересекаются в одной точке.

Но,
как выше упомянуто, для некоторых видов треугольников построение высот и точки
их пересечения отличается. 

Если
треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать
высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот
является общая вершина перпендикулярных сторон.

Если
треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят
вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты,
пересекаются вне треугольника.

Обрати внимание!

Если из одной и той же
вершины провести медиану, биссектрису и высоту, то медиана окажется самым
длинным отрезком, а высота — самим коротким отрезком.

Равнобедренный
треугольник

Если
у треугольника две стороны равны, то такой треугольник называют равнобедренным.

Равные
стороны называют боковыми, а
третью сторону — основанием.

AB=BC — боковые стороны , AC —
основание.

Если
у треугольника все три стороны равны, то такой треугольник является равносторонним.

Равнобедренный
треугольник имеет некоторые свойства, которые не имеют треугольники с разными
сторонами.

1.
В равнобедренном треугольнике углы при основании равны.

2.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является
медианой и высотой.

3.
В равнобедренном треугольнике медиана, проведённая к основанию, является
биссектрисой и высотой.

4. В
равнобедренном треугольнике высота, проведённая к основанию, является
биссектрисой и медианой.

Первое
и второе свойство можно доказать, если докажем равенство двух
треугольников, которые образуются, когда углу напротив основания провести
биссектрису BD.

Рассмотрим
равнобедренный треугольник ABC с
основанием AC и докажем, чтоΔABD=ΔCBD.

Пусть BD — биссектриса треугольника ABC.  ΔABD=ΔCBD по
первому признаку равенства треугольников (AB=BC по условию, BD —
общая сторона, ∡ABD=∡CBD, так как BD —
биссектриса).

У
равных треугольников равны все соответствующие элементы:

1. ∡A=∡C — доказано, что прилежащие основанию углы равны.

2. AD=DC — доказано, что биссектриса является медианой.

3. ∡ADB=∡CDB —
так как смежные углы, сумма которых180°, равны,
то каждый из них равен90°, то есть медиана является
высотой.

Можно
очень легко самостоятельно доказать и третье и четвёртое свойство.

1. Первый признак параллельности.

Если при
пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти
прямые параллельны.

Пусть прямые АВ и СD
пересечены прямой ЕF и / 1 = / 2. Возьмём
точку О — середину отрезка КL секущей ЕF (черт. 189).

Опустим из точки О
перпендикуляр ОМ на прямую АВ и продолжим его до пересечения с прямой СD,
АВ_|_МN. Докажем, что и СD_|_МN. 
Для этого рассмотрим два треугольника: МОЕ и NОК. Эти треугольники равны между
собой. В самом деле: / 1 = / 2 по условию
теоремы; ОK = ОL — по построению;
/ МОL = / NОК, как вертикальные углы. Таким
образом, сторона и два прилежащих к ней угла одного треугольника соответственно
равны стороне и двум прилежащим к ней углам другого треугольника;
следовательно, / МОL =  / NОК, а
отсюда и 
/ LМО =  / КNО, но  / LМО прямой,
значит, и  / КNО тоже прямой. Таким образом, прямые АВ
и СD перпендикулярны к одной и той же прямой МN, следовательно, они
параллельны (§ 33), что и требовалось доказать.

Примечание. Пересечение прямых МО и СD
может быть установлено путём поворота треугольника МОL вокруг точки О на 180°.

2. Второй признак параллельности.

Посмотрим, будут ли
параллельны прямые АВ и СD, если при пересечении их третьей прямой ЕF равны
соответственные углы.

Пусть какие-нибудь
соответственные углы равны, например  /  3 =  / 2
(черт. 190); 
/ 3 =  / 1, как углы вертикальные; значит,  / 2
будет равен  / 1. Но углы 2 и 1 — внутренние накрест лежащие
углы, а мы уже знаем, что если при пересечении двух прямых третьей внутренние
накрест лежащие углы равны, то эти прямые параллельны. Следовательно, АВ || СD.

Если при
пересечении двух прямых третьей соответственные углы равны, то эти две прямые
параллельны.

На этом свойстве основано
построение параллельных прямых при помощи линейки и чертёжного треугольника.
Выполняется это следующим образом.

Приложим треугольник к
линейке так, как это показано на чертеже 191. Будем передвигать треугольник
так, чтобы одна его сторона скользила по линейке, а по какой-либо другой
стороне треугольника проведём несколько прямых. Эти прямые будут параллельны.

3. Третий признак параллельности.

Пусть нам известно, что
при пересечении двух прямых АВ и СD третьей прямой сумма каких-нибудь
внутренних односторонних углов равна 2d (или 180°). Будут ли в этом
случае прямые АВ и СD параллельны (черт. 192).

Пусть / 1
и / 2—внутренние односторонние углы и в сумме составляют 2d. 
Но / 3 + / 2 = 2d, как углы смежные.
Следовательно,  / 1 + / 2 = / 3+ / 2.

Отсюда  / 1
=  / 3, а эти углы внутренние накрест лежащие. Следовательно,
АВ || СD.

Если при
пересечении двух прямых третьей сумма внутренних односторонних углов
равна 2d,
то эти две прямые параллельны.

Признак –
это некоторый факт, благодаря которому мы устанавливаем справедливость
интересующего нас суждения о некотором объекте.

Если при
пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две
прямые параллельны.

Свойство –
если мы уверены в справедливости суждения, мы формулируем свойство
объекта.

Если две
прямые параллельны, то при пересечении их с третьей секущей накрест лежащие
углы равны.

Аксиома,
в свою очередь, такая истина, которую не надо доказывать. В каждой науке есть
свои аксиомы, на справедливость которых строят все дальнейшие суждения и
их доказательства.

Аксиома
параллельных прямых.

В одной
плоскости с заданной прямой через точку, не лежащую на этой прямой, можно
провести только одну прямую, параллельную заданной прямой.

Иногда
эту аксиому называют как одно из свойств параллельных прямых, но на
справедливости этой аксиомы строятся многие доказательства в геометрии.

Другие
свойства параллельных прямых.

1.
Если одна из пары параллельных прямых параллельна третьей прямой, то и другая
прямая параллельна третьей прямой.

2. Если
некая прямая пересекает одну из двух параллельных прямых, то она пересекает и
вторую параллельную прямую.

Эти
свойства в отличии от аксиомы нужно доказать.

Докажем
1. Свойство.  

Даны
две параллельные прямые a и b. Верно ли, если прямая c параллельна
прямой a, то она параллельна и прямой b?

 

Используем
противоположное суждение.

Допустим,
что возможна ситуация, когда прямая c параллельна
одной из параллельных прямых – прямой a,
пересекает другую прямую b в
некоторой точке K.

Получается
противоречие с аксиомой параллельных прямых. Мы имеем ситуацию, когда через
точку проходят две пересекающиеся прямые, которые параллельны одной и той же
прямой a. Такого не может быть, значит прямые b и cпересекаться не могут.

Мы
доказали, что верно – если одна из пары параллельных прямых параллельна третьей
прямой, то и другая прямая параллельна третьей прямой.

Попробуй доказать самостоятельно 2. Свойство.

Если
некая прямая c пересекает
одну из двух параллельных прямых a,
то она пересекает и вторую параллельную прямую b. 

Таким
же методом от противоположного суждения попробуй представить, что возможно
ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает
другую.

Свойства
углов, которые образуются при пересечении двух параллельных прямых с третьей
секущей мы уже назвали в первой части теории.

При
пересечении двух параллельных прямых третьей секущей:

–
накрест лежащие углы равны,

–
соответственные углы равны,

– сумма
односторонних углов равна 180°.

Теорема об
углах, образованных двумя параллельными прямыми и секущей

Теорема об углах, образованных двумя параллельными прямыми и
секущей

Теоремы

1.  
Если две параллельные прямые пересечены секущей, накрест лежащие
углы равны.

2.  
Если две параллельные прямые пересечены секущей, то
соответственные углы равны.

3.  
Если две параллельные прямые пересечены секущей, то сумма односторонних
углов равна 180°.

4.  
Если при пересечении двух прямых секущей накрест лежащие углы
равны, топрямые параллельны.

Доказательство

1. Пусть параллельные прямые a и b пересечены
секущей MN (c). Докажем, что накрест лежащие углы 3 и 6
равны. Допустим, что углы 3 и 6 не равны. Отложим от луча MN угол PMN,
равный углу 6, так, чтобы угол PMN и угол 6 были накрест
лежащими углами при пересечении прямых МР и b секущей MN.
По построению эти накрест лежащие углы равны, поэтому МР||b.
Мы выяснили, что через точку М проходят две прямые
(прямые a и МР), параллельные прямой b.
Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно
и угол 3 равен углу 6.

3.4.
Углы с соответственно параллельными и перпендикулярными сторонами

Дано:  || ,  || .

Требуется доказать , , =, =.

Доказательство:

(соответственные при
параллельных  и  и секущей ). (соответственные при
параллельных  и  и секущей ). . (вертикальные), поэтому . = и = (по свойству смежных углов). Эти
два равенства останутся верными, если  заменим равным углом . Тогда = и =. Что и требовалось доказать. 

Дано: , ,  и .

Требуется доказать: ,,,=, =.

Доказательство:

=— и =—, поэтому . || и ||. (по теореме 1). Отсюда . Тогда , =, =.

1. Сумма углов треугольника

Теория:

Сумма
углов треугольника равна 180°.

Доказательство.

Рассмотрим
произвольный треугольник KLM и докажем, что ∡K+∡L+∡M=180°.

Проведём
через вершину L прямую a, параллельную стороне KM.

Углы, обозначенные 1, являются накрест лежащими углами при пересечении
параллельных прямых a и KMсекущей KL, а углы, обозначенные 2 — накрест лежащими углами при пересечении тех же
параллельных прямых секущей ML.

Очевидно,
сумма углов 1, 2 и 3 равна развёрнутому углу с вершиной L, т. е. 
∡1+∡2+∡3= 180°или ∡K+∡L+∡M=180°.

Теорема
доказана.

Следствия
из теоремы о сумме углов треугольника

Следствие 1. Сумма
острых углов прямоугольного треугольника равна 90°.

Следствие 2.  В равнобедренном
прямоугольном треугольнике каждый острый угол равен 45°.

Следствие 3.  В
равностороннем треугольнике каждый угол равен 60°.

Следствие 4.  В любом
треугольнике либо все углы острые, либо два угла острые, а третий — тупой или
прямой.

Следствие 5. Внешний
угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство.

Из
равенств ∡KML+∡BML= 180° и ∡K+∡L+∡KML=180° получаем, что ∡BML=∡K+∡L.

Остроугольный,
прямоугольный и тупоугольный треугольники

Как
гласит четвёртое следствие из теоремы о сумме углов треугольника, можно
выделить три вида треугольников в зависимости от углов.

У
треугольника KLM все углы острые.

У
треугольника KMN угол K=90°.

У
прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.

На рисунке MN — гипотенуза, MK и KN — катеты.

У
треугольника KLM один угол тупой.

Соотношения
между сторонами и углами треугольника. Неравенство треугольника

Теорема 1. В
треугольнике против большей стороны лежит больший угол.

Доказательство. Пусть
в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).

Рис.1

Докажем, что ∠ С > ∠
В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD
< АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является
частью угла С и, значит, ∠ C > ∠
1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2
равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠
С > ∠ 1, ∠ 1 = ∠
2, ∠ 2 > ∠ B. Отсюда следует, что ∠
С > ∠ В.

Справедлива и обратная теорема (ее доказательство проводится
методом от противного).

Теорема 2. В
треугольнике против большего угла лежит большая сторона.

Из теоремы 1 вытекает

Следствие 1. Если два угла треугольника равны, то
треугольник равнобедренный (признак равнобедренного
треугольника).

Доказательство следствия проводится методом от противного.

Из следствия 1 следует, что если три угла треугольника равны, то
треугольник равносторонний.

Из теоремы 2 получаем

Следствие 3. В прямоугольном треугольнике гипотенуза
больше катета.

С использованием теоремы 2 устанавливается следующая теорема.

Теорема 3. Каждая
сторона треугольника меньше суммы двух других сторон.

Следствие 4. Для любых трех точек А, В и С, не
лежащих на одной прямой, справедливы неравенства: 
АВ < АС + СВ, АС <
АВ + ВС, ВС < ВА + АС.

Каждое из этих неравенств называется неравенством треугольника.

1. Прямоугольные треугольники

Теория:

Свойства
прямоугольного треугольника

Сумма
двух острых углов прямоугольного треугольника равна 90°.

Сумма
углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника∡1+∡2=90°.

Катет
прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее
катета против угла в 30°).

Рассмотрим
прямоугольный треугольник ABC, в котором∡A — прямой, ∡B=30°и значит, что ∡C=60°.

Докажем,
что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD как показано на рисунке.

Получим
треугольник BCD, в котором∡B=∡D=60°, поэтому DC=BC. Но DC=2AC. Следовательно, BC=2AC.

Справедливо
и обратное суждение.

Если
катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в
два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства
прямоугольных треугольников

В прямоугольном треугольнике угол между катетами прямой, а
любые два прямых угла равны. Поэтому согласно теоремам о первом и втором
признаках равенства треугольников справедливы следующие утверждения:

Учитывая, что сумма двух острых углов прямоугольного треугольника равна 90°,
получаем еще два признака равенства прямоугольных треугольников:

В самом деле, в таких треугольниках два других острых угла
также равны, поэтому указанные треугольники равны по второму признаку равенства
треугольников.

Рассмотрим еще один признак равенства прямоугольных
треугольников.

Теорема. Если
гипотенуза и катет одного прямо­угольного треугольника соответственно равны
гипотенузе и катету другого прямоугольного треугольника, то такие треугольники
равны.

Доказательство. Рассмотрим прямоугольные треугольники ABC и A₁B₁C₁, у которых
углы A и A₁ прямые, BC = B₁C₁ и AB = A₁B₁ (рис.
105, а). Докажем, что эти треугольники равны.

Приложим треугольник ABC к треугольнику A₁B₁C₁ так, чтобы
вершина A совместилась с вершиной A₁, вершина B
– с вершиной B₁, а вершины C и C₁ оказались
по разные стороны от прямой A₁B₁ (рис.
105, б). Поскольку ∠CA₁C₁ = 90° +
90° = 180°, то точки C, A₁ и C₁ будут лежать на одной прямой. Треугольник CB₁C₁
равнобедренный, поэтому ∠C = ∠C₁. Следовательно, прямоугольные треугольники ABC и A₁B₁C равны по
гипотенузе (BC = B₁C₁) и острому углу (∠C = ∠C₁). Теорема
доказана.

Расстояние
между двумя параллельными прямыми – определение.

Определение расстояния
между двумя параллельными прямыми дается через расстояние от точки до прямой.

Определение.

Расстояние
между двумя параллельными прямыми – это расстояние
от произвольной точки одной из параллельных прямых до другой прямой.

Для наглядности
изобразим две параллельные прямые a и b,
отметим на прямой апроизвольную
точку М₁, опустим перпендикуляр из
точки М₁ на прямую b,
обозначив его H₁.
Отрезок М₁H₁ соответствует
расстоянию между параллельными прямыми a и b.

Приведенное определение
расстояния между двумя параллельными прямыми справедливо как для параллельных
прямых на плоскости, так и для прямых в трехмерном пространстве. Более того,
такое определение расстояния между двумя параллельными прямыми принято не
случайно. Оно тесно связано со следующей теоремой.

Теорема.

Все
точки одной из двух параллельных прямых удалены на одинаковое расстояние от
другой прямой.

Доказательство.

Рассмотрим параллельные
прямые a и b.
Отметим на прямой a точку М₁,
опустим из нее перпендикуляр на прямую b.
Основание этого перпендикуляра обозначим как H₁.
Тогда длина перпендикуляра М₁H₁ есть
расстояние между параллельными прямыми a и b по
определению. Докажем, что  равно ,
где М₂ – произвольная точка
прямой a, отличная от точки M₁,
а H₂ – основание
перпендикуляра, проведенного из точки М₂ на
прямую b. Доказав этот факт, мы докажем и саму
теорему.

Так как
внутренние накрест лежащие углы, образованные при пересечении двух параллельных
прямых секущей, равны (об этом говорилось в статье параллельные прямые, параллельность прямых),
то , а прямая M₂H₂,
перпендикулярная прямой b по
построению, перпендикулярна и прямой a.
Тогда треугольники М₁H₁H₂ и М₂М₁H₂ прямоугольные,
и, более того, они равны по гипотенузе и острому углу: М₁H₂ –
общая гипотенуза, . Из равенства треугольников следует
равенство их соответствующих сторон, поэтому, . Теорема
доказана.

СОДЕРЖАНИЕ

Введение

1.    
Первый
признак равенства треугольников

2.    
Второй
признак равенства треугольников

3.    
Третий
признак равенства треугольников

4.    
Равнобедренные
треугольники

5.    
Соотношения
между элементами треугольника

Решения

Введение

Обучение
решению задач на доказательство – одна из основных целей преподавания геометрии
в школе. Начинать это обучение желательно с самого начала изучения
систематического курса геометрии. Для этого необходима серия тренировочных
задач на доказательство, решение которых состоит из одного или двух шагов.

Даже
решение задач на непосредственное применение изученных свойств и теорем требует
выработки определенных навыков. Нужно уметь выбрать нужное свойство или
теорему, необходимую для использования при решении задачи; проверить
выполнимость всех условий; провести дополнительные построения; сделать выводы.

Данное
пособие предназначено для тех, кто хочет научиться решать задачи на
доказательство по геометрии. Оно содержит задачи на доказательство,
использующие самые первые свойства и теоремы геометрии, среди которых признаки
равенства треугольников, свойства равнобедренного треугольника, соотношения
между сторонами и углами треугольника.

Решение
этих задач позволяет лучше освоить теоретический материал и научиться применять
его при решении задач. Оно не только способствует выработке соответствующих
умений и навыков, но, что более важно, развивает логическое мышление, учит
рассуждать, анализировать, аргументировать, обосновывать, доказывать.

Утверждения,
сформулированные в пособии в виде задач на доказательство, могут быть
использованы при решении различных вычислительных задач, а сами доказательства
при этом будут являться частью их решений.

Все задачи
сопровождаются рисунками, помогающими лучше понять условия задач, представить
соответствующую геометрическую ситуацию, при необходимости провести
дополнительные построения, наметить план доказательства.

Во второй
части пособия даются решения всех задач.

Задачи, предлагаемые в пособии,
могут быть использованы непосредственно после изучения соответствующих свойств
и теорем в седьмом классе, при обобщающем повторении курса геометрии в девятом
классе, а также при подготовке к ГИА и ЕГЭ по математике.

1. Первый признак равенства треугольников

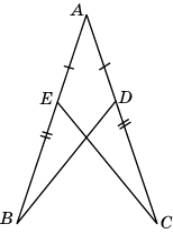
1.                
На рисунке АВ=АС, АЕ=АD.
Докажите, что BD=CE.

 

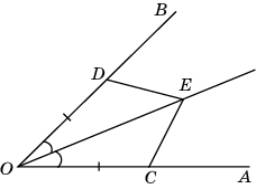
2.                
 На 
сторонах  угла  АОВ  отложены равные отрезки ОС и ОD. Произвольная
точка E биссектрисы этого угла
соединена с точками С и D. Докажите, что ЕС = ЕD.

 

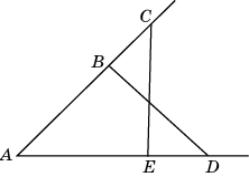
3.                
 На 
сторонах  угла  CAD
отмечены точки B и E так,
что точка B лежит на стороне AC,
а точка E – на стороне AD,
причем AC = AD и AB
= AE. Докажите, что CBD = DEC.

 

4.                
На
рисунке  АО = ОВ и DO = OC. Докажи­те
равенство отрезков AD и ВС.

 

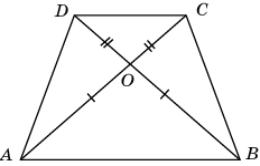5.               
В четырехугольнике ABCD AB = DC и
BAC = ACD. Докажите, что угол  B
равен углу D.

 

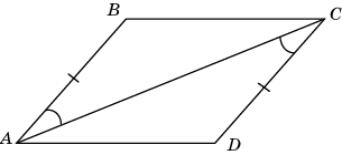6.                
 В
четырехугольнике ABCD AB = DC и
BAC = ACD. Докажите, что AD
= BC.

 

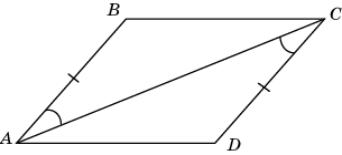7.                
На рисунке АВ = AD и BAC = DAC. Докажите, что BC = CD.

 

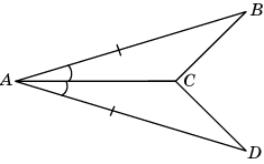8.                
 На рисунке АВ = AD и BAC = DAC. Докажите, что B = D.

 

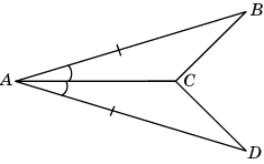9.     На рисунке A = B, AD = BC. 
Докажите, что AC = BD,

 

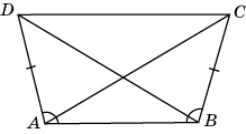10.           
Точки A, B, C
принадлежат одной прямой. Точки D₁ и D₂ лежат
по разные стороны от этой прямой. Докажите, что если треугольники ABD₁ и ABD₂
равны, то треугольники BCD₁ и BCD₂ тоже
равны.

 

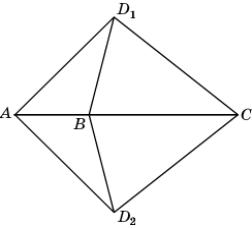11.           
На
каждой стороне правильного треугольника ABC последовательно отложены равные отрезки AD, BE, CF.
Докажите, что треугольник  DEF
тоже правильный.

 

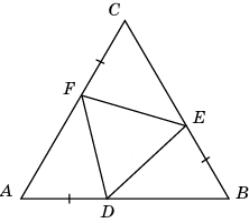12.           
 На продолжении каждой стороны правильного
треугольника ABC последовательно отложены
равные отрезки BD, CE, AF. Докажите, что треугольник DEF
тоже правильный.

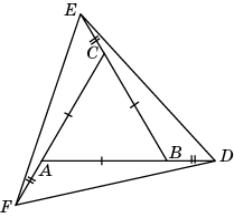2. Второй признак равенства треугольников

1.                
 В
четырехугольнике ABCD 1 = 2 и 3 = 4. Докажите,
что АB = CD.

 

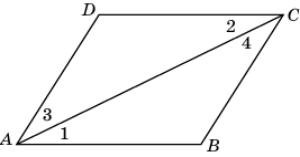2.                
 В
четырехугольнике ABCD 1 = 2 и 3 = 4. Докажите,
что АB = AD.

 

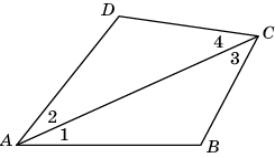3.               
На
рисунке дана фигура, у которой AD = CF, ВAC = EDF, 1 = 2. Докажите,
что АВ = DE.

 

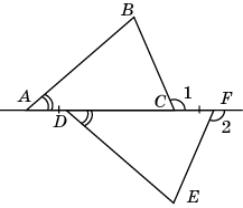4.                
 Отрезки АВ
и CD пересекаются в точке О, 
ОВ = ОС и B = C. Докажите, что АО
= DO.

 

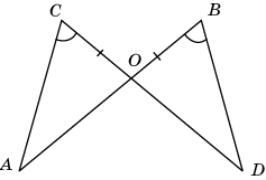5.                
 Отрезки АС
и BD пересекаются в точке О, 
АО = ОС и A = C. Докажите, что ОВ
= OD.

 

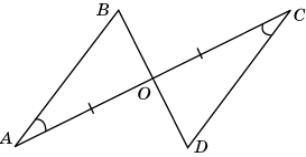6.                
 Лучи AD
и ВС пересекаются в точке О, 1 = 2, OC = OD. Докажите, что OA = OB.

 

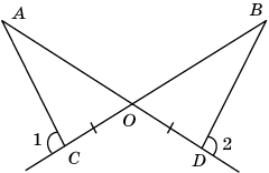7.                
 В
четырехугольнике ABCD DAB = CBА и
диагонали АС и BD
образуют со стороной АВ равные углы.
Докажите, что АС = BD.

 

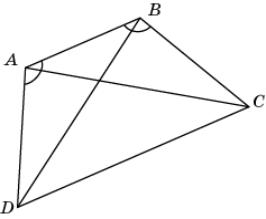8.                
 Треугольники АВС и А₁В₁С₁ равны. Отрезки CD и C₁D₁
образуют со сторонами соответственно СВ
и С₁В₁ равные углы. Докажите, что AD = A₁D₁.

 

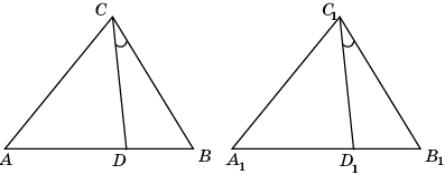9.      На рисунке BC = CD, B = D.
Докажите, что AC = CE.

 

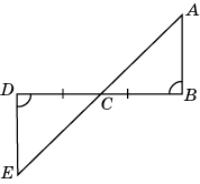3.
Третий признак равенства треугольников

1.                     
В четырехугольнике ABCD АВ = CD и BD = AC.
Докажите, что A = C.

 

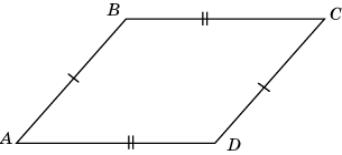2.                     
В четырехугольнике ABCD AD = BC и
AC = BD.
Докажите, что угол  BAD равен углу ABC.

 

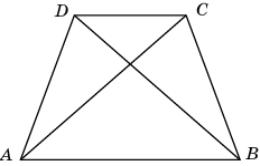3.                
 На рисунке AD = CF, AB = FE, BC = ED. Докажите,
что 1 = 2.

 

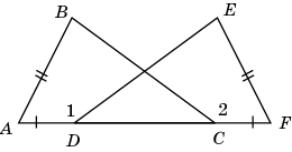4.                     
На рисунке AB = BC, AD = CD. Докажите, что 1 = 2.

 

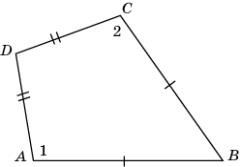5.                     
На рисунке AB = AD, CB = CD. Докажите, что B = D.

 

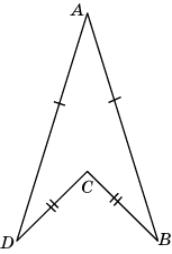6.                
На рисунке AD = CD, AO = OC. Докажите, что AB = BC.

 

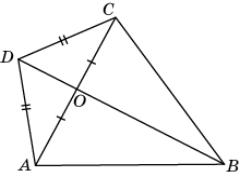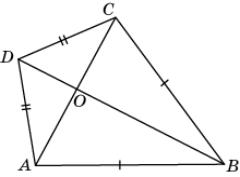
7.               
 На рисунке AB = BC, AD = CD. Докажите, что AO = OC.

 

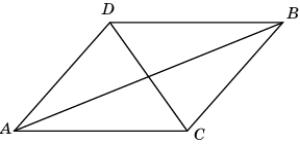
8.                
Треугольники АВС
и BAD равны, причем точки С и D лежат по раз­ные стороны от прямой АВ. Докажите, что треугольники CBD и DAC
равны.

 

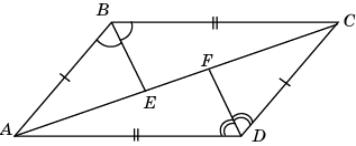
9.                
На рисунке АВ = CD, AD = BC, ВЕ – биссектриса угла АВС,
а DF – биссектриса угла ADC.
Докажите, что треугольники ABE и CDF
равны.

 

4. Равнобедренные
треугольники

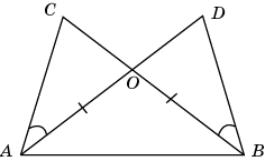
1.     На
рисунке DBC = DAC, BO = AO.
Докажите, что C = D.

 

2.                
На рисунке DBC = DAC, BO = AO.
Докажите, что AC = BD.

 

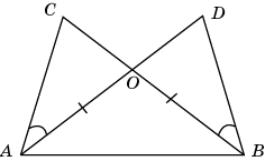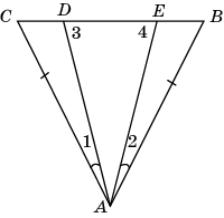
3.               
В треугольнике АВС
АВ = АС и 1=2. 
Докажите, что 3 = 4.

 

4.                
На рисунке AD = AE, CAD = BAE. Докажите, что BD = CE.

 

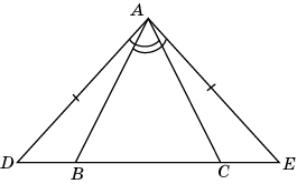5.               
На рисунке ABC AB = BC.
Докажите, что 1 =2.

 

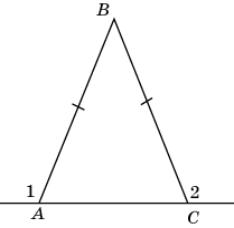6.                
 В треугольнике ABC  AB = BC. Докажите, что 1 =2.

 

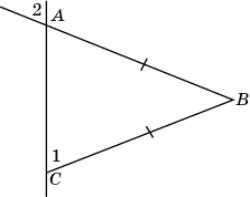7.                
 На рисунке  CD = BD, 1 = 2. Докажите, что ACB = ABC.

 

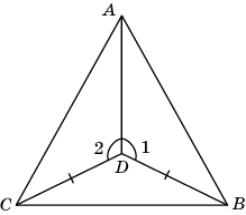8.                
 На рисунке 1 = 2, 5 = 6. Докажите, что 3 = 4.

 

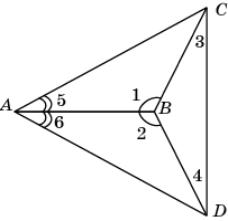9.               
На рисунке АВ = AD и DC = BC. Докажите, что ABC = ADC.

 

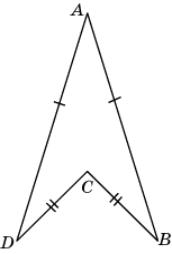10.           
На рисунке DC = BC и B = D. Докажите, что АВ = AD

 

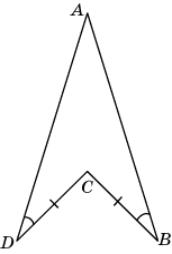11.           
 На рисунке AB = BC, CD = DE.
Докажите, что BAC = CED.

 

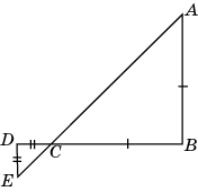12.           
На рисунке AB = BC, 1 = 2. Докажите, что AD = CD.

 

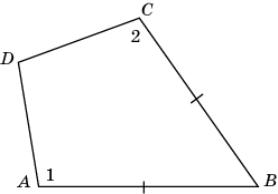5.
Соотношения
между элементами треугольника

1.                
На рисунке  AB > BC.
Докажите, что 1 >2.

 

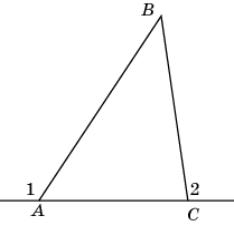2.                
На рисунке  1 >2. Докажите, что  AB > BC.

 

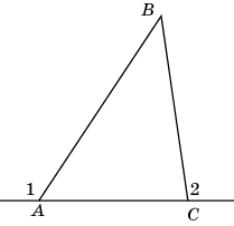3.                
На
рисунке 1 < 2. Докажите, что A < B.

 

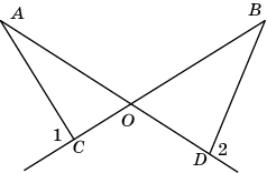4.                
На
рисунке A < B. Докажите, что 1 < 2.

 

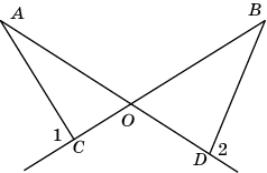5.                
На рисунке 1 = 2, 3 < 4. Докажите, что CD < AB.

 

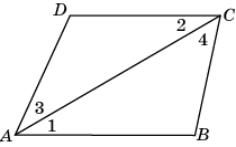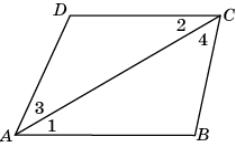
6.                
На рисунке 1 = 2, CD < AB. Докажите, что 3 < 4.

 

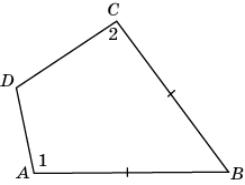
7.                
На рисунке AB = BC,  AD < CD.
Докажите, что 1 > 2.

 

8.                
 На рисунке AB = BC, 1 > 2. Докажите, что AD < CD.

 

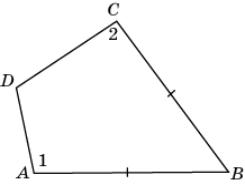9.                
На рисунке AB = AD, BC = CD, AB < BC.
Докажите, что A > C.

 

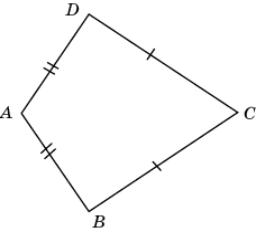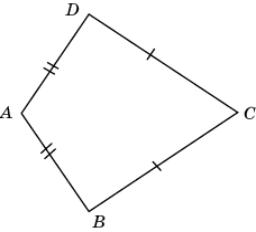
10.           
На рисунке AB = AD, BC = CD, A  > C. Докажите, что AB < BC.

 

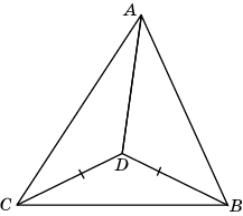
11.           
На рисунке  AC > AB, CD = BD. Докажите, что ACD < ABD.

 

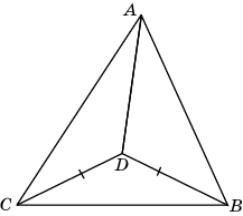
12.           
На рисунке  CD = BD, ACD < ABD.
Докажите, что AC > AB.

 

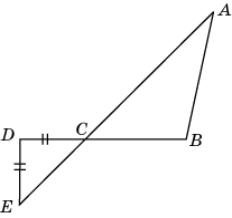
13.           
На рисунке AB > BC, CD = DE. Докажите, что BAC < DEC.

 

14.           
 На рисунке CD = DE, BAC < DEC. Докажите, что AB > BC.

 

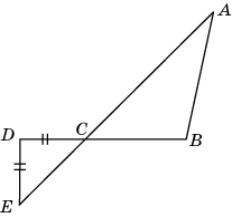15.           
 На рисунке АВ = АС и 1 >2. 
Докажите, что 3 > 4.

 

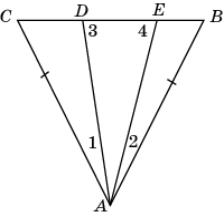16.           
На рисунке АВ = АС
и 3 >4. 
Докажите, что 1 > 2.

 

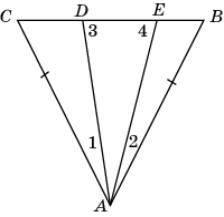17.
 Докажите, что каждая сторона треугольника
меньше его полупериметра.

 

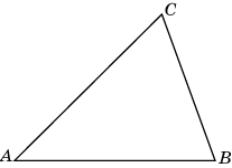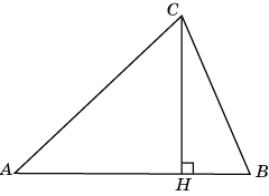
18.
 Докажите, что если в треугольнике ABC выполняется
неравенство AC > BC,
то для высоты CH выполняется неравенство ACH > BCH.

 

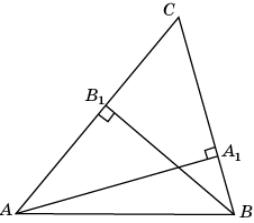
19.
 Докажите, что из двух высот треугольника
больше та, которая опущена на меньшую сторону.

 

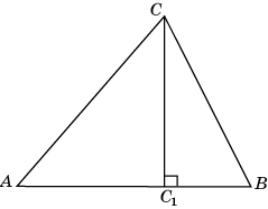
20.  Докажите, что высота треугольника меньше
полусуммы сторон, прилежащих к ней.

 

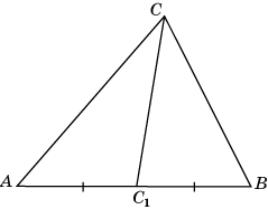
21.   Докажите, что медиана треугольника меньше
его полупериметра.

 

Решения

1. Первый
признак равенства треугольников

1.               
Треугольники
ABD и ACE равны по первому признаку
равенства треугольников (АВ=АС, АD = AE, угол A общий).
Следовательно, равны соответствующие стороны BD и CE этих треугольников.

2.               
Треугольники
OCE и ODE равны по первому признаку
равенства треугольников (OC = OD, COE = DOE, сторона OE общая).
Следовательно, равны соответствующие стороны EC и ED этих треугольников.

3.               
Треугольники
ABD и ACE равны по первому признаку
равенства треугольников (AC = AD,
АВ=АС, угол A общий). Следовательно, равны
соответствующие углы ABD  и AEC. Из
равенства этих углов следует равенство смежных углов CBD и DEC.

4.               
Треугольники
AOD и BOC равны по первому признаку
равенства треугольников (AO = BO,
DO=CO, AOD = BOC). Следовательно, равны
соответствующие стороны  AD и ВС этих треугольников.

5.               
Треугольники ABC и
CDA равны
по первому признаку равенства треугольников (AB = CD, AC –
общая сторона, BAC = ACD). Следовательно, равны
соответствующие углы  B и D этих треугольников.

6.               
Треугольники ABC и
CDA равны
по первому признаку равенства треугольников (AB = CD, AC –
общая сторона, BAC = ACD). Следовательно, равны
соответствующие стороны AD и BC этих треугольников.

7.               
Треугольники ABC и
ADC равны
по первому признаку равенства треугольников (AB = AD, AC –
общая сторона, BAC = DAC). Следовательно, равны
соответствующие стороны BC и CD этих треугольников.

8.               
Треугольники ABC и
ADC равны
по первому признаку равенства треугольников (AB = AD, AC –
общая сторона, BAC = DAC). Следовательно, равны
соответствующие углы B и D этих треугольников.

9.               
Треугольники
ABC и BAD равны по первому признаку
равенства треугольников (AB – общая сторона, BC = AD, ABC = BAD). Следовательно, равны соответствующие
стороны AC и BD этих треугольников.

10.           
Из равенства треугольников ABD₁ и ABD₂
следует равенство соответствующих сторон BD₁ и BD₂, а
также равенство соответствующих углов ABD₁ и ABD₂. Из
равенства указанных углов следует равенство смежных с ними углов CBD₁ и CBD₂.
Треугольники BCD₁ и BCD₂ равны
по первому признаку равенства треугольников (BD₁ = BD₂, BC –
общая сторона, CBD₁ = CBD₂.

11.           
Из
равенства сторон правильного треугольника и равенства отрезков AD, BE и CF следует равенство отрезков AF, CE и BD. Треугольники ADF, BED и CFE равны
по первому признаку равенства треугольников (AD = BE
= CF, AF = BD
= CE, A = B = C).
Следовательно, равны соответствующие стороны DF, DE и EF этих треугольников. Значит, треугольник DEF тоже правильный.

12.           
Из
равенства сторон правильного треугольника ABC и равенства отрезков BD, CE и AF следует равенство отрезков AD, BE и CF. Из равенства углов правильного треугольника ABC следует
равенство углов FAD, DBE и
ECF.  Треугольники
ADF, BED и CFE равны
по первому признаку равенства треугольников (AD = BE
= CF, AF = BD
= CE, FAD = DBE = ECF).
Следовательно, равны соответствующие стороны DF, DE и EF этих треугольников. Значит, треугольник DEF тоже правильный.

2. Второй признак
равенства треугольников

1.               
Треугольники ABC и
CDA равны
по второму признаку равенства треугольников (AC –
общая сторона, 1 = 2, 3 =  4).
Следовательно, равны их соответствующие стороны AB и
CD.

2.               
Треугольники ABC и
ADC равны
по второму признаку равенства треугольников (AC –
общая сторона, 1 = 2, 3 =  4).
Следовательно, равны их соответствующие стороны AB и
AD.

3.               
Из равенства углов 1 и 2
следует равенство смежных углов ACB и DFE. Из равенства отрезков AD и
CF следует
равенство отрезков AC и DF. Треугольники ACB и
DFE равны
по второму признаку равенства треугольников (AC = DF, ВAC
= EDF,
ACB = DFE). Следовательно, равны их соответствующие
стороны AB и DE.

4.                
Треугольники AOC и
DOB равны
по второму признаку равенства треугольников (OC = OB, ACO = DBO, AOC = DOB). Следовательно, равны их соответствующие
стороны AO и DO.

5.                
Треугольники AOB и
COD равны
по второму признаку равенства треугольников (AO = CO, OAB
= OCD,
AOB = DOC). Следовательно, равны их соответствующие
стороны OB и OD.

6.                
Из равенства углов 1 и 2
следует равенство смежных с ними углов ACO и
BDO. Треугольники ACO и
BDO равны
по второму признаку равенства треугольников (CO = DO,  ACO = BDO, AOC = BOD). Следовательно,
равны соответствующие стороны OA и OB этих
треугольников.

7.                
Треугольники
ABC и BAD равны по второму признаку
равенства треугольников (AB – общая сторона, ABC = BАD, BAC = ABD. Следовательно,
равны соответствующие стороны АС и BD этих треугольников.

8.                
Из
равенства треугольников АВС и А₁В₁С₁
следует равенство соответствующих сторон BC и B₁C₁, а также соответствующих углов B и B₁. Треугольники BCD и B₁C₁D₁ равны по первому признаку равенства
треугольников (BC = B₁C₁, B = B₁, BCD = B₁C₁D₁). Следовательно, равны соответствующие стороны BD и
B₁D₁ этих треугольников.  Из равенства треугольников АВС
и А₁В₁С₁ следует
равенство соответствующих сторон AB и A₁B₁. Следовательно, имеет место
равенство отрезков AD и A₁D₁.

9.               
Углы
ACB и ECD равны как вертикальные.
Треугольники ABC и EDC равны по второму признаку
равенства треугольников (BC = DC, ABC = EDC, ACB = ECD). Следовательно, равны
соответствующие стороны AC и CE этих
треугольников.

3. Третий признак равенства
треугольников

1.                                                                
В четырехугольнике ABCD проведем
диагональ BD.  Треугольники
ABD и CDB равны по третьему признаку
равенства треугольников (AB = CD, AD = BC, BD – общая
сторона). Следовательно, равны соответствующие углы BAD и BCD этих
треугольников.

2.                                                                
Треугольники
ABC и BAD равны по третьему признаку равенства
треугольников (AD = BC, AC = BD, AB – общая
сторона). Следовательно, равны соответствующие углы BAD и ABC.

3.                                                                
Из
равенства отрезков AD и CF следует равенство отрезков AC и DF.
Треугольники ABC и FED равны по третьему признаку
равенства треугольников (AB = FE, BC = ED, AC = FD).
Следовательно, равны соответствующие углы ACB и FDE этих треугольников, а, значит,
равны и смежные с ними углы 1 и 2.

4.                                                                
Проведем
отрезок BD. Треугольники ABD и CBD равны по третьему признаку
равенства треугольников (AB = CB, AD = CD, BD – общая
сторона). Следовательно, равны соответствующие углы 1 и 2 этих
треугольников.

5.                                                                
Проведем
отрезок AC. Треугольники ABC и ADC равны по третьему признаку
равенства треугольников (AB = AD, BC = CD, AC – общая
сторона). Следовательно, равны соответствующие углы B и D этих треугольников.

6.                                                                
Треугольники
AOD и COD равны по третьему признаку
равенства треугольников (AO = CO, AD = CD, OD – общая
сторона). Следовательно, равны соответствующие углы ADO и CDO. Треугольники ABD и CBD равны по
первому признаку равенства треугольников (AD = CD, BD – общая
сторона,  ADB = CDB).
Следовательно, равны соответствующие стороны
AB и BC этих треугольников.

7.                                                                
Треугольники
ABD и CBD равны по третьему признаку
равенства треугольников (AB = CB, AD = CD, BD – общая
сторона). Следовательно, равны соответствующие углы ABO и CBO. Треугольники ABO и CBO равны по
первому признаку равенства треугольников (AB = CB, BO – общая
сторона,  ABO = CBO).
Следовательно, равны соответствующие стороны
AO и CO этих треугольников.

8.                                                                
Из
равенства треугольников  АВС и BAD
следует равенство соответствующих сторон AC и BD, BC и AD. Треугольники CBD и DAC равны
по третьему признаку равенства треугольников (CB = DA, BD = AC, CD – общая
сторона.

9.                                                                
Треугольники
ABC и ADC равны по третьему признаку
равенства треугольников (АВ = CD, AD = BC, AC – общая
сторона). Следовательно, равны соответствующие углы ABC и CDA, BAC и DCA. Из
равенства углов ABC и CDA следует равенство углов ABE и  CDF. Треугольники ABE и CDF равны
по второму признаку равенства треугольников (AB = CD, BAE = DCF, ABE = CDF).

4. Равнобедренные треугольники

1.               
Треугольник
ABO равнобедренный и, следовательно, OAB = OBA. Учитывая равенство углов DAC и
DBC, получаем равенство углов ABD и
BAC. Треугольники ABC и
BAD равны по второму признаку
равенства треугольников (AB – общая сторона, ABC = BAC, BAC = ABD).
Следовательно, равны соответствующие углы C и D этих треугольников.

2.                
Треугольник
ABO равнобедренный и, следовательно, OAB = OBA. Учитывая равенство углов DAC и
DBC, получаем равенство углов ABD и
BAC. Треугольники ABC и
BAD равны по второму признаку
равенства треугольников (AB – общая сторона, ABC = BAC, BAC = ABD).
Следовательно, равны соответствующие стороны AC = BD этих
треугольников.

3.               
Треугольник
ABC равнобедренный. Следовательно, B = C. Треугольники ABE и
ACD равны
по второму признаку равенства треугольников (AB = AC, 1=2, B = C). Следовательно, равны соответствующие стороны AE и
AD этих
треугольников. Треугольник AED равнобедренный.
Следовательно, 3 = 4.

4.               
Треугольник
ADE равнобедренный. Следовательно, D = E. Треугольники ACD и
ABE равны
по второму признаку равенства треугольников (AD = AE, D=E, CAD = BAE). Следовательно, равны соответствующие стороны CD и
BE. Значит, равны и отрезки BD и CE.

5.               
Треугольник
ABC равнобедренный. Следовательно, A = C. Значит,
равны и смежные с ними углы 1 и 2.

6.                
Треугольник
ABC равнобедренный. Следовательно, A = 1. Углы A
и 2 равны как вертикальные. Значит, 1 =2.

7.                
Треугольники
ABD и ACD равны по первому признаку
равенства треугольников (AD – общая сторона, BD = CD, ADB = ADC).
Следовательно, равны соответствующие стороны AB и AC этих треугольников. Треугольник ABC равнобедренный
и, значит, ACB = ABC.

8.                
Треугольники
ABС и ABD равны по второму признаку
равенства треугольников (AИ – общая сторона, ABC = ABD, BAC = BAD).
Следовательно, равны соответствующие стороны BC и BD этих треугольников. Треугольник BCD равнобедренный
и, значит, 3 = 4.

9.               
Проведем
отрезок BD. Треугольник ABD равнобедренный (AB = AD).
Следовательно, ABD = ADB. Треугольник CBD равнобедренный
(CB = CD). Следовательно, CBD = CDB. Значит, ABC = ADC.

10.           
Проведем
отрезок BD. Треугольник BCD равнобедренный (BC = DC).
Следовательно, имеет место равенство DBC = BDC. Из этого равенства и
равенства углов ABC и ADC следует равенство углов ABD и ADB. Значит,
треугольник ABD – равнобедренный и,
следовательно, АВ = AD.

11.           
Треугольник
ABC – равнобедренный и, следовательно, BAC = BCA. Треугольник CDE –
равнобедренный и, следовательно, DCE = DEC. Углы BCA и DCE равны
как вертикальные. Следовательно, BAC = DEC.

12.           
Проведем
отрезок AC. Треугольник ABC равнобедренный (AB = BC). Следовательно,
BAC = BCA. Из этого равенства и равенства
углов 1 и 2 следует равенство углов DAC и DCA. Значит, треугольник DAC равнобедренный
и, следовательно, AD = CD.

5. Соотношения между
элементами треугольника

1.         
Так как против большей стороны треугольника лежит
больший угол, то из неравенства  AB > BC
следует неравенство BAC <BCA.
Значит, для соответствующих смежных углов выполняется неравенство 1 >2.

2.         
Из неравенства  1 >2 следует неравенство BAC <BCA. Так
как против большего угла треугольника лежит большая сторона, то выполняется
неравенство  AB > BC.

3.         
В треугольниках AOC и BOD углы AOC и BOD равны
как вертикальные. Так как внешний угол треугольника равен сумме двух
внутренних, не смежных с ним углов, то из неравенства  1 <2 следует неравенство A <B.

4.         
В треугольниках AOC и BOD углы AOC и BOD равны
как вертикальные. Так как внешний угол треугольника равен сумме двух
внутренних, не смежных с ним углов, то из неравенства  A < B следует неравенство 1 < 2.

5.         
Через точку C проведем прямую, параллельную AD, и ее точку пересечения с
прямой AB обозначим E. Так
как 3 < 4 и 3 = ACE, то точка E будет
внутренней точкой  отрезка AB. Четырехугольник ABCE –
параллелограмм и, следовательно, CD = AE < AB.

6.         
На отрезке AB возьмем точку E так,
что AE = CD. Четырехугольник ABCE –
параллелограмм. Следовательно, 3 = ACE и,
значит, 3 < 4.

7.         
В четырехугольнике ABCD проведем
диагональ AC.
Треугольник ABC равнобедренный и, следовательно, BAC = BCA. В треугольнике ACD  AD < CD и,
следовательно, DAC  > DCA. Значит, 
1 > 2.

8.         
В четырехугольнике ABCD проведем
диагональ AC.
Треугольник ABC равнобедренный и, следовательно, BAC = BCA. Из неравенства 1 > 2 следует неравенство DAC  > DCA. Так как против большего угла треугольника лежит
большая сторона, то в треугольнике ACD выполняется неравенство AD < CD.

9.         
В четырехугольнике ABCD проведем
диагональ AC. Так
как против большей стороны треугольника лежит больший угол, то DAC > DCA и  BAC  > BCA. Значит, 
в четырехугольнике ABCD A > C.

10.      В
четырехугольнике ABCD проведем диагональ AC. Треугольники ABC и ADC равны
по третьему признаку равенства треугольников. Следовательно, BAC = DAC, BCA = DCA. Значит, из неравенства A > C следует неравенство BAC > BCA. Так как против большего угла треугольника лежит
большая сторона, то в треугольнике ABC выполняется неравенство AB < BC.

11.      Так
как против большей стороны треугольника лежит больший угол, то в треугольнике ABC выполняется
неравенство ACB < ABC. Треугольник
BCD равнобедренный и, следовательно, DCB = DBC. Значит,
ACD < ABD.

12.      Треугольник BCD равнобедренный и, следовательно, DCB = DBC. Значит,
ACB < ABC. Так
как против большего угла треугольника лежит большая сторона, то в треугольнике ABC выполняется неравенство AC > AB.

13.      Так
как против большей стороны треугольника лежит больший угол, то в треугольнике ABC выполняется
неравенство BAC < BCA. Треугольник
CDE  равнобедренный и, следовательно, DEC = DCA. Углы
BCA и DCE равны как вертикальные.
Значит, BAC < DEC.

14.       Треугольник
CDE равнобедренный и, следовательно,
DEC = DCA. Углы
BCA и DCE равны как вертикальные.
Значит, BAC < DEC. Так как против большего угла треугольника лежит
большая сторона, то в треугольнике ABC выполняется неравенство AB > BC.

15.       Треугольник
ABC равнобедренный и,
следовательно, B = C. Так
как внешний угол треугольника равен сумме двух внутренних, не
смежных с ним углов, то из равенства углов B, C и неравенства 1 >2 следует
неравенство  3 > 4.

16.      Треугольник ABC равнобедренный и, следовательно, B = C. Так
как внешний угол треугольника равен сумме двух внутренних, не
смежных с ним углов, то из равенства углов B, C и неравенства 3 >4 следует
неравенство  1 > 2.

17.     
Воспользуемся
тем, что каждая сторона треугольника меньше суммы двух других сторон. В
треугольнике ABC имеем: AB
< AC + BC. Прибавляя к обеим частям
этого неравенства AB, получим  2AB < AB
+ BC + AC. Следовательно, AB
< ( AB + BC + AC).
 

18.     
Из
неравенства AC > BC
для наклонных следует неравенство AH > BH
для их проекций. На отрезке AH отложим отрезок HD,
равный HB. Прямоугольные треугольники BCH и DCH
равны по двум катетам, следовательно, ACH > CDH = BCH.

19.      Пусть в треугольнике ABC AC > BC, AA₁, BB₁ – высоты. Воспользуемся
тем, что площадь треугольника равна половине произведения стороны на высоту,
опущенную на эту сторону. Получим равенство. Из этого равенства и неравенства AC
> BC, следует, что AA₁ > BB₁.

20.      Пусть CC₁
–  высота треугольника ABC. Воспользуемся тем, что
перпендикуляр короче наклонной, проведенной из той же точки к той же прямой.
Тогда CC₁ < AC и CC₁ < BC. Складывая эти два
неравенства, получим СС₁ < (AC + BC).

21.      Пусть CC₁
–  медиана треугольника ABC. Воспользуемся тем, что
каждая сторона треугольника меньше суммы двух других сторон. Тогда CC₁ < AC + AC₁, CC₁ < BC +
BC₁. Складывая эти неравенства, получим CC₁ < (AC + BC + AB).