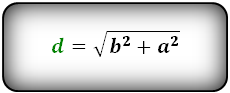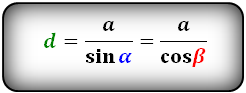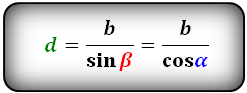Посчитать диагональ прямоугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Посчитать диагональ прямоугольника
Чтобы посчитать диагональ прямоугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).
Просто подставьте их в калькулятор и получите результат.
Чему равна диагональ прямоугольника если сторона
a = ,
а сторона
b = ?
Ответ: d =
0
Теория
Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?
Формула
d = √a2 + b2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
d = √102 + 52 = √100 + 25 ≈ 11.18 см
См. также
Загрузить PDF
Загрузить PDF
Диагональ — это отрезок, который соединяет две противолежащие вершины прямоугольника.[1]
В прямоугольнике две равные диагонали.[2]
Если известны стороны прямоугольника, диагональ можно найти по теореме Пифагора, потому что диагональ делит прямоугольник на два прямоугольных треугольника. Если стороны не даны, но известны другие величины, например, площадь и периметр или отношение сторон, можно найти стороны прямоугольника, а затем по теореме Пифагора вычислить диагональ.
-
1
-
2
-
3
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
4
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[5]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
-
1
Запишите формулу для вычисления площади прямоугольника. Формула:
, где
— площадь прямоугольника,
— длина прямоугольника,
— ширина прямоугольника.[6]
(На рисунке вместо S использовано обозначение А.) -
2
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
-
3
Перепишите формулу так, чтобы обособить
. Для этого разделите обе стороны уравнения на
. Затем полученное выражение нужно подставить в формулу для вычисления периметра.
-
4
Запишите формулу для вычисления периметра прямоугольника. Формула:
, где
— длина прямоугольника,
— ширина прямоугольника.[7]
-
5
В формулу подставьте значение периметра прямоугольника. Это значение подставляется вместо
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
-
6
Разделите обе стороны уравнения на 2. Вы получите сумму сторон прямоугольника, а именно
.
-
7
В формулу подставьте выражение для вычисления
. Это выражение, полученное при обособлении
.
-
8
Избавьтесь от дроби. Для этого обе части уравнения умножьте на
.
-
9
Приравняйте уравнение к 0. Для этого из обеих сторон уравнения вычтите член с переменной первого порядка.
-
10
Упорядочьте члены уравнения. Первым членом будет член с переменной второго порядка, затем член с переменной первого порядка, а затем свободный член. При этом не забудьте про знаки («плюс» и «минус»), которые стоят перед членами. Обратите внимание, что уравнение запишется в виде квадратного уравнения.
-
11
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
12
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (это корни уравнения), которые в случае прямоугольника являются его длиной и шириной.
-
13
-
14
-
15
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
16
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[10]
Вы найдете, то есть гипотенузу треугольника, а значит, и диагональ прямоугольника.
Реклама
-
1
-
2
-
3
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
-
4
В формулу подставьте выражение, характеризующее отношение сторон. В случае прямоугольника можно подставить выражение для вычисления
или
.
-
5
Запишите квадратное уравнение. Для этого раскройте скобки и приравняйте уравнение к нулю.
-
6
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
7
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (так называемые корни уравнения).
-
8
Подставьте найденное значение ширины (или длины) в уравнение, характеризующее отношение сторон. Так можно найти другую сторону прямоугольника.
-
9
-
10
-
11
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
12
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[16]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
Об этой статье
Эту страницу просматривали 556 611 раз.
Была ли эта статья полезной?
Укажите размеры:
Диагональ =
Решение:
Ссылка на страницу с результатом:
# Теория
Прямоугольник – это четырёхугольник у которого все углы прямые (по 90 градусов).
Диагональ прямоугольника – это прямая линия соединяющая противоположные углы. Диагонали прямоугольника обладают следующими свойствами:
- Диагонали прямоугольника равны.
- Диагональ делит прямоугольник на два равных прямоугольных треугольника и является их гипотенузой.
Формула диагонали прямоугольника
Так как диагональ делит прямоугольник на два одинаковых труегольника и является их гипотенузой, то длина и ширина прямоугольника будут катетами образованного треугольника. Поэтому для расчёта диагонали мы применяем теорему Пифагора:
Квадрат гипотенузы равен сумме квадратов катетов: c² = a² + b²
Отсюда, формула для расчётадиагонали прямоугольника выглядит следующим образом:
a
b
d
d = sqrt{a^2 + b^2}
- d – диагональ прямоугольника
- a – длина прямоугольника
- b – ширина прямоугольника
Похожие калькуляторы:
Войдите чтобы писать комментарии
Диагональ прямоугольника делит его на два прямоугольных треугольника и является гипотенузой обеих. Чтобы найти длину, проще всего воспользоваться теоремой Пифагора, которая в нашем случае будет звучать так
Это будет основная формула, но так как не всегда в условии заданы значения сторон прямоугольника, на помощь придут другие:
И теперь на нескольких примерах решим наше задание
Пример 1
найдем длину диагонали прямоугольника, если известна его а)сторона и периметр б) сторона и площадь.
Для этого сначала найдем неизвестную сторону, затем значения обеих сторон подставим в главную формулу
Пример 2
найдем длину диагонали прямоугольника, если известны его периметр и площадь.
Для этого составим систему уравнений, решим ее и подставим значения сторон в основную формулу
Пример 3
нужно найти длину диагонали прямоугольника, если известны его а)площадь и угол между диагональю и стороной б)периметр и угол между диагональю и стороной.
Решение аналогично предыдущему примеру
Как видим, без теоремы Пифагора во всех этих случаях никак не обойтись.
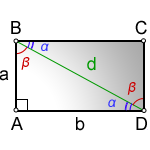
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
d – диагональ прямоугольника
a, b – стороны
α, β – углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
Формулы диагонали через сторону и угол, (d):
Формулы величины углов через диагональ и стороны, (α, β):
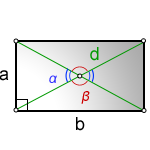
2. Формулы углов между диагоналями в прямоугольнике.
d – диагонали прямоугольника
a, b – стороны
α, β – углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):
- Подробности
-
Опубликовано: 27 октября 2011
-
Обновлено: 13 августа 2021