В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.
Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.
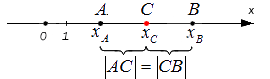
Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = |СВ|. Расстояние между точками определяется модулем разницы их координат, т.е.
|АС| = |СВ|⇔xC-xA=xB-xC
Тогда возможно два равенства: xC-xA=xB-xC и xC-xA=-(xB-xC)
Из первого равенства выведем формулу для координаты точки C : xC=xA+xB2 (полусумма координат концов отрезка).
Из второго равенста получим: xA=xB , что невозможно, т.к. в исходных данных – несовпадающие точки. Таким образом, формула для определения координат середины отрезка AB с концами A(xA) и B(xB):
xA+xB2
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy – проекции точек A, B и C на оси координат (прямые Ох и Оy).
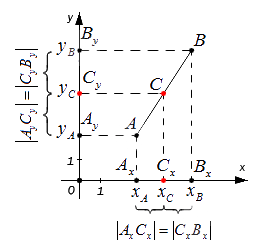
Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy. И тогда, опираясь на полученную ранее формулу, получим:
xC=xA+xB2 и yC=yA+yB2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
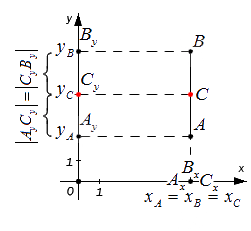
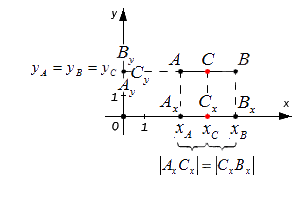
Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:
(xA+xB2, yA+yB2)
Середина отрезка в пространстве
Исходные данные: система координат Оxyz и две произвольные точки с заданными координатами A(xA, yA, zA) и B (xB, yB, zB). Необходимо определить координаты точки C, являющейся серединой отрезка AB.
Ax, Ay, Az ; Bx, By,Bz и Cx, Cy, Cz – проекции всех заданных точек на оси системы координат.
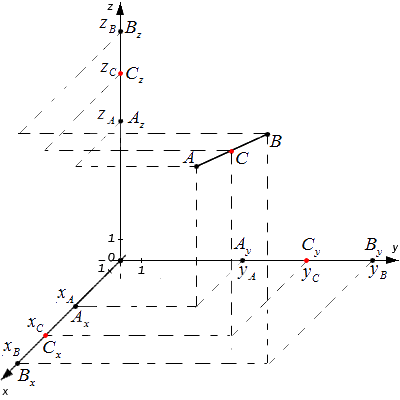
Согласно теореме Фалеса верны равенства: AxCx=CxBx, AyCy=CyBy,AzCz=CzBz
Следовательно, точки Cx, Cy,Cz являются серединами отрезков AxBx, AyBy, AzBz соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
xC=xA+xB2, yc=yA+yB2, zc=zA+ZB2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.
Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) . Выполним некоторые операции над векторами в координатах и получим:
OC→=12·OA→+OB→=xA+xB2, yA+yB2
Следовательно, точка C имеет координаты:
xA+xB2, yA+yB2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C(xA+xB2, yA+yB2, zA+zB2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Исходные данные: на плоскости – точки с заданными координатами А (-7,3) и В (2,4). Необходимо найти координаты середины отрезка АВ.
Решение
Обозначим середину отрезка AB точкой C. Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B.
xC=xA+xB2=-7+22=-52yC=yA+yB2=3+42=72
Ответ: координаты середины отрезка АВ -52, 72.
Исходные данные: известны координаты треугольника АВС: А (-1,0), В (3,2), С (9,-8). Необходимо найти длину медианы АМ.
Решение
- По условию задачи AM – медиана, а значит M является точкой середины отрезка BC. В первую очередь найдем координаты середины отрезка BC, т.е. точки M:
xM=xB+xC2=3+92=6yM=yB+yC2=2+(-8)2=-3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы АМ:
AM=(6-(-1))2+(-3-0)2=58
Ответ: 58
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед ABCDA1B1C1D1 . Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка АС1. Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: xM=xA+xC12 ⇒xA=2·xM-xC1=2·4-1+7yM=yA+yC12⇒yA=2·yM-yC1=2·2-1=3zM=zA+zC12⇒zA=2·zM-zC1=2·(-4)-0=-8
Ответ: координаты точки А (7,3,-8).
В данной публикации мы рассмотрим, что такое середина отрезка, по какой формуле считаются ее координаты (в плоскости и пространстве). Также разберем примеры решения задач по этой теме.
- Расчет координат середины отрезка
- Примеры задач
Расчет координат середины отрезка
Серединой называется точка, лежащая на отрезке и находящаяся на одинаковом расстоянии от его концов.

AC = CB
Если концы отрезка A (xa, ya) и B (xb, yb) расположены в одной плоскости, то координаты его середины (точки C) считаются по формуле:
![]()
Если отрезок с концами A (xa, ya, za) и B (xb, yb, zb) находится в трехмерном пространстве, координаты его середины рассчитываются следующим образом:
![]()
Примеры задач
Задание 1
Вычислим координаты точки C, которая является серединой отрезка AB, образованного точками A (5, -2) и B (11, 10).
Решение:
В данном случае нам подойдут формулы для плоскости:
xc = (5 + 11) / 2 = 8
yc = (-2 + 10) / 2 = 4
Таким образом, точка C имеет координаты (8, 4).
Задание 2
Найдем координаты точки B, являющейся одним из концов отрезка AB. При этом известны координаты точки A (7, 13) и середины отрезка – C (4, -3).
Решение:
Нужные нам формулы можно вывести из выражений для расчета координат середины отрезка:
xb = 2xc – xa = 2 · 4 – 7 = 1
yb = 2yc – ya = 2 · (-3) – 13 = -19
Следовательно, координаты B – (1, -19).
Определение.
Середина отрезка – это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc – xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc – ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc – xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc – ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc – za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
На этой странице можно рассчитать координаты середины отрезка как на плоскости, так и в пространстве. Введите координаты точек и получите ответ, а также подробное решение с помощью наших онлайн-калькуляторов.
Задача нахождения координат середины отрезка довольно часто возникает при решении задач, связанных с нахождением средней линии, медианы а также других вычислениях. На нашем сайте также можно рассчитать длину отрезка, заданного координатами.
Середина отрезка – точка, расположенная на отрезке на равном расстоянии от его конечных точек.
Формула для нахождения координат середины отрезка на плоскости
{x_c=dfrac{x_a + x_b}{2}; ; y_c=dfrac{y_a + y_b}{2}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B,
xc и yc – координаты середины отрезка (точка C).
Формула для нахождения координат середины отрезка в пространстве
{x_c=dfrac{x_a + x_b}{2}; ; y_c=dfrac{y_a + y_b}{2}; ; z_c=dfrac{z_a + z_b}{2}}
xa, ya и za – координаты первой точки A,
xb, yb и zb– координаты второй точки B,
xc, yc и zc – координаты середины отрезка (точка C).
Примеры задач на вычисление середины отрезка
Задача 1
Найдите координаты середины отрезка АВ,если А(-2,3) и В(6,-3).
Решение
Подставим координаты концов отрезка в формулы.
x_c=dfrac{x_a + x_b}{2} = dfrac{-2 + 6}{2} = dfrac{4}{2} = 2
y_c=dfrac{y_a + y_b}{2} = dfrac{3 + (-3)}{2} = dfrac{0}{2} = 0
Мы получили координаты середины отрезка – C(2, 0).
Ответ: C(2, 0)
Калькулятор середины отрезка поможет проверить результат.
Задача 2
Дано: A(1, -1, 2), B(3, 1, -2). Найдите координаты середины отрезка AB.
Решение
Воспользуемся формулами координат середины отрезка в пространстве, подставив в них значение координат концов отрезка.
x_c=dfrac{x_a + x_b}{2} = dfrac{1 + 3}{2} = dfrac{4}{2} = 2
y_c=dfrac{y_a + y_b}{2} = dfrac{-1 + 1}{2} = dfrac{0}{2} = 0
z_c=dfrac{z_a + z_b}{2} = dfrac{2 + (-2)}{2} = dfrac{0}{2} = 0
Мы получили координаты середины отрезка – C(2, 0, 0).
Ответ: C(2, 0, 0)
Проверка
Координаты середины отрезка
Если даны координаты конечных точек отрезка, знания о действиях с векторами и координатами векторов дают возможность определить координаты серединной точки отрезка.
Для этого расположим отрезок (AB) в системе координат.

,
Bx2;y2
— конечные точки отрезка с данными координатами.
— серединная точка с искомыми координатами.
Пусть векторы
OA→
,
OB→
и
OC→
начнутся в начале координат, в таком случае их координаты совпадут с координатами их конечных точек.
Если сосчитать векторы
OA→
и
OB→
по закону параллелограмма, тo
OC→=12OA→+OB→
.
Kак известно, в координатной форме координаты суммы находим как сумму координат слагаемых векторов, а при умножении с числом координаты находим умножением координат.
Следовательно,
OC→x1+x22;y1+y22
,
то есть искомые значения (x) и (y):
