6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вычисление синуса, косинуса и тангенса угла треугольника
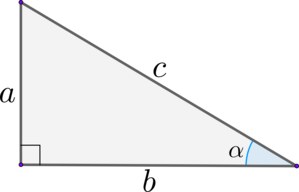
В прямоугольном треугольнике:
(blacktriangleright) Синус острого угла равен отношению противолежащего катета к гипотенузе: [{large{sin alpha =
dfrac{a}{c}}}]
(blacktriangleright) Косинус острого угла равен отношению прилежащего катета к гипотенузе: [{large{cos alpha =
dfrac{b}{c}}}]
(blacktriangleright) Тангенс острого угла равен отношению противолежащего катета к прилежащему: [{large{mathrm{tg}, alpha
= dfrac{a}{b}}}]
(blacktriangleright) Котангенс острого угла равен отношению прилежащего катета к противолежащему: [{large{mathrm{ctg},
alpha =dfrac{b}{a}}}]
Важные формулы:
[{large{begin{array}{|lcl|} hline sin^2 alpha+cos^2 alpha
=1&qquad& mathrm{tg}, alpha cdot mathrm{ctg}, alpha
=1\ &&\
mathrm{tg}, alpha=dfrac{sin alpha}{cos
alpha}&&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha}\&&\
hline
end{array}}}]
[begin{array}{|c|c|c|c|c|c|}
hline & phantom{000}, 0^circ phantom{000}& phantom{000},
30^circ phantom{000} &
phantom{000}, 45^circ phantom{000} & phantom{000}, 60^circ phantom{000}
& phantom{000}, 90^circ phantom{000}\[1ex]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2 & 1\[1ex]
hline cos & 1 & frac{sqrt3}2&frac{sqrt2}2½ & 0\[1ex]
hline mathrm{tg} & 0 & frac{sqrt3}3&1&sqrt3 & text{не сущ.}\[1ex]
hline mathrm{ctg}& text{не сущ.} &sqrt3&1&frac{sqrt3}3 & 0\[1ex]
hline
end{array}]
Задание
1
#612
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 90^{circ}), (sin {angle BAC} = dfrac{2}{3}). Найдите (AC), если (AB = 6sqrt{5}).
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда [dfrac{BC}{AB} = dfrac{2}{3}qquadRightarrowqquad BC = dfrac{2}{3}AB = 4sqrt{5}.]
По теореме Пифагора (AC^2 = AB^2 – BC^2 = 36cdot 5 – 16cdot 5 = 20cdot 5 = 10^2), тогда (AC = 10).
Ответ: 10
Задание
2
#2098
Уровень задания: Равен ЕГЭ
Дан прямоугольный треугольник (ABC), причем (angle C=90^circ). Известно, что (cos angle B=dfrac13), (AB=9). Найдите (BC).

По определению косинуса [cosangle B=dfrac{BC}{AB}=dfrac13 quad
Leftrightarrow quad BC=dfrac13cdot AB=dfrac13cdot 9=3]
Ответ: 3
Задание
3
#2099
Уровень задания: Равен ЕГЭ
Дан треугольник (ABC), причем (angle C=90^circ). Найдите длину его гипотенузы, если (AC=8, cos angle A=dfrac45).

По определению косинуса [cos angle A=dfrac{AC}{AB}=dfrac45
quad Leftrightarrow quad AB=ACcdot dfrac54=10]
Ответ: 10
Задание
4
#3320
Уровень задания: Равен ЕГЭ
Большее основание равнобедренной трапеции равно (34). Боковая сторона равна (14). Синус острого угла равен (dfrac{2sqrt{10}}7). Найдите меньшее основание.

Проведем (BHperp AD). Из (triangle ABH): [dfrac{2sqrt{10}}7=sinangle A=dfrac{BH}{AB}quadRightarrowquad
BH=4sqrt{10}] Тогда по теореме Пифагора [AH=sqrt{14^2-(4sqrt{10})^2}=6] Так как (AH=0,5(AD-BC)), то (BC=AD-2AH=34-12=22).
Ответ: 22
Задание
5
#3305
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=13), (mathrm{tg},angle A=0,2). Найдите (AH).
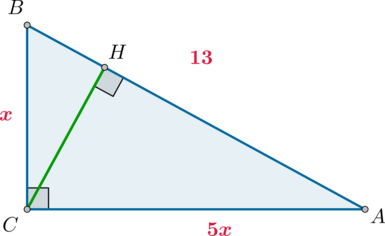
Так как по определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 15] то можно принять (BC=x), (AC=5x). Следовательно, по теореме Пифагора [BC^2+AC^2=AB^2quadRightarrowquad x^2+(5x)^2=13^2quadRightarrowquad
x^2=dfrac{13}2] Из (triangle AHC): [cos angle A=dfrac{AH}{AC}] Из (triangle ABC): [cos angle A=dfrac{AC}{AB}] Следовательно: [dfrac{AH}{AC}=dfrac{AC}{AB}quadRightarrowquad
AH=dfrac{AC^2}{AB}=dfrac{(5x)^2}{13}=dfrac{25}2=12,5]
Ответ: 12,5
Задание
6
#3306
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=26), (mathrm{tg},angle B=5). Найдите (AH).
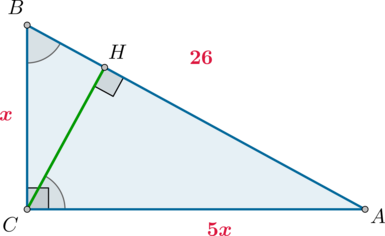
По определению из (triangle ABC): [dfrac{AC}{BC}=mathrm{tg},angle B=dfrac 51] Следовательно, можно принять (AC=5x), (BC=x). Тогда по теореме Пифагора (x^2+(5x)^2=26^2), откуда (x=sqrt{26}).
Тогда [sinangle B=dfrac{AC}{AB}=dfrac5{sqrt{26}}] По свойству прямоугольного треугольника (angle B=angle HCA). Следовательно, из (triangle HCA): [dfrac5{sqrt{26}}=sin angle HCA=dfrac{AH}{AC}quadRightarrowquad
AH=25]
Ответ: 25
Задание
7
#3307
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (AB=17), (mathrm{tg},angle A=0,25). Найдите высоту (CH).
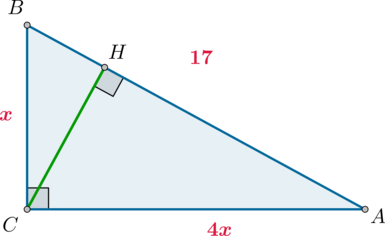
По определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 14] Следовательно, можно принять (AC=4x), (BC=x). Тогда по теореме Пифагора (x^2+(4x)^2=17^2), откуда (x=sqrt{17}).
Так как площадь прямоугольного треугольника (ABC), с одной стороны, равна (0,5CHcdot AB), а с другой стороны, равна (0,5BCcdot AC), то [CHcdot AB=BCcdot ACquadRightarrowquad CH=dfrac{4x^2}{AB}=4]
Ответ: 4
Уметь оперативно и правильно решать задачи ЕГЭ на вычисление элементов многоугольника необходимо всем выпускникам вне зависимости от того, базовый или профильный уровень экзамена они сдают. Причем этой теме традиционно посвящается несколько заданий. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему обязательно стоит уделить внимание задачам, в которых требуется найти синус, косинус и тангенс угла треугольника.
Вместе с образовательным порталом «Школково» вы сможете восполнить пробелы в знаниях и отточить необходимый навык. Весь теоретический и практический материал составлен и изложен таким образом, чтобы все выпускники могли без особых затруднений справляться с задачами ЕГЭ, в которых требуется вычислить тангенс, синус или косинус угла треугольника.
Основные моменты
Первое, что нужно сделать при решении подобных задач в ЕГЭ, – вспомнить, что такое тангенс, косинус и синус угла треугольника. Далее рекомендуется следовать такому алгоритму:
- Выделяем треугольник, в который входит сторона или угол, который требуется найти.
- Определяем известные элементы и выявляем тригонометрическую функцию, которая их связывает.
- Записываем получившееся соотношение и применяем подходящую формулу.
Научившись правильно выполнять упражнения на вычисление элементов многоугольника, а также, например, по теме «Окружность, описанная около многоугольника», которые представлены в данном разделе образовательного портала «Школково», вы сможете закрепить материал и без труда справляться с подобными заданиями на аттестационном экзамене.

УСТАЛ? Просто отдохни
Каталог заданий.
1. Синус, косинус, тангенс, котангенс
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 29 № 1020 

На клетчатой бумаге с размером клетки
изображён угол. Найдите
Решение
·
Помощь
2
Тип 29 № 1024 

На клетчатой бумаге с размером клетки
изображён угол. Найдите
Аналоги к заданию № 1024: 1025 Все
Решение
·
Помощь
3
Тип 29 № 1025 

На клетчатой бумаге с размером клетки
изображён угол. Найдите
Аналоги к заданию № 1024: 1025 Все
Решение
·
Помощь
4
Тип 29 № 1026 

Выведите значения синуса, косинуса, тангенса и котангенса угла 30°.
Решение
·
Помощь
5
Тип 29 № 1027 

Выведите значения синуса, косинуса, тангенса и котангенса угла 45°.
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Инфоурок
›
Алгебра
›Другие методич. материалы›Задачи на теорему синуса, косинуса и площадь треугольника
Задачи на теорему синуса, косинуса и площадь треугольника
Скачать материал
без ожидания
Скачать материал
без ожидания


- Сейчас обучается 27 человек из 19 регионов


- Сейчас обучается 352 человека из 70 регионов


- Сейчас обучается 50 человек из 27 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 251 279 материалов в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы

Презентация по алгебре 7 класс
- Учебник: «Алгебра», Мерзляк А.Г., Полонский В.Б., Якир М.С.
- Тема: § 9. Сложение и вычитание многочленов
- 31.01.2019
- 622
- 11







Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс повышения квалификации «Информационная этика и право»
-
Курс профессиональной переподготовки «Управление качеством»
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Лаптева Евгения Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 6 лет и 7 месяцев
- Подписчики: 7
- Всего просмотров: 87936
-
Всего материалов:
77
Многие ученики путаются в решении задач используя синус и косинус угла, мы подробно разберём решение таких задач, ведь если разобраться и верно нарисовать рисунок, то это не так уж и сложно. В этой статье вместе с myalfaschool.ru мы научимся решать такие задачи, также ты можешь записаться на бесплатный пробный урок здесь.
Задача 1: (10)-метровая лестница опирается на здание таким образом, что угол подъема от земли до здания составляет (30˚) градусов. Найдите расстояние от вершины лестницы до земли, кроме того, найдите расстояние от здания до подножья лестницы.
Решение.
(AB-)длина лестница, (BC-)расстояние от вершины лестницы до земли, (AC-)расстояние от здания до подножья лестницы. Угол (∠BCA) равен (90˚).
- 1. Рассмотрим синус угла (∠BAC) и найдем (BC-) :
(sin30=frac{BC}{AB})
(frac{1}{2}=frac{BC}{10}–>1*10/2=5–>BC=5)
- 2. Далее рассмотрим косинус угла (∠BAC) и найдем (AC:)
(cos30=frac{AC}{AB})
(frac{sqrt{3}}{2}=frac{AC}{10}–>sqrt{3}*10/2=5–>AC=5sqrt{3})
Ответ: (BC=5) м, (AC=5sqrt{3}) м.
Задача 2. Смотритель маяка видит корабль под углом 60˚ . Найдите расстояние от верха маяка до коробля и от низа маяка до корабля, если высота маяка 50 м.
Решение.
(AB-)высота маяка, (BC-)расстояние от верха маяка до коробля, (AC-) расстояние от низа маяка до корабля. Угол (∠BCA) равен (90˚).
- 1. Рассморим синус угла (∠BAC) и найдем (AB):
(sin60=frac{BC}{AB})
(frac{sqrt{3}}{2}=frac{50}{AB}–>2*50/sqrt{3}=10/1,73=57,8–>AB≈57,8)
- 2. Рассморим косинус угла (∠BAC) и найдем (AC) :
(cos60=frac{AC}{AB})
(frac{1}{2}=frac{AC}{57,8}–>1*57,8/2=28,9–>AC≈28,9)
Ответ: (AB≈57,8) м, (AC≈28,9 ) м.
Задача 3. Скалолаз поднимается на 15-градусный уклон у подножья горы. Если он поднимается с постоянной скоростью 3 м в час, то на какой высоте он будет через 5 часов?
Решение.
- 1. Вычислим расстояние (AB) через (5) часов: (5*3=15) м под уклоном (15˚).
- 2. (AB-15) м , угол (∠BAC) = (15˚). Рассмотрим синус угла (∠BAC):
(sin(15)=frac{BC}{AB})
(0,65=frac{BC}{15}–> BC = 9,75)
Ответ: (9,75 ) м.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8 класс. Задачи на синус, косинус, тангенс острого угла прямоугольного треугольника, которые встречаются в 15 задании ОГЭ по математике.
Для начала введем понятия противолежащего и прилежащего катета.
Если катет находится напротив угла, относительно которого находится, то такой катет называется противолежащий. Если катет образует угол с гипотенузой, то катет называется прилежащим.
Определение синуса острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Запишем это определение по другому.
Выделенные буквы помогают определить, какой катет нам нужно взять. (сИнус – прОтиволежащий).
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Запишем это определение по другому.
Выделенные буквы помогают определить, какой катет нам нужно взять. (кОсинус – прИлежащий).
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
Ниже приведу несколько типовых задач, на нахождение синуса, косинуса и тангенса острого угла прямоугольного треугольника:
Задача на нахождение синуса острого угла прямоугольного треугольника
Задача на нахождение косинуса острого угла прямоугольного треугольника
Задача на нахождение тангенса острого угла прямоугольного треугольника
Далее рассмотрим обратные задачи, где нужно будет составить соотношения для синуса, косинуса и тангенса острого угла прямоугольного треугольника и выразить неизвестную сторону.
Найдем сторону треугольника, зная синус острого угла прямоугольного треугольника
Найдем сторону треугольника, зная косинус острого угла прямоугольного треугольника
Найдем сторону треугольника, зная тангенс острого угла прямоугольного треугольника
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
