Гидростатическое давление как найти высоту

Гидростатическое давление как найти высоту

Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:
P=rho gh
Калькулятор позволяет найти

  • давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
  • высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
  • плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
  • ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости

Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения – земное ускорение, и для давления – величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.

PLANETCALC, Гидростатическое давление

Гидростатическое давление

Высота столба жидкости, м

Плотность жидкости, кг/м3

Ускорение свободного падения, м/с2

Точность вычисления

Знаков после запятой: 2

Высота столба жидкости, м

Плотность жидкости, кг/м3

Ускорение свободного падения, м/с2

Гидростатическое давление — давление столба воды над условным уровнем.

Формула гидростатического давления выводится достаточно просто
P=frac{F}{S} longrightarrow P=frac{mg}{S} longrightarrow P=frac{rho Vg}{S} longrightarrow P=frac{rho Shg}{S} longrightarrow P=rho gh

Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Также это приводит к такому явлению как гидростатический парадокс.

Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.

paradox.png

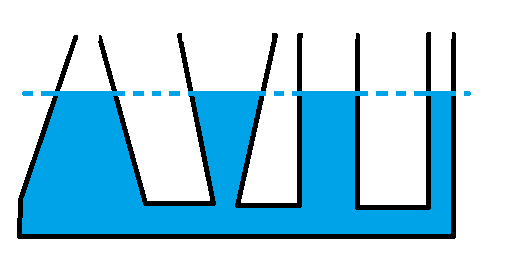
На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда

Источники в википедии: Гидростатическое давление Гидростатический парадокс

Источник

Статика жидкостей и газов.

  • Гидростатическое давление.

  • Закон Паскаля.

  • Гидравлический пресс.

  • Закон Архимеда.

  • Плавание тел.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: давление жидкости, закон Паскаля, закон Архимеда, условия плавания тел.

В гидро- и аэростатике рассматриваются два вопроса: 1) равновесие жидкостей и газов под действием приложенных к ним сил; 2) равновесие твёрдых тел в жидкостях и газах.

Многие из обсуждаемых далее фактов относятся равным образом как к жидкостям, так и к газам. В таких случаях мы будем называть жидкость и газ средой.

При сжатии среды в ней возникают силы упругости, называемые силами давления. Силы давления действуют между соприкасающимися слоями среды, на погружённые в среду твёрдые тела, а также на дно и стенки сосуда.

Сила давления среды обладает двумя характерными свойствами.

1. Сила давления действует перпендикулярно поверхности выделенного элемента среды или твёрдого тела. Это объясняется текучестью среды: силы упругости не возникают в ней при относительном сдвиге слоёв, поэтому отсутствуют силы упругости, касательные к поверхности.

2. Cила давления равномерно распределена по той поверхности, на которую она действует.

Естественной величиной, возникающей в процессе изучения сил давления среды, является давление.

Пусть на поверхность площади S действует сила F, которая перпендикулярна поверхности и равномерно распределена по ней. Давлением называется величина

p=frac{displaystyle F}{displaystyle S}.

Единицей измерения давления служит паскаль (Па). 1 Па – это давление, производимое силой 1 Н на поверхность площадью 1 м ^{2}.

Полезно помнить приближённое значение нормального атмосферного давления: p_{0}=10^{5}Па.

к оглавлению ▴

Гидростатическое давление.

Гидростатическим называется давление неподвижной жидкости, вызванное силой тяжести. Найдём формулу для гидростатического давления столба жидкости.

Предположим, что в сосуд с площадью дна S налита жидкость до высоты h (рис. 1). Плотность жидкости равна rho

Рис. 1. Гидростатическое давление

Объём жидкости равен Sh, поэтому масса жидкости m=rho Sh. Сила F давления жидкости на дно сосуда – это вес жидкости. Так как жидкость неподвижна, её вес равен силе тяжести:

F=mg=rho Shg.

Разделив силу F на площадь S, получим давление жидкости:

p=rho gh.

Это и есть формула гидростатического давления.

Так, на глубине 10 м вода оказывает давление p=1000 cdot 10 cdot 9,8=98000Па, примерно равное атмосферному. Можно сказать, что атмосферное давление приблизительно равно 10 м водного столба.

Для практики столь большая высота столба жидкости неудобна, и реальные жидкостные манометры – ртутные. Посмотрим, какую высоту должен иметь столб ртути (rho=13600 кг/м^{3}), чтобы создать аналогичное давление:

h=frac{p}{rho g}=frac{10^{5}}{13600cdot 9,8}=0.75 м = 750 мм.

Вот почему для измерения атмосферного давления широко используется миллиметр ртутного столба (мм рт. ст.).

к оглавлению ▴

Закон Паскаля.

Если поставить гвоздь вертикально и ударить по нему молотком, то гвоздь передаст действие молотка по вертикали, но не вбок. Твёрдые тела из-за наличия кристаллической решётки передают производимое на них давление только в направлении действия силы.

Жидкости и газы (напомним, что мы называем их средами) ведут себя иначе. В средах справедлив закон Паскаля.

Закон Паскаля. Давление, оказываемое на жидкость или газ, передаётся в любую точку этой среды без изменения по всем направлениям.

(В частности, на площадку, помещённую внутри жидкости на фиксированной глубине, действует одна и та же сила давления, как эту площадку ни поворачивай.)

Например, ныряльщик на глубине h испытывает давление p=p_{0}+rho gh. Почему? Согласно закону Паскаля вода передаёт давление атмосферы p_{0} без изменения на глубину h , где оно прибавляется к гидростатическому давлению водяного столба rho gh.

Отличной иллюстрацией закона Паскаля служит опыт с шаром Паскаля. Это шар с множеством отверстий, соединённый с цилиндрическим сосудом (рис. 2)

Рис. 2. Шар Паскаля

Если налить в сосуд воду и двинуть поршень, то вода брызнет из всех отверстий. Это как раз и означает, что вода передаёт внешнее давление по всем направлениям.

То же самое наблюдается и для газа: если сосуд наполнить дымом, то при движении поршня струйки дыма пойдут опять-таки из всех отверстий сразу. Стало быть, газ также передаёт давление по всем направлениям.

Вы ежедневно пользуетесь законом Паскаля, когда выдавливаете зубную пасту из тюбика. А именно, вы сжимаете тюбик в поперечном направлении, а паста двигается перпендикулярно вашему усилию – в продольном направлении. Почему? Ваше давление передаётся внутри тюбика по всем направлениям, в частности – в сторону отверстия тюбика. Туда-то паста и выходит.

к оглавлению ▴

Гидравлический пресс.

Гидравлический пресс – это устройство, дающее выигрыш в силе. То есть, прикладывая сравнительно небольшую силу в одном месте устройства, оказывается возможным получить значительно большее усилие в другом его месте.

Гидравлический пресс изображён на рис. 3. Он состоит из двух сообщающихся сосудов, имеющих разную площадь поперечного сечения и закрытых поршнями. В сосудах между поршнями находится жидкость.

Рис. 3. Гидравлический пресс

Принцип действия гидравлического пресса очень прост и основан на законе Паскаля.

Пусть S_{1} – площадь малого поршня, S_{2} – площадь большого поршня. Надавим на малый
поршень с силой F_{1}. Тогда под малым поршнем в жидкости возникнет давление:

p=frac{displaystyle F_{displaystyle 1}}{displaystyle S_{displaystyle 1}}.

Согласно закону Паскаля это давление будет передано без изменения по всем направлениям в любую точку жидкости, в частности – под большой поршень. Следовательно, на большой поршень со стороны жидкости будет действовать сила:

F_{displaystyle 2}=pS_{displaystyle 2}=F_{displaystyle 1}frac{displaystyle S_{displaystyle 2}}{displaystyle S_{displaystyle 1}}.

Полученное соотношение можно переписать и так:

frac{displaystyle F_{displaystyle 2}}{displaystyle F_{displaystyle 1}}=frac{displaystyle S_{displaystyle 2}}{displaystyle S_{displaystyle 1}}.

Мы видим, что F_{2} больше F_{1} во столько раз, во сколько S_{2} больше S_{1}. Например, если площадь большого поршня в 100 раз превышает площадь малого поршня, то усилие на большом поршне окажется в 100 раз больше усилия на малом поршне. Вот каким образом гидравлический пресс даёт выигрыш в силе.

к оглавлению ▴

Закон Архимеда.

Мы знаем, что дерево в воде не тонет. Следовательно, сила тяжести уравновешивается какой-то другой силой, действующей на кусок дерева со стороны воды вертикально вверх. Эта сила называется
выталкивающей или архимедовой силой. Она действует на всякое тело, погружённое в жидкость или газ.

Выясним причину возникновения архимедовой силы. Рассмотрим цилиндр площадью поперечного сечения S и высотой h, погружённый в жидкость плотности rho . Основания цилиндра горизонтальны. Верхнее основание находится на глубине h_{1} , нижнее – на глубине h_{2}=h_{1}+h (рис. 4).

На боковую поверхность цилиндра действуют силы давления, которые приводят лишь к сжатию цилиндра. Эти силы можно не принимать во внимание.

На уровне верхнего основания цилиндра давление жидкости равно p_{1}=rho g h_{1}. На верхнее основание действует сила давления F_{1}=p_{1}S=rho g h_{1}S, направленная вертикально вниз.

На уровне нижнего основания цилиндра давление жидкости равно p_{2}=rho g h_{2}. На нижнее основание действует сила давления F_{2}=p_{2}S=rho g h_{2}S, направленная вертикально вверх (закон Паскаля!).

Так как h_{2}>h_{1}, то F_{2}>F_{1}, и поэтому возникает равнодействующая сил давления, направленная вверх. Это и есть архимедова сила F_{A}. Имеем:

F_{A}=F_{2}-F_{1}=rho g h_{2}S-rho g h_{1}S=rho g S(h_{2}-h_{1})=rho gSh.

Но произведение Sh равно объёму цилиндра V. Получаем окончательно:

F_{A}=rho gV. (1)

Это и есть формула для архимедовой силы. Возникает архимедова сила вследствие того, что давление жидкости на нижнее основание цилиндра больше, чем на верхнее.

Формулу (1) можно интерпретировать следующим образом. Произведение rho V – это масса
жидкости m, объём которой равен V : rho V=m. Но тогда rho gV=mg=P, где P – вес жидкости, взятой в объёме V. Поэтому наряду с (1) имеем:

F_{A}=P. (2)

Иными словами, архимедова сила, действующая на цилиндр, равна весу жидкости, объём которой совпадает с объёмом цилиндра.

Формулы (1) и (2) справедливы и в общем случае, когда погружённое в жидкость или газ тело объёма V имеет любую форму, а не только форму цилиндра (конечно, в случае газа rho – это плотность газа). Поясним, почему так получается.

Выделим мысленно в среде некоторый объём V произвольной формы. Этот объём находится в равновесии: не тонет и не всплывает. Следовательно, сила тяжести, действующая на среду, находящуюся внутри выделенного нами объёма, уравновешена силами давления на поверхность нашего объёма со стороны остальной среды – ведь на нижние элементы поверхности приходится большее давление, чем на верхние.

Иными словами, равнодействующая сил гидростатического давления на поверхность выделенного объёма – архимедова сила – направлена вертикально вверх и равна весу среды в этом объёме.

Сила тяжести, действующая на наш объём, приложена к его центру тяжести. Значит, и архимедова сила должна быть приложена к центру тяжести выделенного объёма. В противном случае сила тяжести и архимедова сила образуют пару сил, которая вызовет вращение нашего объёма (а он находится в равновесии).

А теперь заменим выделенный объём среды твёрдым телом того же объёма V и той же самой формы. Ясно, что силы давления среды на поверхность тела не изменятся, так как неизменной осталась конфигурация среды, окружающей тело. Поэтому архимедова сила попрежнему будет направлена вертикально вверх и равна весу среды, взятой в объёме V. Точкой приложения архимедовой силы будет центр тяжести тела.

Закон Архимеда. На погружённое в жидкость или газ тело действует выталкивающая сила, направленная вертикально вверх и равная весу среды, объём которой равен объёму тела.

Таким образом, архимедова сила всегда находится по формуле (1). Заметим, что в эту формулу не входят ни плотность тела, ни какие-либо его геометрические характеристики – при фиксированном объёме величина архимедовой силы не зависит от вещества и формы тела.

До сих пор мы рассматривали случай полного погружения тела. Чему равна архимедова сила при частичном погружении? На ту часть тела, которая находится над поверхностью жидкости, никакая выталкивающая сила не действует. Если эту часть мысленно срезать, то величина архимедовой силы не изменится. Но тогда мы получим целиком погружённое тело, объём которого равен объёму погружённой части исходного тела.

Значит, на частично погружённое в жидкость тело действует выталкивающая сила, равная весу жидкости, объём которой равен объёму погружённой части тела. Формула (1) справедлива и в этом случае, только объём всего тела V нужно заменить на объём погружённой части Vпогр:

F_{A}=rho gVпогр.

Архимед обнаружил, что целиком погружённое в воду тело вытесняет объём воды, равный собственному объёму. Тот же факт имеет место для других жидкостей и газов. Поэтому можно сказать, что на всякое тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом среды.

к оглавлению ▴

Плавание тел.

Рассмотрим тело плотности rho и жидкость плотности rho_{0} . Допустим, что тело полностью погрузили в жидкость и отпустили.

С этого момента на тело действуют лишь сила тяжести mg и архимедова сила F_{A}. Если объём тела равен V, то

mg=rho gV, F_{A}=rho_{0}gV.

Имеются три возможности дальнейшего движения тела.

1. Сила тяжести больше архимедовой силы: mg > F_{A}, или rho > rho_{0}. В этом случае тело тонет.

2. Сила тяжести равна архимедовой силе: mg = F_{A}, или rho = rho_{0}. В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.

3. Сила тяжести меньше архимедовой силы: mg < F_{A}, или rho < rho_{0}. В этом случае тело всплывает, достигая поверхности жидкости. При дальнейшем всплытии начнёт уменьшаться объём погружённой части тела, а вместе с ним и архимедова сила. В какой-то момент архимедова сила сравняется с силой тяжести (положение равновесия). Тело по инерции всплывёт дальше, остановится, снова начнёт погружаться. . . Возникнут затухающие колебания, после которых тело останется плавать в положении равновесия (mg = F_{A}), частично погрузившись в жидкость.

Таким образом, условие плавания тела можно записать в виде неравенства: rho leq rho_{0}.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Статика жидкостей и газов.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

В каждой жидкости существует давление, обусловленное ее собственным весом. Так, например, давление на основание столба воды высотой 10 м составляет около 10 5 Па.

h высота столба жидкости, Метр
p давление в жидкости на глубине h, Паскаль
g ускорение свободного падения, 9.81 м/c 2
ρ плотность жидкости, кг/м 3

давление в жидкости равно ее весу, деленному на площадь,

Так как объем есть произведение высоты на площадь V = Sh, то

Плотность жидкости ρ зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Соотношение между единицами давления. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением.

Калькулятор находит неизвестные величины по заданным, используя формулу давления столба жидкости.

Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости. Сама формула:

Калькулятор позволяет найти

  • давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
  • высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
  • плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
  • ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости

Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения – земное ускорение, и для давления – величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.

Гидростатическое давление

Гидростатическое давление — давление столба воды над условным уровнем.

Формула гидростатического давления выводится достаточно просто

Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление. В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Также это приводит к такому явлению как гидростатический парадокс.

Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.

На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда

Что такое гидростатическое давление

Если на поверхность воды действуют внешние силы, то давление в жидкости будет одинаково передаваться во всех направлениях. Так звучит основной закон гидростатики, который открыл французский ученый Блез Паскаль в 1653 году. А действует на жидкость в основном обычная сила тяжести.

В твердых телах молекулы составляют кристаллическую решетку. И, жестко связанные между собой, могут передать давление только в ту сторону, в которую действует сила, приложенная к предмету. А в состоянии покоя последняя направлена строго вниз.

В жидкостях есть относительная свобода для небольшого движения. Поэтому молекулы газа или любой жидкости могут передать давление в любом направлении. И под действием силы тяжести вода просто растекается в разные стороны, если ее движение не ограничивается стенками сосуда.

Если жидкость находится в покое, то внутри нее полностью отсутствуют касательные и растягивающие силы. Это значит, что давление столба воды направлено строго по внутренней нормали к основанию. То есть, какой бы формы не использовался бы сосуд, давление внутри него всегда будет действовать только под углом в 90 градусов относительно бортов емкости.

Одинаковое давление воды в разных сосудах

Поскольку в бытовых условиях жидкости всегда ограничены какими-либо стенками (бак, трубы), то существует зависимость давления воды от высоты столба. То есть важно, на каком расстоянии находится поверхность жидкости от точки основания, на которую направлена сила.

Смотрите также: Каталог компаний, что специализируются на водоснабжении, канализации и сопутствующих работах

Факторы, влияющие на показатель

При отсутствии внешнего воздействия, играют роль два фактора:

  • высота столба;
  • плотность.

Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.

Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.

Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:

  • внешней силы;
  • веса воды.

При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

Измерение давления воды и формула для расчетов

За единицу измерения давления в жидкости принят 1 мм водяного столба. Он равен 9,8 Па (Н/м²). А на практике давление в воде измеряют в килограмм-силе на квадратный сантиметр (кгс/см²). И в этом случае единица называется одной атмосферой (1 ат). А метр водяного столба будет насчитывать 0,1 ат.

Чтобы точно рассчитать давление жидкости (P) на определенную площадь, необходимо воспользоваться формулой:

P = p × h × g

Для этого нужно знать плотность жидкости (p), высоту столба (h) и скорость свободного падения (g).

Плотность воды зависит от ее температуры. Но общепринято для любых расчетов брать усредненное значение в одну тысячу килограмм на кубический метр. Ускорение свободного падения также привыкли округлять до 10 м/см². Исходя из этих данных, будет нетрудно вычислить, сколько атмосфер имеют 10 метров водяного столба.

Формула водяного давления

На выходе получается 10 кПа, что равно 1 технической атмосфере. Но для предельной точности нужно убрать округления и обязательно еще умножить произведение на величину атмосферного давления, действующего на поверхность воды. Правда для бытовых расчетов это необязательно.

Эпюра двухстороннего давления, когда с двух сторон щита находятся жидкости с разными плотностями

жидкости с разными плотностями

Здесь синим цветом показана эпюра для жидкости справа, которая «вырезается» из эпюры для жидкости слева. Т.е. во всех точках щита в той части, где вода находится с двух сторон, вычисляется разница давлений слева и справа. Эта разница и позволит построить результирующую эпюру давления (показана черным цветом).

Монтаж накопительного бака

В районах, где отсутствует централизованное водоснабжение, для бытовых нужд привыкли брать воду из колодцев или скважин. Чтобы достать питьевую жидкость с глубины, необходимо использовать насос. Но каждый раз, когда нужна лишь одна кружка воды, включение помпы становиться нерентабельным.

Поэтому целесообразен монтаж накопительного бака на определенной высоте. По СНиП, а также Постановлению Правительства за №354 давление воды на выходе из крана минимально должно составлять 0,3 ат. А для этого достаточно поднять бак всего лишь на 3 метра. Для этого даже не нужно строить вышку. Достаточно воспользоваться чердачным помещением одноэтажного дома.

Один раз в определенное время бак наполняется с помощью насоса. Затем вода двигается по трубам самотеком, согласно гидростатическому закону Паскаля. И на выходе из крана будет создаваться достаточный напор, чтобы обеспечить все бытовые нужды.

Кроме проведения разводки от накопительного бака к умывальникам и туалету, необходимо выполнить еще одни обязательные действия. Независимо от того, теплый чердак или нет, нужно дополнительно хорошо изолировать емкость для жидкости. Это будет гарантией, что при усилении морозов зимой дом не останется без воды.

Водяной накопительный бак на чердаке

Применение на практике

Примеры использования знаний свойств воды:

  2. Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
  3. Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
  4. Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.

Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:

  • выжимка масла из семян растений;
  • спуск на воду со стапелей построенного судна;
  • ковка и штамповка деталей;
  • домкраты для подъема грузов.

Обустройство капельного полива

Закон Паскаля давно и с успехом применяется во всех засушливых районах мира. Но наиболее эффективно его использовали в Израиле. В пятидесятые годы прошлого столетия для мелиорации там впервые стали практиковать метод, который впоследствии назвали капельным. А придумали его, чтобы сэкономить и так драгоценную влагу.

Влага к грядкам, как и прежде следовала самотеком, но теперь – дозировано и прямиком под корни растения. Для этого каждый корнеплод снабдили своей персональной «лейкой», а на емкость с водой установили заслонку с таймером. И через определенные промежутки времени саженец получает четко рассчитанную порцию питательной жидкости.

Капельный полив в огороде

Современные средства

Если нет времени либо вы не склонны к математике, рассчитать расход воды через трубопровод с учётом перепада давления можно, воспользовавшись онлайн калькулятором. Интернет изобилует сайтами с таки инструментарием. Чтобы произвести гидравлический расчёт, необходимо учесть коэффициент потерь. Такой подход предполагает выбор:

  • падения напора на погонный метр трубопровода;
  • длины участка;
  • внутреннего диаметра трубы;
  • вида и материала водопроводной системы (пластмасса, железобетон, асбоцемент, чугун, сталь). Современные онлайн калькуляторы учитывают даже, например, меньшую шероховатость пластиковой поверхности по сравнению со стальной;
  • способа расчёта сопротивления.

Кроме того, пользователю доступны опции учёта дополнительных характеристик трубопроводов, в частности, таких, как тип покрытия. Например:

  • цементно-песчаное, нанесённое различными методами;
  • внешнее полимерцементное или пластиковое;
  • новые или проработавшие определённый срок трубопроводы с битумным покрытием либо без защитного внутреннего покрытия.

Если расчёт будет сделан правильно, при условии выполнения монтажа с соблюдением всех требований к водопроводу нарекания не возникнут.

  • Автор: Мария Сухоруких
  • Распечатать

Оцените статью:

  1. 5
  2. 4
  3. 3
  4. 2
  5. 1

(1 голос, среднее: 4 из 5)

Поделитесь с друзьями!

Коротко о главном

Знания школьной программы физики могут значительно облегчить жизнь и сохранить средства. Если воспользоваться законом гидростатики Паскаля, то можно обустроить систему, в которой вода будет поступать в нужную точку самотеком. Причем это может быть, как умывальник в доме, так и грядка с овощами в огороде.

Для этого потребуется подходящую по объему емкость установить на нужной высоте. А чтобы определить последнюю, необходимо воспользоваться специальной формулой, которая определяет давление водяного столба в системе. А всю работу будет делать обычная сила тяжести.

Оценок 0

Прочитать позже

На дно и стенку сосуда – в чем разница?

Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.

Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.

Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.

Инстанции, отвечающие за водоснабжение

Перед тем, как обращаться в какие-либо инстанции по поводу плохого напора воды, необходимо убедиться в том, что причиной этого не является засор устройства известковыми или иными отложениями, неисправность оборудования и т. д.

Если же причина не в вышеперечисленном, то при несоблюдении норм давления подаваемой в МКД воды, можно обратиться в следующие организации:

  • в управляющую компанию (УК), на балансе которой находится данный дом. УК, по определению, является посредником между поставщиком ресурсов жизнеобеспечения МКД и гражданином, являющимся собственником или нанимателем жилья в данном доме. Необходимо предпринять следующее:
  • написать заявление в УК с описанием проблемы, с требованиями устранить нарушение норм подачи воды и произвести перерасчет стоимости оплаченных услуг по содержанию жилья,
  • отнести жалобу в УК в 2 экземплярах, один – оставить в компании, другой, с пометкой о принятии заявления – забрать себе,
  • ожидать устранения проблемы, УК обязаны рассмотреть жалобу не позже 1 месяца после ее принятия.

  • в управление городской администрации, если меры по поданной жалобе не были своевременно рассмотрены УК. При обращении в администрацию следует написать новое заявление и приложить к нему второй экземпляр жалобы, ранее направленной в УК.

Определение

Чтобы водопроводная сеть стабильно функционировала, сотрудники водоканала регулярно поддерживают в ней указанное количество атмосфер. Сила движения жидкости в трубах определяется физической величиной, которая равняется степени воздействия жидкостной среды на их стенки. Систематическая регулировка показателей перемещения H2O позволяет водоносным конструкциям работать полноценно, без вероятности возникновения аварий. Таких, как:

  • прорыв магистралей;
  • поломка вентилей;
  • выход из строя сантехники и т.п.
Источник

В.И.КРЮКОВА

,
МОУ СОШ № 7, г. Прокопьевск, Кемеровская обл.

Гидростатическое давление

Урок объяснения нового матерала.
7-й класс

Цель урока
: рассмотреть природу
давления столба жидкости; выработать
практические навыки при решении задач; развивать
познавательную активность учащихся.

Ход урока

I. Проверка домашнего задания

Фронтальная беседа. Сформулируйте
закон Паскаля. Чем отличается передача давления
жидкостями и газами от передачи давления
твёрдыми телами? Отвечайте, используя сведения о
молекулах. Забавляясь, мы любим выдувать мыльные
пузыри (демонстрация
). Почему они имеют
форму шара? Почему взрыв снаряда губителен для
находящихся поблизости организмов? Каким
простым способом можно удалить вмятину на
оболочке теннисного мяча? (Мяч пластмассовый.)
Почему пустой бумажный мешок, надутый воздухом, с
треском разрывается, если ударить по нему рукой
или обо что-либо твёрдое?

II. Объяснение нового материала

Проблемная ситуация
. Как раньше
добывался жемчуг? Почему ныряльщики часто
погибали? Что вы испытываете при нырянии в воду?
Зачем нужен жёсткий скафандр для водолазов,
работающих на глубине? Камбала обитает на
морском дне. Почему её тело плоское?

Опыт 1
. В трубку, дно которой
затянуто плёнкой, наливаем воду. Дно прогибается.
Почему?

Давление, производимое покоящейся
жидкостью, называется гидростатическим
давлением
.

Выделяем столб жидкости высотой h

и площадью основания S
;

сила давления воды на основание:

F
 = p
 S
. (1)

F
 = P
 – весу жидкости,

F
 = P
 = mg
, m
 = V
,

V
 = S
 h
.

F
 = Shg
.
(2)

Приравниваем формулы (1) и (2):

Анализ формулы
. Давление жидкости
зависит:

1) от
жидкости (чем больше плотность жидкости, тем
больше давление);

2) от h
 (чем больше высота столба
жидкости, тем больше давление).

А зависит ли давление жидкости от
площади дна сосуда? Согласно формуле, не зависит.

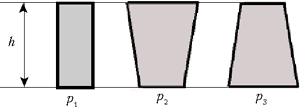
Вывод
: давление жидкости не
зависит от площади дна сосуда и его формы.

При одинаковой высоте h
 давление
одинаково: р
 1 = р
 2 = р
 3 .
А теперь докажем, что внутри жидкости существует
давление.

Опыт 2
. Пластинка (крышка от банки
из-под кофе) закрывает снизу полый стеклянный
цилиндр, опущенный в сосуд с жидкостью, и
удерживается под ним.

Проблемная ситуация
. Если
жидкости нет, пластинка падает. Почему? (Учащиеся
отвечают, что это происходит под действием силы
тяжести
.)

Если в сосуд налита жидкость,
пластинка удерживается под цилиндром до тех пор,
пока внутри цилиндра жидкости нет, и падает,
когда уровни жидкости внутри и снаружи цилиндра
совпадают. (Учащиеся свободно отвечают, что в
последнем случае давление жидкости над
пластинкой равно давлению под пластинкой
.)

(Можно пронаблюдать давление внутри
жидкости, используя манометр, соединённый с
коробочкой, затянутой резиновой мембраной.)

Опыт 3
. В полиэтиленовый пакет
наливаем подкрашенную воду, погружаем его в
аквариум (банку), чтобы уровни жидкостей
совпадали. Если нажать на стенку пакета в
каком-либо месте, то вмятина сохраняется. Почему?
Если пакет погружать глубже, то подкрашенная
жидкость (вода) в пакете поднимается вверх.
Почему?

Аккуратно делаем надрез ножницами
(отрезаем угол пакета) – жидкости не перетекают.
Поднимаем пакет вверх – жидкость из пакета
начинает перетекать в аквариум. Почему?

Вывод
: внутри жидкости существует
давление, которое на одном уровне одинаково во
всех точках и увеличивается с глубиной
погружения.

Отвечаем на проблемные вопросы,
прозвучавшие в начале урока.

А можно ли при помощи небольшого
количества воды создать большое давление? По
рисунку учебника рассматриваем опыт Паскаля.

III. Решение задач

Вызываю к доске троих учащихся и
предлагаю решить задачи:

    В сосуды одинаковой формы и объёма до
    одной высоты 40 см налиты жидкости: в первый –
    керосин, во второй – вода, в третий – ртуть.
    Рассчитайте давление в каждом случае.

После решения учащиеся наглядно
оценивают, сравнивая результаты, что, чем больше
плотность жидкости, тем большее давление она
оказывает.

Дополнительно, если позволяет время,
решаем задачу:

    Определите давление и силу давления
    керосина на дно бака площадью 4,5 дм 2 ,
    наполненного до высоты 25 см. (Ответ
    . 1960 Па; 88,2
    Н.)

IV. Домашнее задание

С.В.Громов
, Н.А.Родина
.
Физика-7 § 37, вопрос № 87.

Напряжение внутри жидкости, находящейся в состоянии покоя, называется гидростатическим давлением.

Средним гидростатическим давлением
 называется среднее для данной площадки напряжение сжатия, вызванное силой . Это давление можно определить как отношение к , то есть

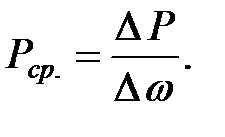(1.8)

Гидростатическое давление в данной точке определяется, как предел отношения к при 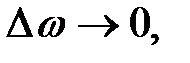то есть

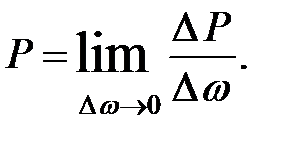(1.9)

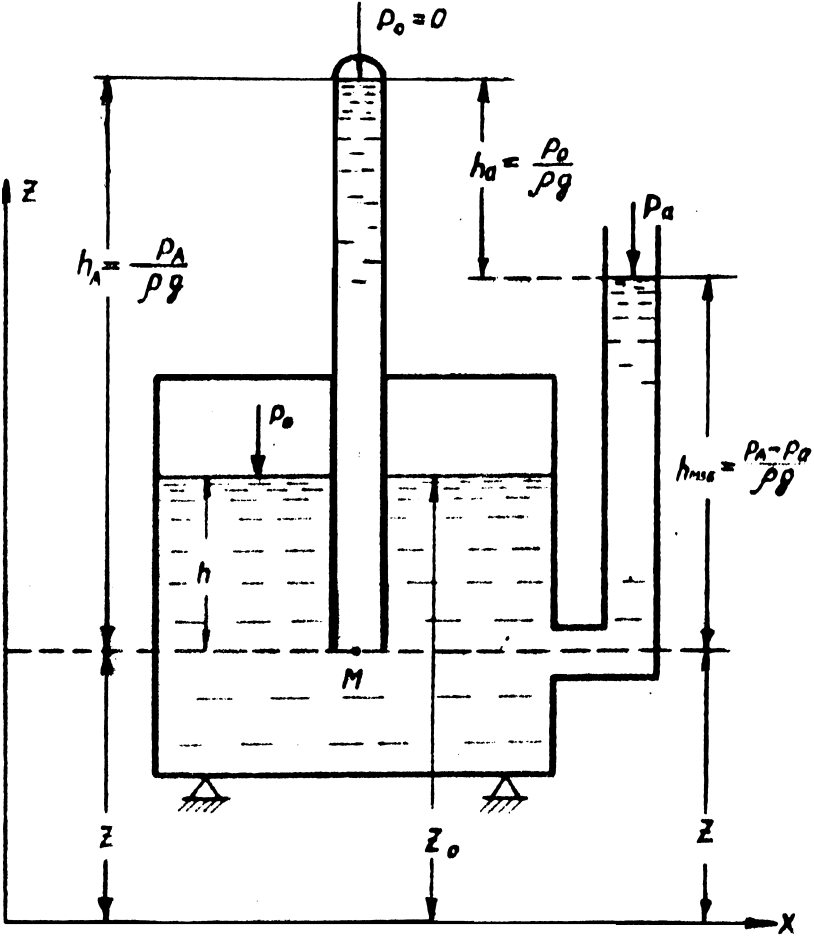
Абсолютное гидростатическое давление в любой точке жидкости складывается из давления на её свободную поверхность и давления столба жидкости, высота которого равна расстоянию от этой точки до свободной поверхности (рис. 1.1).

Основное уравнение гидростатики будет иметь вид

где – полное или абсолютное гидростатическое давление в данной точке М
;

– давление на свободной поверхности;

z
 – координата точки М
;

z
 0 – координата свободной поверхности;

OX
 – плоскость сравнения;

r
 – плотность жидкости;

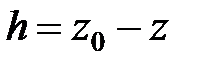– высота слоя жидкости над точкой М
.

Если сосуд открыт, то давление на свободной поверхности равняется атмосферному давлению

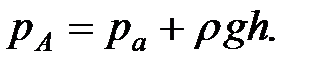(1.11)

Величина превышения абсолютного давления в точке над атмосферным давлением называют избыточным или манометрическим давлением

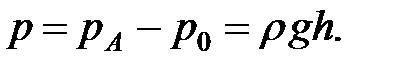(1.12)

Если в какой-либо точке абсолютное давление меньше атмосферного, то состояние жидкости характеризуется так называемым вакуумом. Разность между атмосферным и абсолютным давлением называется вакуумметрическим давлением

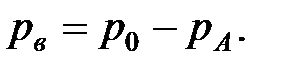(1.13)

На основании основного уравнения гидростатики может быть сформулирован закон Паскаля
: внешнее давление, приложенное к свободной поверхности жидкости в замкнутом сосуде, передаётся в любую точку жидкости без изменения.

На способности жидкости передавать изменение внешнего давления во все точки занятого ею пространства основан принцип действия гидравлических машин. На рис. 1.2 показана схема действия гидравлического пресса.

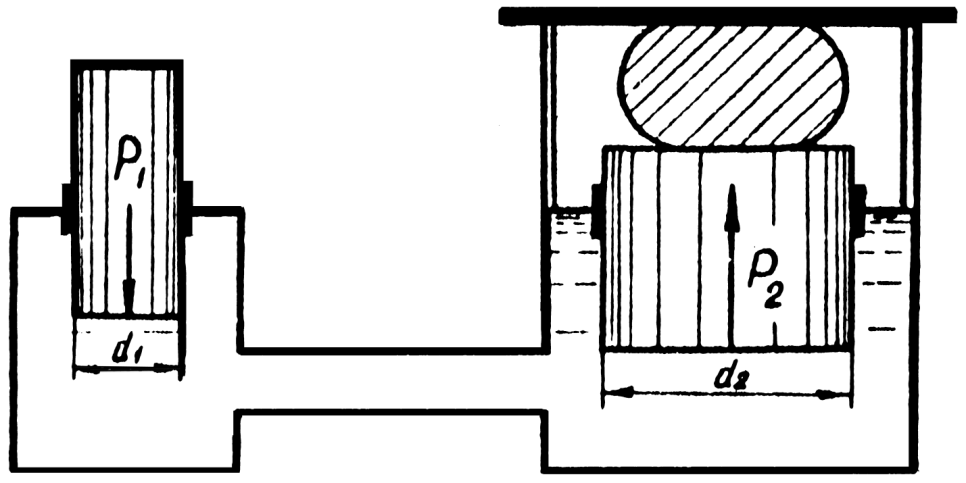
Если на малый поршень действует сила P
 1 , то сила, действующая на большой поршень P
 2 , определяется по уравнению:

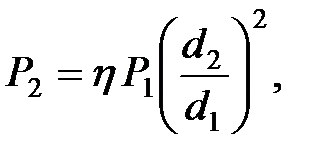(1.14)

где = 0,8-0,85 – коэффициент полезного действия гидравлического пресса, учитывающий потери на трение.

Гидростатическое давление измеряют в паскалях. Паскаль
 (Па
) – давление, вызываемое силой 1 ньютон (Н
), равномерно распределённой по нормальной к ней поверхности площадью 1 м
 2 .

При решении практических задач, где возникает необходимость перевода ранее применявшихся единиц измерения давления в СИ, будем пользоваться соотношениями:

1 ат
 = 1 кг/см
 2 = 10 м
 вод. cт. = 98065 Па
 » 98,1 кПа

760 мм
рт. cт. = 101325 Па
 » 101,3 кПа
.

Задачи

1.18. Какая высота водяного столба соответствует давлению 150 кПа
?

Решение
. Из формулы (1.12) следует, что

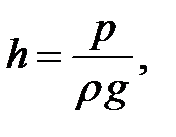
где p
 = 1,5×10 5 Па
– избыточное давление, создаваемое столбом воды;

r
 = 1×10 3 кг
/м
 3 – плотность воды.

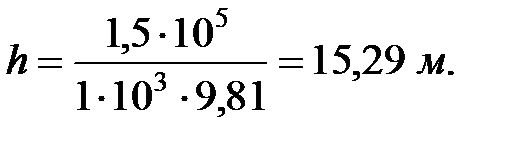
1.19. Какая высота ртутного столба соответствует давлению 80 кПа
?

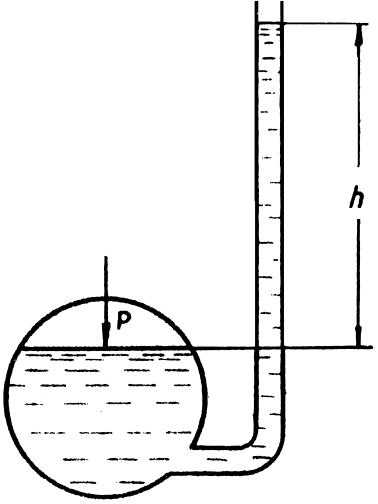
1.20. Определить величину избыточного давления на поверхности жидкости, находящейся в закрытой ёмкости (рис. 1.3) в состоянии покоя, если в трубке пьезометра вода поднялась на высоту h
 = 1,8 м
.

1.21. На какой высоте над манометром, присоединённым к резервуару, находится уровень нефти плотностью 840 кг
/м
 3 . Манометр показывает давление 1,21×10 5 Па
.

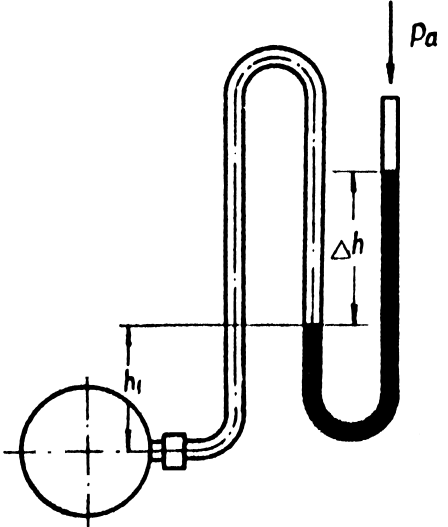
1.22. Определить избыточное давление воды в трубопроводе, если
U
-образный ртутный манометр (рис. 1.4) показал перепад Dh
 = 80 см
,
а h
 1 = 40 см
.

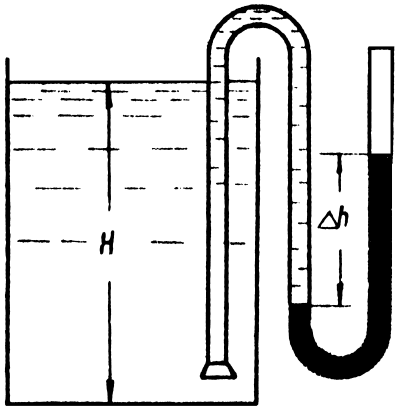
1.23. Определить уровень мазута в баке (рис. 1.5), если при замере
S
-образной трубкой, разность уровней ртути Dh
 = 250 мм
. Плотность мазута r
= 860 кг
/м
 3 .

1.24. Манометр, с помощью которого производилось измерение давления в наружной водопроводной сети, показал 2 кг/см
 2 . Определить абсолютное давление в сети, если атмосферное давление 750 мм
 рт. cт.

Решение
. Абсолютное давление в наружной водопроводной сети определяется по формуле (1.11), где – атмосферное давление

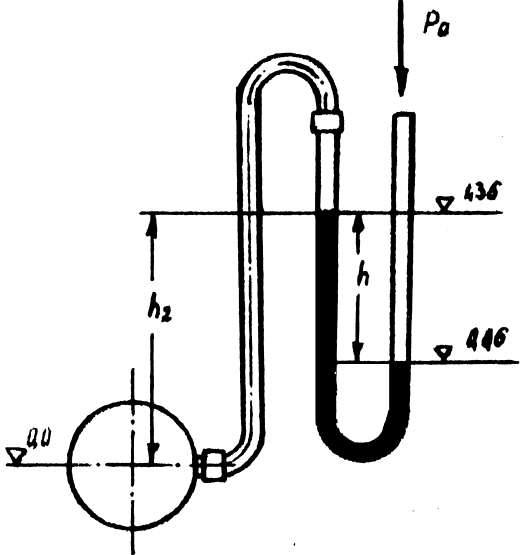
1.25. Определить абсолютное и вакуумметрическое давление воды
в трубопроводе, если U
-образный ртутный манометр (рис. 1.6) показал перепад Dh
 = 50 см
. Атмосферное давление 760 мм
 рт. ст. Высотные отметки относительно оси трубопровода показаны на рис. 1.6.

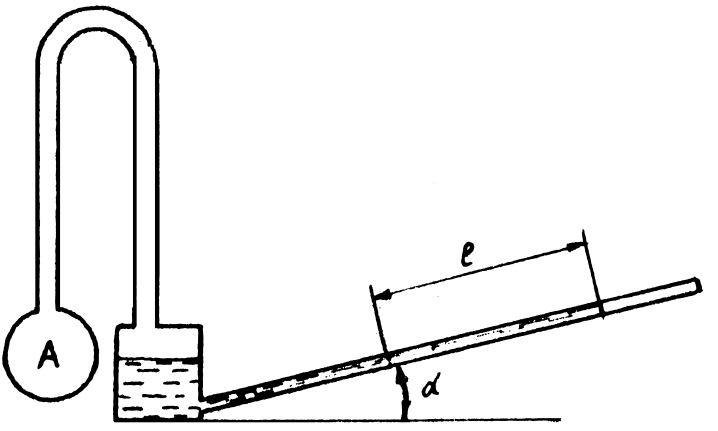
1.26. Давление в газопроводе А
 измеряется с помощью микроманометра, заполненного спиртом плотностью r
 = 790 кг
/м
 3 . Трубка микроманометра наклонена к горизонту под углом a
 = 15° (рис. 1.7). Определить избыточное давление в газопроводе, если мениск переместился на l
 = 62 мм.

1.27. Определить абсолютное и избыточное давление на дно пожарного водоёма глубиной 3,5 м
. Атмосферное давление 735 мм
 рт. ст.

1.28. Определить абсолютное и избыточное давление на дно водонапорного бака диаметром 3 м
, в котором находится 15 м
 3 воды. Атмосферное давление 750 мм
 рт. ст.

1.29. Определить абсолютное и избыточное давление в резервуаре по показанию ртутного дифференциального манометра (рис. 1.8), в правом колене которого над ртутью находится столб масла высотой 15 см
 плотностью 850 кг
/м
 3 . Высота столба ртути 40 см
, атмосферное давление 730 мм
 рт. ст.

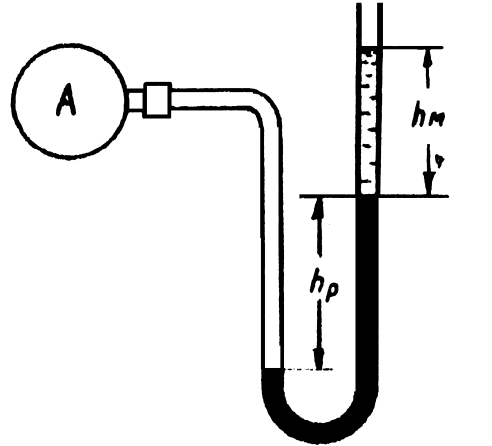
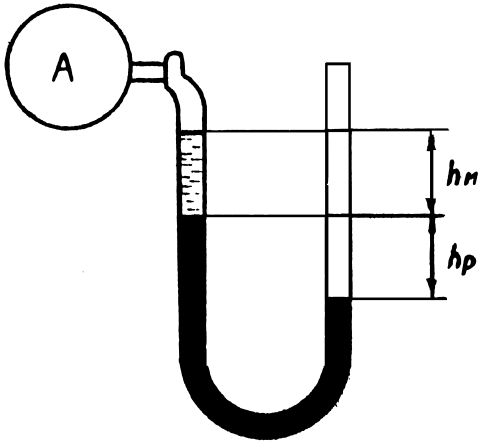
1.30. Определить абсолютное и вакуумметрическое давление во всасывающей линии ацетиленового компрессора по показанию ртутного вакуумметра (рис. 1.9). Ртуть в левом колене поднялась на высоту h
 p = 50 см
, над ртутью налито масло h
 м = 20 см
 плотностью 800 кг
/м
 3 . Атмосферное давление 750 мм
 рт. ст.

1.31. Определить избыточное давление в сети наружного пожарного водопровода, питающегося от водонапорной башни высотой 25 м
.

1.32. Определить максимальную высоту слоя нефти плотностью 900 кг
/м
 3 , чтобы избыточное давление на дно резервуара не превышало 70 кПа
.

1.33. Определить на какую высоту может подняться вода из водяного бака гидропневматической установки, если манометр, установленный на воздушном баке, показывает 3,2 кг/см
 2 .

1.34. Определить максимальную глубину воды в водонапорном баке объемом 30 м
 3 , установленном на перекрытии. Дополнительная нагрузка на перекрытии от установки бака с водой не должна превышать 2×10 4 Па
. Вес бака с арматурой 8 т.

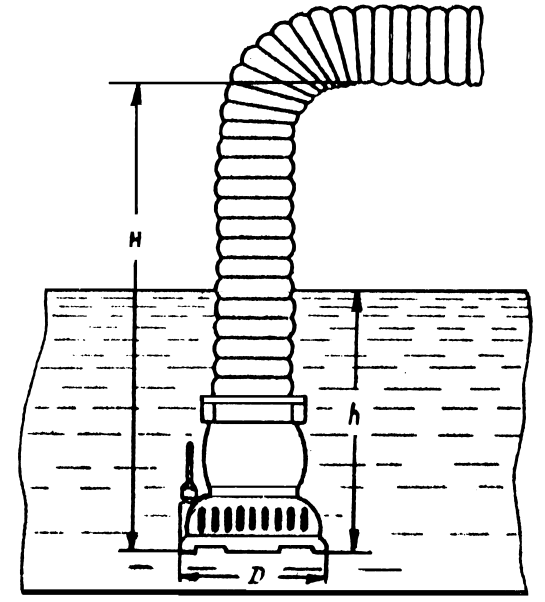
1.35. Определить усилие, необходимое для открытия всасывающего клапана пожарного насоса диаметром 200 мм
, если длина рукава H
 = 6 м
,
а глубина погружения всасывающего клапана h
 = 1 м
 (рис. 1.10)

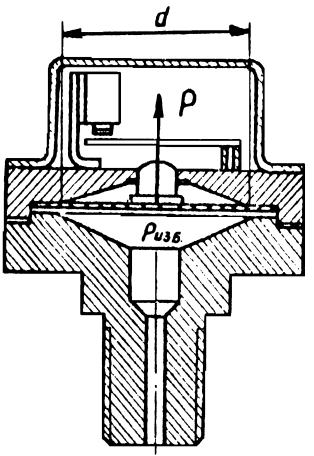
1.36. Определить силу, действующую на шток сигнализатора давления, если давление на мембрану диаметром 40 мм
 составляет 3,5×10 5 Па
 (рис. 1.11).

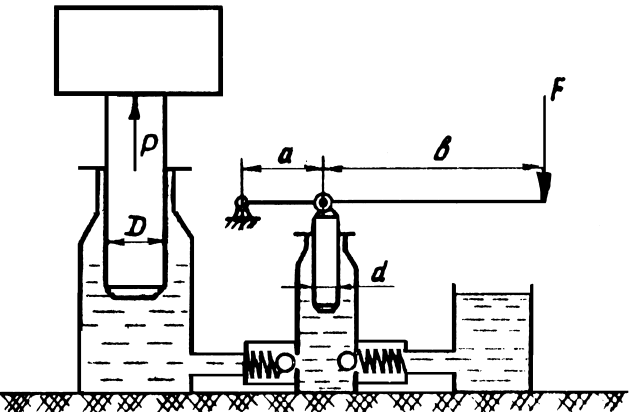
1.37. Для подъёма пожарной техники во время ремонта применяется гидродомкрат (рис. 1.12). Определить силу, развиваемую гидродомкратом, если сила F
, действующая на рукоятку, составляет 20 Н
, а
/в
 = 1/9, d 2 /d 1 = 10. Коэффициент полезного действия h
= 0,85.

1.38. Определить давление масла в цилиндре гидропривода пожарной лестницы (рис. 1.13), если диаметр поршня 100 мм
. Усилие на штоке поршня 30 кН
, коэффициент полезного действия h
= 0,95.

1.3. Эпюры гидростатического давления.
Сила гидростатического давления на плоские стенки.
Закон Архимеда

Графическое изображение распределения гидростатического давления по поверхности тела, погруженного в жидкость, называется эпюрой гидростатического давления
.

При построении эпюр гидростатического давления используются два основных принципа, вытекающие из свойств гидростатического давления:

· гидростатическое давление является векторной величиной
. Вектор гидростатического давления направлен по нормали к поверхности тела, погруженного в жидкость;

· модуль вектора
 гидростатического давления определяется по уравнению (1.11) для построения эпюр абсолютного давления и (1.12) для построения эпюр избыточного гидростатического давления.

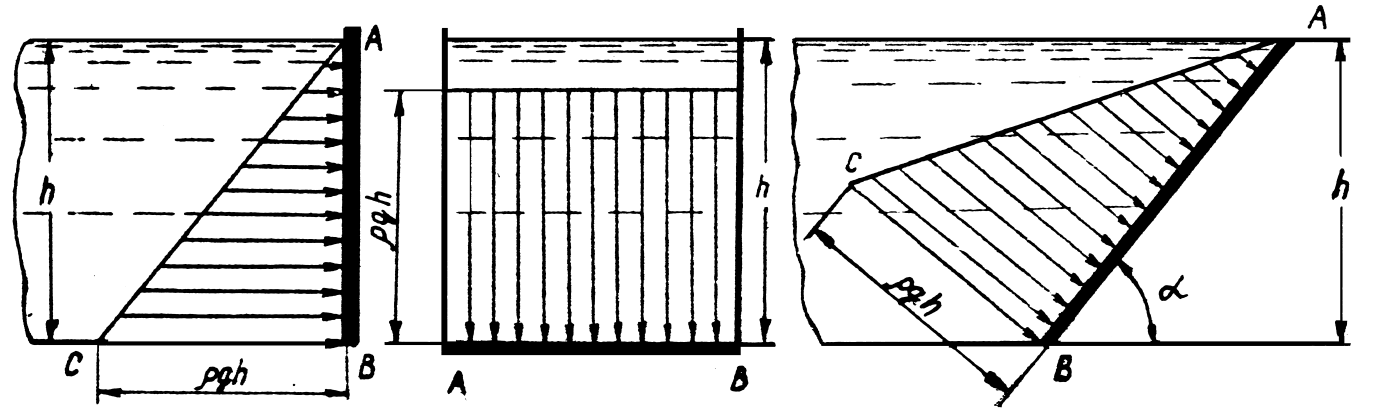
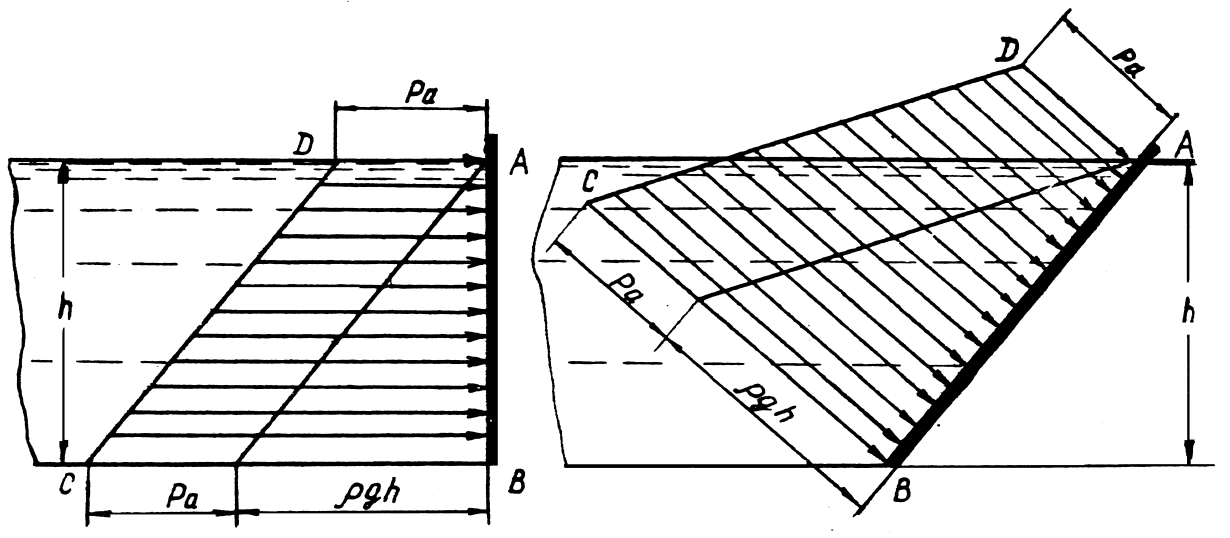
Для плоских прямоугольных стенок эпюры избыточного и абсолютного гидростатического давления имеют вид, представленный на рис. 1.14
и рис. 1.15.

Равнодействующая элементарных сил гидростатического давления, действующих на какую-либо стенку, называется силой гидростатического давления
.

Сила гидростатического давления на площадку определяется произведением её площади на гидростатическое давление в центре тяжести площадки (рис. 1.16).

где P
 – сила гидростатического давления, Н
;

h цт
 – глубина погружения центра тяжести фигуры, м;

p цт
 – гидростатическое давление в центре тяжести фигуры, Па
.

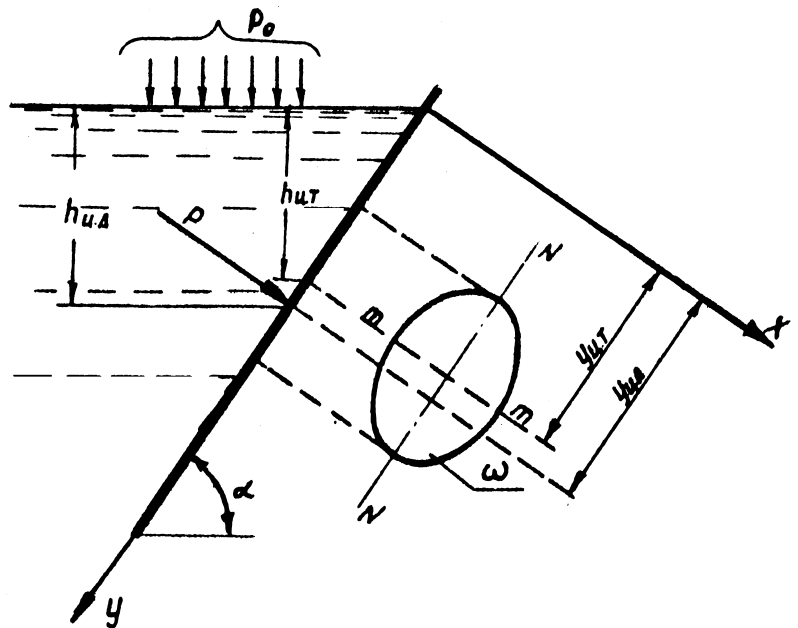
Точка приложения силы Р
 называется центром давления. Координата центра давления 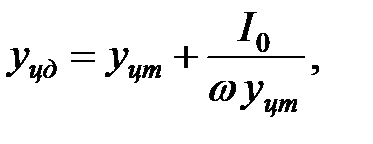для симметричных относительно оси N-N
 фигур определится из уравнения

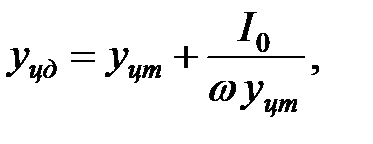(1.16)

где I
 0 – момент инерции площади w
 относительно оси m-m
.

Значения I
 0 и y цт
 для некоторых фигур приведены в приложении 5.

Сила гидростатического давления Р
 может быть определена графическим способом как произведение площади эпюры гидростатического давления на ширину стенки.

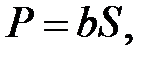(1.17)

где S
 – площадь эпюры гидростатического давления, Н
/м
;

b
 – ширина стенки, м
.

Сила давления проходит через центр тяжести эпюры гидростатического давления и направлена по нормали к поверхности.

Сила избыточного гидростатического давления для плоских прямоугольных стенок, изображенных на рис. 1.14, может быть определена по формулам:

Вертикальная стенка

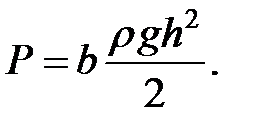(1.18)

Горизонтальная стенка

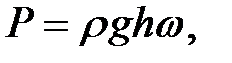(1.19)

где w
 – площадь дна, м
 2 .

Наклонная стенка

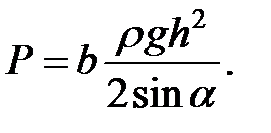(1.20)

Расчёт давления столба жидкости. p. Давление столба жидкости на дно и стенки сосуда пропорци- онально его высоте и плотности. h. ? g. 1. p = 9,8 Н/кг * ? * h. 2. 9,8 Н/кг- коэффициент; p – плотность жидкости; h – высота столба (в м). 3. 4. Единица измерения – 1 Паскаль. 5. 6. 7. [ p] =. 8. Чем выше столб жидкости и больше её плотность, тем давление будет… а) меньше, б) больше, г) не зависит от этих величин.

Слайд 4 из презентации «Давление воды»
 к урокам физики на тему «Давление жидкости»

Размеры: 960 х 720 пикселей, формат: jpg.
Чтобы бесплатно скачать слайд для использования на уроке физики,
щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…».
Скачать всю презентацию «Давление воды.ppt» можно
в zip-архиве размером 661 КБ.

Скачать презентацию

Давление жидкости

«Давление урок» – Физический диктант. 1 2 3. Почему шарик увеличивает свой объем? Изучить влияние атмосферного давления в жизни людей. g. Допишите недостающие величины. S1. «Давление твердых тел, жидкостей и газов.» 7класс учитель Куклина О.Н. Подготовиться к контрольной работе. Этапы урока. F. Цели урока: Обобщающий урок по теме.

«Давление твёрдых тел» – Силу, прикладываемую перпендикулярно поверхности, называют силой давления. S. =. Сила. Давление твёрдых тел. Давление. 1. Площадь. Р. F. 1Па.

«Сообщающиеся сосуды и их применение» – Шлюзование судов. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне. Сообщающиеся сосуды. Р, S, F, h, ?, p, m, g По какой формуле рассчитывают давление жидкости на дно и стенки сосуда? Запишите формулу для расчёта высоты столба жидкости. Выводы: В сообщающихся сосудах любой ширины однородная жидкость устанавливается на одном уровне.

«Давление воды» – В. На рисунке изображена модель фонтана. ЗАДАЧА. p. Давление в неподвижных жидкостях и газах. 9. 10. Все тела притягиваются к Земле. А. если правую трубку наклонить? Проверь себя! Ответы: а3; б2; в12345; в216; г1; д1; е11; е21.

«Давление в природе» – F-приложенная сила,Н. Б.Кирпич лежит на столе. Сила давления. Вычислить давление твёрдого тела на опору.(работа в парах). Мир техники. В Амазонке есть пиранья – С виду рыбка так себе. 1 часть А.Кирпич лежит на столе. F р= — S. Решение задач+ эксперимент. Давление твёрдых тел. У Серой Шейки замерло сердце…».

Жидкости и газы передают по всем направлениям приложенное к ним давление. Об этом гласит закон Паскаля и практический опыт.

Но существует еще и собственный вес, который тоже должен влиять на давление, существующее в жидкостях и газах. Вес собственных частей или слоев. Верхние слои жидкости давят на средние, средние на нижние, а последние – на дно. То есть мы можем говорить о существовании давления столба покоящейся жидкости на дно.

Формула давления столба жидкости

Формула для расчета давления столба жидкости высотой h имеет следующий вид:

где ρ – плотность жидкости,
g – ускорение свободного падения,
h – высота столба жидкости.

Это формула так называемого гидростатического давления жидкости.

Давление столба жидкости и газа

Гидростатическое давление, то есть, давление, оказываемое покоящейся жидкостью, на любой глубине не зависит от формы сосуда, в котором находится жидкость. Одно и то же количество воды, находясь в разных сосудах, будет оказывать разное давление на дно. Благодаря этому можно создать огромное давление даже небольшим количеством воды.

Это очень убедительно продемонстрировал Паскаль в семнадцатом веке. В закрытую бочку, полную воды, он вставил очень длинную узкую трубку. Поднявшись на второй этаж, он вылил в эту трубку всего лишь одну кружку воды. Бочка лопнула. Вода в трубке из-за малой толщины поднялась до очень большой высоты, и давление выросло до таких значений, что бочка не выдержала. То же самое справедливо и для газов. Однако, масса газов обычно намного меньше массы жидкостей, поэтому давление в газах, обусловленное собственным весом можно часто не учитывать на практике. Но в ряде случаев приходится считаться с этим. Например, атмосферное давление, которое давит на все находящиеся на Земле предметы, имеет большое значение в некоторых производственных процессах.

Благодаря гидростатическому давлению воды могут плавать и не тонуть корабли, которые весят зачастую не сотни, а тысячи килограмм, так как вода давит на них, как бы выталкивая наружу. Но именно по причине того же гидростатического давления на большой глубине у нас закладывает уши, а на очень большую глубину нельзя спуститься без специальных приспособлений – водолазного костюма или батискафа. Лишь немногие морские и океанические обитатели приспособились жить в условиях сильного давления на большой глубине, но по той же причине они не могут существовать в верхних слоях воды и могут погибнуть, если попадут на небольшую глубину.

Гидростатическое давление
 – давление столба воды над условным уровнем.

Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р,
 пропорциональной величине этой поверхности, и направленной по нормали к ней. Отношение Pw,
 то есть давление р
 на поверхность равную единице, называется гидростатическим давлением.

Простое уравнение P = pw
 может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах.

Вычисление

В каждой жидкости существует давление, обусловленное её собственным весом
p
=
G
/
S
=
m
g
/
S
{displaystyle p=G/S=mg/S}
; так как
m
=
ρ
V
{displaystyle m=rho V}
 , то
p
=
ρ
g
V
/
S
{displaystyle p=rho gV/S}
, учтем что
V
=
S
h
{displaystyle V=Sh}
 и получим формулу
p
=
ρ
g
h
{displaystyle p=rho gh}

Плотность жидкости ρ зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением .

История открытия

Единица измерения

В практике Гидростатическое давление измеряют в кг на 1 кв. см. Большие давления выражают часто в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0° под широтой, где ускорение силы тяжести = 0,0635 кг на 1 см² = 6,21·10 6 дин на 1 кв. см. 1 атмосфера = 1,0333 кг на 1 см² = 1,0136·10 6 дин на 1 см² для широты Парижа или 1,0132·10 6 для широты в 45°.

На основании гидростатического парадокса можно Г. давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности: так давление в 1 фн. на кв. дм. равно давлению столба воды в 25 дм высотой, так как фн. есть вес 25 куб. дм. воды.

Гидростатический парадокс

Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние каждой такой частицы от свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу Г. давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.

Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, Г. давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.

Закон Паскаля

Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести
 (= несжимаемая жидкость
) подчиняется закону Паскаля
:


p
(h)
=
ρ
g
h
{displaystyle p(h)=rho ,g,h}


ρ
{displaystyle rho }

– плотность
 [для воды : ≈ 1000 кг/м³]

g
{displaystyle g}

–

Источник

    1. Гидростатическое давление и его свойства

Сжимающее
напряжение, возникающее внутри покоящейся
жидкости, называется гидростатическим
давлением. Определяется гидростатическое
давление
как отношение силы давления к площади:

,
(1.4)

где
Р – сила давления; S
– площадь, к которой приложена сила
давления.

Гидростатическое
давление измеряется в Н/м2
(Ньютонах на квадратный метр), 1Н/м2=
1 Па
(Паскаль). В практике широко используется
единица измерения гидростатического
давления – техническая атмосфера (ат),
1 ат=1 кг/см2
≈ 105
Па. Гидростатическое давление может
измеряться высотой столба жидкости, 1
ат = 10 м вод.ст. (метр водного столба
жидкости) или 735,6 мм ртутного столба).

Гидростатическое
давление действует перпендикулярно к
рассматриваемой поверхности и
распространяется во всех направлениях
одинаково.

Задача
1.1.
Определить силу
Р2
для гидравлического пресса (рис. 1), если
известны площади поршней S1
и S2
и сила Р1,
действующая на левый поршень. Р1
= 10 кГ, S1=2см
2,
S2=100см2.

Рис.
1.1. Схема гидравлического пресса

Решение.
Гидростатическое давление под левым
поршнем равно р1=
=
5кГ/см2.
Это давление передается во всех
направлениях одинаково и поэтому под
правым поршнем гидростатическое давление
тоже будет равно 5 кГ/см2.
Так как р2
=Р2/S2
, то Р2=
р2∙S2
= 5∙100 = 500 (кГ).

В
общем виде можно записать

(1.5)

Задача
1.2. Какую
силу необходимо приложить к левому
поршню, имеющем прямоугольную форму
размером 1х2 см, если диаметр правого
поршня d
=12см, а сила Р2=2Т.

Решение.
Площадь левого поршня S1
=1х2=2 (см2),
площадь правого – S2
=3,14х122/4
= 113 (см2).
Из выражения (1.5) Р1
= S1хР2/S2
= 2х2000/113 =
34,4 (кГ).

    1. Основное уравнение гидростатики

Давление
в точке жидкости р
складывается из давления на поверхности
ро
и давления столба жидкости γ∙h.
Полное (или абсолютное) давление в
точке равно

р
= ро
+ γ∙h
(1.6)

Избыточное
давление ризб
= р – рат
= γ∙h
(1.7)

Вакуумметрическое
давление (вакуум) – недостаток давления
до атмосферного

рвак
= рат
– р
 (1.8)

Давление
измеряется при помощи пружинных,
мембранных манометров. Жидкостные
манометры представляют собой U
стеклянную трубку, в которую наливается
ртуть или другая жидкость (необходимо
иметь в виду, что ртуть очень опасна для
здоровья и ее использование в настоящее
время запрещено), один конец трубки
крепится к сосуду, в котором измеряется
давление.

Задача
1.3.
Определить полное и избыточное
гидростатическое давление в водоеме
на глубине 6 м.

Решение.
Полное давление по формуле (1.6) равно
р = ро
+ γ∙h
= 1
+ 0.001·600 = 1.6 ат
[кГ/см2+
кГ/см3·см
= кГ/см2
= ат.], избыточное давление ризб
= γ∙h
 равно
0.001·600 = 0.6 ат.

При
решении этой же задачи в системе Си
р = ро
+ ∙g∙h
= 98100 +
1000·9.81·6 = 98100 + 58860 = 156 960
Па [Н/м2 +
кг/м3·м/с2·м
= Н/м2
+ кг·м/(м2·с2)
= Н/м2+Н/м2
= Па] = 156.96 кПа , ризб
= ∙g∙h
=1000·9.81·6 = 58
кПа.

Задача
1.4. В
герметичном сосуде (рис. 1.2.) поддерживается
давление р = 1,5 ат., определить высоту
столба воды h
в пьезометре.

Рис.
1.2. Схема (к задаче 1.4.)

Решение.
Давление в точке b
слева и справа будет одинаковым. Слева
pb=
р + ∙h1
.

Справа
pb
= pа
+ ∙h1+∙h
или
p
+ ∙h1=
pа
+ ∙h1+
∙h,
p
= pа
+ ∙h.

Отсюда h
= (p
– pa)/

= (1,5 – 1)/ 0.001=500 см [кГ/см2/кГ/см3
= см] =5 м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий