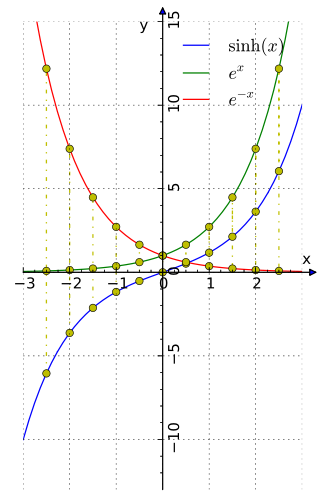
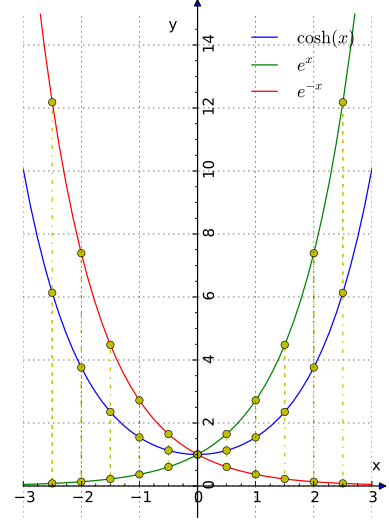
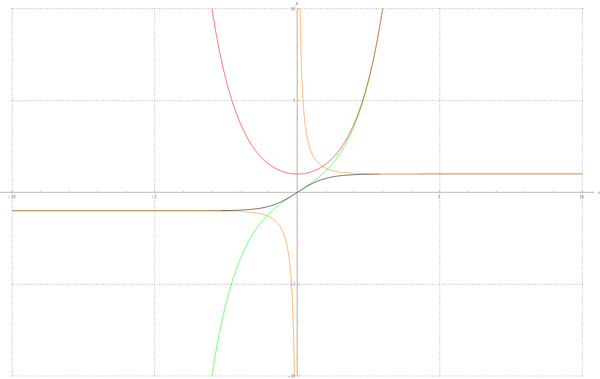
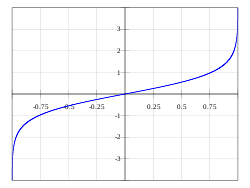
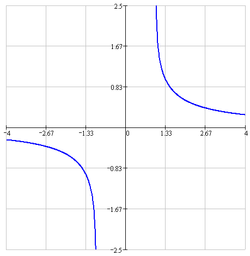
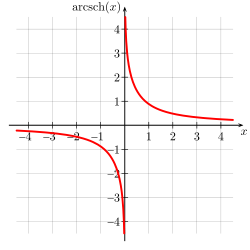
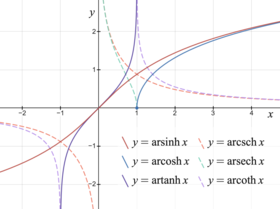
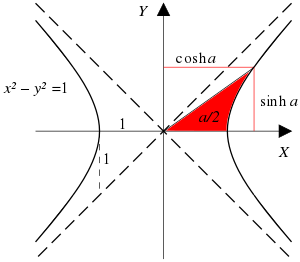
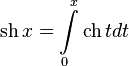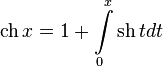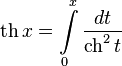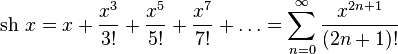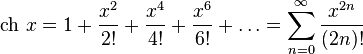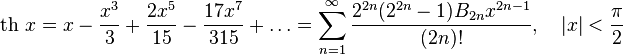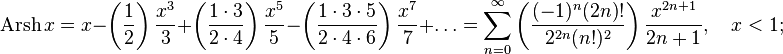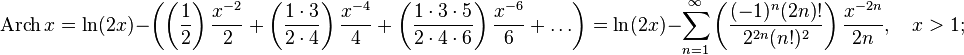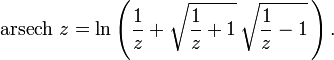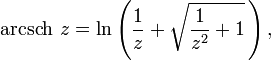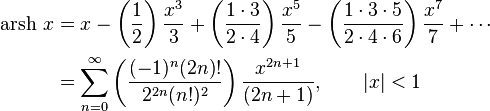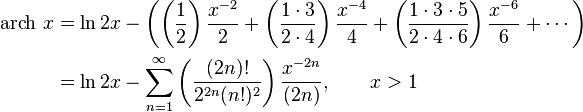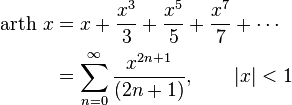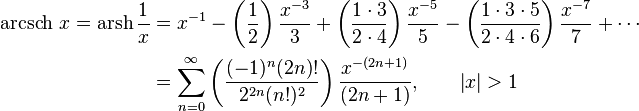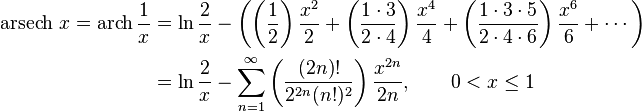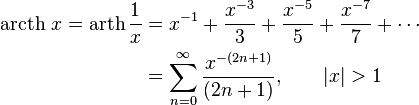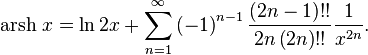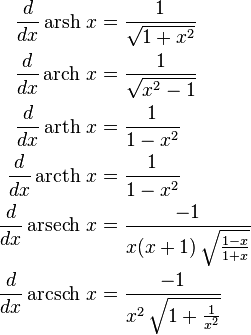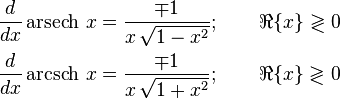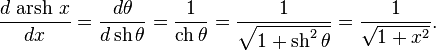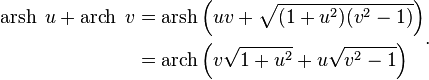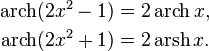Гиперболический синус обратная функция как найти

Обра́тные гиперболи́ческие фу́нкции (известные также как а̀реафу́нкции или ареа-функции) — семейство элементарных функций, определяющихся как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x² − y² = 1 аналогично тому, как обратные тригонометрические функции определяют длину дуги единичной окружности x² + y² = 1. Для этих функций часто используются обозначения arcsinh, arcsh, arccosh, arcch и т.д., хотя такие обозначения являются, строго говоря, ошибочными, так как префикс arc является сокращением от arcus (дуга) и потому относится только к обратным тригонометрическим функциям, тогда как ar обозначает area — площадь. Более правильными являются обозначения arsinh, arsh и т.д. и названия обратный гиперболический синус, ареасинус и т.д. Также применяют^[1] названия гиперболический ареасинус, гиперболический ареакосинус и т.д., но слово «гиперболический» здесь является лишним, поскольку на принадлежность функции семейству обратных гиперболических функций однозначно указывает префикс «ареа». Иногда названия соответствующих функций записывают через дефис: ареа-синус, ареа-косинус и т.д.

В комплексной плоскости гиперболические функции являются периодическими, а обратные им функции — многозначными. Поэтому подобно обратным тригонометрическим функциям обозначения ареафункций принято записывать с большой буквы, если подразумевается множество значений функции (логарифм в соответствующем определении функции также понимается как общее значение логарифма, обозначаемое Ln). С маленькой буквы записываются главные значения соответствующих функций.

В русской литературе обозначения большинства прямых и обратных гиперболических функций (так же как и части тригонометрических) отличаются от английских обозначений.

Название функции	Обозначение в русской литературе	Обозначение в английской литературе
ареасинус	arsh	arsinh, sinh⁻¹
ареакосинус	arch	arcosh, cosh⁻¹
ареатангенс	arth	artanh, tanh⁻¹
ареакотангенс	arcth	arcoth, coth⁻¹
ареасеканс	arsch, arsech	arsech, sech⁻¹
ареакосеканс	arcsch	arcsch, csch⁻¹

Определения функций[править | править код]

Ареасинус для действительного аргумента

Ареакосинус для действительного аргумента

Ареатангенс для действительного аргумента

Ареакотангенс для действительного аргумента

Ареасеканс для действительного аргумента

Ареакосеканс для действительного аргумента

В комплексной плоскости главные значения функций можно определить формулами:

ареасинус

$operatorname {arsh},z=ln(z+{sqrt {z^{2}+1}},);$

ареакосинус

${displaystyle operatorname {arch} ,z=ln(z+{sqrt {z^{2}-1}});}$

ареатангенс

$operatorname {arth},z={tfrac 12}ln left({frac {1+z}{1-z}}right);$

ареакотангенс

$operatorname {arcth},z={tfrac 12}ln left({frac {z+1}{z-1}}right);$

ареасеканс

${displaystyle operatorname {arsech} ,z=ln left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}-1}}right);}$

ареакосеканс

$operatorname {arcsch},z=ln left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}+1}},right).$

Квадратными корнями в этих формулах являются главные значения квадратного корня (то есть ${displaystyle {sqrt {z}}={sqrt {r}},e^{ivarphi /2},}$ если представить комплексное число z как ${displaystyle z=re^{ivarphi }}$ при ), а логарифмические функции являются функциями комплексной переменной. Для действительных аргументов можно осуществить некоторые упрощения, например ${displaystyle {sqrt {x+1}}{sqrt {x-1}}={sqrt {x^{2}-1}},}$ которые не всегда верны для главных значений квадратных корней.

Разложение в ряд[править | править код]

Обратные гиперболические функции можно разложить в ряды:

${displaystyle {begin{aligned}operatorname {arsh} ,x&=x-left({frac {1}{2}}right){frac {x^{3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{5}}{5}}-left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{7}}{7}}+cdots \&=sum _{n=0}^{infty }left({frac {(-1)^{n}(2n-1)!!}{(2n)!!}}right){frac {x^{2n+1}}{(2n+1)}},qquad left|xright|<1.end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arch} ,x&=ln 2x-left(left({frac {1}{2}}right){frac {x^{-2}}{2}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{-4}}{4}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{-6}}{6}}+cdots right)\&=ln 2x-sum _{n=1}^{infty }left({frac {(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{-2n}}{(2n)}},qquad x>1.end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arth} ,x&=x+{frac {x^{3}}{3}}+{frac {x^{5}}{5}}+{frac {x^{7}}{7}}+cdots \&=sum _{n=0}^{infty }{frac {x^{2n+1}}{(2n+1)}},qquad left|xright|<1.end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arcsch} ,x=operatorname {arsh} {frac {1}{x}}&=x^{-1}-left({frac {1}{2}}right){frac {x^{-3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{-5}}{5}}-left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{-7}}{7}}+cdots \&=sum _{n=0}^{infty }left({frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{-(2n+1)}}{(2n+1)}},qquad left|xright|>1.end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arsech} ,x=operatorname {arch} {frac {1}{x}}&=ln {frac {2}{x}}-left(left({frac {1}{2}}right){frac {x^{2}}{2}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{4}}{4}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{6}}{6}}+cdots right)\&=ln {frac {2}{x}}-sum _{n=1}^{infty }left({frac {(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{2n}}{2n}},qquad 0<xleq 1.end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arcth} ,x=operatorname {arth} {frac {1}{x}}&=x^{-1}+{frac {x^{-3}}{3}}+{frac {x^{-5}}{5}}+{frac {x^{-7}}{7}}+cdots \&=sum _{n=0}^{infty }{frac {x^{-(2n+1)}}{(2n+1)}},qquad left|xright|>1.end{aligned}}}$

Асимптотическое разложение arsh x даётся формулой

$operatorname {arsh},x=ln 2x+sum limits _{{n=1}}^{infty }{left({-1}right)^{{n-1}}{frac {{left({2n-1}right)!!}}{{2nleft({2n}right)!!}}}}{frac {1}{{x^{{2n}}}}}.$

Производные[править | править код]

Функция	Производная	Примечание
	${displaystyle {frac {1}{sqrt {x^{2}+1}}}}$	Доказательство ${displaystyle (arsh(x))'=(ln {(x+{sqrt {x^{2}+1}})})'={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (x+{sqrt {x^{2}+1}})'={frac {1}{x+{sqrt {x^{2}+1}}}}cdot ((x)'+({sqrt {x^{2}+1}})')={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (1+({sqrt {x^{2}+1}})')={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (1+{frac {1}{2{sqrt {x^{2}+1}}}}cdot (x^{2}+1)')={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (1+{frac {2x}{2{sqrt {x^{2}+1}}}})={frac {1}{x+{sqrt {x^{2}+1}}}}cdot ({frac {x+{sqrt {x^{2}+1}}}{sqrt {x^{2}+1}}})={frac {x+{sqrt {x^{2}+1}}}{(x+{sqrt {x^{2}+1}})cdot ({sqrt {x^{2}+1}})}}={frac {1}{sqrt {x^{2}+1}}}}$
	${displaystyle {frac {1}{sqrt {x^{2}-1}}}}$	Доказательство ${displaystyle (arch(x))'=(ln {(x+{sqrt {x^{2}-1}})})'={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (x+{sqrt {x^{2}-1}})'={frac {1}{x+{sqrt {x^{2}-1}}}}cdot ((x)'+({sqrt {x^{2}-1}})')={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (1+({sqrt {x^{2}-1}})')={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (1+{frac {1}{2{sqrt {x^{2}-1}}}}cdot (x^{2}-1)')={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (1+{frac {2x}{2{sqrt {x^{2}-1}}}})={frac {1}{x+{sqrt {x^{2}-1}}}}cdot ({frac {x+{sqrt {x^{2}-1}}}{sqrt {x^{2}-1}}})={frac {x+{sqrt {x^{2}-1}}}{(x+{sqrt {x^{2}-1}})cdot ({sqrt {x^{2}-1}})}}={frac {1}{sqrt {x^{2}-1}}}}$
	${displaystyle {frac {1}{1-x^{2}}}}$	Доказательство ${displaystyle ({displaystyle mathrm {arth} x})'={biggl (}{frac {1}{2}}cdot ln {biggl (}{frac {1+x}{1-x}}{biggl )}{biggl )}'={frac {1}{2}}cdot {frac {1-x}{1+x}}cdot {biggl (}{frac {1+x}{1-x}}{biggl )}'={frac {1}{2}}cdot {frac {1-x}{1+x}}cdot {frac {(1+x)'(1-x)-(1+x)(1-x)'}{(1-x)^{2}}}={frac {1}{2}}cdot {frac {1-x}{1+x}}cdot {frac {2}{(1-x)^{2}}}={frac {1}{1-x^{2}}}}$
	${displaystyle {frac {1}{1-x^{2}}}}$	Доказательство ${displaystyle ({displaystyle mathrm {arcth} x})'={biggl (}{frac {1}{2}}cdot ln {biggl (}{frac {x+1}{x-1}}{biggl )}{biggl )}'={frac {1}{2}}cdot {frac {x-1}{x+1}}cdot {biggl (}{frac {x+1}{x-1}}{biggl )}'={frac {1}{2}}cdot {frac {x-1}{x+1}}cdot {frac {(x+1)'(x-1)-(x+1)(x-1)'}{(x-1)^{2}}}={frac {1}{2}}cdot {frac {x-1}{x+1}}cdot {frac {-2}{(x-1)^{2}}}={frac {1}{1-x^{2}}}}$
	${displaystyle -{frac {1}{x(x+1){sqrt {frac {1-x}{1+x}}}}}}$
	${displaystyle -{frac {1}{x(x+1){sqrt {1+{frac {1}{x^{2}}}}}}}}$

Для действительных x:

${displaystyle {begin{aligned}{frac {d}{dx}}operatorname {arsech} ,x&{}=mp {frac {1}{x,{sqrt {1-x^{2}}}}};qquad Re {x}gtrless 0.\{frac {d}{dx}}operatorname {arcsch} ,x&{}=mp {frac {1}{x,{sqrt {1+x^{2}}}}};qquad Re {x}gtrless 0.end{aligned}}}$

Пример дифференцирования: если θ = arsh x, то:

${frac {d,operatorname {arsh},x}{dx}}={frac {dtheta }{doperatorname {sh}theta }}={frac {1}{operatorname {ch}theta }}={frac {1}{{sqrt {1+operatorname {sh}^{2}theta }}}}={frac {1}{{sqrt {1+x^{2}}}}}.$

Комбинация гиперболических и обратных гиперболических функций[править | править код]

${begin{aligned}&operatorname {sh}(operatorname {arch},x)={sqrt {x^{{2}}-1}},quad quad |x|>1;\&operatorname {sh}(operatorname {arth},x)={frac {x}{{sqrt {1-x^{{2}}}}}},quad quad -1<x<1;\&operatorname {ch}(operatorname {arsh},x)={sqrt {1+x^{{2}}}};\&operatorname {ch}(operatorname {arth},x)={frac {1}{{sqrt {1-x^{{2}}}}}},quad quad -1<x<1;\&operatorname {th}(operatorname {arsh},x)={frac {x}{{sqrt {1+x^{{2}}}}}};\&operatorname {th}(operatorname {arch},x)={frac {{sqrt {x^{{2}}-1}}}{x}},quad quad |x|>1.end{aligned}}$

Дополнительные формулы[править | править код]

$operatorname {arsh};upm operatorname {arsh};v=operatorname {arsh}left(u{sqrt {1+v^{2}}}pm v{sqrt {1+u^{2}}}right).$

$operatorname {arch};upm operatorname {arch};v=operatorname {arch}left(uvpm {sqrt {(u^{2}-1)(v^{2}-1)}}right).$

$operatorname {arth};upm operatorname {arth};v=operatorname {arth}left({frac {upm v}{1pm uv}}right).$

${displaystyle {begin{aligned}operatorname {arsh} ;u+operatorname {arch} ;v&=operatorname {arsh} left(uv+{sqrt {(1+u^{2})(v^{2}-1)}}right)\&=operatorname {arch} left(v{sqrt {1+u^{2}}}+u{sqrt {v^{2}-1}}right).end{aligned}}}$

${displaystyle {begin{aligned}2operatorname {arch} x&=operatorname {arch} (2x^{2}-1),&quad quad xgeq 1;\4operatorname {arch} x&=operatorname {arch} (8x^{4}-8x^{2}+1),&quad quad xgeq 1;\2operatorname {arsh} x&=operatorname {arch} (2x^{2}+1),&quad quad xgeq 0;\4operatorname {arsh} x&=operatorname {arch} (8x^{4}+8x^{2}+1),&quad quad xgeq 0.\end{aligned}}}$

См. также[править | править код]

Гиперболические функции
Обратные тригонометрические функции
Таблица интегралов обратных гиперболических функций

Источники[править | править код]

↑ М.Я. Выгодский. Справочник по высшей математике. — Наука, 1963. — С. 594. — 873 с.

Herbert Busemann, Paul J. Kelly (1953) Projective Geometry and Projective Metrics, с. 207, Academic Press.

Ссылки[править | править код]

Inverse hyperbolic functions на сайте MathWorld
Inverse hyperbolic functions

Источник

From Wikipedia, the free encyclopedia

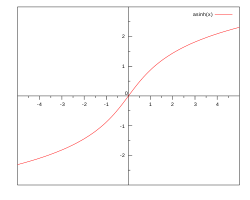
Graphs of the inverse hyperbolic functions

The hyperbolic functions sinh, cosh, and tanh with respect to a unit hyperbola are analogous to circular functions sin, cos, tan with respect to a unit circle. The argument to the hyperbolic functions is a hyperbolic angle measure.

In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangent, inverse hyperbolic cosecant, inverse hyperbolic secant, and inverse hyperbolic cotangent. They are commonly denoted by the symbols for the hyperbolic functions, prefixed with arc- or ar-.

For a given value of a hyperbolic function, the inverse hyperbolic function provides the corresponding hyperbolic angle measure, for example and Hyperbolic angle measure is the length of an arc of a unit hyperbola $x^{2}-y^{2}=1$ as measured in the Lorentzian plane (not the length of a hyperbolic arc in the Euclidean plane), and twice the area of the corresponding hyperbolic sector. This is analogous to the way circular angle measure is the arc length of an arc of the unit circle in the Euclidean plane or twice the area of the corresponding circular sector. Alternately hyperbolic angle it is the area of a sector of the hyperbola Some authors call the inverse hyperbolic functions hyperbolic area functions.^[1]

Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. It also occurs in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace’s equation in Cartesian coordinates. Laplace’s equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity.

Notation[edit]

A ray through the unit hyperbola ${displaystyle x^{2} - y^{2} = 1}$ in the point , where is twice the area between the ray, the hyperbola, and the -axis

The earliest and most widely adopted symbols use the prefix arc- (that is: arcsinh, arccosh, arctanh, arcsech, arccsch, arccoth), by analogy with the inverse circular functions (arcsin, etc.). For a unit hyperbola (“Lorentzian circle”) in the Lorentzian plane (pseudo-Euclidean plane of signature (1, 1))^[2] or in the hyperbolic number plane,^[3] the hyperbolic angle measure (argument to the hyperbolic functions) is indeed the arc length of a hyperbolic arc.

Also common is the notation ${displaystyle sinh ^{-1},}$ ${displaystyle cosh ^{-1},}$ etc.,^[4]^[5] although care must be taken to avoid misinterpretations of the superscript −1 as an exponent. The standard convention is that ${displaystyle sinh ^{-1}x}$ or ${displaystyle sinh ^{-1}(x)}$ means the inverse function while ${displaystyle (sinh x)^{-1}}$ or ${displaystyle sinh(x)^{-1}}$ means the reciprocal Especially inconsistent is the conventional use of positive integer superscripts to indicate an exponent rather than function composition, e.g. ${displaystyle sinh ^{2}x}$ conventionally means ${displaystyle (sinh x)^{2}}$ and not

Because the argument of hyperbolic functions is not the arclength of a hyperbolic arc in the Euclidean plane, some authors have condemned the prefix arc-, arguing that the prefix ar- (for area) or arg- (for argument) should be preferred.^[6] Following this recommendation, the ISO 80000-2 standard abbreviations use the prefix ar- (that is: arsinh, arcosh, artanh, arsech, arcsch, arcoth).

In computer programming languages, inverse circular and hyperbolic functions are often named with the shorter prefix a- (asinh, etc.).

This article will consistently adopt the prefix ar- for convenience.

Definitions in terms of logarithms[edit]

Since the hyperbolic functions are quadratic rational functions of the exponential function they may be solved using the quadratic formula and then written in terms of the natural logarithm.

${displaystyle {begin{aligned}operatorname {arsinh} x&=ln left(x+{sqrt {x^{2}+1}}right)&-infty &<x<infty ,\[10mu]operatorname {arcosh} x&=ln left(x+{sqrt {x^{2}-1}}right)&1&leq x<infty ,\[10mu]operatorname {artanh} x&={frac {1}{2}}ln {frac {1+x}{1-x}}&-1&<x<1,\[10mu]operatorname {arcsch} x&=ln left({frac {1}{x}}+{sqrt {{frac {1}{x^{2}}}+1}}right)&-infty &<x<infty , xneq 0,\[10mu]operatorname {arsech} x&=ln left({frac {1}{x}}+{sqrt {{frac {1}{x^{2}}}-1}}right)&0&<xleq 1,\[10mu]operatorname {arcoth} x&={frac {1}{2}}ln {frac {x+1}{x-1}}&-infty &<x<-1 {text{or}} 1<x<infty .end{aligned}}}$

For complex arguments, the inverse circular and hyperbolic functions, the square root, and the natural logarithm are all multi-valued functions.

Addition formulae[edit]

${displaystyle operatorname {arsinh} upm operatorname {arsinh} v=operatorname {arsinh} left(u{sqrt {1+v^{2}}}pm v{sqrt {1+u^{2}}}right)}$

${displaystyle operatorname {arcosh} upm operatorname {arcosh} v=operatorname {arcosh} left(uvpm {sqrt {(u^{2}-1)(v^{2}-1)}}right)}$

${displaystyle operatorname {artanh} upm operatorname {artanh} v=operatorname {artanh} left({frac {upm v}{1pm uv}}right)}$

${displaystyle operatorname {arcoth} upm operatorname {arcoth} v=operatorname {arcoth} left({frac {1pm uv}{upm v}}right)}$

${displaystyle {begin{aligned}operatorname {arsinh} u+operatorname {arcosh} v&=operatorname {arsinh} left(uv+{sqrt {(1+u^{2})(v^{2}-1)}}right)\&=operatorname {arcosh} left(v{sqrt {1+u^{2}}}+u{sqrt {v^{2}-1}}right)end{aligned}}}$

Other identities[edit]

${displaystyle {begin{aligned}2operatorname {arcosh} x&=operatorname {arcosh} (2x^{2}-1)&quad {hbox{ for }}xgeq 1\4operatorname {arcosh} x&=operatorname {arcosh} (8x^{4}-8x^{2}+1)&quad {hbox{ for }}xgeq 1\2operatorname {arsinh} x&=operatorname {arcosh} (2x^{2}+1)&quad {hbox{ for }}xgeq 0\4operatorname {arsinh} x&=operatorname {arcosh} (8x^{4}+8x^{2}+1)&quad {hbox{ for }}xgeq 0end{aligned}}}$

${displaystyle ln(x)=operatorname {arcosh} left({frac {x^{2}+1}{2x}}right)=operatorname {arsinh} left({frac {x^{2}-1}{2x}}right)=operatorname {artanh} left({frac {x^{2}-1}{x^{2}+1}}right)}$

Composition of hyperbolic and inverse hyperbolic functions[edit]

${displaystyle {begin{aligned}&sinh(operatorname {arcosh} x)={sqrt {x^{2}-1}}quad {text{for}}quad |x|>1\&sinh(operatorname {artanh} x)={frac {x}{sqrt {1-x^{2}}}}quad {text{for}}quad -1<x<1\&cosh(operatorname {arsinh} x)={sqrt {1+x^{2}}}\&cosh(operatorname {artanh} x)={frac {1}{sqrt {1-x^{2}}}}quad {text{for}}quad -1<x<1\&tanh(operatorname {arsinh} x)={frac {x}{sqrt {1+x^{2}}}}\&tanh(operatorname {arcosh} x)={frac {sqrt {x^{2}-1}}{x}}quad {text{for}}quad |x|>1end{aligned}}}$

Composition of inverse hyperbolic and circular functions[edit]

${displaystyle operatorname {arsinh} left(tan alpha right)=operatorname {artanh} left(sin alpha right)=ln left({frac {1+sin alpha }{cos alpha }}right)=pm operatorname {arcosh} left({frac {1}{cos alpha }}right)}$

{displaystyle ln left(left|tan alpha right|right)=-operatorname {artanh} left(cos 2alpha right)}

^[7]

Conversions[edit]

${displaystyle ln x=operatorname {artanh} left({frac {x^{2}-1}{x^{2}+1}}right)=operatorname {arsinh} left({frac {x^{2}-1}{2x}}right)=pm operatorname {arcosh} left({frac {x^{2}+1}{2x}}right)}$

${displaystyle operatorname {artanh} x=operatorname {arsinh} left({frac {x}{sqrt {1-x^{2}}}}right)=pm operatorname {arcosh} left({frac {1}{sqrt {1-x^{2}}}}right)}$

${displaystyle operatorname {arsinh} x=operatorname {artanh} left({frac {x}{sqrt {1+x^{2}}}}right)=pm operatorname {arcosh} left({sqrt {1+x^{2}}}right)}$

${displaystyle operatorname {arcosh} x=left|operatorname {arsinh} left({sqrt {x^{2}-1}}right)right|=left|operatorname {artanh} left({frac {sqrt {x^{2}-1}}{x}}right)right|}$

Derivatives[edit]

${displaystyle {begin{aligned}{frac {d}{dx}}operatorname {arsinh} x&{}={frac {1}{sqrt {x^{2}+1}}},{text{ for all real }}x\{frac {d}{dx}}operatorname {arcosh} x&{}={frac {1}{sqrt {x^{2}-1}}},{text{ for all real }}x>1\{frac {d}{dx}}operatorname {artanh} x&{}={frac {1}{1-x^{2}}},{text{ for all real }}|x|<1\{frac {d}{dx}}operatorname {arcoth} x&{}={frac {1}{1-x^{2}}},{text{ for all real }}|x|>1\{frac {d}{dx}}operatorname {arsech} x&{}={frac {-1}{x{sqrt {1-x^{2}}}}},{text{ for all real }}xin (0,1)\{frac {d}{dx}}operatorname {arcsch} x&{}={frac {-1}{|x|{sqrt {1+x^{2}}}}},{text{ for all real }}x{text{, except }}0\end{aligned}}}$

For an example differentiation: let θ = arsinh x, so (where sinh² θ = (sinh θ)²):

${displaystyle {frac {d,operatorname {arsinh} x}{dx}}={frac {dtheta }{dsinh theta }}={frac {1}{cosh theta }}={frac {1}{sqrt {1+sinh ^{2}theta }}}={frac {1}{sqrt {1+x^{2}}}}.}$

Series expansions[edit]

Expansion series can be obtained for the above functions:

${displaystyle {begin{aligned}operatorname {arsinh} x&=x-left({frac {1}{2}}right){frac {x^{3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{5}}{5}}-left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{7}}{7}}pm cdots \&=sum _{n=0}^{infty }left({frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{2n+1}}{2n+1}},qquad left|xright|<1end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arcosh} x&=ln(2x)-left(left({frac {1}{2}}right){frac {x^{-2}}{2}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{-4}}{4}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{-6}}{6}}+cdots right)\&=ln(2x)-sum _{n=1}^{infty }left({frac {(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{-2n}}{2n}},qquad left|xright|>1end{aligned}}}$

${displaystyle {begin{aligned}operatorname {artanh} x&=x+{frac {x^{3}}{3}}+{frac {x^{5}}{5}}+{frac {x^{7}}{7}}+cdots \&=sum _{n=0}^{infty }{frac {x^{2n+1}}{2n+1}},qquad left|xright|<1end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arcsch} x=operatorname {arsinh} {frac {1}{x}}&=x^{-1}-left({frac {1}{2}}right){frac {x^{-3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{-5}}{5}}-left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{-7}}{7}}pm cdots \&=sum _{n=0}^{infty }left({frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{-(2n+1)}}{2n+1}},qquad left|xright|>1end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arsech} x=operatorname {arcosh} {frac {1}{x}}&=ln {frac {2}{x}}-left(left({frac {1}{2}}right){frac {x^{2}}{2}}+left({frac {1cdot 3}{2cdot 4}}right){frac {x^{4}}{4}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {x^{6}}{6}}+cdots right)\&=ln {frac {2}{x}}-sum _{n=1}^{infty }left({frac {(2n)!}{2^{2n}(n!)^{2}}}right){frac {x^{2n}}{2n}},qquad 0<xleq 1end{aligned}}}$

${displaystyle {begin{aligned}operatorname {arcoth} x=operatorname {artanh} {frac {1}{x}}&=x^{-1}+{frac {x^{-3}}{3}}+{frac {x^{-5}}{5}}+{frac {x^{-7}}{7}}+cdots \&=sum _{n=0}^{infty }{frac {x^{-(2n+1)}}{2n+1}},qquad left|xright|>1end{aligned}}}$

An asymptotic expansion for arsinh is given by

${displaystyle operatorname {arsinh} x=ln(2x)+sum limits _{n=1}^{infty }{left({-1}right)^{n-1}{frac {left({2n-1}right)!!}{2nleft({2n}right)!!}}}{frac {1}{x^{2n}}}}$

Principal values in the complex plane[edit]

As functions of a complex variable, inverse hyperbolic functions are multivalued functions that are analytic, except at a finite number of points. For such a function, it is common to define a principal value, which is a single valued analytic function which coincides with one specific branch of the multivalued function, over a domain consisting of the complex plane in which a finite number of arcs (usually half lines or line segments) have been removed. These arcs are called branch cuts. For specifying the branch, that is, defining which value of the multivalued function is considered at each point, one generally define it at a particular point, and deduce the value everywhere in the domain of definition of the principal value by analytic continuation. When possible, it is better to define the principal value directly—without referring to analytic continuation.

For example, for the square root, the principal value is defined as the square root that has a positive real part. This defines a single valued analytic function, which is defined everywhere, except for non-positive real values of the variables (where the two square roots have a zero real part). This principal value of the square root function is denoted in what follows. Similarly, the principal value of the logarithm, denoted in what follows, is defined as the value for which the imaginary part has the smallest absolute value. It is defined everywhere except for non-positive real values of the variable, for which two different values of the logarithm reach the minimum.

For all inverse hyperbolic functions, the principal value may be defined in terms of principal values of the square root and the logarithm function. However, in some cases, the formulas of § Definitions in terms of logarithms do not give a correct principal value, as giving a domain of definition which is too small and, in one case non-connected.

Principal value of the inverse hyperbolic sine[edit]

The principal value of the inverse hyperbolic sine is given by

$operatorname {arsinh} z=operatorname {Log} (z+{sqrt {z^{2}+1}},),.$

The argument of the square root is a non-positive real number, if and only if z belongs to one of the intervals [i, +i∞) and (−i∞, −i] of the imaginary axis. If the argument of the logarithm is real, then it is positive. Thus this formula defines a principal value for arsinh, with branch cuts [i, +i∞) and (−i∞, −i]. This is optimal, as the branch cuts must connect the singular points i and −i to the infinity.

Principal value of the inverse hyperbolic cosine[edit]

The formula for the inverse hyperbolic cosine given in § Inverse hyperbolic cosine is not convenient, since similar to the principal values of the logarithm and the square root, the principal value of arcosh would not be defined for imaginary z. Thus the square root has to be factorized, leading to

operatorname {arcosh} z=operatorname {Log} (z+{sqrt {z+1}}{sqrt {z-1}},),.

The principal values of the square roots are both defined, except if z belongs to the real interval (−∞, 1]. If the argument of the logarithm is real, then z is real and has the same sign. Thus, the above formula defines a principal value of arcosh outside the real interval (−∞, 1], which is thus the unique branch cut.

Principal values of the inverse hyperbolic tangent and cotangent[edit]

The formulas given in § Definitions in terms of logarithms suggests

${displaystyle {begin{aligned}operatorname {artanh} z&={frac {1}{2}}operatorname {Log} left({frac {1+z}{1-z}}right)\operatorname {arcoth} z&={frac {1}{2}}operatorname {Log} left({frac {z+1}{z-1}}right)end{aligned}}}$

for the definition of the principal values of the inverse hyperbolic tangent and cotangent. In these formulas, the argument of the logarithm is real if and only if z is real. For artanh, this argument is in the real interval (−∞, 0], if z belongs either to (−∞, −1] or to [1, ∞). For arcoth, the argument of the logarithm is in (−∞, 0], if and only if z belongs to the real interval [−1, 1].

Therefore, these formulas define convenient principal values, for which the branch cuts are (−∞, −1] and [1, ∞) for the inverse hyperbolic tangent, and [−1, 1] for the inverse hyperbolic cotangent.

In view of a better numerical evaluation near the branch cuts, some authors^{[citation needed]} use the following definitions of the principal values, although the second one introduces a removable singularity at z = 0. The two definitions of differ for real values of with . The ones of differ for real values of with .

${displaystyle {begin{aligned}operatorname {artanh} z&={tfrac {1}{2}}operatorname {Log} left({1+z}right)-{tfrac {1}{2}}operatorname {Log} left({1-z}right)\operatorname {arcoth} z&={tfrac {1}{2}}operatorname {Log} left({1+{frac {1}{z}}}right)-{tfrac {1}{2}}operatorname {Log} left({1-{frac {1}{z}}}right)end{aligned}}}$

Principal value of the inverse hyperbolic cosecant[edit]

For the inverse hyperbolic cosecant, the principal value is defined as

$operatorname {arcsch} z=operatorname {Log} left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}+1}},right)$

It is defined when the arguments of the logarithm and the square root are not non-positive real numbers. The principal value of the square root is thus defined outside the interval [−i, i] of the imaginary line. If the argument of the logarithm is real, then z is a non-zero real number, and this implies that the argument of the logarithm is positive.

Thus, the principal value is defined by the above formula outside the branch cut, consisting of the interval [−i, i] of the imaginary line.

For z = 0, there is a singular point that is included in the branch cut.

Principal value of the inverse hyperbolic secant[edit]

Here, as in the case of the inverse hyperbolic cosine, we have to factorize the square root. This gives the principal value

${displaystyle operatorname {arsech} z=operatorname {Log} left({frac {1}{z}}+{sqrt {{frac {1}{z}}+1}},{sqrt {{frac {1}{z}}-1}}right).}$

If the argument of a square root is real, then z is real, and it follows that both principal values of square roots are defined, except if z is real and belongs to one of the intervals (−∞, 0] and [1, +∞). If the argument of the logarithm is real and negative, then z is also real and negative. It follows that the principal value of arsech is well defined, by the above formula outside two branch cuts, the real intervals (−∞, 0] and [1, +∞).

For z = 0, there is a singular point that is included in one of the branch cuts.

Graphical representation[edit]

In the following graphical representation of the principal values of the inverse hyperbolic functions, the branch cuts appear as discontinuities of the color. The fact that the whole branch cuts appear as discontinuities, shows that these principal values may not be extended into analytic functions defined over larger domains. In other words, the above defined branch cuts are minimal.

Inverse hyperbolic functions in the complex z-plane: the colour at each point in the plane represents the complex value of the respective function at that point

References[edit]

^ For example: Weltner, Klaus; et al. (2014) [2009]. Mathematics for Physicists and Engineers (2nd ed.). Springer. ISBN 978-364254124-7. Durán, Mario (2012). Mathematical methods for wave propagation in science and engineering. Vol. 1. Ediciones UC. p. 89. ISBN 9789561413146.
^ Birman, Graciela S.; Nomizu, Katsumi (1984). “Trigonometry in Lorentzian Geometry”. American Mathematical Monthly. 91 (9): 543–549. JSTOR 2323737.
^ Sobczyk, Garret (1995). “The hyperbolic number plane”. College Mathematics Journal. 26 (4): 268–280.
^
Weisstein, Eric W. “Inverse Hyperbolic Functions”. Wolfram Mathworld. Retrieved 2020-08-30. “Inverse hyperbolic functions”. Encyclopedia of Mathematics. Retrieved 2020-08-30.
^ Press, W.H.; Teukolsky, S.A.; Vetterling, WT; Flannery, B.P. (1992). “§ 5.6. Quadratic and Cubic Equations”. Numerical Recipes in FORTRAN (2nd ed.). Cambridge University Press. ISBN 0-521-43064-X. Woodhouse, N.M.J. (2003). Special Relativity. Springer. p. 71. ISBN 1-85233-426-6.
^ Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 539. ISBN 039304002X. Another form of notation, arcsinh x, arccosh x, etc., is a practice to be condemned as these functions have nothing whatever to do with arc, but with area, as is demonstrated by their full Latin names, ¶ arsinh area sinus hyperbolicus ¶ arcosh area cosinus hyperbolicus, etc. Zeidler, Eberhard; Hackbusch, Wolfgang; Schwarz, Hans Rudolf (2004). “§ 0.2.13 The inverse hyperbolic functions”. Oxford Users’ Guide to Mathematics. Translated by Hunt, Bruce. Oxford University Press. p. 68. ISBN 0198507631. The Latin names for the inverse hyperbolic functions are area sinus hyperbolicus, area cosinus hyperbolicus, area tangens hyperbolicus and area cotangens hyperbolicus (of x)….. Zeidler & al. use the notations arsinh, etc.; note that the quoted Latin names are back-formations, invented long after Neo-Latin ceased to be in common use in mathematical literature. Bronshtein, Ilja N.; Semendyayev, Konstantin A.; Musiol, Gerhard; Heiner, Mühlig (2007). “§ 2.10: Area Functions”. Handbook of Mathematics (5th ed.). Springer. p. 91. doi:10.1007/978-3-540-72122-2. ISBN 3540721215. The area functions are the inverse functions of the hyperbolic functions, i.e., the inverse hyperbolic functions. The functions sinh x, tanh x, and coth x are strictly monotone, so they have unique inverses without any restriction; the function cosh x has two monotonic intervals so we can consider two inverse functions. The name area refers to the fact that the geometric definition of the functions is the area of certain hyperbolic sectors … Bacon, Harold Maile (1942). Differential and Integral Calculus. McGraw-Hill. p. 203.
^ “Identities with inverse hyperbolic and trigonometric functions”. math stackexchange. stackexchange. Retrieved 3 November 2016.

Bibliography[edit]

Herbert Busemann and Paul J. Kelly (1953) Projective Geometry and Projective Metrics, page 207, Academic Press.

External links[edit]

“Inverse hyperbolic functions”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Источник

ГИПЕРБОЛИЧЕСКИЕ
ФУНКЦИИ

ОБРАТНЫЕ
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

ГИПЕРБОЛИЧЕСКИЕ
ФУНКЦИИ

Гиперболические
функции

Определение

Гиперболические
функции задаются следующими формулами:

гиперболический
синус:

(в
англоязычной литературе обозначается
)

гиперболический
косинус:

(в
англоязычной литературе обозначается
)

гиперболический
тангенс:

(в
англоязычной литературе обозначается
)

гиперболический
котангенс:

гиперболические
секанс и косеканс:

Свойства

Связь
с тригонометрическими функциями:

Гиперболические
функции выражаются через тригонометрические
функции от мнимого
аргумента.

Важные
соотношения:

Чётность:
Формулы
сложения:
Формулы
двойного угла:
Формулы
кратных углов:
Произведения
Суммы
Формулы
понижения степени
Производные:
Интегралы:

Неравенства:

Для
всех
выполняется:

Разложение
в степенные ряды:

(Ряд
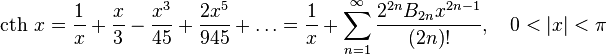
Лорана)

Здесь
—
числа
Бернулли.

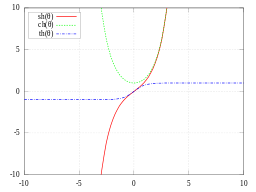
Графики:

sh(x),
ch(x),
th(x),
cth(x)

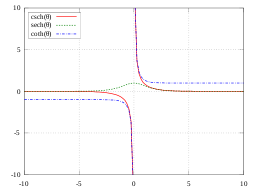
sh,
ch
и th

csch,
sech
и cth

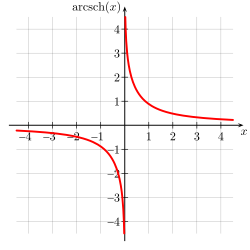
Обратные
гиперболические функции

—
обратный
гиперболический синус, гиперболический
арксинус, ареасинус:

—
обратный
гиперболический косинус, гиперболический
арккосинус, ареакосинус.

—
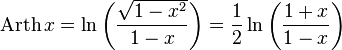
обратный
гиперболический тангенс, гиперболический
арктангенс, ареатангенс.

—
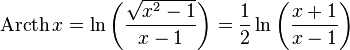
обратный
гиперболический котангенс, гиперболический
арккотангенс, ареакотангенс.

—
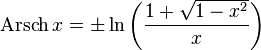
обратный
гиперболический секанс, гиперболический
арксеканс, ареасеканс.

—
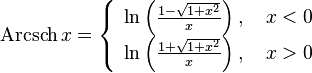
обратный
гиперболический косеканс, гиперболический
арккосеканс, ареакосеканс.

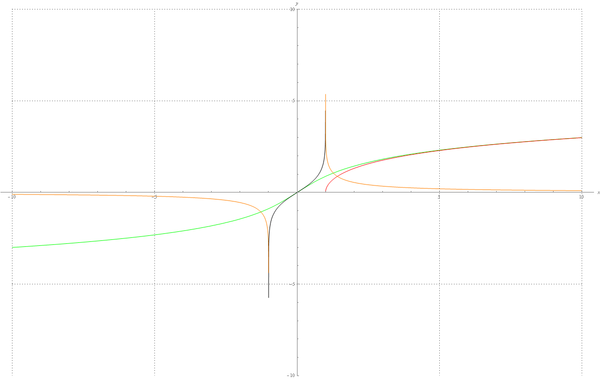
Графики:

arsh(x),
arch(x),
arth(x),
arcth(x)

Связь
между некоторыми обратными гиперболическими
и обратными тригонометрическими
функциями:

где
i
— мнимая единица.

Эти
функции имеют следующее разложение в
ряд:

ОБРАТНЫЕ
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Обратные
гиперболические функции

Название функции	Обозначение в русской литературе	Обозначение в английской литературе
ареасинус	arsh	arsinh, sinh⁻¹
ареакосинус	arch	arcosh, cosh⁻¹
ареатангенс	arth	artanh, tanh⁻¹
ареакотангенс	arcth	arcotanh, cotanh⁻¹
ареасеканс	arsech	arsech, sech⁻¹
ареакосеканс	arcsch	arcsch, csch⁻¹

Определения
функций

Гиперболический
ареасинус для действительного аргумента

Гиперболический
ареакосинус для действительного
аргумента

Гиперболический
ареатангенс для действительного
аргумента

Гиперболический
ареакотангенс для действительного
аргумента

Гиперболический
ареасеканс для действительного аргумента

Гиперболический
ареакосеканс для действительного
аргумента

В
комплексной
плоскости функции можно определить
формулами:

Гиперболический
ареасинус:

Гиперболический
ареакосинус:

Гиперболический
ареатангенс:

Гиперболический
ареакотангенс:

Гиперболический
ареасеканс:

Гиперболический
ареакосеканс:

Разложение
в ряд

Обратные
гиперболические функции можно разложить
в ряды:

Асимптотическое
разложение arsh x
даётся формулой:

Производные

Для
действительных x:

Пример
дифференцирования: если θ = arsh x,
то:

Комбинация
гиперболических и обратных гиперболических
функций

Дополнительные
формулы

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Макеты страниц

Если то, желая выразить зависимость у от х, обозначают у символом (читается «ареасинус гиперболический») или, более подробно, у есть площадь, гиперболический синус которой равен — латинское слово, означающее в переводе площадь). Подобным же образом определяются и другие обратные гиперболические функции, а именно:

Графики обратных гиперболических функций с их краткими описаниями приводятся ниже.

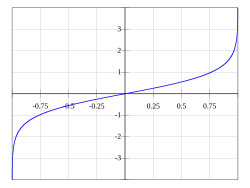
Ареасинус (рис. 7). Функция нечетная, область определения — монотонно возрастает от до . В начале координат — точка перегиба и центр симметрии графика. Угол образованный с осью абсцисс касательной в этой точке, равен Асимптот не имеет.

Ареакосинус (рис. 8). Функция двузначная, область определения каждой ветви График симметричен относительно оси в точке А (1,0)

имеется вертикальная касательная при возрастании по абсолютной величине возрастает.

Ареатангенс (рис. 9). Функция нечетная, область определения — монотонно возрастает от до

Рис. 7.

Рис. 8.

В начале координат — точка перегиба и центр симметрии графика. Угол образованный с осью абсцисс касательной в этой точке, равен Вертикальные асимптоты .

Ареакотангенс (рис. 10). Функция нечетная, область определения

Рис. 9.

Рис. 10.

При убывает от 0 до при убывает от до 0. Экстремумов и точек перегиба нет. Имеются горизонтальная асимптота и вертикальные асимптоты

Любую из обратных гиперболических функций можно выразить через остальные функции. Приведем соответствующую таблицу.

Следует иметь в виду, что при выражении функций через ареакосинус последний надо брать со знаком плюс при и со знаком минус при Это объясняется двузначностью ареакосинуса и нечетностью остальных функций, которые при положительны, а при отрицательны. Выражения же самого ареакосинуса через остальные функции (вторая строка) надо брать с двумя знаками, что также объясняется его двузначностью.

Легко убедиться в справедливости приведенных в таблице соотношений. Для примера выразим через остальные функции. Пусть тогда , следовательно, откуда

Аналогично проверяются и остальные соотношения. Суммы и разности обратных гиперболических функций выражаются следующим образом:

Для вывода формулы (8) исходим из того, что если откуда минус здесь необходимо сохранить, так как правая часть будет положительной и в этом случае). Логарифмируя последнее равенство, получим формулу (8).

Заметим, что формуле (8) можно придать несколько иной вид, а именно:

Для этого достаточно показать, что Но в этом легко убедиться с помощью следующего преобразования:

Если взять то откуда или следовательно,

Наконец, если взять то откуда или и, следовательно, Приведенные формулы позволяют выяснить вопрос об области определения обратных гиперболических функций. Из формулы (7) следует, что существует при любом действительном х, так как как при положительном, так и при отрицательном х. Формула (8) показывает, что существует только при так как имеет действительные значения при но х

Оглавление

ПРЕДИСЛОВИЕ
ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ
1. Введение. Определение гиперболических функций
2. Соотношения между гиперболическими функциями
3. Обратные гиперболические функции
4. Показательные, тригонометрические и гиперболические функции от комплексного аргумента. Формулы Эйлера
5. Соотношения между тригонометрическими и гиперболическими функциями
6. Соотношения между логарифмическими, обратными тригонометрическими и обратными гиперболическими функциями
7. Гиперболическая амплитуда (гудерманиан)
8. Дифференцирование и интегрирование гиперболических и обратных гиперболических функций
9. Разложение гиперболических функций в степенные ряды и в тригонометрические ряды Фурье
ГЛАВА II. ПРИМЕНЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ К ИНТЕГРИРОВАНИЮ
10. Интегрирование функций (гиперболические подстановки)
11. Интегрирование некоторых дифференциальных уравнений
ГЛАВА III. ПРИМЕНЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ В ГЕОМЕТРИИ, МЕХАНИКЕ И ФИЗИКЕ
Касательная и нормаль.
Параметрические уравнения цепной линии.
Кривизна и радиус кривизны.
Эвольвента цепной линии (трактриса).
Натуральное уравнение линии.
Цепная линия как рулета.
Площадь криволинейной трапеции и длина дуги.
Центр тяжести криволинейной трапеции и дуги.
Катеноид.
Минимальные свойства цепной линии.
Задачи, связанные с цепной линией.
13. Некоторые прикладные задачи
Движение материальной точки.
Скольжение цепочки.
Движение шарика во вращающейся трубке.
Включение электродвижущей силы в контур.
Установившееся распределение температуры в стержне.
Ионизация газа.
Диффузия, сопровождаемая химической реакцией.
Размножение бактерий.
ПРИЛОЖЕНИЯ
ЛИТЕРАТУРА

Источник

Раздаточный материал №5 по теме

“Гиперболические и обратные
гиперболические функции”

Содержание

§1. Гиперболические функции
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . 159

§2. Определение
и свойства обратных гиперболических
функций. . . . . . . . . . 166

§3. Соотношения
между обратными гиперболическими
функциями. . . . . . . . 171

§4. Связь
обратных гиперболических функций с
логарифмами. . . . . . . . . . . . 176

§5. Производные
от обратных гиперболических функций.
. . . . . . . . . . . . . . . . 178

§6. Интегралы
и первообразные с гиперболическими и
обратными гиперболическими
функциями. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . 180

Контрольные
вопросы. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . 182

Примеры и
упражнения. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . 184

Ответы к
упражнениям . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 192

Приложение
1. Таблица значений функции Arsh x. . . . . .
. . . . . . . . . . . . . . . . . 193

Литература. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194

§1.
Гиперболические функции

Линейные
комбинации показательных функций вида

и

рассматриваются как новые функции и
обозначаются так

и
.
Они называются соответственно
гиперболическим синусом и гиперболическим
косинусом. С помощью этих функций
определяются еще две функции

и
,
которые называются соответственно
гиперболическим тангенсом и гиперболическим
котангенсом. При этом
,
.

Из определений
вытекают следующие свойства гиперболических
функций:

функции shx, chx и thx определены для
всех значений аргумента;

функция cthx определена всюду, за
исключением точки х=0;
функции shx, cthx и thx являются
нечетными;
функция chx является четной;
предельные значения гиперболических
функций соответственно равны:

,
;

6). прямая y=1
является правосторонней асимптотой
функций thx и сthx;

7). прямая y=-1
является левосторонней асимптотой
функций thx и cthx;

8). ось 0у является
вертикальной асимптотой функции cthx.

Графики
гиперболических функций представлены
на рисунках 1 – 4.

Рис.1
Рис.2

Рис.3
Рис.4

Название
“гиперболические функции” связано
с тем обстоятельством, что формулы
x=a·ch t и y=a·sh t (*) параметрически задают
гиперболу, подобно тому, как формулы
x=a·cos t и y=a·sin t параметрически задают
окружность. Действительно, если возвести
в квадрат соотношения (*) и вычесть из
первого соотношения второе, то получим
x²–
y²=a²(ch²t
– sh²t).
Учитывая соотношение ch²t
– sh²t=1,
получим x²– y²=а²,
то есть каноническое
уравнение гиперболы.

Исходя
из определений гиперболических функций,
можно получить различные соотношения
между этими функциями, схожие с
соответствующими соотношениями между
тригонометрическими функциями или
отличающиеся знаком перед некоторыми
слагаемыми. Получать эти соотношения
проще, руководствуясь мнемоническим
правилом (оно доказывается в комплексном
анализе): вместо
пишем
ch x,
а вместо

пишем i
, где i
– мнимая единица ( i=
,
i
=-1).
Таким образом, имеем :

;

По аналогии с табличными
интегралами от тригонометрических
функций некоторые простые интегралы,
содержащие гиперболические функции,
тоже можно считать табличными. Зная
производные от гиперболических функций

,
нетрудно видеть, что:

Например,

Будем считать табличными еще два
интеграла:

Покажем
справедливость формулы (VII), используя
так называемую универсальную
гиперболическую подстановку:

Ясно, что,

кроме того:
,
,
.Итак,
имеем:
=,
что и требовалось доказать. Исходя из
определения гиперболического косинуса,
покажем справедливость формулы (VIII):
.

Другой вид первообразной в
интеграле (VIII) получим, используя
универсальную гиперболическую
подстановку:

Разные
первообразные для интеграла (VIII) должны
отличаться на постоянную величину,
которая может быть и нулем. Покажем, что
,
то есть:
.
Если это равенство имеет место, то оно
справедливо для всех значений
.
Пусть
=0,
тогда имеем

.
Таким образом,
.
Покажем справедливость этого соотношения
при любом
.
Пусть
>0,
тогда имеем
,

,
(*)

,
тогда
;
на этом интервале операция взятия
тангенса от обеих частей соотношения
(*) будет однозначной, ибо функции слева
и справа монотонно возрастают. Итак,
получаем
,

,
(**).
В левой части полученного соотношения
используем формулы:
,
,
,
что дает

,
то есть то же самое, что и в правой части
(**). Если
,
то в соотношении (*) имеем

возьмем
тангенсы от обеих частей полученного
соотношения
,
,
.
Так как знаменатель дроби отличен от
нуля (в самом деле,),
то имеем
.
Умножим обе части равенства на
:
,

,
,
то есть то, что в соотношении (**). Таким
образом, показано, что разность между
первообразными

и

постоянна и равна
.
Кстати,

для случая

равно
,
а для

она равно
;
следовательно, при любом

множества значений функций

и

одинаковы и равны
,
что ясно из вида правой части соотношения
(*), где
,
ибо
.

Если в интеграле (VII)
использовать определение гиперболического
синуса, то получим первообразную, равную
.
В самом деле,

.
Покажем, что разность первообразных
интеграла (VII) равна нулю, то есть,
.
Имеем
.
При

равенство справедливо, при

имеем:
,
так как
,

,
то получим:
,

+=+–++-1,
что дает
;
при
имеем
=,

,
что уже было рассмотрено ранее.

§2.
Oпределение
и свойства обратных гиперболических
функций

О
братные
гиперболические функции определяются
как функции, обратные cоответствующим
гиперболическим функциям. Если у
= Ar sh x, то x
= sh у, где D:
xR,
E: yR.

Рис.5

На рис.5 показана
прямая функция y=sh
x и ей обратная
y = Arsh x.
Графики этих функций симметричны
относительно прямой у=х.
Кроме того, прямая функция и ей обратная
имеют один и тот же характер монотонности:
обе функции в данном случае возрастающие.

Из самого определения функции
ареа-синус следует, что

(1). Ar
sh(sh x)=x,

(2). sh(Ar
sh x)=x.

Функция ареа-синус нечетна, то
есть

(3). Ar
sh(-x)= -Ar sh(x).

Доказательство:
так как E(Ar
sh α) и E(-Ar
sh β) совпадают
с D(sh γ),
то операция взятия синусов гиперболических
от обеих частей доказываемого равенства
будет однозначной: sh(Ar
sh(-x)) =
sh(-Ar sh x); с
учетом формулы (2) и того обстоятельства,
что синус гиперболический есть функция
нечетная, имеем
-x = – sh(Ar sh x), -x =-x,
что доказывает справедливость
соотношения(3).

Е
сли
у =Ar ch x,
то x= ch y,
где D:x[1;+),
E: y[0;+).

Рис.6.

Будем учитывать
только положительную часть графика
функции ареа-косинус, которая представлена
на рис.6 сплошной линией и которая
симметрична правой ветви графика прямой
функции у
= ch
х (функция у
= ch х монотонна
при х[0,
+)
и, следовательно, имеет обратную функцию,
определенную на множестве своих значений
[1, +)).
Характер монотонности прямой и обратной
функций одинаков: обе функции в данном
случае возрастают.

Из самого определения функции
ареа-косинус следует, что

(4). Ar ch(ch x)
=x, x
0;

(5). ch(Ar ch x)
=x, x1.

Функция ареа-косинус не является
ни четной, ни нечетной.

Докажем
соотношение (8):

с учетом формулы (2); знак плюс перед
корнем выбираем по той причине, что
множество значений косинуса гиперболического
положительно.

Если
y=Ar th x,
то
x= th y,
где
D:

E : yR.

Рис. 7.

На рис.7
представлены графики прямой и обратной
ей функций: y=th
x и y
=Ar th x, которые
имеют один и тот же характер монотонности:
обе функции возрастающие. Из самого
определения функции ареа-тангенс
следует, что

(10). th(Ar
th x) = x,

(11). Ar
th(th x) = x, xR.

Функция y=Ar
th x нечетна:

что нетрудно
доказать по аналогии с тем, как это было
сделано при обосновании формулы (3); при
этом необходимо учитывать то, что E(Ar
th α) и Е(-Ar
th β) совпадают
с D(th γ).

Если y = Ar cth x,
то x = cth y, где D:
,
E:
.

Рис. 8.

На рис.8
представлены графики прямой функции y
= cth x (пунктирная линия) и обратной ей
функции y = Ar cth x (сплошная линия). Эти
функции имеют один и тот же характер
монотонности: обе функции убывающие.
Из определения функции ареа-котангенс
следует, что

Функция у= Ar cth(x) нечетна

что нетрудно
доказать по аналогии с тем, как это было
сделано при обосновании формулы (3) с
учетом того обстоятельства, что E(Ar cth
α) и
E(-Аr cth β) совпадают с D(cth γ). Имеют
место соотношения:

Если рассматривать эти соотношения
с точки зрения определения обратных
гиперболических функций, то имеем:

Доказательство формул (16) и
(17) простое. Докажем соотношение (16):

с учетом
формулы (13).

§3.
Соотношения между обратными гиперболическими
функциями

Сходные обратные
гиперболические функции связаны
соотношениями:

(7).
,
;

(9.)
,
;

(18).
,
;

(19).
,
.

Приведем возможное доказательство
формулы (9). Пусть
,
где

подлежит определению; E

и E

совпадают на участке
,
где они монотонны; стало быть, операция
взятия косинуса гиперболического от
обеих частей доказываемого равенства
будет однозначной, но только на участке
множества значений косинуса
гиперболического, равного
.
Итак имеем:
.
Если
,
то

и надо определить
.
Так как
,
то
,
где знак перед корнем определяется тем,
что E
;
в итоге получаем
,
то есть
,
что требовалось доказать.

Нетрудно показать, что разные
обратные гиперболические функции
связаны между собой соотношениями:

(20).
,
;

(21).
,
;

(22).
,
;

(23).
,
;

(24).
,
;

(25).
,
;

(26).
,
;

(27).
,
.

Докажем формулу (20). Так как
области изменения функций ареа-синус
и ареа-тангенс совпадают с областью
определения тангенса гиперболического,
то операция взятия тангенса гиперболического
от обеих частей доказываемого равенства
будет однозначной:
;

(с учетом формулы (10)); пусть
,
тогда
,
и осталось показать, что
;
так как
,
то
;
при

имеем
;
при

с учетом нечетности функций ареа-синус
и ареа-тангенс получаем:
,
,
что требовалось доказать при
.

Доказательства других соотношений
между нечетными обратными гиперболическими
функциями (формулы (21), (24) и (26)) аналогичны
приведенному.

Доказательство
формул, содержащих функцию ареа-косинус,
требует учета того, что эта функция не
является четной или нечетной. Докажем
соотношение (22). Так как область определения
тангенса гиперболического включает в
себя множество значений ареа-косинуса
и совпадает со множеством значений
ареа-тангенса, то операция взятия
тангенсов гиперболических от обеих
частей доказываемого равенства будет
однозначна на участке, не выходящем за
пределы множества значений ареа-косинуса,
где эти функции монотонны. Получим
;

(с учетом формулы (10)); пусть
,
тогда

и надо показать, что
.
Так как
,
то
;
при

,
что и требовалось доказать.

Если стоит
обратная задача: установить связь между
любыми обратными гиперболическими
функциями, то ее всегда можно решить,
получив одну из приведенных выше формул
(7), (9), (18) – (27). Для примера найдем связь
между двумя нечетными разными обратными
гиперболическими функциями; например,
между функциями ареа-тангенс и ареа-синус:
пусть
,
где

подлежит определению; так как множества
значений ареа-тангенса и ареа-синуса
совпадают с D (ареа-синус) и монотонны,
то операция взятия синуса гиперболического
от обеих частей исходного равенства
будет однозначной:
,
;
пусть
,
тогда

и надо определить
;
так как
,
то
,
;
при

получаем
,
где
,
то есть связь между функциями ареа-тангенс
и ареа-синус в виде

при,
что совпадает с формулой (24) при данных
ограничениях для
;
при

с учетом нечетности функций ареа-тангенс
и ареа-синус имеем:
;
;

,
что дает полное совпадение с формулой
(24) при
.

Найдем еще
связь между обратными гиперболическими
функциями, одна из которых есть
ареа-косинус. Пусть надо выразить
ареа-тангенс через ареа-косинус;
следовательно,
,
где

подлежит определению. Так как D

совпадает с E
,
то операция взятия косинуса гиперболического
от обеих частей исходного соотношения,
не превышающей E
,
где эти функции монотонны, будет
однозначной
,
;
пусть
,
тогда

и надо определить
;
так как
,
то

и
,
где знак плюс перед корнем определяется
тем, что косинус гиперболический всегда
положителен; итак,
,
откуда следует, что

при

(формула (25)).

По аналогии с
двумя приведенными примерами по
установлению связей между разными
обратными гиперболическими функциями
можно найти связи между сходными
обратными гиперболическими функциями
ареа-синус и ареа-косинус: пусть
,
где

подлежит определению. Так как E

включает в себя E
,
то операция взятия косинуса гиперболического
от обеих частей исходного соотношения
будет однозначной на участке, равном E
,
где эти функции монотонны; итак, имеем

(с учетом формулы (5)); далее, пусть
,
тогда
,
и надо определить
;
так как
,
то
,
где знак перед корнем определяется тем,
что E
;
итак, имеем окончательно

при
,
что совпадает с формулой (9).

§4.
Связь обратных гиперболических функций

с логарифмами

Рассмотрим
связи между обратными гиперболическими
функциями и натуральными логарифмами,
которые можно использовать и как
определения обратных гиперболических
функций. Имеют место соотношения:

(28)).
,
;

(29).
,
;

(30).
,
;

(31).
,
.

Покажем
справедливость соотношения (28): если
,
то
,
;
умножаем последнее равенство на
:
,
,
;
так как
,
то перед корнем выбираем знак плюс;
окончательно получаем:
,
что требовалось доказать.

Доказательство
формулы (29): если

при
,
то
;
;
умножаем на
,
получаем
,
;
при

равенство справедливо при любом знаке
перед корнем, то есть обе части соотношения
положительны, а потому
;
так как при

справедливо, что
,
,
следовательно,
;
рассматривая только положительную
ветвь функции ареа-косинус, имеем
окончательно:
,
,
что и требовалось доказать.

Формулы,
связывающие натуральные логарифмы с
тангенсом и котангенсом гиперболическими
доказываются еще проще. Так, например,
если

при
,
то
,
;
умножаем обе части этого равенства на
:
,
;
так как
,
то правая часть тоже положительна, что
реализуется при
;
,
,
что требовалось доказать.

§5.
Производные от обратных гиперболических
функций

Можно
найти производные обратных гиперболических
функций, используя ранее рассмотренные
соотношения. Так согласно (2),
,
;
тогда
,
,

,

(перед корнем берется знак плюс, так как
множество значений косинуса гиперболического
положительно).

Так
как
,
,
то
,
,
,

(знак перед корнем определяется тем,
что E
,
а потому

тоже положителен).

Формулы
для производных ареа-тангенса и
ареа-котангенса оказываются одинаковыми,
но они относятся к функциям, которые
определены в разных непересекающихся
областях. Пусть

при
,
тогда
, ,

.
Пусть
,
;
тогда
,
,
.

Приведем
перечень формул с производными от
обратных гиперболических функций:

(32).
,
;

(33).
,
;

(34).
,
;

(35).
,
.

§6.
Интегралы и первообразные с
гиперболическими
и обратными
гиперболическими функциями

Учитывая
производные от обратных гиперболических
функций нетрудно видеть, что:

IX.
;

X.
,

;

XI.

;

XII.
,
.

Обобщая
соотношения (IX)-(XII), получим следующие
формулы:

XIII.
,
,
;

XIV.
,
,
;

XV.
,
,
;

XVI.
,
;
.

Так,
например, в формуле (XIII) при

имеем

,
где
.
Ограничения на отношение

определяют выбор соответствующей
ареа-функции в качестве первообразной.
Если ограничений нет (кроме
),
то формулы (XIII) и (XIV), а также (XV) и (XVI)
можно объединить, используя лишь их
логарифмические представления в качестве
первообразных. Получим тогда известные
табличные интегралы:

XVII.
,
;

XVIII.
,
.

Интегралы
типа

XIX.
,

содержащие
обратные гиперболические функции,
берутся по частям.

Контрольные
вопросы.

Вопрос 1.
Используя
мнемоническое правило, получить для
гиперболических функций формулы: суммы
и разности
двух углов, двойного угла и понижения
порядка:

а).
;

б).
;

в).
;

г).
;

д).
;

е).
;

ж).
.

Вопросы
2-5. Рассказать
об одной из гиперболических функций
(определение, область определения,
область значений, график; указать на
соотношения, вытекающие из определения
ареа-функции).

Вопросы
6, 7. Доказать,
что функции ареа-тангенс и ареа-котангенс
являются нечетными (смотри доказательство
формулы (3) и замечания к формулам (12) и
(15)).

Вопросы
8-10.
Доказать формулы:

а)
,
;

б)
,
;

в)
,
.

Вопросы
11-13. Доказать
формулы:

а)
,
;

б)
,
;

в)
,
.

Вопросы
14-16. Установить
связи между различными нечетными
обратными гиперболическими функциями
(смотри доказательство формулы (24)), а в
качестве ответов необходимо получить
формулы (20), (21), (26)).

Вопросы
17-19. Установить
связи между различными обратными
гиперболическими функциями, одна из
которых есть ареа-косинус (смотри
доказательство формулы (25), а в качестве
ответов необходимо получить формулы
(22), (23), (27)).

Вопросы
20-22. Установить
связи между сходными обратными
гиперболическими функциями.

Вопросы
23-26. Получить
соотношения, связывающие обратные
гиперболические функции с натуральными
логарифмами.

Вопросы
27-29. Получить
производные от обратных гиперболических
функций тремя способами, используя:
правило взятия производной от обратной
функции, связи между обратными
гиперболическими функциями и натуральными
логарифмами, а также соотношения,
вытекающие из определений обратных
гиперболических функций.

Примеры
и упражнения

Упражнение
1. Получить
для гиперболических функций синуса и
косинуса формулы тройного угла.

Упражнение
2. Установить
эквивалентность функций
,
,
,

относительно функции

при
.

Упражнение
3.
Функция

не определена при
.
Определить

так, чтобы

была непрерывна при
,
если:

а).
;

б).
.

Упражнение
4. Найти
производные следующих функций:

а).
;

б).
;

в).
;

г).
;

д).
;

е).
;

ж).
;

з).
;

и).;

к).
;

л).
;

м).
;

н).
;

о).
;

п).
;

р).
.

Упражнение
5. Вычислить
предел
.

Дополнительно
можно использовать примеры из “Задач
и упражнений по математическому анализу
для ВТУЗов” под редакцией Демидовича
Б. П. (Москва 1997 год), а именно №№: 103-105,
263 (а, б), 401, 402, 404, 406-408, 528, 537-539, 541, 542, 671,
674, 728, 779, 844, 976, 997.

Пример 1.
Вычислить
.

Решение.
Так как
,
тоmимеем

,
где

,
а возможные варианты ответов подчеркнуты.

Пример 2.
Вычислить интеграл

Решение. ОДЗ
подынтегральной функции:
Так
как
,
тотимеем:

,
где
,а
модуль под знаком логарифма раскрыт с
учётом ОДЗ.

Упражнение
6. Вычислить
интегралы:

а).
;
б).
.

Пример 3.
Вычислить интеграл:
.

Решение.
Так как
,
тоmимеем

Упражнение
7. Вычислить
интеграл
.

Наряду с
тригонометрическими подстановками при
интегрировании в ряде случаев удобнее
использовать гиперболическиеиподстановки.
Так, в интегралах,
содержащих
радикалы

,
можно использовать соответственно
следующие подстановки:

,
где вне скобок указаны предположительные
замены.

Пример 4.
Вычислить интеграл.

Решение.
Пусть
,
где
,
;
тогда в исходном интеграле имеем

,мгдемм,

Пример 5.
Вычислить
интеграл:
.

Решение.
ОДЗ подынтегральной функции:.
Пусть
.
Тогда

и далее имеем

где

Упражнение
8. Вычислить
интегралы:

а).
; б).

Обратные гиперболические функции
удобно использовать в качестве
первообразных, так как они хорошо
изучены, и работать с ними проще, чем с
“длинными” или “дробными”
логарифмами, причём ОДЗ первообразных
фиксируется выбором соответствующей
ареа-функции.

К интегралам, содержащим
гиперболические функции, относятся все
те рекомендации, которые используются
при интегрировании тригонометрических
функций. При этом, естественно, учитывается
специфика связей между гиперболическими
функциями. Приведём некоторые примеры
интегрирования гиперболических функций.

Пример 6.
Вычислить
интеграл
.

Решение.
I способ: пусть cth
x = t, тогда
x = Arcth t и
,
причём
;
в исходном интеграле имеем

II способ: так
как
,
то

Упражнение
9. Вычислить
интегралы:

а)
; б)
.

Пример 7.
Вычислить интеграл
.

Решение.
.

Пример 8.
Вычислить интеграл
.

Решение.

то

Пример 9.
Вычислить
интеграл

Решение.
Так как
,
тоиимеем

Пример 10.
Вычислить интеграл
.

Решение.
Пусть x=sh t,
тогда t=Arsh x,
а
;
имеем

Пример 11.
Вычислить интеграл
.

Решение.

В качестве упражнений можно
использовать номера из ранее упомянутого
задачника под редакцией Б.П. Демидовича,
а именно №№: 1048(б), 1138, 1139, 1142, 1189, 1190, 1209,
1210, 1253, 1254, 1334, 1391-1394, 1396, 1399, 1400, 1406, 1408,
1414, 1426, 1484-1487, 1543-1545, 1641,1666, 1687, 1718.

Ответы
к упражнениям

Упр.1.

;

У

пр.3.
a).
f(0)=2;
б). f(0)=2.

Упр.4. а). -th²x;
б).

в). 2сth 2x; г). sec 2x д). -cosec x;

e).

ж).
x Arth x; з).
2x
Arshx;
и).

к).

Замечание:

м).

н).

о).

п).

р).

У
пр.5.
{1}.

Упр.6.

Упр.7.

Упр.8.

Упр.9. a).
ln(chx)-(th²x)/2+C;
б).
x+thx+C.

Литература

Математическая энциклопедия.
М. 1982.
Берман А.Ф. , Араманович И. Г.-
Краткий курс математического анализа
для втузов. М. , “Наука”, главное
издательство физ-мат литературы, 1971.
Задачи и упражнения по
математическому анализу для втузов.
Под ред. Б.П.Демидовича. М.,”Интеграл-пресс”,
1997.

Приложение
I. Таблица значений функции

x	Ar shx	x	Ar shx	x	Ar shx
0.0	0	3.4	1.938	6.8	2.615
0.1	0.1	3.5	1.966	6.9	2.63
0.2	0.199	3.6	1.993	7	2.644
0.3	0.296	3.7	2.019	7.1	2.658
0.4	0.39	3.8	2.045	7.2	2.672
0.5	0.481	3.9	2.07	7.3	2.686
0.6	0.569	4	2.095	7.4	2.699
0.7	0.653	4.1	2.119	7.5	2.712
0.8	0.733	4.2	2.142	7.6	2.726
0.9	0.809	4.3	2.165	7.7	2.739
1	0.881	4.4	2.187	7.8	2.751
1.1	0.95	4.5	2.209	7.9	2.764
1.2	1.016	4.6	2.231	8	2.776
1.3	1.078	4.7	2.252	8.1	2.789
1.4	1.138	4.8	2.272	8.2	2.801
1.5	1.195	4.9	2.293	8.3	2.813
1.6	1.249	5	2.312	8.4	2.825
1.7	1.301	5.1	2.332	8.5	2.837
1.8	1.35	5.2	2.351	8.6	2.848
1.9	1.398	5.3	2.37	8.7	2.8б
2.0	1.444	5.4	2.388	8.8	2.871
2.1	1.487	5.5	2.406	8.9	2.882
2.2	1.53	5.6	2.424	9	2.893
2.3	1.57	5.7	2.441	9.1	2.904
2.4	1.609	5.8	2.458	9.2	2.915
2.5	1.647	5.9	2.475	9.3	2.92б
2.6	1.684	6	2.492	9.4	2.937
2.7	1.719	6.1	2.508	9.5	2.947
2.8	1.753	6.2	2.524	9.6	2.958
2.9	1.786	6.3	2.54	9.7	2.968
3	1.818	6.4	2.555	9.8	2.978
3.1	1.85	6.5	2.571	9.9	2.988
3.2	1.88	6.6	2.586	10.0	2.998
3.3	1.909	6.7	2.601	20.0	3.690

Источник

Определения функций[править | править код]

Разложение в ряд[править | править код]

Производные[править | править код]

Комбинация гиперболических и обратных гиперболических функций[править | править код]

Дополнительные формулы[править | править код]

См. также[править | править код]

Источники[править | править код]

Ссылки[править | править код]

Notation[edit]

Definitions in terms of logarithms[edit]

Addition formulae[edit]

Other identities[edit]

Composition of hyperbolic and inverse hyperbolic functions[edit]

Composition of inverse hyperbolic and circular functions[edit]

Conversions[edit]

Derivatives[edit]

Series expansions[edit]

Principal values in the complex plane[edit]

Principal value of the inverse hyperbolic sine[edit]

Principal value of the inverse hyperbolic cosine[edit]

Principal values of the inverse hyperbolic tangent and cotangent[edit]

Principal value of the inverse hyperbolic cosecant[edit]

Principal value of the inverse hyperbolic secant[edit]

Graphical representation[edit]

See also[edit]

References[edit]

Bibliography[edit]

External links[edit]

Содержание

Приложение
1. Таблица значений функции Arsh x. . . . . .
. . . . . . . . . . . . . . . . . 193

Литература. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194

Добавить комментарий Отменить ответ

Определения функций[править | править код]

Разложение в ряд[править | править код]

Производные[править | править код]

Комбинация гиперболических и обратных гиперболических функций[править | править код]

Дополнительные формулы[править | править код]

См. также[править | править код]

Источники[править | править код]

Ссылки[править | править код]

Notation[edit]

Definitions in terms of logarithms[edit]

Addition formulae[edit]

Other identities[edit]

Composition of hyperbolic and inverse hyperbolic functions[edit]

Composition of inverse hyperbolic and circular functions[edit]

Conversions[edit]

Derivatives[edit]

Series expansions[edit]

Principal values in the complex plane[edit]

Principal value of the inverse hyperbolic sine[edit]

Principal value of the inverse hyperbolic cosine[edit]

Principal values of the inverse hyperbolic tangent and cotangent[edit]

Principal value of the inverse hyperbolic cosecant[edit]

Principal value of the inverse hyperbolic secant[edit]

Graphical representation[edit]

See also[edit]

References[edit]

Bibliography[edit]

External links[edit]

Содержание

Приложение 1. Таблица значений функции Arsh x. . . . . . . . . . . . . . . . . . . . . . . 193

Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194

Вам также может понравиться

Как найти площадь комнаты вики огэ

Как найти имена рыб

Как найти мощность авто

Добавить комментарий Отменить ответ

Приложение
1. Таблица значений функции Arsh x. . . . . .
. . . . . . . . . . . . . . . . . 193

Литература. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194