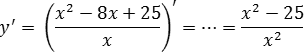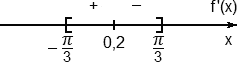Глобальный максимум функции как найти

8.3.1. Понятие глобального экстремума функции

Рассмотрим
функцию
,
которая задана на замкнутом множестве.
Точканазывается точкойглобального
максимума
или наибольшим
значением
функции на множестве
,
если
.

Если же
,
то точка
называется точкойглобального
минимума
или наименьшим
значением
функции на множестве
.

Точка
называется точкойглобального
экстремума
функции
на множестве,
если точкаявляется глобальным минимумом или
глобальным максимумом функциина множестве.

Если функция
непрерывна на замкнутом и ограниченном
множестве
,
то из теоремы Вейерштрасса следует,
что во множественайдутся точки глобального максимума
и минимума функции.

Точки глобального
экстремума функции могут быть внутренними
точками множества
или принадлежать границе множества.
Если точка глобального экстремума
является внутренней, то она является
локальным экстремумом функции.Отсюда
вытекает алгоритм отыскания глобальных
экстремумов функции
на множестве
:

1. Во множестве
найти все критические точки функции, а
также точки, в которых функция не
дифференцируема.

2. Найти все точки,
в которых функция может принимать
наибольшее и наименьшее значения на
границе множества
.

3. Вычислить
значения функции в точках, найденных в
пунктах 1 и 2.

4. Среди значений,
найденных в пункте 3, выбрать наибольшее
и наименьшее значения.

Примеры

1. Найти глобальный
экстремум функции
на множестве.

Решение.
Множество
является ограниченным, таки.
Из теоремы 4.9. вытекает, чтоявляется замкнутым множеством.
Следовательно функцияна множествеимеет глобальный минимум и максимум.
Множествопредставляет собой треугольник,
ограниченный осями координат и прямой(рис. 8.7).

Рис.8.7.

Найдем критические
точки функции
.
Так как

,
,

то функция
имеет единственную критическую точку,
которая принадлежит множеству.

Исследуем функцию
на отрезке
,.
Подставляяв выражение для функции, получим.
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке.
Отсюда следует, что на отрезке,функция принимает наименьшее и наибольшее
значение только в точках

,
и.

Исследуем функцию
на отрезке
,.
Подставляяв выражение для функции, получим.
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке.
Отсюда следует, что на отрезке,функция принимает наименьшее и наибольшее
значение только в точках

,
и.

Исследуем функцию
на отрезке
,.
Подставляяв выражение для функции, получим

.

Функция принимает
наименьшее и наибольшее значение на
концах отрезка и в критической точке
.
Отсюда следует, что на отрезке,функция принимает наименьшее и наибольшее
значение только в точках

,
и.

В таблице 8.1
приведены значения функции во всех
найденных точках.

Таблица
8.1

Из таблицы 8.1
следует, что
и—
точки соответственно глобального
минимума и максимума функция,
и

,
.
●

Задачи

Найти глобальные
экстремумы функции
на множестве.

1.
,.

2.
,.

3.
,.

4.
,.

5.
,.

Ответы

1.
,.

2.
,.

3.
,.

4.
,.

5.
,.
▲

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Наибольшее и наименьшее значения функции.
Глобальные максимумы и минимумы

Краткая теория

---

Наибольшее значение
функции

 на
множестве

 называют глобальным максимумом, а ее
наименьшее значение – глобальным минимумом.

Чтобы найти глобальные
экстремумы функции

 на
отрезке

, на котором она непрерывна, надо: найти
критические точки, принадлежащие интервалу

, и вычислить значения функции в этих
точках; вычислить значения функции в граничных точках отрезка, то есть

 и

; из всех полученных значений выбрать
наименьшее и наибольшее.

Общая схема решения
прикладных задач такова:

Устанавливается
зависимость рассматриваемой величины

 от
некоторой независимой величины

 (обозначения, разумеется, могут быть другими).
Из условия задачи
определяется тот промежуток, в котором может изменяться аргумент

.
Когда величина

 представлена как функция аргумента

, к ней применяется теория экстремумов.

В прикладных задачах чаще
всего встречается случай, когда внутри рассматриваемого промежутка (отрезка,
полуинтервала или интервала) оказывается лишь одна критическая точка

. Если в этой точке непрерывная функция
имеет локальный максимум (минимум), то он является ее наибольшим (наименьшим)
значением.

Примеры решения задач

---

Задача 1

Определить наибольшее и
наименьшее значения функции

 на
отрезке

:

на отрезке

Решение

Найдем критические точки
этой функции, лежащие на отрезке 

.

Для этого найдем
производную функции:

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Приравняем производную к
нулю:

 -критическая
точка, лежащая на отрезке

Вычислим значение функции
в найденной точке и на концах отрезка:

Сравнивая полученные значения,
находим:

---

Задача 2

Найти наибольшее и
наименьшее значения функции

 на
отрезке

.

Решение

Найдем критические точки
этой функции, лежащие на отрезке 

.

Для этого найдем
производную функции:

Приравняем производную к
нулю и решим полученное уравнение:

Найденная
точка

 лежит в заданном интервале

Вычислим
значение функции в найденных точках и на концах отрезка:

Сравнивая полученные
значения, находим:

Экстре́мум (лат. extremum — крайнее) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Задачи нахождения экстремума возникают во всех областях человеческого знания: теория автоматического управления, проблемы экономики, биология, физика и т. д.^[1]

Определения[править | править код]

Пусть дана функция и  — внутренняя точка области определения Тогда

Если неравенства выше строгие, то называется точкой строгого локального или глобального максимума или минимума соответственно.

Значение функции называют соответственно (строгим) локальным или глобальным максимумом или минимумом. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

Замечание[править | править код]

Функция определённая на множестве может не иметь на нём ни одного локального или глобального экстремума. Например,

Необходимые условия существования локальных экстремумов[править | править код]

• Из леммы Ферма вытекает следующее^[2]:

Пусть точка является точкой экстремума функции , определенной в некоторой окрестности точки .

Тогда либо производная не существует, либо .

Эти условия не являются достаточными, так, функция может иметь нуль производной в точке, но эта точка может не быть точкой экстремума, а являться, скажем, точкой перегиба, как точка (0,0) у функции .

Достаточные условия существования локальных экстремумов[править | править код]

является точкой строгого локального максимума. А если

то является точкой строгого локального минимума.

Заметим, что при этом функция не обязательно дифференцируема в точке .

и

является точкой локального максимума. А если

и

то является точкой локального минимума.

Если чётно и , то  — точка локального максимума.
Если чётно и , то  — точка локального минимума.
Если нечётно, то экстремума нет.

См. также[править | править код]

• Критическая точка (математика)
• Методы оптимизации
• Условный экстремум

Примечания[править | править код]

Литература[править | править код]

• Пшеничный Б.Н. Необходимые условия экстремума. — М.: Наука, 1969. — 150 с.

Глобальный экстремум или
наибольшее и наименьшее значение функции
Глобальным экстремумом функции нескольких переменных называют
наибольшее и наименьшее значение функции в замкнутой ограниченной области D .
Пусть функция f ( x; y ) , определена и непрерывна в некоторой замкнутой
ограниченной области D с границей g ( x; y ) = 0 . Тогда заведомо функция в области D
имеет наибольшее и наименьшее значение. Кроме того, функция также может достигать
наибольшее и наименьшее значение функции на границе области. Таким образом,
исследование функции на глобальный экстремум
Правило нахождения наибольшего и наименьшего значений дифференцируемой в
области D функции z = f ( x; y ) состоит в следующем:
1.
Найти все критические точки функции z = f ( x; y ) , принадлежащие D . Для
этого вычислить частные производные функции z ′x , z ′y .
полученные частные производные к нулю
 z ′x = 0
получившуюся систему уравнений 
, определив координаты точек;
′
z
=
 у
2.
Приравнять
и
решить
3.
Построить область D и посмотреть принадлежит ли найденные точки
области D;
4.
Найти точки, лежащие на границе области. Для этого, уравнение каждого
графика, которым ограничена область, подставить в функцию z = f ( x; y ) вместо
соответствующей переменной. Затем найти производную, приравнять ее к нулю и
определить координаты точек;
5.
Найти значения функции z = f ( x; y ) в критических точках, принадлежащих
области D , и на границах области;
6.
Сравнить все найденные значения функции и выбрать из них наибольшее и
наименьшее значение.
Пример 1. Найти наибольшее и наименьшее значение функции z = 3 − x 2 − y 2 в
области D , ограниченной прямыми x = ±1 , у = ±1 .
Решение. Найти все критические точки функции, для этого вычислим частные
производные первого порядка
z ′x ( y = const ) = (3 − x 2 − у 2 )′ = −2 х ,
z ′y ( x = const ) = (3 − x 2 − y 2 )′ = −2 у .
 z′x = −2 х = 0  х = 0
Для поиска точек решим систему 
. Отсюда получаем точку
′
z
=
−
2
y
=

у
=
y

O (0;0) . Строим график
Точка O (0;0) не принадлежит области D .
Исследуем поведение функции на границе области, т.е. на контуре ABCD , где
A(−1;−1) , B(1;−1) , C (1;1) , D(−1;1) .
1. AB : y = −1  z = 3 − x 2 − 1 = 2 − x 2 .
Найдем производную: z ‘ = (2 − x 2 )’ = −2 x = 0  x = 0 . Получаем точку M 2 (0;−1) .
2. BС : х = 1  z = 3 − 1 − у 2 = 2 − у 2 .
Найдем производную: z ‘ = (2 − у 2 )’ = −2 у = 0  у = 0 . Получаем точку M 3 (1;0) .
3. DC : y = 1  z = 3 − x 2 − 1 = 2 − x 2 .
Найдем производную: z ‘ = (2 − x 2 )’ = −2 x = 0  x = 0 . Получаем точку M 2 (0;1) .
4. AD : х = −1  z = 3 − 1 − у 2 = 2 − у 2 .
Найдем производную: z ‘ = (2 − у 2 )’ = −2 у = 0  у = 0 . Получаем точку M 3 (−1;0) .
Найдем значения функции z = 3 − x 2 − y 2 в критических точках и на границах
области:
z (0;−1) = 2 ;
z (1;0) = 2 ;
z (0;1) = 2 ;
z (−1;0) = 2 ;
z ( A) = z (−1;−1) = 1 ;
z ( B ) = z (1;−1) = 1 ;
z (C ) = z (1;1) = 1 ;
z ( D) = z (−1;1) = 1 .
Сравнивая полученные результаты, имеем: точки (0;−1) , (1;0) , (0;1) , (−1;0)
является точками глобального максимума, а точки A, B, C , D – точками глобального
минимума.
Пример 2. Найти наибольшее и наименьшее значение функции
z = x 2 + 2 xy − y 2 − 4 x в замкнутой области D , ограниченной прямыми y = x + 1, x = 3 ,
у = 0.
Решение. Найти все критические точки функции, для этого вычислим частные
производные первого порядка
z ′x ( y = const ) = ( x 2 + 2 xy − y 2 − 4 x)′ = 2 х + 2 y − 4 ,
z ′y ( x = const ) = ( x 2 + 2 xy − y 2 − 4 x)′ = 2 x − 2 y .
Для поиска точек решим систему
 z ′x = 2 x + 2 y − 4 = 0
,
 ′
z
=
2
x
−
2
y
=
y

2 y + 2 y − 4 = 0


=
x
y

4 y − 4 = 0
.

x
=
y

Получаем точку M 1 (1;1) . Строим график
Точка M 1 (1;1) не принадлежит области D .
Исследуем поведение функции на границе области, т.е. на контуре ABC , где
A(−1;0) , B(3;4) , C (3;0) .
1. y = 0  z = x 2 + 2 xy − y 2 − 4 x = x 2 − 4 x .
Найдем производную: z ‘ = ( x 2 − 4 x)’ = 2 x − 4 = 0  x = 2 . Получаем точку M 2 (2;0) .
2. х = 3  z = x 2 + 2 xy − y 2 − 4 x = 9 + 6 у − у 2 − 12 = − у 2 + 6 у − 3 .
Найдем производную:
M 3 (3;3) .
z ‘ = (− у 2 + 6 у − 3)’ = −2 у + 6 = 0  у = 3 . Получаем точку
3. y = х + 1  z = x 2 + 2 x( х + 1) − ( х + 1) 2 − 4 x = x 2 + 2 x 2 + 2 х − х 2 − 2 х − 1 − 4 х =
= 2×2 − 4х + 1.
Найдем производную:
M 2 (1;2) .
z ‘ = (2 x 2 − 4 х + 1)’ = 4 x − 4 = 0
 x = 1 . Получаем точку
Найдем значения функции z = x 2 + 2 xy − y 2 − 4 x в критических точках и на
границах области:
z (2;0) = 4 + 0 − 0 − 8 = −4 ;
z (3;3) = 9 + 18 − 9 − 12 = 6 ;
z (1;2) = 1 + 4 − 4 − 4 = −3 ;
z ( A) = z (−1;0) = 1 + 0 − 0 + 4 = 5 ;
z ( B ) = z (3;4) = 9 + 24 − 16 − 12 = 5 ;
z (C ) = z (3;0) = 9 + 0 − 0 − 12 = −3 .
Сравнивая полученные результаты, имеем: точка
(3;3) является точкой
глобального максимума, а точка (2;0) – точкой глобального минимума.
Пример 3. Найти наибольшее и наименьшее значение функции z = 10 + 2 ху − x 2 в
замкнутой области D , ограниченной y ≤ 4 − х 2 , у ≥ 0 .
Решение. Найти все критические точки функции, для этого вычислим частные
производные первого порядка
z ′x ( y = const ) = (10 + 2 ху − x 2 )′ = 2 у − 2 х ,
z ′y ( x = const ) = (10 + 2 ху − x 2 )′ = 2 x .
 z ′x = 2 y − 2 х = 0
Для поиска точек решим систему 
,
′
z
=
2
x
=
y

Получаем точку О (0;0) .
Строим график
Точка О (0;0) принадлежит области D .
Исследуем поведение функции z = 10 + 2 ху − x 2 на границе области.
1. y = 0  z = 10 + 2 ху − x 2 = 10 − х 2 .
Найдем производную: z ‘ = (10 − x 2 )’ = −2 x = 0  x = 0 . Получаем точку (0;0) .
2. у = 4 − х 2  z = 10 + 2 ху − x 2 = 10 + 2 х(4 − х 2 ) − х 2 = 10 + 8 х − 2 х 3 − х 2 =
= −2 х 3 − х 2 + 8 х + 10 .
Найдем производную: z ‘ = (−2 х 3 − х 2 + 8 х + 10)’ = −6 х 2 − 2 х + 8 = 0
6 х 2 + 2 х − 8 = 0  3х 2 + х − 4 = 0 .
D = 1 − 4 ⋅ (−4) ⋅ 3 = 49 ,
−1+ 7
−1− 7
8
4
x1 =
= 1 , x1 =
=− =− .
6
6
3
6
16 20
 4
у1 = 4 − 1 = 3 , у2 = 4 −  −  = 4 − =
.
9
9
 3
 4 20 
Получаем точки M 1 (1;3) и M 2  − ;  .
 3 9 
Найдем значения функции z = 10 + 2 ху − x 2 в критических точках и на границах
области:
z (0;0) = 10 ;
z (1;3) = 10 + 6 − 1 = 15 ;
2
160 16 270 − 160 − 48 62
 4 20 
 4  20  4 
z  − ;  = 10 + 2 ⋅  −  ⋅ −  −  = 10 −
− =
= .
27 9
27
27
 3 9 
 3 9  3
Сравнивая полученные результаты, имеем: точка
(1;3) является точкой
 4 20 
глобального максимума, а точка  − ;  – точкой глобального минимума.
 3 9 

4 марта 2011

В задаче B15 предлагается исследовать на экстремумы функцию, заданную формулой. Это стандартная задача по математическому анализу, и ее сложность сильно меняется зависимости от рассматриваемой функции: некоторые из них решаются буквально устно, другие же требуют серьезных размышлений.

Прежде чем изучать методы решения, надо усвоить некоторые термины из области математического анализа. Итак, в задаче B15 требуется найти с помощью производной следующие величины:

1. Точки локального максимума (минимума) — значение переменной, при которой функция достигает своей наибольшей (наименьшей) величины. Такие точки еще называются точками экстремума.
2. Глобальный максимум (минимум) функции — наибольшее (наименьшее) значение функции при указанных ограничениях. Другое название — глобальные экстремумы.

При этом глобальные экстремумы обычно ищутся не на всей области определения функции, а лишь на некотором отрезке [a; b]. Важно понимать, что глобальный экстремум и значение функции в точке экстремума далеко не всегда совпадают. Поясним это на конкретном примере:

Задача. Найти точку минимума и минимальное значение функции y = 2x³ − 3x² − 12x + 1 на отрезке [−3; 3].

Сначала найдем точку минимума, для чего вычислим производную:
y’ = (2x³ − 3x² − 12x + 1)’ = 6x² − 6x − 12.

Найдем критические точки, решив уравнение y’ = 0. Получим стандартное квадратное уравнение:
y’ = 0 ⇒ 6x² − 6x − 12 = 0 ⇒ … ⇒ x₁ = −1, x₂ = 2.

Отметим эти точки на координатной прямой, добавим знаки производной и ограничения — концы отрезка:

Масштаб картинки не имеет значения. Самое главное — отметить точки в правильной последовательности. Из школьного курса математики известно, что в точке минимума производная меняет знак с минуса на плюс. Отсчет всегда идет слева направо — в направлении положительной полуоси. Поэтому точка минимума одна: x = 2.

Теперь найдем минимальное значение функции на отрезке [−3; 3]. Оно достигается либо в точке минимума (тогда она становится точкой глобального минимума), либо на конце отрезка. Заметим, что на интервале (2; 3) производная всюду положительна, а значит y(3) > y(2), поэтому правый конец отрезка можно не рассматривать. Остались лишь точки x = −3 (левый конец отрезка) и x = 2 (точка минимума). Имеем:
y(−3) = 2(−3)³ − 3(−3)² − 12(−3) + 1 = −44;
y(2) = 2*2³ − 3*2² − 12*2 + 1 = −19.

Итак, наименьшее значение функции достигается на конце отрезка и равно −44.

Ответ: x_min = 2; y_min = −44

Из приведенных рассуждений следует важный факт, о котором многие забывают. Функция принимает максимальное (минимальное) значение не обязательно в точке экстремума. Иногда такое значение достигается на конце отрезка, и производная там не обязана равняться нулю.

Схема решения задач B15

Если в задаче B15 требуется найти максимальное или минимальное значение функции f(x) на отрезке [a; b], выполняем следующие действия:

1. Найти производную функции: f’(x).
2. Решить уравнение f’(x) = 0. Если корней нет, пропускаем третий шаг и переходим сразу к четвертому.
3. Из полученного набора корней вычеркнуть все, что лежит за пределами отрезка [a; b]. Оставшиеся числа обозначим x₁, x₂, …, x_n — их, как правило, будет немного.
4. Подставим концы отрезка [a; b] и точки x₁, x₂, …, x_n в исходную функцию. Получим набор чисел f(a), f(b), f(x₁), f(x₂), …, f(x_n), из которого выбираем наибольше или наименьшее значение — это и будет ответ.

Небольшое пояснение по поводу вычеркивания корней, когда они совпадают с концами отрезка. Их тоже можно вычеркнуть, поскольку на четвертом шаге концы отрезка все равно подставляются в функцию — даже если уравнение f’(x) = 0 не имело решений.

Также следует внимательно читать условие задачи. Когда требуется найти значение функции (максимальное или минимальное), концы отрезка и точки x₁, x₂, …, x_n подставляются именно в функцию, а не в ее производную.

Задача. Найти наибольшее значение функции y = x³ + 3x² − 9x − 7 на отрезке [−5; 0].

Для начала найдем производную: y’ = (x³ + 3x² − 9x − 7)’ = 3x² + 6x − 9.

Затем решаем уравнение: y’ = 0 ⇒ 3x² + 6x − 9 = 0 ⇒ … ⇒ x = −3; x = 1.

Вычеркиваем корень x = 1, потому что он не принадлежит отрезку [−5; 0].

Осталось вычислить значение функции на концах отрезка и в точке x = −3:
y(−5) = (−5)³ + 4·(−5)² − 9·(−5) − 7 = −12;
y(−3) = (−3)³ + 4·(−3)² − 9·(−3) − 7 = 20;
y(0) = 0³ + 4·0² − 9·0 − 7 = −7.

Очевидно, наибольшее значение равно 20 — оно достигается в точке x = −3.

Теперь рассмотрим случай, когда требуется найти точку максимума или минимума функции f(x) на отрезке [a; b]. Если отрезок не задан, функция рассматривается на своей области определения. В любом случае, схема решения такова:

1. Найти производную функции: f’(x).
2. Решить уравнение f’(x) = 0. Если производная — дробно-рациональная функция, дополнительно выясняем, когда ее знаменатель равен нулю. Полученные корни обозначим x₁, x₂, …, x_n.
3. Отметить x₁, x₂, …, x_n на координатной прямой и расставить знаки, которые принимает производная между этими числами. Если задан отрезок [a; b], отмечаем его и вычеркиваем все, что лежит за его пределами.
4. Среди оставшихся точек ищем такую, где знак производной меняется с минуса на плюс (это точка минимума) или с плюса на минус (точка минимума). Такая точка должна быть только одна — это и будет ответ.

Вдумчивый читатель наверняка заметит, что для некоторых функций этот алгоритм не работает. Действительно, существует целый класс функций, для которых нахождение точек экстремума требует более сложных выкладок. Однако такие функции в ЕГЭ по математике не встречаются.

Внимательно отнеситесь к расстановке знаков между точками x₁, x₂, …, x_n. Помните: при переходе через корень четной кратности знак у производной не меняется. Когда ищутся точки экстремума, знаки всегда просматриваются слева направо, т.е. по направлению числовой оси.

Задача. Найти точку максимума функции

на отрезке [−8; 8].

Найдем производную:

Поскольку это дробно-рациональная функция, приравниваем к нулю производную и ее знаменатель:
y’ = 0 ⇒ x² − 25 = 0 ⇒ … ⇒ x = 5; x = −5;
x² = 0 ⇒ x = 0 (корень второй кратности).

Отметим точки x = −5, x = 0 и x = 5 на координатной прямой, расставим знаки и границы:

Очевидно, что внутри отрезка осталась лишь одна точка x = −5, в которой знак производной меняется с плюса на минус. Это и есть точка максимума.

Еще раз поясним, чем отличаются точки экстремума от самих экстремумов. Точки экстремума — это значения переменных, при которых функция принимает наибольшее или наименьшее значение. Экстремумы — это значения самих функций, максимальные или минимальные в некоторой своей окрестности.

Помимо обычных многочленов и дробно-рациональных функций, в задаче B15 встречаются следующие виды выражений:

1. Иррациональные функции,
2. Тригонометрические функции,
3. Показательные функции,
4. Логарифмические функции.

С иррациональными функциями проблем, как правило, не возникает. Остальные случаи стоит рассмотреть более подробно.

Тригонометрические функции

Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение sin x = 0 имеет корни x = πn, где n ∈ Z. Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?

Ответ прост: надо подставлять конкретные значения n. Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — отрезок [a; b]. Поэтому для начала берем n = 0, а затем увеличиваем n до тех пор, пока соответствующий корень не «вылетит» за пределы отрезка [a; b]. Аналогично, уменьшая n, очень скоро получим корень, который меньше нижней границы.

Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, на отрезке [a; b] не существует. Рассмотрим теперь этот процесс на конкретных примерах.

Задача. Найти точку максимума функции y = sin x − 5x·sin x − 5cos x + 1, принадлежащую отрезку [−π/3; π/3].

Вычисляем производную: y’ = (sin x − 5x·sin x − 5cos x + 1)’ = … = cos x − 5x·cos x = (1 − 5x)·cos x.

Затем решаем уравнение: y’ = 0 ⇒ (1 − 5x)·cos x = 0 ⇒ … ⇒ x = 0,2 или x = π/2 + πn, n ∈ Z.

С корнем x = 0,2 все понятно, а вот формула x = π/2 + πn требует дополнительной обработки. Будем подставлять разные значения n, начиная с n = 0.

n = 0 ⇒ x = π/2. Но π/2 > π/3, поэтому корень x = π/2 не входит в исходный отрезок. Кроме того, чем больше n, тем больше x, поэтому нет смысла рассматривать n > 0.

n = −1 ⇒ x = − π/2. Но −π/2 < −π/3 — этот корень тоже придется отбросить. А вместе с ним — и все корни для n < −1.

Получается, что на отрезке [−π/3; π/3] лежит только корень x = 0,2. Отметим его вместе со знаками и границами на координатной прямой:

Чтобы удостовериться, что справа от x = 0,2 производная действительно отрицательна, достаточно подставить в y’ значение x = π/4. Мы же просто отметим, что в точке x = 0,2 производная меняет знак с плюса на минус, а следовательно это точка максимума.

Задача. Найти наибольшее значение функции y = 4tg x − 4x + π − 5 на отрезке [−π/4; π/4].

Вычисляем производную: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.

Затем решаем уравнение: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ … ⇒ x = πn, n ∈ Z.

Выделим из этой формулы корни, подставляя конкретные n, начиная с n = 0:
n = 0 ⇒ x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π. Но π > π/4, поэтому корень x = π и значения n > 1 надо вычеркнуть.
n = −1 ⇒ x = −π. Но π < −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

Из всего многообразия корней остался лишь один: x = 0. Поэтому вычисляем значение функции для x = 0, x = π/4 и x = −π/4.
y(0) = 4tg 0 − 4·0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4·π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4·(−π/4) + π − 5 = … = 2π − 9.

Теперь заметим, что π = 3,14… < 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее — очевидно, это y = −1.

Заметим, что в последней задаче можно было и не сравнивать числа между собой. Ведь из чисел π − 5, 1 и 2π − 9 в бланк ответов может быть записана лишь единица. Действительно, как написать в бланке, скажем, число π? А никак. Это важная особенность первой части ЕГЭ по математике, которая значительно упрощает решение многих задач. И работает она не только в B15.

Иногда при исследовании функции возникают уравнения, у которых нет корней. В таком случае задача становится еще проще, поскольку остается рассмотреть лишь концы отрезка.

Задача. Найти наименьшее значение функции y = 7sin x − 8x + 5 на отрезке [−3π/2; 0].

Сначала находим производную: y’ = (7sin x − 8x + 5)’ = 7cos x − 8.

Попробуем решить уравнение: y’ = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7. Но значения cos x всегда лежат на отрезке [−1; 1], а 8/7 > 1. Поэтому корней нет.

Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:
y(−3π/2) = 7sin (−3π/2) − 8·(−3π/2) + 5 = … = 12π + 12;
y(0) = 7sin 0 − 8·0 + 5 = 5.

Поскольку число 12π + 12 в бланк ответов не записать, остается лишь y = 5.

Показательные функции

Вообще говоря, показательная функция — это выражение вида y = a^x, где a > 0. Но в задаче B15 встречаются только функции вида y = e^x и, в крайнем случае, y = e^{kx + b}. Причина в том, что производные этих функций считаются очень легко:

1. (e^x)” = e^x. Ничего не изменилось.
2. (e^{kx +} b)” = k·e^{kx + b}. Просто добавляется множитель, равный коэффициенту при переменной x. Это частный случай производной сложной функции.

Все остальное абсолютно стандартно. Разумеется, настоящие функции в задачах B15 выглядят более сурово, но схема решения от этого не меняется. Рассмотрим пару примеров, выделяя лишь основные моменты решения — без основательных рассуждений и комментариев.

Задача. Найти наименьшее значение функции y = (x² − 5x + 5)e^{x − 3} на отрезке [−1; 5].

Производная: y’ = ((x² − 5x + 5)e^{x − 3})’ = … = (x² − 3x)e^{x − 3} = x(x − 3)e^{x − 3}.

Находим корни: y’ = 0 ⇒ x(x − 3)e^{x − 3} = 0 ⇒ … ⇒ x = 0; x = 3.

Оба корня лежат на отрезке [−1; 5]. Осталось найти значение функции во всех точках:
y(−1) = ((−1)² − 5·(−1) + 5)e^{− 1 − 3} = … = 11·e⁻⁴;
y(0) = (0² − 5·0 + 5)e^{0 − 3} = … = 5·e⁻³;
y(3) = (3² − 5·3 + 5)e^{3 − 3} = … = −1;
y(5) = (5² − 5·5 + 5)e^{5 − 3} = … = 5·e².

Из четырех полученных чисел в бланк можно записать лишь y = −1. К тому же, это единственное отрицательное число — оно и будет наименьшим.

Задача. Найти наибольшее значение функции y = (2x − 7)·e^{8 − 2x} на отрезке [0; 6].

Производная: y’ = ((2x − 7)·e^{8 − 2x})’ = … = (16 − 4x)·e^{8 − 2x} = 4(4 − x)·e^{8 − 2x}.

Находим корни: y’ = 0 ⇒ 4(4 − x)·e^{8 − 2x} = 0 ⇒ x = 4.

Корень x = 4 принадлежит отрезку [0; 6]. Ищем значения функции:
y(0) = (2·0 − 7)e^{8 − 2·0} = … = −7·e⁸;
y(4) = (2·4 − 7)e^{8 − 2·4} = … = 1;
y(6) = (2·6 − 7)e^{8 − 2·6} = … = 5·e⁻⁴.

Очевидно в качестве ответа может выступать лишь y = 1.

Логарифмические функции

По аналогии с показательными функциями, в задаче B15 встречаются только натуральные логарифмы, поскольку их производная легко считается:

1. (ln x)’ = 1/x;
2. (ln(kx + b))’ = k/(kx + b). В частности, если b = 0, то (ln(kx))’ = 1/x.

Таким образом, производная всегда будет дробно-рациональной функцией. Остается лишь приравнять эту производную и ее знаменатель к нулю, а затем решить полученные уравнения.

Для поиска максимального или минимального значения логарифмической функции помните: натуральный логарифм обращается в «нормальное» число только в точках вида eⁿ. Например, ln 1 = ln e⁰ = 0 — это логарифмический ноль, и чаще всего решение сводится именно к нему. В остальных случаях «убрать» знак логарифма невозможно.

Задача. Найти наименьшее значение функции y = x² − 3x + ln x на отрезке [0,5; 5].

Считаем производную:

Находим нули производной и ее знаменателя:
y’ = 0 ⇒ 2x² − 3x + 1 = 0 ⇒ … ⇒ x = 0,5; x = 1;
x = 0 — тут решать нечего.

Из трех чисел x = 0, x = 0,5 и x = 1 внутри отрезка [0,5; 5] лежит только x = 1, а число x = 0,5 является его концом. Имеем:
y(0,5) = 0,5² − 3·0,5 + ln 0,5 = ln 0,5 − 1,25;
y(1) = 1² − 3·1 + ln 1 = −2;
y(5) = 5² − 3·5 + ln 5 = 10 + ln 5.

Из полученных трех значений лишь y = −2 не содержит знака логарифма — это и будет ответ.

Задача. Найти наибольшее значение функции y = ln(6x) − 6x + 4 на отрезке [0,1; 3].

Вычисляем производную:

Выясняем, когда производная или ее знаменатель равны нулю:
y’ = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 — уже решено.

Вычеркиваем число x = 0, поскольку оно лежит за пределами отрезка [0,1; 3]. Считаем значение функции на концах отрезка и в точке x = 1/6:
y(0,1) = ln(6·0,1) − 6·0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = ln(6·1/6) − 6·1/6 + 4 = ln 1 + 3 = 3;
y(3) = ln(6·3) − 6·3 + 4 = ln 18 − 14.

Очевидно, только y = 3 может выступать в качестве ответа — остальные значения содержат знак логарифма и не могут быть записаны в бланк ответов.

Смотрите также:

1. Задача B15: Решение сложных задач и производная частного
2. Общая схема решения задач B15
3. Формула полной вероятности
4. Решение задач B1: №17—32
5. Сложные задачи на проценты
6. Задача B4: Цены на продукты в трех городах