Глубина функции как найти

Рекурсивная функция в C++ – это функция, которая вызывает сама себя. Вот пример плохо написанной рекурсивной функции:

#include <iostream>
 
void countDown(int count)
{
    std::cout << "push " << count << 'n';
    countDown(count-1); // countDown() вызывает себя рекурсивно
}
 
int main()
{
    countDown(5);
 
    return 0;
}

Когда вызывается countDown(5), печатается “push 5” и вызывается countDown(4). countDown(4) печатает “push 4” и вызывает countDown(3). countDown(3) печатает “push 3” и вызывает countDown(2). Последовательность countDown(n), вызывающих countDown(n-1), повторяется бесконечно, образуя рекурсивный эквивалент бесконечного цикла.

В уроке «11.8 – Стек и куча» вы узнали, что каждый вызов функции вызывает размещение данных в стеке вызовов. Поскольку функция countDown() никогда не возвращается (она просто снова вызывает countDown()), эта информация никогда не извлекается из стека! Следовательно, в какой-то момент на компьютере закончится стековая память, произойдет переполнение стека, и программа вылетит со сбоем или завершится. На машине автора эта программа отсчитала до -11732 перед завершением!

Условия завершения рекурсии

Рекурсивные вызовы функций обычно работают так же, как и обычные вызовы функций. Однако приведенная выше программа иллюстрирует наиболее важное отличие рекурсивных функций: вы должны включить условие завершения рекурсии, иначе они будут работать «вечно» (на самом деле, пока стек вызовов не исчерпает память). Завершение рекурсии – это условие, при выполнении которого рекурсивная функция перестает вызывать себя.

Завершение рекурсии обычно включает в себя использование оператора if. Вот наша функция, переработанная с условием завершения (и некоторым дополнительным выводом):

#include <iostream>
 
void countDown(int count)
{
    std::cout << "push " << count << 'n';
 
    if (count > 1) // условие завершения
        countDown(count-1);
 
    std::cout << "pop " << count << 'n';
}
 
int main()
{
    countDown(5);
    return 0;
}

Теперь, когда мы запустим нашу программу, countDown() будет выводить следующий текст:

push 5
push 4
push 3
push 2
push 1

Если вы посмотрите на стек вызовов на этом этапе, вы увидите следующее:

countDown(1)
countDown(2)
countDown(3)
countDown(4)
countDown(5)
main()

Из-за условия завершения countDown(1) не вызывает countDown(0) (поскольку «условная инструкция if» не выполнится), и поэтому функция печатает “pop 1” и затем завершается. В этот момент countDown(1) извлекается из стека, а управление возвращается к countDown(2). countDown(2) возобновляет выполнение в точке после вызова countDown(1), выводит “pop 2” и затем завершается. Рекурсивные вызовы функций последовательно извлекаются из стека до тех пор, пока не будут удалены все экземпляры countDown.

Таким образом, эта программа в итоге печатает:

push 5
push 4
push 3
push 2
push 1
pop 1
pop 2
pop 3
pop 4
pop 5

Стоит отметить, что вывод сообщений “push” происходит в прямом порядке, поскольку они выводятся до вызова рекурсивной функции. Вывод сообщений “pop” происходит в обратном порядке, потому что они выводятся после вызова рекурсивной функции по мере того, как функции извлекаются из стека (что происходит в порядке, обратном порядку, в котором они были помещены).

Более полезный пример

Теперь, когда мы обсудили базовую механику рекурсивных вызовов функций, давайте взглянем на другую рекурсивную функцию, которая немного более типична:

// возвращаем сумму всех целых чисел от 1 (включительно) до sumto (включительно)
// возвращает 0 для отрицательных чисел
int sumTo(int sumto)
{
    if (sumto <= 0)
    {
        // базовый случай (условие завершения), когда пользователь передал
        // неожиданный параметр (0 или отрицательное значение)
        return 0; 
    }
    else if (sumto == 1)
    {
        // нормальный базовый случай (условие завершения)
        return 1;
    }
    else
    {
        // рекурсивный вызов функции
        return sumTo(sumto - 1) + sumto;
    }
}

Рекурсивные программы часто трудно понять, просто взглянув на них. Часто бывает информативнее посмотреть, что происходит, когда мы вызываем рекурсивную функцию с определенным значением. Итак, давайте посмотрим, что произойдет, когда мы вызовем эту функцию с параметром sumto = 5.

Вызывается sumTo(5), 5 <= 1 ложно, поэтому мы возвращаем sumTo(4) + 5.
Вызывается sumTo(4), 4 <= 1 ложно, поэтому мы возвращаем sumTo(3) + 4.
Вызывается sumTo(3), 3 <= 1 ложно, поэтому мы возвращаем sumTo(2) + 3.
Вызывается sumTo(2), 2 <= 1 ложно, поэтому мы возвращаем sumTo(1) + 2.
Вызывается sumTo(1), 1 <= 1 истинно, поэтому мы возвращаем 1. Это условие завершения.

Теперь мы раскручиваем стек вызовов (извлекая каждую функцию из стека вызовов по мере ее возврата):

sumTo(1) возвращает 1.
sumTo(2) возвращает sumTo(1) + 2, что равно 1 + 2 = 3.
sumTo(3) возвращает sumTo(2) + 3, что равно 3 + 3 = 6.
sumTo(4) возвращает sumTo(3) + 4, что равно 6 + 4 = 10.
sumTo(5) возвращает sumTo(4) + 5, что равно 10 + 5 = 15.

На этом этапе легче увидеть, что мы складываем числа между 1 и переданным значением (оба включительно).

Поскольку рекурсивные функции трудно понять, просто посмотрев на них, особенно важны хорошие комментарии.

Обратите внимание, что в приведенном выше коде мы рекурсивно используем значение sumto - 1, а не --sumto. Мы делаем это, потому что operator-- имеет побочный эффект, а использование переменной, к которой применяется побочный эффект, более одного раза в заданном выражении, приведет к неопределенному поведению. Использование sumto - 1 позволяет избежать побочных эффектов, что делает более безопасным использование sumto в выражении более одного раза.

Рекурсивные алгоритмы

Рекурсивные функции обычно решают задачу, сначала находя решение подмножества задачи (рекурсивно), а затем, изменяя это подрешение, чтобы перейти к решению. В приведенном выше алгоритме sumTo(value) сначала решает sumTo(value-1), а затем добавляет значение переменной value, чтобы найти решение для sumTo(value).

Во многих рекурсивных алгоритмах некоторые входные данные дают тривиальные результаты. Например, sumTo(1) имеет тривиальный результат 1 (вы можете вычислить это в уме), и нет выигрыша от дальнейшей рекурсии. Входные данные, для которых алгоритм создает выходные данные тривиально, называются базовым случаем. Базовые случаи действуют как условия завершения работы алгоритма. Базовые случаи часто можно определить, рассматривая выходные данные для входных значений 0, 1, “”, ” или null.

Числа Фибоначчи

Одним из самых известных математических рекурсивных алгоритмов является последовательность Фибоначчи. Последовательности Фибоначчи появляются во многих местах в природе, таких как ветвление деревьев, спираль ракушек, плоды ананаса, раскручивающаяся ветка папоротника и устройство сосновой шишки.

Вот изображение спирали Фибоначчи:

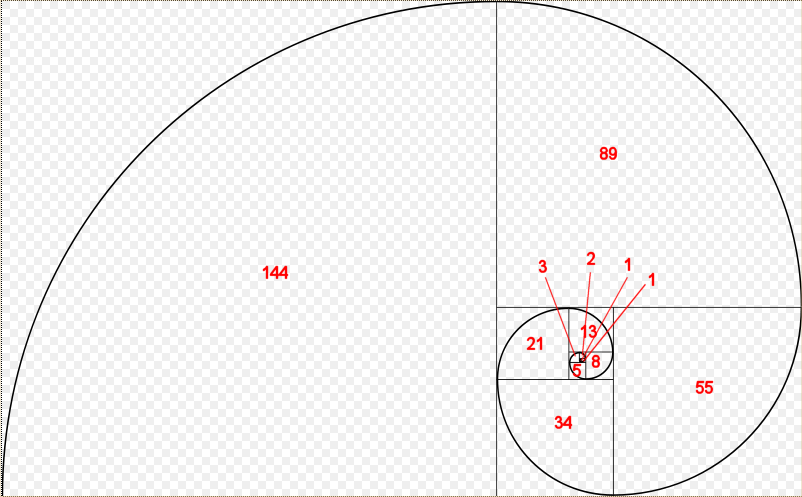
Каждое из чисел Фибоначчи – это длина стороны квадрата, в которой находится это число.

Числа Фибоначчи определяются математически как:

(begin{equation*} F(n) = begin{cases} 0 & если n = 0\ 1 & если n = 1\ f(n-1) + f(n-2) & если n > 0\ end{cases} end{equation*})

Следовательно, для вычисления n-го числа Фибоначчи довольно просто написать (не очень эффективную) рекурсивную функцию:

#include <iostream>
 
int fibonacci(int count)
{
    if (count == 0)
        return 0; // базовый случай (условие завершения)
    if (count == 1)
        return 1; // базовый случай (условие завершения)
    return fibonacci(count-1) + fibonacci(count-2);
}
 
// И основная программа для отображения первых 13 чисел Фибоначчи
int main()
{
    for (int count=0; count < 13; ++count)
        std:: cout << fibonacci(count) << " ";
 
    return 0;
}

Запуск этой программы дает следующий результат:

0 1 1 2 3 5 8 13 21 34 55 89 144

Вы можете заметить, что это именно те числа, которые появляются на диаграмме спирали Фибоначчи.

Алгоритмы мемоизации

Показанный выше рекурсивный алгоритм Фибоначчи не очень эффективен отчасти потому, что каждый вызов небазового случая Фибоначчи приводит к еще двум вызовам Фибоначчи. Это приводит к экспоненциальному росту количества вызовов функции (фактически, в приведенном выше примере функция fibonacci() вызывается 1205 раз!). Существуют методы, которые можно использовать для уменьшения количества необходимых вызовов. Один метод, называемый мемоизацией, кэширует результаты дорогостоящих вызовов функций, чтобы результат мог быть возвращен, когда те же входные данные повторяются снова.

Вот мемоизированная версия рекурсивного алгоритма Фибоначчи:

#include <iostream>
#include <vector>
 
int fibonacci(int count)
{
	// Мы будем использовать статический std::vector
    // для кеширования вычисленных результатов
	static std::vector<int> results{ 0, 1 };
 
	// Если мы уже видели этот count, то используем результат кеширования
	if (count < static_cast<int>(std::size(results)))
		return results[count];
	else
	{
		// В противном случае вычисляем новый результат и складываем его
		results.push_back(fibonacci(count - 1) + fibonacci(count - 2));
		return results[count];
	}
}
 
//  И основная программа для отображения первых 13 чисел Фибоначчи
int main()
{
	for (int count = 0; count < 13; ++count)
		std::cout << fibonacci(count) << " ";
 
	return 0;
}

Эта мемоизированная версия выполняет 35 вызовов функции, что намного лучше, чем 1205 вызовов у исходного алгоритма.

Рекурсия против итераций

О рекурсивных функциях часто задают вопрос: «Зачем использовать рекурсивную функцию, если вы можете выполнять многие из тех же задач итеративно (используя цикл for или while)?». Оказывается, вы всегда можете решить рекурсивную задачу итеративно, однако для нетривиальных задач рекурсивную версию часто намного проще написать (и читать). Например, хотя функцию Фибоначчи можно написать итеративным способом, но это будет немного сложнее! (Попробуйте!)

Итерационные функции (использующие цикл for или while) почти всегда более эффективны, чем их рекурсивные аналоги. Это связано с тем, что каждый раз, когда вы вызываете функцию, появляются некоторые накладные расходы, связанные с добавлением и извлечением кадров стека. Итерационные функции избегают этих накладных расходов.

Это не значит, что итерационные функции всегда лучший выбор. Иногда рекурсивная реализация функции настолько чище и проще в использовании, что небольшие дополнительные накладные расходы более чем окупаются с точки зрения поддерживаемости, особенно если алгоритму не требуется повторяться слишком много раз, чтобы найти решение.

В общем, рекурсия – хороший выбор, когда выполняется большинство из следующих утверждений:

• рекурсивный код реализовать намного проще;
• глубина рекурсии может быть ограничена (например, нет способа предоставить входные данные, которые заставят функцию рекурсивно пройти вниз 100 000 уровней);
• итерационная версия алгоритма требует управления стеком данных;
• это не критичный для производительности раздел кода.

Однако если рекурсивный алгоритм реализовать проще, может иметь смысл начать с него, а затем, позже оптимизировать до итеративного алгоритма.

Небольшой тест

Вопрос 1

Факториал целого числа N (пишется N!) определяется как произведение всех чисел от 1 до N (0! = 1). Напишите рекурсивную функцию с именем factorial, которая возвращает факториал входных данных. Проверьте это с первыми 7 факториалами.

Подсказка: помните, что (x * y) = (y * x), поэтому произведение всех чисел от 1 до N равно произведению всех чисел от N до 1.

Ответ

Вопрос 2

Напишите рекурсивную функцию, которая принимает на вход целое число и возвращает сумму отдельных цифр этого целого числа (например, 357 = 3 + 5 + 7 = 15). Выведите ответ на входное значение 93427 (то есть 25). Предположим, что входные значения положительны.

Ответ

Вопрос 3

Немного сложнее. Напишите программу, которая просит пользователя ввести положительное целое число, а затем использует рекурсивную функцию для печати двоичного представления этого числа. Воспользуйтесь методом 1 из урока «O.4 – Преобразование между двоичной и десятичной системами счисления».

Подсказка: используя метод 1, мы хотим печатать биты «снизу вверх», что означает в обратном порядке. Это означает, что ваша инструкция печати должна быть после рекурсивного вызова.

Ответ

Вопрос 4

Обновите свой код из задания 3, чтобы обработать случай, когда пользователь может ввести 0 или отрицательное число.

Вот пример вывода программы (при условии, что int занимает 32 бита):

Enter an integer: -15
11111111111111111111111111110001

Подсказка: отрицательное число int можно превратить в положительное значение, преобразовав его в unsigned int. Они имеют идентичные битовые представления (тип используется для определения того, как интерпретировать число в десятичном виде).

Ответ

Теги

C++ / CppLearnCppДля начинающихМемоизацияОбучениеПрограммированиеРекурсияСтек вызововЧисла Фибоначчи / Fibonacci numbers