В последнее время Интернет просто ломится от желающих поделиться секретами простого обучения школьников любого возраста. Больше достаётся малышам. Один советует не учить таблицу умножения, а выполнять умножение многозначных чисел диковинным японским способом — при помощи подсчёта точек пересечения прямых.
При этом советующий не думает о последствиях, ведь надо будет учить не только умножению, но и делению, где используется умножение, а также действиям с обыкновенными и десятичными дробями.
https://zen.yandex.ru/media/shevkin/tablica-umnojeniia-bolshe-ne-nujna-5f8dee7cb5e4d5370eefe9f6
Второй предлагает складывать и вычитать обыкновенные дроби по правилу «бабочки».
И при этом не задумывается о громоздкости вычислений даже в простом примере: 5/36 + 7/72.
https://zen.yandex.ru/media/tehno_chtivo/genialnyi-metod-slojeniia-drobei-i-ego-podvodnye-kamni-5f5f94295622142b93db0f92
Разумеется, я прокомментировал и это предложение. Критикуя, предложил, как надо учить сложению и вычитанию дробей самым традиционным способом — без лайфхаков, вызывающих у читателей этих лайфхаков оглушительные восторги.
https://zen.yandex.ru/media/shevkin/sovet-protiv-laifhaka-5f5a36b98279b40946603e1a
Про ролик, прославивший молодого учителя миллионными просмотрами, написала МК (10.09.2020) и блогер, указавший на “подводные камни” метода на примере 4/6 + 2/12 = 60/72. Блогер решил задачу проще: 4/6 + 2/12 = 10/12, но не заметил ещё более простого решения: 4/6 + 2/12 = 4/6 + 1/6 = 5/6.
Хорошо, что у него были внимательные читатели. Вот и решайте, чему надо учить: тупо применять единственный алгоритм, показанный учителем, или учить анализировать ситуацию и поступать по ситуации.
На днях я прочитал на Дзене предложение некоей KUMONo-мамы об упрощении запоминания правил нахождения уменьшаемого и вычитаемого. Вот начало статьи Как находить уменьшаемое и вычитаемое — Простая техника запоминания для малышей.
«Ваши первоклашки уравнения уже решают по Петерсон? Ну второклашки-то уж точно!
Малыши, не знакомые с отрицательными числами, решают уравнения, запоминая адские правила про «сложить разность и вычитаемое».
Ага, осталось только запомнить, что из них что…
Я, кстати, в школе была отличницей и прекрасно знала математику… и до сих пор помню, как чудовищно сложно (и, главное, в 1-2 классе непонятно, ради чего) было запомнить эти слова: вычитаемое, уменьшаемое…»
https://zen.yandex.ru/media/kumon/kak-nahodit-umenshaemoe-i-vychitaemoe-prostaia-tehnika-zapominaniia-dlia-malyshei-5f85864fa144c35a271d1920
Итак, мама видит проблему в том, что ребёнку, не знающему отрицательных чисел, трудно запомнить термины «уменьшаемое» и «вычитаемое». Она старается помочь, называя уменьшаемое, вычитаемое и разность одинаково — «числа».
Неужели так сложно донести до ребёнка, наученного вычитать, что при вычитании первое число уменьшается, его называют уменьшаемое? Это надо делать обязательно, так как развитие понятийного мышления, если хотите, научного мышления, предполагает использования терминов для обозначения изучаемых объектов. Станет ли ребёнку легче учиться, если мы избавим его от заучивания двух терминов из десяти, используемых для обозначения компонентов арифметических действий? Ребёнок и дальше будет обходиться без терминологии и называть словом «числа» каждое из чисел в следующих равенствах?
4 + 3 = 7
6 – 1 = 5
3 ∙ 2 = 6
8 : 4 = 2
Без терминов, которыми советчица пользуется, ребёнку станет легче выражать свои мысли и описывать свои действия? Чем же именно? Или термины знать всё-таки надо, но трудно запомнить, какое действие надо выполнить при поиске неизвестного компонента?
Раскрою секрет: обсуждаемые здесь термины гораздо важнее для развития речи и мышления школьника, чем для изучения математики, так как в старших классах эти правила уже не используются. Там говорят о переносе слагаемого в другую часть уравнения с противоположным знаком, о прибавлении к двум частям уравнения одного и того же числа, об умножении (делении) обеих частей уравнения на одно и то же число. Очевидно, что с этого нельзя начинать в начальной школе. А вот приучать малыша использовать речевые «шаблоны»: «чтобы найти… надо…» полезно именно для развития речи и мышления обучаемого.
В чём суть предложения KUMONo-мамы? Она записывает на листке уравнение х – 6 = 22 «на нахождение уменьшаемого», далее пишет: «Скажите ребенку, что числа стоят рядышком — так просто представить, что они ВМЕСТЕ, так и просят сложиться, чтобы стать ещё поближе друг к другу».
Интересный аргумент! А в уравнении x ∙ 2 = 6 числа 2 и 6 стоят так же близко. Они тоже будут просить сложиться? Ведь основание для выбора действия (они близко) одно и то же. А вот и рисунок, советующий ребёнку действие, а под ним умилительная запись с использованием тех самых терминов, которые детям трудно запомнить.
Что из этого поймёт ребёнок ещё вопрос, и поймёт ли?
Ещё изобретательнее KUMONo-мама объясняет нахождение вычитаемого. Она пишет на листке уравнение 12 – x = 7 «на нахождение вычитаемого». Далее пишет: «Предложите ребенку представить, что минус пытается выыыытянуться и дотянуться до ближайшего числа:
Теперь можно вычесть и получить вычитаемое.
Осталось только запомнить, как искать слагаемые. Если знаете такие же техники про них — обязательно напишите в комментариях».
Наша советчица ещё не придумала, как объяснять поиск неизвестного слагаемого. А там ещё неизвестные множители, делимое и делитель…
Но ещё больше, чем советы блогерши, меня огорчили «лайки» и восторги читателей.
Я оставил краткий комментарий: «Прекрасные примеры того, как не надо учить детей. Пытаясь придумать про “рядышком” и “выыыытянуть” автор хочет дать детям какой-то рецепт, никак не связанный с математикой. Не проще ли показывать связь операций на очевидных примерах?
1 + 2 = 3.
Накроем пальцем (монеткой…) первое слагаемое:
x + 2 = 3.
Каким действием можно найти спрятанное слагаемое?
И вопреки мнению автора, надо формулировать: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Также со вторым слагаемым, уменьшаемым,… всего шесть правил. Это и развитие речи, и развитие наблюдательности, умения замечать закономерности».
Развиваю мысль. В начале 80-х годов прошлого века я недолго увлекался идеей использования опорных конспектов (В.Ф. Шаталов). В 5 классе у меня был такой опорный конспект, возникавший в процессе работы с классом.
Глядя на него, ребята лучше запоминали упомянутые выше термины (первая буква термина стоит над числом), а также действия, с помощью которых находится неизвестная компонента (знак действия под числом). Ребята на отметку сдавали мне зачёт — формулировали каждое правило и приводили пример на его применение, я уточнял: а как называется это число, а это? Первые сдавшие зачёт увлечённо и строго экзаменовали одноклассников…
Может быть, и в начальной школе стоит попробовать применить этот опорный конспект? Только надо двигаться постепенно. Изучили сложение и вычитание — учим правила нахождения неизвестных слагаемого, уменьшаемого и вычитаемого.
Вместо заключения. Говорят, что лечить и учить умеет каждый. Не знаю, как насчёт лечить, но желающих учить — хоть отбавляй. Это явление, к сожалению, подстёгивают наши «учёные», твердящие из каждого утюга: «учитель утратил монополию на знание». Ну и чего хорошего мы дождёмся от этой утраты? От появления новых непрофессиональных желающих “сеять разумное, доброе, вечное”? Чему радуемся? Много ли пользы получим от непрофессионалов?
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
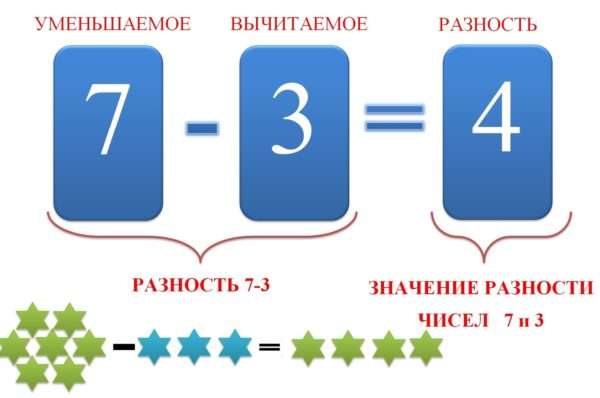
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
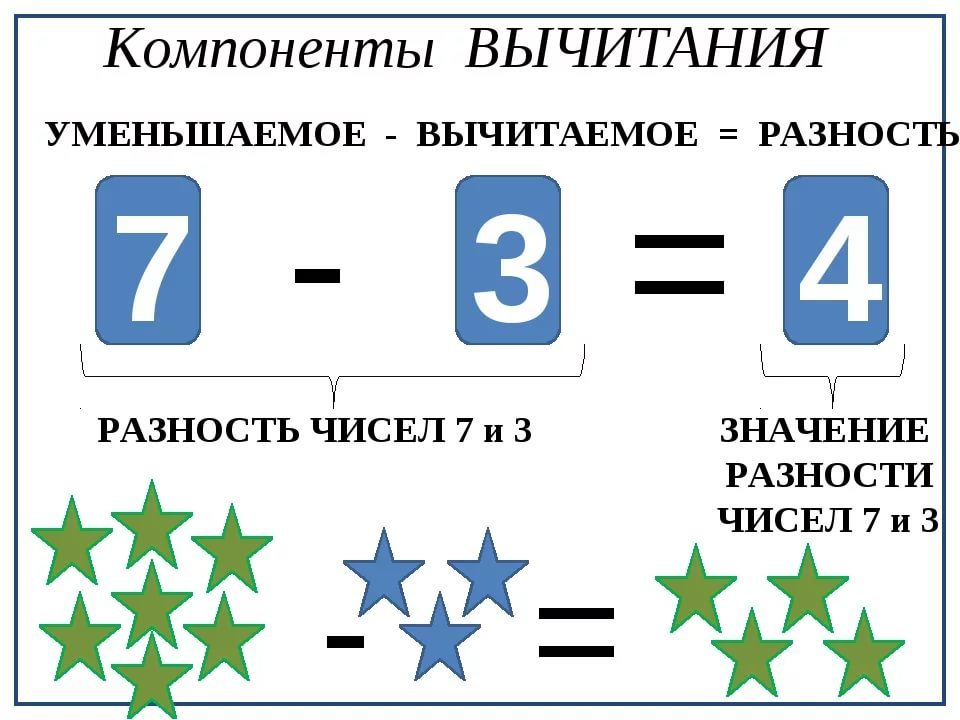
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Вычитать числа в реальной жизни не составляет труда. Мы учимся делать это так рано в жизни, что даже не думаем об этом как об умении. С появлением калькуляторов стало проще вычитать даже большие числа.
С другой стороны, вычитание значений данных в Google Таблицах — совсем другое дело. Когда вы имеете дело с большими объемами данных, становится непрактичным использовать калькулятор для выполнения вычитания по одному. На самом деле, зачем работать с данными по одному, если вы можете выполнить тысячи вычитаний за один раз?
В Google Таблицах используются формулы и функции, помогающие выполнять вычитание. В этом руководстве мы покажем вам два быстрых способа вычитания значений ячеек в Google Таблицах .
Таблицы Google и более или менее все программы для работы с электронными таблицами используют функции и формулы. Оба предоставляют отличные способы выполнения расчетов и получения результатов. Именно поэтому из всех различных способов вычитания в Google Таблицах мы решили выделить эти два метода.
Чтобы понять, как быстро вычесть значения ячеек в Google Таблицах, мы воспользуемся следующим набором данных:

Метод 1: вычитание в Google Таблицах с использованием простой формулы
Формула — это просто заявление, которое пользователь делает для выполнения вычисления. Формула состоит из комбинации значений с одной или несколькими операциями, такими как сложение, вычитание и т. Д.
Значения, используемые в формуле, могут быть числовыми или текстовыми значениями, ссылками на ячейки или заданными именами.
Формула может быть простой, как показано ниже, всего с двумя переменными и операцией:
= 6 - 5
= A2 - B2
Также он может быть сложным, состоящим из серии операций.
В любом случае формула всегда должна начинаться со знака «равно» (=). Всякий раз, когда вы используете формулу в ячейке, она отображается в строке формул.
Когда вы заканчиваете вводить формулу в ячейку, она выполняет операции, как только вы нажимаете клавишу возврата.
На этом этапе результат формулы отображается в ячейке, а фактическая формула отображается в строке формул, когда ячейка выбрана:

- Выберите ячейку, в которой вы хотите отобразить результат (ячейка C2)
- Поставьте в ячейку знак равенства (=), чтобы начать формулу. Если вы посмотрите на строку формул, вы также заметите знак равенства (=).
- Выберите ячейку, содержащую число, из которого вы хотите вычесть, или уменьшаемое (ячейка A2)
- После этого поставьте знак минус (-).
- Выберите ячейку, содержащую число, которое вы хотите вычесть, или вычитаемое (ячейка B2)
- Нажмите клавишу возврата.
- Разница между значениями в A2 и B2 теперь должна отображаться как результат в ячейке C2.
- Как только вы подготовите первую формулу, легко получить результаты для остальных ячеек в том же столбце. Вы заметите небольшой квадрат в правом нижнем углу ячейки C2. Это называется ручкой заполнения. Наведите указатель мыши на него.
- Когда ваша мышь изменится на знак плюса, просто дважды щелкните квадрат. Вы найдете формулу, скопированную во все ячейки в столбце C. В качестве альтернативы вы можете просто перетащить маркер заполнения вниз по столбцу, пока не дойдете до последней строки.
Каждая ячейка в столбце C должна теперь содержать значение соответствующих расходов, вычтенное из дохода!
Разве это не было просто?

Метод 2: вычитание в Google Таблицах с помощью функции МИНУС
Функция — это своего рода формула, которая была заранее создана для выполнения определенных задач. Например, есть функции для поиска сумм, разностей, средних значений и т. Д.
Как и формулы, функции всегда начинаются со знака «равно» (=). За ним следует имя функции и круглые скобки. В скобках вы можете указать параметры (или аргументы), если применимо.
Аргументы — это входные значения, которые функция использует для выполнения своей задачи. Количество и тип аргументов зависят от синтаксиса функции. Например, в Google Таблицах есть функция МИНУС, которая используется для вычитания двух чисел. Синтаксис этой функции принимает два параметра — вычитаемое и убываемое.
Если аргументов несколько, они разделяются запятыми. Итак, синтаксис функции МИНУС следующий:
=MINUS(value1, value2)
Здесь:
- значение1 — вычитаемое.
- значение2 — это уменьшенное значение.
В этой формуле value1 и value2 могут быть числами, датами или ссылками на ячейки, содержащие числа и / или даты.
Итак, вы можете написать либо:
=MINUS(6, 5)
или же
=MINUS(A1 , B1)
Как и формулы, всякий раз, когда вы используете функцию в ячейке, она отображается в строке формул.
Когда вы заканчиваете вводить функцию в ячейку, она выполняет операции, как только вы нажимаете клавишу возврата.
На этом этапе результат функции отображается в ячейке, а фактическая формула отображается в строке формул, когда ячейка выбрана:

- Выберите ячейку, в которой вы хотите отобразить результат (ячейка C2)
- Поставьте в ячейку знак равенства (=), чтобы начать формулу. Если вы посмотрите на строку формул, вы также заметите знак равенства (=).
- Введите имя функции MINUS и заключите его в открывающие скобки. В строке формул теперь должно отображаться:
- Выберите ячейку, содержащую число, из которого вы хотите вычесть, или уменьшаемое (ячейка A2). Это отобразит ссылку на выбранную ячейку после открывающих скобок.
- После этого поставьте запятую (,)
- Выберите ячейку, содержащую число, которое вы хотите вычесть, или вычитаемое (ячейка B2)
- Закройте круглые скобки. В строке формул теперь должно отображаться:
- Нажмите клавишу возврата.
- Разница между значениями в A2 и B2 теперь должна отображаться как результат в ячейке C2.
- Как только вы подготовите первую формулу, легко получить результаты для всех остальных ячеек в том же столбце. Наведите указатель мыши на маркер заливки (расположенный в нижнем левом углу ячейки C2).
- Когда курсор мыши изменится на знак плюса, дважды щелкните квадрат. Вы найдете формулу, скопированную во все ячейки в столбце C. В качестве альтернативы вы можете перетащить маркер заполнения вниз по столбцу, пока не дойдете до последней строки.
Каждая ячейка в столбце C теперь должна содержать значение соответствующих расходов, вычтенное из дохода.

Надеюсь, эта статья оказалась для вас полезной!
Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».
Содержание
- Что значит число уменьшаемое, число вычитаемое и разность чисел?
- Как найти уменьшаемое и вычитаемое число?
- Видео: Уменьшаемое, вычитаемое, разность
В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением. Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные. Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.
Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже. Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.
Что значит число уменьшаемое, число вычитаемое и разность чисел?
Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.
Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница». А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами. Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.
Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:
- 8 – 5 = 3
То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».
Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).
Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.
Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.
Как найти уменьшаемое и вычитаемое число?
Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:
- Y – 10 = 18, где Y – число уменьшаемое
- Значит, Y = 18 + 10
- 18 + 10 = 28
- Y = 28
Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:
- 28 – B = 10, где B – число вычитаемое
- Значит, B = 28 – 10
- 28 – 10 = 18
- B = 18
Видео: Уменьшаемое, вычитаемое, разность
Поиск вычитаемого, уменьшаемого и разности для первоклассников
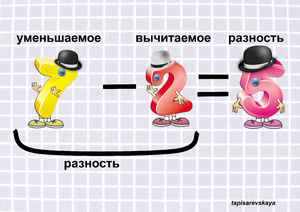
Теперь рассмотрим правила вычисления каждого из этих компонентов на простых примерах.
Чтобы сделать юным математикам понимание азов науки проще и доступнее, представим эти сложные и пугающие термины именами чисел в уравнении. Ведь у каждого человека есть имя, по которому к нему обращаются, чтобы о чем-то спросить, что-то рассказать, обменяться информацией. Учитель в классе, вызывая ученика к доске, смотрит на него и называет по имени. Так и мы, глядя на числа в уравнении, можем очень легко понять, какое число как зовут. А после уже и обратиться к числу, чтобы правильно решить уравнение или даже найти потерявшееся число, об этом чуть позже.
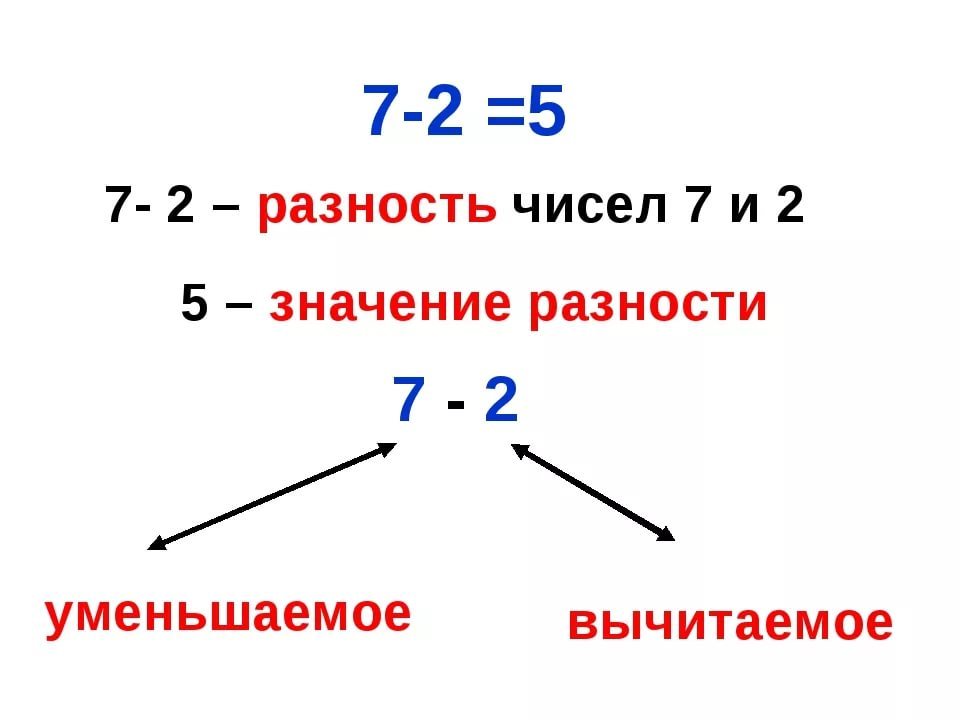
Но, ничего не зная о числах в уравнении, давайте сначала с ними познакомимся. Для этого приведем пример: уравнение 5−3= 2. Первое и самое большое число 5 после того, как мы от него отняли 3, становится меньше, уменьшается. Поэтому в мире математики его так и называют — Уменьшаемое. Второе число 3, которое мы отнимаем от первого, тоже легко узнать и запомнить — оно Вычитаемое. Глядя на третье число 2, мы видим разницу между Уменьшаемым и Вычитаемым — это Разность, то, что мы получили в результате вычитания. Вот так.
Как найти неизвестные

Но бывают случаи, когда какое-то из чисел теряется или просто неизвестно. Что же делать? Все очень просто — для того, чтобы такое число найти, нам нужно знать только два других значения, а также несколько правил математики, и, конечно, уметь ими пользоваться. Начнём с самой лёгкой ситуации, когда нам нужно найти Разность.
Как найти разность
Представим, что мы купили 7 яблок, подарили 3 яблока своей сестре и оставили какое-то количество себе. Уменьшаемое — это наши 7 яблок, число которых уменьшилось. Вычитаемое — это те 3 подаренных нами яблока. Разность — это количество оставшихся яблок. Что сделать, чтобы узнать это количество? Решить уравнение 7−3= 4. Таким образом, хотя мы и подарили 3 яблока сестре, у нас ещё осталось 4.
Правило поиска уменьшаемого
Теперь узнаем, что делать, если потерялось Уменьшаемое.
Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
- Теперь, чтобы быть уверенными, сделаем небольшую проверку — подставим все на свои места и вычислим разность. Итак, 10 -4= 6. Разность совпадает, а значит мы сделали все верно. У нас было 10 яблок, мы съели 4, осталось 6.
Как найти вычитаемое
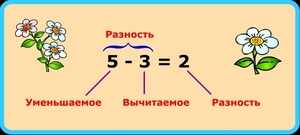
На всякий случай можно проверить наши успехи и подставить отыскавшееся Вычитаемое в исходный пример. 7−3= 4. Разность не изменилась, а значит мы сделали все правильно. Было 7 яблок, съели 3, осталось 4.
Правила очень простые, но, чтобы быть уверенными и ничего не забыть, можно поступить так — самому для себя придумать лёгкий и понятный пример на вычитание и, решая другие примеры, отыскивать неизвестные значения, просто подставляя цифры и легко находить правильный ответ. Например, 5−3= 2. Мы уже знаем, как найти и Уменьшаемое 5, и Вычитаемое 3, поэтому решая более сложное уравнение, скажем, 25-Х= 13, мы можем вспомнить наш простой пример и понять, что, чтобы найти неизвестное Вычитаемое, нужно лишь отнять от 25 число 13, то есть 25 -13= 12.
Ну вот, теперь мы познакомились с вычитанием, его главными участниками.
Мы умеем отличать их друг от друга, находить, если они неизвестны и решать любые уравнения с их участием. Пусть эти знания помогут и пригодятся вам в начале интересного и увлекательного пути в страну Математики. Удачи!
Памятка “Нахождение неизвестных компонентов сложения и вычитания в уравнениях”
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
ПРАВИЛА НАХОЖДЕНИЯ НЕИЗВЕСТНЫХ КОМПОНЕНТОВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
Нужно найти неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое
Нужно найти сумму
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое
Нужно найти уменьшаемое
Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое
Нужно найти вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность
Нужно найти разность
Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого
ПРАВИЛА НАХОЖДЕНИЯ НЕИЗВЕСТНЫХ КОМПОНЕНТОВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
Нужно найти неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое
Нужно найти сумму
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое
Нужно найти уменьшаемое
Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое
Нужно найти вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность
Нужно найти разность
Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 574 056 материалов в базе
Материал подходит для УМК
«Математика (в 2 частях)», Муравин Г.К., Муравина О.В.
3. Нахождение неизвестных компонентов сложения и вычитания
Другие материалы
- 02.05.2020
- 249
- 3
- 02.05.2020
- 207
- 2
- 02.05.2020
- 186
- 1
- 02.05.2020
- 175
- 0
- 01.05.2020
- 423
- 30
- 01.05.2020
- 375
- 4
- 01.05.2020
- 434
- 3
- 01.05.2020
- 198
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 02.05.2020 7385
- DOCX 14.9 кбайт
- 528 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Логинов Вячеслав Дмитриевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 4 года и 11 месяцев
- Подписчики: 1
- Всего просмотров: 14262
- Всего материалов: 24
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
Минобрнауки создаст для вузов рекомендации по поддержке молодых семей
Время чтения: 1 минута
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Решение уравнений. Нахождение неизвестного уменьшаемого
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы рассмотрим решение уравнений с неизвестным уменьшаемым или неизвестным вычитаемым. Вначале дадим определение понятию «уравнение» и вспомним, как узнавать его на письме. Вспомним, что такое «уменьшаемое», «вычитаемое» и «разность» и как они связаны между собой. Решим несколько уравнений на нахождение неизвестного уменьшаемого и вычитаемого.
[spoiler title=”источники:”]
http://infourok.ru/pamyatka-nahozhdenie-neizvestnyh-komponentov-slozheniya-i-vychitaniya-v-uravneniyah-4279339.html
http://interneturok.ru/lesson/matematika/4-klass/operatsii-s-mnogoznachnymi-chislami/reshenie-uravneniy-nahozhdenie-neizvestnogo-umenshaemogo
[/spoiler]
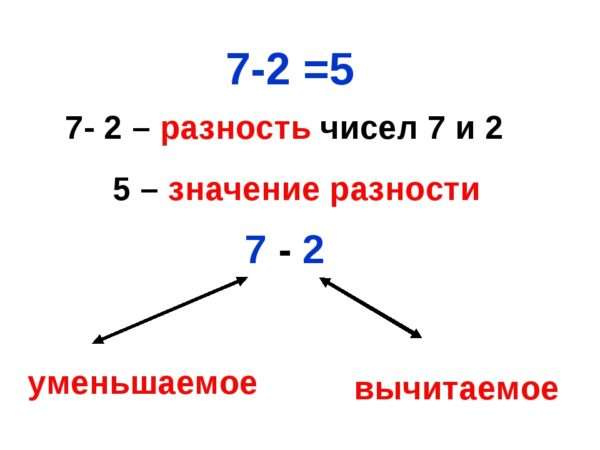








 Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.

