Горизонтальная асимптота как найти онлайн

Горизонтальная асимптота как найти онлайн

Асимптоты кривой

Прямая линия называется асимптотой кривой y=f(x), если расстояние точки кривой до этой прямой стремится к нулю при стремлении точки к бесконечности.

Назначение сервиса. Данный сервис предназначен для нахождения асимптот к графику функции в онлайн режиме. Решение оформляется в формате Word.

  • Решение онлайн
  • Видеоинструкция
  • Оформление Word

Правила ввода функции

Примеры

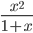≡ x^2/(x+2)

cos2(2x+π) ≡ (cos(2*x+pi))^2

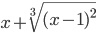≡ x+(x-1)^(2/3)

Классификация асимптот

  1. Вертикальные асимптоты.
  2. Горизонтальные асимптоты.
  3. Наклонные асимптоты.

Вертикальные асимптоты

Уравнение любой вертикальной прямой, то есть прямой, параллельной оси OY, имеет вид x=a.

Вертикальные асимптоты

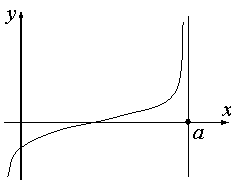
Если прямая x=a является вертикальной асимптотой графика функции y=f(x), то очевидно, что хотя бы один из односторонних пределов 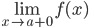или 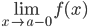равен бесконечности (+∞ или -∞).

Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.

Пример 1. Найти уравнение вертикальных асимптот графика функции .

Решение. Видим, что y→∞, если x→1, точнее , , то есть прямая x=1 является вертикальной асимптотой, причем двусторонней.

Горизонтальные асимптоты

Горизонтальные асимптоты

Всякая горизонтальная прямая имеет уравнение y=A.

Если прямая y=A является горизонтальной асимптотой кривой y=f(x), то .

Пример 2. Найти горизонтальные асимптоты кривой .

Решение. Найдем , то есть y→0 при x→+∞ и при x→-∞, значит прямая y=0 – горизонтальная асимптота данной кривой.

Наклонные асимптоты

Уравнения наклонных асимптот обычно ищут в виде y=kx+b. По определению асимптоты или (1)

Разделим обе части этого равенства на x:
, откуда

(2)

Теперь из (1):

(3)

Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при x→+∞ и при x→-∞, так как пределы могут быть разными (функция имеет две разные асимптоты).

Пример 4. Найти наклонные асимптоты графика функции .

Решение. По формуле (2) найдем .

Теперь найдем . Получаем уравнение наклонной асимптоты y=x+1.

Пример 5. Найти асимптоты кривой y=(x-1)2(x+3).

Решение. Вертикальных и горизонтальных асимптот нет, так как y→∞ при x→∞. Ищем наклонные:

.

Таким образом, кривая асимптот не имеет.

Пример 6. Найти асимптоты кривой .

Решение. Поскольку y→∞ при x→0 и при x→4, то прямые x=0 и x=4 являются вертикальными асимптотами. Так как , то y=2 – горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот: , следовательно, кривая наклонных асимптот не имеет (искать “b” не имеет смысла, так как горизонтальные асимптоты уже найдены).

Пример 7. Построить все виды асимптот к функции

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:



Находим коэффициент k:



Находим коэффициент b:



Получаем уравнение наклонной асимптоты: y = -x

Найдем вертикальные асимптоты. Для этого определим точки разрыва:





Находим переделы в точке





– является вертикальной асимптотой.

Находим переделы в точке





– является вертикальной асимптотой.

Источник

Горизонтальной асимптотой
функции
f(x)
называется прямая параллельная оси
x
к которой неограниченно приближается функция
f(x)
при стремлении к бесконечности. Уравнение горизонтальной асимптоты записывается в виде

y = y0,
где
y0
– некоторая константа (конечное число)

Для того, чтобы найти горизонтальную асимптоту функции
f(x),
очевидно, необходимо найти
y0.
Получить значение
y0
можно
вычислив пределы

limx∞fx

и
limx∞fx

Если значение хотя бы одного предела равно конечному числу
y0,
тогда

y = y0
– горизонтальная асимптота функции
f(x).

Для вычисления горизонтальных асимптот своей функции Вы можете воспользоваться нашим бесплатным онлайн калькулятором, построенным на основе системы Wolfram Alpha.

Источник

Данный калькулятор предназначен для нахождения асимптот графика функции онлайн, вычислит вертикальные, горизонтальные и наклонные асимптоты.

Асимптота – это прямая, к которой бесконечно близко приближается график функции, и график при этом бесконечно удаляется от начала координат. Знание уравнения асимптоты функции может быть полезно при анализе функции и построении ее графика.
В зависимости от поведения аргумента асимптоты разделяются на вертикальные, горизонтальные и наклонные. Вертикальная асимптота – это вертикальная линия вида x=α, если .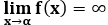

Точки разрыва функции и границы области определения являются основанием для нахождения вертикальных асимптот. Горизонтальная асимптота – горизонтальная прямая линия вида x=α, если 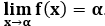. Наклонная асимптота – прямая вида y=kx+b; для существования наклонных асимптот, необходимо одновременное существование пределов .
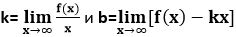Преимуществом онлайн калькулятора является то, что нет необходимости знать, как находить асимптоты графика функции. Достаточно только ввести функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже.

Для получения полного хода решения нажимаем в ответе Step-by-step.

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник
bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • асимптоты:y=frac{x^2+x+1}{x}

  • асимптоты:f(x)=x^3

  • асимптоты:f(x)=ln (x-5)

  • асимптоты:f(x)=frac{1}{x^2}

  • асимптоты:y=frac{x}{x^2-6x+8}

  • асимптоты:f(x)=sqrt{x+3}

  • Показать больше

Описание

Найдите шаг за шагом вертикальные и горизонтальные асимптоты функций

function-asymptotes-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

  • Functions

    A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Исследование функции по-шагам

    Примеры исследуемых функций

    • График логарифмической функции
    • y = log(x)/x
    • График показательной функции
    • y = 2^x - 3^x
    • График степенной функции
    • f(x) = x^5 - x^4 + x^2 - x + 1
    • График гиперболы
    • f(x) = (x - 1)/(x + 1)
    • y = 1/x
    • График квадратичной функции
    • x^2 - x + 5
    • График тригонометрической функции
    • sin(x) - 2*cos(x) + 3*sin(2*x)
    • Функция Гомпертца
    • e/2*e^(-e^-x)
    • e^(-e^-x)
    • -1/2*e^(-e^-x)
    • e^(-1/4*e^(-x))
    • e^(-e^(-2*x))
    • Логистическая кривая
    • 1/(1 + exp(-x))

    Что исследует?

    • Область определения функции. Умеет определять только точки, в которых знаменатель функции обращается в нуль
    • Умеет определять точки пересечения графика функции с осями координат
    • Экстремумы функции: интервалы (отрезки) возрастания и убывания функции, а также локальные (или относительные) и глобальные (или абсолютные) минимумы и максимумы функции
    • Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости)
    • Вертикальные асимптоты: область определения функции, точки, где знаменатель функции обращается в нуль
    • Горизонтальные асимптоты графика функции
    • Наклонные асимптоты графика функции
    • Четность и нечетность функции

    Подробнее про Исследование функции.

    Указанные выше примеры содержат также:

    • модуль или абсолютное значение: absolute(x) или |x|
    • квадратные корни sqrt(x),
      кубические корни cbrt(x)
    • тригонометрические функции:
      синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
    • показательные функции и экспоненты exp(x)
    • обратные тригонометрические функции:
      арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
      арккотангенс acot(x)
    • натуральные логарифмы ln(x),
      десятичные логарифмы log(x)
    • гиперболические функции:
      гиперболический синус sh(x), гиперболический косинус ch(x),
      гиперболический тангенс и котангенс tanh(x), ctanh(x)
    • обратные гиперболические функции:
      гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
      гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
    • другие тригонометрические и гиперболические функции:
      секанс sec(x), косеканс csc(x), арксеканс asec(x),
      арккосеканс acsc(x), гиперболический секанс sech(x),
      гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
      гиперболический арккосеканс acsch(x)
    • функции округления:
      в меньшую сторону floor(x), в большую сторону ceiling(x)
    • знак числа:
      sign(x)
    • для теории вероятности:
      функция ошибок erf(x) (интеграл вероятности),
      функция Лапласа laplace(x)
    • Факториал от x:
      x! или factorial(x)
    • Гамма-функция gamma(x)
    • Функция Ламберта LambertW(x)
    • Тригонометрические интегралы: Si(x),
      Ci(x),
      Shi(x),
      Chi(x)

    Правила ввода

    Можно делать следующие операции

    2*x
    – умножение
    3/x
    – деление
    x^2
    – возведение в квадрат
    x^3
    – возведение в куб
    x^5
    – возведение в степень
    x + 7
    – сложение
    x – 6
    – вычитание
    Действительные числа
    вводить в виде 7.5, не 7,5

    Постоянные

    pi
    – число Пи
    e
    – основание натурального логарифма
    i
    – комплексное число
    oo
    – символ бесконечности
    Источник

    Добавить комментарий