Горизонтальные проложения линий как найти

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Горизонтальные проложения. Приведение длин наклонных линиййк горизонту

Горизонтальное проложение– проекция линии местности на горизонтальную плоскость. Для определения Г.п линии АВ необходимо знать угол ν наклона или превышение hмежду конечными точками А и В линии: d=Dcosν=D-ΔD_ν, где D- длина отрезка АВ. Разность d-D=ΔD_ν называют поправкой за наклон линии к горизонту и вычисляют по формуле ΔD_ν=-2Dsin(ν/2). Эту же велічіну можно вычісліть по прібліженной формуле ΔD_ν≈-h 2 /(2D)

28. Теодолитная съёмка. Способы съёмки ситуации при теодолитной съёмке

Целью теодолитной (горизонтальной) съемки является составление контурного плана местности. Съемка элементов ситуации на местности производится относительно пунктов и сторон теодолитного хода съемочного обоснования. Для съемки объектов и угодий местности применяют следующие способы: а) Полярный способ

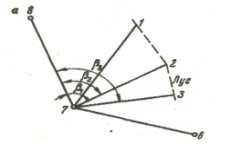Положение полярной точки определяется полярным углом bi и расстоянием Si

Полярный способ целесообразно применять на открытой местности при съемке внутриквартальной застройки. Горизонтальные углы bi измеряют теодолитом с точностью до 1¢ а расстояние Si — мерной лентой. Расстояния до снимаемых контуров при масштабе съемки 1:1000 не должны превышать 180 м до четких контуров капитальных сооружений и 250 м – до нечетких контуров. При измерении длин линий нитяным дальномером эти расстояния не должны превышать соответственно 60, 150

б) Способ перпендикуляров (прямоугольных координат)

Положение точки (рис.9.3-б) определяется абсциссой Х – вдоль стороны теодолитного хода и длиной перпендикуляра – У. Величины перпендикуляров, восстановленные на глаз для масштаба съемки 1:1000 не должны превышать 40 м при съемке четких капитальных контуров и 125 м при съемке нечетких контуров. Указанные расстояния можно увеличить в 2 раза, если перпендикуляры восстанавливать при помощи экера

в) Способ прямых угловых засечек

Способ прямых угловых засечек (рис. 9.3-в) целесообразно применять на открытых участках, где затруднительно выполнять измерения непосредственным образом. Положение снимаемой точки определяют по двум измеренным углам bi с точек съемочного обоснования одним полуприемом, с точностью до 1¢. Угол gi при определяемой точке должен быть не менее 30°и не более 150°– этот угол не измеряется.

Этот способ применяют в тех случаях, когда можно легко выполнить линейные измерения. Расстояния до снимаемых точек четких капитальных и некапитальных сооружений не должны превышать соответственно 60 и 180 м. Положение теодолит точки местности определяется измерением расстояний лентой, рулеткой между точкой съемочного обоснования и точкой местности. Лучшая форма линейной засечки, когда расстояния примерно равны (рис. 9.3-г)

Рисунок 9.3-в,г Способ угловых засечек

в- угловых засечек; г- линейных засечек

д) Способ створов

Способ створов (рис. 9.3-д) позволяет снимать контуры объектов линий теодолитного хода, одновременно с измерением длин линий теодолитного хода. Этот способ применяется при съемке точек, расположенных в створе линии теодолитного хода (съемочного обоснования), фиксируются расстояния от точек теодолитного хода до точки местности.

Источник

Определение горизонтальных проложений линий измеренных дальномером

При выводе формулы D = K ∙ n предполагалось, что визирная ось горизонтальна, а дальномерная рейка установлена перпендикулярно ей. В этом случае мы получим горизонтальное проложение линии S = D = K ∙ n.

Однако на практике в большинстве случаев визирная ось имеет некоторый угол наклона v (рис. 57), и вследствие этого вертикально расположенная рейка не будет перпендикулярна визирной оси.

Если рейку наклонить на угол v так, чтобы она была установлена перпендикулярно визирной оси, то наклонное расстояние будет равно

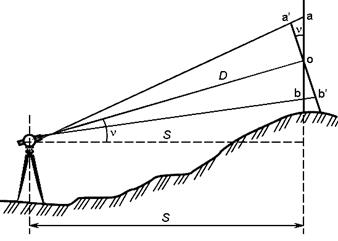
Рис. 57. Схема определения горизонтального проложения линии нитяным дальномером.

D = K ∙ n ,

где n’= a’b’ = ab ∙ cos ν = n ∙ cos ν.

D = K ∙ n ∙ cos v .

Отсюда получаем следующую формулу для расчета горизонтального проложения линии при её измерении нитяным дальномером

S = D ∙ cos v = K ∙ n ∙ cos 2 v .

Точность измерения расстояний нитяным дальномером невысокая и характеризуется относительной ошибкой 1/300. На точность определения расстояний нитяным дальномером влияют следующие факторы:

1) толщина дальномерных нитей;

2) рефракция воздуха;

3) промежуток времени между взятием отсчетов по верхней и нижней нитям.

Определение коэффициента дальномера

Коэффициент дальномера K определяют путем измерения дальномером отложенных на местности расстояний в 50, 100 и 200 м (рис. 58)

Рис. 58. Схема определения коэффициента дальномера

; ; .

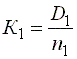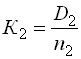вычисляют три значения коэффициента дальномера и по ним рассчитывают среднее арифметическое K_ср .

Принцип измерения расстояний электромагнитными дальномерами

Развитие электроники и радиотехники позволило создать новые приборы для линейных измерений – электромагнитные дальномеры (свето- и радиодальномеры).

Принцип работы этих приборов основан на определении промежутка времени t, необходимого для прохождения электромагнитных волн (световых и радиоволн) в прямом и обратном направлении от точки А, в которой центрирован прибор, до точки В, где установлен отражатель.

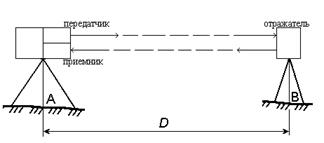
Рис. 59. Схема определения расстояния светодальномером.

Зная скорость распространения электромагнитных колебаний, можно записать

Из-за большой скорости света ( в атмосфере v ≈ 299710 км/с) измерение времени t необходимо выполнять с очень высокой точностью. Так, для измерения расстояния с точностью 1 см, время надо измерить с ошибкой не более 10 -10 сек.

Измерения выполняют фазовым или импульсным методом.

В светодальномерах лазерный источник излучения периодически посылает световой импульс. Одновременно запускается счетчик временных импульсов. Счетчик останавливается, когда светодальномер получает световой импульс, возвращенный призменным отражателем. Световой импульс, отразившись от призменного отражателя, останавливает счетчик. Для повышения точности измерения выполняют многократно. Измеренное расстояние высвечивается на цифровом табло.

Способы съемки ситуации

Съемка ситуации – геодезические измерения на местности для последующего нанесения на план ситуации (контуров и предметов местности).

Выбор способа съемки зависит от характера и вида снимаемого объекта, рельефа местности и масштаба, в котором должен быть составлен план .

Съемку ситуации производят следующими способами: перпендикуляров; полярным; угловых засечек; линейных засечек; створов (рис. 60).

Способы съемки ситуации:

1) способ перпендикуляров;

2) полярный способ;

3) способ угловых засечек;

4) способ линейных засечек;

5) способ створов.

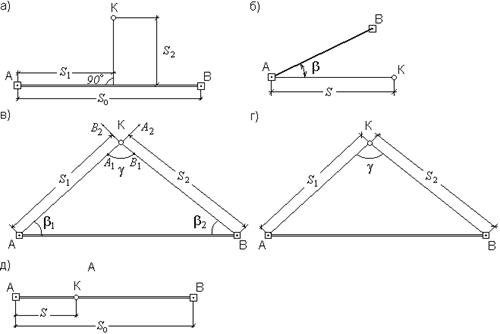
Рис. 60. Способы съемки ситуации:

а – перпендикуляров, б – полярный, в – угловых засечек, г – линейных засечек, д – створов.

Способ перпендикуляров (способ прямоугольных координат) – применяется обычно при съемке вытянутых в длину контуров, расположенных вдоль и вблизи линий теодолитного хода, проложенных по границе снимаемого участка. Из характерной точки К (рис. 60, а) опускают на линию хода А – В перпендикуляр, длину которого S₂ измеряют рулеткой. Расстояние S₁ от начала линии хода до основания перпендикуляра отсчитывают по ленте.

Полярный способ (способ полярных координат) – состоит в том, что одну из станций теодолитного хода (рис.60, б) принимают за полюс, например, станцию А, а положение точки К определяют расстоянием S от полюса до данной точки и полярным углом β между направлением на точку и линией А – В. Полярный угол измеряют теодолитом, а расстояние дальномером. Для упрощения получения углов, теодолит ориентируют по стороне хода.

Приспособе засечек (биполярных координат) положение точек местности определяют относительно пунктов съемочного обоснования путем измерения углов β₁ и β₂ (рис.60, в) – угловая засечка, или расстояний S₁ и S₂ (рис.60, г) – линейная засечка.

Угловую засечку применяют для съемки удаленных или труднодоступных объектов.

Линейную засечку – для съемки объектов, расположенных вблизи пунктов съемочного обоснования. При этом необходимо чтобы угол γ, который получают между направлениями при засечке был не менее 30° и не более 150°.

Способ створов (промеров). Этим способом определяют плановое положение точек лентой или рулеткой.(рис. 60, д). Способ створов применяется при съемке точек, расположенных в створе опорных линий, либо в створе линий, опирающихся на стороны теодолитного хода. Способ применяется при видимости крайних точек линии. Результат съемки контуров заносят в абрис. Абрис называют схематический чертеж, который составляется четко и аккуратно.

Вопросы для самоконтроля

1. Каков принцип измерения расстояний нитяным дальномером?

2. К какому типу относится нитяный дальномер?

3. По какой формуле определяют расстояние, измеренное нитяным дальномером?

4. С какой точностью можно измерить расстояние нитяным дальномером?

5. Как определяют поправку за наклон линии, измеренной нитяным дальномером?

6. Какой физический принцип используют для измерения расстояний свето- и радиодальномерами?

Источник

2.3.3. Вычисление горизонтальных проложений сторон теодолитного хода

Измерения сторон теодолитного хода выполняют мерной лентой, рулеткой, светодальномером или тахеометром. В результате получают наклонные длины линий. Наклонные линии следует при обработке хода привести к горизонту. Вычисление горизонтальных проложений сторон теодолитного хода для нашего примера приведено в табл. 2.6.

Горизонтальные проложения линий находят по формуле

где D – измеренная на местности длина линии;  — угол наклона линии.

Значения косинусов углов наклона могут быть определены по таблицам тригонометрических функций или на микрокалькуляторе. При использовании таблиц тригонометрических функций их значения выбираются с не менее чем пятью знаками после запятой. При использовании микрокалькулятора необходимо минуты перевести в доли градуса. Например: 242  2,70 (2+42/ 602,70).

В нашем примере (табл. 2.6) горизонтальное проложение линии I — II равно: d_I—II м.

Как видно из табл. 2.6, линии II  III и III  IV состоят из двух участков, имеющих разный наклон (рис. 2.4). В этом случае сначала находят по формуле (9) горизонтальные проложения каждого участка отдельно, после чего длина всей стороны хода определяется их суммированием, например, для линии II  III:

м;

м;

d_II—III м.

Рис. 2.4. Схема измерения линии II  III.

Аналогично находят горизонтальное проложение линии III  IV.

Полученные вычисления округляют до сотых долей метра и записывают в графу 5 табл. 2.5.

Суммируя горизонтальные проложения всех сторон хода, находят длину хода Р, и записывают ее значение в нижней части графы 5 (табл. 2.5).

2.3.4. Вычисление приращений координат

Приращения координат вычисляют по формулам:

где d — горизонтальное проложение стороны хода;

 — дирекционный угол стороны хода.

Значения х и у могут быть определены с использованием таблиц тригонометрических функций, на микрокалькуляторе или компьютере. Приращения координат могут иметь как знак «+», так и «», в зависимости от величины дирекционного угла . Необходимо определять знак приращений координат, используя табл. 2.7. Результаты вычислений округляют до сотых долей метра и записывают в графы 6 и 7 табл. 2.5.

Источник

Ekzamen_geodezia (1) / 25.Измерение линий лентой. Компарирование мерных лент. Приведение наклонных линий к горизонту

25. Измерение линий лентой. Компарирование мерных лент. Приведение наклонных линий к горизонту.

Измерения линий на местности могут выполняться непосредственно, путем откладывания мерного прибора в створе измеряемой линии, с помощью специальных приборов дальномеров и косвенно. Косвенным методом измеряют вспомогательные параметры (углы, базисы), а длину вычисляют по формулам.

Порядок измерения линий штриховой лентой

Измерение линий на местности штриховыми лентами производят двое рабочих. По направлению измерения один из них считается задним, второй – передним. Ленту аккуратно разматывают с кольца. Её оцифровка должна возрастать по ходу измерения. Для закрепления мерной ленты в створе линии используется 6 шпилек. Перед началом измерения 5 шпилек берет передний мерщик и одну – задний. Задний мерщик совмещает с началом линии нулевой штрих ленты. Используя прорезь в ленте, закрепляет шпилькой её конец рядом с колышком, обозначающим начальную точку линии.

Передний мерщик, имея в руке 5 шпилек, по указанию заднего мерщика, встряхнув ленту, натягивает её в створе линии и фиксирует первой шпилькой передний конец ленты. Затем задний мерщик вынимает свою шпильку из земли, вешает её на кольцо, и оба мерщика переносят ленту вперед вдоль линии. Дойдя до воткнутой в землю передним мерщиком шпильки, задний мерщик закрепляет на ней свой конец ленты, а передний, натянув ленту, закрепляет её передний конец следующей шпилькой. В таком порядке мерщики укладывают ленту в створе линии 5 раз.

После того как передний мерщик зафиксирует пятой шпилькой свой конец ленты, задний мерщик передает ему кольцо с пятью шпильками, которые он собрал в процессе измерения. Число таких передач (т.е. отрезков по 100 м при длине ленты в 20 м) записывают в журнале измерений. Последний измеряемый остаток линии обычно меньше полной длины ленты. При определении его длины метры и дециметры отсчитывают по ленте, а сантиметры оценивают на глаз

Измеренная длина линии D вычисляется по формуле :

D = 100 · a + 20 · b + c,

где a – число передач шпилек;

b – число шпилек у заднего мерщика на кольце;

Для контроля линию измеряют вторично 24-метровой или той же 20-метровой в обратном направлении. За окончательный результат принимают среднее арифметическое из двух измерений, если их расхождение не превышает:

– 1/3000 части от длины линии при благоприятных условиях измерений;

– 1/2000 – средних условиях измерений;

– 1/1000 – неблагоприятных условиях измерений.

Т.е. допускаются абсолютные ошибки на 100 м длины линии 3 см, 5 см и 10 см.

Компарирование мерных лент и рулеток

Мерные ленты и рулетки перед измерением ими линий должны быть проверены. Данная проверка называется компарированием и состоит в установлении действительной длины мерного прибора путем его сравнения с образцовым прибором, длина которого точно известна.

Для компарирования штриховых лент за образцовый мерный прибор принимают одну из лент, имеющихся на производстве, длину которой выверяют в лаборатории Государственного надзора за стандартами и измерительной техникой Государственного комитета стандартов РФ и пользуются ею при сравнении с рабочими лентами. Компарирование шкаловых лент производят на специальных приборах, называемых стационарными компараторами.

Простейший способ компарирования штриховых лент состоит в следующем. На горизонтальной поверхности, например, на полу, укладывают образцовую ленту. Рядом с ней кладут проверяемую ленту так, чтобы их края касались друг друга, а нулевые штрихи совмещались. Жестко закрепив концы с нулевыми штрихами, ленты натягивают с одинаковой силой и измеряют миллиметровой линейкой величину несовпадения конечных штрихов на других концах лент. Данная величина показывает на сколько миллиметров рабочая лента короче или длиннее образцовой и называется поправкой за компарирование Δℓ.

Длина проверяемой 20-метровой ленты не должна отличаться от длины образцовой ленты более чем на ±2 мм. В противном случае в результаты измерения линий вводят поправки. При этом, выполняя измерения линий рабочей лентой, полагают, что её длина равняется 20 м. Поправки определяют по формуле

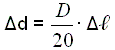
где D – длина измеренной линии.

Поправку вычитают из результатов измерения, когда рабочая лента короче образцовой, и прибавляют, когда она длиннее.

Вычисление горизонтальной проекции наклонной линии местности

При создании планов местности вычисляют горизонтальную проекцию каждой линии, т.е. её горизонтальное проложение S.

Рис. 50. Горизонтальная проекция линии

Если линия АВ (рис. 50) наклонена к горизонту под углом ν, то определить горизонтальное проложение можно, воспользовавшись формулой

,

где D – длина измеренной наклонной линии АВ; ν – угол наклона.

Иногда для определения горизонтального проложения используют поправку за наклон

,

.

Поправку за наклон вводят при углах наклона более 1°. Углы наклона измеряют теодолитом.

Источник

Перейти к контенту

В своей практике мы не раз сталкивались с проблемой, когда заказчик работ не уверен в получившихся промерах границ участка. В этих случаях мы часто слышим: «Я проверил рулеткой, там больше вышло!» Так почему же рулеткой не точнее.

По закону для определения координат точек границ земельного участка допускаются погрешности в зависимости от того, где Ваш участок расположен. Например, для населенных пунктов это погрешность составляет не более 0,1 м, то есть 10 см. Причем следует учесть, что, когда мы говорим о координатах границ, учитывается горизонтальное проложение, а не фактически «искривлённая» поверхность земли.

Исходя из этого при измерении длины участка рулеткой не получится измерить его правильно, так как просто невозможно держать ее горизонтально ровно. Да и к тому же длина участка чаще превышают длину имеющейся рулетки. Чем больше раз Вы ее разложите, тем больше увеличится погрешность измерений.

Многие скажут, что прогресс не стоит на месте и почему бы этим не воспользоваться. Взять смартфон с навигатором или одноименный прибор и сделать все самому. Но! Даже далеко недешевый вариант дает погрешность в несколько метров. Может быть плохая связь со спутником, плохая погода, высотки – все это влияет на качество определения местоположения.

Для съемки границ и в последующем подготовки качественного кадастрового документа используют, конечно, специализированное геодезическое оборудование. Так, например, часто используют тахеометр. Прибор позволяет снимать координаты с помощью отражателя, то есть съемка происходит «в паре». Также одним из минусов является привязка к нескольким пунктам для обеспечения необходимой точности, которые зачастую находятся вне зон видимости. Тем самым придется тянуть ход и точность от такой съемки снижается. Но даже в этом случае погрешность будет в допустимых пределах.

Сейчас одним из фаворитов среди геодезического оборудования, конечно, является GPS (GNSS)-приемник, который работает за счет связи со спутников. В случае плохого сигнала использует специальные базовые станции. Точность от такой съемки зачастую измеряется в миллиметрах.

Таким образом, не стоит не доверять специалисту с оборудованием за несколько сотен тысяч рублей. Рулеткой или навигатором самостоятельно измерить границы с необходимой точностью точно не выйдет! Проверено!

Ставьте ЛАЙК, подписывайтесь и читайте дальше:

Как бесплатно увеличить свой участок?

Как признать садовый дом жилым?

Как бесплатно узаконить “прирезку”: 3 простых шага