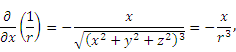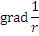, где r – расстояние от начала прямоугольной системы координат до точки M (x, y, z).Решение.
Согласно определению,
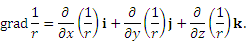
Учитывая равенства
,
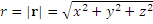
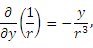
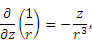
получим
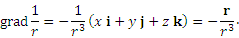
4
Скалярные и
векторные поля.
Определение 1.
Скалярным полем точки М называется
скалярная функция
точки М вместе с областью ее определения.
В пространственной
системе координат Oxyz
для каждой точки с координатами
,
скалярное поле является функцией этих
координат:
.
Примерами скалярных
полей являются поле температуры
атмосферы, поле плотности массы и т.д.
В дальнейшем будем
предполагать, что скалярные поля являются
однозначными, непрерывными и
дифференцируемыми достаточное число
раз.
Если частные
производные одновременно не равны нулю,
то уравнение
(С= const)
определяет поверхность, вдоль которой
функция
сохраняет постоянное значение; такая
поверхность называется поверхностью
уровня функции
.
Очевидно, что рассматриваемая область
Т заполнена поверхностями уровня и
через каждую точку проходит одна и
только одна такая поверхность. Очевидно
также, что поверхности уровня не
пересекаются между собой. Аналогично
определяются линии уровня
непрерывно дифференцируемой функции
,
заданной в области
.
Аналогично
определяются линии уровня
непрерывно дифференцируемой функции
,
заданной в области
.
Производная
по направлению
Рассмотрим единичный
вектор
произвольного направления, где
– углы, образуемые вектором
с осями координат.
Параметрические
уравнения прямой , проходящей через
точку
в направлении вектора
,
имеют вид
,
,
(1)
.
Тогда для точек
этой прямой функция
является функцией
одной переменной
:
(2)
Определение 3.
Производной
скалярного поля
в точке
по направлению
называется производная функции
по
при
,
если она существует, и обозначается
.
Можно сказать, что
производная по направлению
есть скорость изменения скалярного
поля по отношению к величине перемещения
точки М вдоль выбранного направления.
Дифференцируя
правую часть равенства (2) по
,
получаем
(3)
где
– направляющие косинусы вектора
.
Для плоского случая
Пример 1.
Вычислить производную функции
в точке
по направлению вектора
,
где
.
Решение. Определим
единичный вектор
заданного направления
.
Имеем
.
,
.
Отсюда
.
Найдем частные производные функции в
точке
:
,
.
По формуле (3) получаем
.
3. Градиент
Определение 4.
Градиентом
дифференцируемого скалярного поля
называется векторное поле точки М,
обозначаемое
и определяемое формулой
(4)
Градиентами
некоторых скалярных полей являются
поле сил тяготения, поле заряда и т.д.
Пользуясь известными
формулами для нахождения модуля вектора,
получим
,
(5)
,
,
.
Используя понятие
градиента и формулу для скалярного
произведения, представим формулу (3) в
виде скалярного произведения векторов
и
:
(6)
Так как
,
то получаем
,
(7)
Из (7) следует, что
в каждой точке, не являющейся особой,
градиент направлен в сторону максимального
возрастания функции, а модуль градиента
равен величине скорости этого возрастания.
Действительно. В случае
вектор
имеет то же направление, что и
,
и тогда
. (8)
Формула (8) позволяет
вместо предыдущего определения градиента,
в котором используется система координат,
дать другое, инвариантное определение.
Определение 5.
Градиентом скалярного поля
называется вектор, характеризующий
наибольшую (по модулю и направлению)
скорость изменения этого скалярного
поля.
Это определение
градиента инвариантно, т.е. не зависит
от выбора системы координат.
Если
,
то производная по направлению является
наименьшей, равной
.
Если же
,
то производная по направлению равна
нулю. Направление градиента совпадает
с направлением нормали к поверхности
уровня
.
Пример 2.
Найти градиент скалярного поля
в точке
.
Вычислить его величину и направление.
Решение:
Имеем
,
,
Следовательно
;
;
,
,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Векторный анализ
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано поле данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.
Скалярное поле
Скалярное поле задается скалярной функцией точки и = /(М). Если в пространстве введена декартова с истема координат, то и есть функция трех переменных х, yt z — координат точки М: Определение. Поверхностью уровня скалярного поля называется множество точек, в которых функция f(M) принимает одно и то же значение. Уравнение поверхности уровня Пример 1. Найти поверхности уровня скалярного поля ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению.
Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента -4 Согласно определению уравнением поверхности уровня будет . Это уравнение сферы (с Ф 0) с центром в начале координат. Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же.
Если указанную плоскость принять за плоскость хОу, то функция поля не будет зависеть от координаты z, т. е. будет функцией только аргументов х и у, Плоское поле можно характеризовать помощьюлиний уровня — множестваточек плоскости, в которых функция /(ж, у) имеетодно и тоже значение. Уравнение линии уровня — Пример 2.
Найти линии уровня скалярного поля Линии уровня задаются уравнениями При с = 0 получаем пару прямых получаем семейство гипербол (рис. 1). 1.1. Производная по направлению Пусть имеется скалярное поле, определяемое скалярной функцией и = /(Af). Возьмем точку Afo и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис. 2). Обозначим длину вектора МоМ через А/, а приращение функции /(Af) – /(Afo), соответствующее перемещению Д1, через Ди.
Отношение определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению Пусть теперь стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I. Определение. Если при Д/ О существует конечный предел отношения (5), то его называют производной функции в данной точке Afo поданному направлению I и обозначают символом зг!^ . Так что, по определению, Это определение не связано с выбором системы координат, т. е. носит**вариантный характер.
Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция / дифференцируема в точке . Рассмотрим значение /(Af) в точке . Тогда полное приращение функции можно записать в следующем виде: где а символы означают, что частные производные вычислены в точке Afo. Отсюда Здесь величины jfi, , ^ суть направляющие косинусы вектора . Так как векторы МоМ и I сонаправлены , то их направляющие косинусы одинаковы:
Так как M Afo, осгавая сь все время на прямой, параллельной вектору 1, то углы постоянные потому Окончательно из равенств (7) и (8) получаем Эамуан ис 1. Частные производные , являются производными функции и по направлениям координатныхосей ссчлвешне нно- Пример 3. Найти производную функции по направлению к точке Вектор имеет длину .
Его направляющие косинусы: По формуле (9) будем иметь Тот факт, что , означает, что скалярное поле в точке в данном направлении возраста- Для плоского поля производная по направлению I в точке вычисляется по формуле где а — угол, образованный вектором I с осью Ох. Зммчмм 2. Формула (9) для вычисления производной по направлению I в данной точке Afo остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке ПрИШр 4.
Вычислить производную скалярного поля в точке Afo(l, 1). принадлежащей параболе по направлению этой кривой (в направлении возрастания абсциссы). Направлением ] параболы в точке считается направление касательной к параболе в этой точке (рис.3). Пусть касательная к параболе в точке Afo образует с осью Ох угол о.
Тогда откуда направляющие косинусы касательной Вычислим значения и в точке . Имеем Теперь по формуле (10) получаем.
Найти производную скалярного поля в точке по направлению окружности Векторное уравнение окружности имеет вид . Находим единичный вектор т касательной к окружности Точке соответствует значение параметра Значение г в точке Afo будет равно Отсюда получаем направляющие косинусы касательной к окружности в точке Вычислим значения частных производных данного скалярного поля в точке Значит, искомая производная .
Возможно вам будут полезны данные страницы:
Градиент скалярного поля Пусть скалярное поле определяется скалярной функцией которая предполагается дифференцируемой. Определение. Градиентом скалярного поля » в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством Ясно, что этот вектор зависиткак от функции /, так и отточки М, в которой вычисляется ее производная.
Пусгь 1 — единичный вектор в направлении Тогда формулу дл я производной по направлению можно записать в следующем виде: . тем самым производная от функ ии и по направлению 1 равна скалярному произведению градиента функ ии и(М) на орт 1° направления I. 2.1. Основные свойства градиента Теорема 1.
Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское). (2) Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть I — векгор, касательный к кривой L в точке М. Так как на поверхности уровня и(М) = и(М|) для любой точки Мj е L, то С другой стороны, = (gradu, 1°). Поэтому .
Это означает, что векторы grad и и 1° ортогональны, Итак, векгор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М. Теорема 2. Градиент направлен в сторону возрастания функции поля. Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.
Векторный анализ
Обозначим через п нормальк поверхности уровня, ориентированную в сторону возрастания функции ti(M), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем Так как по условию рис.5 и поэтому ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т. е. в сторону возрастания функции и(М).
Теорема 3. Длина градиента равна наибольшей производной по направлению в данной точке поля, (здесь шах $ берется по всевозможным направлениям в данной точке М паю). Имеем где — угол между векторами 1 и grad п. Так как наибольшее значени Пример 1. Найти направление наибольшего иэмонония скалярного поля в точке а также величину этого наибольшего изменения в указанной точке. Направление наибольшего изменения скалярного поля указывается вектором .
Имеем так что Этот вектор определяет направление наибольшего возрастания поля в точко . Величина наибольшого изменения поля в этой точке равна 2.2. Инвариантное определение градиента Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта.
Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант. Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента. Определение. Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).
нормали, направленный в сторону возрастания поля. Тогда Пример 2. Найти градиент расстояния — некоторая фиксированная точка, a M(x,y,z) — текущая. 4 Имеем где — единичный вектор направления . Правила вычисления градиента где с — постоянное число. Приведенные формулы получаются непосредственно из определения градиента и свойств производных.
По правилу дифференцирования произведения Доказательство аналогично доказательству свойства Пусть F(и) — дифференцируемая скалярная функция. Тогда 4 По определению фадиента имеем Применим ко всем слагаемым правой части правило дифференцирования сложной функции. Получим В частности, Формула (6) следует из формулы Пример 3. Майти производную по направлению радиус-воктора г от функции По формуле (3) а по формуле В результате получим, что Пример 4.
Пусть дано плоское скалярное поле — расстояния от некоторой точки плоскости до двух фиксированных точек этой плоскости. Рассмотрим произвольный эллипс с фокусами Fj и F] и докажем, что всякий луч свота, вышедший из одного фокуса эллипса, после отражения от эллипса попадает в другой его фокус. Линии уровня функции (7) суть ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению.
Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента Уравнения (8) описывают семейство эллипсов с фокусами в точках F) и Fj. Согласно результату примера 2 имеем Тем самым градиент заданного поля равен вектору PQ диагонали ромба, построенного на ортах г? и радиус-векторов. проведенных к точке Р(х, у) из фокусов F| и Fj, и значит, лежит на биссектрисе угла можду этими радиус-векторами (рис. 6).
По тооромо 1 градиент PQ перпендикулярен к эллипсу (8) в точке. Следова- Рис.6 тельно. нормаль к эллипсу (8) в любой ого точке делит пополам угол между радиус-векторами, проведенными в эту точку. Отсюда и из того, что угол падения равон углу отражения, получаем: луч света, вышедший из одного фокуса эллипса, отразившись от него, непременно попадает в другой фокус этого эллипса.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Градиент скалярного поля и его физический смысл
В заключение рассмотрим меру скалярного поля, называемую градиентом, что в переводе с латинского означает шагающий или растущий. Термин впервые появился в метеорологии, а в математику и физику был введен Джеймсом Максвеллом, который предложил его обозначение в виде – grad.
Градиент – вектор, своим направлением указывающий направление наискорейшего возрастания некоторой физической величины, значение которой меняется от одной точки скалярного поля к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.
Для раскрытия физического смысла градиента, рассмотрим пример скалярного поля, в котором изменяется один параметр – высота поверхности земли над уровнем моря (см. рис. 2.7). Тогда градиент в каждой точке поверхности будет показывать «направление самого крутого подъема», и своей величиной характеризовать крутизну склона.
Рисунок 2.7 – Пример скалярного поля и его градиента.
Из рисунка видно, что операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и тем длиннее, чем круче наклон.
С математической точки зрения градиент – это производная скалярной функции, определенной на векторном пространстве. Для случая трехмерного пространства градиентом скалярной функции
Использовав в качестве единичных векторов векторы (орты) еЛЛ- 110 осям прямоугольных декартовых координат, получаем
В общем, размерность вектора градиента определяется размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.
Математический смысл градиента любой скалярной функции/в том, что его скалярное произведение с бесконечно малым вектором перемещения dx дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена/, то есть линейную часть изменения / при смещении на dx. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат лт.е. от природы параметров х вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат. В тоже время dx – это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, т.е. вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного) вектора, т.е. вектором, записанным в обычном базисе.
В различных отраслях физики используется понятие градиента различных физических полей. Например, напряженность электростатического поля есть минус градиент электрического потенциала, напряженность гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Консервативная сила в классической механике есть минус градиент потенциальной энергии.
[spoiler title=”источники:”]
http://bstudy.net/816679/informatika/gradient_skalyarnogo_polya_fizicheskiy_smysl
[/spoiler]
