Графический метод
довольно прост и нагляден для решения
задач ЛП с двумя переменными. Он основан
на геометрическом
представлении
допустимых решений и ЦФ задачи. Каждое
из неравенств задачи ЛП определяет на
координатной плоскости (x1,
x2
) некоторую полуплоскость, а система
неравенств в целом – пересечение
соответствующих полуплоскостей.
Множество точек пересечения данных
полуплоскостей называется областью
допустимых решений (ОДР).
ОДР всегда представляет собой выпуклую
фигуру, т.е.
обладающую следующим свойством: если
две точки А и В принадлежат этой фигуре,
то и весь отрезок АВ принадлежит ей. ОДР
графически может быть представлена
выпуклым многоугольником, неограниченной
выпуклой многоугольной областью,
отрезком, лучем, одной точкой. В случае
несовместности системы ограничений
задачи ОДР является пустым множеством.
Оптимальное решение
всегда находится на границе ОДР т.е. ЦФ
L(X)=c1x1+c2x2
принимает свое max(min)
значение на границе области, точнее в
ее угловых точках.
При поиске
оптимального решения задач ЛП возможны
следующие ситуации: существует
единственное решение задачи; существует
бесконечное множество решений
(альтернативный
оптиум); ЦФ
не ограничена; область допустимых
решений – единственная точка; задача
не имеет решений.
Методика решения задач лп графическим методом
-
В ограничениях
задачи замените знаки неравенств на
знаки точных равенств и постройте
соответствующие прямые. -
Найдите и заштрихуйте
полуплоскости, разрешенные каждым из
ограничений-неравенств задачи. Для
этого подставьте в конкретное неравенство
координаты какой-либо точки [например,
(0;0)], и проверьте истинность полученного
неравенства.
Если неравенство
истинное, то
надо
заштриховать полуплоскость, содержащую
данную точку; иначе
(неравенство
ложное) надо заштриховать полуплоскость,
не содержащую данную точку.
Поскольку x1
и x2
должны быть неотрицательными, то их
допустимые значения всегда будут
находиться выше оси x1
и правее оси x2
, т.е. в I-м квадранте. Ограничения-равенства
разрешают только те точки, которые лежат
на соответствующей прямой, поэтому
выделите на графике такие прямые.
III. Определите
ОДР как часть плоскости, принадлежащую
одновременно всем разрешенным областям,
и выделите ее. При отсутствии ОДР задача
не имеет
решений,
о чем сделайте соответствующий вывод.
IV. Если
ОДР – не пустое множество, то определите
координаты угловых точке. Определение
координат сводится к решению системы
соответствующих линейных уравнений.
-
Подставьте
координаты угловых точек в уравнение
для Ц.Ф. и найдите max
(min)
значение целевой функции.
Можно вместо
перебора всех угловых точек (пункт
IV,
V)
произвести
следующие действия:
IV.а Провести
вектор координатами которого служат
коэффициенты в уравнении с целевой
функцией. Сдвигать прямую перпендикулярную
построенному вектору, от начала по
направлению вектора, до момента, когда
пресечение сдвигаемой прямой с ОДР
будет составлять одну точку.
V.а Координаты
найденной точки будут являться оптимальным
планом, а если их подставить в уравнение
целевой функции, то получим ее max
(min)
значение.
Задача
Найдем оптимальное
решение задачи о красках, математическая
модель которой имеет вид:
Построим прямые
ограничений (рис. 1).
Рис. 1. Графическое
решение задачи
Определим ОДР.
Например, подставим точку (0;0) в исходное
ограничение (3), получим 0≤1 , что является
истинным неравенством, поэтому стрелкой
(или штрихованием) обозначим полуплоскость,
содержащую
точку
(0;0), т.е. расположенную правее и ниже
прямой (3). Аналогично определим допустимые
полуплоскости для остальных ограничений
и укажем их стрелками у соответствующих
прямых ограничений (см. рис. 1.). Общей
областью, разрешенной всеми ограничениями,
т.е. ОДР является многоугольник ABCDEF.
Найдем координаты
точек пересечения прямых ограничений,
т.е. координаты угловых точек. В некоторых
случаях хороший рисунок позволяет сразу
определять координаты угловых точек.
;
;
;
;
Для определения
координаты точки Е решим систему
уравнений с ограничениями (1) и (2).
Решая данную
систему получаем:
.
Найдем значение
целевой функции в угловых точках, т.е.
подставим их координаты в уравнение
.
Е – это точка
максимума ЦФ.
Таким образом,
наилучшим режимом работы фирмы является
ежесуточное производство краски 1-го
вида в объеме 3 1/3 т. и краски 2-го вида в
объеме 1 1/3 т. Доход от продажи красок
составит 12 2/3 тыс. руб. в сутки.
Решая графическим
методом предполагающим построение
целевого вектора, проводим
вектор координатами которого служат
коэффициенты в уравнении с целевой
функцией
,
сдвигая прямую перпендикулярную
построенному вектору (от начала к концу)
найдем точку, являющуюся последней в
пресечении сдвигаемой прямой сОДР,
(это точка Е) ее координаты найденные
из решении системы соответствующих
уравнений будут являться оптимальным
планом, а значение целевой функции в
ней будет max.
В более общем
случае, разработан и широко применяется
универсальный метод решения любой
задачи ЛП, называемый симплекс-методом.
Симплекс метод,
как метод решения задач ЛП был предложен
в американским математиком-экономистом
Данцигом в 1951 году.
Графически симплекс
метод представляет из себя передвижение
по выпуклому многограннику от вершине
к вершине, при этом значение целевой
функции на каждом шаге улучшается до
тех пор, пока не достигается оптимум.
Идея
симплекс метода состоит в том, чтобы
преобразовать уравнение содержащее
целевую функцию к виду:
,
т.к. в этом случае становиться возможным
выразить,
а в силу того что перед нами ставится
задача максимизироватьL,
то эта задача достигается в случае когда
все переменные присутствующие в данном
уравнении принимают нулевые значения
(т.к. переменные не отрицательны по
условию).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в графический метод
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.
Возможно эта страница вам будет полезна:
Задача линейного программирования в стандартной форме с двумя переменными имеет вид:
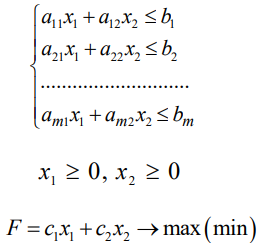
Эти задачи допускают простое геометрическое истолкование.
Рассмотрим вначале геометрическое истолкование системы ограничений задачи. Каждую совокупность значений переменных 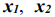


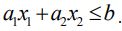
Рассмотрим прямую на плоскости с уравнением:
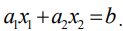
Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо наше неравенство, а в другой — противоположное. Для того чтобы проверить, какая из полуплоскостей состоит из решений нашего неравенства, следует взять точку из какой-либо полуплоскости и проверить, выполняется ли наше неравенство в этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находиться во всех соответствующих полуплоскостях, т. е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет, таким образом, некоторую выпуклую многоугольную область (область допустимых решений). Условия неотрицательности переменных 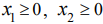
При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР — область допустимых решений):
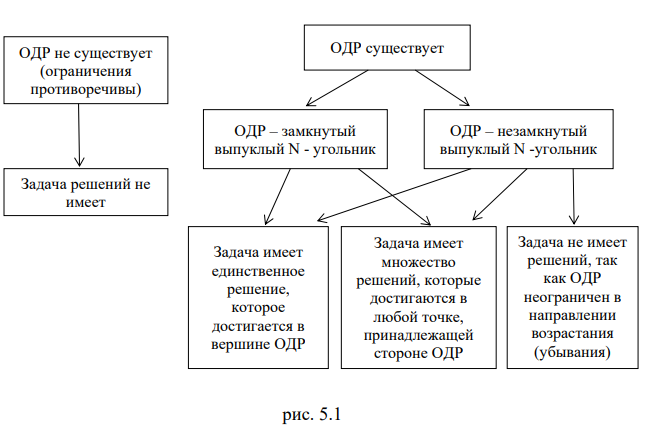
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция 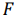
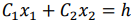
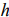
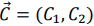
Отметим, что при нахождении решения задачи (5.1)-(5.3) могут встретиться случаи, изображенные на рис. 5.2- 5.5. Рис.5.2 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке 
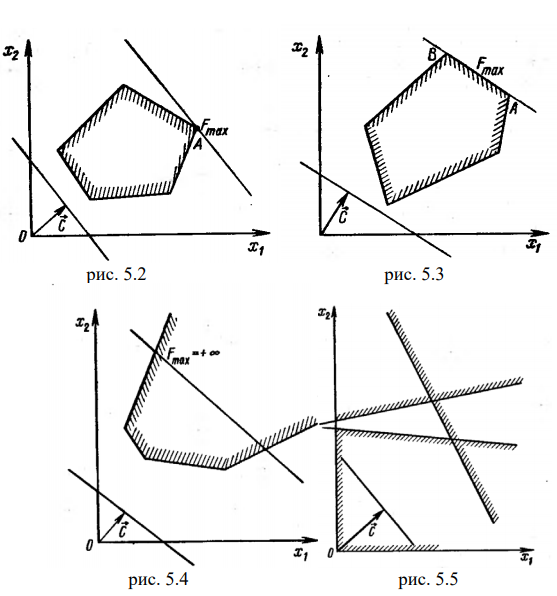
Также отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня 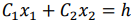
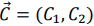
Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Алгоритм графического метода решении задач линейного программирования
- Построить область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, построить нормаль линий уровня
и одну из линий уровня, имеющую общие точки с этой областью.
- Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
- Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.
Пример задачи №1
Пусть имеется два станка 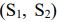
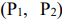
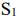

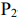
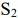

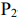
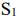
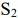

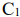
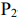
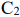

Решение:
Для наглядности сведем условие задачи в таблицу 5.1.
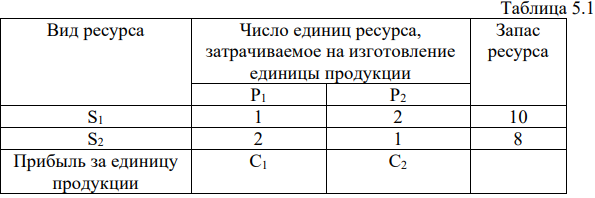
Составим математическую модель задачи. Обозначим через 


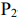
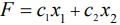


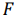
Переменные 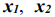

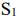
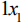
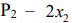
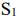


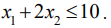
Аналогично можно получить неравенство для станка 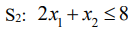


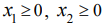
по смыслу задачи. Такие задачи кратко записываются следующим образом:
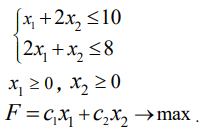
Итак, математическая модель задачи: найти такой план выпуска продукции 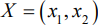
Решения, удовлетворяющие системе ограничений (5.4) и требованиям неотрицательности (5.5), являются допустимыми, а решения, удовлетворяющие одновременно и требованию (5.6) — оптимальными.
Рассмотрим геометрическое истолкование задачи:
Возьмем 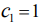
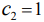
Математическая модель задачи:
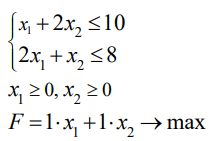
Построение области допустимых решений целевой функции 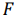
1.Построим прямоугольную систему координат. Так как, 

Рассмотрим первое ограничение:
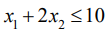
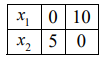
Рассмотрим второе ограничение:
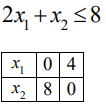
Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют данным ограничениям.
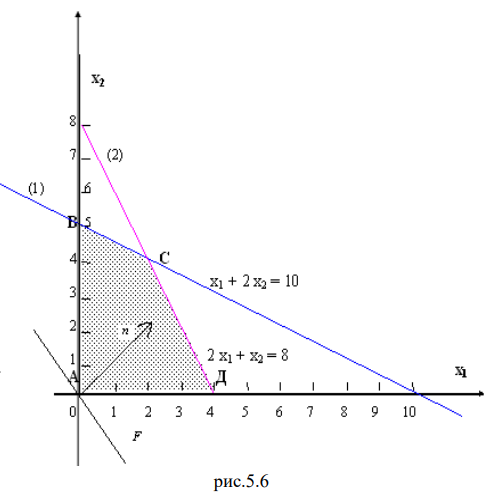
Двумерные задачи линейного программирования решаются графически.
Для случая 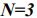
В общем виде, когда в задаче участвуют 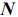
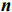
Для решения ЗЛП любой размерности существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Графический метод решения задач линейного программирования
Множество решений системы ограничений задачи ЛП образует область допустимых решений (ОДР).
Графический метод решения задач ЛП основывается на возможности графического изображения ОДР и нахождении среди них оптимального решения. Этот метод применяется для задач ЛП с одной, двумя или тремя переменными, для которых система ограничений стандартна (состоит из неравенств), и задач со многими переменными, для которых система ограничений содержит 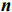
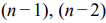
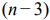
ОДР задачи строится как пересечение областей решений каждого из ограничений и представляет собой выпуклый многогранник (многоугольник, интервал). Область допустимых решений может содержать бесконечное число точек. Для того чтобы найти решение ЗЛП, нужно рассмотреть поведение целевой функции в ОДР.
I. Одномерное пространство переменных
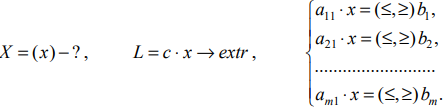
Решение системы ограничений есть пересечение лучей, что определяет интервал решений (ОДР): точку, отрезок, луч или всю числовую прямую.
Значения целевой функции в угловых точках интервала решений определяют наименьшее (наибольшее) значение исследуемой целевой функции, монотонно убывающей (если 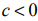
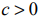
В случае неограниченности ОДР задача ЛП может и не иметь оптимума.
II. Двумерное пространство переменных
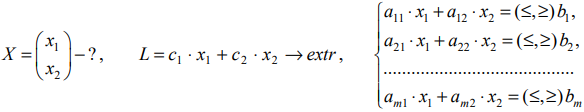
Областью решений линейного неравенства
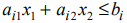
является одна из полуплоскостей, на которые прямая делит всю координатную плоскость. Для того, чтобы определить, какая из двух координатных полуплоскостей является областью допустимых решений неравенства, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку; если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Решение системы ограничений есть пересечение полуплоскостей с граничными прямыми
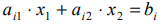
многоугольник решений (ОДР).
Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение
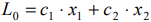
задаёт семейство линий уровня исследуемой целевой функции 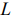
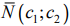
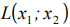
Замечание.
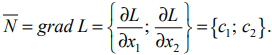
Т. о., если линию уровня 


• Прямая
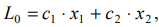
имеющая с многоугольником решений, расположенным по одну сторону от неё, хотя бы одну общую точку, называется опорной. ОДР любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
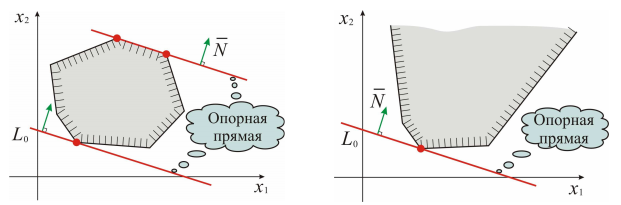
Значение 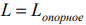
Графически опорная прямая определяет оптимум целевой функции в угловой точке многоугольника решений. Поэтому перебором значений целевой функции во всех угловых точках можно так же выбрать искомый оптимум.
Замечание. Если заданы ограничения неотрицательности переменных, то все построения проводятся в первой четверти.
Особые случаи

Алгоритм графического метода решения задач линейного программирования с двумя переменными
- Находим область допустимых решений из системы ограничений. Если ОДР является пустым множеством, то задача ЛП неразрешима (не имеет решения) в виду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, строим направляющий вектор
прямой
и параллельно ему проводим линию уровня
.
- Строим вектор нормали
перпендикулярно прямой
.
- Линию уровня
перемещаем до положения опорной прямой в направлении вектора
для задач на максимум или в направлении, противоположном
для задач на минимум. Т. е. перемещение проводится до тех пор, пока линия уровня не коснется области допустимых решений. Общая точка (точки) будет точкой экстремума (оптимума) целевой функции в ОДР.
- Находим координаты точки экстремума и значение целевой функции в ней, т. е. оптимум задачи ЛП.
Пример задачи №2
Найти 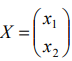
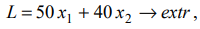
если имеются ограничения:
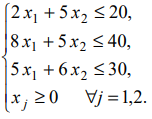
Решение:
Система ограничений определяет граничные прямые:
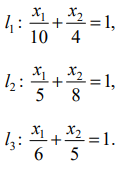
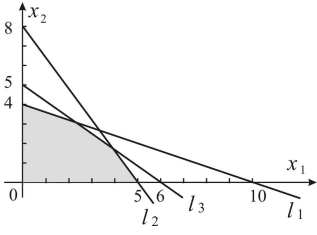
С учётом исходной системы неравенств строим ОДР.
Прямая
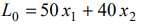
имеет вектор нормали 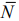
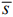
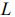
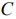
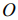
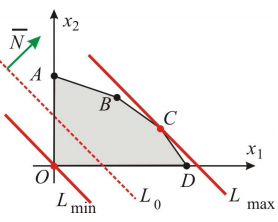
Т. о. имеем:
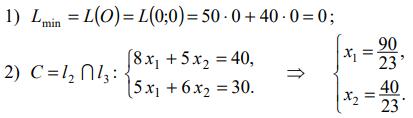
Тогда
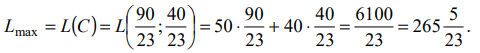
Ответ:
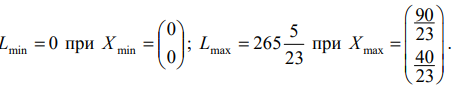
Пример задачи №3
Найти план
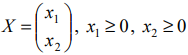
при котором:
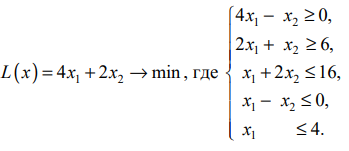
Решение:
Строим ОДР, проводим линии уровня 
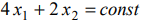
и вектор 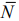
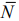
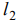
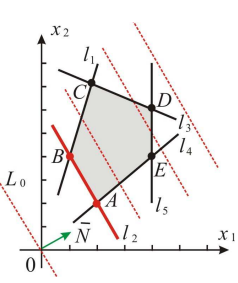
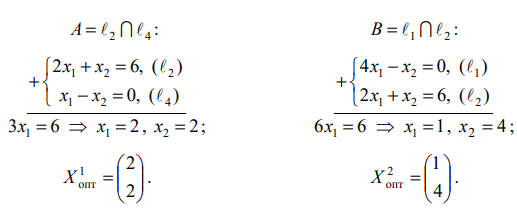
Общее решение (выпуклая линейная комбинация точек отрезка 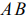
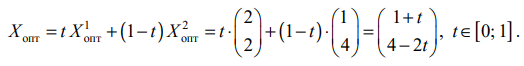
Вычисляем
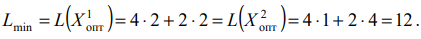
Ответ:
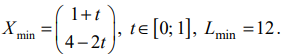
Пример задачи №4
Найти план
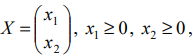
при котором
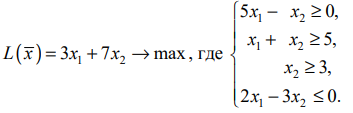
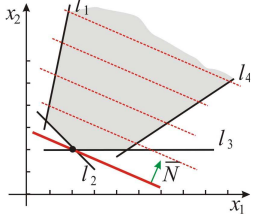
Решение:
Строим ОДР, проводим линию уровня 
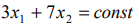
и вектор 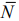
Таким образом, задача ЛП не имеет решения в виду неограниченности целевой функции.
Пример задачи №5
Найти план
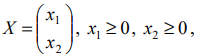
при котором
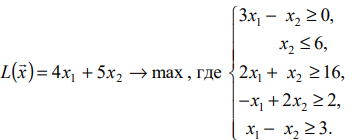
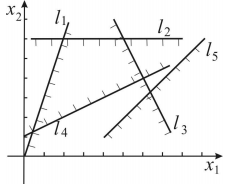
Решение:
Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств. Область допустимых решений задачи является пустым множеством. Задача не имеет решения в виду несовместности системы ограничений.
III. Трёхмерное пространство переменных
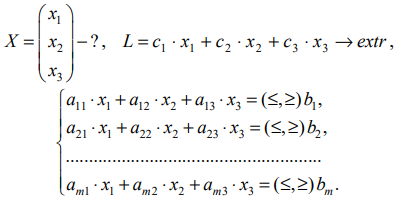
Решение системы ограничений — многогранник решений (ОДР) — пересечение полупространств с граничными плоскостями
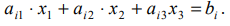
Уравнение
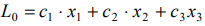
задаёт семейство поверхностей уровня функции 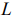
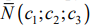
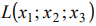
Плоскость
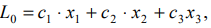
имеющая с многогранником решений, расположенным по одну сторону от нее, хотя бы одну общую точку, называется опорной. Значение 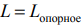
Графический метод в виду большой размерности реальных практических задач ЛП достаточно редко применяется, однако он позволяет уяснить одно из основных свойств ЛП- если в задаче ЛП существует оптимальное решение, то, по крайней мере, одна из вершин допустимой области определяет собой оптимальное решение.
IV. С помощью графического метода может быть решена основная ЗЛП, система ограничений (уравнений) которой удовлетворяет условию 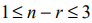
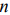
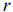
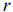
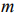
Основной случай: система ограничений содержит 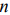
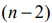
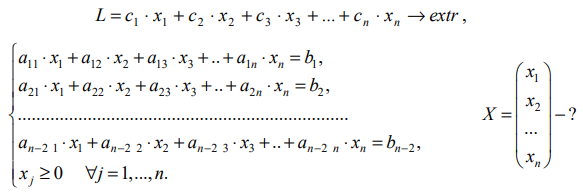
Расширенную матрицу системы с помощью элементарных преобразований строк можно привести к виду:
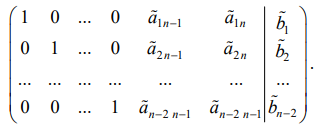
Тогда соответствующая система уравнений примет вид:
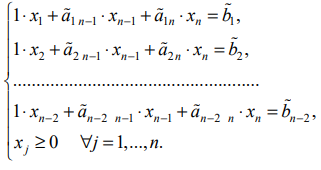
Выражая базисные неизвестные 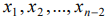
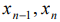
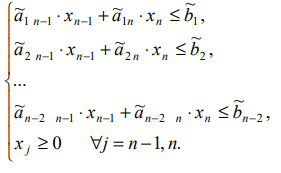
Подставляя полученные выражения для базисных неизвестных в целевую функцию, получим:
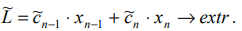
Преобразованная задача ЛП содержит только два неизвестных. Следовательно, возможен графический способ её решения на плоскости.
Найденное решение 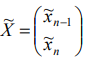
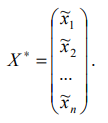
При этом оптимум:
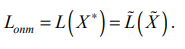
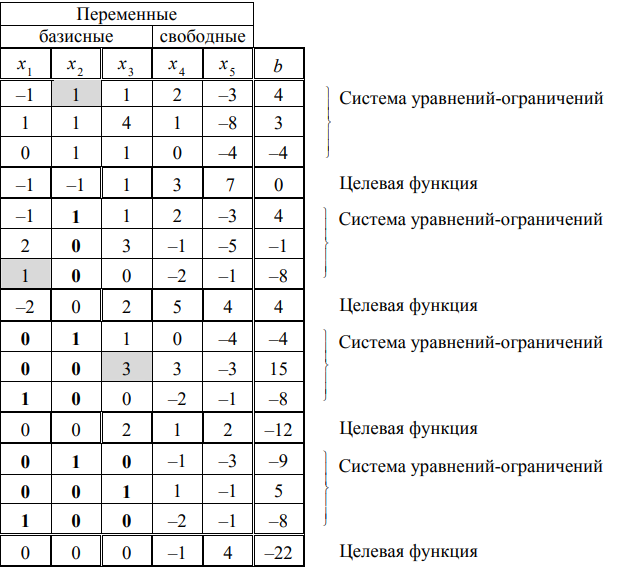
Пример. Решить задачу ЛП:
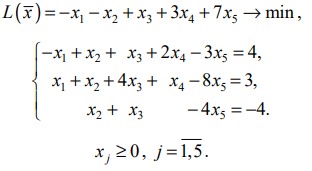
Решение. Метод применим,так как 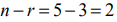
Используя последнюю часть табл., запишем задачу ЛП в преобразованном виде:
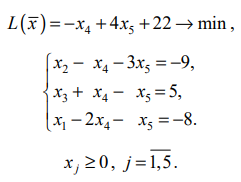
Отбросим в уравнениях-ограничениях неотрицательные базисные переменные 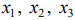
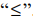
Получим вспомогательную задачу ЛП с двумя переменными:

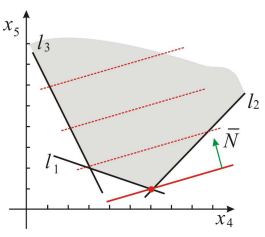
Решаем задачу графическим методом. Свободный член 22 в целевой функции не влияет на отыскание оптимального решения и учитывается только при вычислении значения целевой функции.
Находим оптимальное решение вспомогательной задачи 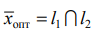
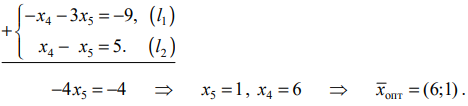
Вычисляем минимальное значение целевой функции
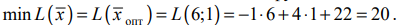
Находим оптимальное решение исходной задачи:
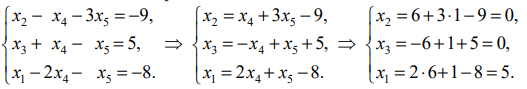
Т. о., получаем:
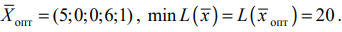
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюЛинейное программирование в ExcelКурсовая работа по линейному программированию
- »
- »
Уравнения с параметром. Задача 18 (С6)
Графический метод в задачах с параметром
Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.
Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.
Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.
Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.
Пример 1
Решить графическим методом уравнение (x^2+3x=5x+3).
Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.
(y=5x+3) – красный график; (y=x^2+3x) – синий график.
Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: ({x}_{1}=-1; {x}_{2}=3).
Ответ: ({x}_{1}=-1; {x}_{2}=3).
Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).
В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac{10+5y}{2}) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):
Все точки, принадлежащие этому графику, будут решениями нашего уравнения. Например, при (x=0) ⇔ (y=-2). Аналогично можно выразить (y=frac{2x-10}{5}). График будет выглядеть так (Рис. 3):
И, разумеется, будет задавать точно такие же пары решений (x) и (y).
Теперь перейдем к уравнениям с параметром. Заметим, что параметр – это обычная переменная, которая ничем не отличается от рассмотренных выше переменных (x) и (y). Поэтому, если мы вместо (y) в уравнении (1) запишем параметр (a), то суть уравнения от этого не поменяется. То есть уравнение (1) можно рассматривать относительно (x) с параметром (y) или наоборот. В дальнейшем параметр будем обозначать за (a).
Разберем уравнение с параметром (6x-5a=15). Будем работать в системе координат ((aOx)). Выразим (x=frac{15+5a}{6}) – это будет общий вид решения. Для того чтобы проиллюстрировать ответ, построим график (x(a)) (Рис. 4).
Пример 2
Найти все значения параметра (a), при которых корни уравнения (6x-5a=15) лежат на отрезке ([-5;5]).
График (x(a)) для этого же примера на рисунке 4.
Иногда для решения удобно построить график зависимости (a(x): a=frac{6x-15}{5}). Давайте так и поступим. Построим график (Рис. 5). И красной областью покажем интервал, который нас интересует по условию задачи. Из рисунка видно, что (a∈[-9;3]) (при (x=5) ⇔(a=3); и при (x=-5) ⇔(a=-9))
На мой взгляд, будет более наглядно, если показывать графический метод на примерах. Поэтому, давайте разберем примеры от простых к сложным, которые могут встретиться на ЕГЭ.
Пример 3
Определить, при каких значениях параметра (a) уравнение (x^2-3x-2a=0) имеет: а) 2 корня; б) 1 корень; в) не имеет корней;
Решение:
1 способ решения:
Приведем уравнение к виду (x^2-3x=2a). И построим графики (y=1/2*(x^2-3x)) (показан красной линией) и (y=a) (синяя линия). Обратите внимание, график (y=a) – это просто семейство прямых параллельных оси (x) в плоскости ((xOy)) (Рис. 6). Точки пересечения красной линии с семейством синих линий – это корни нашего уравнения. Если, например, (a=5), то графики (y=5) и (y=1/2*(x^2-3x)) имеют две общие точки, а значит, и два решения. При (a=-1.125) оба графика имеют только одну общую точку ((1.5;-1.125)) – это единственное решение.
Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.
2 способ решения:
Таким же образом можно решить данное уравнение, построив графики в плоскости ((xOa)). Для этого выразим (a=1/2*(x^2-3x).)
Различным значениям параметра (a) можно поставить значения искомого (x), для это проведем горизонтальные линии.
Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.
Пример 4
Решить уравнение: (cos^2x-2 cosx+a=0)
Сделаем замену (t=cosx,) тогда ( t^2-2t+a=0,) при (t∈[-1;1].)
Построим в плоскости ((tOa)) график нашей функции (a=2t-t^2:)
Точки пересечения горизонтальных (фиолетовых) прямых с графиком нашей функции соответствуют решениям. Но (t∈[-1;1]), покажем это при помощи зеленой области (Рис.8). Таким образом, нас устраивают решения, которые принадлежат кусочку параболы, попавшей в зеленую область. Как видно из рисунка, (a) может принимать значения (a∈[-3;1]), и каждому значению (a) из этой области соответствует единственное решение. Найдем его, решив уравнение (t^2-2t+a=0;)
$$ {t}_{1}=frac{4-sqrt{4-4a}}{2};$$
$$ {t}_{2}=frac{4+sqrt{4-4a}}{2}.$$
({t}_{2}) не подходит, так как он не удовлетворяет условию (t∈[-1;1]).
Сделаем обратную замену:
$$ cosx=frac{4-/sqrt{4-4a}}{2};$$
$$ x=±arccos(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$
Ответ: При (a∈[-3;1]); $$ x=±arccos(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$
Пример 5
Решить уравнение (sin^4x-(a-1) sin^2x-(2a+2)=0.)
Решение:
Сделаем замену: (t=sin^2x ) ⇔ (t^2-(a-1)t-2a-2=0;)
Обратите внимание: (t∈[0;1];)
Выразим (a=frac{t^2+t-2}{t+2}=frac{(t+2)(t-1)}{t+2}=t-1),при (t≠-2).
Таким образом, необходимо решить систему:
$$ begin{cases} a=t-1, \t∈[0;1]. end{cases} $$
Построим решения данной системы на координатной плоскости ((tOa)).
Красной линией показан график (a=t-1), а зеленая область показывает интервал, в котором могут лежать корни. Выделенная часть графика соответствует всем возможным корням при (a∈[-1;0].) Если (a) не принадлежит этому интервалу, то корней нет. Найдем эти решения:
$$ t=a+1,$$ $$sin^2x=a+1,$$ $$ 1-cos2x=a+1,$$ $$ cos2x=-a,$$
$$x=±1/2$$ $$ arccos(-a)+πn,n∈Z.$$
Ответ:При (a∈[-1;0];) $$ x=±1/2 arccos(-a)+πn,n∈Z.$$
Пример 6
Решить уравнение (9^{-|x+1|}-3^{1-|x+1|}-a=0.)
Сделаем замену (t=3^{-|x+1|}), получим (t^2-3t-a=0), где (t∈(0;1].)
Построим график функции (a(t)=t^2-3t), при (t∈(0;1]) в системе координат ((tOa)).
Зеленой областью покажем допустимый интервал, в котором могут находиться корни. Выделенная часть параболы соответствует корням нашего уравнения при (a∈[-2;0)). Таким образом, при (a<-2) и (a≥0) корней нет.
Решим уравнение (t^2-3t-a=0).
При (a∈[-2;0)) $$ {t}_{1}=frac{3-sqrt{9+4a}}{2};$$ $$ {t}_{2}=frac{3+sqrt{9+4a}}{2},$$ так как (t∈(0;1]), то ({t}_{2}) не подходит.
Сделаем обратную замену:
$$ 3^{-|x+1|}=frac{3-sqrt{9+4a}}{2};$$
$$-|x+1|=log_3 (frac{3-sqrt{9+4a}}{2});$$
$$|x+1|=-log_3 (frac{3-sqrt{9+4a}}{2});$$
$$x=-1±log_3 (frac{3-sqrt{9+4a}}{2}).$$
Ответ: (x=-1±log_3 (frac{3-sqrt{9+4a}}{2})) при (a∈[-2;0).)
Пример 7
Решить уравнение (sqrt{a(3^x+1)+9}=2-3^x.)
Сделаем замену (t=3^x, t>0) ⇔ (sqrt{a(t+1)+9}=2-t.)
Данному уравнению равносильна система:
$$ begin{cases} a(t+1)+9=(2-t)^2, \ 2-t ≥ 0, \ t > 0. end{cases} $$
$$ begin{cases} a=frac{(t-5)(t+1)}{t+1}, \ 0 < t ≤ 2. end{cases} $$
$$ begin{cases} a = t-5, \ 0 < t <= 2. end{cases}$$
Построим множество точек, которые удовлетворяют полученной системе:
При (a∈(-5;-3]) ⇔ (t=a+5,) сделаем обратную замену 3(^x=a+5), ⇔ (x=log_3 (a+5).)
При (a∈(-∞;-5]∪(-3;+∞)) корней нет.
Ответ: При (a∈(-5;-3]) ⇔ ( x=log_3 (a+5).)
Пример 8
Решить неравенство (9^x-(a-1) 3^x-a≥0)
Сделаем замену: (t=3^x,) ⇔ (t>0;)
Получаем
$$ begin{cases} t^2-(a-1)t-a≥0, \t>0. end{cases} $$
$$ t(t+1)≥a(t+1); $$
Заметим, что решение (t=-1) не подходит, так как (t>0). Поделим наше неравенство на
(t+1). Так как (t+1>0), то знак неравенства не меняется. Будьте внимательны! В случае, когда нам неизвестен знак выражения, на которое мы делим неравенство, необходимо рассмотреть два случая, когда выражение отрицательно (меняем знак неравенства) и когда положительно (не меняем).
$$ begin{cases} t≥a, \t>0. end{cases} $$
Построим график, получившейся системы неравенств на плоскости ((tOa)).
Оранжевой областью выделено решение первого неравенства системы, синей областью – второго неравенства. Их пересечение – это решение все системы.
Получаем, что при (a≤0) $$ t∈(0;+∞) ⇔ 3^x>0 ⇔ x∈(-∞;+∞)$$
При ( a>0) $$ t∈[a;+∞) ⇔ 3^x≥a ⇔ x≥log_3 a.$$
Ответ: при( a≤0) $$ x∈(-∞;+∞)$$
при (a>0) $$ x≥log_3 a.$$
Пример 9
Найти все значения параметра, при которых функция
$$ f(x)=ln{(p-1)*3^x-4*3^{x/2}+(p+2)} $$
определена при всех (x∈R.)
Решение:
Наша функция будет определена при условии, что выражение под логарифмом будет больше нуля:
$$ (p-1)*3^x-4*3^{x/2}+(p+2) > 0.$$
Сделаем замену: (t=3^{x/2},t > 0).
Получим
$$ begin{cases} (p-1)*t^2-4*t+p+2>0, \ t>0. end{cases} $$
Если (p=1),
$$ begin{cases} -4t+3>0, \ t>0; end{cases} $$
$$ begin{cases} t<0.75, \ t>0; end{cases} $$
Сделаем обратную замену: (0 < 3^{x/2} < 0.75.) Очевидно, что это неравенство не будет выполняться при всех (x), как того требует условие задачи.
Если (p≠-1,)
$$ begin{cases} pt^2-t^2-4t+p+2>0, \t>0; end{cases} $$
$$ begin{cases} p(t^2+1)>t^2+4t-2, \t>0; end{cases} $$
$$ begin{cases} p > frac{t^2+4t-2}{1+t^2}, \t>0. end{cases} $$
Теперь нужно построить график функции (p=frac{t^2+4t-2}{1+t^2}). Для этого исследуем функцию на монотонность и найдем экстремумы.
Найдем производную:
$$ p^{‘}=frac{-4(t-2)(t+1/2)}{1+t^2}^2 ;$$
Как видно из рисунка 13, точка ((-1/2;-3)) – точка минимума; а ((2;2)) – точка максимума.
Найдем асимптоты. Напомню, что вертикальные асимптоты бывают только в точках разрыва, поэтому наличие вертикальной асимптоты можно проверить, взяв предел от функции в точке разрыва. В нашем случае нет точек разрыва, поэтому вертикальных асимптот не будет.
График функции будет иметь горизонтальные асимптоты, если (lim_{t→+∞} p(t)=const) или (lim_{t→-∞} p(t)=const.) Проверим нашу функцию:
$$lim_{t→∞} frac{t^2+4t-2}{1+t^2}=1.$$
Значит, есть горизонтальная асимптота (p=1).
И асимптоты могут быть наклонными: Прямая (p=kt+b) будет наклонной асимптотой к нашему графику ( p=frac{t^2+4t-2}{1+t^2}), если существуют пределы (lim_{t→∞} {frac{p(t)}{t}}=k) и (lim_{t→∞} {(p(t)-kt)}=b.)
В нашей случае наклонной асимптоты не будет.
Подробнее можно посмотреть здесь.
Из полученных данных построим примерный график функции (p=frac{t^2+4t-2}{1+t^2}) :
На рисунке 14 при помощи штриховки показаны точки, которые будут корнями системы
$$ begin{cases} p < frac{t^2+4t-2}{1+t^2}, \ t > 0. end{cases}$$
Если (p>2),то (t>0) или (3^(x/2)>0), а значит и функция (f(x)) определена при любых (x∈R).
Ответ: (p∈(2;+∞).)
Пример 10
Найти при каких значениях параметра (a) система
$$ begin{cases} (2+log_{3} {(frac{1}{9} a+frac{1}{3}-frac{2}{9} y)}=log_{3}{(2a+x-y-6)}, \ sqrt{x}=2+y. end{cases}$$
имеет решение?
Решение:
Преобразуем исходную систему:
$$ begin{cases} a+3-2y=2a+x-y-6, \ frac{1}{9} a+frac{1}{3}-frac{2}{9} y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=3-2y-(2+y)^2+y+6, \ a+3-2y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=-y^2-5y+5, \ a>2y-3, \ x=(2+y)^2. end{cases}$$
Построим график полученной системы:
Из рисунка 15 видно, что (a∈(-19;11.25].)
Ответ: (a∈(-19;11.25].)
Пример 11
Найти значения параметра a, при которых система
$$ begin{cases} x+y-1=0, \ 2y=sqrt{ax-1} end{cases} $$
имеет единственное решение.
Решение:
Из второго уравнения следует, что (x=frac{y^2+1}{a}).
Тогда
$$ begin{cases} frac{y^2+1}{a}+y-1=0, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
$$ begin{cases} a=frac{y^2+1}{1-y}, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
Обратите внимание, что (y=1), (x=0) не может быть решением системы при любых значениях параметра (a).
Исследуем, полученную зависимость (a=frac{y^2+1}{1-y}) на монотонность и найдем экстремумы.
$$ {a}^{‘}=frac{2y(1-y)+(y^2+1)}{1-y}^2 ;$$
$$ {a}^{‘}=frac{-y^2+2y+1}{(1-y)^2} =-frac{(y-1-sqrt{2})(y-1+sqrt{2})}{(1-y)^2} ;$$
Из рисунка 16 видно, что ({y}_{1}=1-sqrt{2}) – точка минимума функции (a=frac{y^2+1}{1-y};) Ей соответствует значение (a=2sqrt{2}-2).
({y}_{2}=1+sqrt{2}) – точка максимума. (a=-2sqrt{2}-2).
Найдем асимптоты (см. пример 9):
$$lim_{y→1} {frac{y^2+1}{1-y}}=∞;$$
Значит (y=1) – вертикальная асимптота.
$$lim_{y→∞} {frac{y^2+1}{1-y}}=∞;$$
Значит горизонтальные асимптоты отсутствуют.
И проверим на наличие наклонных асимптот:
$$ lim_{y→∞} {frac{a(y)}{y}}=lim_{y→∞} {frac{(frac{y^2+1}{1-y})}{y}}=lim_{y→∞} {frac{y^2+1}{y-y^2 }}=$$
$$=lim_{y→∞} {frac{1+frac{1}{y^2}}{-1+frac{1}{y}}}=-1=k;$$
$$lim_{y→∞} {(a(y)-ky)}=lim_{y→∞} {frac{y^2+1}{1-y}+y}=lim_{y→∞} {frac{1+y}{1-y}}=-1;$$
Получим уравнение наклонной асимптоты (a=-y-1).
Красным показа график функции (a=frac{y^2+1}{1-y};) Зеленым – показаны найденные асимптоты; Синяя область удовлетворяет условию (y≥0);
Выделенная бардовым часть графика указывает на возможные корни исходной системы. По условию задачи необходимо найти такие значения параметра (a), чтобы система имела единственное решение. Таким образом, из рисунка следует, что при (a=-2sqrt{2}-2) и (a ≥ 1) система будет иметь единственное решение.
Ответ: (a=-2sqrt{2}-2) и (a≥1)
Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.
Использование свойств функции при решении заданий с параметром из ЕГЭ по математике профильного уровня. Симметрия функций и приемы решения.
Квадратные уравнения с параметром. Умение исследовать квадратный многочлен поможет решать задачи с параметром аналитическим методом. Квадратное уравнение решается при помощи дискриминанта или теоремы Виета.
Разбор линейных уравнений с параметром. Для того, чтобы решить такое уравнение, нужно найти все x при всех значениях параметра a
Решение показательных и логарифмических уравнений с параметром
Знакомимся с понятием параметра в уравнениях. Краткие рекомендации к выполнению.






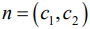 и одну из линий уровня, имеющую общие точки с этой областью.
и одну из линий уровня, имеющую общие точки с этой областью.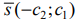 прямой
прямой 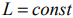 и параллельно ему проводим линию уровня
и параллельно ему проводим линию уровня 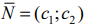 перпендикулярно прямой
перпендикулярно прямой