Материал из Викиконспекты
Перейти к: навигация, поиск
Содержание
- 1 Теорема о существовании простого пути в случае существования пути
- 1.1 Конструктивное доказательство
- 1.2 Неконструктивное доказательство
- 2 Замечания
- 3 См. также
Теорема о существовании простого пути в случае существования пути
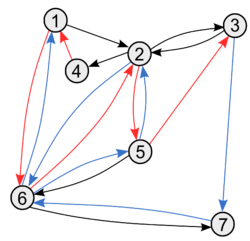
Ориентированный граф. Красным выделен вершинно-простой путь. Синим — реберно-простой путь.
| Теорема: | ||
| Доказательство: | ||
Конструктивное доказательствоРассмотрим путь: между вершинами и , причём . Возьмем — вершина на данном пути. Если она лежит на данном пути более одного раза, то она принадлежит какому-то (не обязательно простому) циклу . Удалим этот цикл. Получившаяся последовательность вершин и рёбер графа останется путём , но не будет содержать найденный цикл. Начнём процесс с вершины и будем повторять его каждый раз для следующей вершины нового пути, пока не дойдём до последней. По построению, получившийся путь будет содержать каждую из вершин графа не более одного раза, а значит, будет вершинно-простым. Неконструктивное доказательствоВыберем из всех путей между данными вершинами путь наименьшей длины.
Тогда в нём содержатся две одинаковые вершины , . Удалим из исходного пути отрезок от до , включительно. Конечная последовательность также будет путём от до и станет короче исходной. Получено противоречие с условием: взятый нами путь оказался не кратчайшим. Значит, предположение неверно, выбранный путь — простой. |
||
| Утверждение: |
|
Данная теорема не верна для случая . |
| В данном случае мы не сможем найти вершинно-простой путь, так как путь начинается и заканчивается в одной и той же вершине. |
Замечания
- Так как вершинно-простой путь всегда является рёберно-простым, данная теорема справедлива и для рёберно-простого пути.
- Теорема может быть сформулирована как для ориентированного, так и для неориентированного графа.
См. также
- Основные определения теории графов
- Теорема о существовании простого цикла в случае существования цикла
Поиск в глубину, поиск в ширину, алгоритмы Дейкстры и А* — это один и тот же алгоритм
Время на прочтение
7 мин
Количество просмотров 9.5K

В алгоритмических задачах на графах мы часто используем четыре известных алгоритма. Два из них — это алгоритмы обхода графа: Поиск в ширину и Поиск в глубину. Ещё два, A* и алгоритм Дейкстры, используются для нахождения оптимального пути внутри графа от одного узла до другого.
Я покажу, что все эти четыре алгоритма — это по сути один и тот же алгоритм. И вся разница между ними — только в разных структурах данных, используемых для хранения непосещённых узлов графа.
Задачка для примера
Сначала рассмотрим задачу поиска пути в небольшом простом графе:

Двигаясь от узла к узлу, мы хотим найти путь от start до target.
Самое очевидное, что мы можем сделать, — это использовать один из известных алгоритмов обхода графа: поиск в глубину или в ширину. Опишем типовой алгоритм поиска пути между двумя узлами в общем виде.
Тот самый один алгоритм
Мы начинаем с узла start и можем двигаться по рёбрам графа от узла к узлу. На каждой итерации алгоритма у нас есть некоторый узел, который мы называем текущим, и именно на нём сосредоточено наше внимание. Мы исследуем его соседей, то есть узлы, к которым потенциально можем перейти на следующей итерации.
Помимо текущего узла нам нужно где-то хранить ещё не посещённые узлы, куда можно перейти на следующей итерации. Это узлы, которые мы уже встречали как соседей, но не рассматривали в качестве текущего. Хранить такие узлы будем в специальном хранилище, которое назовём nodes_storage.
Для текущего узла всегда проверяем, является ли он целевым. Если да, значит мы прибыли: путь от start до target найден, и алгоритм поиска может быть прерван. В противном случае мы должны рассмотреть узлы, соседние с текущим, и добавить их в хранилище nodes_storage.
Чтобы не запутаться и не ходить по одним и тем же узлам несколько раз, мы будем раскрашивать узлы графа следующим образом:
-
белый — мы ещё не посещали и даже не встречали этот узел;
-
серый — мы встречали этот узел в качестве соседа и уже добавили его в
nodes_storage, но ещё не посещали его; -
чёрный — этот узел посещён и больше не нуждается в анализе.
Изначально все узлы белые. Если мы встречаем узел как соседа, мы окрашиваем его в серый. И только когда мы посетили узел, обработали всех его соседей, и он больше не нужен — красим его в чёрный цвет.

Важно отдельно рассмотреть случай, если сосед текущего узла имеет цвет, отличный от белого; то есть мы встречаем этот узел уже не в первый раз. Это означает, что мы уже приходили в узел по другому пути, и теперь нужно решить, какой из путей нам подходит больше. Поскольку зачастую мы хотим найти кратчайший путь, то конфликт решается просто: нужно выбрать путь с кратчайшим расстоянием до этого узла от start.
Переходим к коду
Когда мы описали алгоритм в общих чертах, пришло время погрузиться в код — напишем этот алгоритм на языке Python.
Пока мы не будем прямо указывать структуру данных для хранения непосещённых узлов, назвав её AbstractNodeStorageClass. Нам нужно только знать, что этот класс содержит три метода: insert — для добавления узла в хранилище, get_first — для извлечения одного элемента из хранилища и is_empty — для проверки, не опустело ли хранилище.
Получается вот такой код:
def find_path(
graph: Graph,
start_node: int,
target_node: int,
nodes_storage_structure_name: AbstractNodeStorageClass,
) -> bool:
"""
Универсальный алгоритм обхода графа в поисках пути между
начальным (start) и целевым (target) узлами, используя
структуру графа и вспомогательную структуру nodes_storage.
Возвращает True, если путь найден.
"""
# красим все узлы в белый
color = ['white'] * graph.number_of_nodes()
# в начале поиска расстояние до всех узлов кроме начального равны ∞
dist = [float('Inf')] * graph.number_of_nodes()
dist[start_node] = 0
# положим start_node внутрь nodes_storage
nodes_storage.insert(start_node)
# цикл пока внутри nodes_storage есть узлы
while not nodes_storage.is_empty():
current_node = nodes_storage.get_first()
if current_node == target_node:
# конец поиска, целевой узел найден, а значит и путь до него
return True
# возьмём всех соседей текущего узла
neighbours = list(graph.adj[current_node])
for node_to_go in neighbours:
# если этот узел встречается впервые
if color[node_to_go] == 'white':
# красим его в серый
color[node_to_go] = 'grey'
# обновляем расстояние от стартового узла
dist[node_to_go] = dist[current_node] +
graph.get_edge_data(node_to_go, current_node)['weight']
# добавляем узел в nodes_storage
nodes_storage.insert(node_to_go)
else:
# иначе нам нужно решить конфликт дублирования (два пути
# к одному узлу). Выбираем из двух путей более короткий.
weight_from_current_node = graph.get_edge_data(node_to_go, current_node)['weight']
if dist[current_node] + weight_from_current_node < dist[node_to_go]:
dist[node_to_go] = dist[current_node] + weight_from_current_node
# красим текущий узел в чёрный, он нам больше не интересен
color[current_node] = 'black'
return FalseВот и всё! Это единственный алгоритм, который нам понадобится. Подставляя разные структуры данных в качестве хранилища, мы получим разные классические алгоритмы поиска пути в графе.
Поиск в глубину
Если мы используем стек в качестве хранилища непосещённых узлов, то описанный выше алгоритм превращается в Поиск в глубину.
Давайте проверим. Возьмём класс, который реализует хранение непосещённых узлов по принципу стека. То есть метод get_first возвращает элемент, добавленный последним:
Код стека
class Stack(AbstractNodeStorageClass):
"""
Стек работает по принципу LIFO - первым возвращается
последний добавленный элемент.
"""
def __init__(self):
self.nodes = []
def get_first(self):
return self.nodes.pop()
def insert(self, node_number):
self.nodes.append(node_number)
def is_empty(self):
return len(self.nodes) == 0Результат использования этого класса показан ниже. На каждой итерации мы копаем как можно глубже в поисках целевого узла.

Чтобы поиграть в этой анимации с кнопками управления, жми сюда.
Поиск в ширину
Чтобы выполнить Поиск в ширину, нужно вместо стека использовать очередь:
Код очереди
class Queue(AbstractNodeStorageClass):
"""
Очередь работает по принципу FIFO - первым возвращается
элемент, добавленный раньше всех.
"""
def __init__(self):
self.nodes = []
def get_first(self):
return self.nodes.pop(0)
def insert(self, node_number):
self.nodes.append(node_number)
def empty(self):
return len(self.nodes) == 0Единственная разница со стеком заключается в том, что первый элемент берётся с помощью функции pop(0) вместо того, чтобы брать последний элемент с помощью pop(). Результат работы алгоритма с такой структурой показан ниже.

Чтобы поиграть в этой анимации с кнопками управления, жми сюда.
Теперь мы проходим по всем узлам, расположенным на одной горизонтали, т. е. перебираем узлы как можно шире. Также обратите внимание, как зелёный узел target проходит через очередь от входа до выхода.
Алгоритм Дейкстры
Изначально алгоритм Дейкстры был разработан для нахождения кратчайшего пути к заданному узлу (и одновременно ко всем остальным), начиная с начального узла start. Мы можем применить его к нашей задаче поиска пути между двумя узлами.
Но перед этим, чтобы сделать задачу интереснее, укажем для каждого ребра графа его длину:

Это означает, что расстояние между узлами 0 и 1 в три раза больше, чем расстояние между узлами 0 и 2.
Теперь запишем структуру данных хранения узлов для алгоритма Дейкстры. В алгоритме Дейкстры мы каждый раз выбираем непосещённый узел с наименьшим расстоянием до начального узла, поэтому будем использовать очередь с приоритетом.
Основное отличие этой очереди от обычной состоит в том, что в методе get_first мы выбираем узел с наименьшим расстоянием от начального узла. В Python есть уже готовая реализация очереди с приоритетом внутри встроенной библиотеки heapq:
Код очереди с приоритетом
class DijkstraQueue(AbstractNodeStorageClass):
"""
Очередь с приоритетом. Внутри метода get_first() выбирается
узел с минимальным расстоянием distance от начального узла.
"""
def __init__(self, distances):
self.nodes = []
self.distances = distances
def get_first(self):
closest_node_distance, closest_node = heappop(self.nodes)
return closest_node
def insert(self, element):
heappush(self.nodes, (self.distances[element], element))
def is_empty(self):
return len(self.nodes) == 0Результат алгоритма на такой структуре данных выглядит следующим образом:

Чтобы поиграть в этой анимации с кнопками управления, жми сюда.
Интересно, что в трёх случаях мы получили три разных пути, хотя и действовали в рамках одного графа и с помощью одного алгоритма. Изменялась только структура данных.
Усложним задачу до лабиринта
Прежде чем идти дальше, давайте усложним задачу и заменим простой граф лабиринтом. Начальный и конечный узлы — соответственно вход и выход из лабиринта, а остальная часть доступного пространства заполнена узлами графа. Наша цель — найти путь от входа к выходу через граф.
Сразу посмотрим, как решает эту задачу алгоритм Дейкстры. Не меняем ни алгоритм, ни структуру данных из предыдущего пункта — только граф.

Чтобы поиграть в этой анимации с кнопками управления, жми сюда.
Мы видим, как алгоритм последовательно перебирает узлы. При этом каждый следующий узел выбирается по принципу приоритетной очереди — как ближайший к начальному узлу start.
Используя этот подход, алгоритм перебирает почти все узлы в лабиринте. Но интуитивно кажется, что мы можем добраться до финиша быстрее, если будем целиться в сторону конечного узла target. Именно такие рассуждения привели к созданию алгоритма A*.
Алгоритм А*
Алгоритм А* учитывает как расстояние до начального узла, так и примерную оценку расстояния до целевого узла. Эта приблизительная оценка эвристически рассчитывается как евклидово расстояние от выбранного узла до целевого. Единственное изменение, которое нам нужно сделать, — это вычисление приоритета узла в очереди приоритетов. Вот код:
Код очереди с приоритетом (А*)
class AStarQueue(AbstractNodeStorageClass):
"""
Очередь с приоритетом для алгоритма А*.
В методе get_first() выбирается узел, для которого минимальна
сумма расстояния до начального узла и оценки расстояния
(оценивается евклидова норма) до конечного узла.
"""
def __init__(self, graph, distances, goal_node):
self.nodes = []
self.graph = graph
self.x_goal, self.y_goal = graph.nodes[goal_node]['position']
self.distances = distances
def calc_heuristic(self, node):
x_node, y_node = self.graph.nodes[node]['position']
estimated_distance_to_goal = sqrt(
(x_node - self.x_goal) ** 2 +
(y_node - self.y_goal) ** 2
)
return estimated_distance_to_goal
def get_first(self):
optimal_node_value, optimal_node = heappop(self.nodes)
return optimal_node
def insert(self, element):
heappush(self.nodes,
(self.distances[element] +
self.calc_heuristic(element), element)
)
def is_empty(self):
return len(self.nodes) == 0Здесь мы видим дополнительный метод calc_heuristic(), оценивающий расстояние до целевого узла. Теперь отдадим структуру данных алгоритму и получим следующий результат:

Чтобы поиграть в этой анимации с кнопками управления, жми сюда.
Обратите внимание, что благодаря использованию эвристики алгоритм A* быстрее находит правильный ответ — всего за 80 шагов вместо 203.
Вместо заключения
В случае с поиском пути в графе можно применять четыре разных классических алгоритма, которые на самом деле один — разница только в структуре данных. Наглядно это показано в таблице:

Иногда нам кажется, что алгоритмы и структуры данных – это два разных раздела computer science, но на практике они очень тесно связаны, и описанное выше – яркое тому подтверждение. На курсе “Алгоритмы и структуры данных” в Яндекс Практикуме мы стараемся не только научить людей писать эффективные алгоритмы, но и показать эту важную связь.
Если вам понравилась статья, вы можете посмотреть полный туториал и поиграться с кодом в google colab, либо посмотреть весь код на github.
У этого термина существуют и другие значения, см. Путь.
![]()
Путь в графе — последовательность вершин, в которой каждая вершина соединена со следующей ребром.
Определения[править | править код]
Пусть G — неориентированный граф.
Путём в G называется такая конечная или бесконечная последовательность рёбер и вершин[1]

что каждые два соседних ребра 


Таким образом, можно написать

Отметим, что одно и то же ребро может встречаться в пути несколько раз.
Если нет рёбер, предшествующих 



Любая вершина, принадлежащая двум соседним рёбрам, называется внутренней.
Так как рёбра и вершины в пути могут повторяться, внутренняя вершина может оказаться начальной или конечной вершиной.
Если начальная и конечная вершины совпадают, путь называется циклическим.
Путь называется цепью, а циклический путь — циклом, если каждое его ребро встречается не более одного раза (вершины могут повторяться).
Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется.
Цикл с концом 

К сожалению, эта терминология не вполне устоялась. Уилсон[2] писал:
То, что мы назвали маршрутом, называют также путём, рёберной последовательностью.
Цепь называют путём, полупростым путём; простую цепь – цепью, путём, дугой, простым путём, элементарной цепью; замкнутую цепь – циклической цепью, контуром; цикл – контуром, контурной цепью, простым циклом, элементарным циклом.
— [3][4][5]

Ориентированный цикл. Без стрелок это просто цикл. Это не простой цикл, поскольку синие вершины используются дважды.
Пути, цепи и циклы являются фундаментальными концепциями теории графов и определяются во вводной части большинства книг по теории графов. Смотрите, например, Бонди и Марти[6], Гиббонс[7] или Дистель[8].
Различные виды путей[править | править код]
Путь, для которого никакие рёбра графа не соединяют две вершины пути, называется индуцированным путём.
Простая цепь, содержащая все вершины графа без повторений, известна как Гамильтонов путь.
Простой цикл, содержащий все вершины графа без повторений, известен как Гамильтонов цикл.
Цикл, получаемый добавлением ребра графа к остовному дереву исходного графа, известен как Фундаментальный цикл.
Свойства путей[править | править код]
Два пути вершинно независимы, если они не имеют общих внутренних вершин. Аналогично два пути рёберно независимы, если они не имеют общих внутренних рёбер.
Длина пути — это число рёбер, используемых в пути, при этом многократно используемые рёбра считаются соответствующее число раз. Длина может равняться нулю, если путь состоит только из одной вершины.
Взвешенный граф ставит в соответствие каждому ребру некоторое значение (вес ребра). Весом пути во взвешенном графе называется сумма весов рёбер пути. Иногда вместо слова вес употребляется цена или длина.
Примечания[править | править код]
- ↑ Оре, 2008, 2.1 Маршруты, цепи и простые цепи, с. 34—38.
- ↑ Уилсон, 1977, Новые определения, с. 37.
- ↑ Харари, 2003, Маршруты и связность, с. 232.
- ↑ Харари, 2003, Орграфы и соединимость., с. 232.
- ↑ Кристофидес, 1978, Глава 1. Введение 2. Пути и маршруты, с. 13.
- ↑ Bondy, Murty, 1976.
- ↑ Gibbons, 1985.
- ↑ Дистель, 2002.
См. также[править | править код]
|
|
Литература[править | править код]
- Харари Ф. Теория графов. — М.: УРСС, 2003. — 300 с. — ISBN 5-354-00301-6.
- Оре, Ойстин. Теория графов. — М.: УРСС, 2008. — 352 с. — ISBN 978-5-397-00044-4.
- Н. Кристофидес. Теория графов. Алгоритмический подход. — 2-е.. — М.: Издательство «Мир», 1978.
- Р. Уилсон. Введение в теорию графов. — М.: Издательство «Мир», 1977. — (Современная математика. Вводные курсы).
- J.A. Bondy, U.S.R. Murty. Graph Theory with Applications. — North Holland, 1976. — С. 12—21. — ISBN 0-444-19451-7.
- Рейнгард Дистель. Теория графов. — Новосибирск: Изд-во Ин-та математики, 2002. — ISBN 5-86134-101-X.
- Gibbons, A. Algorithmic Graph Theory. — Cambridge University Press, 1985. — С. 5—6. — ISBN 0-521-28881-9.
- Bernhard Korte, László Lovász, Hans Jürgen Prömel Alexander Schrijver. Paths, Flows, and VLSI-Layout. — Algorithms and Combinatorics 9, Springer-Verlag, 1990. — ISBN 0-387-52685-4.
Ссылки[править | править код]
- Weisstein, Eric W. Path Graph (англ.) на сайте Wolfram MathWorld.
%saved0% Граф — это (упрощенно) множество точек, называемых вершинами, соединенных какими-то линиями, называемыми рёбрами (необязательно все вершины соединены). Можно представлять себе как города, соединенные дорогами.
Любое клетчатое поле можно представить в виде графа. Вершинами будут являться клетки, а ребрами — смежные стороны клеток.
Наглядное представление о работе перечисленных далее алгоритмов можно получить благодаря визуализатору PathFinding.js.
Поиск в ширину (BFS, Breadth-First Search)
Алгоритм был разработан независимо Муром и Ли для разных приложений (поиск пути в лабиринте и разводка проводников соответственно) в 1959 и 1961 годах. Этот алгоритм можно сравнить с поджиганием соседних вершин графа: сначала мы зажигаем одну вершину (ту, из которой начинаем путь), а затем огонь за один элементарный промежуток времени перекидывается на все соседние с ней не горящие вершины. В последствие то же происходит со всеми подожженными вершинами. Таким образом, огонь распространяется «в ширину». В результате его работы будет найден кратчайший путь до нужной клетки.
Алгоритм Дейкстры (Dijkstra)
Этот алгоритм назван по имени создателя и был разработан в 1959 году. В процессе выполнения алгоритм проверит каждую из вершин графа, и найдет кратчайший путь до исходной вершины. Стандартная реализация работает на взвешенном графе — графе, у которого каждый путь имеет вес, т.е. «стоимость», которую надо будет «заплатить», чтобы перейти по этому ребру. При этом в стандартной реализации веса неотрицательны. На клетчатом поле вес каждого ребра графа принимается одинаковым (например, единицей).
А* (А «со звездочкой»)
Впервые описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Данный алгоритм является расширением алгоритма Дейкстры, ускорение работы достигается за счет эвристики — при рассмотрении каждой отдельной вершины переход делается в ту соседнюю вершину, предположительный путь из которой до искомой вершины самый короткий. При этом существует множество различных методов подсчета длины предполагаемого пути из вершины. Результатом работы также будет кратчайший путь. О реализации алгоритма читайте в здесь.
Поиск по первому наилучшему совпадению (Best-First Search)
Усовершенствованная версия алгоритма поиска в ширину, отличающаяся от оригинала тем, что в первую очередь развертываются узлы, путь из которых до конечной вершины предположительно короче. Т.е. за счет эвристики делает для BFS то же, что A* делает для алгоритма Дейкстры.
IDA* (A* с итеративным углублением)
Расшифровывается как Iterative Deeping A*. Является измененной версией A*, использующей меньше памяти за счет меньшего количества развертываемых узлов. Работает быстрее A* в случае удачного выбора эвристики. Результат работы — кратчайший путь.
Jump Point Search
Самый молодой из перечисленных алгоритмов был представлен в 2011 году. Представляет собой усовершенствованный A*. JPS ускоряет поиск пути, «перепрыгивая» многие места, которые должны быть просмотрены. В отличие от подобных алгоритмов JPS не требует предварительной обработки и дополнительных затрат памяти.
Материалы по более интересным алгоритмам мы обозревали в подборке материалов по продвинутым алгоритмам и структурам данных.
Определение.
Маршрутом
![]()
в графе ![]()
называется последовательность вершин
![]() ,
,
где пара соседних вершин ![]()
является ребром графа.
![]()
![]() -1
-1
В
этом случае будем говорить, что маршрут
M
соединяет вершины ![]() .
.
Пример.
![]()

Определение.
Путем,
соединяющим пару вершин ![]()
будем называть маршрут, соединяющий
данную пару вершин и не содержащий
повторяющихся ребер.
Определение.
Простым
путем,
соединяющим пару вершин ![]() будем
будем
называть путь, соединяющий данную пару
и не содержащий повторяющихся вершин.
Определение.
Пару вершин ![]()
в графе ![]()
будем называть связной,
если либо вершины совпадают, либо
существует маршрут, соединяющий две
эти вершины.
Пример.
Любая
пара вершин в следующем графе связана:

В
следующем графе связанными являются
не все вершины:

Вершины
1 и 2 связаны, а, например, вершины 2 и 3 не
связаны.
Утверждение.
Если в графе существует маршрут,
соединяющий пару вершин, то существует
простой
путь,
который соединяет данную пару вершин.
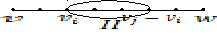
Рассмотрим
маршрут, соединяющий вершины ![]() .
.
Предположим, что вершина ![]()
повторяется на маршруте. Тогда вырежем
участок маршрута ![]()
между повторяющимися вершинами и
соединим полученные части. Данную
операцию будем повторять до тех пор,
пока в маршруте не будет повторяющихся
вершин.
Таким
образом, получен простой путь, соединяющий
пару вершин ![]() .
.
Поэтому для связности вершин достаточно
наличие простого пути, который их
соединяет.
Определение.
Циклом
называется путь, в котором начальная и
конечная врешины совпадают.
Пример.
![]()

Определение.
Простым
циклом
называется путь, в котором вершины не
повторяются, за исключением первой и
последней. Другими словами, простой
цикл – это цикл без самопересечения.
Пример.
Простой цикл:![]() .
.
Связные графы
Отношение
связности
между вершинами в графе обладает тремя
свойствами:
1.
Рефлексивность (отражение).
Любая
вершина связана сама с собой.
2.
Симметричность.
Если
вершина ![]()
связана с вершиной ![]() ,
,
то верно и обратное: вершина ![]()
связана с вершиной ![]() .
.
3.
Транзитивность.
Если
вершина ![]()
связана с вершиной ![]() ,
,
а вершина ![]()
связана с вершиной ![]() ,
,
то вершина ![]()
связана с вершиной ![]() .
.
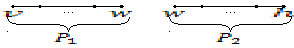
Путь,
который связывает ![]()
и ![]() ,
,
можно получить соединением путей ![]()
и ![]() .
.
Отношение
связности разбивает все вершины графа
на компоненты связанности:
![]()
Любая
пара вершин, входящая в одну компоненту
связности связана. Любые вершины из
разных компонент связности между собой
не связаны.
Пример.
Представленный граф состоит из двух
компонент связности. В первой компоненте
находятся вершины ![]()
и ![]() ,
,
а вторая компонента включает в себя
вершину ![]() .
.

4.3 Методы анализа графа. Поиск в ширину. Нахождение кратчайших путей в графе.
Вход
алгоритма:
граф ![]()
и фиксированная вершина ![]() .
.
Выход
алгоритма:
компонента связности графа, в которую
входит вершина ![]() .
.
Описание
алгоритма:
на этапах алгоритма строится
последовательность расширяющихся
множеств вершин
![]()
по
следующему рекуррентному принципу: ![]()
– исходная фиксированная вершина ![]() .
.
Пусть построены множества ![]() .
.
Тогда множество ![]()
включает вершины множества ![]() ,
,
а также вершины, которые смежны с
вершинами ![]() :
:
![]()
Таким
образом, ![]()
– сама вершина ![]() .
.
![]()
– те вершины, которые достижимы из
начальной вершины ![]()
не более чем за один шаг.![]()
– те вершины, которые достижимы из
начальной вершины ![]()
не более чем за два шага…![]() Место
Место
для формулы.

Как
только два соседних множества совпадут,
алгоритм завершает свою работу.
П ример.
ример.
Пусть
начальная вершина – ![]() .
.
Тогда:
![]()
![]()
![]()
![]()
![]()
Поиск
в ширину позволяет находить длины
кратчайших путей и сами пути. Из
фиксированной вершины ![]()
во все вершины графа (для простоты
считаем, что граф связан).
Определение.
Кратчайший
путь
между вершиной ![]()
и ![]()
– это путь, соединяющий данные вершины
и содержащий наименьшее число ребер.
Утверждение.
Вершины, впервые помеченные на k-ом
этапе алгоритма поиска в ширину есть
те вершины графа, кратчайший путь от
которых до начальной вершины ![]()
равен ![]() .
.

Доказательство:
Проведем
доказательство методом индукции по
номеру этапа алгоритма.
Для
начального нулевого этапа утверждение
очевидно. Начальная вершина множества
![]()
![]()
и кратчайший путь от вершины ![]()
до нее равен ![]() .
.
Пусть
утверждение справедливо для k-ого
этапа алгоритма. Докажем справедливость
утверждения для ![]() -ого
-ого
этапа. Так как по построению алгоритма
на ![]()
этапе вновь помеченные вершины есть
вершины, которые смежны с вершинами,
помеченными на предыдущем k-ом
этапе, то из данных вершин обязательно
найдется путь в вершину ![]() ,
,
содержащий не более чем ![]()
ребро.
Более
короткого пути, чем из k+1-ого
ребра в вновь помеченные вершины на k+1
этапе бытьть не может. В последнем случае
эти вершины были бы отмечены на более
раннем этапе (по предположению индукции).
Утверждение
доказано.
Рассмотрим
более общую задачу поиска кратчайшего
пути в графе, в котором каждому ребру
предписано положительное число – его
длина (расстояние между соответствующей
парой вершин). Считаем, что это число
положительное целое.
Таким
образом, на вход алгоритма подается
сеть ![]()
и начальная вершина ![]() ,
,
где ![]()
– неориентированный связный граф, а
![]()
– положительная целочисленная
(стоимостная) функция длины, заданная
на ребрах графа.
![]()
На
выходе алгоритма должны быть получены
значения кратчайших путей ![]()
из вершины ![]()
в любую другую вершину графа ![]() .
.
Если вершина ![]() не
не
связана с вершиной ![]() ,
,
считаем, что расстояние равно ![]() .
.
Сведем
рассматриваемую задачу к предыдущей
задаче поиска кратчайших путей для
графа, в котором функция длины единичная.
Для этого совершим следующее преобразование:
Рассмотрим
произвольное ребро ![]()
в заданном графе. Длина данного ребра
равна ![]() .
.

В
данное ребро добавим ![]()
вершину, а длину каждого полученного
ребра будем считать равной ![]() .
.

Данное
преобразование применим к каждому ребру
графа. При этом длины кратчайших путей
между вершинами исходного графа не
изменятся, а функция длины в полученном
графе единичная. Исходя из этого, можно
применить алгоритм поиска в ширину для
полученного графа.
Примечание.
Данный
алгоритм будет неэффективным в силу
того, что числа в компонентах связности
хранятся в двоичной системе исчисления,
поэтому целое число длины ![]()
будет требовать лишь ![]()
битов памяти. Преобразованный граф
будет требовать экспоненциальную
память, по сравнению с памятью
первоначального графа, т.к. ребро длины
![]()
преобразуется в ![]()
ребер. Если в первоначальной задаче для
записи числа ![]()
требуется ![]()
бит, то в полученной задаче будет
необходимо ![]()
бит для хранения новых вершин в графе.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
