Группа ассура как найти - Сайт, где вы сможете решить свои вопросы

Группы Ассура и их классификация

Кинематическая
цепь, которая после присоединения её
всеми свободными элементами кинематических
пар к стойке получает подвижность,
равную нулю, называется группой Асура.
Таким образом,

W_гр.Асс.
= 0.

В
состав группы Асура входят только
кинематические пары 5 класса, поэтому,
согласно формуле Чебышёва:

W_гр.Асс.
= 3n
– 2 p₅
= 0,

откуда
получаем 3n
= 2p₅_, или p₅
= 3/2∙n,
как условие существования группы Ас-

сура.
Составим таблицу из нескольких сочетаний
количества звеньев и кинематических
пар в группах Ассура согласно приведённому
выше соотношению

n	2	4	6…
p₅	3	6	9…

Группы Ассура
делятся на классы и порядки.

Класс
группы определяется классом наиболее
сложного замкнутого контура в составе
группы:

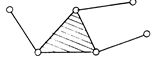
II класс
III класс IV
класс V класс и т.
д.

Кинематические
пары в контуре III
класса, могут быть расположены по одной
прямой, не образуя никакой контур, однако
считается, что и в этом случае имеется
контур III
класса. Порядок групп Ассура определяется
количеством свободных элементов
кинематических пар, которыми группы
Ассура присоединяются к друг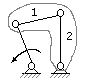
им
звеньям.

Рассмотрим
несколько примеров групп Ассура и
механизмов с этими группами.

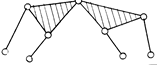
Группа
Ассура II
класса, 2-го порядка
Четырёхшарнирный

1-го
вида
механизм

Группы II
класса делятся также на виды (модификации)
в зависимости от количества и расположения
в них поступательных и вращательных
кинематических

пар.
Приведённая выше группа Ассура относится
к первому
виду. Если
в этой группе один из крайних элементов
вращательной пары заменить поступательным,
то получится группа второго
вида. Если
заменить среднюю вращательную пару
поступательной, то такая группа Ассура
получится группой Ассура третьего
вида.

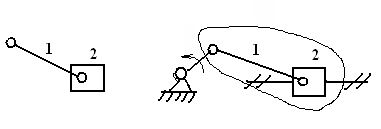
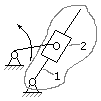
Группа Ассура
Кривошипно-ползунный

II
класса, 2-го механизм

порядка, 2-го вида

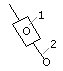
Группа Ассура II
класса, Кривошипно-кулисный

2-го порядка, 3-го вида
механизм

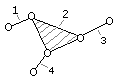
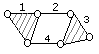
n
= 4

p₅
= 6

Группа Ассура III
класса, Группа Ассура IV
класса

3-го порядка
4-го порядка

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
31.05.20151.29 Mб2581.doc
#
24.09.20192.41 Mб231.doc
#
31.05.201587.04 Кб641.doc
#
#
#
#

Источник

Группа Ассура (структурная группа) – это такая кинематическая цепь, присоединение которой к любому механизму не изменяет его числа степеней свободы. При этом такая цепь не должна распадаться на более простые цепи с тем же свойством.

Так как группа Ассура не изменяет числа степеней свободы механизма после присоединения к нему или отсоединения от него, то она обладает собственной нулевой степенью свободы. Таким образом:

W_гр=3n_гр–2p_5гр=0,
откуда
p_5гр=3_nгр/2
или
n_гр=2p_5гр/3,

где:
n_гр – число звеньев в группе Ассура, включая фиктивные звенья, полученные при замене высших пар,
p_5гр – число кинематических пар пятого класса в группе Ассура, включая пары, полученные при замене высших пар.

Примечание: рассматриваются структурные группы, включающие только низшие пары 5 класса, т.к. при наличии высших кинематических пар в механизме их можно заменить цепями с низшими парами.

Так как количество звеньев и кинематических пар заведомо целые числа, то число звеньев в группе Ассура всегда четное, а число кинематических пар кратно трем. Таким образом группы Ассура имеют следующие сочетания чисел звеньев и кинематических пар (таблица 2.1):

Таблица 2.1

n_гр	2	4	6	8	10	12	…
p_5гр	3	6	9	12	15	18	…

Группы Ассура подразделяются на классы, порядки.

Класс группы Ассура

Класс группы Ассура определяется числом сторон замкнутого контура (многоугольника), входящего в состав этой группы. При этом все группы, имеющие два звена, относятся к группам II класса, а контур с числом сторон больше трех должен быть подвижным (т.е. иметь изменяемую форму при работе механизма).

Порядок группы Ассура

Порядок группы Ассура определяется числом элементов кинематических пар, которыми группа присоединяется к механизму.

Группы Ассура второго класса одновременно являются группами второго порядка (иногда их называют двухповодковыми группами), но они еще подразделяются на виды.

Вид группы Ассура

Вид группы Ассура зависит от сочетания вращательных (шарниров) и поступательных (ползунов) кинематических пар в данной группе. Всего существует пять видов групп Ассура второго класса.

Класс механизма >
Курсовой проект по ТММ >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Для выполнения структурного
синтеза (проектирования схемы) многозвенных плоских механизмов с числом
звеньев более четырех непосредственный перебор всех возможных вариантов по
формуле Чебышева оказывается затруднительным. Наиболее удобно проектировать
схемы механизмов путем наслоения (присоединения) кинематических цепей, называемых структурными
группами, или группами
Ассура.
Понятие о структурных группах введено в 1916 г. Л.В. Ассуром.

NB 3.3. Группой Ассура называется такая плоская кинематическая
цепь, которая, будучи
присоединенной к другой кинематической цепи, не меняет числа степеней свободы последней.

Иначе говоря, число степеней свободы группы
Ассура W = 0. Группа Ассура содержит только низшие кинематические
пары. При таких условиях структурная формула группы Ассура имеет
вид:

W = 3n – 2p₁=
0, или

p₁
= (3/2) n. (3.4)

Это условие в
целых числах удовлетворяется только при четных числах звеньев n и
числах низших кинематических пар p₁, кратных трем, и может быть представлено
соотношениями, приведенными в табл. 3.3:

Таблица
3.3

Число подвижных звеньев	n	2	4	6	8
Число кинематических пар	p₁	3	6	9	12

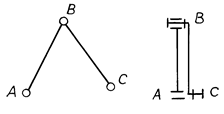
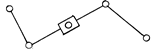
Рис. 3.5

Из табл. 3.3
видно, что простейшая
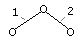
группа Ассура состоит из двух звеньев и трех низших кинематических пар. Базовая
группа Ассура содержит два звена и три вращательные пары (рис. 3.5). В
точке B находится действительная кинематическая
пара (цилиндрический шарнир). В
точках A и C — потенциальные пары, которыми группа Ассура, входящая в состав механизма, присоединяется к соседним звеньям.

NB 3.4.

1. Группа
Ассура — плоская кинематическая цепь с числом степеней свободы, равным нулю.

2. Группа
Ассура содержит только низшие пары.

3.
Простейшая группа Ассура состоит из двух звеньев и трех пар.

3.5. Классификация групп Ассура

Группы Ассура
характеризуются классом и порядком.

NB 3.5.

1. Класс
группы Ассура определяется числом кинематических пар, входящих в наиболее
сложный контур.

2. Порядок
группы Ассура определяется числом внешних (потенциальных) кинематических пар.

Таким образом, в
соответствии с данными определениями простейшая группа Ассура (рис. 3.5)
является группой II класса и 2-го
порядка: каждый из
контуров (AB и BC) входит в две кинематические пары,
потенциальными являются две пары — A и C. Простейшая группа
Ассура называется двухповодковой, или диадой. В формуле строения порядок
группы Ассура указывают в индексе класса, например III₃. Так как
двухповодковые группы всегда второго порядка, то в индексе их класса ставится
вид. Базовой диаде (рис. 3.5) присвоен вид 1
и обозначение II₁. В табл.
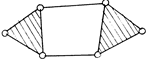
3.4 приведены некоторые виды контуров и групп Ассура.

Таблица
3.4

Обозн. группы	Число звеньев группы	Схема	Класс и порядок
А)	2		II₂
Б)	4		III₃
В)	4		III₃
Г)	4		IV₂
Д)	6		III₄
Е)	6		VI₃

Разновидности
групп Ассура, приведенные в табл. 3.4, не исчерпывают их многообразия. Однако
на практике преимущественно применяют механизмы с группами Ассура II класса (диадами).
Использование структурных групп позволяет существенно упростить кинематический
и динамический анализ механизмов. Таким образом, введение понятия «структурная
группа» преследует следующие цели:

а) классификация
механизмов;

б)
кинематический анализ;

в)
кинетостатический анализ.

3.6. Виды двухповодковых групп
и начальных механизмов

Большинство
современных механизмов, применяемых в технике, содержит группы Ассура II класса
2-го порядка (диады). Такие механизмы называют диадными. Диады 2-го,
3-го и других видов получаются из диады 1–го вида путем замены одной
или двух вращательных пар поступательными. Так, диада 2-го вида получается заменой
одной крайней вращательной пары поступательной (рис. 3.6). Такая замена
правомерна, так как цилиндрический шарнир с радиусом r = по сути преобразуется в поступательную
пару.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Источник

Что такое структурный синтез механизма

Структурный синтез механизма – проектирование структурной схемы механизма, под которой понимается схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение.

Основная схема механизма (схема с оптимальной структурой) – схема механизма, отражающая наличие только необходимых подвижностей звеньев для обеспечения заданного числа степеней свободы при отсутствии избыточных контурных связей.

Основная схема механизма обладает определенными свойствами:

элементы кинематических пар удовлетворяют условию сборки замкнутых контуров механизма без деформации звеньев и натягов в кинематических парах;
изменяемость положения элементов кинематических пар, расположенных на стойке, при возможной деформации стойки и звеньев не оказывает существенного влияния на силы в кинематических парах;
при заданных активных нагрузках, положениях, скоростях и ускорениях входных звеньев имеется возможность найти положения, скорости и ускорения всех остальных точек и определить реакции в кинематических парах.

При анализе реальных конструкций и их кинематических схем выявляются:

1) дополнительные подвижности

местные подвижности звена (Реализация местной подвижности звена не вызывает перемещения остальных звеньев механизма. Местная подвижность звена позволяет уменьшить износ элементов кинематической пары, улучшить условия смазки, повысить КПД, надежность, долговечность узлов машины);
местные подвижности группы звеньев;
групповая подвижность (групповая подвижность части звеньев кинематических цепей, не вызывающая перемещения остальных звеньев в механизме. Для некоторых механизмов групповая подвижность недопустима, т.к. приводит к неопределенности движения выходного звена);

2) избыточные структурные связи (относительно основной схемы механизма с заданным числом степеней свободы).

Основной принцип образования механизмов состоит в последовательном присоединении к начальным звеньям и стойке групп, степень свободы которых равна нулю.

Группа Ассура – кинематическая цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы её звеньев, и не распадающаяся на более простые цепи, обладающие также нулевой степенью свободы.

Группы Ассура подразделяются на классы в зависимости от их строения.

Класс структурной группы определяется числом кинематических пар, образующих наиболее сложный замкнутый контур группы.

Порядок структурной группы определяется числом элементов звеньев, которыми она присоединяется к имеющемуся механизму.

Число звеньев в группе Ассура – всегда четное число, а число кинематических пар 5 класса кратно трем.

Если в состав механизма входят группы различных классов, то класс механизма определяется по той группе, которая относится к наивысшему классу. При определении класса механизма необходимо указать, какие из звеньев являются начальными, т.к. в зависимости от выбора начальных звеньев может изменяться класс механизма.

Последовательность расчленения механизма на группы следующая. Пусть дан механизм, состоящий из стойки, начального звена (или начальных звеньев) и нескольких групп различных классов. Начинать надо с попытки отсоединить от механизма группы II класса. При этом необходимо каждый раз после отсоединения группы проверить, обладает ли оставшаяся кинематическая цепь той же степенью свободы, что и первоначальный механизм, и чтобы не оставалось вообще элементов звеньев, не входящих в кинематические пары. Если попытки отсоединения групп II класса не дадут решения, то надо переходить к попыткам отсоединения групп III класса. После групп III класса следует переходить к группам IV класса и т.д. После выделения всех групп должны остаться стойка и начальное звено (начальные звенья).

Источники:

Фролов К.В. Теория механизмов и машин/ К.В. Фролов, С.А. Попов, А.К. Мусатов; Под ред. К.В. Фролова. – М.: Высш. шк., 1987. – 496 с.

Кожевников С.Н. Теория механизмов и машин/ С.Н. Кожевников. — М.: Машиностроение, 1969. — 584 с.

Левитский Н.И. Теория механизмов и машин/ Н.И. Левитский. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 592 с.

Артоболевский И.И. Теория механизмов и машин/ И.И. Артоболевский. – 4-е изд., перераб. и доп. – М.: Наука, 1988. – 640 с.

Дополнительно на Геноне: Что такое механизм?

Источник

Обновлено: 14.05.2023

Структу́рная гру́ппа Ассу́ра (также просто гру́ппа Ассу́ра) — это такая кратчайшая кинематическая цепь, образованная низшими парами пятого класса, при присоединении которой к любому плоскому механизму степень его подвижности не меняется [1] .

Группа названа именем Леонида Владимировича Ассура, который и разработал методику их образования в 1916 году.

Группы Ассура делятся на классы, виды и порядки.

Класс группы Ассура определяется классом наивысшего контура, входящего в неё.
Вид группы Ассура определяется сочетанием вращательных (шарниров) и поступательных (ползунов) кинематических пар в данной группе.
Порядок группы Ассура определяется по числу кинематических пар, которыми она крепится к механизму.

Профессор Дворников создал альтернативную универсальную структурную классификацию [2]

Группы Ассура подразделяются на классы, порядки.

Класс группы Ассура

Порядок группы Ассура

Вид группы Ассура

Для выполнения структурного синтеза (проектирования схемы) многозвенных плоских механизмов с числом звеньев более четырех непосредственный перебор всех возможных вариантов по формуле Чебышева оказывается затруднительным. Наиболее удобно проектировать схемы механизмов путем наслоения (присоединения) кинематических цепей, называемых структурными группами, или группами Ассура. Понятие о структурных группах введено в 1916 г. Л.В. Ассуром.

NB 3.3. Группой Ассура называется такая плоская кинематическая цепь, которая, будучи присоединенной к другой кинематической цепи, не меняет числа степеней свободы последней.

Иначе говоря, число степеней свободы группы Ассура W = 0. Группа Ассура содержит только низшие кинематические пары. При таких условиях структурная формула группы Ассура имеет вид:

W = 3n – 2p₁ = 0, или

Это условие в целых числах удовлетворяется только при четных числах звеньев n и числах низших кинематических пар p₁, кратных трем, и может быть представлено соотношениями, приведенными в табл. 3.3:

Число подвижных звеньев

Число кинематических пар

Из табл. 3.3 видно, что простейшая группа Ассура состоит из двух звеньев и трех низших кинематических пар. Базовая группа Ассура содержит два звена и три вращательные пары (рис. 3.5). В точке B находится действительная кинематическая пара (цилиндрический шарнир). В точках A и C — потенциальные пары, которыми группа Ассура, входящая в состав механизма, присоединяется к соседним звеньям.

NB 3.4.

1. Группа Ассура — плоская кинематическая цепь с числом степеней свободы, равным нулю.

2. Группа Ассура содержит только низшие пары.

3. Простейшая группа Ассура состоит из двух звеньев и трех пар.

3.5. Классификация групп Ассура

Группы Ассура характеризуются классом и порядком.

NB 3.5.

1. Класс группы Ассура определяется числом кинематических пар, входящих в наиболее сложный контур.

2. Порядок группы Ассура определяется числом внешних (потенциальных) кинематических пар.

Таким образом, в соответствии с данными определениями простейшая группа Ассура (рис. 3.5) является группой II класса и 2-го порядка: каждый из контуров (AB и BC) входит в две кинематические пары, потенциальными являются две пары — A и C. Простейшая группа Ассура называется двухповодковой, или диадой. В формуле строения порядок группы Ассура указывают в индексе класса, например III₃. Так как двухповодковые группы всегда второго порядка, то в индексе их класса ставится вид. Базовой диаде (рис. 3.5) присвоен вид 1 и обозначение II₁. В табл. 3.4 приведены некоторые виды контуров и групп Ассура.

Группой Ассура называется кинематическая цепь, которая в случае ее присоединения элементами внешних пар к стойке получает нулевую степень подвижности, т.е. образует ферму. Группа Ассура характеризуется классом, порядком и видом.

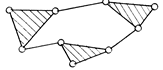
Класс группы Ассура определяется максимальным классом контура входящего в группу. Класс контура – наибольшее число кинематических пар образующих в группе замкнутый контур. Если группа Ассура образована двумя звеньями ей в качестве исключения присваивается 2-й класс.

Порядок группы Ассура определяется числом кинематических пар, которыми она присоединяется к основному механизму.

Вид группы Ассура (её характеристика) определяется соотношением входящих в неё вращательных и поступательных кинематических пар. Поводком называется звено, входящее в группе в две кинематические пары, одна из которых свободная и служит для присоединения к одному из подвижных звеньев механизма или к стойке. Порядок структурных групп определяется числом поводков.

Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура – их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая конструкция. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 2-го класса 2-го порядка.

Число разновидностей таких групп для плоских механизмов с низшими парами невелико, их всего пять (см. рис. 1 б, в, г, д, е)

Структурный анализ механизмов с высшими кинематическими парами.

Под структурным анализом механизма понимается определение количества звеньев и кинематических пар, классификация кинематических пар, определение степени подвижности механизма, а также установление класса и порядка механизма.

Простейшей является структурная группа, у которой число подвижных звеньев: n=2 и число низших КП: p_H = 3. Она называется структурной группой 2-го класса, 2-го порядка и существует в пяти видах.

Порядок структурной группы определяется числом ее внешних кинематических пар. Группы, у которых n=4 и p_H=6, могут быть 3 и 4 класса.

Класс структурной группы определяется числом внутренних кинематических пар, образующих наиболее сложный замкнутый контур.

Задачи и методы кинематического анализа механизмов.

Кинематический анализ механизмов состоит в определении движения его звеньев по заданному движению начальных звеньев.

· определение положений звеньев и траекторий отдельных точек;

· определение линейных скоростей и ускорений точек и угловых скоростей и ускорений звеньев;

· определение передаточных функций или отношений между звеньями.

Методы кинематического анализа:

· графический – основан на графическом дифференцировании и интегрировании.;

· аналитические – в общем случае сложны и требуют громоздких вычислений.

Читайте также:

Иоанн скот эриугена философия кратко

Сочетание объективных и субъективных факторов преступности в современных условиях кратко

Балочные системы определение реакций опор и моментов защемления кратко

Мероприятия по гимнастике в школе

Программа по волейболу 6 часов в неделю в школе секция

Источник

Группы Ассура и их классификация

Класс группы Ассура

Порядок группы Ассура

Вид группы Ассура

3.5. Классификация групп Ассура

3.6. Виды двухповодковых групп и начальных механизмов

Класс группы Ассура

Порядок группы Ассура

Вид группы Ассура

3.5. Классификация групп Ассура

Вам также может понравиться

Как найти своих друзей в друг вокруг

Нашел смартфон как вернуть владельцу

Как найти путешественников во времени

Добавить комментарий Отменить ответ

3.6. Виды двухповодковых групп
и начальных механизмов