О степенях свободы в статистике
Время на прочтение
8 мин
Количество просмотров 196K
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.
Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:
Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
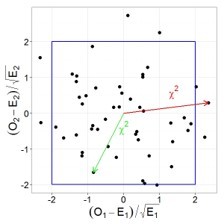
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
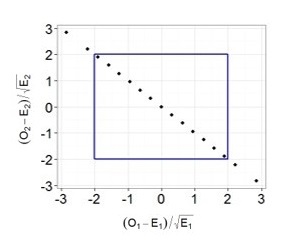
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.
Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.
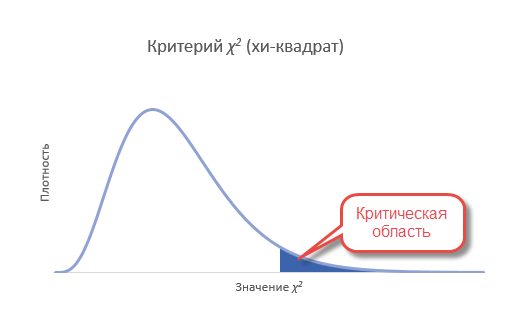
До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
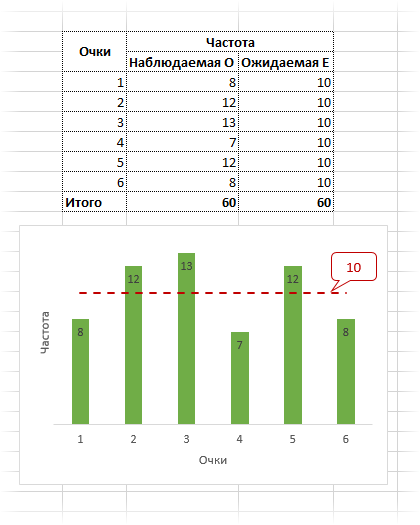
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
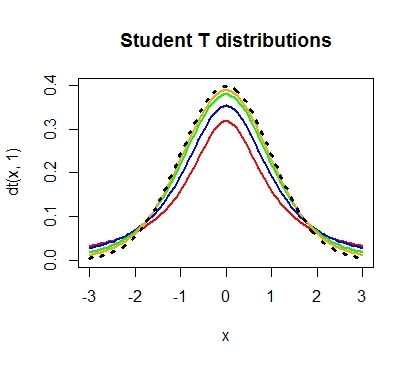
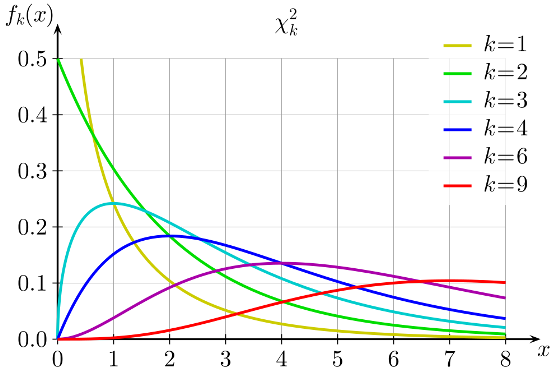
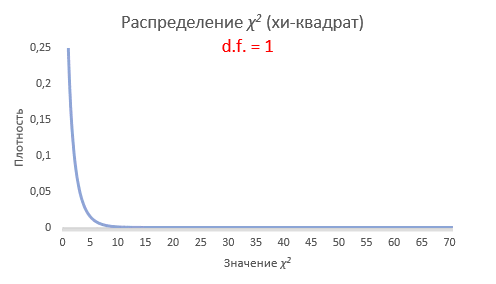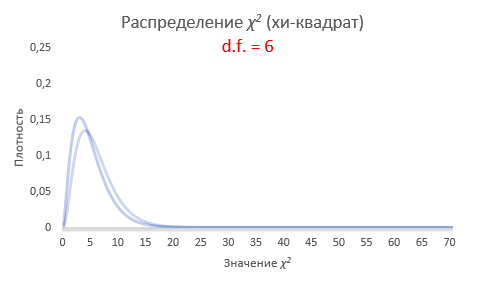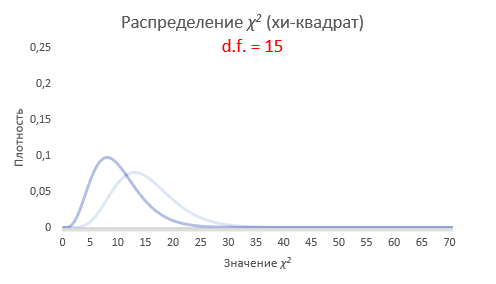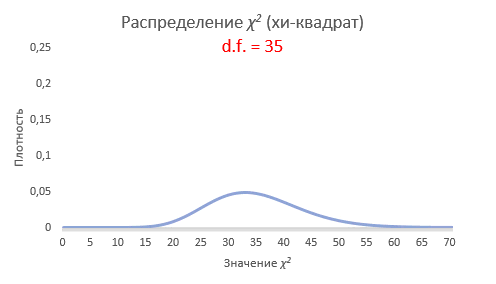
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию Хи квадрат Пирсона
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
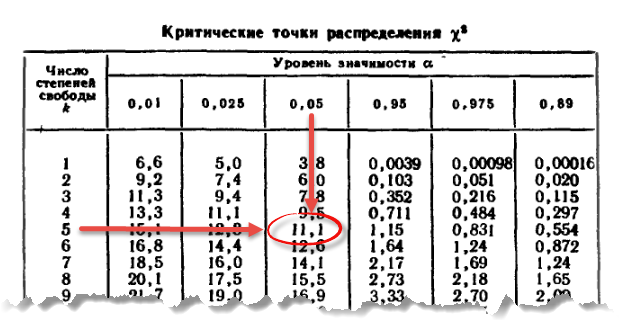
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
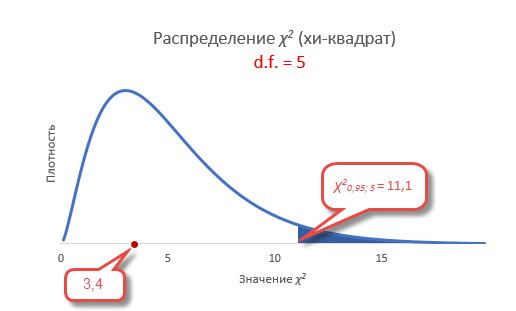
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
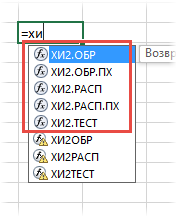
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
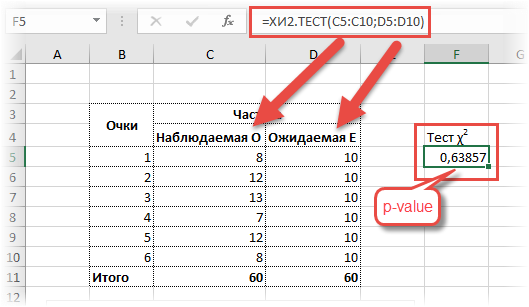
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
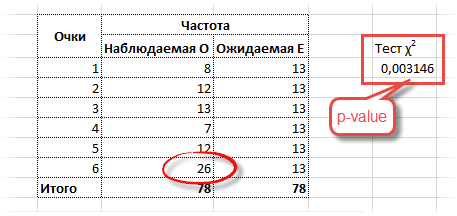
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
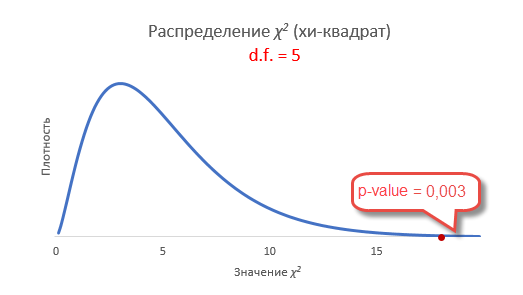
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
Критерий хи-квадрат – метод в математической статистике. Он показывает различия между фактическими данными в выборке и теоретическими результатами, которые предположил исследователь. С помощью метода оценивают, соответствует ли выборка законам распределения. Частный случай – критерий согласия Пирсона, который употребляется чаще всего.
При начале анализа информации исследователь предполагает, что фактические данные соответствуют какому-нибудь закону распределения. Например, результаты распределены равномерно. Это предположение называют нулевой гипотезой. Затем с помощью критерия хи квадрат исследователь проверяет, насколько фактические результаты отклоняются от предполагаемых. Так удается проверить, насколько верна нулевая гипотеза.
Понятие критерия хи-квадрат общее. В него входят разные методы. Но критерий Пирсона – самый популярный из них, поэтому названия иногда используют как синонимы. Критерий Пирсона помогает проверять гипотезы с помощью таблиц сопряженности, которые уже существуют и рассчитаны для многих распространенных ситуаций. Поэтому его удобно использовать.
Кто пользуется критерием хи-квадрат
Критерий часто используется в научных исследованиях, в маркетинге, в медицине и в других областях – везде, где бывает нужна статистика. Это популярный метод анализа, который помогает найти корреляцию или отвергнуть ее – а знание корреляции между разными факторами важно для прогнозов и стратегий.
- Ученые и статисты используют критерий хи-квадрат в расчетах, исследованиях, при интерпретации экспериментов и в других похожих задачах.
- ·Дата-аналитики и дата-саентисты применяют критерий в бизнес-целях. Например, с его помощью делают выводы о поведении пользователей или о тенденциях на рынке.
- Врачи и другие сотрудники здравоохранения могут использовать критерий при проведении клинических исследований и написании научных работ.
- Маркетологи и прочие диджитал-специалисты пользуются результатами, которые показывает критерий хи-квадрат, чтобы составить стратегию развития продукта.
Когда применяют критерий хи-квадрат
Критерий хи-квадрат используют, когда нужно определить наличие или отсутствие связи между двумя категориальными переменными — такими, которые могут принимать ограниченное количество уникальных значений. Категориальные переменные обычно не имеют числовых значений: например, цвет волос или любимое блюдо. Еще употребляют фразу «переменные, распределенные по номинальной шкале» – это означает примерно то же.
Например, исследование может пытаться установить, есть ли связь между образованием и доходом, или между полом и предпочтениями в музыке. В обоих случаях переменные категориальные – значит, критерий хи-квадрат использовать можно.
Есть еще несколько правил.
- С самого начала нужно отобрать правильные показатели – такие, которые вероятнее окажутся наглядными и репрезентативными. Они должны быть качественными и целочисленными, категориальными.
- Группы, которые сравниваются между собой, должны быть независимы друг от друга. Например, для сравнения одной и той же группы «до» и «после» какой-то манипуляции критерий не подойдет.
- Количество наблюдений для точных результатов – не менее 20 (иногда считается, что не менее 50).
- Ожидаемая частота – то, сколько раз значение теоретически должно появиться в выборке – должна быть больше или равна 5-10 для критерия Пирсона. Если она меньше, понадобится критерий Фишера.
Как выглядит распределение хи-квадрат
В критерии хи-квадрат используют определенное распределение – то, как распределяются показатели из выборки на графике. Распределение хи-квадрат описывается как «распределение суммы квадратов n независимых стандартных нормальных случайных величин». На практике это означает вот что.
Если реальные показатели распределяются по хи-квадрату – значит, наблюдаемые величины независимы друг от друга.
Первая картинка — это плотность распределения (вероятность получить в выборке каждое из чисел на горизонтальной оси), вторая — интегральная функция распределения (вероятность получить значение меньше, чем на горизонтальной оси).
Стандартная нормальная величина – такая, которая подчиняется нормальному распределению. Нормальное распределение – это пик посередине графика, который сглаживается по краям. Если измерить подчиняющийся ему показатель много раз и построить график – получится такая картинка. Нормальное распределение значит, что на величину действует много случайных факторов.
Как выглядит распределение хи квадрат – зависит от количества степеней свободы (df). Степени свободы – это количество величин, которые мы измеряем. Например, распределение хи-квадрат с 5 степенями свободы представляет собой график, построенный по сумме квадратов 5 случайных переменных с нормальным распределением.
Как рассчитываются результаты по критерию Пирсона
Самый часто применяемый среди семейства критериев хи квадрат – критерий Пирсона. Он довольно универсален, и под его требования подпадает довольно много исследований. При использовании этого метода наблюдаемые значения сравниваются с ожидаемыми. Наблюдаемые значения – фактические результаты, которые исследователь получил в ходе эксперимента. Ожидаемые значения вычисляются по формуле: составляется таблица, потом сумма ее строк и столбцов умножается на определенное значение. Подбор значений зависит от количества степеней свободы.
Рассмотрим этот процесс подробнее.
Создание таблицы. Первый шаг в применении критерия – составление таблицы реальных и ожидаемых значений. В таблице перечислены категориальные переменные, взаимосвязь которых проверяет исследователь. Таблица состоит из строк и столбцов, в каждой ячейке записано количество наблюдений в соответствующей категории.
Разобраться проще, если посмотреть на пример. Скажем, таблица может выглядеть вот так.
Формирование гипотез. Исследователь составляет две гипотезы — нулевую и альтернативную. Нулевая гипотеза говорит, что переменные не связаны друг с другом. Альтернативная гипотеза предполагает наличие связи между переменными. Обычно нулевую гипотезу формулируют так, чтобы ее опровержение доказывало существование связи между переменными.
Например, мы хотим узнать, есть ли связь между полом и предпочтениями в музыкальных жанрах. Тогда нулевая гипотеза будет говорить, что пол не влияет на предпочтения в музыке.
Ожидаемые значения. Затем нужно подсчитать ожидаемые значения — такие, какие должны получиться, если нулевая гипотеза верна. Их тоже нужно занести в таблицу, для этого в ней создают отдельный столбец. Так будет легче сравнить ожидаемые значения с реальными.
Ожидаемые значения рассчитываются так:
- берется общее число наблюдений для каждой переменной, записанной в таблице;
- общее число для каждого столбца умножается на общее число для каждой строки;
- полученные значения делятся на полное количество наблюдений.
Понять, как это работает, поможет картинка.
Расчеты. Когда исследователь подсчитал ожидаемые значения для каждой ячейки, он переходит к расчету статистики критерия хи-квадрат. Для каждой ячейки таблицы нужно:
- подсчитать квадрат разности между наблюдаемым и ожидаемым значением;
- разделить получившееся число на ожидаемое значение.
Подсчитанные значения нужно сложить. Получится число, которое называется статистикой критерия хи-квадрат. Чем больше это число, тем сильнее отличия между наблюдаемыми и ожидаемыми значениями — и тем вероятнее, что между факторами действительно есть связь.
Выводы. Маленькое значение статистики критерия хи-квадрат говорит, что нулевую гипотезу отвергнуть нельзя — но нельзя и подтвердить. А большое значение позволяет отвергнуть нулевую гипотезу и подтвердить связь между факторами. Остается вопрос: как понять, достаточно ли большое получилось число?
Специально для этого существуют таблицы критических значений. В них описаны «пограничные» значения статистики критерия хи-квадрат для разных условий. Если рассчитанный результат больше табличного — значит, нулевая гипотеза неверна, и связь есть. Если меньше — нулевую гипотезу нельзя отвергнуть.
Все, что должен сделать исследователь на этом этапе, — найти в таблице критическое значение критерия для своего случая. То есть — для нужного количества степеней свободы и уровня значимости. Уровень значимости — это число, которое показывает вероятность получить статистически значимый результат по ошибке. Исследователь выбирает этот уровень сам.
Некоторые другие критерии хи-квадрат
Критерий Пирсона — не единственный критерий хи квадрат. Выше мы говорили в основном о нем, но существуют и другие методики для разных ситуаций. Вот несколько примеров — в реальности их больше.
Критерий Тьюки. В отличие от критерия Пирсона, этот метод используется для сравнения нескольких групп – обычно трех и более. Он помогает оценить различия между средними значениями в группах и сделать вывод, насколько они значимы.
Критерий Фишера. Его применяют, если ожидаемая частота меньше 5. Ожидаемая частота говорит, сколько раз тот или иной результат должен появиться в таблице ожидаемых значений.
Поправка Йейтса. Это модификация критерия хи квадрат, которая используется для сравнения небольших выборок с ожидаемой частотой меньше 5. Дело в том, что если значения в таблице маленькие, классический критерий даст большую вероятность ошибки. Поправка помогает уменьшить этот риск. Она проще, чем критерий Фишера: от значений в таблице просто отнимается 0,5 или 1. После этого вычисляется статистика: она будет меньше, чем без поправки, поэтому риск ошибки окажется ниже.
Тесты семейства хи-квадрат
Критерий можно использовать для тестирования разных показателей. Тесты семейства хи-квадрат помогают проанализировать выборку, подтвердить или опровергнуть какую-нибудь гипотезу. Чаще всего говорят о тестах гомогенности, независимости и дисперсии.
Гомогенность. Тест гомогенности проверяет гипотезу, что распределение какой-либо переменной в разных группах – одинаковое. Например, с его помощью можно оценить, одинаково ли распределяются доходы населения в разных городах. При этом сам по себе критерий хи квадрат – непараметрический, то есть параметры распределения для него неважны. Значение имеют только наблюдения.
Независимость. Тест независимости проверяет, верно ли, что две категориальные переменные не связаны друг с другом. Он помогает определить, есть ли связь между разными переменными: пол и предпочтения в еде, образование и любимая музыка, и так далее. Обычно критерий хи-квадрат используют как раз для оценки независимости и поиска связей между переменными.
Дисперсия. С помощью этого теста исследователи оценивают дисперсию – то, насколько велик разброс между результатами в выборке. Тест дисперсии помогает оценить, одинакова ли дисперсия в разных выборках, соответствует ли она какому-то принятому значению – и так далее. Например, с помощью этого теста можно проанализировать разброс оценок учеников в разных классах: одинаковый ли этот разброс, соответствует ли он какому-то стандарту, и так далее.
Как начать применять критерий хи-квадрат
Объяснения выше могут показаться сложными. Это нормально. Статистические критерии редко рассчитывают вручную – обычно для этого используют специальное ПО или привычный всем Excel. «Ручные» расчеты чаще всего нужны при обучении, когда важно, чтобы ученик понял, как это работает.
Понять критерий хи-квадрат до конца можно, если начать им пользоваться. Так легче разобраться, чем при изучении теории. Поэтому мы рекомендуем тренироваться и выполнять задачи – можно начать с заданий из учебников и уроков в открытом доступе. Сначала будет сложно, но со временем понять принципы расчета будет легче.
Распределение  . Распределение Пирсона . Распределение Пирсона |
|
|---|---|
 Плотность вероятности Плотность вероятности |
|
 Функция распределения Функция распределения |
|
| Обозначение |
 или или  |
| Параметры |
 — число степеней свободы — число степеней свободы |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
примерно  |
| Мода |
0 для   если если  |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
|
| Производящая функция моментов |
 , если , если  |
| Характеристическая функция |
 |
Распределе́ние 


Определение[править | править код]
Пусть 

имеет распределение хи-квадрат с 

.
Распределение хи-квадрат является частным случаем гамма-распределения, и его плотность имеет вид:
,
где 

Функция распределения имеет следующий вид:
,
где 

Свойства распределения хи-квадрат[править | править код]
- Из определения легко получить моменты распределения хи-квадрат. Если
, то
,
.
по распределению при
.
Связь с другими распределениями[править | править код]
имеет распределение 
- Если
, то распределение хи-квадрат совпадает с экспоненциальным распределением:
.
имеет распределение Фишера со степенями свободы 
Вариации и обобщение[править | править код]
Дальнейшим обобщением распределения хи-квадрат является так называемое нецентральное распределение хи-квадрат[en], возникающее в некоторых задачах статистики.
Квантили[править | править код]
Квантиль — это число (аргумент), на котором функция распределения равна заданной, требуемой вероятности. Грубо говоря, квантиль — это результат обращения функции распределения, но есть тонкости с разрывными функциями распределения.
История[править | править код]
Критерий 
Общее обсуждение критерия 
Приложения[править | править код]
Распределение хи-квадрат имеет многочисленные приложения при статистических выводах, например при использовании критерия хи-квадрат и при оценке дисперсий. Оно используется в проблеме оценивания среднего нормально распределённой популяции и проблеме оценивания наклона линии регрессии благодаря его роли в распределении Стьюдента. Оно используется в дисперсионном анализе.
Далее приведены примеры ситуаций, в которых распределение хи-квадрат возникает из нормальной выборки:
| Название | Статистика |
|---|---|
| распределение хи-квадрат | 
|
| нецентральное распределение хи-квадрат | 
|
| распределение хи | 
|
| нецентральное распределение хи | 
|
Таблица значений χ2 и p-значений[править | править код]
Для любого числа p между 0 и 1 определено p-значение — вероятность получить для данной вероятностной модели распределения значений случайной величины такое же или более экстремальное значение статистики (среднего арифметического, медианы и др.), по сравнению с наблюдаемым, при условии верности нулевой гипотезы. В данном случае это распределение 
В таблице даны p-значения для соответствующих значений 
| Степени свободы (df) | Значение  [3] [3]
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,004 | 0,02 | 0,06 | 0,15 | 0,46 | 1,07 | 1,64 | 2,71 | 3,84 | 6,63 | 10,83 |
| 2 | 0,10 | 0,21 | 0,45 | 0,71 | 1,39 | 2,41 | 3,22 | 4,61 | 5,99 | 9,21 | 13,82 |
| 3 | 0,35 | 0,58 | 1,01 | 1,42 | 2,37 | 3,66 | 4,64 | 6,25 | 7,81 | 11,34 | 16,27 |
| 4 | 0,71 | 1,06 | 1,65 | 2,20 | 3,36 | 4,88 | 5,99 | 7,78 | 9,49 | 13,28 | 18,47 |
| 5 | 1,14 | 1,61 | 2,34 | 3,00 | 4,35 | 6,06 | 7,29 | 9,24 | 11,07 | 15,09 | 20,52 |
| 6 | 1,63 | 2,20 | 3,07 | 3,83 | 5,35 | 7,23 | 8,56 | 10,64 | 12,59 | 16,81 | 22,46 |
| 7 | 2,17 | 2,83 | 3,82 | 4,67 | 6,35 | 8,38 | 9,80 | 12,02 | 14,07 | 18,48 | 24,32 |
| 8 | 2,73 | 3,49 | 4,59 | 5,53 | 7,34 | 9,52 | 11,03 | 13,36 | 15,51 | 20,09 | 26,12 |
| 9 | 3,32 | 4,17 | 5,38 | 6,39 | 8,34 | 10,66 | 12,24 | 14,68 | 16,92 | 21,67 | 27,88 |
| 10 | 3,94 | 4,87 | 6,18 | 7,27 | 9,34 | 11,78 | 13,44 | 15,99 | 18,31 | 23,21 | 29,59 |
| p-значение | 0,95 | 0,90 | 0,80 | 0,70 | 0,50 | 0,30 | 0,20 | 0,10 | 0,05 | 0,01 | 0,001 |
Эти значения могут быть вычислены через квантиль (обратную функцию распределения) распределения хи-квадрат[4]. Например, квантиль 



В таблице дано округление до сотых; более точные таблицы для большего количества степеней свободы см., например, здесь[5].
См. также[править | править код]
- Критерий согласия Пирсона (критерий
)
Примечания[править | править код]
- ↑ Pearson K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling (англ.) // Philosophical Magazine, Series 5. — Vol. 50, no. 302. — P. 157—175. — doi:10.1080/14786440009463897.
- ↑ Cochran W. G. The
Test of Goodness of Fit (англ.) // Annals Math. Stat. — 1952. — Vol. 23, no. 3. — P. 315—345.
- ↑ Chi-Squared Test Архивная копия от 18 ноября 2013 на Wayback Machine Table B.2. Dr. Jacqueline S. McLaughlin at The Pennsylvania State University. Этот источник, в свою очередь, ссылается на: R. A. Fisher and F. Yates, Statistical Tables for Biological Agricultural and Medical Research, 6th ed., Table IV. Два значения были исправлены, 7,82 на 7,81 и 4,60 на 4,61.
- ↑ R Tutorial: Chi-squared Distribution. Дата обращения: 19 ноября 2019. Архивировано 16 февраля 2021 года.
- ↑ StatSoft: Таблицы распределений — Хи-квадрат распределение. Дата обращения: 29 января 2020. Архивировано 26 января 2020 года.
Many statistical inference problems require us to find the number of degrees of freedom. The number of degrees of freedom selects a single probability distribution from among infinitely many. This step is an often overlooked but crucial detail in both the calculation of confidence intervals and the workings of hypothesis tests.
There is not a single general formula for the number of degrees of freedom. However, there are specific formulas used for each type of procedure in inferential statistics. In other words, the setting that we are working in will determine the number of degrees of freedom. What follows is a partial list of some of the most common inference procedures, along with the number of degrees of freedom that are used in each situation.
Standard Normal Distribution
Procedures involving standard normal distribution are listed for completeness and to clear up some misconceptions. These procedures do not require us to find the number of degrees of freedom. The reason for this is that there is a single standard normal distribution. These types of procedures encompass those involving a population mean when the population standard deviation is already known, and also procedures concerning population proportions.
One Sample T Procedures
Sometimes statistical practice requires us to use Student’s t-distribution. For these procedures, such as those dealing with a population mean with unknown population standard deviation, the number of degrees of freedom is one less than the sample size. Thus if the sample size is n, then there are n – 1 degrees of freedom.
T Procedures With Paired Data
Many times it makes sense to treat data as paired. The pairing is carried out typically due to a connection between the first and second value in our pair. Many times we would pair before and after measurements. Our sample of paired data is not independent; however, the difference between each pair is independent. Thus if the sample has a total of n pairs of data points, (for a total of 2n values) then there are n – 1 degrees of freedom.
T Procedures for Two Independent Populations
For these types of problems, we are still using a t-distribution. This time there is a sample from each of our populations. Although it is preferable to have these two samples be of the same size, this is not necessary for our statistical procedures. Thus we can have two samples of size n1 and n2. There are two ways to determine the number of degrees of freedom. The more accurate method is to use Welch’s formula, a computationally cumbersome formula involving the sample sizes and sample standard deviations. Another approach, referred to as the conservative approximation, can be used to quickly estimate the degrees of freedom. This is simply the smaller of the two numbers n1 – 1 and n2 – 1.
Chi-Square for Independence
One use of the chi-square test is to see if two categorical variables, each with several levels, exhibit independence. The information about these variables is logged in a two-way table with r rows and c columns. The number of degrees of freedom is the product (r – 1)(c – 1).
Chi-Square Goodness of Fit
Chi-square goodness of fit starts with a single categorical variable with a total of n levels. We test the hypothesis that this variable matches a predetermined model. The number of degrees of freedom is one less than the number of levels. In other words, there are n – 1 degrees of freedom.
One Factor ANOVA
One factor analysis of variance (ANOVA) allows us to make comparisons between several groups, eliminating the need for multiple pairwise hypothesis tests. Since the test requires us to measure both the variation between several groups as well as the variation within each group, we end up with two degrees of freedom. The F-statistic, which is used for one factor ANOVA, is a fraction. The numerator and denominator each have degrees of freedom. Let c be the number of groups and n is the total number of data values. The number of degrees of freedom for the numerator is one less than the number of groups, or c – 1. The number of degrees of freedom for the denominator is the total number of data values, minus the number of groups, or n – c.
It is clear to see that we must be very careful to know which inference procedure we are working with. This knowledge will inform us of the correct number of degrees of freedom to use.
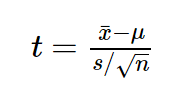
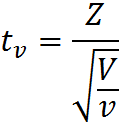
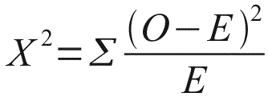
![{frac {k}{2}}!+!ln left[2Gamma left({k over 2}right)right]!+!left(1!-!{frac {k}{2}}right)psi left({frac {k}{2}}right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f01393e5f33aee251e935c9fdb24c42d85af2a)






![mathbb {E} [Y]=k](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff84e6269cf601498b736b9b4d51f6eb5db8884f)
![{displaystyle mathrm {D} [Y]=2k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a242253f2365176400f50d43c9a66566132d3d92)






