Хи квадрат пирсона как найти

До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.

Так был изобретен критерий χ² (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.

Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.

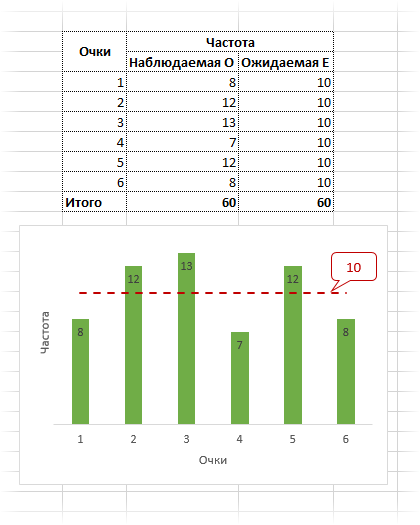
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.

Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
Распределение этой меры при справедливости гипотезы о том, что различий нет.

Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.

Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной E_i будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение

имеет стандартное нормальное распределение.

Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.

У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.

Это и есть статистика для критерия Хи-квадратПирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.

«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.

Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ² – это целое семейство распределений.

И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.

По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).

Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.

Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.

Таким образом, распределение хи квадрат (χ²) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ² (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.

Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.

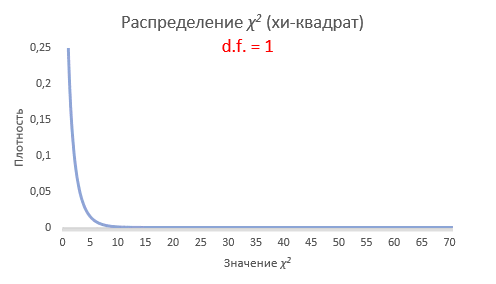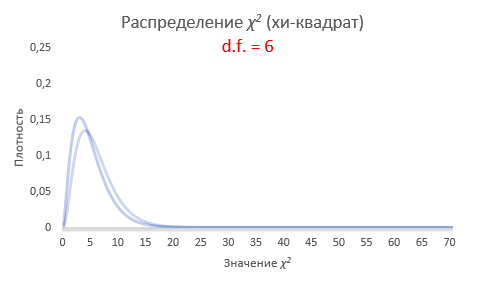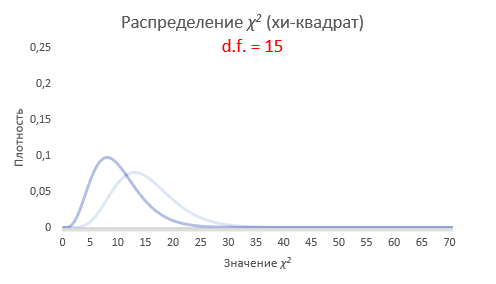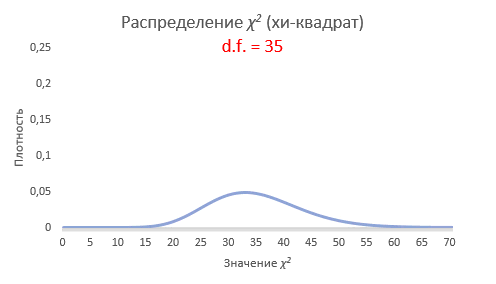
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).

Проверка гипотезы по критерию Хи квадрат Пирсона

Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.

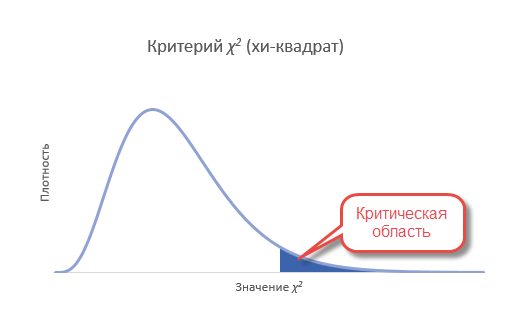
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.

Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.

Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.

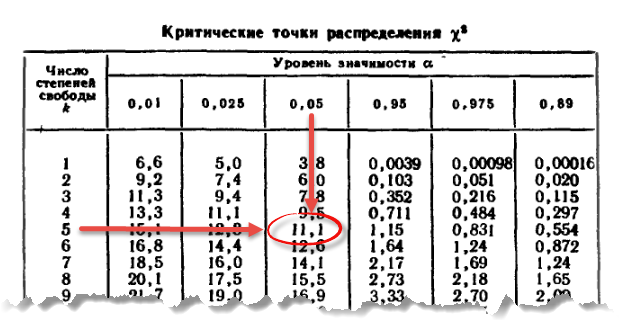
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ²_{0,05; 5} = 11,1.

Сравним фактическое и табличное значение. 3,4 (χ²) < 11,1 (χ²_{0,05; 5}). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.

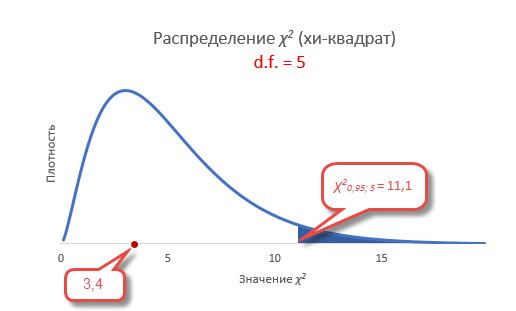
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.

Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.

Ниже их краткое описание.

ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)

ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.

ХИ2.РАСП – p-value слева (можно рассчитать плотность).

ХИ2.РАСП.ПХ – p-value справа.

ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.

Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:

=ХИ2.ОБР(0,95;5)

Или так

=ХИ2.ОБР.ПХ(0,05;5)

Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).

Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ² = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)

=ХИ2.РАСП.ПХ(3,4;5) = 0,63857

Значит, при 5-ти степенях свободы вероятность получить значение критерия χ² = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.

А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.

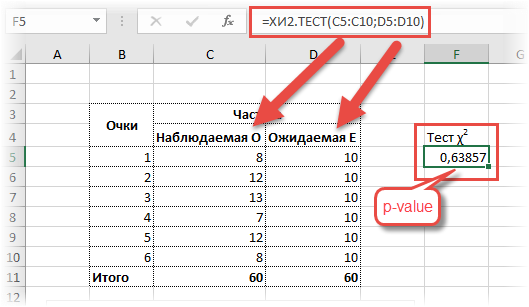
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.

Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).

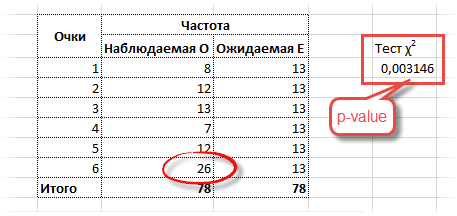
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.

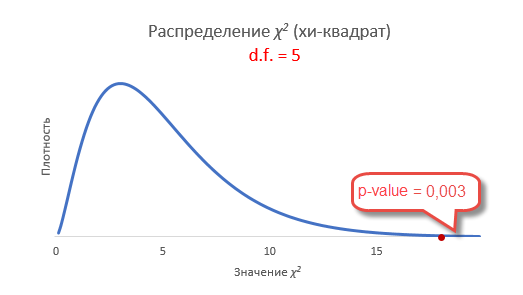
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).

Надеюсь, мне удалось объяснить, что такое критерий согласия χ² (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.

Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.

Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 марта 2023 года; проверки требуют 2 правки.

Критерий согласия Пирсона или критерий согласия ${displaystyle chi ^{2}}$ (хи-квадрат) — непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).

Является наиболее часто употребляемым критерием для проверки гипотезы о принадлежности наблюдаемой выборки $x_{1},x_{2},...,x_{n}$ объёмом некоторому теоретическому закону распределения .

Критерий хи-квадрат для анализа таблиц сопряжённости был разработан и предложен в 1900 году основателем математической статистики английским учёным Карлом Пирсоном.

Критерий может использоваться при проверке простых гипотез вида

${displaystyle H_{0}:F_{n}(x)=F(x,theta ),}$

где theta — известный вектор параметров теоретического закона, и при проверке сложных гипотез вида

${displaystyle H_{0}:F_{n}(x)in left{F(x,theta ),theta in Theta right},}$

когда оценка скалярного или векторного параметра распределения вычисляется по той же самой выборке.

Статистика критерия[править | править код]

Процедура проверки гипотез с использованием критериев типа $chi ^{2}$ предусматривает группирование наблюдений. Область определения случайной величины разбивают на непересекающихся интервалов граничными точками

${displaystyle x_{(0)},x_{(1)},...,x_{(k-1)},x_{(k)},}$

где $x_{(0)}$ — нижняя грань области определения случайной величины; $x_{(k)}$ — верхняя грань.

В соответствии с заданным разбиением подсчитывают число $n_{i}$ выборочных значений, попавших в -й интервал, и вероятности попадания в интервал

${displaystyle P_{i}(theta )=F(x_{(i)},theta )-F(x_{(i-1)},theta ),}$

соответствующие теоретическому закону с функцией распределения

При этом

$n=sum _{i=1}^{k}n_{i}$

и ${displaystyle sum _{i=1}^{k}P_{i}(theta )=1.}$

При проверке простой гипотезы известны как вид закона , так и все его параметры (известен скалярный или векторный параметр theta ).

В основе статистик, используемых в критериях согласия типа $chi ^{2}$ , лежит измерение отклонений $n_{i}/n$ от $P_{i}(theta )$ .

Статистика критерия согласия $chi ^{2}$ Пирсона определяется соотношением

${displaystyle chi ^{2}=nsum _{i=1}^{k}{frac {left(n_{i}/n-P_{i}(theta )right)^{2}}{P_{i}(theta )}}.}$

В случае проверки простой гипотезы, в пределе при эта статистика подчиняется $chi _{r}^{2}$ -распределению с r=k-1 степенями свободы, если верна проверяемая гипотеза $H_{0}$ . Плотность $chi _{r}^{2}$ -распределения, которое является частным случаем гамма-распределения, описывается формулой

${displaystyle g(s)={frac {1}{2^{r/2}Gamma (r/2)}}s^{r/2-1}e^{-s/2}.}$

Проверяемая гипотеза $H_{0}$ отклоняется при больших значениях статистики, когда вычисленное по выборке значение статистики ${displaystyle chi _{n}^{2}}$ больше критического значения ${displaystyle chi _{r,alpha }^{2},}$

${displaystyle Pleft(chi _{n}^{2}>chi _{r,alpha }^{2}right)={frac {1}{2^{r/2}Gamma (r/2)}}int _{chi _{r,alpha }^{2}}^{infty }s^{r/2-1}e^{-s/2}ds}$

или достигнутый уровень значимости (p-значение) меньше заданного уровня значимости (заданной вероятности ошибки 1-го рода) alpha .

Проверка сложных гипотез[править | править код]

При проверке сложных гипотез, если параметры закона по этой же выборке оцениваются в результате минимизации статистики ${displaystyle chi _{n}^{2}}$ или по сгруппированной выборке методом максимального правдоподобия, то статистика ${displaystyle chi _{n}^{2}}$ при справедливости проверяемой гипотезы подчиняется $chi _{r}^{2}$ -распределению с r=k-m-1 степенями свободы, где — количество оценённых по выборке параметров.

Если параметры оцениваются по исходной негруппированной выборке, то распределение статистики не будет являться ${displaystyle chi _{k-m-1}^{2}}$ -распределением^[1]. Более того, распределения статистики при справедливости гипотезы $H_{0}$ будут зависеть от способа группирования, то есть от того, как область определения разбивается на интервалы^[2].

При оценивании методом максимального правдоподобия параметров по негруппированной выборке можно воспользоваться модифицированными критериями типа $chi ^{2}$ ^[3]^[4]^[5]^[6].

О мощности критерия[править | править код]

При использовании критериев согласия, как правило, не задают конкурирующих гипотез: рассматривается принадлежность выборки конкретному закону, а в качестве конкурирующей гипотезы — принадлежность любому другому. Естественно, что критерий по-разному будет способен отличать от закона, соответствующего $H_{0}$ , близкие или далёкие от него законы. Если задать конкурирующую гипотезу $H_{1}$ и соответствующий ей некоторый конкурирующий закон $F_{1}(x,theta )$ , то можно рассуждать уже об ошибках двух видов: не только об ошибке 1-го рода (отклонении проверяемой гипотезы $H_{0}$ при её справедливости) и вероятности этой ошибки alpha , но и об ошибке 2-го рода (неотклонении $H_{0}$ при справедливости $H_{1}$ ) и вероятности этой ошибки beta .

Мощность критерия по отношению к конкурирующей гипотезе $H_{1}$ характеризуется величиной 1-beta . Критерий тем лучше распознаёт пару конкурирующих гипотез $H_{0}$ и $H_{1}$ , чем выше его мощность.

Мощность критерия согласия $chi ^{2}$ Пирсона существенно зависит от способа группирования^[7]^[8] и от выбранного числа интервалов^[8]^[9].

При асимптотически оптимальном группировании, при котором максимизируются различные функционалы от информационной матрицы Фишера по группированным данным (минимизируются потери, связанные с группированием), критерий согласия $chi ^{2}$ Пирсона обладает максимальной мощностью относительно «(очень) близких» конкурирующих гипотез^[10]^[8]^[9].

При проверке простых гипотез и использовании асимптотически оптимального группирования критерий согласия $chi ^{2}$ Пирсона имеет преимущество в мощности по сравнению с непараметрическими критериями согласия. При проверке сложных гипотез мощность непараметрических критериев возрастает и такого преимущества нет^[11]^[12]. Однако для любой пары конкурирующих гипотез (конкурирующих законов) за счёт выбора числа интервалов и способа разбиения области определения случайной величины на интервалы можно максимизировать мощность критерия^[13].

См. также[править | править код]

Точный критерий Фишера

Примечания[править | править код]

↑ Chernoff H., Lehmann E. L. The use of maximum likelihood estimates in $chi ^{2}$ test for goodness of fit (англ.) // The Annals of Mathematical Statistics. — 1954. — Vol. 25. — P. 579—586.
↑ Лемешко Б. Ю., Постовалов С. Н. О зависимости предельных распределений статистик $chi ^{2}$ Пирсона и отношения правдоподобия от способа группирования данных // Заводская лаборатория. — 1998. — Т. 64, вып. 5. — С. 56-63. Архивировано 24 мая 2015 года.
↑ Никулин М. С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и её применение. — 1973. — Т. XVIII, вып. 3. — С. 583—591.
↑ Никулин М. С. О критерии хи-квадрат для непрерывных распределений // Теория вероятностей и её применение. — 1973. — Т. XVIII, вып. 3. — С. 675—676.
↑ Rao K. C., Robson D. S. A chi-squared statistic for goodness-of-fit tests within the exponential family (англ.) // Commun. Statist. — 1974. — Vol. 3. — P. 1139—1153.
↑ Greenwood P. E., Nikulin M. S. A guide to chi-squared testing (англ.). — New York: John Wiley & Sons, 1996. — 280 p.
↑ Лемешко Б. Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория. — 1998. — Т. 64, вып. 1. — С. 56—64. Архивировано 29 октября 2013 года.
↑ ¹ ² ³ Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. — М.: Изд-во стандартов, 2006. — 87 с. Архивировано 30 сентября 2021 года.
↑ ¹ ² Лемешко Б. Ю., Чимитова Е. В. О выборе числа интервалов в критериях согласия типа $chi ^{2}$ // Заводская лаборатория. Диагностика материалов. — 2003. — Т. 69, вып. 1. — С. 61—67. Архивировано 6 сентября 2007 года.
↑ Денисов В. И., Лемешко Б. Ю. Оптимальное группирование при обработке экспериментальных данных // Измерительные информационные системы. — Новосибирск, 1979. — С. 5—14.
↑ Лемешко Б. Ю., Лемешко С. Б., Постовалов С. Н. Сравнительный анализ мощности критериев согласия при близких конкурирующих гипотезах. I. Проверка простых гипотез // Сибирский журнал индустриальной математики. — 2008. — Т. 11, вып. 2(34). — С. 96—111. Архивировано 29 октября 2013 года.
↑ Лемешко Б. Ю., Лемешко С. Б., Постовалов С. Н. Сравнительный анализ мощности критериев согласия при близких альтернативах. II. Проверка сложных гипотез // Сибирский журнал индустриальной математики. — 2008. — Т. 11, вып. 4(36). — С. 78—93. Архивировано 29 октября 2013 года.
↑ Лемешко Б. Ю., Лемешко С. Б., Постовалов С. Н., Чимитова Е. В. Статистический анализ данных, моделирование и исследование вероятностных закономерностей. Компьютерный подход. — Новосибирск: Изд-во НГТУ, 2011. — 888 с. — (Монографии НГТУ). — ISBN 978-5-7782-1590-0. Архивировано 29 октября 2013 года. — Раздел 4.9.

Литература[править | править код]

Кендалл М., Стьюарт А. Статистические выводы и связи. — М.: Наука, 1973.

См. также[править | править код]

Критерий хи-квадрат
Распределение хи-квадрат
Квантили распределения хи-квадрат

Ссылки[править | править код]

Критерий Пирсона на сайте Новосибирского государственного университета
Критерии типа хи-квадрат на сайте Новосибирского государственного технического университета (Рекомендации по стандартизации Р 50.1.033-2001)

Источник

Критерий согласия Пирсона (или хи-квадрат) вычисляется по формуле:

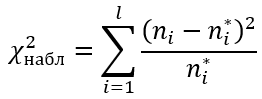
n_i – эмпирические частоты;

n_i^* – теоретические частоты;

l – количество интервалов (вариант)

Объем выборки по критерию Пирсона:

n>30

Теоретические частоты должны быть больше 5.

Распределение Пирсона с k степенями свободы рассчитывается по формуле:

k=l−r−1

r – число параметров предполагаемого распределения

Если предполагаемое распределение имеет нормальный закон распределения, то число степеней свободы оценивают по двум параметрам (математическое ожидание и СКО) и формула имеет вид:

k=l−3

Пример

Проверить гипотезу о нормальном распределении по критерию Пирсона при уровне значимости 0,01. Дана выборка данных измерений в виде таблицы

Найдем выборочное среднее по формуле: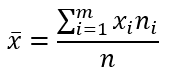

Отсюда

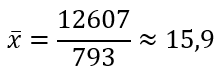
Формула выборочной исправленной дисперсии:

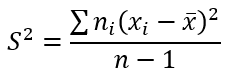
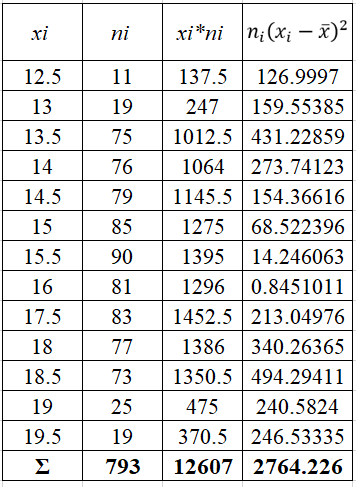
Тогда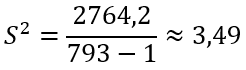

Откуда получаем выборочную исправленную СКО:

Получаем параметры нормального распределения m_x=15,9, σ=1,87.

Найдем теоретические частоты по формуле:

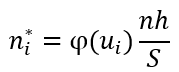
h – шаг между вариантами, h=0,5

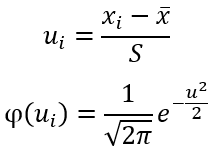
При уровне значимости α=0,01 и число степеней свободы k=13−3=10 по таблице Пирсона найдем критическое значение:

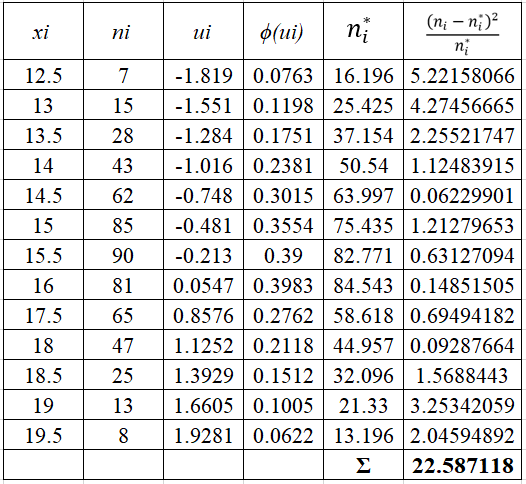
Наблюдаемое значение критерия равно:

Ввиду того, что

следовательно, нулевую гипотезу о нормальном распределении принимаем.

14555

Источник

Использование
этого критерия основано на применении
такой меры (статистики) расхождения
между теоретическим F(x)
и эмпирическим распределением F*_п(x),
которая приближенно подчиняется закону
распределения χ². Гипотеза
Н₀
о согласованности распределений
проверяется путем анализа распределения
этой статистики. Применение критерия
требует построения статистического
ряда.

Итак,
пусть выборка представлена статистическим
рядом с количеством разрядов M.
Наблюдаемая частота попаданий в i–й
разряд n_i.
В соответствии с теоретическим законом
распределения ожидаемая частота
попаданий в i-й
разряд составляет F_i.
Разность между наблюдаемой и ожидаемой
частотой составит величину (n_i
– F_i).
Для нахождения общей степени расхождения
между F(x)
и F*_п(x)
необходимо подсчитать взвешенную сумму
квадратов разностей по всем разрядам
статистического ряда

(3.7)

Величина
χ²
при неограниченном увеличении n
имеет
χ²-распределение
(асимптотически распределена как χ²).
Это распределение зависит от числа
степеней свободы k,
т.е. количества независимых значений
слагаемых в выражении (3.7). Число степеней
свободы равно числу y
минус число линейных связей, наложенных
на выборку. Одна связь существует в силу
того, что любая частота может быть
вычислена по совокупности частот в
оставшихся M–1
разрядах. Кроме того, если параметры
распределения неизвестны заранее, то
имеется еще одно ограничение, обусловленное
подгонкой распределения к выборке. Если
по выборке определяются S
параметров
распределения, то число степеней свободы
составит k=M
–S–1.

Область
принятия гипотезы Н₀
определяется условием χ²<
χ²(k;a),
где χ²(k;a)
– критическая точка
χ2-распределения с уровнем значимости
a.
Вероятность ошибки первого рода равна
a,
вероятность ошибки второго рода четко
определить нельзя, потому что существует
бесконечно большое множество различных
способов несовпадения распределений.
Мощность критерия зависит от количества
разрядов и объема выборки. Критерий
рекомендуется применять при n>200,
допускается применение при n>40,
именно при таких условиях критерий
состоятелен (как правило, отвергает
неверную нулевую гипотезу).

Алгоритм проверки
по критерию

1. Построить
гистограмму равновероятностным способом.

2. По виду гистограммы
выдвинуть гипотезу

H₀
: f(x)
= f₀(x),

H₁
: f(x)
¹
f₀(x),

где
f₀(x)
– плотность вероятности гипотетического
закона распределения
(например, равномерного,
экспоненциального,
нормального).

Замечание.
Гипотезу об экспоненциальном законе
распределения можно выдвигать в том
случае, если все числа в выборке
положительные.

3. Вычислить значение
критерия по формуле

где частота
попадания вi-тый интервал;

p_i– теоретическая вероятность
попадания случайной величины вi–
тый интервал при условии, что гипотезаH₀верна.

Формулы
для расчета p_i
в случае экспоненциального, равномерного
и нормального законов соответственно
равны.

Экспоненциальный
закон

. (3.8)

При
этом A₁= 0, B_m
= +¥.

Равномерный
закон

.
(3.9)

Нормальный закон

. (3.10)

При
этом A₁= -¥,
B_M
= +¥.

Замечания.
После вычисления всех вероятностей p_i
проверить, выполняется ли контрольное
соотношение

Функция
Ф(х)-
нечетная. Ф(+¥)
= 1.

4.
Из таблицы ” Хи-квадрат” Приложения
выбирается значение
,
гдеa
– заданный уровень значимости (a
= 0,05 или a
= 0,01), а k–
число степеней свободы, определяемое
по формуле

k
= M
– 1 – S.

Здесь
S
– число параметров, от которых зависит
выбранный гипотезой H₀
закон распределения. Значения S
для равномерного закона равно 2, для
экспоненциального – 1, для нормального
– 2.

5.
Если
,
то гипотезаH₀
отклоняется. В противном случае нет
оснований ее отклонить: с вероятностью
1 – b
она верна, а с вероятностью – b
неверна, но величина b
неизвестна.

Пример3.1.
С помощью критерия c²
выдвинуть и проверить гипотезу о законе
распределения случайной величины X,
вариационный ряд, интервальные
таблицы и гистограммы распределения
которой приведены в примере 1.2. Уровень
значимости a
равен 0,05.

Решение.
По виду гистограмм выдвигаем гипотезу
о том, что случайная величина X
распределена по нормальному закону:

H₀
: f(x)
= N(m,
s);

H₁
: f(x)
¹
N(m,
s).

Значение критерия
вычисляем по формуле :

(3.11)

Как отмечалось
выше, при проверке гипотезы предпочтительнее
использовать равновероятностную
гистограмму. В этом случае

Теоретические
вероятности p_i
рассчитываем по формуле (3.10). При этом
полагаем, что

p₁
= 0,5(Ф((-4,5245+1,7)/1,98)-Ф((-¥+1,7)/1,98))
= 0,5(Ф(-1,427)-Ф(-¥))
=

=
0,5(-0,845+1) = 0,078.

p₂=
0,5(Ф((-3,8865+1,7)/1,98)-Ф((-4,5245+1,7)/1,98)) =

=
0,5(Ф(-1,104)+0,845) = 0,5(-0,729+0,845) = 0,058.

p₃=
0,094; p₄=
0,135; p₅=
0,118; p₆=
0,097; p₇=
0,073; p₈=
0,059; p₉=
0,174;

p₁₀=
0,5(Ф((+¥+1,7)/1,98)-Ф((0,6932+1,7)/1,98))
= 0,114.

После этого
проверяем выполнение контрольного
соотношения

Тогда

=
100 ×
(0,0062 + 0,0304 + 0,0004 + 0,0091 + 0,0028 + 0,0001 + 0,0100 +

+
0,0285 + 0,0315 + 0,0017 ) = 100 ×
0,1207 = 12,07.

После этого из
таблицы “Хи – квадрат” выбираем
критическое значение

Так
как
то гипотезаH₀
принимается (нет основания ее отклонить).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Pearson’s chi-squared test ( $chi ^{2}$ ) is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900.^[1] In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to Pearson χ-squared test or statistic are used.

It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable.
A simple example is the hypothesis that an ordinary six-sided die is “fair” (i. e., all six outcomes are equally likely to occur.)

Definition[edit]

Pearson’s chi-squared test is used to assess three types of comparison: goodness of fit, homogeneity, and independence.

A test of goodness of fit establishes whether an observed frequency distribution differs from a theoretical distribution.
A test of homogeneity compares the distribution of counts for two or more groups using the same categorical variable (e.g. choice of activity—college, military, employment, travel—of graduates of a high school reported a year after graduation, sorted by graduation year, to see if number of graduates choosing a given activity has changed from class to class, or from decade to decade).^[2]
A test of independence assesses whether observations consisting of measures on two variables, expressed in a contingency table, are independent of each other (e.g. polling responses from people of different nationalities to see if one’s nationality is related to the response).

For all three tests, the computational procedure includes the following steps:

Calculate the chi-squared test statistic, $chi ^{2}$ , which resembles a normalized sum of squared deviations between observed and theoretical frequencies (see below).
Determine the degrees of freedom, df, of that statistic.
1. For a test of goodness-of-fit, df = Cats − Parms, where Cats is the number of observation categories recognized by the model, and Parms is the number of parameters in the model adjusted to make the model best fit the observations: The number of categories reduced by the number of fitted parameters in the distribution.
2. For a test of homogeneity, df = (Rows − 1)×(Cols − 1), where Rows corresponds to the number of categories (i.e. rows in the associated contingency table), and Cols corresponds to the number of independent groups (i.e. columns in the associated contingency table).^[2]
3. For a test of independence, df = (Rows − 1)×(Cols − 1), where in this case, Rows corresponds to the number of categories in one variable, and Cols corresponds to the number of categories in the second variable.^[2]
Select a desired level of confidence (significance level, p-value, or the corresponding alpha level) for the result of the test.
Compare $chi ^{2}$ to the critical value from the chi-squared distribution with df degrees of freedom and the selected confidence level (one-sided, since the test is only in one direction, i.e. is the test value greater than the critical value?), which in many cases gives a good approximation of the distribution of $chi ^{2}$ .
Sustain or reject the null hypothesis that the observed frequency distribution is the same as the theoretical distribution based on whether the test statistic exceeds the critical value of $chi ^{2}$ . If the test statistic exceeds the critical value of $chi ^{2}$ , the null hypothesis ( $H_{0}$ = there is no difference between the distributions) can be rejected, and the alternative hypothesis ( $H_{1}$ = there is a difference between the distributions) can be accepted, both with the selected level of confidence. If the test statistic falls below the threshold $chi ^{2}$ value, then no clear conclusion can be reached, and the null hypothesis is sustained (we fail to reject the null hypothesis), though not necessarily accepted.

Test for fit of a distribution[edit]

Discrete uniform distribution[edit]

In this case observations are divided among cells. A simple application is to test the hypothesis that, in the general population, values would occur in each cell with equal frequency. The “theoretical frequency” for any cell (under the null hypothesis of a discrete uniform distribution) is thus calculated as

$E_i=frac{N}{n}, ,$

and the reduction in the degrees of freedom is p=1 , notionally because the observed frequencies $O_{i}$ are constrained to sum to .

One specific example of its application would be its application for log-rank test.

Other distributions[edit]

When testing whether observations are random variables whose distribution belongs to a given family of distributions, the “theoretical frequencies” are calculated using a distribution from that family fitted in some standard way. The reduction in the degrees of freedom is calculated as p=s+1 , where is the number of parameters used in fitting the distribution. For instance, when checking a three-parameter Generalized gamma distribution, p=4 , and when checking a normal distribution (where the parameters are mean and standard deviation), p=3 , and when checking a Poisson distribution (where the parameter is the expected value), p=2 . Thus, there will be n-p degrees of freedom, where is the number of categories.

The degrees of freedom are not based on the number of observations as with a Student’s t or F-distribution. For example, if testing for a fair, six-sided die, there would be five degrees of freedom because there are six categories or parameters (each number); the number of times the die is rolled does not influence the number of degrees of freedom.

Calculating the test-statistic[edit]

Upper-tail critical values of chi-square distribution^[3]
Degrees of freedom	Probability less than the critical value
0.90	0.95	0.975	0.99	0.999
1	2.706	3.841	5.024	6.635	10.828
2	4.605	5.991	7.378	9.210	13.816
3	6.251	7.815	9.348	11.345	16.266
4	7.779	9.488	11.143	13.277	18.467
5	9.236	11.070	12.833	15.086	20.515
6	10.645	12.592	14.449	16.812	22.458
7	12.017	14.067	16.013	18.475	24.322
8	13.362	15.507	17.535	20.090	26.125
9	14.684	16.919	19.023	21.666	27.877
10	15.987	18.307	20.483	23.209	29.588
11	17.275	19.675	21.920	24.725	31.264
12	18.549	21.026	23.337	26.217	32.910
13	19.812	22.362	24.736	27.688	34.528
14	21.064	23.685	26.119	29.141	36.123
15	22.307	24.996	27.488	30.578	37.697
16	23.542	26.296	28.845	32.000	39.252
17	24.769	27.587	30.191	33.409	40.790
18	25.989	28.869	31.526	34.805	42.312
19	27.204	30.144	32.852	36.191	43.820
20	28.412	31.410	34.170	37.566	45.315
21	29.615	32.671	35.479	38.932	46.797
22	30.813	33.924	36.781	40.289	48.268
23	32.007	35.172	38.076	41.638	49.728
24	33.196	36.415	39.364	42.980	51.179
25	34.382	37.652	40.646	44.314	52.620
26	35.563	38.885	41.923	45.642	54.052
27	36.741	40.113	43.195	46.963	55.476
28	37.916	41.337	44.461	48.278	56.892
29	39.087	42.557	45.722	49.588	58.301
30	40.256	43.773	46.979	50.892	59.703
31	41.422	44.985	48.232	52.191	61.098
32	42.585	46.194	49.480	53.486	62.487
33	43.745	47.400	50.725	54.776	63.870
34	44.903	48.602	51.966	56.061	65.247
35	46.059	49.802	53.203	57.342	66.619
36	47.212	50.998	54.437	58.619	67.985
37	48.363	52.192	55.668	59.893	69.347
38	49.513	53.384	56.896	61.162	70.703
39	50.660	54.572	58.120	62.428	72.055
40	51.805	55.758	59.342	63.691	73.402
41	52.949	56.942	60.561	64.950	74.745
42	54.090	58.124	61.777	66.206	76.084
43	55.230	59.304	62.990	67.459	77.419
44	56.369	60.481	64.201	68.710	78.750
45	57.505	61.656	65.410	69.957	80.077
46	58.641	62.830	66.617	71.201	81.400
47	59.774	64.001	67.821	72.443	82.720
48	60.907	65.171	69.023	73.683	84.037
49	62.038	66.339	70.222	74.919	85.351
50	63.167	67.505	71.420	76.154	86.661
51	64.295	68.669	72.616	77.386	87.968
52	65.422	69.832	73.810	78.616	89.272
53	66.548	70.993	75.002	79.843	90.573
54	67.673	72.153	76.192	81.069	91.872
55	68.796	73.311	77.380	82.292	93.168
56	69.919	74.468	78.567	83.513	94.461
57	71.040	75.624	79.752	84.733	95.751
58	72.160	76.778	80.936	85.950	97.039
59	73.279	77.931	82.117	87.166	98.324
60	74.397	79.082	83.298	88.379	99.607
61	75.514	80.232	84.476	89.591	100.888
62	76.630	81.381	85.654	90.802	102.166
63	77.745	82.529	86.830	92.010	103.442
64	78.860	83.675	88.004	93.217	104.716
65	79.973	84.821	89.177	94.422	105.988
66	81.085	85.965	90.349	95.626	107.258
67	82.197	87.108	91.519	96.828	108.526
68	83.308	88.250	92.689	98.028	109.791
69	84.418	89.391	93.856	99.228	111.055
70	85.527	90.531	95.023	100.425	112.317
71	86.635	91.670	96.189	101.621	113.577
72	87.743	92.808	97.353	102.816	114.835
73	88.850	93.945	98.516	104.010	116.092
74	89.956	95.081	99.678	105.202	117.346
75	91.061	96.217	100.839	106.393	118.599
76	92.166	97.351	101.999	107.583	119.850
77	93.270	98.484	103.158	108.771	121.100
78	94.374	99.617	104.316	109.958	122.348
79	95.476	100.749	105.473	111.144	123.594
80	96.578	101.879	106.629	112.329	124.839
81	97.680	103.010	107.783	113.512	126.083
82	98.780	104.139	108.937	114.695	127.324
83	99.880	105.267	110.090	115.876	128.565
84	100.980	106.395	111.242	117.057	129.804
85	102.079	107.522	112.393	118.236	131.041
86	103.177	108.648	113.544	119.414	132.277
87	104.275	109.773	114.693	120.591	133.512
88	105.372	110.898	115.841	121.767	134.746
89	106.469	112.022	116.989	122.942	135.978
90	107.565	113.145	118.136	124.116	137.208
91	108.661	114.268	119.282	125.289	138.438
92	109.756	115.390	120.427	126.462	139.666
93	110.850	116.511	121.571	127.633	140.893
94	111.944	117.632	122.715	128.803	142.119
95	113.038	118.752	123.858	129.973	143.344
96	114.131	119.871	125.000	131.141	144.567
97	115.223	120.990	126.141	132.309	145.789
98	116.315	122.108	127.282	133.476	147.010
99	117.407	123.225	128.422	134.642	148.230
100	118.498	124.342	129.561	135.807	149.449

The value of the test-statistic is

${displaystyle chi ^{2}=sum _{i=1}^{n}{frac {(O_{i}-E_{i})^{2}}{E_{i}}}=Nsum _{i=1}^{n}{frac {left(O_{i}/N-p_{i}right)^{2}}{p_{i}}}}$

where

The chi-squared statistic can then be used to calculate a p-value by comparing the value of the statistic to a chi-squared distribution. The number of degrees of freedom is equal to the number of cells , minus the reduction in degrees of freedom, .

The result about the numbers of degrees of freedom is valid when the original data are multinomial and hence the estimated parameters are efficient for minimizing the chi-squared statistic. More generally however, when maximum likelihood estimation does not coincide with minimum chi-squared estimation, the distribution will lie somewhere between a chi-squared distribution with n-1-p and n-1 degrees of freedom (See for instance Chernoff and Lehmann, 1954).

Bayesian method[edit]

In Bayesian statistics, one would instead use a Dirichlet distribution as conjugate prior. If one took a uniform prior, then the maximum likelihood estimate for the population probability is the observed probability, and one may compute a credible region around this or another estimate.

Testing for statistical independence[edit]

In this case, an “observation” consists of the values of two outcomes and the null hypothesis is that the occurrence of these outcomes is statistically independent. Each observation is allocated to one cell of a two-dimensional array of cells (called a contingency table) according to the values of the two outcomes. If there are r rows and c columns in the table, the “theoretical frequency” for a cell, given the hypothesis of independence, is

$E_{{i,j}}=Np_{{icdot }}p_{{cdot j}},$

where is the total sample size (the sum of all cells in the table), and

$p_{{icdot }}={frac {O_{{icdot }}}{N}}=sum _{{j=1}}^{c}{frac {O_{{i,j}}}{N}},$

is the fraction of observations of type i ignoring the column attribute (fraction of row totals), and

${displaystyle p_{cdot j}={frac {O_{cdot j}}{N}}=sum _{i=1}^{r}{frac {O_{i,j}}{N}}}$

is the fraction of observations of type j ignoring the row attribute (fraction of column totals). The term “frequencies” refers to absolute numbers rather than already normalized values.

The value of the test-statistic is

$chi ^{2}=sum _{{i=1}}^{{r}}sum _{{j=1}}^{{c}}{(O_{{i,j}}-E_{{i,j}})^{2} over E_{{i,j}}}$

$=Nsum _{{i,j}}p_{{icdot }}p_{{cdot j}}left({frac {(O_{{i,j}}/N)-p_{{icdot }}p_{{cdot j}}}{p_{{icdot }}p_{{cdot j}}}}right)^{2}$

Note that $chi ^{2}$ is 0 if and only if $O_{i,j} = E_{i,j} forall i,j$ , i.e. only if the expected and true number of observations are equal in all cells.

Fitting the model of “independence” reduces the number of degrees of freedom by p = r + c − 1. The number of degrees of freedom is equal to the number of cells rc, minus the reduction in degrees of freedom, p, which reduces to (r − 1)(c − 1).

For the test of independence, also known as the test of homogeneity, a chi-squared probability of less than or equal to 0.05 (or the chi-squared statistic being at or larger than the 0.05 critical point) is commonly interpreted by applied workers as justification for rejecting the null hypothesis that the row variable is independent of the column variable.^[4]
The alternative hypothesis corresponds to the variables having an association or relationship where the structure of this relationship is not specified.

Assumptions[edit]

The chi-squared test, when used with the standard approximation that a chi-squared distribution is applicable, has the following assumptions:^[5]

Simple random sample: The sample data is a random sampling from a fixed distribution or population where every collection of members of the population of the given sample size has an equal probability of selection. Variants of the test have been developed for complex samples, such as where the data is weighted. Other forms can be used such as purposive sampling.^[6]
Sample size (whole table): A sample with a sufficiently large size is assumed. If a chi squared test is conducted on a sample with a smaller size, then the chi squared test will yield an inaccurate inference. The researcher, by using chi squared test on small samples, might end up committing a Type II error. For small sample sizes the Cash test is preferred.^[7]^[8]
Expected cell count: Adequate expected cell counts. Some require 5 or more, and others require 10 or more. A common rule is 5 or more in all cells of a 2-by-2 table, and 5 or more in 80% of cells in larger tables, but no cells with zero expected count. When this assumption is not met, Yates’s correction is applied.
Independence: The observations are always assumed to be independent of each other. This means chi-squared cannot be used to test correlated data (like matched pairs or panel data). In those cases, McNemar’s test may be more appropriate.

A test that relies on different assumptions is Fisher’s exact test; if its assumption of fixed marginal distributions is met it is substantially more accurate in obtaining a significance level, especially with few observations. In the vast majority of applications this assumption will not be met, and Fisher’s exact test will be over conservative and not have correct coverage.^[9]

Derivation[edit]

Examples[edit]

Fairness of dice[edit]

A 6-sided die is thrown 60 times. The number of times it lands with 1, 2, 3, 4, 5 and 6 face up is 5, 8, 9, 8, 10 and 20, respectively. Is the die biased, according to the Pearson’s chi-squared test at a significance level of 95% and/or 99%?

The null hypothesis is that the die is unbiased, hence each number is expected to occur the same number of times, in this case, 60/n = 10. The outcomes can be tabulated as follows:

	${displaystyle O_{i}}$	$E_{i}$	${displaystyle O_{i}-E_{i}}$	${displaystyle (O_{i}-E_{i})^{2}}$
1	5	10	−5	25
2	8	10	−2	4
3	9	10	−1	1
4	8	10	−2	4
5	10	10	0	0
6	20	10	10	100
Sum	134

We then consult an Upper-tail critical values of chi-square distribution table, the tabular value refers to the sum of the squared variables each divided by the expected outcomes. For the present example, this means

${displaystyle {X^{2}}=25/10+4/10+1/10+4/10+0/10+100/10=13.4}$

This is the experimental result whose unlikeliness (with a fair die) we wish to estimate.

Degrees of freedom	Probability less than the critical value
0.90	0.95	0.975	0.99	0.999
5	9.236	11.070	12.833	15.086	20.515

The experimental sum of 13.4 is between the critical values of 97.5% and 99% significance or confidence (p-value). Specifically, getting 20 rolls of 6, when the expectation is only 10 such values, is unlikely with a fair die.

Chi-Squared Goodness of Fit Test

In this context, the frequencies of both theoretical and empirical distributions are unnormalised counts, and for a chi-squared test the total sample sizes of both these distributions (sums of all cells of the corresponding contingency tables) have to be the same.

For example, to test the hypothesis that a random sample of 100 people has been drawn from a population in which men and women are equal in frequency, the observed number of men and women would be compared to the theoretical frequencies of 50 men and 50 women. If there were 44 men in the sample and 56 women, then

$chi^2 = {(44 - 50)^2 over 50} + {(56 - 50)^2 over 50} = 1.44.$

If the null hypothesis is true (i.e., men and women are chosen with equal probability), the test statistic will be drawn from a chi-squared distribution with one degree of freedom (because if the male frequency is known, then the female frequency is determined).

Consultation of the chi-squared distribution for 1 degree of freedom shows that the probability of observing this difference (or a more extreme difference than this) if men and women are equally numerous in the population is approximately 0.23. This probability is higher than conventional criteria for statistical significance (0.01 or 0.05), so normally we would not reject the null hypothesis that the number of men in the population is the same as the number of women (i.e., we would consider our sample within the range of what we would expect for a 50/50 male/female ratio.)

Problems[edit]

The approximation to the chi-squared distribution breaks down if expected frequencies are too low. It will normally be acceptable so long as no more than 20% of the events have expected frequencies below 5. Where there is only 1 degree of freedom, the approximation is not reliable if expected frequencies are below 10. In this case, a better approximation can be obtained by reducing the absolute value of each difference between observed and expected frequencies by 0.5 before squaring; this is called Yates’s correction for continuity.

In cases where the expected value, E, is found to be small (indicating a small underlying population probability, and/or a small number of observations), the normal approximation of the multinomial distribution can fail, and in such cases it is found to be more appropriate to use the G-test, a likelihood ratio-based test statistic. When the total sample size is small, it is necessary to use an appropriate exact test, typically either the binomial test or, for contingency tables, Fisher’s exact test. This test uses the conditional distribution of the test statistic given the marginal totals, and thus assumes that the margins were determined before the study; alternatives such as Boschloo’s test which do not make this assumption are uniformly more powerful.

It can be shown that the $chi ^{2}$ test is a low order approximation of the Psi test.^[12] The above reasons for the above issues become apparent when the higher order terms are investigated.

Notes[edit]

^ Pearson, Karl (1900). “On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling”. Philosophical Magazine. Series 5. 50 (302): 157–175. doi:10.1080/14786440009463897.
^ ^a ^b ^c David E. Bock, Paul F. Velleman, Richard D. De Veaux (2007). “Stats, Modeling the World,” pp. 606-627, Pearson Addison Wesley, Boston, ISBN 0-13-187621-X
^ “1.3.6.7.4. Critical Values of the Chi-Square Distribution”. Retrieved 14 October 2014.
^ “Critical Values of the Chi-Squared Distribution”. NIST/SEMATECH e-Handbook of Statistical Methods. National Institute of Standards and Technology.
^ McHugh, Mary (15 June 2013). “The chi-square test of independence”. Biochemia Medica. 23 – via National Library of Medicine.
^ See Field, Andy. Discovering Statistics Using SPSS. for assumptions on Chi Square.
^ Cash, W. (1979). “Parameter estimation in astronomy through application of the likelihood ratio”. The Astrophysical Journal. 228: 939. Bibcode:1979ApJ…228..939C. doi:10.1086/156922. ISSN 0004-637X.
^ “The Cash Statistic and Forward Fitting”. hesperia.gsfc.nasa.gov. Retrieved 19 October 2021.
^ “A Bayesian Formulation for Exploratory Data Analysis and Goodness-of-Fit Testing” (PDF). International Statistical Review. p. 375.
^ Statistics for Applications. MIT OpenCourseWare. Lecture 23. Pearson’s Theorem. Retrieved 21 March 2007.
^ “Seven Proofs of the Pearson Chi-Squared Independence Test and its Graphical Interpretation”. SSRN (preprint). p. 5-6. SSRN 3239829.
^ Jaynes, E.T. (2003). Probability Theory: The Logic of Science. C. University Press. p. 298. ISBN 978-0-521-59271-0. (Link is to a fragmentary edition of March 1996.)

References[edit]

Chernoff, H.; Lehmann, E. L. (1954). “The Use of Maximum Likelihood Estimates in $chi ^{2}$ Tests for Goodness of Fit”. The Annals of Mathematical Statistics. 25 (3): 579–586. doi:10.1214/aoms/1177728726.
Plackett, R. L. (1983). “Karl Pearson and the Chi-Squared Test”. International Statistical Review. International Statistical Institute (ISI). 51 (1): 59–72. doi:10.2307/1402731. JSTOR 1402731.
Greenwood, P.E.; Nikulin, M.S. (1996). A guide to chi-squared testing. New York: Wiley. ISBN 0-471-55779-X.

Источник

Проверка гипотезы по критерию Хи квадрат Пирсона

Статистика критерия[править | править код]

Проверка сложных гипотез[править | править код]

О мощности критерия[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Definition[edit]