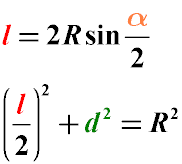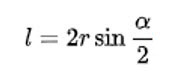Как посчитать хорду окружности
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
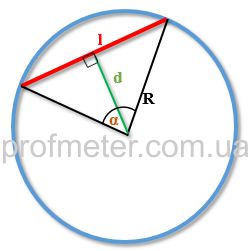
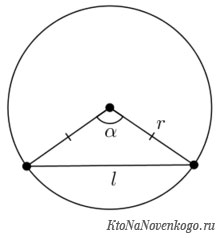
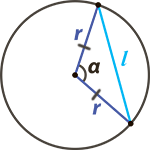
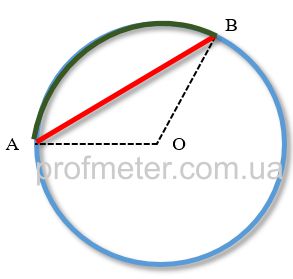
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
Пример
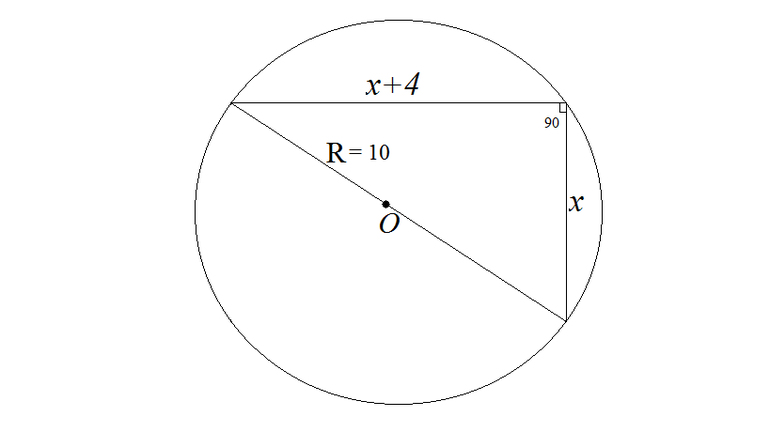
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
Хорда окружности – определение, свойства, теорема
Хорда в геометрии
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
- Это отрезок с наибольшей длиною в окружности это диаметр. Он обязательно будет проходить через центр круга.
- Если есть две равные дуги, то их отрезки, которые их стягивают, будут равны.
- Хорда, которая перпендикулярна диаметру, будет делить этот отрезок и его дугу на две одинаковые части (справедливо и обратное утверждение).
- Самый маленький отрезок в окружности это точка.
- Хорды будут равны, если они находятся на одном расстоянии от центра окружности (справедливо и обратное утверждение).
- При сравнении двух отрезков в кругу большая из них окажется ближе к центру окружности.
- Дуги, которые находятся между двумя параллельными хордами, равны.
Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
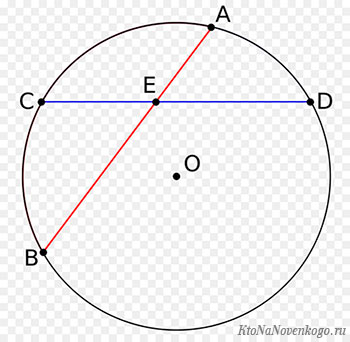
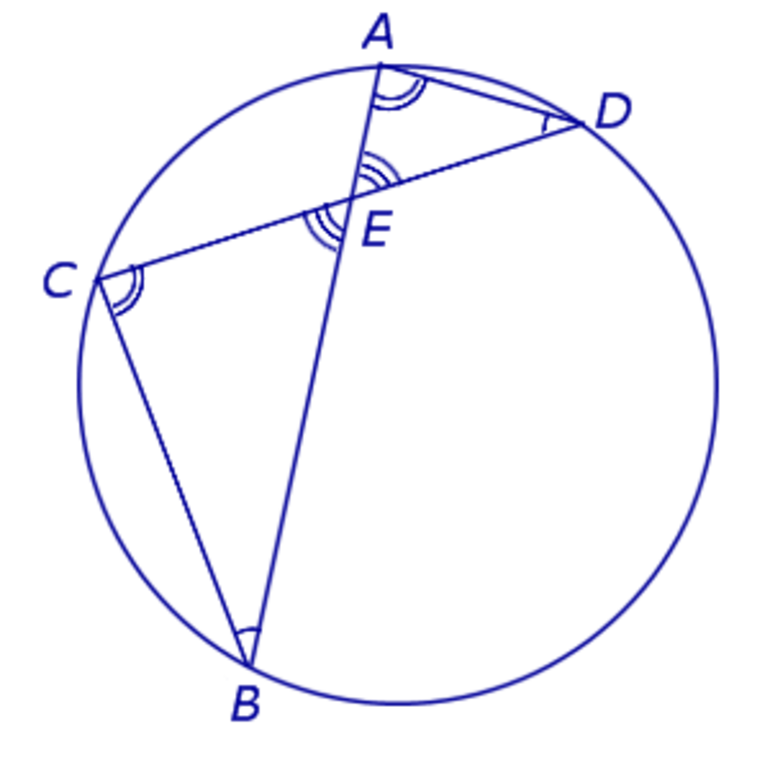
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
Касательная и секущая
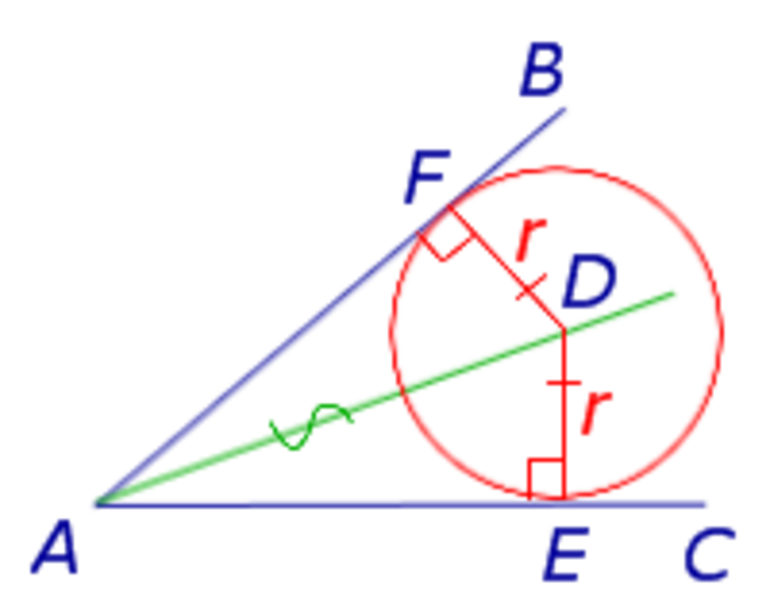
Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
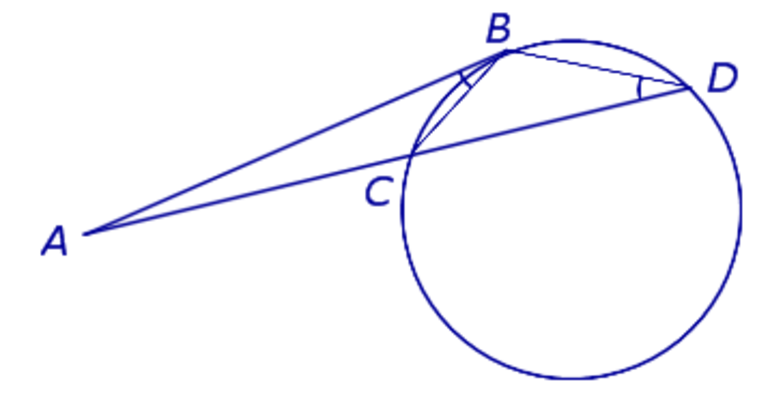
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Как найти хорду окружности пример
| Учебный курс | Решаем задачи по геометрии |
Определение хорды Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности – самая длинная хорда окружности. Свойства хорды к окружности
Свойства хорды и вписанного углаСвойства хорды и центрального углаФормулы нахождения хордыОбозначения в формулах: Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задачПримечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника. Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается. 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ; [spoiler title=”источники:”] http://nauka.club/matematika/geometriya/khorda-okruzhnosti.html http://profmeter.com.ua/communication/learning/course/course7/lesson318/ [/spoiler] |
Секущая и хорда окружности
Зачем что-то знать о секущих и хордах в окружности?
Как обычно, знание свойств и закономерностей сильно облегчает жизнь.
Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ!
Поехали!
Секущая и хорда окружности — коротко о главном
Секущая окружности
Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Хорда окружности
Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.
Длина хорды
Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle AСB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB). Тогда:
( displaystyle AB=2Rsin alpha).
Произведение длин отрезков хорд и секущих
Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется:
( displaystyle ABcdot AC=ADcdot AE).
Теорема о секущей и касательной
Для любых секущей и касательной, проходящих через точку ( A), верно:
( displaystyle A{{C}^{2}}=ADcdot AE).
А теперь подробнее…
Определения секущей и хорды окружности
Давай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки.
Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.
Кстати, заметил ли ты, что на первом рисунке хорда ( displaystyle BC) является кусочком секущей ( displaystyle AC)?
Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас ( displaystyle AB) – она же снаружи, верно?
Что же мы должны знать о секущей и хорде окружности?
Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности.
Длина хорды окружности
Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle ACB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB).
Тогда ( Largefrac{AB}{sin alpha }=2R)
Узнал теорему синусов?
Значит, длину хорды окружности можно найти по формуле:
Произведение длин отрезков хорд и секущих
Сейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности.
Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами.
Произведение длин отрезков хорд окружности
Для любых двух хорд окружности, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)
Произведение длин отрезков секущих окружности
Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)
Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком?
Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом.
Вопрос второй: Как не перепутать, что на что умножать?
Произведение длин отрезков хорд окружности — доказательство
Повторим формулировку.
Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)
А теперь докажем.
Рассмотрим ( triangle ABD) и ( triangle AEC). У них углы ( displaystyle A) равны как вертикальные и ( angle DBC=angle DEC), потому что они опираются на одну дугу ( displaystyle DC).
Значит, ( displaystyle triangle ABDsim triangle AEC) по двум углам (вспоминаем признаки подобия треугольников).
Запишем, что же нам даёт это подобие (и откроем маленький секрет!).
Произведение длин отрезков секущих окружности — доказательство
Еще раз формулировку…
Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)
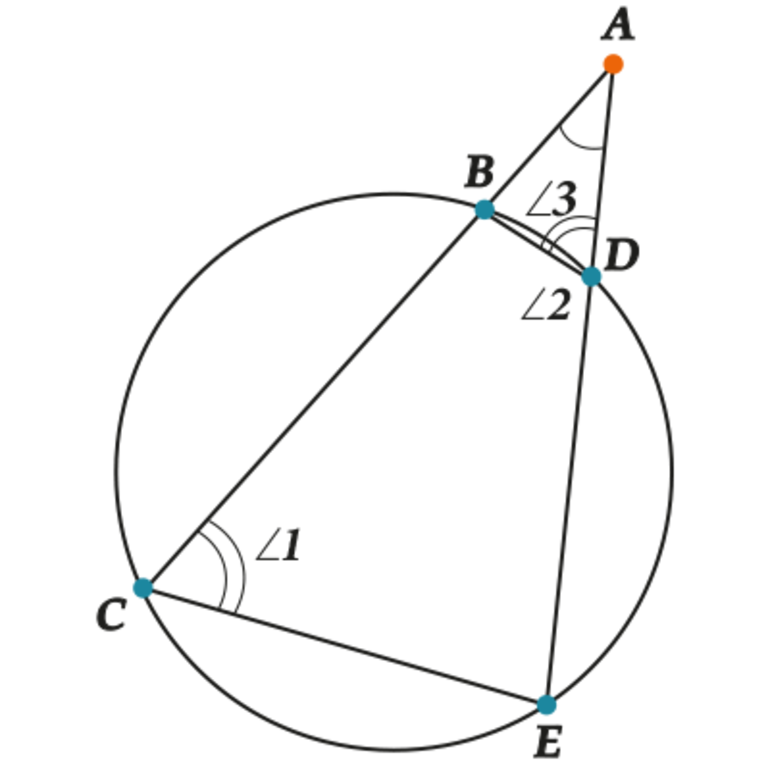
Снова рассмотрим ( displaystyle triangle ABD) и ( displaystyle triangle AEC).
- У них есть общий ( angle A);
- Четырехугольник ( BCED) — вписанный (срочно повторяем или читаем тему «Окружность. Вписанный угол»).
Значит, ( angle 1+angle 2=180{}^circ ) (сумма противоположных углов вписанного четырехугольника равна ( 180{}^circ )). Но ( angle 2+angle 3=180{}^circ ) — как смежные углы (смотри на картинку).
Что же получилось?
( left{ begin{array}{l}angle 1+angle 2=180{}^circ \angle 2+angle 3=180{}^circ end{array} right.Rightarrow angle 1=angle 3)
То есть ( underbrace{angle ACE}_{в triangle AEC}=underbrace{angle ADB}_{в triangle ABD }).
Из всего этого следует, что ( triangle AECsim triangle ABD) по двум углам (( angle A) – общий и ( angle ACE=angle ADB)).
Снова запишем отношение соответствующих сторон:
Теорема о секущей и касательной (секретное оружие)
А сейчас «секретное» оружие — теорема о секущей и касательной. Почему секретное?
Потому что множество задач ОГЭ и ЕГЭ можно решить с помощью этой теоремы. А акцент на ней в учебнике не делается. То есть ее как бы нет…
В предыдущем пункте мы выяснили, что ( ABcdot AC=ADcdot AE)
Но возникает вопрос: а что будет, если секущая ( AC) и «превратится» в касательную?
Видишь: осталось всего три зелёных точки? Оказывается, ничего страшного, всё почти так же. Формулируем:
Для любых секущей и касательной, проходящих через точку ( A), верно: ( Large A{{C}^{2}}=ADcdot AE).
Тут точки ( B) и ( C) как бы слились в одну – и на рисунке, и в формуле. Заметил?
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
| Учебный курс | Решаем задачи по геометрии |
Определение хорды Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности – самая длинная хорда окружности. Свойства хорды к окружности
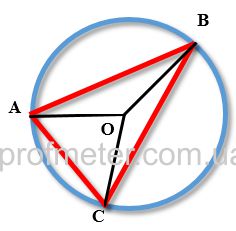
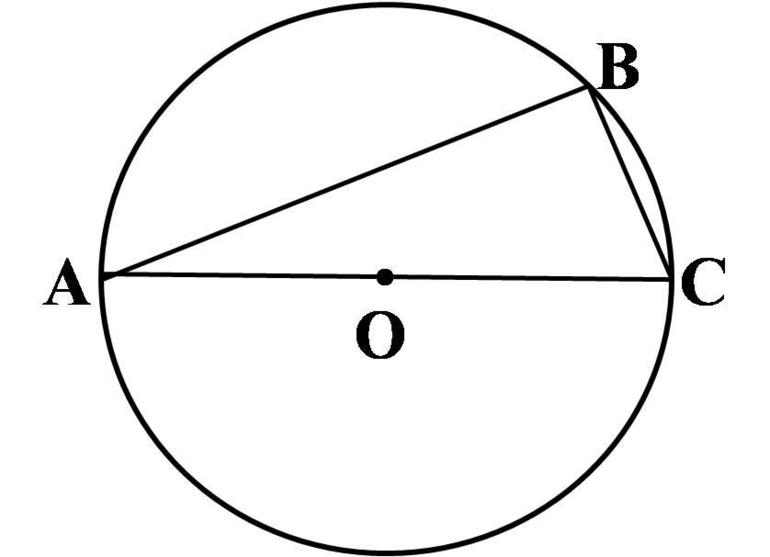
Свойства хорды и вписанного углаНа рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности – AB
Свойства хорды и центрального углаНа рисунке [2] центральный угол обозначен как AOB, хорда как AB.
Формулы нахождения хорды Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задач Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда Ответ: 5√10 Задача. Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
Задачи про окружность | Описание курса | Треугольник (Трикутник) |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!
Хорда — это геометрическая струна
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы подробно расскажем, что такое ХОРДА.
Слово это имеет древнегреческие корни и переводится как «струна».
Это очень точно характеризует ее внешний вид, так как хорда представляет собой прямую линию.
Хорда — это…
Термин этот применяется сразу в нескольких областях:
-
В геометрии хорда – это часть прямой, которая проходит между двумя точками на окружности или эллипсе;
- В биологии – скелетная позвоночная ось у всех животных, включая человека;
- В авиации хорда – это расстояние между двумя наиболее удаленными точками на крыле любого летательного аппарата;
- В медицине и анатомии – нервные волокна, которые соединяют стенки желудочков сердца и края желудочковой стороны створок клапанов (трехстворчатого и митрального);
- В ботанике хорда – это разновидность бурых водорослей, которая бывает двух видов – пушистая и нитевидная.
Но в рамках этой статьи мы подробно рассмотрим первый вариант значения термина ХОРДА. Тот, который применяют в геометрии, и который школьники подробно изучают в 7 классе.
Что такое хорда в геометрии
Хорда – это отрезок прямой, которая проходит через две точки на любой кривой линии. Это могут быть окружность, эллипс, гипербола или парабола.
Выглядит она вот так:
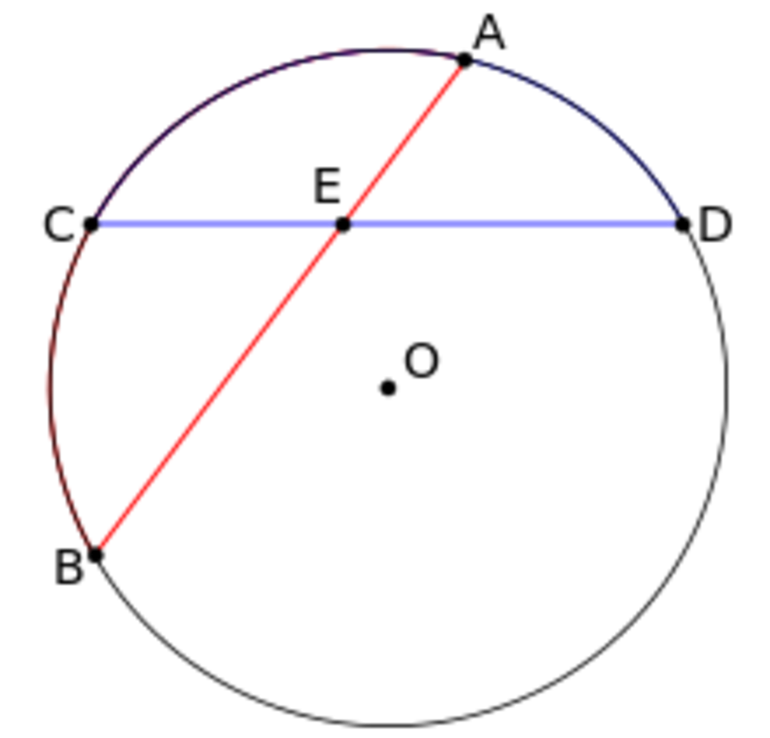
На этом рисунке изображены сразу две хорды – AB и CD. А есть еще частный случай, когда хорда проходит через центр окружности.
На данном рисунке это отрезок AB, будет являться диаметром окружности. И как нетрудно догадаться, это самая длинная хорда, которая может быть для данного примера.
Свойства хорды
Если сравнивать ее с другими частями окружности, то можно вывести целый ряд закономерностей.
Например, хорда и радиус:
- Если радиус поделил хорду пополам, то оба отрезка перпендикулярны друг другу. И наоборот – если хорда и радиус перпендикулярны, то радиус поделит хорду на две равные части.
- Если радиус поделил хорду на две равные половины, то он точно так же поделит на равные части и дугу окружности, которая «стягивает» эту хорду. Аналогично правдиво и обратное утверждение – если пополам делится дуга окружности, то пополам будет делиться и хорда.
- И наконец, объединяя первые два пункта. Если радиус может поделить дугу пополам, то он пересекает хорду под прямым углом.
Хорда и диаметр:
- Если диаметр разделяет хорду на две равные части, то они перпендикулярны друг другу. Верно и противоположное утверждение.
- Если диаметр разделяет пополам хорду, то точно так же делится и дуга, образованная этой хордой. Верно и обратное свойство.
- Если диаметр и хорда пересекаются под прямым углом, то он делит ее дугу пополам. Точно так же и в обратном случае.
Хорда и центр окружности:
- Если две или несколько хорд равны между собой, то они находятся на одном расстоянии до центра окружности. Верна и обратная зависимость между расстоянием от центра и длиной хорд.
- Чем длиннее хорда, тем ближе она находится к центру фигуры. И чем она короче, тем дальше она от центра и ближе к дуге.
- Если у хорды максимально возможная длина, то она является диаметром. А если наименьшая, то речь идет о точке.
И еще одно свойство. Если взять уже знакомый нам рисунок расположенный сразу под определением, то при пересечении хорд получается вот такая зависимость – произведение частей одной хорды равна произведению частей другой:
AE * EB = CE * ED
Как рассчитать ее длину
Длина хорды – это расстояние от одной точки пересечения с окружностью до другой. Чаще всего она обозначается латинской буквой «L».
Чтобы рассчитать длину хорды, надо знать значение радиуса и центрального угла. Формула выглядит так:
Вот и все, что мы хотели рассказать о ХОРДЕ.
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.
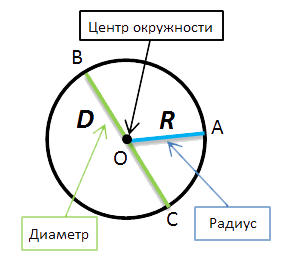
Рассмотрим более подробно окружность. Разберёмся, что называют центром,
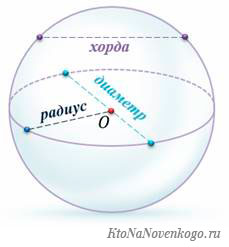
радиусом и диаметром окружности.
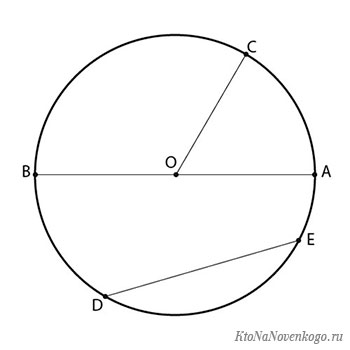
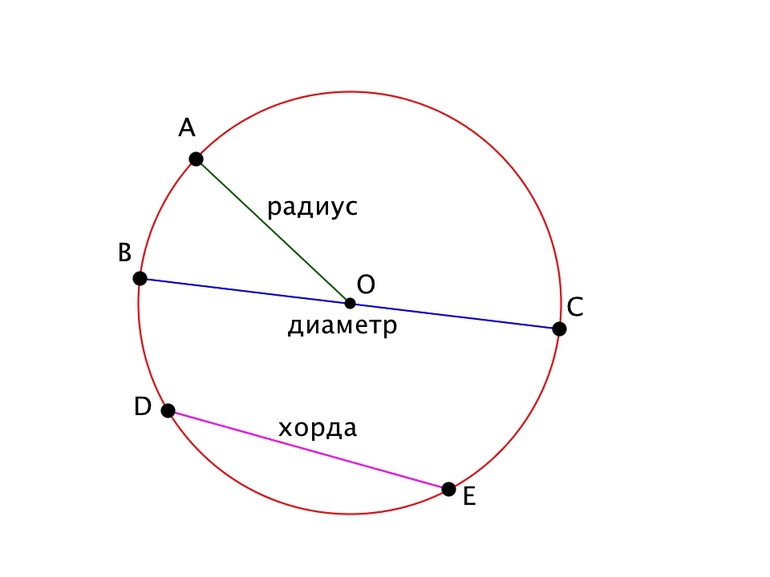
- (·)O — называется центром окружности.
- Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности.
Радиус окружности обозначается буквой «R». На рисунке выше —
это отрезок «OA». - Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.Диаметр окружности обозначается буквой «D».
На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому
справедливо выражение «D = 2R».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,
округленное до разряда сотых
π ≈ 3,14…
Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.
Запомните!
Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).
C = πD
C = 2πR
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD
D = С / π
D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
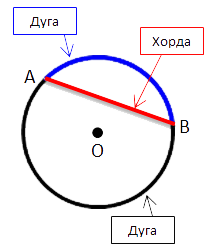
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.
Важно!
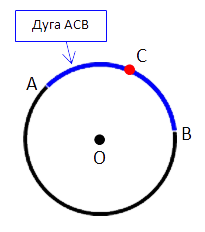
Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 мая 2020 в 10:27
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
, Радиус одной окружности равен 12 см, а второй-36см.Чему равно отношения длины первой окружности к длине второй окружности?
0
Спасибо
Ответить
6 мая 2020 в 15:48
Ответ для Владислав Заступневич
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
С=2πR
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=
0
Спасибо
Ответить
22 сентября 2016 в 19:03
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Помогите 2) чему равен деаметр если радиус равен а)12см б)10 децеметров
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12мСРОЧНО СЕГОДНЯ! ПРОШУ!!!
0
Спасибо
Ответить
23 сентября 2016 в 14:51
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус равен половине диаметра. Обратно диаметр равен двум радиусам. Подробнее здесь.
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м
0
Спасибо
Ответить
22 сентября 2016 в 18:54
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
1)Начертить окружность радиусом а)2 см пот буквой б)4 см 5 мм
0
Спасибо
Ответить
23 сентября 2016 в 14:46
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус окружности это расстояние от центра до любой точки окружности. Подробнее можно посмотреть вот здесь. На линейке циркулем отмеряем необходимый радиус и чертим окружность.
0
Спасибо
Ответить
24 января 2016 в 13:45
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Длина окружности и площадь круга.
Я не понимаю как найти площадь круга.
0
Спасибо
Ответить
19 сентября 2016 в 10:56
Ответ для Инна Шабрашина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
7 сентября 2015 в 21:08
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
радиус — 2,1 м.Найти длинну круга и его площадь(помогите плз)
0
Спасибо
Ответить
2 сентября 2016 в 15:18
Ответ для Игорь Желтоновский
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Длина окружности(l) вычисляется по формуле: l=2?r
Площадь круга(S) вычисляется по формуле: S=?r2
Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,12=13,8474
Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php
0
Спасибо
Ответить

![Хорда к окружности вместе с вписанным [1] и центральными углами [2] Хорда к окружности вместе с вписанным [1] и центральными углами [2]](https://profmeter.com.ua/upload/medialibrary/b1c/horda2.jpg)