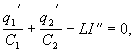Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
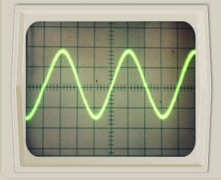
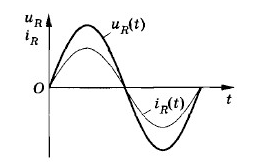
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
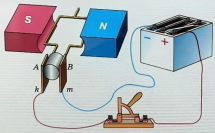
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
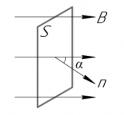
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
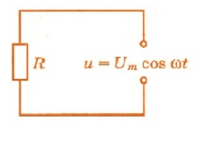
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
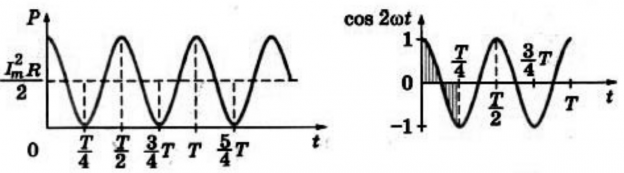
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
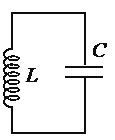
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
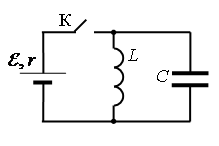
Задание EF18735
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
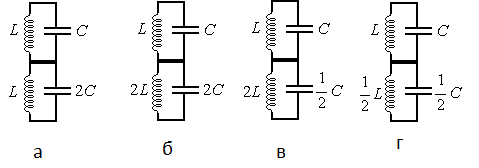
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
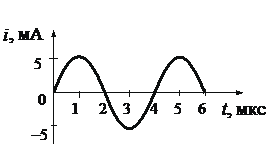
Задание EF18656
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.5k
Лучший ответ
Мореход
Искусственный Интеллект
(524249)
1 год назад
Найти ГДЕ?? Нагрузи по максимуму!
Yan Arefiev …Ученик (80)
1 год назад
В електр. поле. Задачу написать?
Yan Arefiev …Конечно
Остальные ответы
Не местный
Искусственный Интеллект
(238872)
1 год назад
Он достигается при максимальном напряжении и/или минимальном сопротивлении. Хотя если мы говорим об амплитуде при комплексной или реактивной нагрузке – там сложнее.
Вольный ветер
Искусственный Интеллект
(283175)
1 год назад
А и правда, как найти? Если нет вводных данных? Ты на столько ёбнутый?
Магистр схемы
Гуру
(4096)
1 год назад
Значение максимального тока можно найти по формуле корень из двух умножить на действующее значение, а вообще исходя из каких известных параметров находим? Можем и заряд на время поделить или на корень произведения индуктивности на емкость
Содержание:
- Определение и формула мощности тока
- Единицы измерения мощности тока
- Примеры решения задач
Электрический ток, на каком угодно участке цепи совершает некоторую работу (А). Допустим, что у нас есть произвольный участок
цепи (рис.1) между концами которого имеется напряжение U.
Работа, которая выполняется при перемещении заряда равного 1 Кл между точками A и B (рис.1) будет равна
U. В том случае, если через проводник протекает ток силой I за время равное
$Delta t$ по указанному выше участку пройдет заряд (q) равный:
$$q=I Delta t(1)$$
Следовательно, работа, которую совершает электрический ток на данном участке, равна:
$$A=U cdot I cdot Delta t(2)$$
Надо отметить, что выражение (2) является справедливым при I=const для любого участка цепи
(в таком участке могут содержаться проводники 1–го и 2–го рода).
Определение и формула мощности тока
Определение
Мощность тока – есть работа тока в единицу времени:
$$P=frac{A}{Delta t}$$
Формулой для вычисления мощности можно считать выражение:
$$P=U cdot I=I^{2} R(4)$$
В том случае, если участок цепи содержит источник тока, то формулу мощности можно представить в виде:
$$P=left(varphi_{1}-varphi_{2}right) I+varepsilon I$$
где $left(varphi_{1}-varphi_{2}right)$ – разность потенциалов,
$varepsilon$ – ЭДС источника, который включен в цепь.
Выражение (5) является интегральной записью. Это выражение можно представить в дифференциальной форме, если использовать понятие
удельной мощности ($P_{u d}=frac{Delta P}{Delta V}$ – мощность, развиваемая током в
единице объема проводника):
$$P_{u d}=rho j^{2}(6)$$
где j – плотность тока, $rho$ – удельное сопротивление.
Единицы измерения мощности тока
Основной единицей измерения мощности тока (как и мощности вообще) в системе СИ является: [P]=Вт=Дж/с.
В СГС: [P]=эрг/с.
1 Вт=107 эрг/( с).
Выражение (4) применяют в системе СИ для того, чтобы дать определение единицы напряжения.
Так, единицей напряжения (U) является вольт (В), который равен: 1 В= (1 Вт)/(1 А).
Вольтом называют электрическое напряжение, которое порождает в электроцепи постоянный ток силы 1 А при мощности 1 Вт.
Примеры решения задач
Пример
Задание. Какой должна быть сила тока, которая течет через обмотку электрического мотора для того,
чтобы полезная мощность двигателя (PA) стала максимальной?Какова максимальная полезная мощность?
Если двигатель постоянного тока подключен к напряжению U, сопротивление обмотки якоря – R.
Решение. Мощность, которую потребляет электроприбор, идет на нагревание (PQ) и совершение
работы (PA):
$$P=P_{Q}+P_{A}(1.1)$$
Мощность, идущую на нагревание можно рассчитать как:
$$P_{Q}=I^{2} R(1.2)$$
Потребляемую мощность найдем как:
$$P=I U(1.3)$$
Выразим $P_A$ из (1.1) и используем (1.2) и (1.3):
$$P_{A}=I U-I^{2} R$$
Для нахождения экстремума функции, которая представлена в выражении (1.4) найдем производную
$frac{d P_{A}}{d I}$ и приравняем ее к нулю:
$$frac{d P_{A}}{d I}=frac{d}{d I}left(I U-I^{2} Rright) ; U-2 I_{max } R=0 rightarrow I_{max }=frac{U}{2 R}(1.5)$$
Найдем максимальную полезную мощность,используя выражение (1.4) и Imax:
$$P_{A max }=frac{U}{2 R} U-left(frac{U}{2 R}right)^{2} R=frac{U^{2}}{4 R}$$
Ответ. $I_{max }=frac{U}{2 R} . P_{text {Amax}}=frac{U^{2}}{4 R}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
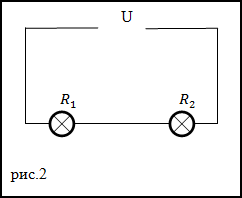
Задание. Электрические лампочкис мощностями
P1 и P2 номинальным напряжением U1=U2 соединяют последовательно
(рис.2) и включают в сеть с постоянным напряжением U. Какова мощность, потребляемая первой лампочкой P1*).
Решение. Лампочки по условию задачи соединены последовательно, значит сила тока, текущая через лампочки
одинакова, а падение напряжения на каждой из лампочек зависит от их сопротивлений. Искомую мощность можно найти как:
$$P_{1}^{*}=I^{2} R_{1}(2.1)$$
Сопротивления лампочек можно найти из данных в условиях номинальных мощностей:
$$R_{1}=frac{U_{1}^{2}}{P_{1}} ; R_{2}=frac{U_{2}^{2}}{P_{2}}(2.2)$$
Силу тока можно найти по закону Ома, учитывая, что лампочки соединены последовательно:
$$I=frac{U}{R_{1}+R_{2}}(2.3)$$
Решая уравнения (2.1) – (2.3) совместно получим:
$$P_{1}^{*}=frac{U^{2} U_{1}^{2}}{U_{1}^{2}+frac{P_{1} U_{2}^{2}}{P_{2}}}$$
Читать дальше: Формула напряжения электрического поля.
Колебательный контур ― это электрическая цепь, содержащая катушку индуктивности и конденсатор. В такой электрической цепи происходят колебания электрического тока и напряжения, и взаимная трансформация энергии электрического поля и энергии магнитного поля.
Процессы в колебательном контуре
У заряженного конденсатора на одной пластине находится определенное количество отрицательного заряда, а на другой ― положительного. Поскольку между пластинами конденсатора расположен диэлектрик (или воздух, и пластины не соприкасаются) ― заряд не может прямо перейти из одной пластины на другую. Но как только такой конденсатор оказывается подключенным к проводящей цепи, один конец которой связан с одной пластиной ― а другой с другой, заряды начинают переходить от пластины к пластине по «длинному пути» ― через всю цепь. Постепенно конденсатор разряжается ― теряет заряд, а в цепи наблюдается ток, ведь ток ― это направленные движения зарядов.
Если в цепи, кроме проводов и резисторов, находится катушка индуктивности, в равномерный и быстрый процесс перераспределения заряда вмешивается ЭДС самоиндукции катушки. Согласно правилу Ленца, втекающий в катушку ток вызывает ЭДС самоиндукции ― а ЭДС самоиндукции создает индуцированный ток, направленный так, чтобы препятствовать изменению тока в цепи. Если ток в цепи вдруг резко увеличивается ― индукционный ток стремиться его уменьшить, если ток в сети вдруг уменьшается ― индукционный ток стремиться его увеличивать.
Поэтому из―за катушки индуктивности заряд не переходит сразу через всю цепь, от одной обкладки конденсатора к другой. Сила тока в цепи медленно увеличивается ― потому что ее быстрому росту препятствует ЭДС самоиндукции катушки. Максимальной сила тока становится в тот момент, когда конденсатор разряжен (обе его обкладки обладают нулевым зарядом). В этот момент сила тока максимальна благодаря тому, что как только ее перестает наращивать конденсатор за счет потерянных зарядов ― ЭДС самоиндукции прекращает ей препятствовать.
Но разряженный конденсатор больше не может поддерживать силу тока ― ведь заряда на его обкладках нет, и не будь в цепи катушки индукции, ток бы прекратился. Однако здесь вновь срабатывает правило Ленца: после того как сила тока достигла максимума и начала уменьшаться ― в катушке возникает ЭДС и индукционные токи, которые стремятся вернуть силу тока такой, как она была ― максимальной. Поэтому, даже после того, как конденсатор разряжен, в цепи продолжает течь ток. Заряды попадают на обкладку конденсатора и постепенно заряжают ее. На этот раз, та обкладка конденсатора, которая была заряжена положительно и принимала заряд, начинает накапливать отрицательный заряд, а так обкладка, которая была заряжена отрицательно, становится заряженной положительно.
После того как конденсатор зарядится ― он вновь начинает разряжаться. Таким образом, в контуре происходят колебания заряда, силы тока, напряжения и энергий магнитного и электрического поля в катушке индуктивности и конденсаторе.
Цикл процессов, происходящих в колебательном контуре:
1: Начальное состояние ― конденсатор заряжен до максимального заряда Qm, но силы тока в цепи пока нет.
2. Конденсатор разряжается ― заряд переходит от одной обкладки на другую через всю цепь, сила тока в цепи постепенно увеличивается.
3. Конденсатор разряжен ― весь заряд с обкладок уже ушел, сила тока в цепи максимальна и равна Im.
4. Конденсатор заряжается ― сила тока в цепи уменьшается, а конденсатор получает заряд.
5. Конденсатор перезаряжен ― но теперь та обкладка, которая была положительно заряженной, стала отрицательно заряженной, и наоборот. Тока в цепи нет.
6. Конденсатор вновь разряжается, но в обратную сторону ― и ток течет в сторону, обратную тому, что был на этапе 2.
7. Конденсатор разряжен ― ток достиг максимума, а заряда на конденсаторе нет.
Для постоянного тока сила тока определялась как количество заряда, прошедшее через сечение проводника за некоторый промежуток времени: I =∆q/ ∆t, где
I ― сила тока, [А];
∆q ― количество заряда, [Кл];
∆t ― время, [c].
Но переменный ток изменяет в цепи свою величину и свое направление, поэтому силу переменного тока определяют как производную количества заряда по времени:
I = = qt‘, где
I ― сила тока, [А];
q ― количество заряда, [Кл];
t ― время, [c].
Заряд в колебательном контуре изменяется по гармоническому закону q(t) = Qmaxsin(ωt + φ0), где
q ― количество заряда, [Кл];
Qmax ― максимальный заряд (амплитуда колебаний заряда), [Кл];
ω ― циклическая частота колебаний [рад/с];
φ0 ― начальная фаза колебаний, [рад];
t ― время, [c].
Следовательно, сила тока в контуре изменяется по закону I = qt‘ = (Qmaxsin(ωt + φ0))t‘ = Qmaxωcos(ωt + φ0). При этом Qmaxω ― максимальная сила тока в цепи: Imax = Qmaxω.
Сила тока в цепи переменного тока равна I = Imaxcos(ωt + φ0), где
Imax ― максимальная сила тока в цепи, [A];
ω ― циклическая частота колебаний [рад/с];
φ0 ― начальная фаза колебаний, [рад];
t ― время, [c].
В колебательном контуре происходит трансформация энергии электрического поля в энергию магнитного поля.
Энергия электрического поля заряженного конденсатора равна We = = = , где
We ― энергия электрического поля конденсатора, [Дж];
C ― электроемкость конденсатора, [Ф];
U ― напряжение на обкладках конденсатора, [В];
q ― заряд на обкладках конденсатора, [Кл].
Так как напряжение на обкладках конденсатора в цепи переменного тока величина переменная, то и энергия электрического поля конденсатора ― переменна.
Энергия электрического поля конденсатора всегда положительна.
Энергия магнитного поля индукционной катушки равна Wm = , где
Wm ― энергия магнитного поля индукционной катушки, [Дж];
L ― индуктивность катушки, [Гн];
I ― сила тока, [А].
Как видно из формулы, энергия магнитного поля катушка также всегда положительна ― вне зависимости от того, какое из направлений силы тока принято в качестве положительного, а какое ― в качестве отрицательно, сила тока, возведенная в квадрат, всегда будет положительной величиной.
Согласно закону сохранения энергии, полная энергия колебательного контура постоянна в любой момент времени: W = Wm max = We max = We + Wm, где
W ― полная энергия свободных электромагнитных колебаний, W = const, [Дж];
Wm max ― максимальная энергия магнитного поля катушки индуктивности, [Дж];
We max ― максимальная энергия электрического поля конденсатора, [Дж];
Wm ― энергия магнитного поля катушки индуктивности, [Дж];
We ― энергия электрического поля конденсатора, [Дж];
или W = CU^2/2 + LI^2/2, где
W ― полная энергия свободных электромагнитных колебаний, W = const, [Дж];
C ― электроемкость конденсатора, [Ф];
U ― напряжение на обкладках конденсатора, [В];
Umax ― максимальное напряжение на обкладках конденсатора, [В];
L ― индуктивность катушки, [Гн];
I ― сила тока в катушке индуктивности, [А];
Imax ― максимальная сила тока в катушке индуктивности, [A].
Частота колебаний силы тока и напряжения в колебательном контуре определяются формулой Томпсона и зависят только от индуктивности катушки и электроемкости конденсатора. Частота и период гармонических колебаний в колебательном контуре равны v = и T = 2π√LC, где
v ― частота колебаний [Гц];
Т ― период колебаний [c];
L ― индуктивность катушки [Гн];
С ― электроёмкость конденсатора [Ф].
В курсе средней школы задачи по физике, при
решении которых требуется явное применение
дифференциального и интегрального исчисления
встречаются нечасто и в большинстве своем
вызывают значительные затруднения у
выпускников. Конечно, формулировки многих из
этих задач требуют ответы на вопросы, которые
можно легче получить не из явного решения
описывающих протекающие в них явления
дифференциальных уравнений, а привлекая
известные в физике законы сохранения.
Однако, сравнительный анализ различных
способов решения заданий, а также умение
использовать изученный в курсе алгебры и начал
анализа математический аппарат, безусловно
пригодятся выпускникам средней школы для
продолжения образования в стенах высшей.
Кроме того, весьма важно установление четкой
связи в умах учеников между различными ветвями
познания окружающего мира, их
взаимодополняющего влияния на точность и
четкость воссоздаваемой картины реальности. Я
полагаю, что задумываться об этом человек должен
как можно раньше, для того чтобы в будущей
деятельности плодотворно заниматься творческой
исследовательской работой.
Для начала рассмотрим задачу №1,
предлагавшуюся на вступительных экзаменах в
МФТИ , так как её результаты можно будет
использовать при решении последующих задач.
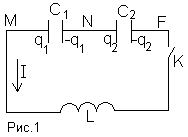
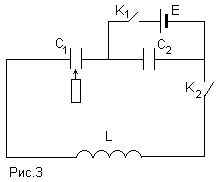
Задача 1. В цепи, изображенной на рис.1 , при
разомкнутом ключе К заряд на конденсаторе с
емкостью С2 (С2=С1/3) равен q2,
а конденсатор с емкостью С1 не заряжен.
Через какое время после замыкания ключа заряд на
конденсаторе С1 будет иметь максимальное
значение? Чему будет равен этот заряд? Омическими
потерями в катушке с индуктивностью L пренебречь.
Как показывает опыт работы, простая замена
преподавателем схемы из двух последовательно
соединенных конденсаторов С1 и С2
эквивалентным конденсатором хотя бы для
расчетов частоты колебаний контура может
совершенно запутать учеников, если они
предварительно сами не придут к осознанию
равносильности такой замены для ответа на
некоторые вопросы задачи. Попробуем составить
дифференциальное уравнение для описания
колебательных явлений в контуре. Хочется
отметить, что то, что близкому к радиотехнике
человеку кажется очевидным, вызывает кучу
вопросов у учеников, и преподаватель не должен
оставлять у них ощущения, что какие-то члены в
уравнении или, допустим, их знаки появляются
из-за случайных догадок, и подробно
последовательно остановиться на всех этапах
решения.
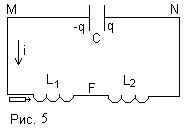
Обозначим буквами М, N, F соответствующие точки
схемы. Изначально на левой пластине конденсатора
С2 был заряд q20, на правой – (-q20).По
закону сохранения заряда сумма зарядов на левой
пластине конденсатора С2 правой пластине
конденсатора С1 остается постоянной, так
как заряды в эту часть схемы извне не поступают q1+q2=q20.
j M-j N=q1/C1; (1) j N-j F=q2/C2
(2). Выберем направление тока в цепи против
часовой стрелки, при этом заряд q2 должен
уменьшаться.
Падение напряжения на катушке индуктивности IR=j
M-j F+e сам. инд. По закону
электромагнитной индукции e cам.инд=Так как активное
сопротивление катушки индуктивности равно 0, то j M-j
FСкладывая
уравнения (1) и (2),получим j M-j F=q1/C1+q2/C2.
Подставляя данное соотношение в (3), мы получим
уравнение (4), справедливое для любого момента
времени:
q1/C1+q2/C2–
Продифференцируем это уравнение по времени,
получим:
учитывая, что
мы приходим к
дифференциальному уравнению
которое является уравнением гармонических
колебаний.
Общее решение этого уравнения I(t) = Imax sin(w
t+j ), где w 2=.
Инерционной частью в данной модели являются
заряды на конденсаторах q1 и q2,
которые не могут измениться мгновенно из-за
наличия индуктивности в цепи.
В момент замыкания ключа j M=j N, так
как конденсатор C1 не заряжен.
j M-j F=j N-j F=q20/C2.
Скорость изменения тока в начальный момент
времени конечна и равна q20/(C2L)(см.(3)),
его значение в этот момент времени также равно 0,
откуда в общем уравнении гармонических
колебаний находим первую const: j =0,
тогда I(t)=Imax sinw t.
w t;
так как
q2(0)=q20, то const=, а зависимость величин
зарядов конденсаторов от времени имеет вид:
В
моменты времени, когда ток в цепи максимален, Поскольку
активное сопротивление цепи равно 0, энергия
электромагнитного поля в процессе колебаний
сохраняется, т.е. в любой момент времени
справедливо соотношение
а
при максимальном значении тока из этого
соотношения получаем: отсюда
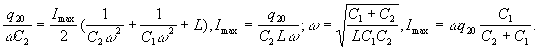
Данный результат можно получить и иначе. Найдем
равновесное распределение зарядов на
конденсаторах, которое отвечает отсутствию
протекания тока в цепи. При этом конденсаторы С1
и С2 оказываются включенными параллельно
друг другу.
U1=U2=q1p/C1=q2p/C2.Сумма
же зарядов на конденсаторах равна q20. Из
этих условий получаем, чтоВокруг этих положений и
осуществляются колебания зарядов на
конденсаторах с течением времени, амплитуда же
колебаний соответствует величине Imax/w , что
позволяет определить Imax.
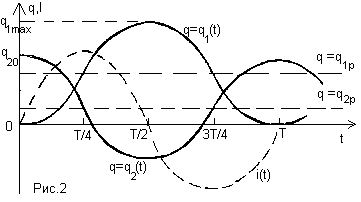
В нашем конкретном случае 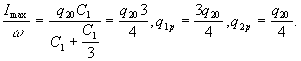
заряда q1 будет равняться 3q20/2, а
достигаться она будет в моменты времени t=T/2+n? T,
где Т – период колебаний, а n=0,1,2… На рис.2
приведены зависимости от времени величины
зарядов на конденсаторах и тока, протекающего в
цепи.
Подробный анализ данной задачи позволяет
подойти к решению более сложного задания,
предложенного на вступительных экзаменах в МФТИ.
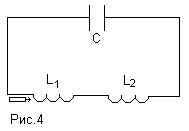
Задача 2. В схеме, предложенной на рисунке,
сначала замыкают ключ К1 и после того, как
конденсатор емкостью С2 полностью
зарядится от батареи с ЭДС E , ключ К1 раз-
мыкают и замыкают ключ К2. После замыкания
ключа К2 в схеме происходят свободные
незатухающие колебания. Когда напряжение на
конденсаторе емкостью С1 достигает
максимального значения, в него быстро (за время,
малое по сравнению с периодом колебаний)
вставляют диэлектрическую пластину, что
приводит к увеличению его емкости в e раз.
1)Чему равен начальный ток в цепи после
замыкания ключа К2?
2)Определить максимальный ток в цепи после
вставки пластины.
После замыкания ключа К1 конденсатор С2
заряжается до напряжения U= E , на его пластинах
скапливаются заряды q20 и -q20, q20=UC2.
После размыкания ключа К1 источник ЭДС не
играет роли в дальнейших процессах и
промежуточный этап после замыкания ключа К2
описывается найденными в задаче №1
соотношениями. Из зависимости зарядов q1 и q2
от времени следует, что а
За
время, малое по сравнению с периодом колебаний, в
процессе внесения в конденсатор C1 диэлектрической
пластины заряды на пластинах конденсаторов не
могут измениться, т.к. до начала процесса ток в
цепи равнялся 0,а максимальную скорость его
изменения можно оценить из уравнения (3).
Она конечна, следовательно, сразу после внесения
диэлектрической пластины ток в цепи по-прежнему
будет равняться 0.
Колебания зарядов на конденсаторах после
внесения диэлектрической пластины будут
осуществляться около новых равновесных
положений, определяемых условиями: Отсюда
находим равновесные распределения зарядов: В
момент времени, когда система проходит это
равновесное положение, ток в цепи достигает
своего максимального значения. Найдем величину
этого тока из закона сохранения энергии
электромагнитного поля в контуре в процессе
колебаний после помещения в него
диэлектрической пластины.
Данное уравнение относительно Imax является
квадратным, одно из его решений Imax=0
соответствует тривиальному случаю отсутствия
колебаний в контуре, а после упрощений можно
найти и его второе, интересующее нас решение:
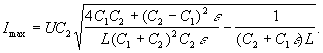
Следующие схемы предлагались на экзамене в
МФТИ в качестве наиболее сложных задач.
Задача №3. В колебательном контуре,
состоящем из двух последовательно соединенных
катушек с индуктивностью L1 и L2 и
конденсатора с емкостью С, происходят свободные
незатухающие колебания, при которых амплитуда
колебаний тока равна I0. Когда сила тока в
катушке L1 максимальна, в неё быстро ( за
время, малое по сравнению с периодом колебаний)
вставляют сердечник, что приводит к увеличению
её индуктивности в m раз.
1)Определить максимальное напряжение на
конденсаторе до вставки сердечника.
2)Определить максимальное напряжение на
конденсаторе после вставки сердечника.
Составим дифференциальное уравнение
колебаний, описывающее поведение данной цепи.
Все её элементы соединены последовательно, пусть
ток , протекающий в цепи, будет i(t), выберем его
направление так, как показано на рис.5. Пусть
заряд на правой пластине конденсатора q, тогда j N-j
M=q(t)/C; (1).
Падение напряжения на катушке L1 равно 0,
так как её активное сопротивление равно 0
( колебания в контуре по условию задачи
незатухающие.)
Складывая уравнения (2) и (3) и учитывая (1), получаем
уравнение (4), справедливое для любого момента
времени до вставки сердечника.
(4)
Продифференцируем его по времени: Данное
дифференциальное уравнение показывает, что
колебания в контуре происходят по
гармоническому закону, а квадрат частоты
собственных колебаний равен .
Максимальное напряжение на конденсаторе
соответствует максимальному заряду на нем;
учитывая, что в точках экстремума
дифференцируемой функции q(t) её производная
обращается в 0, получаем, что ток в этот момент в
цепи равен 0.
По закону сохранения электромагнитной энергии
в контуре:
,
где Umax– максимальное напряжение на
конденсаторе до вставки сердечника.
Рассмотрим процесс введения в катушку L1
сердечника. В это время конденсатор полностью
разряжен, j M=j N.
j M-j F+e инд 1=0, j F-j N+e инд
2=0, тогда e инд 1+e инд 2=0, т.е. поскольку
вставка сердечника происходит быстро и
конденсатор всё это время остается незаряженным.
Получаем равенство, вытекающее из сохранения
магнитного потока в системе: (L1+L2) Imax
нач=(m L1+L2)Imax кон.
Следовательно, к моменту окончания вставки
сердечника Imax кон= Тогда для максимального
напряжения на конденсаторе после вставки
сердечника имеем: