Автор – Лада Борисовна Есакова.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Пример:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.

Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.

Ответ: 11
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №15. Графы. Поиск количества путей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
| A | B | C | D | E | F | |
| A | 4 | |||||
| B | 4 | 6 | 3 | 6 | ||
| C | 6 | 4 | ||||
| D | 3 | 2 | ||||
| E | 6 | 4 | 2 | 5 | ||
| F | 5 |
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
2
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице значает, что прямой дороги между пунктами нет.
| A | B | C | D | E | F | G | |
| A | 5 | 12 | 25 | ||||
| B | 5 | 8 | |||||
| C | 2 | 4 | 5 | 10 | |||
| D | 12 | 8 | 2 | ||||
| E | 4 | 5 | |||||
| F | 5 | 5 | |||||
| G | 25 | 10 | 5 | 5 |
Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).
3
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
| A | B | C | D | E | F | |
| A | 2 | 4 | 8 | 16 | ||
| B | 2 | 3 | ||||
| C | 4 | 3 | ||||
| D | 8 | 3 | 3 | 5 | 3 | |
| E | 5 | 5 | ||||
| F | 16 | 3 | 5 |
Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт E. Передвигаться можно только по указанным дорогам.
4
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
| A | B | C | D | E | F | G | |
| A | 2 | 6 | |||||
| B | 2 | 5 | 3 | ||||
| C | 5 | 1 | 8 | ||||
| D | 6 | 3 | 1 | 9 | 7 | ||
| E | 9 | 5 | |||||
| F | 7 | 7 | |||||
| G | 8 | 5 | 7 |
Определите длину кратчайшего пути между пунктами A и G. Передвигаться можно только по указанным дорогам.
5
Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
| A | B | C | D | E | F | G | |
| A | 2 | 6 | |||||
| B | 2 | 5 | 2 | ||||
| C | 5 | 4 | 8 | ||||
| D | 6 | 2 | 4 | 2 | 7 | ||
| E | 2 | 5 | |||||
| F | 7 | 7 | |||||
| G | 8 | 5 | 7 |
Определите длину кратчайшего пути между пунктами A и G. Передвигаться можно только по указанным дорогам.
Пройти тестирование по этим заданиям
Урок посвящен тому, как решать 1 задание ЕГЭ по информатике
Содержание:
- Объяснение заданий 1 ЕГЭ по информатике
- Структурирование информации и информационные модели
- Поиск кратчайшего пути (перебор)
- Решение заданий 1 ЕГЭ по информатике
1-я тема характеризуется, как:
— задания базового уровня сложности,
— требуется использование специализированного программного обеспечения — нет,
— время выполнения – примерно 3 минуты,
— максимальный балл — 1
Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)
До ЕГЭ 2021 года — это было задание № 3 и задание № 7 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
“Как и в большинстве простых заданий, основные ошибки происходят из-за торопливости и невнимательности”
ФГБНУ “Федеральный институт педагогических измерений”
* Некоторые изображения страницы взяты из материалов презентации К. Полякова
Структурирование информации и информационные модели
Рассмотрим кратко необходимые для решения 1 задания ЕГЭ понятия.
Структурирование информации — это установление главных элементов в информационных сообщениях и установление связей между ними.
Структурирование выполняется с целью облегчения восприятия и поиска информации.
Структурирование возможно при помощи следующих структур (информационных моделей):
перечисление элементов, собранных по характерному признаку;
Вася, Петя, Коля 1, 17, 22, 55
В множестве упорядочивание элементов не обязательно, т.е. порядок следования не важен.
Важна упорядоченность следования элементов.

В таблицах выделяются объекты (отдельные записи таблиц) и свойства (названия столбцов или названия строк):


Уровни в дереве
Рассмотрим родственные отношения в дереве:

Корень – узел без предков (A).
Лист – узел без потомков (D, E, F, G).
Высота – наибольшее расстояние от корня до листа (количество уровней).
Допустим, на жестком диске компьютера имеются следующие папки (каталоги) с файлами:

Получим дерево:

Иногда очень трудно структурировать информацию описанными структурами из-за сложных «взаимоотношений» между объектами. Тогда можно использовать графы:
Граф – это набор вершин и связей между ними, называющихся рёбрами:

Граф, отображающий дороги между поселками

Связный граф – это граф, между любыми вершинами которого существует путь.

Связный граф
Дерево – это связный граф без циклов (замкнутых участков).

Дерево — связный граф без циклов
У взвешенных графов указан «вес ребра»:

Из взвешенных графов получается весовая матрица, обратное преобразование тоже возможно.

Весовая матрица
Поиск кратчайшего пути (перебор)

Определение кратчайшего пути между пунктами A и D
- В заданиях ЕГЭ этой темы чаще всего используются две информационные модели — таблицы и схемы.
- Информация в таблице строится по следующим правилам: на пересечении строки и столбца находится информация, характеризующая комбинацию этой строки и столбца.
- На схеме информация строится по следующему правилу: если между объектами схемы имеется связь, то она отображается линией, соединяющей названия этих объектов на схеме.
Егифка ©:

Решение заданий 1 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube: 
Задание демонстрационного варианта 2022 года ФИПИ
1_3: Решение 1 задания ЕГЭ по информатике:
Между населенными пунктами A, B, C, D, E, F построены дороги, протяженность которых приведена в таблице (если ячейка пуста — дороги нет).
| A | B | C | D | E | F | |
| A | 7 | 3 | ||||
| B | 7 | 2 | 4 | 1 | ||
| C | 3 | 2 | 7 | 5 | 9 | |
| D | 4 | 7 | 2 | 3 | ||
| E | 1 | 5 | 2 | 7 | ||
| F | 9 | 3 | 7 |
Определите длину кратчайшего пути между пунктами A и F.
Подобные задания для тренировки
✍ Решение:
- Для решения задачи используем построение дерева с подсчетом значений для каждой ветви (протяженности дорог).
- При движении от корня дерева (А) вниз будем иметь в виду, что:
- рассматривать вершины, которые уже есть в текущей «ветви», — не нужно,
- если получаемое число (суммарная протяженность дорог) превышает какое-либо из найденных вариантов от A до F, то дальше эту ветвь можно не рассматривать.
- В итоге получим дерево:
- Самый короткий путь: A -> C -> B -> E -> D -> F = 11

Результат: 11
Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
1_4: Решение 1 задания ЕГЭ по информатике:
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
| A | B | C | D | E | F | |
| A | 3 | 7 | 6 | |||
| B | 3 | 4 | 4 | |||
| C | 7 | 5 | 9 | |||
| D | 4 | 5 | 5 | |||
| E | 6 | 4 | 8 | |||
| F | 9 | 5 | 8 |
Определите длину кратчайшего пути между пунктами A и F при условии, что передвигаться можно только по указанным в таблице дорогам.
✍ Решение:
- Решим задание при помощи построения дерева, вершиной которого является отправной пункт — A. На ребрах дерева будем записывать числа — результат протяженности пути до конкретной вершины.
- Кратчайший путь: A -> B -> D -> F = 12

Результат: 12
1_5: Решение 1 задания ЕГЭ по информатике:
Между населенными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяженность каждой дороги (отсутствие числа в таблице означает, что прямой дороги между пунктами нет).
| A | B | C | D | E | F | Z | |
| A | 3 | 5 | 14 | ||||
| B | 2 | 8 | |||||
| C | 2 | 7 | |||||
| D | 1 | 4 | 4 | ||||
| E | 1 | 5 | |||||
| F | 12 | 1 | 9 | ||||
| Z |
Сколько существует таких маршрутов из A в Z, которые проходят через пять и более населенных пунктов? Пункты A и Z при подсчете учитывайте. Два раза проходить через один пункт нельзя.
* в учебниках 2018 года задания 2 и 3 поменяли местами: теперь 2 — Поиск кратчайшего пути, а 3 — Алгебра логики
✍ Решение:
- Для решения будем использовать дерево:
- Розовым отмечены неподходящие маршруты, а голубым — подходящие.
- Заметим, что после 4-го уровня сверху, все варианты будут подходить.

Результат: 6
1_2:
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта А в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.
Подобные задания для тренировки
✍ Решение:
- Посчитаем сколько ребер у каждой вершины:
A -> 3 (В Г Д) Б -> 1 (В) В -> 4 (А Б Г Е) Г -> 4 (А В Д К) Д -> 2 (А Г) Е -> 1 (В) К -> 1 (Г)
Г -> 4 (А В Д К)). В весовой матрице с вершиной Д пресекается П5. Значит вершина Г соответствует П5.Результат: 6
Подробное решение данного 1 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
1_1:
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова длина дороги из пункта Д в пункт К. В ответе запишите целое число — так, как оно указано в таблице.
✍ Решение:
- Рассмотрим граф и посчитаем количество ребер из каждой вершины:
А - > 2 ребра (Г, В) В - > 4 ребра (А, Г, К, Д) Г - > 4 ребра (А, В, К, Д) Б - > 2 ребра (Г, К) К - > 5 ребер (Б, Г, В, Д, Е) Е - > 2 ребра (К, Д) Д - > 3 ребра (В, К, Е)
Результат: 20
Кроме того, Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
1_6: Разбор 1 задания ЕГЭ:
На рисунке изображена схема дорог Н-ского района, в таблице звездочкой обозначено наличие дороги из одного населенного пункта в другой, отсутствие звездочки означает, что такой дороги нет. Каждому населенному пункту на схеме соответствует его номер в таблице, но неизвестно, какой именно номер.

|
|
Определите, какие номера населенных пунктов в таблице могут соответствовать населенным пунктам D и E на схеме? В ответе запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.
Подобные задания для тренировки
✍ Решение:
- Для начала найдем уникальные вершины — у которых уникальное число ребер: это A (2 ребра) и H (6 ребер). В таблице им соответствуют номера 3 и 4:
- По схеме находим, что смежными вершинами для A являются B и G. В таблице определяем соответствующие им цифры — 1 и 2. Поскольку по заданию они нас не интересуют, обозначим их вместе:
- У обеих вершин B и G смежными являются уже известные A и H и, кроме того, вершины F и C. По первому столбцу или первой строке находим, что F или C будет соответствовать цифра 7, а по второй строке — цифра 8. Обозначим их в таблице:
- В результате получаем, что искомым вершинам — D и E — соответствуют цифры 5 и 6. Поскольку не имеет значения, какой именно цифре должна соответствовать та или иная вершина, то в ответе просто запишем эти цифры в порядке возрастания.
| 1 | 2 | A | H | 5 | 6 | 7 | 8 | |
| 1 | * | * | * | |||||
| 2 | * | * | * | |||||
| A | * | * | ||||||
| H | * | * | * | * | * | * | ||
| 5 | * | * | * | |||||
| 6 | * | * | * | |||||
| 7 | * | * | * | |||||
| 8 | * | * | * |
| B,G | B,G | A | H | 5 | 6 | 7 | 8 | |
| B,G | * | * | * | |||||
| B,G | * | * | * | |||||
| A | * | * | ||||||
| H | * | * | * | * | * | * | ||
| 5 | * | * | * | |||||
| 6 | * | * | * | |||||
| 7 | * | * | * | |||||
| 8 | * | * | * |
| B,G | B,G | A | H | 5 | 6 | F,C | F,C | |
| B,G | * | * | * | |||||
| B,G | * | * | * | |||||
| A | * | * | ||||||
| H | * | * | * | * | * | * | ||
| 5 | * | * | * | |||||
| 6 | * | * | * | |||||
| F,C | * | * | * | |||||
| F,C | * | * | * |
Результат: 56
Сегодня разберём одно из самых лёгких заданий из ЕГЭ по информатике – задание 13. Вы с похожим типом задач могли встретится на экзамене в 9 классе по информатике.
Приступим к практическим тренировкам решения 13 задания ЕГЭ по информатике 2022.
Задача (Стандартная)
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
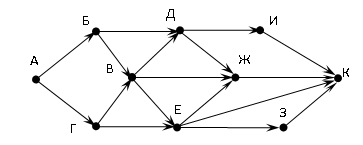
Решение:
Нужно подсчитать количество путей от начальной точки А до конечной точки К.
Будем использовать специальную технику для решения 13 задания из ЕГЭ по информатике 2022
Техника:
Ставим 1 (единицу) возле начальной точки A. Далее, просматриваем ближайшие точки и анализируем, сколько входит стрелок в эти точки. В точку Б “перетекает” 1 из точки А. В точку Г тоже входит одна стрелка из точки А. Значит, тоже в эту точку “перетекает” 1 из А.
В точку В входят две стрелки. Значит, в точку В “втекает” сумма двух точек, из которых выходят эти стрелки! Получается 1 + 1 = 2.
И продолжаем в том же духе.
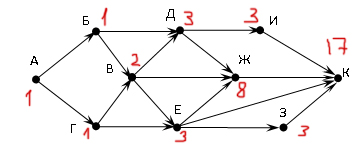
Число в конечной точке показывает правильный ответ!
Ответ: 17
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е,
Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном
направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих
через город Ж?

Решение:
Отличие этой задачи от предыдущей заключается в том, что пути, которые будем засчитывать, обязательно должны проходить через пункт Ж. Чтобы выполнить это условие, зачеркнём стрелку из пункта Е в пункт И. Так же зачеркнём стрелку из пункта З в пункт И. По этим стрелкам ходить нельзя, т.к. если мы по ним пойдём, не будет пройден пункт Ж.
Основная техника же решения будет такой же, как и в прошлой задаче.

Ответ: 51
Продолжаем отработку 13 задания ЕГЭ по информатике 2022
Задача (Избегаемая вершина)
На рисунке – схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П
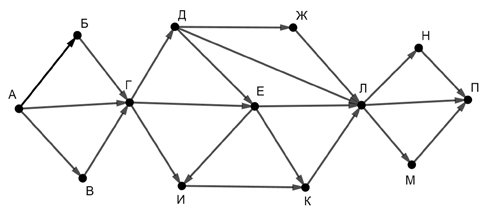
Сколько существует различных путей из пункта А в пункт П, не проходящих через пункт Е?
Решение:
Такая же задача, как и предыдущие две, только здесь, при построении путей, мы не должны проходить через точку E.
Зачеркнём те дороги, которые поведут наши пути через пункт E.
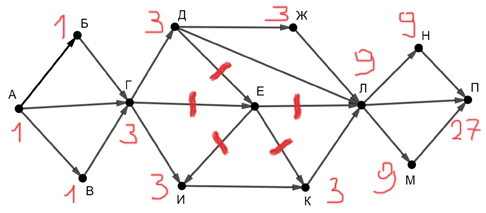
Далее, применим старый метод, который использовали ранее.
Получается ответ 27.
Ответ: 27
Рассмотрим задачу, которая была на реальном экзамене по информатике в этом году.
Задача (ЕГЭ по информатике, 2020, Москва)
На рисунке – схема дорог, связывающих города А, Б, В, Г, Е, Ж, К, Л, М. По каждой дороге можно двигаться в одном направлении, указанном стрелкой. Какая наибольшая длина пути из А в М ?
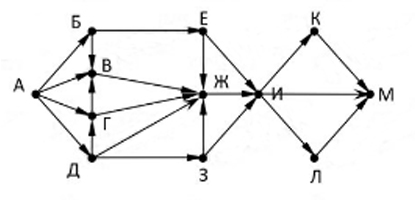
Решение:
В этой задаче отличается вопрос от привычного нахождения количества путей. Здесь нужно найти наибольшую длину пути из начального пункта в конечный.
Возле начальной точки ставим число 0.
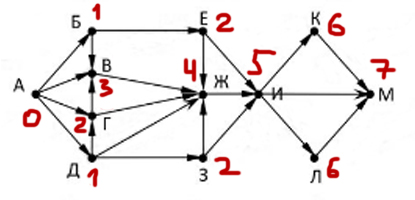
Смотрим сколько входит в узел стрелок. Выбираем стрелку, которая идёт из узла с наибольшим числом. При переходе по стрелочке добавляем 1.
Число, которое получится возле конечной точки и будет ответом. В этой задачке стрелок получилось 7, это и будет ответ.
Ответ: 7

Tom Clancy’s Rainbow Six Siege

31 ratings

Как решать задание №1 ЕГЭ по информатике?
Теория. Алгоритм решения
Алгоритм решения на примере задачи:
Задача:
2. Обозначаем количество дорог из точек на графе. Обозначаем количество дорог в таблице рядом с соответствующими пунктами. (Сколько у вас в строчке чисел столько и дорог исходит из этого пункта)
Берем по каждому пункту и смотрим по столбикам, сколько дорог они пересекают. Пункты 3 и 7 не подходят, т.к они пересекают пункты с меньшим количеством дорог. Значит, буква “С” – пункт №4. Обозначаем букву рядом с пунктом. (Для наглядности я выписал отдельно)
4. Можем найти букву “D”, т.к. она соединена с пунктом №4 (буквой “С”) и с пунктом с 2 дорогами (“Е”). Соответственно “D” связана с двумя пунктами с двумя дорогами(“Е” и “С”).
5. Решаем дальше, “Е” связана с “F”, а “F” с “G” -> значит “F” – п7, а “G” – п6:

8. Находим сумму и пишем ответ: 25
Originally posted by author:
Соре, я каждый раз заново переписывал, кое-где отсутствуют цифорки и другие обозначения(например в конце не подписан пункт “А”, но я думаю и так понятно)
Базовые заданий
Задание №1:

“Г” – 3 дороги – пункт №2;
“Е” – 4 дороги – пункт №4;
“В” – 4 дороги – пункт №6;
Аналогично “Д” с “Е” связана, тогда “Д” -П7

Задание №2:



У “Д” – 3 дороги – значит “Д” это П2
“Г” – 2 дороги – значит “Г” это П4
Осталось найти, что хотят в задании, а хотят сумму БВ и ГД,
Средние задания
Средние задания подразумевают предположения, то есть представление нескольких пунктов какой-либо буквой или наоборот нескольких букв каким-то пунктом. Как правило это происходит из-за того, что конкретно выделить особенности пункта или буквы невозможно. Обычно в таких случаях нам дают доп. информацию, по которой мы потом судим совпал пункт или нет; или мы делаем предположение и проверяем правильно или нет – выходит.
Задание №1

Далее придётся делать предположения; П5/П4 может быть либо “D”, либо “В”. В связи с условием логичнее взять за букву “D” такую дорогу, которая будет наибольшей. Так как П3-П5=12, а П3-П4=16; то за “D” берём пункт с наибольшей длиной дороги – П4. Следовательно за “В” берём П5.
Значит оставшиеся определяем по количеству дорог, “H” – П1 и “G” – П2.

Задание №2


Сложные задания
Задание №1




Задание №2

2. Расписываем все пункты и делаем предположения какие буквы им соответствуют.
3. Проходимся по всем вариантам прохода из “А” в “Д”(в данном случае берём самый короткий “АГД”) и пишем все вариации сложения пунктов, которые мы можем взять. Нам будет подходить 1 при условии того, что “А..Д” < 30. Получаем:
П1 – “Б”
П2 – “Е”
П3 – “Д”
П4 – “В”
П5 – “Г”
П6 – “А”
П7 – “Ж”

.




