Информатика как найти силу

Формулы и Задачи (Информатика 10)

Формулы

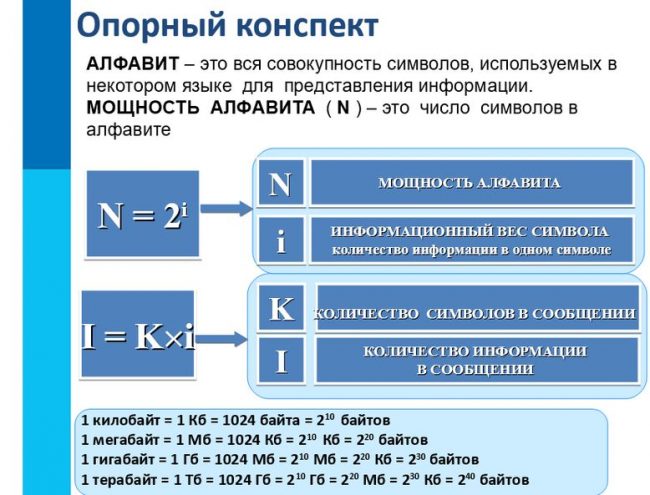
N = 2 i

N – мощность алфавита (количество знаков в алфавите)
i – информационный вес символа алфавита (количество информации в одном символе)

I = K * i

I – количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K – число символов в сообщении
i – информационный вес символа (количество информации в одном символе)

Q = N L

Q – количество разных сообщений
N – количество символов
L – длина сообщения

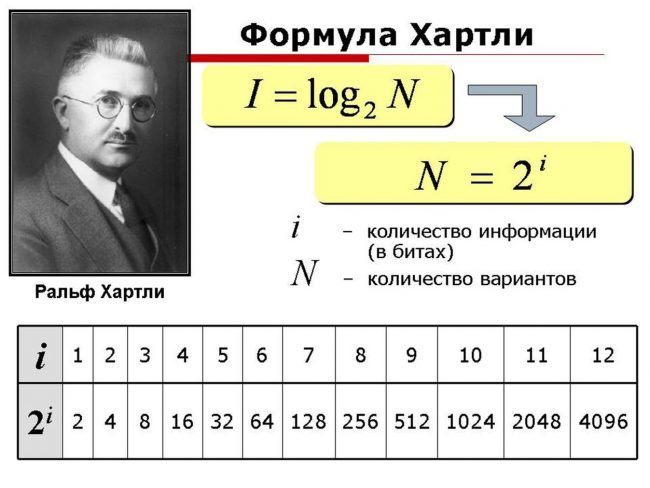
Формула Хартли:

I = log₂N

I – количество информации, содержащееся в выбранном сообщении
N – количество сообщений

Римская система счисления

I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

Перевод чисел из других систем счисления в десятичную систему счисления

Развернутая запись целого числа:

a 3a 2a 1a 0 = a 3 * p 3 + a 2 * p 2 + a 1 * p 1 + a 0 * p 0

Правило перевода числа из любой системы счисления в десятичную систему счисления – умножаем каждую цифру исходного числа на основание системы счисления в степени разряда , в котором находится эта цифра, а затем всё складываем.

Запись через схему Горнера:

p – основание системы счисления в котором представлено число.

Пример:

6 3 7 5 ₁₀ = 6 * 10 3 + 3 * 10 2 + 7 * 10 1 + 5 * 10 0
6 3 7 5 ₁₀ = (( 6 * 10 + 3 ) * 10 + 7 ) * 10 + 5
1 2 3 4 ₅ = 1 * 5 3 + 2 * 5 2 + 3 * 5 1 + 4 * 5 0 = 194₁₀
1 2 3 4 ₅ = (( 1 * 5 + 2 ) * 5 + 3 ) * 5 + 4 = 194₁₀

Развернутая запись дробного числа:

Запись через схему Горнера:

p – основание системы счисления в котором представлено число.

Пример:

0,6375 = 6 * 10 -1 + 3 * 10 -2 + 7 * 10 -3 + 5 * 10 -4
0,6375 = 10 -1 * (6 + 10 -1 * (3 + 10 -1 * (7 + 10 -1 * 5)))
0,1234 ₅ = 1 * 5 -1 + 2 * 5 -2 + 3 * 5 -3 + 4 * 5 -4
0,1234 ₅ = 5 -1 * (1 + 5 -1 * (2 + 5 -1 * (3 + 5 -1 * 4)))

Задачи

Алфавитный подход к измерению количества информации

Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.

1. информационная ёмкость символа: 256 = 2 8 =>> i = 8 бит = 1 байт
2. количество символов на странице:
   32 * 64 = 2 5 * 2 6 = 2 11
3. общее количество символов:
   L = 10 * 2 11
4. информационный объём сообщения:
   I = L * i = 10 * 2 11 * 1 байт = 20 Кбайт

Системы счисления

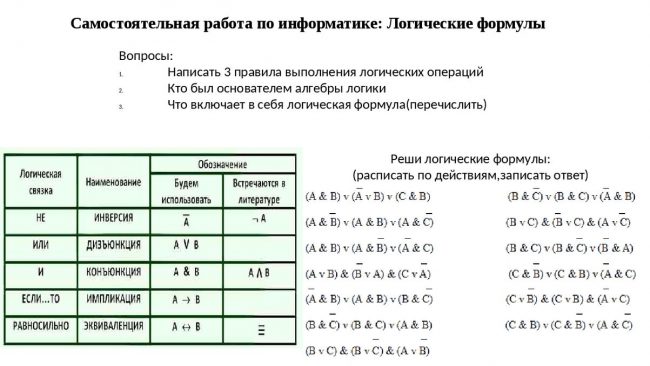
Логические операции

Логической операцией называется выбор решения (действия), исходя из заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.

Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.

Таблица истинности для операции НЕ имеет вид:

Действие, связанное с операцией НЕ можно записать следующим образом:

Логическая операция И ( конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).

Таблица истинности для операции И имеет вид:

A	B	X=A^B
0	0	0
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией И можно записать следующим образом:

X = AB = A*B = A ^ B

Логическая операция ИЛИ ( дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.

Таблица истинности для операции ИЛИ имеет вид:

A	B	X=A v B
0	0	0
0	1	1
1	0	1
1	1	1

Действие, связанное с операцией ИЛИ можно записать следующим образом:

Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.

Таблица истинности имеет вид:

A	B	X=AB
0	0	0
0	1	1
1	0	1
1	1	0

Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:

X = A B

Действие, связанное с операцией Импликации можно записать следующим образом:

Таблица истинности Импликации имеет вид:

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

Операция тождество. Операция тождество определяет тождественность аргументов.

Таблица истинности для операции тождество имеет вид:

A	B	A Ξ B
0	0	1
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией тождество можно записать следующим образом:

X = A B.

Диаграммы Венна (круги Эйлера)

Поиск номера сети

Необходимо найти номер сети по IP-адресу 12.16.196.10 и маске 255.255.224.0.

Картинки формулы по информатике (43 фото)

Решение задач с формулами по информатике позволяет лучше понять устройство вычислительной техники. Понимание основ данной науки необходимо каждому человеку. Во многих формулах по информатике используются такие понятия как бит и байт. Они являются единицами измерения информации, которой оперирует компьютер. Предлагаем тут посмотреть красивые картинки про формулы по информатике.

Скорость передачи файла.

Число возможных вариантов.

Прикольная формула по информатике.

Глубина кодирования в бит.

Количество символов в тексте.

Картинка формулы по информатике.

Важное уравнение информационной науки.

Формулы по информатике в опорном конспекте.

Задача на кодирование текста.

Ученый Ральф Хартли.

Замечательная формула по информатике.

Самостоятельная работа на логику.

Красивая картинка формул по информатике.

Символы в одном сообщении.

Информационный вес символа.

Познавательный материал с формулами по информатике.

Сумма элементов в задаче.

Символьный алфавит компьютера.

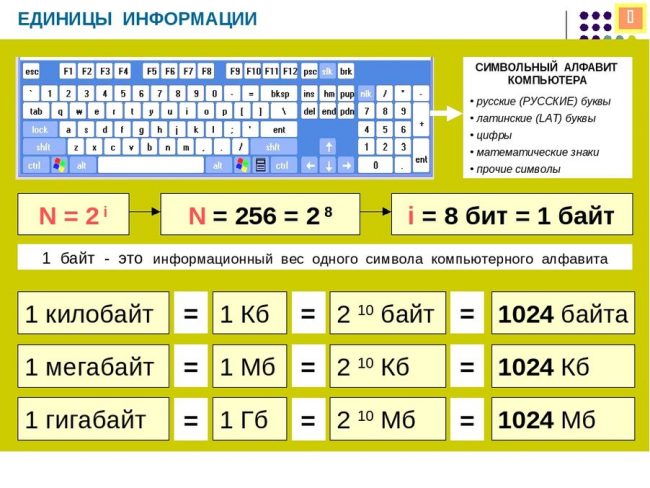
Сложная формула по информатике.

Алфавитный подход к измерению.

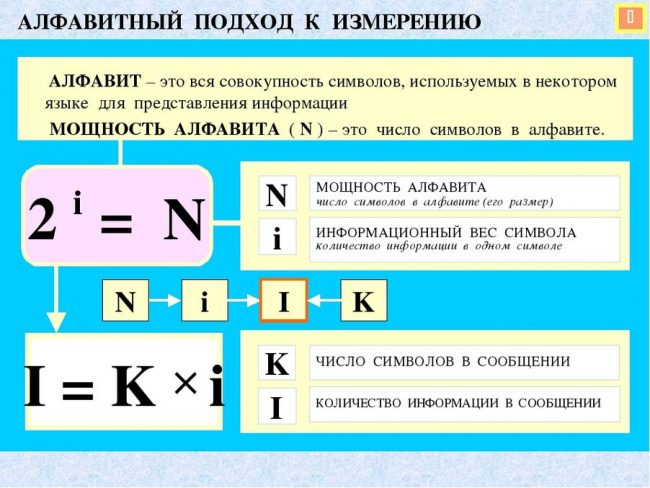
Небольшие подсказки для экзамена.

Формулы по информатике на картинке.

Количество информации как степень.

Символы, используемые в некотором языке.

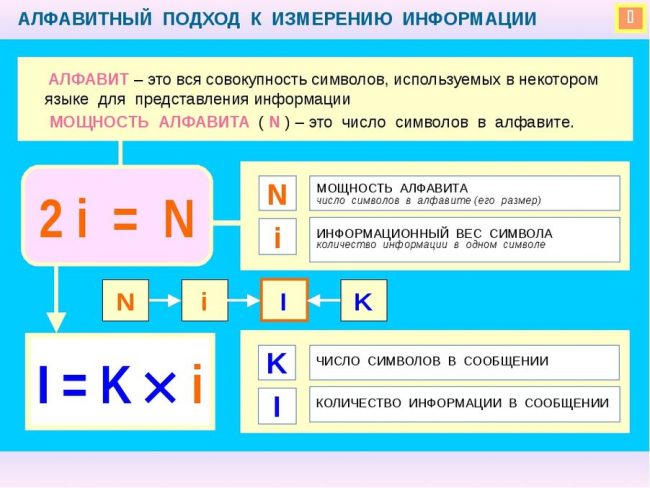
Главная формула информатики.

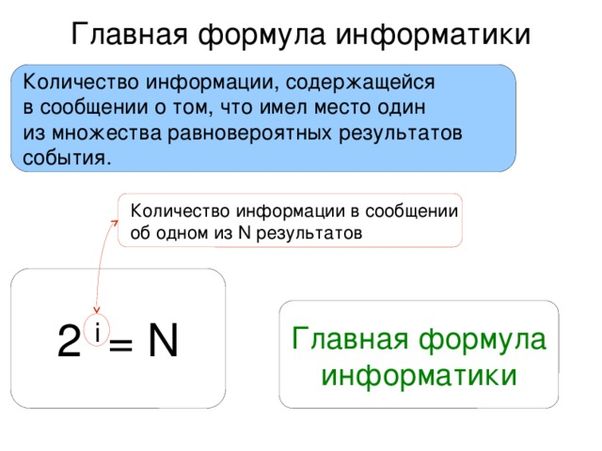
Простое задание с логарифмом.

Измерение информации в битах.

Красные рамки для формул по информатике.

Символы на темном фоне.

Вес символа алфавита.

Целые разряды числа в формуле по информатике.

Дано, решение, ответ.

Цветная картинка формулы по информатике.

Двоичное кодирование целых чисел.

Преобразуем логические выражения.

Разные события для формул по информатике.

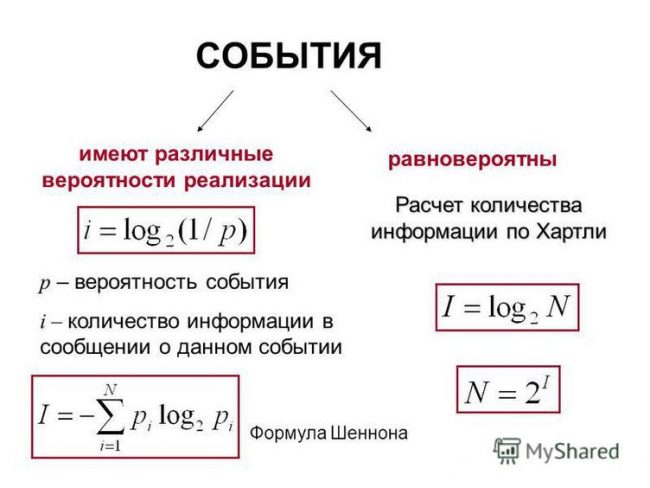
Важная пометка в синей рамке.

Определения для обозначений.

Запоминаем формулу по информатике.

Количество возможных равновероятных альтернатив.

Формулы и уравнения по информатике

2) Логическое сложение или дизъюнкция:

Дизъюнкция – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.

Таблица истинности для дизъюнкции

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

3) Логическое отрицание или инверсия:

Инверсия – это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Обозначение: F = ¬ A.

Таблица истинности для инверсии

4) Логическое следование или импликация:

Импликация – это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

«A → B» истинно, если из А может следовать B.

Обозначение: F = A → B.

Таблица истинности для импликации

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

5) Логическая равнозначность или эквивалентность:

Эквивалентность – это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

[spoiler title=”источники:”]

http://proprikol.ru/kartinki/kartinki-formuly-po-informatike-43-foto.html

http://www.sites.google.com/site/uvarovaap/family-map/11-klass/osnovy-logiki-logiceskie-operacii-i-tablicy-istinnosti

[/spoiler]

Задачи, связанные с определением количества информации, занимают довольно большое место как в общем курсе 9-11 классов, так и при итоговой аттестации разного типа.

Обычно решение подобных задач не представляет трудности для учащихся с хорошими способностями к анализу ситуаций. Но большинство учеников поначалу путаются в понятиях и не знают, как приступить к решению.

Тем не менее, к 9-му классу учащиеся уже имеют определенный опыт решения задач по другим предметам (более всего – физика) с применением формул. Определить, что в задаче дано, что необходимо найти, и выразить одну переменную через другую – действия довольно привычные, и с ними справляются даже слабые ученики. Представляется возможным ввести некоторые дополнительные формулы в курсе информатики и найти общий стиль их применения в решении задач.

Оттолкнемся от одной из главных формул информатики – формулы Хартли N=2ⁱ. При ее использовании учащиеся могут еще не знать понятия логарифма, достаточно вначале иметь перед глазами, а затем запомнить таблицу степеней числа 2 хотя бы по 10-й степени.

При этом формула может применяться в решении задач разного типа, если правильно определить систему обозначений.

Выделим в системе задач на количество информации задачи следующих типов:

1. Количество информации при вероятностном подходе;
2. Кодирование положений;
3. Количество информации при алфавитном подходе (кодирование текста);
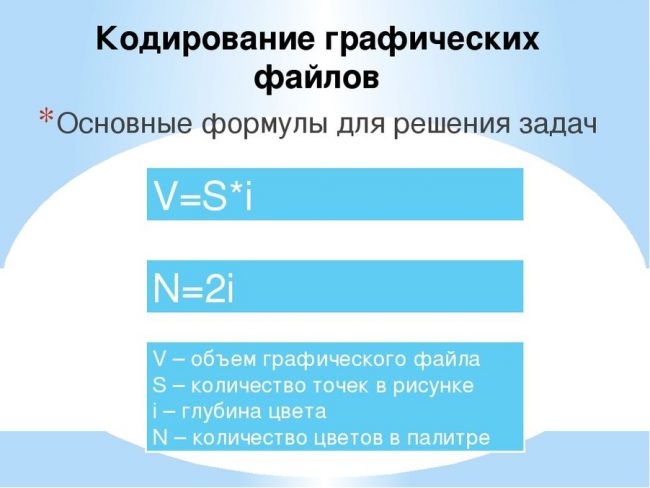
4. Кодирование графической информации;
5. Кодирование звуковой информации

Все задачи группы A (в случае, если мы имеем дело с равновероятными событиями) решаются непосредственно по формуле Хартли с ее привычными обозначениями:

• N – количество равновероятных событий;
• i – количество бит в сообщении о том, что событие произошло,

Причем в задаче может быть определена любая из переменных с заданием найти вторую. В случае если число N не является непосредственно числом, представляющим ту или иную степень числа 2, количество бит нам необходимо определить «с запасом». Так для гарантированного угадывания числа в диапазоне от 1 до 100 необходимо задать минимально 7 вопросов (27=128).

Решение задач для случаев неравновероятных событий в этой статье не рассматривается.

Для решения задач групп B-E дополнительно введем еще одну формулу:

Q=k*i

и определим систему обозначений для задач разного типа.

Для задач группы B значение переменных в формуле Хартли таково:

• i – количество «двоичных элементов», используемых для кодирования;
• N – количество положений, которые можно закодировать посредством этих элементов.

Так:

• два флажка позволяют передать 4 различных сообщения;
• с помощью трех лампочек можно потенциально закодировать 8 различных сигналов;
• последовательность из 8 импульсов и пауз при передаче информации посредством электрического тока позволяет закодировать 256 различных текстовых знаков;

и т.п.

Рассмотрим структуру решения по формуле:

Задача 1: Сколько существует различных последовательностей из символов «плюс» и «минус» длиной ровно в пять символов?

Дано: i = 5

Найти: N

Решение: N = 2⁵

Ответ: 5

Каждый элемент в последовательности для кодирования несет один бит информации.

Очевидно, что при определении количества элементов, необходимых для кодирования N положений, нас всегда интересует минимально необходимое для этого количество бит.

При однократном кодировании необходимого количества положений мы определяем необходимое количество бит и ограничиваемся формулой Хартли. Если кодирование проводится несколько раз, то это количество мы обозначаем как k и, определяя общее количество информации для всего кода (Q), применяем вторую формулу.

Задача 2: Метеорологическая станция ведет наблюдение за влажностью воздуха, результатом которых является целое число от 1 до 100%, которое кодируется посредством минимально возможного количества бит. Станция сделала 80 измерений. Какой информационный объем результатов наблюдений.

Дано: N = 100; k = 80

Найти: Q

Решение:

По формуле Хартли i = 7 (с запасом); Q = 80 * 7 = 560

Ответ: 560 бит

(Если в задаче даны варианты ответов с использованием других единиц измерения количества информации, осуществляем перевод: 560 бит = 70 байт).

Отметим дополнительно, что, если для кодирования используются нe «двоичные», а скажем, «троичные» элементы, то мы меняем в формуле основание степени.

Задача 3: Световое табло состоит из лампочек. Каждая из лампочек может находиться в одном из трех состояний («включено», «выключена» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов.

В данном случае N = 18, основание степени – 3. Необходимо найти i. Если логарифмы еще не знакомы, определяем методом подбора – 5. Ответ: 5 лампочек

Далее рассмотрим решение задач на кодирование текстовой, графической и звуковой информации.

Здесь важно провести параллели:

Информация, которая обрабатывается на компьютере, должна быть представлена в виде конечного множества элементов (символ для текста, точка – для графики, фрагмент звуковой волны – для звука), каждый из которых кодируется отдельно с использованием заданного количества бит. Зависимость количества элементов, которые могут быть закодированы, от количества бит, отводимых, на кодирование одного элемента, как и раньше, определяем по формуле Хартли.

А путем умножения количества элементов (k) на «информационный вес» одного из них, определяем общее количество информации в текстовом, графическом, звуковом фрагменте (Q).

Каждую задачу можно решить, обозначив заданными переменными известные данные, и выразив одну переменную через другую. Только необходимо помнить, что непосредственно расчеты чаще всего производятся в минимальных единицах измерения (битах, секундах, герцах), а потом, если необходимо, ответ переводится в более крупные единицы измерения.

Рассмотрим конкретные примеры:

Алфавитный подход позволяет определить количество информации, заключенной в тексте. Причем под «текстом» в данном случае понимают любую конечную последовательность знаков, несущую информационную нагрузку. Поэтому обозначения переменных для задач группы C одинаково применимы как для задач на передачу обычной текстовой информации посредством компьютера (i = 8, N = 256 или i = 16, N = 16256) так и для задач на передачу сообщений посредством любых других алфавитов (здесь и далее используются разные названия, встречающиеся в задачах):

• i – количество бит, используемое для кодирования одного текстового знака, равнозначно: количество информации (в битах), в нем содержащееся, информационный «вес», информационный «объем» одного знака;
• N – полное количество знаков в алфавите, используемом для передачи сообщения, мощность алфавита;
• k – количество знаков в сообщении;
• Q – количество информации в сообщении (информационный «вес», «объем» сообщения), количество памяти, отведенное для хранения закодированной информации;

Задача 4: Объем сообщения – 7,5 кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность алфавита?

Дано:

Q = 7,5 Кбайт = 7680 байт ( в данном случае нет необходимости перевода в биты);

k = 7680

Найти: N

Решение: i = Q / k = 1 байт = 8 бит; N = 2⁸ = 256

Ответ: 256 знаков

Задача 5: Дан текст из 600 символов. Известно, что символы берутся из таблицы размером 16 на 32. Определите информационный объем текста в битах.

Дано:

k = 600; N = 16 * 32

Найти: Q

Решение:

N = 2⁴ * 2⁵ = 2⁹; i = 9; Q = 600 * 9 = 5400 бит;

Ответ: 5400 бит

Задача 6: Мощность алфавита равна 64. Сколько кбайт памяти потребуется, чтобы сохранить 128 страниц текста, содержащего в среднем 256 символов на каждой странице?

Дано:

N = 64; k = 128 * 256

Найти: Q

Решение:

64 = 2ⁱ; i = 6; Q = 128 * 256 * 6 = 196608 бит = 24576 байт = 24 Кбайт;

Ответ: 24 Кбайт

Задача 7: Для кодирования нотной записи используется 7 значков-нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?

Дано:

N = 7; k = 180

Найти: Q

Решение:

7 = 2ⁱ; i = 3 (с запасом); Q = 180 * 3 = 540 бит;

Ответ: 540 бит

Рассматривая задачи групп D и E, вспоминаем, что при кодировании графики и звука производится дискретизация, то есть разбиение изображения на конечное множество элементов (пикселей) и звуковой волны на конечное множество отрезков, количество которых зависит от количества измерений в секунду уровня звука (частоты дискретизации) и времени звучания звукового файла.

То есть –

• общее количество элементов в графическом файле (k) равно разрешению изображения или разрешению экрана монитора, если изображение формируется на весь экран,
• общее количество элементов в звуковом файле (k) равно произведению частоты дискретизации на время звучания (важно при этом использовать в качестве единиц измерения минимальные единицы – герцы и секунды).

Рассмотрим всю систему обозначений для данного типа задач:

• i – количество бит, используемое для кодирования одного элемента изображения или звукового фрагмента, равнозначно: глубина цвета, звука;
• N – насыщенность цвета, равнозначно: количество цветов в палитре изображения, цветовое разрешение изображения; насыщенность звука (в задачах обычно не используется);
• k – количество точек в изображении, равнозначно: разрешение изображения (или экрана) или количество фрагментов дискретной звуковой волны (равно произведению частоты дискретизации на время звучания);
• Q – количество информации, содержащееся в графическом (звуковом) файле, равнозначно: информационный «объем», «вес» графического (звукового) файла, объем памяти (видеопамяти), необходимый для хранения заданного файла.

Задача 8: Для хранения растрового изображения размером 64 на 64 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения?

Дано:

k = 64 * 64 = 212; Q = 512 байтов = 29 * 23 = 212 бит;

Найти: N

Решение:

i = Q / k = 2¹² / 2¹² = 1; N = 21 = 2

Ответ: 2 цвета

Задача 9: Сколько памяти нужно для хранения 64-цветного растрового графического изображения размером 32 на 128 точек?

Дано:

N = 64; k = 32 * 128;

Найти: Q

Решение:

i = 6 (по формуле Хартли); Q = 32 * 128 * 6 = 24576 бит = 3072 байт = 3 Кбайт

Ответ: 3 Кбайт

Задача 10: Оцените информационный объем моноаудиофайла длительностью звучания 1 минута, если глубина кодирования равна 16 бит при частоте дискретизации 8 кГц

Дано:

k = 60 * 8000; i = 16;

Найти: Q

Решение:

Q = 60 * 8000 * 16 = 7680000 бит = 960000 байт = 937,5 Кбайт

Ответ: 937,5 Кбайт

(Если файл стерео, Q будет больше в 2 раза).

Задача 11: Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 625 Кбайт

Дано:

i = 16; k = 32000 * t; Q = 625 кбайт = 640000 байт = 5120000 бит;

Найти: t

Решение:

k = Q / i; k = 5120000 / 16 = 320000; t = 320000 / 32000 = 10 сек

Ответ: 10 секунд

В эту же схему укладывается решение задач на скорость передачи информации любого типа, если в хорошо известной учащимся формуле:

S = V * t принять S = Q (количество переданной информации вместо расстояния).

Задача 12: Сколько секунд потребуется обычному модему, передающему сообщения со скоростью 28800 бит/сек, чтобы передать цветное растровое изображение размером 640 на 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами?

Дано:

V = 28800 бит/сек; k = 640 * 480; i = 3 байт = 24 бит;

Найти: t

Решение:

t = S (Q) / V; Q = k * i = 640 * 480 * 24 = 7372800 бит; t = 7372800 / 28800 = 256 сек.

Ответ: 256 сек

В заключение отметим, что после определенной тренировки решения задач по формулам, многие учащиеся перестают нуждаться в их прописывании в задаче, сразу определяя порядок необходимых арифметических действий для ее решения.

Если к этим задачам добавить задачи на соотношение величин, записанных в разных единицах измерения, с использованием представления величин в виде степеней двойки мы получим 9 типов задач.
Рассмотрим задачи на все типы. Договоримся, что при переходе от одних единиц измерения информации к другим будем строить цепочку значений. Тогда уменьшается вероятность вычислительной ошибки.

Задача 3. Компьютер имеет оперативную память 512 Мб. Количество соответствующих этой величине бит больше:

1) 10 000 000 000бит 2) 8 000 000 000бит 3) 6 000 000 000бит 4) 4 000 000 000бит Решение: 512*1024*1024*8 бит=4294967296 бит.
Ответ: 4.

Задача 4. Определить количество битов в двух мегабайтах, используя для чисел только степени 2.
Решение: Поскольку 1байт=8битам=2³битам, а 1Мбайт=2¹⁰Кбайт=2²⁰байт=2²³бит. Отсюда, 2Мбайт=2²⁴бит.
Ответ: 2²⁴бит.

Задача 5. Сколько мегабайт информации содержит сообщение объемом 2²³бит?
Решение: Поскольку 1байт=8битам=2³битам, то
2²³бит=2²³*2²³*2³бит=2¹⁰2¹⁰байт=2¹⁰Кбайт=1Мбайт.
Ответ: 1Мбайт

Задача 6. Один символ алфавита “весит” 4 бита. Сколько символов в этом алфавите?
Решение:
Дано:

i=4	По формуле N=2i находим N=24, N=16
Найти: N – ?

Ответ: 16

Задача 7. Каждый символ алфавита записан с помощью 8 цифр двоичного кода. Сколько символов в этом алфавите?
Решение:
Дано:

i=8	По формуле N=2i находим N=28, N=256
Найти:N – ?

Ответ: 256

Задача 8. Алфавит русского языка иногда оценивают в 32 буквы. Каков информационный вес одной буквы такого сокращенного русского алфавита?
Решение:
Дано:

N=32	По формуле N=2i находим 32=2i, 25=2i,i=5
Найти: i– ?

Ответ: 5

Задача 9. Алфавит состоит из 100 символов. Какое количество информации несет один символ этого алфавита?
Решение:
Дано:

N=100	По формуле N=2i находим 32=2i, 25=2i,i=5
Найти: i– ?

Ответ: 5

Задача 10. У племени “чичевоков” в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет. Какое минимальное количество двоичных разрядов им необходимо для кодирования всех символов? Учтите, что слова надо отделять друг от друга!
Решение:
Дано:

N=24+8=32	По формуле N=2i находим 32=2i, 25=2i,i=5
Найти: i– ?

Ответ: 5

Задача 11. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге? Ответ дайте в килобайтах и мегабайтах
Решение:
Дано:

K=360000	Определим количество символов в книге 150*40*60=360000. Один символ занимает один байт. По формуле I=K*iнаходим I=360000байт 360000:1024=351Кбайт=0,4Мбайт
Найти: I– ?

Ответ: 351Кбайт или 0,4Мбайт

Задача 12. Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт. Определить количество символов в тексте книги.
Решение:
Дано:

I=128Кбайт,i=2байт	В кодировке Unicode один символ занимает 2 байта. Из формулыI=K*i выразимK=I/i,K=128*1024:2=65536
Найти: K– ?

Ответ: 65536

Задача 13.Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Определить информационный вес одного символа использованного алфавита
Решение:
Дано:

I=1,5Кбайт,K=3072	Из формулы I=K*i выразимi=I/K,i=1,5*1024*8:3072=4
Найти: i– ?

Ответ: 4

Задача 14.Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
Решение:
Дано:

N=64, K=20	По формуле N=2i находим 64=2i, 26=2i,i=6. По формуле I=K*i I=20*6=120
Найти: I– ?

Ответ: 120бит

Задача 15. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составил 1/16 часть мегабайта?
Решение:
Дано:

N=16, I=1/16 Мбайт	По формуле N=2i находим 16=2i, 24=2i,i=4. Из формулы I=K*i выразим K=I/i, K=(1/16)*1024*1024*8/4=131072
Найти: K– ?

Ответ: 131072

Задача 16. Объем сообщения, содержащего 2048 символов,составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
Решение:
Дано:

K=2048,I=1/512 Мбайт	Из формулы I=K*i выразим i=I/K, i=(1/512)*1024*1024*8/2048=8. По формулеN=2iнаходим N=28=256
Найти: N– ?

Ответ: 256

• 
  
  

Как найти F (силу тока) если известны:
B (индукция) = 100Тл
I (сила тока) = 2А
L (длина проводника) = 0.5м

Формулы

N = 2ⁱ

N – мощность алфавита (количество знаков в алфавите)
i – информационный вес символа алфавита (количество информации в одном символе)

I = K * i

I – количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K – число символов в сообщении
i – информационный вес символа (количество информации в одном символе)

Q = N^L

Q – количество разных сообщений
N – количество символов
L – длина сообщения

Формула Хартли:

I = log₂N

I – количество информации, содержащееся в выбранном сообщении
N – количество сообщений

---

Римская система счисления

I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

Перевод чисел из других систем счисления в десятичную систему счисления

Развернутая запись целого числа:

a₃a₂a₁a₀ = a₃ * p³ + a₂ * p² + a₁ * p¹ + a₀ * p⁰

Правило перевода числа из любой системы счисления в десятичную систему счисления – умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.

Запись через схему Горнера:

a₃a₂a₁a₀ = ((a₃ * p + a₂) * p + a₁) * p + a₀

p – основание системы счисления в котором представлено число.

Пример:

6375₁₀ = 6 * 10³ + 3 * 10² + 7 * 10¹ + 5 * 10⁰

6375₁₀ = ((6 * 10 + 3) * 10 + 7) * 10 + 5

1234₅ = 1 * 5³ + 2 * 5² + 3 * 5¹ + 4 * 5⁰ = 194₁₀

1234₅ = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 194₁₀

Развернутая запись дробного числа:

0,a₁a₂a₃a₄ = a₁*p^-1 + a₂*p^-2 + a₃*p^-3 + a₄*p^-4

Запись через схему Горнера:

0,a₁a₂a₃a₄ = p^-1 * (a₁ + p^-1 * (a₂ + p^-1 * (a₃ + p^-1 * a₄)))

p * (0,a₁a₂a₃a₄) = a₁ + p^-1 * (a₂ + p^-1 * (a₃ + p^-1 * a₄))

p – основание системы счисления в котором представлено число.

Пример:

0,6375 = 6 * 10^-1 + 3 * 10^-2 + 7 * 10^-3 + 5 * 10^-4

0,6375 = 10^-1 * (6 + 10^-1 * (3 + 10^-1 * (7 + 10^-1 * 5)))

0,1234₅ = 1 * 5^-1 + 2 * 5^-2 + 3 * 5^-3 + 4 * 5^-4

0,1234₅ = 5^-1 * (1 + 5^-1 * (2 + 5^-1 * (3 + 5^-1 * 4)))

Задачи

Алфавитный подход к измерению количества информации

Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.

1. информационная ёмкость символа:
   256 = 2⁸      =>>      i = 8 бит = 1 байт
2. количество символов на странице:
   32 * 64 = 2⁵ * 26 = 2¹¹
   
3. общее количество символов:
   L = 10 * 2¹¹
4. информационный объём сообщения:
   I = L * i = 10 * 2¹¹ * 1 байт = 20 Кбайт

---

Системы счисления


  X10     X16     X8       X2


Логические операции

Логической операцией называется выбор решения (действия), исходя из  заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.

---

Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.

Таблица истинности для операции НЕ имеет вид:

A
0	1
1	0

Действие, связанное с операцией НЕ можно записать следующим образом:

---

Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).

Таблица истинности для операции И имеет вид:

A	B	X=A^B
0	0	0
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией И можно записать следующим образом:

X = AB = A*B = A ^ B

---

Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.

Таблица истинности для операции ИЛИ имеет вид:

A	B	X=A v B
0	0	0
0	1	1
1	0	1
1	1	1

Действие, связанное с операцией ИЛИ можно записать следующим образом:

X = A + B = A v B

---

Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.

Таблица истинности имеет вид:

A	B	X=AB
0	0	0
0	1	1
1	0	1
1	1	0

Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:

X = A B

---

Действие, связанное с операцией Импликации можно записать следующим образом:

X = A → B

Таблица истинности Импликации имеет вид:

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

---

Операция тождество. Операция тождество определяет тождественность аргументов.

Таблица истинности для операции тождество имеет вид:

A	B	A Ξ B
0	0	1
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией тождество можно записать следующим образом:

X = A Ξ B

---

---

 
 

Диаграммы Венна (круги Эйлера)

 

Поиск номера сети

Необходимо найти номер сети по IP-адресу 12.16.196.10 и маске 255.255.224.0.

маска сети	255.	255.	224.	0
IP-адрес	12.	16.	196.	10	– ip-адрес (узла, компьютера и т.п.)
IP-адрес	0000 1100.	0001 0000.	1100 0100.	0000 1010
маска сети	1111 1111.	1111 1111.	1110 0000.	0000 0000
адрес сети	0000 1100.	0001 0000.	110x xxxx.	xxxx xxxx	– эта часть относится к адресу сети – она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее:
адрес сети	0000 1100.	0001 0000.	1100 0000.	0000 0000	– полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем:
адрес сети	12.	16.	192.	0	– полный адрес сети (в десятичном виде)