Интегральная теплота растворения как найти

Определение
интегральной теплоты

растворения
соли

Теоретическая
часть

1.
Основные понятия термодинамики

Термодинамика – наука, изучающая
взаимные переходы теплоты и работы в
равновесных системах и при переходе к
равновесию. Химическая термодинамика
– раздел физической химии, в котором
термодинамические методы применяются
для анализа химических явлений:
химических реакций, фазовых переходов
и процессов в растворах.

Объект
изучения термодинамики – термодинамические
системы, т.е. макроскопические
объекты, отделенные от окружающего
пространства реальной или мысленной
поверхностью. Системы бывают:

• открытые,
  в которых существует обмен энергией
  и веществом с окружающей средой;

• закрытые,
  в которых существует обмен энергией
  с окружением, но нет обмена веществом;

• изолированные,
  в которых нет обмена с окружением ни
  энергией, ни веществом.

Состояние
системы описывают с помощью макроскопических
параметров. Параметры бывают:

• внутренние,
  которые определяются только координатами
  тел системы, например: плотностьили внутренняя энергияU;

• внешние,
  которые определяются координатами
  тел в окружающей среде, например, объемV(при фиксированном положении
  стенок сосуда) или напряженность
  электрического поляE;

• экстенсивные,
  которые прямо пропорциональны массе
  системы или числу частиц, например,
  объемV, энергияU, энтропияS,
  теплоемкостьC;

• интенсивные,
  которые не зависят от массы системы
  или числа частиц, например, температураT, плотность,
  давлениеp. Отношение любых двух
  экстенсивных параметров является
  интенсивным параметром, например
  парциальный мольный объемVили мольная доляx.

Среди термодинамических параметров
выделяют обобщенные силыиобобщенные координаты. Обобщенные
силы описывают состояние равновесия.
К ним относят давлениеp, химический
потенциал,
электрический потенциал,
поверхностное натяжение.
Обобщенные силы – интенсивные параметры.

Обобщенные координаты – это величины,
которые изменяются под действием
соответствующих обобщенных сил. К ним
относятся объем V, количество
веществаn, зарядe, площадь W .
Все обобщенные координаты – экстенсивные
параметры.

Состояние системы описывается также
с помощью термодинамических функций,
которые зависят от параметров. Различают:

• функции
  состояния, которые зависят только
  от состояния системы и не зависят от
  пути, по которому это состояние получено;

• функции
  перехода, значение которых зависит
  от пути, по которому происходит изменение
  системы.

Примеры функций состояния: внутренняя
энергия – U, энтальпия –H, энергия
Гельмгольца –F, энергия Гиббса –G, энтропия –S. Термодинамические
параметры: объем –V, давление –p,
температуру –Tтакже можно считать
функциями состояния, т.к. они однозначно
характеризуют состояние системы.
Примеры функций перехода: теплотаQ
и работаA.

Функции состояния характеризуются
следующими свойствами:

1. бесконечно
   малое изменение функции fявляется
   полным дифференциалом (обозначаетсяdf);

2. изменение
   функции при переходе из состояния 1в состояние2определяется только
   этими состояниями:

;

1. в результате любого циклического
   процесса функция состояния не изменяется:
   .

Параметры системы могут зависеть или
не зависеть от времени. В зависимости
от этого различают следующие состояния
термодинамических систем:

• стационарное,
  когда параметры системы не зависят от
  времени, но в системе есть потоки
  (например, массы или энергии);

• равновесное,
  когда параметры системы не зависят от
  времени и нет потоков;

• неравновесное,
  когда параметры системы зависят от
  времени.

Если
хотя бы один из параметров системы
меняется со временем, то говорят, что
в системе происходит процесс.
Процессы бывают:

• обратимые,
  когда переход системы из одного
  состояния в другое и обратно может
  происходить по одному и тому же пути,
  и после возвращения в исходное состояние
  в окружающей среде не остается
  макроскопических изменений;

• квазистатические,
  илиравновесные, которые
  происходят под действием бесконечно
  малой разности обобщенных сил;

• необратимые,
  илинеравновесные, когда
  параметры меняются с конечной скоростью.

Все выводы и соотношения термодинамики
основаны на двух постулатах (исходных
положениях)итрех законах (началах).

Первое исходное положение, или
основной постулат термодинамики:

Любая изолированная система с
течением времени приходит в равновесное
состояние и самопроизвольно не может
из него выйти.

Это положение ограничивает размер
систем, которые описывает термодинамика.
Оно не выполняется для систем
астрономического масштаба и
микроскопических систем с малым числом
частиц. Системы галактического размера
самопроизвольно не приходят в состояние
равновесия благодаря дальнодействующим
гравитационным силам. Микроскопические
системы могут самопроизвольно выходить
из состояния равновесия; это явление
называют флуктуациями. В статистической
физике показано, что отклонение от
положения равновесия имеет амплитуду
порядка,
гдеN– число частиц в системе. Таким
образом, нижний предел для числа частиц
в термодинамической системе – порядка
10¹⁸.

Переход системы в равновесное состояние
называют релаксацией. Основной
постулат термодинамики ничего не
говорит о времени релаксации. В
классической равновесной термодинамикевообще нет времени. Термодинамика
позволяет установить только возможность
протекания процессов, но не может
определить скорость этих процессов.

Второе исходное положение, или
нулевой закон термодинамики описывает
свойства систем, находящихся в состоянии
теплового равновесия:

Если система А находится в тепловом
равновесии с системой В, а та, в свою
очередь, находится в равновесии с
системой С, то системы А и С также
находятся в тепловом равновесии.

Это свойство говорит о существовании
особого интенсивного параметра,
характеризующего состояние теплового
равновесия. Этот параметр называют
температурой. Системы, находящиеся
в тепловом равновесии, имеют одинаковую
температуру. Таким образом,нулевой
закон– это постулат о существовании
температуры.

Из нулевого закона следует, что при
равновесии внутренние параметры системы
являются функциями внешних параметров
и температуры. Уравнение, связывающее
внутренние параметры с внешними
параметрами и с температурой, называют
уравнением состояниятермодинамической системы.

Простейшее уравнение состояния описывает
систему невзаимодействующих частиц
точечного размера – идеальный газ: PV=nRT, (1.3) гдеn–
количество вещества (в молях),R–
универсальная газовая постоянная:

R= 8,314 Дж/(моль^.К) = 1,987 кал/(моль^.К) = 0,0821 латм/(моль^.К).

2. Первый закон термодинамики

Первый закон (первое начало) термодинамики
– это, фактически, закон сохранения
энергии. Он утверждает, что

энергия
изолированной системы постоянна. В
неизолированной системе энергия может
изменяться за счет: а) совершения работы
над окружающей средой; б) теплообмена
с окружающей средой.

Для описания этих изменений вводят
функцию состояния – внутреннюю энергию
Uи две функции перехода – теплотуQи работуA. Математическая
формулировка первого закона:

Q
= dU + A(дифференциальная форма) (2.1)

Q
= U
+ A(интегральная форма) (2.2)

Буква в уравнении
(2.1) отражает тот факт, чтоQиA– функции перехода и их бесконечно
малое изменение не является полным
дифференциалом.

В уравнениях (2.1) и (2.2) знаки теплоты и
работы выбраны следующим образом.
Теплота считается положительной, если
она передается системе. Напротив,
работа считается положительной, если
она совершаетсясистемойнад
окружающей средой.

Существуют разные виды работы:
механическая, электрическая, магнитная,
поверхностная и др. Бесконечно малую
работу любого вида можно представить
как произведение обобщенной силы на
приращение обобщенной координаты,
например:

A_мех=p^.
dV;A_эл=^.dе;A_пов=^.dW (2.3)

(- электрический потенциал,e– заряд,- поверхностное
натяжение, W – площадь поверхности). С
учетом (2.3), дифференциальное выражение
первого закона можно представить в
виде:

Q = dU
+ p
dV 
A_немех(2.4)

В дальнейшем изложении немеханическими
видами работы мы будем, по умолчанию,
пренебрегать.

Механическую работу, производимую при
расширении против внешнего давления
p_ex, рассчитывают по формуле:

(2.5)

Если процесс расширения обратим, то
внешнее давление отличается от давления
системы (например, газа) на бесконечно
малую величину: p_ex=p_in–dpи в формулу (2.5) можно подставлять
давление самой системы, которое
определяется по уравнению состояния.

Проще
всего рассчитывать работу, совершаемую
идеальным газом, для которого известно
уравнение состояния

Таблица
1.

Работа
идеального газа в некоторых процессах
расширения V₁

V₂:

Процесс	A
Изохорный процесс V = const	0
Расширение против постоянного внешнего давления p = const	p (V2–V1)
Изотермическое обратимое расширение T = const
Адиабатическое обратимое расширение Q = const	nCV(T1–T2)

При обратимом процессе совершаемая
работа максимальна.

Теплота может переходить в систему при
нагревании. Для расчета теплоты
используют понятие теплоемкости,
которая определяется следующим образом:

(2.6)

Если нагревание происходит при постоянном
объеме или давлении, то теплоемкость
обозначают соответствующим нижним
индексом:

;
. (2.7)

Из определения (2.6) следует, что конечную
теплоту, полученную системой при
нагревании, можно рассчитать как
интеграл:

(2.8)

Теплоемкость – экспериментально
измеряемая экстенсивная величина. В
термодинамических таблицах приведены
значения теплоемкости при 298 К и
коэффициенты, описывающие ее зависимость
от температуры. Для некоторых веществ
теплоемкость можно также оценить
теоретически методами статистической
термодинамики. Так, при комнатной
температуре для одноатомных идеальных
газов мольная теплоемкость C_V= 3/2R, для двухатомных газовC_V= 5/2R.

Теплоемкость определяется через
теплоту, переданную системе, однако ее
можно связать и с изменением внутренней
энергии. Так, при постоянном объеме
механическая работа не совершается и
теплота равна изменению внутренней
энергии: Q_V=dU, поэтому

(2.9)

При постоянном давлении теплота равна
изменению другой функции состояния,
которую называют энтальпией:

Q_p=dU+pdV=d(U+pV)= dH,
(2.10)

где H=U +pV–энтальпиясистемы.
Из (2.10) следует, что теплоемкостьC_pопределяет зависимость энтальпии от
температуры.

(2.11)

Из соотношения между внутренней энергией
и энтальпией следует, что для моля
идеального газа

C_p–C_V=R. (2.12)

Внутреннюю энергию можно рассматривать,
как функцию температуры и объема:

(2.13)

Для
идеального газа экспериментально
обнаружено, что внутренняя энергия не
зависит от объема,
,
откуда можно получить калорическое
уравнение состояния:

dU=C_V dT, (2.14)

В изотермических процессах с участием
идеального газа внутренняя энергия не
изменяется, и работа расширения
происходит только за счет поглощаемой
теплоты.

Возможен и совсем иной процесс. Если в
течение процесса отсутствует теплообмен
с окружающей средой (Q= 0), то такой процесс называютадиабатическим. В адиабатическом
процессе работа может совершаться
только за счет убыли внутренней энергии.
Работа обратимого адиабатического
расширения идеального газа:

A=
-U=nC_V
(T₁–T₂) (2.15)

(n– число молей,C_V– мольная
теплоемкость). Эту работу можно также
выразить через начальные и конечные
давление и объем:

(2.16)

где =C_p/C_V.

При обратимом адиабатическом расширении
идеального газа давление и объем связаны
соотношением (уравнением адиабаты):

pV^
= const (2.17)

В уравнении (2.17) важны два момента:
во-первых, это уравнение процесса, а не
уравнение состояния; во-вторых, оно
справедливо только для обратимогоадиабатического процесса. Это же
уравнение можно записать в эквивалентном
виде:

TV^-1=const, (2.18)

T^
p^1-
=const. (2.19)

3. Термохимия

Термохимия изучает тепловые эффекты
химических реакций. Во многих случаях
эти реакции протекают при постоянном
объеме или постоянном давлении. Из
первого закона термодинамики следует,
что при этих условиях теплота является
функцией состояния. При постоянном
объеме теплота равна изменению внутренней
энергии:

Q_V=dU,Q_V=U(3.1)

а при
постоянном давлении – изменению
энтальпии:

Q_P
=dH,Q_P=H(3.2)

Эти равенства в применении к химическим
реакциям составляют суть закона
Гесса:

Тепловой эффект химической реакции,
протекающей при постоянном давлении
или постоянном объеме, не зависит от
пути реакции, а определяется только
состоянием реагентов и продуктов
реакции.

Другими словами, тепловой эффект
химической реакции равен изменению
функции состояния.

В
термохимии, в отличие от других приложений
термодинамики, теплота считается
положительной, если она выделяется в
окружающую среду, т.е. если H< 0 илиU< 0.
Под тепловым эффектом химической
реакции понимают значениеH(которое называют просто “энтальпией
реакции”) илиUреакции.

Если
реакция протекает в растворе или в
твердой фазе, где изменение объема
незначительно, то

H=U+(pV)U(3.3)

Если же в реакции участвуют идеальные
газы, то при постоянной температуре

H=U+(pV)
=U+nRT,
(3.4)

где n
– изменение числа молей газов в реакции.

Для того чтобы облегчить сравнение
энтальпий различных реакций, используют
понятие “стандартного состояния”.
Стандартное состояние – это
состояние чистого вещества при давлении
1 бар (= 10⁵
Па) и заданной температуре.Для газов – это гипотетическое состояние
при давлении 1 бар, обладающее свойствами
бесконечно разреженного газа. Энтальпию
реакции между веществами, находящимися
в стандартных состояниях при температуреT, обозначают
(r- означает “reaction”).
В термохимических уравнениях указывают
не только формулы веществ, но и их
агрегатные состояния или кристаллические
модификации.

Из закона Гесса вытекают важные
следствия, которые позволяют рассчитывать
энтальпии химических реакций.

Следствие
1.Стандартная энтальпия химической
реакции равна разности стандартных
энтальпий образования продуктов реакции
и реагентов (с учетом стехиометрических
коэффициентов):

(3.5)

Стандартной энтальпией (теплотой)
образования вещества
(fозначает “formation”) при
заданной температуре называют энтальпию
реакции образования одного моля этого
веществаиз элементов, находящихся
в наиболее устойчивом стандартном
состоянии. Согласно этому определению,
энтальпия образования наиболее
устойчивых простых веществ в стандартном
состоянии равна 0 при любой температуре.
Стандартные энтальпии образования
веществ при температуре 298 К приведены
в справочниках.

Понятия
“энтальпия образования” используют
не только для обычных веществ, но и для
ионов в растворе. При этом за точку
отсчета принят ион H⁺, для которого
стандартная энтальпия образования в
водном растворе полагается равной
нулю:
(H⁺)
= 0

Следствие 2.Стандартная энтальпия химической
реакции равна разности энтальпий
сгорания реагентов и продуктов реакции
(с учетом стехиометрических коэффициентов):

(3.6)

(cозначает “combustion”). Стандартной
энтальпией (теплотой) сгорания вещества
называют энтальпию реакции полного
окисления одного моля вещества. Это
следствие обычно используют для расчета
тепловых эффектов органических реакций.

Следствие 3.Энтальпия химической реакции равна
разности энергий разрываемых и
образующихся химических связей.

Энергией
связиA-B называют энергию,
необходимую для разрыва связи и
разведения образующихся частиц на
бесконечное расстояние:

AB_(г)A_(г)+ B_(г).

Энергия
связи всегда положительна.

Большинство термохимических данных в
справочниках приведено при температуре
298 К. Для расчета тепловых эффектов при
других температурах используют уравнение
Кирхгофа:(дифференциальная форма) (3.7)

(интегральная форма) (3.8)

где
C_p–
разность изобарных теплоемкостей
продуктов реакции и исходных веществ.
Если разницаT₂–T₁невелика, то можно принятьC_p= const.

Лабораторная работа Определение интегральной теплоты растворения соли

Задачу калориметрии составляет измерение
количества тепла, выделяющегося или
поглощающегося при различных
физико-химических процессах. Но теплота
процесса не всегда является характеристикой
для данного процесса, т.к., согласно
первому закону термодинамики, она
зависит не только от начального и
конечного состояния системы, но и от
пути перехода системы из одного состояния
системы в другое.

Если ограничиться такими процессами,
при которых единственным видом работы
может быть работа против внешнего
давления, то теплота процесса будет
характерной величиной процесса при
двух условиях: для изохорических
процессов, где тепловой эффект равен
изменению внутренней энергии:

Q_V = U₂ – U₁ =U

Для изобарных процессов, где тепловой
эффект равен убыли энтальпии системы:

Q_P = H₁ – H₂ =H

При растворении в воде наблюдается
либо поглощение, либо выделение тепла.
Изучением тепловых процессов,
сопровождающихся изменением состояния
системы, занимается термохимия. По
закону Гесса тепловой эффект реакции
зависит только от начального и конечного
состояния реагирующих веществ и не
зависит от пути перехода от одного
состояния к другому.

Пользуясь этим законом можно рассчитать
тепловой эффект процесса там, где
невозможно произвести точное прямое
измерение.

При растворении вещества в воде протекают
одновременно следующие процессы:

1.
Разрушение кристаллической решетки
вещества. При этом происходит поглощение
тепла в количестве равном Q кристаллической
решетки.

2.
Гидратация ионов, сопровождаемая
выделением определенного количества
тепла, равного Q гидратации. Теплота
растворения соли равна алгебраической
сумме тепловых эффектов этих процессов:

Q _раств = Q_{крист.реш.} + Q_гидр

Вещества, обладающие прочной
кристаллической решеткой и слабо
гидратирующиеся в растворе, будут
растворяться с поглощением тепла.
Вещества с непрочной кристаллической
решеткой или образующие в растворе
сильно гидратированные ионы, например
ионы водорода или гидроксила, будут
растворяться с выделением тепла.

Теплота растворения, помимо природы
растворенного вещества и растворителя,
зависит от температуры растворителя
и концентрации полученного раствора.

Различают интегральную и дифференциальную
теплоты растворения.

Интегральная теплота растворения
– это тепловой эффект растворения
одного грамма (удельная) и одного моля
(мольная) вещества в определенном
количестве растворителя, при данной
температуре.

Дифференциальная или парциальная
теплота растворения– это тепловой
эффект, сопровождающий процесс
растворения одного моля или одного
грамма вещества в настолько большом
количестве растворителя определенной
концентрации, что изменение ее, вызванное
растворением этого количества вещества,
можно считать равным нулю.

Интегральные теплоты растворения
находятся экспериментально, а
дифференциальные – методом расчета.

Калориметрическая установка

Большинство калориметрических измерений
сводятся к тому, что процесс проводят
в калориметре и наблюдают вызванное
этим процессом температуры калориметра.

Простейший калориметр с изотермической
оболочкой изображен на рис.1. Тефлоновый
нетеплопроводный стакан (4) вставлен в
оболочку (8) на подставке из материала
с малой теплопроводностью. Для уменьшения
испарения калориметрической жидкости
и для придания всей установке в собранном
виде механической жесткости, стакан
закрывают крышкой (3).

Рис.1. Калориметрическая
установка:

1 – мешалка, 2 –
воронка для ввода вещества, 3 – крышка,

4
– внутренний стакан, 5 – муфта, 6 –
электромотор,

7
– термометр Бекмана, 8 – внешний стакан.

В крышке сделаны отверстия для мешалки,
термометра и для ввода соли (2). Для
быстрого установления теплового
равновесия между всеми частями
калориметрической установки и для
энергичного смешивания исследуемых
веществ используют мешалку (1), приводимую
в движение электрическим мотором (6).
Изменение температур и хода опыта
определяют с помощью термометра Бекмана
(7). Вся шкала его охватывает интервал
температур в 5⁰С.

Цена наименьшего деления – 0,01⁰С.
(Рис.2)

	1 – нижний резервуар большого объема для ртути, 2 – капилляр и измерительная шкала, 3 – верхний запасной резервуар, 4 – шкала верхнего резервуара для грубой настройки термометра. Количество ртути в основном резервуаре А можно изменять путем перевода ртути в трубку В и обратно. Это дает возможность работать с термометром Бекмана при температурах от –90 до +2000С.
Рис.2. Метастатический термометр Бекмана:

Таким образом, следует помнить, что
шкала такого термометра имеет условный
характер.

1. Определение постоянной калориметра

Для расчета теплового процесса,
протекающего в калориметрической
установке, необходимо знать постоянную
калориметра, т.е. количество тепла в
калориях, необходимые для нагревания
всех частей калориметра на 1⁰С.
Эту величину можно определить разными
методами. В приближенных измерениях,
когда допустимая погрешность опыта
составляет несколько процентов,
постоянную калориметра можно вычислить,
зная, что теплоемкость всей системы
слагается из теплоемкостей калориметрической
жидкости и соприкасающихся с ней всех
частей калориметра, участвующих в
теплообмене: растворителя (в данном
случае – воды), мешалки, термометра.

Теплоемкость каждой части калориметра
рассчитывают, умножая ее удельную
теплоемкость на массу: c_i ^.m_i, а или постоянную калориметра
системы:

K = c_i
^. m_i

Значения масс частей калориметра смотри
на установке, а значения теплоемкости
находят в таблице 1.

Теплоемкость погруженной в раствор
нижней части термометра Бекмана по
необходимости определяют с меньшей
точностью, чем теплоемкость остальных
деталей калориметра, но эта величина
мала и погрешность определения
незначительно сказывается на точности
опыта. Теплоемкость термометра
рассчитывают из того, что разные объемы
стекла и ртути обладают приблизительно
одинаковыми теплоемкостями (ртуть –
0,45, а стекло – 0,47, в среднем – 0,46
кал/мл^.град).

Таблица 1.

Значения удельной теплоемкости для некоторых веществ

Вещество	Al	Hg + стекло	Cu	Fe	H2O
Удельная теплоемкость, кал/гград	0,21	0,46	0,09	0,107	1,00

Объем погруженной части термометра
определяют погружением термометра в
мензурку на ту же глубину, что и в
калориметре. Изменение уровня воды в
мензурке равно объему погруженной
части термометра.

Порядок проведения опыта

1. Взять навеску хлорида калия из расчета,
что концентрация раствора должна быть
1 моль соли на 200 молей воды (рассчитать
m_KCl, необходимую для проведения
опыта в 400 мл воды).

2. В тефлоновый стакан налить 400 мл
дистиллированной воды, закрыть стакан
крышкой (7), опустить термометр Бекмана
(термометр перед работой настраивает
лаборант).

3. Включить мешалку.

4. Через 3 – 4 минуты, при включенной
мешалке, когда все части калориметра
примут одинаковую температуру и резкого
изменения температуры не происходит,
проводят измерения температуры через
каждые 30 секунд (используя секундомер).

Весь опыт делится на три периода:

а) предварительный;

б) главный – время растворения соли;

в) заключительный период.

5. Предварительный период проводят в
течение 5 минут, замеряя значения
температуры каждые 30 секунд. В это время
устанавливается равномерный ход
температуры. Сразу после десятого
замера через отверстие в крышке
калориметра вводят соль и начинается
главный период.

6. Главный период длится до тех пор, пока
не прекратится падение температуры
(измерение температуры производят
также каждые 30 секунд).

7. После этого делают еще 10 отсчетов
через каждые 30 секунд – заключительный
период.

Если из-за быстрого изменения температуры
какой-либо отсчет не удалось записать,
ставят прочерк, а потом на этом месте
указывают среднее значение температур
из предыдущего и последующего отсчетов.
Если процесс протекает слишком быстро,
то в главном периоде допускается запись
температур с меньшей точностью, чем в
начальном периоде.

Результаты опыта заносят в таблицу:

Таблица
2.

Время, мин (№ измерения)	Температура, 0С
KCl	Задача №___
1 2 3 .

3. Определение изменения температуры (t)

Для расчета точного изменения температуры
растворения соли вычерчивают график,
где на оси абсцисс откладывают время,
а на оси ординат – изменение температуры
за каждые 0,5 минуты.

Если соединить найденные таким образом
точки, получаются две наклонные прямые,
наклон которых будет зависеть от
разности температур между калориметром
и окружающей средой. Чтобы определить
действительное изменение температуры,
продолжают линии АВ и СД до пересечения
с вертикальной прямой ЕГ.

Положение линии ЕГ находится построением:
расстояние между В и С делят пополам и
в точке О проводят прямую ЕГ, параллельную
оси ординат до пересечения с продолжением
прямых АВ и СД. Отрезок ЕГ будет
действительным изменением температуры
системы (t), т.е.
таким изменением, которое сопровождало
бы растворение хлорида калия в условиях,
исключающих потери в окружающую среду.

4. Вычисления

По найденной величине постоянной
калориметра К и величине действительного
изменения температуры t
вычисляют удельную теплоту растворения
соли по формуле:

,

где Q –
удельная теплота растворения,

m – рассчитанная навеска соли.

Для вычисления молярной теплоты
растворения соли удельную теплоту
умножают на молярный вес соли.

Q_мол. = Q^. М_соли

Сравнить полученное значение интегральной
теплоты растворения соли со справочной
величиной (Краткий справочник
физико-химических величин).

5. Определение теплоты растворения неизвестной соли

Определив тепловое значение калориметра,
приступают к контрольной работе –
определению теплоты растворения
неизвестной соли. Соль выдается
преподавателем после проверки
правильности выполнения опыта с хлоридом
калия.

Порядок проведения опыта

1. Взять количество соли, указанное в
задаче, отвесить на технических весах
(указано на банке с задачей).

2. В тефлоновый стакан налить 400 мл
дистиллированной воды, закрыть стакан
крышкой (7), опустить термометр Бекмана
(термометр перед работой настраивает
лаборант).

3. Включить мешалку.

4. Через 2-3 минуты, при включенной мешалке,
когда все части калориметра примут
одинаковую температуру и резкого
изменения температуры не происходит,
проводят измерения температуры через
каждые 30 секунд (используя секундомер).

Весь опыт делится на три периода:

а) предварительный – в
течение 5 минут, замеряют значения
температуры каждые 30 секунд. В это время
устанавливается равномерный ход
температуры. Сразу после десятого
замера через отверстие в крышке
калориметра вводят соль, и начинается
главный период.

б) главный– время растворения
соли;

Главный
период длится до тех пор, пока не
прекратится падение температуры
(измерение температуры производят
также каждые 30 секунд).

в) заключительный период– делают
еще 10 отсчетов через каждые 30 секунд –
заключительный период.

По найденной величине постоянной
калориметра К и величине действительного
изменения температуры t,
которую определяют по графику, вычисляют
удельную теплоту растворения соли по
формуле:

,

где Q – удельная теплота растворения,

К – постоянная калориметра, (K = c_i
^.m_i,)

t – изменение температуры,

m – навеска неизвестной соли.

2

23

3

22

4

21

5

20

6

19

7

18

8

17

9

16

10

15

11

14

12

13

    В очень разбавленных растворах Xj, т совпадает с первой интегральной теплотой растворения AHq. В концентрированных растворах интегральная и дифференциальная теплоты растворения нередко различаются не только значением, но и знаком. Наиболее важна дифференциальная теплота растворения в насыщенном растворе h, S, называемая последней теплотой растворения. Знак 2, s определяет зависимость растворимости твердых тел и газов от температуры. [c.49]

    Первой интегральной теплотой растворения называют изменение энтальпии при растворении одного моля вещества в бесконечно боль- [c.374]

    Промежуточной энтальпией растворения называют изменение энтальпии при растворении 1 моля вещества в растворе, уже содержащем некоторое количество этого вещества. Если растворение 1 моля вещества происходит в бесконечно большом количестве раствора, тепловой эффект называют дифференциальной энтальпией растворения. В этом процессе концентрация раствора остается неизменной, или, точнее, возрастает на бесконечно малую величину, которой пренебрегают. Дифференциальная теплота растворения зависит от концентрации раствора. Очевидно, дифференциальная теплота растворения в чис-том растворителе характеризует, по сути дела, энергетику образования бесконечно разбавленного раствора и поэтому совпадает с первой интегральной теплотой растворения. Дифференциальную теплоту растворения в насыщенном растворе, или, точнее, в растворе, концентрация которого отличается от концентрации насыщенного на бесконечно малую величину, называют последней теплотой растворения. [c.65]

Рис. 1. Зависимость первой интегральной теплоты растворения K I от содержания воды в спирте при 25° С (в мольн. %)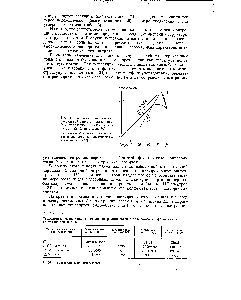

    Дифференциальная теплота растворения зависит от концентрации раствора. Дифференциальная теплота растворения в чистом растворителе совпадает с первой интегральной теплотой растворения. Дифференциальную теплоту растворения в насыщенном растворе называют последней теплотой растворения. [c.375]

    На рис. 125 приведена зависимость интегральной теплоты растворения от числа молей растворенного вещества в одном и том же количестве растворителя (п пропорционально моляльности раствора). Экстраполяция кривой на = О дает первую интегральную теплоту растворения, экстраполяция на п , при котором раствор становится насыщенным, дает полную теплоту растворения. Отрезок, отсекаемый касательной на оси ординат, равен дифференциальной теплоте растворения в растворе, концентрация которого определяется абсциссой точки касания. Действительно, уравнение касательной имеет вид [c.376]

    Полное изменение энтальпии при растворении П2 молей второго компонента в П1 молях растворителя называется интегральной теплотой растворения и обозначается чаще всего АЯ . Интегральная теплота растворения зависит от концентрации, поэтому, как правило, в справочной литературе приводят так называемую первую интегральную теплоту растворения, определяемую как теплота растворения П2 молей растворяемого вещества в бесконечном количестве растворителя. [c.135]

    Теплоту, энтропию и энергию гидратации исследовали, основываясь на экспериментально определяемых теплотах растворения и энергиях решеток солей. Для случая бесконечного разведения раствора кристаллического электролита первая интегральная теплота растворения АЯо равна сумме энергии решетки и общей теплоты гидратации (сольватации) катионов и анионов. Энергия решетки определяется как изменение энтальпии, отвечающее взаимному удалению ионов решетки на бесконечно большое расстояние  [c.254]

    Изменение энергии системы в процессе растворения кристаллов при полной ионизации с образованием бесконечно разбавленного раствора (см. разд. 4.3.1) определяется первой интегральной теплотой растворения АНт->о- [c.215]

    Особый интерес представляют первая интегральная энтальпия (теплота) растворения и полная энтальпия растворения. Первой интегральной теплотой растворения называют изменение энтальпии при растворении 1 моля вещества в бесконечно большом количестве растворителя. В результате процесса образуется бесконечно разбавленный раствор. Например, для растворения Ь(ЫОз),2 это выражается схемой [c.64]

    Первые интегральные теплоты растворения хлорида калия в воде (АЯо) по данным различных авторов и вычисленные из них значения интегральной теплоты растворения последнего (ЛЯ, =0,2,3) при 25° С [c.38]

    В нроцессе обработки наших экспериментальных данных мы применили иной путь для объективной проверки подвергавшегося сомнению метода, используя для этого более близкие к непосредственным результатам величины — температурные коэффициенты первых интегральных теплот растворения А//о- [c.217]

    Параллельно для ряда понов вычисление химических теплот гидратации проведено другим способом. Как известно, суммарная химическая теплота гидратации электролита Л//, при бесконечном разведении связана с энергией кристаллической решетки ДЯре,,, тг с первой интегральной теплотой раствореиия ДЯ соотпоптением (28) (стр. 56) [c.70]

    Первые интегральные теплоты растворения (в нал/моль) различных электролитов в смесях [c.249]

    Первые интегральные теплоты растворения [c.86]

    При рассмотрении зависимости теплот растворения солей от свойств растворителя естественно в качеств. ) стандартного состояния принять бесконечное.разведение. Именно поэтому большой интерес представляет накопление данных по первым интегральным теплотам растворения одних и тех же солей в различных растворителях (табл. VI. 2).- [c.86]

    МОЖНО получить целый ряд дифференциальных теплот растворения. Очевидно, первая дифференциальная теплота растворения, отвечающая образованию раствора концентрации /Ио, совпадает по величине с первой интегральной теплотой растворения. [c.61]

    В табл. 3 приведены первые интегральные теплоты растворения компонентов, вычисленные нами из литературных данных по теплотам [c.33]

    Уравнение (159.2) позволяет определить стандартную энтальпию образования кристаллических соединений по энтальпии их растворения с образованием стандартного раствора. Если ДЯ°(СаС12) — первая интегральная теплота растворения СаС , то стандартная энтальпия образования кристаллического СаСЬ может быть рассчитана по уравнению [c.447]

    Однако точность величин 7г, являющихся температурным коэффициентом о. п. м. э., во многих случаях неудовлетворительна, что ограничивает возможности применения уравнения (У.ЗО) для расчета С ,, В методе интегральных теплот Коббла рекомендуется использовать для этой цели температурные коэффициенты первых интегральных теплот растворения. Так как [c.95]

    Сопоставление первых интегральных теплот растворения (в ккал моль) некоторых солей в формамлде, измеренных Сомсеном и Коопеом [74], с результатами, полученными А. М. Сухотиным [49] (25° С) [c.157]

    При растворении кристаллического электролита с образованием весьма разбавленного раствора первая интегральная теплота растворения может бьпь представлена как сумма энергии кристаллической решетки и суммарной энтальпии сольватации катионов и анионов. Энергия решетки и сум- [c.205]

    В таблице приведены значения интегральных теплот растворения некоторых солей в водных растворах на границе полной гидратации А Нгиг и первых интегральных теплот растворения АНо, а также их разности, которые, в принципе, представляют собой энергию взаимодействии данной соли [c.138]

    Учитывая, что при одновременном переходе катионов и анионов все добавочные электрические влияния взаимно компенсируются и на границах кристалл—газ и кристалл—раствор, мы возвращаемся к строгому термодинамическому уравнению (7.7), содержащему только энергию решетки, суммарную химическую теплоту сольватации и первую интегральную теплоту растворения. Подводные камни здесь ограничиваются только погрешностями экспериментальных данных для теплот растворения и энер ГИИ решетки. Первые теплоты растворения при современной технике термохимических измерений в случае водных растворов известны с точностью до 0,1%, для неводных систем — с точностью от О, 5% до 1,0%. Правда, экстраполяция измеренных значений тепловых эффектов при т Q в ряде случаев возможна с большой достоверностью благодаря прецизион ным измерениям теплоты разведения в калориметрах с чувствительностью около С. В случае растворов в спиртах, ацетоне, этиленгликоле, [c.142]

    Учитывая, что при одновременном переходе катионов и анионов все добавочные электрические влияния взаимно компенсируются и на границах кристалл—газ и кристалл—раствор, мы возвращаемся к строгому термодинамическому уравнению (IV. 1), содержащему только энергию решетки, суммарную химическую теплоту сольватации и первую интегральную теплоту растворения. Подводные камни здесь ограничиваются только погрешностями экспериментальных данных для АЯо и АЯрдщ. Первые теплоты растворения при современной технике термохимических измерений в случае водных растворов известны с точностью до 0,1%, для неводных систем — с точностью от i l до 0,5%. Правда, и здесь только [c.62]

    Сопоставление первых интегральных теплот растворения некоторых солей в формамиде, измеренных Сомсеном и Коопсом [164 12, р. 111], с результатами, полученными А. М. Сухотиным [305] (25 °С) [c.164]

    Однако, подводя теоретическую базу под правило Мессона— Россини, Г. И. Микулин не решает поставленного нами выше вопроса об экстраполяции значений Ср или Фс к /и = О для точного нахождения их предельных значений. Уравнения, описывающие участок 1, позволяют определить наклон в зоне бесконечного разведения, но не могут предсказать места пересечения изотермы с ординатой. В то же время даже точная оценка коэффициентов ап Ьв уравнении (IX. 12) позволяет найти пересечение с нулевой ординатой только прямой 3. Естественно, что оба пересечения не совпадают и вопрос об оправданности нахождения Фс = Ср путем экстраполяции прямых Мессона—Россини остается открытым. Удовлетворительное совпадение этих величин, найденных таким путем, с температурными коэффициентами первых интегральных теплот растворе- [c.240]

    Мы видим, что даже первые интегральные теплоты растворения ДНо, при/и = О не совпадают. Так, в ацетоне ДНо = —44,1 кДж/моль (—10,54 ккал/моль), а в псевдоацетоне —27,74 кДж/моль (—6,63 ккал/моль). Те же величины для пары метанол и псевдометанол соответственно равны —32,05 (—7,66) и —22,76 кДж/моль (—5,44 ккал/моль). Следовательно, химические теплоты сольватации в ацетоне и метаноле заметно экзотермичнее, чем в изодиэлектри- [c.283]

    Термохимическое исследование растворов ассоциирован-ньЕХ жидкостей в алканах часто используется для оценки энергии ассоциации этих соединений. В работе показано, что величина первой интегральной теплоты растворения в гексане близка к энергии ассоциации изучаемых жидкостей, если эта энергия не очень значительна / меньше 10 ккал/моль /. По нашим данным ата величина составляет 3,6 ккал/моль для [c.435]

    Величина ДЯт , полученная при растворении одного моля соли в бесконечно большом количестве растворителя (концентрация Ото приближается к нулю), называется первой, интегральной теплотой растворения. Практически для получения АЯот достаточно взять 400 и боле молей растворителя на один моль растворяемой соли. [c.60]

    Вслшчины интегральных тоилот растворения АН,,, могут быть использованы для характеристики сольватирующей способности растворителей. Для этого необходимо иметь первые интегральные теплоты растворения АЯ(), из которых рассчитывают суммарные химические теплоты сольватации электролитов при бесконечном разведении [c.130]

---

Интегральная теплота – растворение

Cтраница 1

Интегральные теплоты растворения и набухания некоторых по-лимеров приведены в табл. 23, ил которой следует, что растворение полиморов может быть атермическим, экзо – и эндотермическим.
 [2]

Интегральные теплоты растворения MgS04 ( безводн.
 [3]

Интегральные теплоты растворения MgSQ4 ( безвенн.
 [4]

Интегральные теплоты растворения и набухания некоторых по-лимеров приведены в табл. 23, ил которой следует, что растворение полимеров может быть атермическим, экзо – и эндотермическим.
 [5]

Интегральная теплота растворения зависит от концентрации полученного раствора.
 [7]

Интегральная теплота растворения 1 моль вещества зависит от концентрации получившегося раствора. Значения интегральных теплот растворения приводятся в справочниках. Эта величина может иметь как положительный, так и отрицательный знак.
 [8]

Интегральная теплота растворения равна в среднем 360 ккал / кг СО 2, в зависимости от условий работы она колеблется от 320 до 430 ккал / кг. Чем сильнее нагрет насыщенный раствор на выходе из абсорбера за счет теплоты абсорбции, тем выше температура регенерированного раствора на выходе из теплообменника и тем большее количество тепла будет потеряно в холодильнике.
 [9]

Интегральные теплоты растворения некоторых полимеров приведены в табл. 22, из которой следует, что растворение полимеров может быть атермическим, экзо – и эндотермическим.
 [10]

Интегральная теплота растворения полимера может быть измерена калориметрическим методом. Это достигается смешением па-вески полимера с определенным количеством низкомолекулярного компонента, находящегося в калориметрическом сосуде. При соприкосновении с растворителем полимер набухает, а затем растворяется. Процесс в целом, даже при очень малых навесках полимера, продолжается от 20 до 60 мин.
 [12]

Интегральная теплота растворения полимера может быть измс-рена калориметрическим методом. Это достигается смешением навески полимера с определенным количеством низкомолекулярного компонента, находящегося в калориметрическом сосуде. При соприкосновении с растворителем полимер набухает, а затем растворяется. Процесс в целом, даже при очень малых навесках полимера, продолжается от 20 до 60 мин.
 [13]

Интегральная теплота растворения NaCl, отвечающая образованию насыщенного раствора ( 6 15 моль Nad на 1000 г Н2О), равна 0 466 ккал / моль.
 [14]

Интегральная теплота растворения электролитов является алгебраической суммой двух величин: 1) поглощения теплоты при разрушении кристаллической решетки ( АЯреш) и удаления ионов на расстояния в соответствии с объемом раствора и 2) выделения теплоты при гидратации или сольватации ДЯГИДр каждого иона молекулами растворителя.
 [15]

Страницы:  

   1

   2

   3

   4