Интегральные уравнения как составить

Интегральные уравнения как составить

Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.

Классификация интегральных уравнений[править | править код]

Линейные интегральные уравнения[править | править код]

Это интегральные уравнения, в которые неизвестная функция входит линейно:

{displaystyle varphi (x)=lambda int limits _{a}^{b}K(x,;s)varphi (s),ds+f(x)}

где varphi (x) — искомая функция, f(x), K(x,;s) — известные функции, lambda  — параметр. Функция K(x,;s) называется ядром интегрального уравнения. В зависимости от вида ядра и свободного члена линейные уравнения можно разделить ещё на несколько видов.

Уравнения Фредгольма[править | править код]

Уравнения Фредгольма 2-го рода[править | править код]

Уравнения Фредгольма 2-го рода — это уравнения вида:

varphi(x)=lambdaintlimits_a^b K(x,;s)varphi(s),ds+f(x).

Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: aleqslant x,;sleqslant b, а ядро и свободный член должны быть непрерывными: K(x,;s)in C(aleqslant x,;sleqslant b),;f(x)in C([a,;b]), либо удовлетворять условиям:

intlimits_a^bintlimits_a^b|K(x,;s)|^2,dx,ds<+infty,qquadintlimits_a^b|f(x)|^2,dx<+infty.

Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если f(x)equiv 0 на [a,;b], то уравнение называется однородным, иначе оно называется неоднородным интегральным уравнением.

Уравнения Фредгольма 1-го рода[править | править код]

Уравнения Фредгольма 1-го рода выглядят так же, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:

intlimits_a^b K(x,;s)varphi(s),ds=f(x),

при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 2-го рода.

Уравнения Вольтерры[править | править код]

Уравнения Вольтерры 2-го рода[править | править код]

Уравнения Вольтерры отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:

varphi(x)=lambdaintlimits_a^x K(x,;s)varphi(s),ds+f(x),qquad aleqslant xleqslant b.
Уравнения Вольтерры 1-го рода[править | править код]

Также, как и для уравнений Фредгольма, в уравнениях Вольтерры 1-го рода отсутствует неизвестная функция вне интеграла:

intlimits_a^x K(x,;s)varphi(s),ds=f(x).

В принципе, уравнения Вольтерры можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:

mathcal{K}(x,;s)=begin{cases}K(x,;s), & aleqslant sleqslant x, \ 0, & x<sleqslant b.end{cases}

Однако некоторые свойства уравнений Вольтерры не могут быть применены к уравнениям Фредгольма.

Нелинейные уравнения[править | править код]

Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.

Уравнения Урысона[править | править код]

Основная статья: Интегральное уравнение Урысона

varphi(x)=intlimits_a^b K(x,;s,;varphi(s)),ds,qquad K(x,;s,;varphi)in C(aleqslant x,;sleqslant b;;-Mleqslantvarphileqslant M).

Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.

Уравнения Гаммерштейна[править | править код]

Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:

varphi(x)=intlimits_a^b K(x,;s)F(s,;varphi(s)),ds,

где K(x,;s) — фредгольмово ядро.

Уравнения Ляпунова — Лихтенштейна[править | править код]

Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:

varphi(x)=f(x)+lambdaintlimits_a^b K_{[1]}(x,;s)varphi(s),ds+muintlimits_a^bintlimits_a^b K_{[1,;1]}(x,;s,;z)varphi(x)varphi(z),ds,dz+ldots

Нелинейное уравнение Вольтерры[править | править код]

varphi(x)=intlimits_a^x F(x,;s,;varphi(s)),ds,

где функция F(x,;s,;varphi) непрерывна по совокупности своих переменных.

Методы решения[править | править код]

Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений, не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.

Преобразование Лапласа[править | править код]

Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:

intlimits_0^x f(x-t)g(t),dtrisingdotseq F(p)G(p),

то есть, когда ядро является функцией разности двух переменных:

varphi(x)=f(x)+intlimits_0^x K(x-s)varphi(s),ds.

Например, дано такое уравнение:

varphi(x)=sin x+2intlimits_0^x cos(x-s)varphi(s),ds.

Применим преобразование Лапласа к обеим частям уравнения:

varphi(x)risingdotseqPhi(p),
Phi(p)=frac{1}{1+p^2}+2frac{p}{1+p^2}Phi(p)RightarrowPhi(p)=frac{1}{(p-1)^2}.

Применяя обратное преобразование Лапласа, получим:

varphi(x)=underset{p=1}{mathrm{res}},frac{1}{(p-1)^2}e^{px}=(e^{px})'_pBig|_{p=1}=xe^x.

Метод последовательных приближений[править | править код]

Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:

|lambda||b-a|max_{aleqslant x,;sleqslant b}|K(x,;s)|<1.

Это условие необходимо для сходимости ряда Лиувилля — Неймана:

varphi(x)=sum_{k=0}^inftylambda^k(K^kf)(x),

который и является решением уравнения. (K^kf)(x) — k-ая степень интегрального оператора (Kf)(x):

(Kf)(x)=intlimits_a^b K(x,;s)f(s),ds.

Впрочем, такое решение является хорошим приближением лишь при достаточно малых |lambda|.

Этот метод применим также и при решении уравнений Вольтерры 2-го рода. В таком случае ряд Лиувилля – Неймана сходится при любых значениях |lambda|, а не только при малых.

Метод резольвент[править | править код]

Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.

Если ввести следующие обозначения:

begin{align} K_0(x,;t)=K(x,;t),\ K_1(t,;s)=K(t,;s), end{align}

то повторными ядрами ядра K(x,;s) будут ядра K_p(x,;s):

K_p(x,;s)=intlimits_a^b K(x,;t)K_{p-1}(t,;s),dt.

Ряд, составленный из повторных ядер,

mathcal{R}(x,;s,;lambda)=sum_{k=0}^inftylambda^k K_{k+1}(x,;s),

называется резольвентой ядра K(x,;s) и является регулярно сходящимся при aleqslant x, sleqslant b и вышеупомянутому условию сходимости ряда Лиувилля — Неймана. Решение интегрального уравнения представляется по формуле:

varphi(x)=f(x)+lambdaintlimits_a^bmathcal{R}(x,;s,;lambda)f(s),ds.

Например, для интегрального уравнения

varphi(x)=f(x)+lambdaintlimits_0^1 xsvarphi(s),ds

повторными будут следующие ядра:

K_0(x,;s)=xs,
K_1(x,;t)=xt,
K_2(x,;t)=intlimits_0^1 xs,st,ds=frac{xt}{3},
K_3(x,;t)=intlimits_0^1 xsfrac{st}{3},ds=frac{xt}{9},
ldots
K_{n+1}=frac{xt}{3^n},

а резольвентой — функция

mathcal{R}(x,;t,;lambda)=sum_{n=0}^inftylambda^n K_{n+1}=sum_{n=0}^inftylambda^nfrac{xt}{3^n}=xtfrac{1}{1-dfrac{lambda}{3}}=frac{3xt}{3-lambda}.

Тогда решение уравнения находится по формуле:

varphi(x)=f(x)+lambdaintlimits_0^1frac{3xt}{3-lambda}f(t),dt.

Метод сведения к алгебраическому уравнению[править | править код]

В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть K(x,;s)=sum_{i=1}^N f_i(x)g_i(s), само интегральное уравнение можно свести к системе алгебраических уравнений. Действительно, в этом случае уравнение можно переписать так:

varphi(x)=lambdasum_{i=1}^N f_i(x)intlimits_a^b g_i(s)varphi(s),ds+f(x)=lambdasum_{i=1}^N c_if_i(x)+f(x),

где c_i=intlimits_a^bvarphi(s)g_i(s),ds. Умножив предыдущее равенство на g_i(x) и проинтегрировав его по x на отрезке [a,;b], приходим к системе алгебраических уравнений для неизвестных чисел c_{i}:

c_i=lambdasum_{k=0}^N a_{ik}c_k+b_i,qquad i=1,;ldots,;N,

где a_{ik}=intlimits_a^b g_i(x)f_k(x),dx и b_i=intlimits_a^b g_i(x)f(x),dx — числовые коэффициенты.

Приближённо этим методом можно решить интегральное уравнение Фредгольма с любым ядром, если в качестве вырожденного ядра, близкого к действительному, взять отрезок ряда Тейлора для функции K(x,;s).[1]

Замена интеграла конечной суммой[править | править код]

Рассмотрим интегральное уравнение Фредгольма 2-го рода: varphi(x) - lambda int_{a}^{b} K(x,t) varphi(t) dt = f(x), где K(x,t) и f(x) имеют непрерывные производные нужного порядка, lambda – заданное число. Используем квадратурную формулу: int_{a}^{b}Phi(x)dxapproxsum_{k=1}^{n}A_{k}Phi(x_{k}), где x_{1}, x_{2}, ... x_{n} – точки на отрезке [a,b], а коэффициенты A_{1}, A_{2}, ... , A_{n} не зависят от вида функции Phi (x). Рассмотрим исходное уравнение в точках x_{k}: varphi(x_{k}) - lambda int_{a}^{b} K(x_{k},t) varphi(t) dt = f(x_{k}). Заменим интеграл в левой части уравнения с помощью квадратурной формулы: varphi(x_{k}) - lambda sum_{m=1}^{n} K(x_{k}, x_{m}) varphi(x_{m}) = f(x_{k}). Получаем линейную систему n алгебраических уравнений с n неизвестными varphi(x_{1}), varphi(x_{2}), ... varphi(x_{n}), которые являются приближёнными значениями решения varphi (x) в точках x_{1}, x_{2}, ... x_{n}. В качестве приближённого решения исходного интегрального уравнения можно принять функцию: overline{varphi(x)} = lambda sum_{m=1}^{n} A_{m}K(x, x_{m}) varphi(x_{m})[1].

Приложения[править | править код]

Термин «интегральное уравнение» ввёл в 1888 году П. Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.

Формула обращения Фурье[править | править код]

Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x):

g(x)=frac{1}{sqrt{2pi}}intlimits_{-infty}^{+infty}e^{ixy}f(y),dy.

Фурье получил выражение для функции f(y):

f(y)=frac{1}{sqrt{2pi}}intlimits_{-infty}^{+infty}e^{-ixy}g(x),dx.

Сведение задачи Коши к интегральному уравнению[править | править код]

К нелинейным интегральным уравнениям Вольтерры приводит задача Коши для обыкновенных дифференциальных уравнений:

frac{dx}{dt}=F(t,;x(t)),qquad x(a)=x_0.

В самом деле, это уравнение можно проинтегрировать по t от a до t:

x(t)=x_0+intlimits_a^t F(s,;x(s)),ds.

Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерры 2-го рода. Этим ещё в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:

x''(t)+[lambda^2-nu(t)]x(t)=0qquad (lambda=mathrm{const}),;x(a)=1,;x'(a)=0.

Для уравнения с постоянными коэффициентами с теми же начальными условиями:

x''(t)+lambda^2x(t)=g(t)

решение может быть найдено методом вариации постоянных и представлено в виде:

x(t)=coslambda(t-a)+frac{1}{lambda}intlimits_a^t g(tau)sinlambda(t-tau),dtau.

Тогда для исходного уравнения получается:

x(t)=coslambda(t-a)+frac{1}{lambda}intlimits_a^t nu(tau)sinlambda(t-tau)x(tau),dtau

— интегральное уравнение Вольтерры 2-го рода.

Линейное дифференциальное уравнение n-го порядка

frac{d^nx}{dt^n}+a_1(t)frac{d^{n-1}x}{dt^{n-1}}+ldots+a_n(t)x(t)=F(t),qquad t>a,
x(a)=C_0,;x'(a)=C_1,;ldots,;x^{(n-1)}(a)=C_{n-1}

также может быть сведено к интегральному уравнению Вольтерры 2-го рода.

Задача Абеля[править | править код]

Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:

f(x)=intlimits_0^xfrac{varphi(eta)}{sqrt{x-eta}},deta,

где f(x) — заданная функция, а varphi (x) — искомая. Это уравнение есть частный случай линейного интегрального уравнения Вольтерры 1-го рода. Уравнение Абеля интересно тем, что к нему непосредственно приводит постановка той или иной конкретной задачи механики или физики (минуя дифференциальные уравнения). Например, к уравнению такого вида приводит задача об определении потенциальной энергии по периоду колебаний[2]

У Абеля формулировка задачи выглядела примерно так:

Материальная точка под действием силы тяжести движется в вертикальной плоскости (xi ,;eta ) по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав своё движение без начальной скорости в точке кривой с ординатой x, достигла оси Oxi за время t=f_1(x), где f_1(x) — заданная функция.

Если обозначить угол между касательной к траектории и осью Oxi как beta и применить законы Ньютона, можно прийти к следующему уравнению:

intlimits_0^xfrac{varphi(eta)}{sqrt{x-eta}},deta=-sqrt{2g}f_1(x),qquadvarphi(beta)=frac{1}{sinbeta}.

Примечания[править | править код]

  1. ↑ 1 2 Краснов М. Л., Киселев А. И., Макаренко Г. И. Интегральные уравнения. — М.: Наука, 1976. — С. 214.
  2. ↑ Ландау Л. Д., Лившиц Е. М. Теоретическая физика: учеб. пособ.: Для вузов. В 10 т. Т. I. Механика.. — 5-е изд. стереот.. — М.: ФИЗМАТЛИТ, 2004. — С. 42-43. — 224 с. — ISBN 5-9221-0055-6.

Литература[править | править код]

  • Краснов М. Л. Интегральные уравнения: введение в теорию. — М.: Наука, 1975.
  • Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
  • Петровский И. Г. Лекции об уравнениях с частными производными, 3-е изд. — 1961.
  • Васильева А. Б., Тихонов Н. А. Интегральные уравнения. — 2-е изд., стереотип. — М.: ФИЗМАТЛИТ, 2002. — 160 с. — ISBN 5-9221-0275-3.
  • Забрейко П. П., Кошелев А. И., Красносельский М. А. Интегральные уравнения. — М.: Наука, 1968.
Источник

ГЛАВА I. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

1. Примеры составления интегральных уравнений.

Интегральным уравнением называется всякое уравнение, содержащее искомую функцию под знаком интеграла. Пусть ищется решение дифференциального уравнения удовлетворяющее начальному условию Мы видели раньше [II; 51], что эта задача сводится к решению интегрального уравнения:

Совершенно так же задача интегрирования дифференциального уравнения порядка с начальными данными приводится к интегральному уравнению

Преобразуя двукратный интеграл в простой [II; 17], можем переписать это уравнение в следующем виде:

Общее решение уравнения получится из интегрального уравнения

где — произвольные постоянные, а нижний предел интегрирования мы положили равным нулю. Рассмотрим теперь для нашего уравнения второго порядка предельную задачу, а именно, будем искать решение уравнения, удовлетворяющее предельным условиям Полагая в уравнении (1) сначала

а потом получим два уравнения для определения произвольных постоянных, которые дадут нам

Подставляя найденные значения в формулу (1), приведем нашу предельную задачу к интегральному уравнению:

где

Мы можем переписать уравнение (2) в следующем виде:

Введем функцию двух переменных:

Уравнение (3) может быть переписано при помощи этой функции следующим образом:

Применим полученные результаты к линейному уравнению

Мы можем утверждать, что задача нахождения решения этого уравнения при предельных условиях

равносильна нахождению функции из линейного интегрального уравнения.

где

есть известная функция независимой переменной

Отметим, что в уравнении (1) верхний предел интегрирования переменный, тогда как в уравнении (8) оба предела интегрирования постоянны. Отметим еще, что как в уравнении (1), так и в уравнении (8) искомая функция входит не только под знак интеграла, но и вне знака интеграла. Это обстоятельство, как мы видели выше [II; 50], является существенным при применении к решению уравнения метода последовательных приближений.

Умножим коэффициент в уравнении (6) на некоторый параметр Я и рассмотрим однородное уравнение

при однородных предельных условиях:

Эта однородная предельная задача приведет нас к однородному интегральному уравнению, содержащему параметр X:

Одним из основных вопросов в дальнейшем будет вопрос о том, при каких значениях параметра X поставленная задача имеет решения, не равные тождественно нулю. Мы уже встречались с этой задачей раньше при применении метода Фурье к предельным задачам математической физики. Отметим еще некоторые характерные свойства функции , которая называется ядром нашего интегрального уравнения. Это ядро — непрерывная функция и квадрате определяемом неравенствами . На диагонали этого квадрата, т. е. при первая производная от ядра терпит разрыв:

Далее, упомянутое ядро, как функция от вне диагонали есть решение однородного уравнения , удовлетворяющее однородным предельным условиям (10). Отметим, наконец, свойство симметрии ядра, выражаемое равенством

Все эти свойства ядра непосредственно вытекают из формулы (4).

Ядро имеет простой физический смысл. Напомним, что при действии сосредоточенной силы в точке на струну,

закрепленную на концах, мы должны иметь в точке приложения силы условие [II; 176]:

где Р — величина действующей силы. Нетрудно проверить, что функция

дает форму статического прогиба струны под влиянием упомянутой выше сосредоточенной силы. Отметим при этом, что уравнение колебаний струны в статическом случае сводится просто к уравнению . Все эти идеи приведения предельной задачи к интегральному уравнению, изложенные нами здесь для простейшего случая, будут подробно развиты во 2-й части тома.

Укажем еще на один характерный метод приведения предельных задач математической физики к интегральному уравнению. Мы определили раньше потенциал сферического слоя следующей формулой:

где — заданная на поверхности сферы S функция, – элемент площади поверхности сферы и d — расстояние от переменной точки пространства М до переменной точки поверхности сферы. Пусть — направление нормали в некоторой точке сферы.

Обозначим через и предельные значения, которые имеет производная при приближении переменной точки М пространства к точке изнутри или извне сферы. Мы вывели раньше следующие формулы:

где d — расстояние от точки до переменной точки М сферы и — угол, образованный радиусом-вектором с направлением .

В следующей главе мы увидим, что эти формулы справедливы не только для сферы. Поставим теперь внутреннюю задачу Неймана для сферы, т. е. положим, что ищется функция, гармоническая

внутри сферы, нормальная производная которой имеет заданные предельные значения на поверхности сферы:

Будем искать функцию и в виде потенциала сферического слоя. Этот потенциал является гармонической функцией внутри сферы, и нам надо только подобрать плотность этого потенциала так, чтобы удовлетворялось и предельное условие (14). Принимая во внимание первую из формул (13) и предельное условие (14), мы получаем для определения искомой плотности следующее интегральное уравнение:

Заметим, что в данном случае функции должны быть определены на поверхности сферы, и интегрирование производится не по интервалу оси ОХ, как это было выше, а по поверхности сферы.

Источник

ФЕДЕРАЛЬНОЕ
АГЕНСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ

ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ВОДНЫХ
КОММУНИКАЦИЙ»

Васин
А.В.

Интегральные
уравнения.

Рекомендовано
редакционно-издательским советом
Санкт-Петербургского Государственного
университета водных коммуникаций

Санкт-Петербург

2011 г.

УДК
517.7

ББК

Рецензенты

Кандидат
физико-математических нау доцент Гулевич
Н.М.

доктор
технических наук, профессор Нырков
А.П.

Васин
А.В.

Интегральные
уравнения: конпект лекций
–СПб:СПБГУВК, 2011.-23
стр.

Учебно-методическое
пособие содержит основной теоритический
материал и конкретные примеры по
дисциплине «Интегральные уравнения»,
и соответствует рабочим программам
дисциплины, стандартам, указанной
специальности, и может быть использовано
при подготовке к экзамену студентами
и преподавателями.

Предназначен
для студентов четвертого курса (8-ой
семестр) специальности 010501.65 «Прикладная
математика и информатика».

УДК 517.7

ББК

Васин А.В, 2011

СПБГУВК, 2011

  1. Интегральные уравнения Вольтерра

  1. Основные
    понятия

Уравнение

где


–
известные функции,

– искомая функция,

– числовой параметр, называется линейным
интегральным уравнением Вольтерра 2-го
рода.
Функция


называется ядром
уравнения
Вольтерра. Если
,
то уравнение (1) принимает вид

и
называется однородным
уравнением Вольтерра 2-го рода.

Уравнение

где


– искомая функция, называют интегральным
уравнением Вольтерра 1-го рода.
Не нарушая общности, можем считать
нижний предел

равным нулю, что мы и будем предполагать
в дальнейшем.

Решением
интегрального уравнения (1), (2) или (3)
называют функцию
,
которая, будучи подставлена в это
уравнение, обращает его в тождество (по

).

  1. Связь
    между линейными дифференциальными
    уравнениями и интегральными уравнениями
    Вольтерра

Решение
линейного дифференциального уравнения

с
непрерывными коэффициентами

(

при начальных условиях

может
быть сведено к решению интегрального
уравнения Вольтерра 2-го рода.

Покажем
это на примере дифференциального
уравнения 2-го порядка

Полагаем

Отсюда,
принимая во внимание начальные условия
(2’), последовательно находим

При
этом мы использовали формулу

Учитывая
(3) и (4), дифференциальное уравнение (1’)
запишем так:

или

Полагая

приведем
(5) к виду

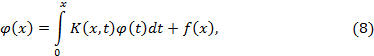
т.е.
придем к интегральному уравнению
Вольтерра 2-го рода.

Существование
единственного решения уравнения (8)
следует из существования и единственности
решения задачи Коши (1’) – (2’) для линейного
дифференциального уравнения с непрерывными
коэффициентами в окрестности точки

И
наоборот, решая интегральное уравнение
(8) с

и
,
определенными по формулам (6) и (7), и
подставляя выражение, полученное для

,
в последнее из уравнений (4), мы получим
единственное решение уравнения (1’),
удовлетворяющее начальным условиям
(2’).

Задача
1.
Составить интегральное уравнение,
соответствующее дифференциальному
уравнению

и
начальным условиям

Решение.
Полагаем

Тогда

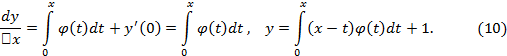
Подставляя
(9) и (10) в данное дифференциальное
уравнение, найдем

или

  1. Резольвента интегрального уравнения Вольтерра

  1. Определение
    резольвенты

Пусть
имеем интегральное уравнение Вольтерра
2-го рода

где


есть непрерывная функция при

а

непрерывна при
.

Будем
искать решение интегрального уравнения
(1) в виде бесконечного степенного ряда
по степеням
:

Подставляя
формально этот ряд в (1), получим

Сравнивая
коэффициенты при одинаковых степенях

,
найдем

Соотношения
(3) дают способ последовательного
определения функций
.
Можно показать, что при сделанных
предположениях относительно

и

полученный таким образом ряд (2) сходится
равномерно по

и

при любом

и

и его сумма есть единственное решение
уравнения (1).

Далее,
из (3) следует:

где

Аналогично
устанавливается, что вообще

Функции


называются повторными
или итерированными
ядрами.
Они, как нетрудно показать, определяются
при помощи рекуррентных формул

Используя
(4) и (5), равенство (2) можно записать так:

Функция

,
определяемая при помощи ряда

называется
резольвентой
(или разрешающим ядром) интегрального
уравнения (1). Ряд (6) в случае непрерывного
ядра

сходится абсолютно равномерно.

Повторные
ядра, а также резольвента не зависят от
нижнего предела в интегральном уравнении.

Резольвента


удовлетворяет следующему функциональному
уравнению:

С
помощью резольвенты решение интегрального
уравнения (1) запишется в виде

  1. Нахождение
    резольвенты

Задача
2.
Найти резольвенту интегрального
уравнения Вольтерра с ядром
.

Решение.
Имеем

Далее, согласно формулам (5)

Таким
образом, согласно определению

Соотношения
(3) дают способ последовательного
определения функций

Можно показать, что при сделанных
предположениях относительно

полученный таким образом ряд (2) сходится
равномерно по

при любом

и его сумма есть единственное решение
уравнения (1).

Далее,
из (3) следует:

где

Аналогично
устанавливается, что вообще

Функции


называются повторными
или итерированными
ядрами.
Они, как нетрудно показать, определяются
при помощи рекуррентных формул

Используя
(4) и (5), равенство (2) можно записать так:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Mojo Risin’🌳🌲🌳

Search IconIcon to open search

Light ModeDark Mode

Last updated Unknown

# Интегральное уравнение

  • #π/определение:
    • Интегральное уравнение — уравнение, содержащее неизвестную функцию под знаком интеграла.
  • #π/формула интегрального уравнения и его составные части:
    • $displaystyle y(x)=lambda int_{a}^b K(x,t)y(t) , dt + f(x), , (aleq x leq b)$, где:
      • $K(x,t)$ — ядро интегрального уравнения;
      • $f(x)$ — некая заданная функция;
      • $y(x)$ — искомое решение.
      • $lambda$ — некий параметр;
  • Смежные понятия:
    • Резольвента интегрального уравнения

# Классификация интегральных уравнений

  • Линейное интегральное уравнение
    • 1-го рода:
      • неоднородное;
    • 2-го рода:
      • однородное;
      • неоднородное.
  • Нелинейное интегральное уравнение

# Задачи на интегральные уравнения

  • Метод последовательных приближений
  • Метод определителей Фредгольма
  • Метод решения уравнений Фредгольма с вырожденными ядрами
  • Нахождение характеристических чисел и собственных функций
  • Задачи на проверку решения

# Пример 1

  • Решить уравнение разными способами:
    • $displaystyle varphi(x)=1+lambda int_{-1}^{1} (xt+x^{2}t^{2})varphi(t) , dt.$

# Метод последовательных приближений

  • Решение:
    • Перепишем уравнение:
      • $displaystyle varphi(x)-lambda int_{-1}^{1} (xt+x^{2}t^{2})varphi(t) , dt = 1;$
    • Проверим условие:
      • $displaystyle |lambda| < dfrac{1}{B_{k}} = left(iint_{-1}^{1} |K(x,t)^{2}| , dx, dtright)^{-dfrac{1}{2}}=dfrac{4}{9};$
    • $y_{0}(x)=1;$
    • $displaystyle y_{1}(x)=1-lambda int_{-1}^{1} (xt+x^{2}t^{2}) , dt =1 – dfrac{2lambda x^{2}}{3};$
    • $displaystyle y_{2}(x)=1-lambda int_{-1}^{1} (xt+x^{2}t^{2})cdotleft(1 – dfrac{2lambda x^{2}}{3} right) , dt=1 + dfrac{2lambda x^{2}(2lambda x^{2}-3)}{9};$
    • $displaystyle y_{3}(x)=1-lambda int_{-1}^{1} (xt+x^{2}t^{2})cdotleft(1 + dfrac{2lambda x^{2}(2lambda x^{2}-3)}{9} right) , dt=1 – dfrac{2lambda x^{2}(2lambda x^{2}(2lambda x^{2}-3)+9)}{27};$
    • ???

# Метод определителей Фредгольма

  • Решение:
    • $B_{0}=xt+x^{2}t^{2};$
    • $displaystyle C_{1}=int_{-1}^{1} zz+z^{2}z^{2} , dz= int_{-1}^{1} z^{6} , dz=dfrac{2}{7};$
    • $displaystyle B_{1}=int_{-1}^{1} begin{vmatrix}(xt+x^{2}t^{2}) & (xt_{1}+x^{2}t_{1}^{2}) (t_{1}t+t_{1}^{2}t^{2}) & t_{1}^{6} end{vmatrix} , dt_{1}=int_{-1}^{1} t_{1}^{6}(xt+x^{2}t^{2})-(xt_{1}+x^{2}t_{1}^{2})(t_{1}t+t_{1}^{2}t^{2}) , dt_{1}=-dfrac{4tx(3tx+10)}{105}.$
    • $displaystyle C_{2}=int_{-1}^{1} -left( dfrac{4z^{2}(3z^{2}+10)}{105} right) , dz=-dfrac{472}{1575}.$
    • $displaystyle B_{2}=-dfrac{472}{1575}(xt+x^{2}t^{2}) -2int_{-1}^{1} (xz+x^{2}z^{2})left( -dfrac{4zt(3zt+10)}{105} right) , dz= dfrac{16tx(9tx+50)}{1575}-dfrac{472}{1575}(xt+x^{2}t^{2})=dfrac{144t^{2}x^{2}+80tx-472xt+472x^{2}t^{2}}{1575}=-dfrac{+328x^{2}t^{2}+392xt}{1575}.$
    • $displaystyle C_{3}=int_{-1}^{1} -dfrac{328z^{4}+392z^{2}}{1575} , dz=-dfrac{5888}{23625}.$
    • $B_{3}=-dfrac{5888}{23625}(xt+x^{2}t^{2})-3int_{-1}^{1} (xz+x^{2}z^{2})left( -dfrac{328z^{2}t^{2}+392zt}{1575} right) , dz$
    • …
Источник

Добавить комментарий