Когда мы чертим график функции, важно определить интервалы выпуклости и точки перегиба. Они, наряду с промежутками убывания и возрастания, нужны нам для четкого представления функции в графическом виде.
Понимание этой темы требует знания того, что такое производная функции и как ее вычислить до некоторого порядка, а также умения решать разные виды неравенств.
В начале статьи определяются основные понятия. Потом мы покажем, какая связь существует между направлением выпуклости и значением второй производной на определенном интервале. Далее мы укажем условия, в которых можно определить точки перегиба графика. Все рассуждения будут проиллюстрированы примерами решений задач.
Что такое выпуклость/вогнутость функции и точки перегиба графика функции
Дифференцируемая функция является выпуклой по направлению вниз на некотором интервале в том случае, когда ее график располагается не ниже касательной к нему в любой точке этого интервала.
Дифференцируемая функция является выпуклой по направлению вверх на некотором интервале в том случае, если график данной функции располагается не выше касательной к нему в любой точке этого интервала.
Выпуклую вниз функцию можно иначе назвать вогнутой. Оба определения наглядно показаны на графике ниже:
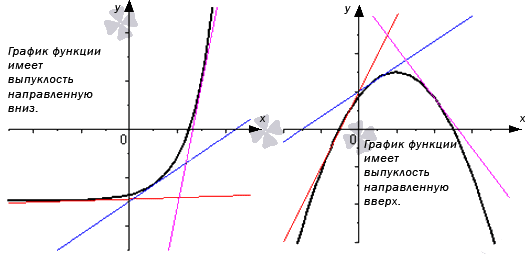
Точка перегиба функции – это точка M(x0; f(x0)), в которой существует касательная к графику функции, при условии существования производной в окрестности точки x0 , где с левой и правой стороны график функции принимает разные направления выпуклости.
Проще говоря, точка перегиба – это место на графике, в котором есть касательная, и направление выпуклости графика при прохождении через это место будет менять направление выпуклости. Если вы не помните, при каких условиях возможно существование вертикальной и невертикальной касательной, советуем повторить раздел о касательной графика функции в точке.
Ниже указан график функции, имеющей несколько точек перегиба, которые выделены красным. Уточним, что наличие точек перегиба не является обязательным. На графике одной функции их может быть одна, две, несколько, бесконечно много или ни одной.
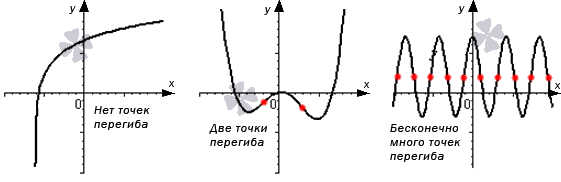
Как найти интервалы выпуклости функции
В этом пункте мы расскажем о теореме, с помощью которой можно определить промежутки выпуклости на графике конкретной функции.
График функции будет иметь выпуклость по направлению вниз или вверх в том случае, если у соответствующей ему функции y=f(x) будет вторая конечная производная на указанном интервале x при условии, что неравенство f”(x)≥0 ∀x∈X (f”(x)≤0 ∀x∈X) будет верным.
Используя данную теорему, можно найти промежутки вогнутости и выпуклости на любом графике функции. Для этого нужно просто решить неравенства f”(x)≥0 и f”(x)≤0 на области определения соответствующей функции.
Уточним, что те точки, в которых вторая производная не существует, но функция y=f(x) определена, будут включаться в интервалы выпуклости и вогнутости.
Посмотрим на примере конкретной задачи, как правильно применять эту теорему.
Условие: дана функция y=x36-x2+3x-1. Определите, на каких промежутках ее график будет иметь выпуклости и вогнутости.
Решение
Областью определения данной функции является все множество действительных чисел. Начнем с вычисления второй производной.
y’=x36-x2+3x-1’=x22-2x+3⇒y”=x22-2x+3=x-2
Мы видим, что область определения второй производной совпала с областью самой функции Значит, для выявления интервалов выпуклостей нам надо решить неравенства f”(x)≥0 и f”(x)≤0 .
y”≥0⇔x-2≥0⇔x≥2y”≤0⇔x-2≤0⇔x≤2
Мы получили, что график заданной функции будет иметь вогнутость на отрезке [2; +∞) и выпуклость на отрезке (-∞; 2].
Для наглядности изобразим график функции и отметим на нем выпуклую часть синим, а вогнутую – красным цветом.
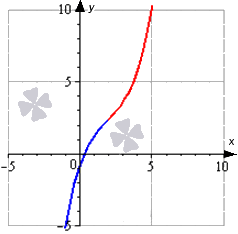
Ответ: график заданной функции будет иметь вогнутость на отрезке [2; +∞) и выпуклость на отрезке (-∞; 2].
А что же делать в случае, если область определения второй производной не совпадает с областью определения функции? Здесь нам пригодится замечание, сделанное выше: те точки, где конечная вторая производная не существует, мы тоже будем включать в отрезки вогнутости и выпуклости.
Условие: дана функция y=8xx-1 . Определите, в каких промежутках ее график будет иметь вогнутость, а в каких – выпуклость.
Решение
Для начала выясним область определения функции.
x≥0x-1≠0⇔x≥0x≠1⇔x∈[0; 1)∪(1;+∞)
Теперь вычисляем вторую производную:
y’=8xx-1’=8·12x·(x-1)-x·1(x-1)2=-4·x+1x·(x-1)2y”=-4·x+1x·(x-1)2’=-4·1·x·x-12-(x+1)·x·x-12’x·(x-1)4==-4·1·x·x-12-x+1·12x·(x-1)2+x·2(x-1)x·x-14==2·3×2+6x-1×32·(x-1)3
Область определения второй производной – это множество x∈(0; 1)∪(1; +∞). Мы видим, что x, равный нулю, будет принадлежать области определения исходной функции, но не области определения второй производной. Эту точку нужно обязательно включить в отрезок вогнутости или выпуклости.
После этого нам надо решить неравенства f”(x)≥0 и f”(x)≤0 на области определения заданной функции. Используем для этого метод интервалов: при x=-1-233≈-2,1547 или x=-1+233≈0,1547 числитель 2·(3×2+6x-1)x23·x-13 обращается в 0, а знаменатель равен 0 при x, равном нулю или единице.
Нанесем получившиеся точки на график и определим знак выражения на всех интервалах, которые войдут в область определения исходной функции. На графике эта область обозначена штриховкой. Если значение положительно, отмечаем интервал плюсом, если отрицательно, то минусом.

Следовательно,
f”(x)≥0x∈[0; 1)∪(1; +∞)⇔x∈0; -1+233∪(1; +∞), а f”(x)≤0x∈[0; 1)∪(1; +∞)⇔x∈[-1+233; 1)
Включаем ранее отмеченную точку x=0 и получаем нужный ответ. График исходной функции будет иметь выпуклость по направлению вниз при 0; -1+233∪(1; +∞) , и вверх – при x∈[-1+233; 1) .
Изобразим график, отметив на нем выпуклую часть синим, а вогнутую красным цветом. Вертикальная асимптота отмечена черным пунктиром.
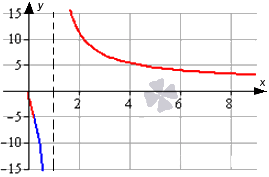
Ответ: График исходной функции будет иметь выпуклость по направлению вниз при 0; -1+233∪(1; +∞) , и вверх – при x∈[-1+233; 1) .
Условия перегиба графика функции
Начнем с формулировки необходимого условия перегиба графика некоторой функции.
Допустим, что у нас есть функция y=f(x), график которой имеет точку перегиба. При x=x0 у него есть непрерывная вторая производная, следовательно, будет выполняться равенство f”(x0)=0.
Учитывая данное условие, нам следует поискать точки перегиба среди тех, в которых вторая производная будет обращаться в 0. Это условие не будет достаточным: не все такие точки нам подойдут.
Также обратите внимание, что, согласно общему определению, нам нужна будет касательная прямая, вертикальная или невертикальная. На практике это означает, что для нахождения точек перегиба следует взять те, в которых вторая производная данной функции обращается в 0. Следовательно, чтобы найти абсциссы точек перегиба, нам нужно взять все x0 из области определения функции, где limx→x0-0f'(x)=∞ и limx→x0+0f'(x)=∞. Чаще всего это такие точки, в которых знаменатель первой производной обращается в 0.
Первое достаточное условие существования точки перегиба графика функции
Мы нашли все значения x0, которые можно взять в качестве абсцисс точек перегиба. После этого нам нужно применить первое достаточное условие перегиба.
Допустим, что у нас есть функция y=f(x), которая является непрерывной в точке M(x0; f(x0)). При этом она имеет на этой точке касательную, а сама функция имеет вторую производную в окрестности этой точки x0. В таком случае если с левой и правой стороны вторая производная приобретает противоположные знаки, то данную точку можно считать точкой перегиба.
Мы видим, что данное условие не требует, что в этой точке непременно существовала вторая производная, достаточно ее наличия в окрестности точки x0.
Все сказанное выше удобно представить в виде последовательности действий.
Как найти точки перегиба графика функции
- Для начала нужно найти все абсциссы x0 возможных точек перегиба, где f”(x0)=0, limx→x0-0f'(x)=∞, limx→x0+0f'(x)=∞.
- Выясним, в каких точках производная будет менять знак. Эти значения и есть абсциссы точек перегиба, а точки M(x0; f(x0)) , соответствующие им, – это сами точки перегиба.
Для наглядности разберем две задачи.
Условие: дана функция y=110·x412-x36-3×2+2x . Определите, где график данной функции будет иметь точки перегиба и выпуклости.
Решение
Указанная функция определена на всем множестве действительных чисел. Считаем первую производную:
y’=110·x412-x36-3×2+2x’=110·4×312-3×26-6x+2==110·x33-x22-6x+2
Теперь найдем область определения первой производной. Это также множество всех действительных чисел. Значит, равенства limx→x0-0f'(x)=∞ и limx→x0+0f'(x)=∞ не могут быть выполнены ни при каких значениях x0.
Вычисляем вторую производную:
y”==110·x33-x22-6x+2’=110·3×23-2×2-6=110·x2-x-6
Далее определяем, когда она будет обращаться в 0:
y”=0⇔110·(x2-x-6)=0⇔x2-x-6=0D=(-1)2-4·1·(-6)=25×1=1-252=-2, x2=1+252=3
Мы нашли абсциссы двух вероятных точек перегиба –2 и 3. Все, что нам осталось сделать – это проверить, в какой точке производная изменит свой знак. Изобразим числовую ось и нанесем на нее данные точки, после чего расставим знаки второй производной на получившихся промежутках.
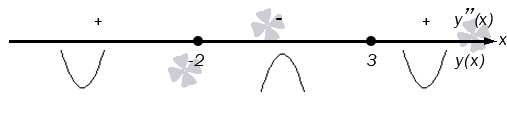
Дуги показывают направление выпуклости графика в каждом интервале.
Вторая производная меняет знак на противоположный (с плюса на минус) в точке с абсциссой 3, проходя через нее слева направо, и также делает это (с минуса на плюс) в точке с абсциссой 3. Значит, мы можем сделать вывод, что x=-2 и x=3– это абсциссы точек перегиба графика функции. Им будут соответствовать точки графика -2; -43 и 3; -158.
Взглянем вновь на изображение числовой оси и получившиеся знаки на интервалах, чтобы сделать выводы о местах вогнутости и выпуклости. Получается, что выпуклость будет расположена на отрезке -2; 3 , а вогнутость на отрезках (-∞; -2] и [3; +∞).
Решение задачи наглядно изображено на графике: синий цвет – выпуклости, красный – вогнутость, черный цвет означает точки перегиба.
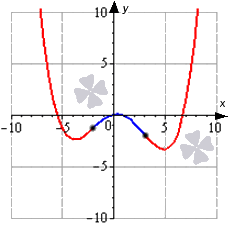
Ответ: выпуклость будет расположена на отрезке -2; 3 , а вогнутость на отрезках (-∞; -2] и [3; +∞).
Условие: вычислите абсциссы всех точек перегиба графика функции y=18·x2+3x+2·x-335.
Решение
Область определения заданной функции – множество всех действительных чисел. Вычисляем производную:
y’=18·(x2+3x+2)·x-335’==18·x2+3x+2’·(x-3)35+(x2+3x+2)·x-335’==18·2x+3·(x-3)35+(x2+3x+2)·35·x-3-25=13×2-6x-3940·(x-3)25
В отличие от функции, ее первая производная не будет определена при значении x, равном 3, но:
limx→3-0y'(x)=13·(3-0)2-6·(3-0)-3940·3-0-325=+∞limx→3+0y'(x)=13·(3+0)2-6·(3+0)-3940·3+0-325=+∞
Это значит, что через данную точку будет проходить вертикальная касательная к графику. Следовательно, 3 может быть абсциссой точки перегиба.
Вычисляем вторую производную. Также находим область ее определения и точки, в которых она обращается в 0:
y”=13×2-6x-3940·x-325’==140·13×2-6x-39’·(x-3)25-13×2-6x-39·x-325′(x-3)45==125·13×2-51x+21(x-3)75, x∈(-∞; 3)∪(3; +∞)y”(x)=0⇔13×2-51x+21=0D=(-51)2-4·13·21=1509×1=51+150926≈3,4556, x2=51-150926≈0,4675
У нас получились еще две возможные точки перегиба. Нанесем их все на числовую прямую и разметим получившиеся интервалы знаками:
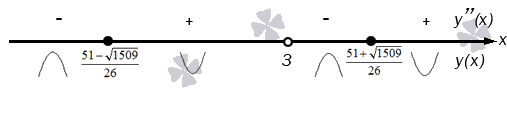
Перемена знака будет происходить при прохождении через каждую указанную точку, значит, они все являются точками перегиба.
Ответ: Изобразим график функции, отметив вогнутости красным, выпуклости синим и точки перегиба – черным:
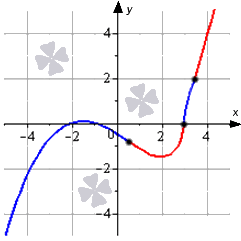
Зная первое достаточное условие перегиба, мы можем определить нужные точки, в которых не обязательно наличие второй производной. Исходя из этого, первое условие можно считать наиболее универсальным и пригодным для решения разных типов задач.
Отметим, что существует еще два условия перегиба, однако их можно применять только тогда, когда в указанной точке есть конечная производная.
Второе достаточное условие перегиба графика функции
Если мы имеем f”(x0)=0 и f”'(x0)≠0, то x0 будет абсциссой точки перегиба графика y=f(x).
Условие: задана функция y=160×3-320×2+710x-25 . Определите, будет ли график функции иметь перегиб в точке 3; 45.
Решение
Первое, что нужно сделать, – это убедиться в том, что данная точка вообще будет принадлежать графику этой функции.
y(3)=160·33-320·32-25=2760-2720+2110-25=9-27+42-820=45
Заданная функция определена для всех аргументов, являющихся действительными числами. Вычислим первую и вторую производные:
y’=160×3-320×2+710x-25’=120×2-310x+710y”=120×2-310x+710’=110x-310=110(x-3)
Мы получили, что вторая производная будет обращаться в 0, если x будет равен 0. Значит, необходимое условие перегиба для этой точки будет выполнено. Теперь используем второе условие: найдем третью производную и выясним, будет ли она обращаться в 0 при 3:
y”’=110(x-3)’=110
Третья производная не будет обращаться в нуль ни при одном значении x. Поэтому можно заключить, что данная точка будет точкой перегиба графика функции.
Ответ: Покажем решение на иллюстрации:
Третье достаточное условие перегиба графика функции
Допустим, что f'(x0)=0, f”(x0)=0, …, f(n)(x0)=0 и f(n+1)(x0)≠0 .В таком случае при четном n мы получим, что x0 – это абсцисса точки перегиба графика y=f(x).
Условие: дана функция y=(x-3)5+1. Вычислите точки перегиба ее графика.
Решение
Данная функция является определенной на всем множестве действительных чисел. Вычисляем производную: y’=((x-3)5+1)’=5·x-34 . Поскольку она тоже будет определена для всех действительных значений аргумента, то в любой точке ее графике будет существовать невертикальная касательная.
Теперь вычислим, при каких значениях вторая производная будет обращаться в 0:
y”=5·(x-3)4’=20·x-33y”=0⇔x-3=0⇔x=3
Мы получили, что при x=3 график функции может иметь точку перегиба. Используем третье условие, чтобы подтвердить это:
y”’=20·(x-3)3’=60·x-32, y”'(3)=60·3-32=0y(4)=60·(x-3)2’=120·(x-3), y(4)(3)=120·(3-3)=0y(5)=120·(x-3)’=120, y(5)(3)=120≠0
Имеем n=4 по третьему достаточному условию. Это четное число, значит, x=3 будет абсциссой точки перегиба и ей соответствует точка графика функции (3;1).
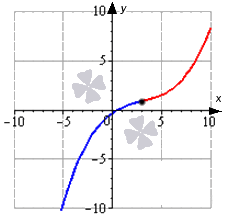
Ответ: Вот график данной функции с отмеченными выпуклостями, вогнутостями и точкой перегиба:
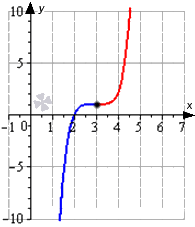
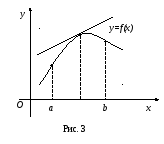
График функции
называется выпуклым в интервале
![]() ,
,
если он расположен ниже касательной,
проведенной в любой точке этого интервала
(рис.3).
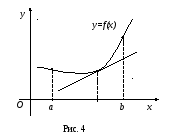
График функции
называется вогнутым в интервале
![]() ,
,
если он расположен выше касательной,
проведенной в любой точке этого интервала
(рис. 4).
Достаточное
условие выпуклости (вогнутости).Пусть
функция![]() имеет вторую производную на интервале
имеет вторую производную на интервале![]() .
.
Тогда, если![]() на этом интервале, то функция выпукла,
на этом интервале, то функция выпукла,
если![]() ,
,
то график функции вогнутый на этом
интервале.
Точка графика
непрерывной функции
![]() ,
,
отделяющая его части выпуклости и
вогнутости, называетсяточкой перегиба(рис. 5).
Необходимое
условие точки перегиба. Если![]() – точка перегиба функции
– точка перегиба функции![]() ,
,
то в этой точке вторая производная
функции либо равна нулю (![]() ),
),
либо не существует.
Точки, в которых
вторая производная функции равна нулю
или не существует, называются критическими
точками 2 –го рода.
Точки перегиба
следует искать среди критических точек
2- го рода.
Первое достаточное
условие точки перегиба. Пусть функция![]() имеет первую производную в точке
имеет первую производную в точке![]() и вторую производную в некоторой
и вторую производную в некоторой
окрестности этой точки (кроме, быть
может самой точки). Тогда если при
переходе через точку![]() вторая производная меняет знак, то
вторая производная меняет знак, то![]() – точка перегиба.
– точка перегиба.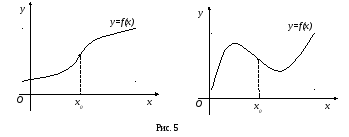
Второе достаточное
условие точки перегиба.Пусть в точке![]() функция
функция![]() имеет производные до третьего порядка
имеет производные до третьего порядка
включительно. Тогда если![]() ,
,
а![]() ,
,
то![]() – точка перегиба этой функции.
– точка перегиба этой функции.
-
Асимптоты.
П
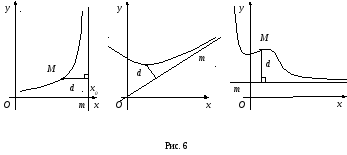 рямая
рямая
линияmназываетсяасимптотойграфика функции![]() ,
,
если расстояниеdот
точкиM, лежащей на
этом графике, до прямойmстремится к нулю при неограниченном
удалении этой точки по графику от начала
координат в бесконечность (Рис. 6 а),
б), в)).
б
в
а
Асимптоты бывают
трех видов: вертикальные (рис.6а), наклонные
(рис.6б) и горизонтальные (рис.6в).
Прямая
![]() называетсявертикальной асимптотойграфика функции
называетсявертикальной асимптотойграфика функции![]() ,
,
если хотя бы один из односторонних
пределов![]() и
и![]() равен бесконечности.
равен бесконечности.
Обычно вертикальными
асимптотами являются прямые в точках
разрыва 2-го рода. Поэтому для отыскания
вертикальных асимптот определяют точки
![]() бесконечного
бесконечного
разрыва
функции. Тогда уравнение вертикальных
асимптот
![]() .
.
Вертикальные асимптоты могут быть и на
границе области определения функции.
Например, как у функции![]() .
.
Прямая
![]() называется
называется
наклонной асимптотойграфика
функции![]()
при![]() (при
(при![]() ),
),
если![]() (соответственно,
(соответственно,![]() ).
).
Уравнение наклонной
асимптоты к графику функции
![]() ищем
ищем
виде![]() ,
,
где
![]() (*)
(*)
и
![]() (**)
(**)
Если хотя бы один
из пределов (*) и (**) не существует или
равен бесконечности, то кривая
![]() наклонной асимптоты не имеет. Асимптоты
наклонной асимптоты не имеет. Асимптоты
графика функции![]() при
при![]() и
и![]() могут быть разными. Поэтому при нахождении
могут быть разными. Поэтому при нахождении
пределов (*) и (**) следует отдельно
рассматривать случай, когда![]() и когда
и когда![]() .
.
Частным случаем
наклонной асимптоты (при
![]() )
)
являетсягоризонтальная асимптота.
Прямая
![]() является горизонтальной асимптотой
является горизонтальной асимптотой
графика функции![]() при
при![]() (при
(при![]() )
)
тогда и только тогда, когда![]() (соответственно,
(соответственно,![]() ).
).
-
Общая
схема исследования функции и построение
графиков функций.
При построении
графика данной функции
![]() целесообразно пользоваться следующей
целесообразно пользоваться следующей
схемой:
-
найти
область определения функции; -
исследовать
функцию на четность, нечетность и
периодичность; -
найти
точки пересечения графика с осями
координат (если это возможно); -
найти
интервалы знакопостоянства функции
(промежутки, на которых
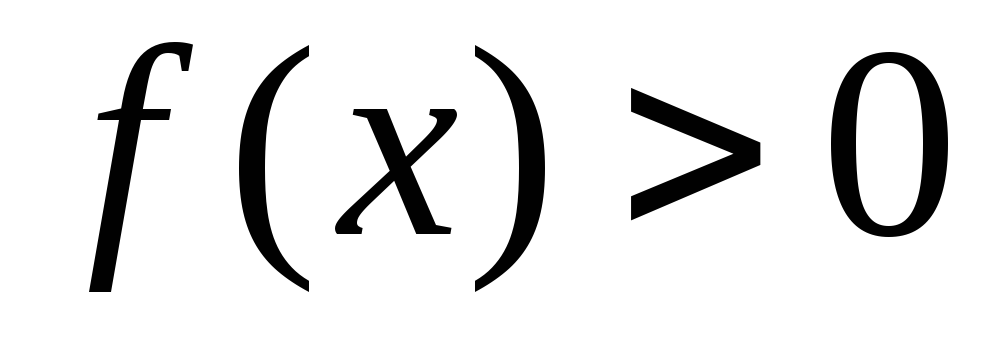 и
и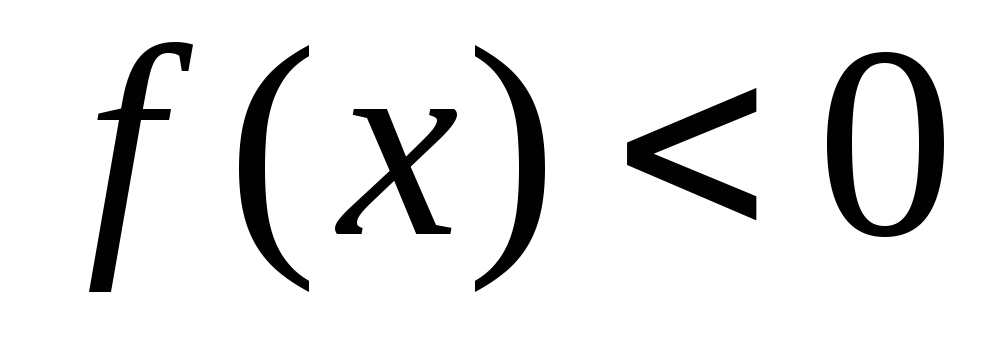 );
); -
найти
асимптоты; -
найти
интервалы возрастания и убывания,
экстремумы функции; -
найти
интервалы выпуклости и вогнутости,
точки перегиба; -
построить
график функции.
Приведенная схема
исследования не является обязательной.
В более простых случаях достаточно
выполнить лишь несколько операций,
например 1, 3, 4, 6. Иногда бывает необходимым
вычислить несколько дополнительных
точек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интервалы выпуклости и вогнутости графика функции
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.
- Решение онлайн
- Видеоинструкция
Направление выпуклости графика функции. Точки перегиба
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.
Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
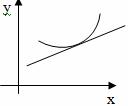
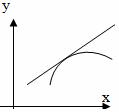
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
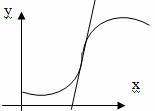
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x).
- Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x2–x3.
Решение: Находим f ‘(x) = 12x – 3x2, f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.

f(2) = 6*22 – 23 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).
Пример 2. Имеет ли точки перегиба функция: f(x)=x3-6x2+2x-1
Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x3-6x2+12x+4
Содержание:
- Теоремы о выпуклости функции и точках перегиба
- Схема исследования функции на выпуклость, вогнутость
График функции $y=f(x)$, дифференцируемой на интервале
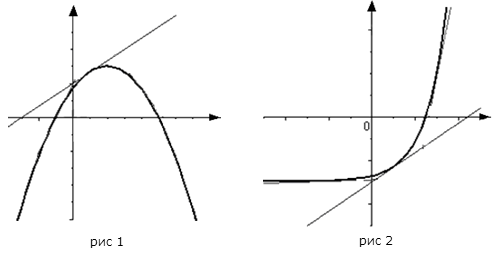
$(a ; b)$, является на этом интервале выпуклым, если график
этой функции в пределах интервала $(a ; b)$ лежит не выше любой
своей касательной (рис. 1).
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале вогнутым, если график
этой функции в пределах интервала $(a ; b)$ лежит не ниже любой
своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция $y=f(x)$ определена на интервале
$(a ; b)$ и имеет непрерывную, не равную нулю в точке
$x_{0} in(a ; b)$ вторую производную. Тогда, если
$f^{prime prime}(x)>0$ всюду на интервале
$(a ; b)$, то функция имеет вогнутость на этом интервале,
если $f^{prime prime}(x) lt 0$, то функция имеет выпуклость.
Определение
Точкой перегиба графика функции $y=f(x)$
называется точка $Mleft(x_{1} ; fleft(x_{1}right)right)$, разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция $y=f(x)$ имеет перегиб в точке
$Mleft(x_{1} ; fleft(x_{1}right)right)$, то
$f^{prime prime}left(x_{1}right)=0$ или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
- первая производная $f^{prime}(x)$
непрерывна в окрестности точки $x_{1}$; - вторая производная $f^{prime prime}(x)=0$ или не существует в точке $x_{1}$;
- $f^{prime prime}(x)$ при переходе через точку $x_{1}$ меняет свой знак,
тогда в точке $Mleft(x_{1} ; fleft(x_{1}right)right)$ функция $y=f(x)$ имеет перегиб.
Схема исследования функции на выпуклость, вогнутость
- Найти вторую производную функции.
- Найти точки, в которых вторая производная равна нулю или не существует.
- Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
Пример
Задание. Найти интервалы выпуклости/вогнутости функции
$y=frac{x^{3}}{6}-x^{2}+3 x+1$
Решение. Найдем вторую производную заданной функции:
$y^{prime prime}=left(frac{x^{3}}{6}-x^{2}+3 x+1right)^{prime prime}=left(frac{x^{2}}{2}-2 x+3right)^{prime}=x-2$
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
$y^{prime prime}(x)=0$:
$y^{prime prime}(x)=x-2=0 Rightarrow x=2$
Исследуем знак второй производной слева и справа от полученной точки:
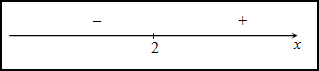
Так как на промежутке $(-infty ; 2)$ вторая производная
$y^{prime prime}(x) lt 0$, то на этом промежутке функция
$y(x)$ выпукла; в силу того, что на промежутке
$(2 ;+infty)$ вторая производная
$y^{prime prime}(x)>0$ – функция вогнута. Так как при переходе через
точку $x=2$ вторая производная сменила знак, то
эта точка является точкой перегиба графика функции.
Ответ. Точка $x=2$ – точка перегиба графика функции.
На промежутке $(-infty ; 2)$ функция выпукла, на промежутке
$(2 ;+infty)$ функция вогнута.
Читать дальше: асимптоты графика функции.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
График функции y=f(x) называется выпуклым на интервале (a;
b), если он расположен ниже любой своей касательной на
этом интервале.
График функции y=f(x) называется вогнутым на интервале (a;
b), если он расположен выше любой своей касательной на
этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).

Примеры.
- Полуокружность
 выпукла на [–1; 1].
выпукла на [–1; 1].
- Парабола y = x2 вогнута на интервале (-∞; +∞).
- График функции в одних интервалах может быть
выпуклым, а в других вогнутым. Так график функции y = sin x на
[0,2; π], выпуклый в интервале (0; π) и вогнутый в (π;
2π).

Рассмотрим достаточный признак, позволяющий установить,
будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a;
b). Если во всех точках интервала (a;
b) вторая производная функции y = f(x) отрицательная, т.е. f ”(x) < 0, то график функции
на этом интервале выпуклый, если же f”(x) > 0 – вогнутый.
Доказательство.
Предположим для определенности, что f”(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение ![]() . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
. Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.

Итак, уравнение кривой имеет вид y
= f(x). Обозначим ![]() ординату касательной,
ординату касательной,
соответствующую абсциссе x. Тогда ![]() . Следовательно, разность ординат кривой и касательной при
. Следовательно, разность ординат кривой и касательной при
одном и том же значении x будет ![]() .
.
Разность f(x)
– f(x0) преобразуем по теореме
Лагранжа ![]() , где c между x и x0.
, где c между x и x0.
Таким образом,
![]() .
.
К выражению, стоящему в квадратных скобках
снова применим теорему Лагранжа: ![]() , где c1 между c0 и x0. По условию теоремы f ”(x) < 0. Определим знак
, где c1 между c0 и x0. По условию теоремы f ”(x) < 0. Определим знак
произведения второго и третьего сомножителей.
- Предположим, что x>x0. Тогда x0<c1<c<x,
следовательно, (x – x0)
(x – x0)
> 0 и (c – x0) > 0. Поэтому .
.
- Пусть x<x0, следовательно, x < c
< c1 < x0 и (x – x0)
< 0, (c – x0) < 0. Поэтому вновь .
.
Таким образом, любая
точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î
(a; b), а это значит, что кривая
выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
- Установить интервалы
выпуклости и вогнутости кривой y = 2 – x2.Найдем y ” и определим, где вторая
производная положительна и где отрицательна. y‘ = –2x, y” = –2 < 0 на (–∞; +∞), следовательно, функция всюду
выпукла. - y = ex. Так как y” = ex
> 0 при любых x, то кривая всюду вогнута.


- y = x3. Так как y” = 6x, то y” < 0 при x
< 0 и y” > 0 при x
> 0. Следовательно, при x < 0 кривая выпукла, а
при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной
стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные
условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется
уравнением y = f(x). Если f ”(x0) = 0 или f ”(x0) не существует и при переходе
через значение x = x0 производная f ”(x) меняет знак, то точка
графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть
f ”(x) < 0 при x
< x0 и f
”(x) > 0 при x
> x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с
абсциссой x0 есть точка перегиба. Аналогично можно
рассматривать второй случай, когда f
”(x) > 0 при x
< x0 и f
”(x) < 0 при x
> x0.

Таким образом, точки перегиба следует искать только
среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы
выпуклости и вогнутости кривых.

Найдем производные
заданной функции до второго порядка. .
. . Вторая производная не существует при x =
. Вторая производная не существует при x =
1. Исследуем эту точку на возможный перегиб.Итак, точка
перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞;
1).

Возможные точки
перегиба найдем, решив уравнение 2x2 – 1 = 0. Отсюда .
.Точки перегиба
 . Функция выпукла на
. Функция выпукла на  и вогнута на
и вогнута на  .
.
- y = ln (1 – x2). Область определения функции D(y) = (-1; 1).
 .
. при всех x из
при всех x из
(–1; 1).Следовательно,
f(x) выпуклая на (–1; 1).
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции
важно установить форму ее графика при неограниченном удалении точки графика от
начала координат.
Особый интерес
представляет случай, когда график функции при удалении его переменной точки в
бесконечность неограниченно приближается к некоторой
прямой.


Прямая называется асимптотой графика функции y = f(x), если расстояние от
переменной точки M графика до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении
в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от
нее или с разных сторон, бесконечное множество раз пересекая асимптоту и
переходя с одной ее стороны на другую.
Если обозначим
через d расстояние от точки M
кривой до асимптоты, то ясно, что d стремится к нулю при
удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной
величине, т.е. ![]() или
или ![]() или
или ![]() . Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное,
. Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное,
если прямая x = x0 является асимптотой, т. о. ![]() .
.

Таким образом, вертикальной
асимптотой графика функции y = f(x)
называется прямая, если f(x) → ∞ хотя бы при одном из условий x→
x0 – 0 или x → x0 + 0, x = x0
Следовательно,
для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный
разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Примеры.
- Найти вертикальные асимптоты графика функции
 .
.
Так как
 , то прямая x =
, то прямая x =
2 является вертикальной асимптотой.  .
.
Прямая x = 0 – вертикальная асимптота.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку
асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту,
то ее уравнение будет y = kx + b. Наша задача найти
коэффициенты k и b.

Теорема. Прямая y = kx + b служит наклонной
асимптотой при x → +∞
для графика функции y
= f(x) тогда и только тогда,
когда ![]() . Аналогичное утверждение верно и при x → –∞.
. Аналогичное утверждение верно и при x → –∞.
Доказательство. Пусть MP –
длина отрезка, равного расстоянию от точки M до асимптоты. По условию ![]() . Обозначим через φ угол наклона асимптоты к
. Обозначим через φ угол наклона асимптоты к
оси Ox. Тогда из ΔMNP
следует, что ![]() . Так как φ постоянный угол (φ ≠ π/2), то
. Так как φ постоянный угол (φ ≠ π/2), то ![]() , но
, но
MN = MK – NK = y – yас = f(x) – (kx+b).
Следовательно, мы можем
записать следующее равенство ![]() .
.
Так как x → +∞, то должно
выполняться равенство ![]() . Но при постоянных k и b
. Но при постоянных k и b ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() , т.е.
, т.е. ![]() .
.
Если число k
уже известно, то ![]() , поэтому
, поэтому ![]() .
.
Для
доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное
утверждение. Предположим, что существуют пределы, определяющие числа k и b.
Тогда несложно заметить, что выполняется равенство ![]() . Действительно
. Действительно

Следовательно,
прямая y = kx + b
есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема
показывает, что для нахождения асимптот достаточно найти два указанных предела.
Причем, если хотя бы один из пределов не существует или обращается в бесконечность,
то кривая асимптот не имеет.
Замечание 2. В случае,
когда k = 0 асимптота y = b
называется горизонтальной асимптотой. Наличие горизонтальной асимптоты
означает, что существуют пределы
![]() .
.
Замечание 3. Пределы для отыскания k и b могут
быть различны при x
→ +∞ и x
→ – ∞ и, следовательно, график функции может иметь две различные
асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
 .
.
- Вертикальные:

x = 0 – вертикальная асимптота.
- Наклонные:
 .
.При x → – ∞ получим те
же значения k и b. Следовательно, прямая
y = x + 2 является наклонной асимптотой.
- Вертикальные:
- y = e–x sin x + x.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
вертикальных асимптот нет. -
а)
 .
.Итак, при x
→ +∞ наклонная асимптота у=
х.б)
 , т. к.
, т. к. , поэтому при x
, поэтому при x
→ – ∞ наклонных асимптот нет.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
- y = x – 2arctg x.
- Вертикальных асимптот нет.
-
а)
 .
. . Наклонная асимптота y = x – π
. Наклонная асимптота y = x – π
при .
.б)
 при
при  .
.
