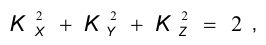0 голосов
3.1k просмотров
Рисунок 63 Сделать фронтальную диметрическую проекцию и изометрическую размеры увеличить в два раза(М 2:1) на карандаш не надо обращать внимание… начертите по клеточкам пж)
- рисунок
- сделать
- проекцию
- размеры
- увеличить
- карандаш
- 5 – 9 классы
- другие предметы
Другие предметы
Cпиcывaльщик_zn
29 Май, 20
|
3.1k просмотров
Дан 1 ответ
0 голосов
Правильный ответ
++++++++++++++++++++++++++++++++++++++
Букса_zn
29 Май, 20
Описание презентации по отдельным слайдам:
-
1 слайд
Построение диметрических
проекций
МНОГОПРОФИЛЬНЫЙ ЛИЦЕЙ
Преподаватель: Рафальский Ю.В. -
2 слайд
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Аксонометрические проекции
Косоугольная фронтальная диметрическая проекция
Прямоугольная изометрическая проекция -
3 слайд
РАСПОЛОЖЕНИЕ ОСЕЙ
Косоугольная фронтальная диметрическая проекция -
4 слайд
ПОСТРОЕНИЕ ОСЕЙ
Косоугольная фронтальная диметрическая проекция -
5 слайд
Вдоль оси z и параллельно ей откладывают высоты, а вдоль оси y – сокращенный в два раза размер ширины, натуральный размер длины предмета вдоль x – натуральный размер.
-
6 слайд
Построение осей диметрических плоскостей.
– Построение нижнего основания прямоугольного параллелепипеда.
Шаг 1. -
7 слайд
Построение вертикальных ребер
Шаг 2. -
8 слайд
Построение боковых граней и верхнего основания
Шаг 3. -
9 слайд
Шаг 4. Определение видимости граней.
Шаг 5. Обводка. -
10 слайд
Шаг 6. Размеры на изображении детали наносят так, чтобы цифровые значения «лежали» в плоскостях V, H и W.
-
11 слайд
Запомните!!!
В аксонометрических проекциях из каждой вершины предмета всегда выходят три ребра (видимых или невидимых).
-
12 слайд
Графическая работа
Задания:
1. Оформить формат А4. Выполнить упражнения 1 и 2.
2. Оформить формат А4. Выполнить упражнение 3, по наглядному изображению детали построить фронтальную диметрическую проекцию. -
13 слайд
Упражнение 1. Построение диметрических проекций прямоугольной призмы
-
14 слайд
Упражнение 2. Построение фронтальной диметрической проекции детали
-
15 слайд
Образец
выполнения
задания -
16 слайд
Упражнение 3. По наглядному изображению детали построить фронтальную диметрическую проекцию. Масштаб 2:1.
-
17 слайд
Образец
выполнения
задания
cerdoungenke968
Вопрос:
Постройте фронтальную диметрическую и изометрическую проекции детали, приведенной на рисунке. Величину увеличьте в 2 раза.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
dirdoalounsi
Размеры даны с учетом масштаба 2:1

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Другие предметы.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
В данном разделе публикуются вопросы и ответы на них к непопулярным предметам.
Аксонометрическое черчение — способ изображения на чертеже геометрических предметов при помощи параллельных проекций. Аксонометрические проекции выполняют в соответствии с ГОСТ 2.317-69.
При построении аксонометрических проекций объект относят к прямоугольной декартовой системе координат и проецируют его вместе с осями координат пучком параллельных лучей на некоторую плоскость проекций, называемую аксонометрической. Полученное изображение, нанесенное на некоторую плоскость проекций, называют аксонометрическим (или просто аксонометрией), а проекции координатных осей – аксонометрическими осями координат.
При выполнении технических чертежей, иногда помимо изображения объектов в прямоугольных проекциях, необходимо иметь и визуальные изображения. Это необходимо для того, чтобы более полно раскрыть конструктивные решения, присущие изображаемому объекту, правильно отобразить его положение в пространстве, а также оценить пропорции его частей и их размеры,
Построение аксонометрических проекций заключается в том, что геометрическую фигуру вместе с осями прямоугольных координат, к которым эта фигура отнесена в пространстве, параллельным, прямоугольным или косоугольным способом проецируют на выбранную плоскость проекций.
Содержание:
Основные правила оформления чертежей
Вес чертежи должны соответствовать государственным стандартам (ГОСТ) ЕСКД и отличаться четким и аккуратным выполнением. Чертежи выполняют на листах чертежной бумаги. Для этого необходимо иметь следующие инструменты и принадлежности: чертежную доску, рейсшину, готовальню, два угольника (один – с углами 45°, 45° и 90°, другой – 30°, 60°, 90° и длиной катетов 130—200 мм), линейку длиной 250—300 мм, набор лекал разных типов, транспортир, чертежные карандаши (для построения чертежа рекомендуются карандаши марки Т или 2Т, для обводки чертежа – марки ТМ или М), мягкую резинку для удаления карандашных линий.
При выполнении чертежей источник света должен находиться слева и сверху от чертежной доски, так как в этом случае тень от правой руки и кромки угольника не будет мешать проводить линию.
Единая система конструкторской документации
Единая система стандартов обеспечивает единство оформления и обозначения чертежей, правила учета и хранения чертежей, а также внесения в них изменений с обязательным распространением этих правил на все виды изделий и все отрасли промышленности.
Характерным для этой системы является то, что она охватывает не только графическую часть, но включает и все элементы, связанные с использованием иной технической документации.
Единая система конструкторской документации (ЕСКД) регламентирует положения относящиеся к конструкторской документации. Она включает в себя десять классификационных групп – от 0 до 9 (первая цифра после точки в обозначении стандарта, например ГОСТ 2.104-2006):
- 0 группа – общие положения;
- 1 группа – основные положения;
- 2 группа – обозначение изделий и конструкторской документации;
- 3 группа – общие правила выполнения чертежей;
- 4 группа – правила выполнения чертежей изделий;
- 5 группа – учет и обращение конструкторской документации;
- 6 группа – эксплуатационная и ремонтная документация;
- 7 группа – правила выполнения схем;
- 8 группа – правила выполнения документов строительных и судостроительных;
- 9 группа – прочие стандарты.
В курсе «Инженерная графика» изучают стандарты преимущественно третьей группы (например, ГОСТ 2.301-68 «Форматы», ГОСТ 2.304-81 «Шрифты чертежные», ГОСТ 2.303-2011 «Нанесение размеров и предельных отклонений», ГОСТ 2.317-2011 «Аксонометрические проекции»), выборочно – первой (например, ГОСТ 2.104-2006 «Основные надписи», ГОСТ 2.105-95 «Общие требования к текстовым документам»), четвертой (например, 2.412-81 «Правила выполнения чертежей и схем оптических изделий») и седьмой (например, ГОСТ 2.755-87 «Обозначения условные графические в электрических схемах. Устройства коммутационные и контактные соединения»).
Форматы
Чертежи и другие конструкторские документы всех отраслей промышленности и строительства должны выполняться на листах определенных стандартных размеров форматов.
Форматы листов чертежей определяются размерами внешней рамки, ограниченной тонкой линией. Каждый чертеж оформляется рамкой поля чертежа, проведенной с трех сторон на расстоянии 5 мм от границы формата, а с четвертой (левой) стороны – на расстоянии 20 мм для брошюровки в альбом (рис. 1.1). В правом нижнем углу каждого листа вплотную к рамке выполняется основная надпись, форма, размеры и содержание которой приведены на рис. 1.3. В верхнем углу формата располагается дополнительная графа, содержащая обозначение чертежа, повернутое на 180° к длинной стороне рамки (рис. 1.6 и 1.7).
ГОСТ 2.301-68 устанавливает форматы листов чертежей и других документов, предусмотренных стандартами на конструкторскую документацию всех отраслей промышленности и строительства. Площадь формата АО равна 1 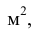
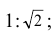
- при помощи циркуля и линейки просто построить прямоугольник с соотношением сторон
- легко получить любой другой формат, опять же при помощи линейки и циркуля. Каждый меньший последующий формат получается делением пополам предыдущего формата параллельно его меньшей стороне (рис. 1.2, б и табл. 1.1) или делением большей стороны пополам.
Обозначение и размеры основных форматов чертежа приведены в табл. 1.1.
Дополнительные форматы образуются путем увеличения сторон основных форматов на величину, кратную размерам формата А4. Обозначение производного формата составляется из обозначения основного формата и его кратности согласно табл. 1.2, например, 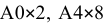
Иногда допускается применение формата А5 с размерами сторон 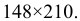
Основные надписи
Формы, размеры и порядок заполнения основной надписи и дополнительных граф к ней в чертежах, схемах и текстовых документах устанавливает ГОСТ 2.104-2006.
Основная надпись, дополнительные графы к ней и рамки выполняют сплошными основными и сплошными тонкими линиями, а именно: тонкие линии наносятся там, где вносятся фамилии и подписи лиц, ответственных за разработку данной детали или изделия, и
графы литеры, остальные линии – основные.
Основная надпись всегда располагается в правом нижнем углу формата, вплотную к рамке (см. рис. 1.1).
Содержание, расположение и размеры граф основной надписи, дополнительных граф к ней, также размеры рамок на чертежах и схемах должны соответствовать форме 1 (рис. 1.3), а в текстовых документах должны соответствовать форме 2 (рис. 1.4) и форме 2а (рис. 1.5) указанного выше ГОСТа:
- наименование чертежа (начинается с существительного в единственном числе);
- обозначение чертежа (состоит из индекса раздела курса, номера задания, варианта, порядкового номера чертежа, например ИГО 1.22.001);
- обозначение материала (заполняют только на чертежах и эскизах деталей);
- литера чертежа (обычно на учебных чертежах используют литеру У);
- масса изделий (на учебных чертежах не указывается);
- масштаб;
- порядковый номер листа (на документах, состоящих из одного листа, графу не заполняют);
- количество листов (графу заполняют только на первом листе, если документ состоит из одного листа, указывают – /);
- наименование предприятия, выпустившего чертеж (на учебных чертежах указывают наименование учебного заведения и шифр группы, например Г1И СФУ гр. МТ10-12);
- характер работы, выполняемой лицом, подписавшим чертеж;
- фамилии лиц, подписавших чертеж;
- подписи лиц, фамилии которых указаны в графе 11;
- даты, когда были сделаны подписи.
Основная надпись, форма 2 – для текстовых конструкторских документов первый или заглавный лист (рис. 1.4).
Основная надпись, форма 2а – для текстовых конструкторских документов второй и последующие листы (рис. 1.5).
Для второго и последующих листов чертежей и схем допускается применять форму 2а (рис. 1.5).
На формате Л4 основную надпись размещают только вдоль короткой стороны, дополнительную графу – в левом верхнем углу вдоль короткой стороны (рис. 1.6, а).
На форматах больше А4 при расположении основной надписи вдоль длинной стороны листа дополнительная графа располагается так, как показано на рис. 1.6, 6.
На форматах больше А4 при расположении основной надписи вдоль короткой стороны листа дополнительная графа располагается, как показано на рис. 1.7.
Масштабы
Все чертежи выполняют в масштабах, утвержденных ГОСТ 2.302-68.
Масштабы изображений в чертежах, в зависимости от сложности и величины изображаемых изделий или их составных частей, а также от вида чертежа, нужно выбирать из представленного в табл. 1.3 ряда.
Масштаб, указанный в предназначенной для этого графе основной надписи чертежа, должен обозначаться по типу 1:1; 1:2; 2:1 и т. д.
Масштаб изображения, отличающийся от указанного в основной надписи, помещают справа от надписи, относящейся к изображению. Например: А (1:2), А-А (1:2).
Вес чертежи выполняют линиями различного типа и толщины, причем толщина линий зависит от величины, сложности и назначения чертежа.
ГОСТ 2.303-68 устанавливает начертания и основные назначения линий на чертежах (рис. 1.8).
Указанный стандарт устанавливает назначение и начертание девяти типов линий, это – сплошная (основная, тонкая, волнистая и тонкая с изломами), штриховая, штрихпунктирная (тонкая, утолщенная и с двумя точками) и разомкнутая линии (табл. 1.4).
Сплошная тонкая линия предназначена для построения, выносных и размерных линий, штриховки разрезов и сечений, линии контура наложенного сечения, линии-выноски, полки линий выносок и подчеркивание надписей и др. (см. табл. 1.4). Расстояние между линиями штриховки принимают от 1 до 10 мм в зависимости от величины площади штриховки.
Волнистой линией показывают линии обрыва и линии разграничения вида и разреза.
Штриховую линию применяют для изображения на чертежах линий невидимого контура.
Штрихпунктирной тонкой линией проводят осевые и центровые линии, линии сечений, являющиеся осями симметрии для наложенных или вынесенных сечений.
Штрихпунктирная тонкая линия с двумя точками применяется для изображения линий сгиба и частей изделий в крайних или промежуточных положениях, а также для изображения развертки, совмещенной с видом.
Утолщенная штрихпунктирная линия применяется для обозначения поверхности, подлежащей термической обработке или нанесению покрытий.
Длину штрихов в штриховых линиях следует выбирать в пределах от 2 до 8 мм в соответствии с толщиной линий, а расстояние между штрихами выбирают примерно 1-2 мм.
Длина штрихов в штрихпунктирных тонких линиях должна быть в пределах от 5 до 30 мм, при малых изображениях длину штрихов лучше выбирать меньшей длины. Промежутки между штрихами в этих линиях рекомендуется брать для линии с одной точкой от 3 до 5 мм, а с двумя точками примерно 4—6 мм.
Длина штрихов в штрихпунктирных утолщенных линиях должна быть в пределах от 3 до 8 мм, при малых изображениях длину штрихов рекомендуется выбирать меньшей длины. Промежутки между штрихами в этих линиях выбирают от 3 до 4 мм.
Разомкнутую линию применяют для обозначения линий разрезов и сечений (см. рис. 1.8, А-А). Длину штрихов в этих линиях выбирают в пределах от 8 до 20 мм в зависимости от величины изображения.
При выполнении чертежа необходимо руководствоваться следующими требованиями:
- толщина линий одного типа должна быть одинаковой для всех изображений на данном чертеже, вычерченных в одном масштабе;
- штрихи в линии должны быть приблизительно одинаковой длины;
- штриховые и штрихпунктирные линии должны начинаться и заканчиваться штрихами, которые рекомендуется выводить за контур изображения предмета на 3-5 мм;
- штриховые и штрихпунктирные линии должны пересекаться между собой и другими линиями чертежа штрихами;
- если диаметр окружности в изображении менее 12 мм, то штрихпунктирные линии, применяемые в качестве центровых, следует заменять сплошными тонкими;
- центр окружности во всех случаях должен определяться пересечен и ем штрихов.
Шрифты чертежные
ГОСТ 2.304-81 регламентирует правила написания шрифтов (букв, цифр, условных знаков). Необходимость строгого соблюдения этого ГОСТа продиктована проблемой быстрого и безошибочного распознавания надписей невооруженным глазом или вооруженным, или «читающим» устройством при изменяющихся условиях (при различной освещенности, когда наблюдатель неподвижен, а движется чертеж или наоборот). Кроме того, чертежи со временем могут изнашиваться и надписи становятся менее четкими. Ошибки при чтении размерных чисел недопустимы. Поэтому к качеству шрифта на чертежах предъявляют особые требования.
В соответствии с требованиями ГОСТ 2.304-81 шрифты, применяемые при оформлении чертежей и других технических документов всех отраслей промышленности и строительства, установлены двух типов: тип А с толщиной линии 1:14h (табл. 1.5) и тип Б с толщиной 1:10h (табл. 1.6) с наклоном под углом 75° к основанию строки (рис. 1.9) или без наклона (рис. 1.10).
Устанавливаются следующие размеры шрифта: 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Применение шрифта типа Л с размером 1,8 не рекомендуется и допускается только для типа Б.
Стандарт предусматривает следующие термины, обозначения и определения (рис. 1.11):
- Размер шрифта h – величина, определенная высотой прописных букв в миллиметрах.
- Высота прописных букв h измеряется перпендикулярно к основанию строки. Высота строчных букв с определяется из отношения их высоты (без отростков k) к размеру шрифта h, например с = 7/10h.
- Ширина буквы g, толщина линии шрифта d, расстояние между буквами а и минимальное расстояние между строками b определяются в зависимости от типа шрифта (табл. 1.5 и 1.6).
При выполнении надписей шрифтом вначале необходимо построить карандашом сетку (рис. 1.12) в виде тонких линий, а затем от руки нанести на эту сетку буквы и цифры тонкими линиями. Необходимая толщина линий букв и цифр достигается при обводке мягким карандашом.
На рис. 1.13 показано построение шрифта типа А (рис. 1.13, а) и типа Б (рис. 1.13, 6) по вспомогательной сетке.
При выполнении чертежей часто используются специальные знаки, начертание которых приведены на рис. 1.14.
При нанесении знака 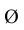
Примечание. Нижние горизонтальные отростки у прописных и строчных букв Ц и Щ типов А и Б делают за счет промежутков между смежными буквами, а вертикальные (также черта над И) – за счет промежутка между строками.
При нанесении знака □ перед размерным числом высота знака должна быть равна 5/7h.
При нанесении знака R перед размерным числом высота знака должна быть равна h – высоте размерного числа.
Примеры начертания цифр и знаков чертежного шрифта представлены на рис. 1.15.
Дроби, показатели, индексы и предельные отклонения выполняют шрифтом на одну ступень меньшим, чем размер шрифта основной величины, или одинакового размера с ним (рис. 1.16). Следует десятичные знаки отделять четко выполненной запятой (в виде черты), оставляя для нее достаточный промежуток между смежными цифрами.
Применение шрифта размера, меньшего чем 3,5, при нанесении размерных чисел на чертежах, выполненных в карандаше, не допускается.
Нанесение размеров
Простановка размеров на чертеже является одним из важных элементов, поэтому необходимо познакомиться с правилами их нанесения.
Нанесение размеров на чертеже регламентирует ГОСТ 2.307-2011. Основанием для определения величины изображенного изделия и его элементов служат размерные числа, проставленные на чертеже. Общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления и контроля изделия. Требование минимальности простановки размеров обусловлено тем, что лишний размер увеличивает время чтения чертежа из-за его загруженности. Пропуск или ошибка в размерах приводят к браку при изготовлении изделия. Повторять размеры одного и того же элемента детали на изображениях не допускается.
Размеры выражают геометрические величины объектов, расстояния и углы между ними, координаты отдельных точек. Величина изображенного на чертеже изделия и его элементов (частей) определяется размерными числами, нанесенными на чертеже.
Размеры подразделяются на линейные и угловые. Линейные определяют длину, ширину, высоту, толщину, диаметр и радиус элементов детали. Угловые определяют углы между линиями и плоскостями элементов детали, а также углы между элементами.
Линейные размеры на чертежах указывают в миллиметрах, без обозначения единицы измерения. Угловые размеры указывают в градусах, минутах и секундах с обозначением единицы измерения, например: 45°, 45° 30′, 60°
Для размерных чисел применять простые дроби не допускается, за исключением размеров в дюймах.
Размеры на чертеже наносят без учета масштаба изображения, т. е. значения размерных чисел определяют действительные размеры, которые должно иметь изготовленное изделие.
Размеры на чертежах указывают размерными числами и размерными линиями, ограничиваемыми с одного или обоих концов стрелками или засечками. Размерная линия – это отрезок, графически выражающий величину, а также ориентацию размера. Размерные линии (рис. 1.17. а) проводят параллельно тому отрезку, линейный размер которого наносят. Выносные линии, а также заменяющие их осевые, проводят перпендикулярно размерным линиям. В случаях, подобных изображенному на рис. 1.17, б, выносные линии следует проводить так, чтобы они вместе с измеряемым отрезком образовывали параллелограмм.
Размерные линии не должны являться продолжениями линий контура, центровых и выносных линий.
Размерную линию желательно наносить вне контура изображения. Размерные и выносные линии следует выполнять сплошными тонкими линиями. Необходимо избегать пересечения размерных и выносных линий.
Размерный текст обычно состоит из размерного числа, при необходимости в размерный текст могут включаться различные специальные обозначения, а также допуски. Центровые линии – это штрихпунктирные линии (рис. 1.17, б), обозначающие центр окружности или дуги.
Рис. 1.17. Расположение на чертеже размерных линий и чисел
Расстояние между контурной и размерной линией должно быть не менее 10 мм, а между размерными линиями не менее 7 мм, выносные линии должны выходить за концы стрелок или засечек на 1…5 мм (рис. 117, а).
Размерные числа наносят над размерной линией как можно ближе к ее середине, причем промежуток между размерным числом и размерной линией должен быть 0,5… 1,0 мм (рис. 1.17, а). В пределах одного чертежа размерные числа выполняют шрифтом одного размера – 3,5 или 5 мм. Предпочтительная высота размерных чисел равна 5 мм.
Если вид или разрез симметричного предмета или отдельных симметрично расположенных элементов изображают только до оси симметрии (рис. 1.18) или с обрывом, то размерные линии, относящиеся к этим элементам, проводят с обрывом, и обрыв размерной линии делают дальше оси или линии обрыва предмета.
Величину стрелки выбирают в зависимости от толщины линий видимого контура и вычерчивают их приблизительно одинаковыми на всем чертеже.
Форма, размер стрелки и примерное соотношение ее элементов показаны на рис. 1.19.
При нанесении размера угла размерную линию проводят в виде дуги с центром в его вершине, а выносные линии – радиально (рис. 1.20).
При нанесении размера дуги окружности размерную линию проводят концентрично дуге, а выносные линии – параллельно биссектрисе угла, и над размерным числом наносят знак 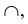
При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии перпендикулярно к размерным (рис. 1.22).
При изображении изделия с разрывом размерную линию не прерывают (рис. 1.23).
Если длина размерной линии недостаточна для размещения на ней стрелок, то размерную линию продолжают за выносные (или за контурные, осевые, центровые и т. д.) и стрелки наносят так, как показано на рис. 1.24.
При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допускается заменить засечками, наносимыми под углом 45° к размерным линиям (рис. 1.25. а) или четко наносимыми точками (рис. 1.25, б).
При нанесении нескольких параллельных (рис. 1.26) или концентрических (рис. 1.27) размерных линий на небольшом расстоянии друг от друга размерные числа над ними рекомендуется располагать в шахматном порядке.
Размерные числа линейных размеров при различных наклонах размерных линий располагают так, как показано на рис. 1.28. Причем все размерные числа и надписи должны читаться со стороны основной надписи или при повороте формата вправо. Данное требование продиктовано тем, что изображения в основном располагают относительно основной надписи так, как располагается деталь на станке. Если необходимо указать размер в заштрихованной зоне (рис. 1.28), то размерное число наносят на полке линии-выноски.
Для указания размера угла размерная линия проводится в виде дуги с центром в его вершине, а выносные линии – радиально. Знаки градусов наносят на уровне высоты цифры размерного числа (рис. 1.29).
В зоне, расположенной выше горизонтальной осевой линии, размерные числа угловых размеров наносятся над размерными линиями со стороны их выпуклости; в зоне, расположенной ниже горизонтальной осевой линии, со стороны вогнутости размерных линий. Размерное число, расположенное в отмеченной штрихами зоне, должно располагаться на горизонтальной полке линии выноски (размеры 30° и 40°) (рис. 1.29).
При указании размера диаметра всегда перед размерным числом наносят знак 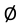
Если для написания размерного числа над размерной линией недостаточно места, то размеры наносят так, как показано на рис, 1.30. Если недостаточно места для нанесения стрелок, то размеры наносят так, как показано на рис. 1.3 1.
Способ нанесения размерного числа при различных положениях размерных линий (стрелок) на чертеже определяется наибольшим удобством чтения (рис. 1.30, 1.31).
Размерные числа нельзя разделять или пересекать какими бы то ни было линиями чертежа. Нс допускается разрывать линию контура для нанесения размерного числа и наносить размерные числа в местах пересечения размерных, осевых или центровых линий.
В месте нанесения размерного числа осевые, центровые линии (рис. 1.32, л) и линии штриховки (рис. 1.32, 6) прерывают.
Размеры, относящиеся к одному и тому же конструктивному элементу (пазу, выступу, отверстию и т. п.), рекомендуется группировать в одном месте, располагая их на том изображении, на котором геометрическая форма данного элемента показана наиболее полно, более наглядно (рис. 1.33).
При нанесении размера радиуса перед размерным числом помещают прописную букву R (рис. 1.34).
Если при нанесении размера радиуса дуги окружности необходимо указать размер, определяющий положение ее центра, то центр изображают в виде пересечения центровых или выносных линий. При большой величине радиуса центр допускается приближать к дуге, в этом случае размерную линию можно приближать к дуге, а размерную линию радиуса показывать с изломом под углом 90° (рис. 1.34, а).
Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается нс доводить до центра и смещать ее относительно центра (рис. 1.34, б).
При проведении нескольких радиусов из одного центра размерные линии любых двух радиусов не располагают на одной прямой (рис. 1.34.г)•
При совпадении центров нескольких радиусов их размерные линии допускается не доводить до центра, кроме крайних (рис. 1.34, г).
Размеры радиусов наружных скруглений наносят так, как показано на рис. 1.35, а. Размеры внутренних скруглений показаны на рис. 1.35, б.
Радиусы скруглений, размер которых в масштабе чертежа 1 мм и менее, на чертеже не изображают, а размеры наносят так, как показано на рис. 1.36.
Способ нанесения размерных чисел при различных положениях размерных линий (стрелок) на чертеже определяется наибольшим удобством чтения.
Размеры одинаковых радиусов допускается указывать на общей полке (рис. 1.37).
Перед размерным числом диаметра (рис. 1.38) или радиуса (рис. 1.39) сферической поверхности (или ее части) наносят соответственно знак 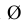
Размеры элементов квадратной формы наносят так, как показано на рис. 1.40, причем знак квадрата должен выглядеть как квадрат (не параллелограмм, не прямоугольник). Высота знака 
Перед размерными числами, характеризующими конусность, наносят специальный знак 
Знак конуса и конусность в виде соотношения следует наносить над основной линией или на полке линии-выноски (рис. 1.41).
Примечание. При выполнении чертежей на компьютере знак □ проставляется автоматически, равным высоте размерных чисел (рис. 1.40). Размеры фасок под углом 45° наносят так, как показано на рис. 1.42.
Если деталь имеет несколько одинаковых фасок на цилиндрических (или конических) поверхностях разного диаметра, то размер фаски наносят только один раз, с указанием их количества под размерной линией (рис. 1.42, 6). Когда деталь имеет две симметрично расположенные одинаковые фаски на одинаковых диаметрах, то размер фаски наносят один раз без указания их количества (рис. 1.42, а).
Размеры фасок под другими углами указывают по общим правилам – линейными угловыми размерами или двумя линейными размерами. Нанесение размеров углов показано на рис. 1.43 и 1.44.
При расположении элементов предмета (отверстий, пазов, зубьев и т. п.) на одной оси или на одной окружности размеры, определяющие взаимное расположение, наносят следующим образом:
а) задание размеров между смежными элементами цепочкой (рис.1.45);
б) задание линейных размеров от общей базы (рис. 1.46);
в) задание угловых размеров от общей базы (рис. 1.47);
г) заданием размеров нескольких групп элементов от нескольких общих баз (рис. 1.48).
Размеры на чертежах не наносят в виде замкнутой цепи, за исключением случаев, когда один из элементов указывается как справочный (рис. 1.49). Справочными называют размеры, нанесенные на чертеже, но не подвергающиеся контролю. Справочные размеры на чертеже отмечаются знаком *.
Размеры, определяющие положение симметрично расположенных элементов у симметричных изделий, наносят так, как показано на рис. 1.50, 1.51.
Размеры нескольких одинаковых элементов изделия, как правило, наносят один раз с указанием на полке линии-выноски количества этих элементов (рис. 1.52. а, б, 1.53). Полку линии-выноски необходимо вычерчивать горизонтально, параллельно основной надписи.
При нанесении размеров, определяющих расстояние между равномерно расположенными одинаковыми элементами (например отверстиями), рекомендуется вместо размерных цепей наносить размер между соседними элементами и размер между крайними элементами в виде произведения количества промежутков между элементами на размер промежутка линейных размеров, как показано на рис. 1.53, угловых размеров на рис. 1.54.
При нанесении размеров одинаковых элементов, например отверстий (рис. 1.55, рис. 1.56), расположенных в разных частях изделия:
- а) эти элементы рассматривают как один элемент, если между ними нет промежутка (рис. 1.55, а) или они соединены тонкими сплошными линиями (рис. 1.55, б);
- б) рассматривают как разные элементы, если между ними есть промежуток и они не соединены тонкими сплошными линиями (рис. 1.56). В этом случае указывают полное количество элементов.
При изображении детали в одной проекции (рис. 1.57) размер ее толщины наносят так, как показано на рис. 1.57, а, длины – на рис. 1.57, 6.
Размер детали или отверстия прямоугольного сечения могут быть указанны на полке линии-выноски размерами сторон через знак умножения, как показано на рис. 1.58. При этом на первом месте должен быть указан размер той стороны прямоугольника, от которой проводиться линия-выноска.
Допускается не наносить размеры радиуса дуги окружности сопрягающихся параллельных линий (рис. 1.59).
На чертежах необходимо проставлять габаритные размеры. Габаритными размерами называют размеры, определяющие предельные величины внешних очертаний изделий. К габаритным размерам относятся размеры длины, ширины, высоты изделия. Габаритные размеры всегда больше других, поэтому их на чертеже располагают дальше от изображения, чем остальные.
Обозначения графические материалов и правила их нанесения на чертежах
Для большей наглядности при выполнении и чтении чертежей изображение в сечениях покрывают штриховкой. Графическое обозначение материалов в сечениях должно способствовать легкому различению деталей, а также показывать вид материала детали, не затрудняя чтение чертежа.
Правила графического обозначения и нанесения материалов в сечениях на чертежах устанавливает ГОСТ 2.306-68.
Графические обозначения материалов в сечениях в зависимости от вида материалов должны соответствовать приведенным в табл. 1.7.
Допускается применять дополнительные обозначения материалов, не предусмотренных указанным стандартом, но в этом случае необходимо их пояснение на чертеже.
Нанесение штриховки на чертежах должны выполняться по правилам, предусмотренным стандартом.
Наклонные параллельные линии штриховки должны проводиться под углом 45° к линиям рамки чертежа (рис. 1.60), или к линии контура изображения (рис. 1.61), или к его оси (рис. 1.62).
Если линии штриховки, приведенные к линии рамки чертежа под углом 45°, совпадают с линиями контура или осевыми линиями, то вместо угла 45°следует брать угол 30° (рис. 1.63, а) или угол 60° (рис. 1.63,б)
Линии штриховки должны наноситься с наклоном влево или вправо, но, как правило, в одну и ту же сторону на всех сечениях, относящихся к одной и той же детали, независимо от количества листов, на которых эти сечения расположены.
Расстояние между параллельными прямыми линиями штриховки (частота) должно быть одинаковым для всех выполняемых в одном и том же масштабе сечений данной детали и выбираться в зависимости от площади штриховки и необходимости разнообразить штриховку смежных сечений. Указанное расстояние должно быть от 1 до 10 мм (рис. 1.61) в зависимости от площади штриховки и необходимости разнообразить штриховку смежных сечений.
Узкие и длинные площади сечения (например, штампованных и других подобных деталей), ширина которых на чертеже от 2 до 4 мм, рекомендуется штриховать полностью только на концах и у контуров отверстий, а остальную площадь сечения – небольшими участками в нескольких местах (рис. 1.64), а в случаях штриховки стекла (рис. 1.65) линии штриховки следует наносить с наклоном 15-20° к линиям большей стороны контура сечения. Штриховка в этих случаях выполняется от руки.
Узкие площади сечений, ширина которых на чертеже менее 2 мм, допускается показывать зачерненными с оставлением просветов между смежными сечениями не менее 0,8 мм (примерно равными толщине основной линии S), как показано на рис, 1.66.
Рис. 1.66. Штриховка узких площадей, толщиной менее 2 мм Для смежных сечений двух деталей следует брать наклон линий штриховки для одного сечения вправо, для другого – влево (встречная штриховка).
В смежных сечениях со штриховкой одинакового наклона и направления следует изменять расстояние между линиями штриховки (рис. 1.67) или сдвигать эти линии в одном сечении по отношению к другому, не изменяя угла их наклона (рис. 1.68).
При штриховке в клетку для смежных сечений двух деталей расстояние между линиями штриховки в каждом сечении должно быть разным (рис. 1.69).
При больших площадях сечений, а также при указании профиля грунта допускается наносить обозначение лишь у контура сечения узкой полоской равномерной ширины (рис. 1.70).
Аксонометрические проекции
При выполнении технических чертежей иногда наряду с изображением предметов в прямоугольных проекциях следует иметь и наглядные изображения. Это необходимо для обеспечения возможности более полно выявить конструктивные решения, заложенные в изображаемом предмете, правильно представить положение его в пространстве, оценить пропорции частей, их размеры,
Наглядные изображения на некоторых чертежах могут располагаться и независимо от прямоугольных изображений. Например, при изображении схем электроснабжения и теплоснабжения зданий и сооружений.
Существуют различные способы построения наглядных изображений. Сюда относятся аксонометрические аффинные и векторные проекции, а также линейная перспектива. Рассмотрим аксонометрические проекции.
Аксонометрические проекции выполняют в соответствии с ГОСТ 2.317-2011. При построении аксонометрических проекций объект относят к прямоугольной декартовой системе координат и проецируют его вместе с осями координат пучком параллельных лучей на некоторую плоскость проекций, называемую аксонометрической. Полученное изображение, нанесенное на некоторую плоскость проекций, называют аксонометрическим (или просто аксонометрией), а проекции координатных осей – аксонометрическими осями координат.
Проекции прямых, параллельных в действительности натуральным осям координат, параллельны соответствующим аксонометрическим. Именно в использовании этого свойства параллельных проекций и заключается простота построения параллельной аксонометрии.
Здесь возможны три случая, когда все три оси координат составляют с аксонометрической плоскостью проекций некоторые острые углы (равные или неравные) и когда одна или две оси параллельны. В первом случае применяется только прямоугольное проецирование (прямоугольная или ортогональная аксонометрия), а во втором и третьем -только косоугольное проецирование (косоугольная аксонометрия). На практике используют несколько видов как прямоугольной, так и косоугольной аксонометрии с наиболее простыми соотношениями между показателями искажений.
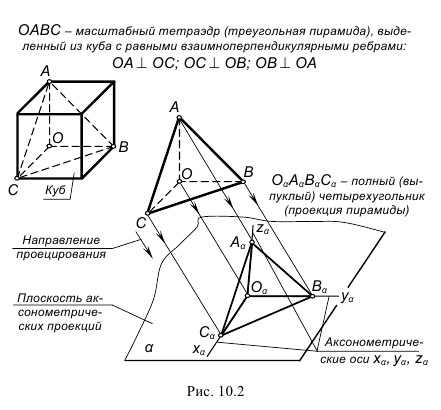
Обратимость аксонометрического чертежа (возможность определения натуральных размеров изображенного объекта) обеспечивается указанием на нем показателей искажения (или наличием условий для их определения) и возможностью построения аксонометрической координатной ломаной (рис. 4.5) любой точки поверхности, принадлежащей изображенному объекту.
Разрезы на аксонометрических проекциях выполняют, как правило, путем сечения объекта координатными плоскостями. При этом ребра жесткости, спицы колес и другие тонкостенные элементы штрихуют (рис. 4.1).
ГОСТ 2.317-2011 рекомендует к применению на чертежах всех отраслей промышленности и строительства пять видов аксонометрий: две ортогональных (прямоугольных) – изометрическую и диметриче-скую и три косоугольных – фронтальную и горизонтальную изометрические и фронтальную диметрическую. В машиностроении в основном применяют ортогональные: изометрическую (она является единствено возможной) и диметрическую проекции.
Прямоугольные аксонометрические проекции, изометрическая и диметрическая, дают более наглядные изображения и в связи с этим применяются на практике наиболее часто.
Прямоугольная изометрическая проекция
Углы между осями х, у и z равны между собой, линейные размеры предмета, параллельные этим осям, искажаются одинаково (рис. 4.2).
При построении аксонометрии дробные показатели искажений усложняют расчет размеров, для его упрощения пользуются приведёнными показателями искажений: в изомстрии все три показателя увеличивают в 1,22 раза (1:0,82 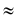
Известно, что любая линия или поверхность есть множество точек. Поэтому рассмотрение построения изометрической проекции рационально начать с построения точки.
Точка А задана своими проекциями 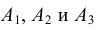
Построение изометрической проекции точки (рис. 4.5). Сначала строим оси, как показано на рис. 4.2. Откладываем от точки О (начала координат) последовательно отрезки на одной из осей и параллельные двум другим осям, равные величинам координат, мы всегда придем в точку А. Порядок построения координатной ломаной может быть любым из шести, представленных на рис. 4.5.
Коэффициент искажения в изометрии 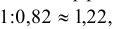
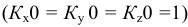
Линии штриховки сечении наносят параллельно одной из диагоналей проекции квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям («спроецированная» штриховка, рис. 4.6).
Если основание многогранника – правильный многоугольник (например треугольник), то построенные прямоугольные изометрические проекции многогранника выполняют просто, а именно: построение вершин основания по координатам упрощается, достаточно провести одну из осей координат через центр основания. На рис 4,7 оси х, у, z проведены через центры правильных треугольников призмы.
Построив изометрические проекции треугольников – оснований призмы (рис. 4.7), из их вершин проводим прямые, параллельные соответственно осям х, у или z. На этих прямых от вершин основания откладываем высоту призмы и получаем изометрию вершин других основания призмы. Соединив эти точки прямыми, получим изометрические проекции призмы.
Построение прямоугольной изометрической проекции правильной шестиугольной призмы показано на рис. 4.8.
Для построения необходимо провести оси прямоугольной изометрической проекции так (рис. 4,8, б), чтобы изображение призмы не вышло за пределы выбранного формата чертежа. И далее: построить прямоугольную изометрическую проекцию дальнего основания призмы 123456; провести из построенных точек 1, 2, 2, 4, 5, 6 прямые линии параллельно оси у и отложить на них ординаты вершин ближнего основания призмы, равные длине ее боковых ребер 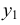
Соединить между собой полученные на прямых, параллельных оси у , точки так, чтобы точки дальнего и ближнего пятиугольников, расположенных в основаниях призмы, были параллельны между собой. Определяем видимость ребер призмы и ее граней, исходя из того, что ближнее основание и крайние ребра (контур изображения) видимы (рис. 4.8, б).
Прямоугольная изометрическая проекция окружности. Если построить изометрическую проекцию куба, в грани которого вписаны окружности диаметра D (рис. 4.9, а), то квадратные грани куба будут изображаться в виде ромбов, а окружности – в виде эллипсов (рис. 4.9, 6). Малая ось C’D’ каждого эллипса всегда должна быть перпендикулярна большой оси
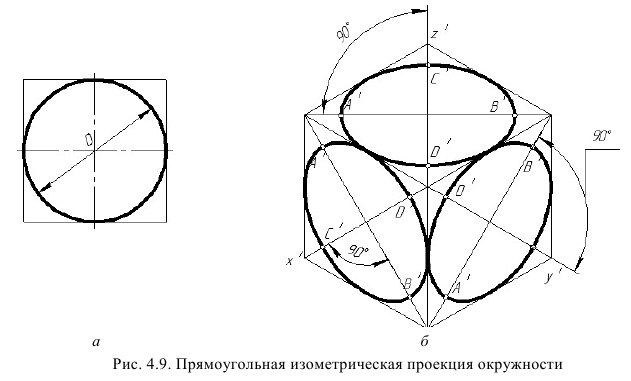
Если окружность расположена в плоскости, параллельной горизонтальной плоскости, то большая ось А’В’ должна быть горизонтальной, а малая ось C’D’ – вертикальной (рис. 4.9, 6). Если окружность расположена в плоскости, параллельной фронтальной плоскости, то большая ось эллипса должна быть проведена под углом 90° к оси у.
При расположении окружности в плоскости, параллельной профильной плоскости, большая ось эллипса располагается под углом 90° к оси
Большие оси эллипсов всегда перпендикулярны соответствующим осям, а малые – им параллельны.
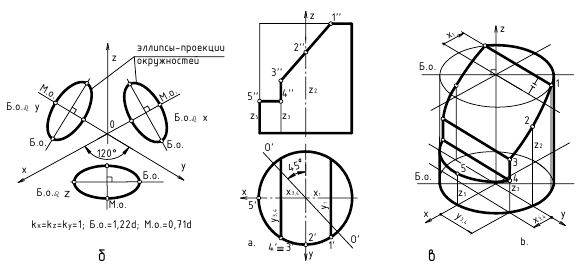
При построении изометрической проекции окружности без сокращения по осям х, у и z длина большой оси эллипса берется равной 1,22 диаметра D изображаемой окружности, а длина малой оси эллипса -0,71D (рис. 4.10).
На рис. 4,11, 4.13 и 4.15 показаны поверхности вращения, выполненные в изометрии с овалами, расположенными параллельно горизонтальной плоскости проекций (рис. 4.11), фронтальной плоскости проекций (рис. 4.13), профильной плоскости проекций (рис. 4.15).
Рис. 4.10. Построение изометрической проекции окружности без сокращения
Рис. 4.11. Поверхность вращения, выполненная в изометрии с овалами, расположенными параллельно горизонтальной плоскости проекций
Рис. 4.12. Построение изометрического овала в плоскости, параллельной горизонтальной плоскости проекций
В учебных чертежах для упрощения построения изометрических проекций окружности вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения изометрических овалов приведен на рис. 4.12, 4.14, 4.16.
Для построения овала в плоскости, параллельной горизонтальной плоскости проекций (рис. 4.12), проводим вертикальную и горизонтальную оси овала, оси x и у (рис. 4,2).
Из точки пересечения осей О проводим вспомогательную окружность диаметром 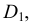
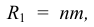
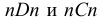
Из центра О радиусом ОС, равным половине малой оси овала, находим на большой оси овала АВ точки 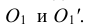
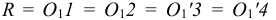
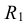
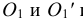
На рис. 4.14 показано упрощенное построение изометрической проекции окружности, расположенной в плоскости, параллельной фронтальной плоскости проекций. Построение аналогично построению изометрического овала, расположенного в плоскости, параллельной горизонтальной плоскости проекций, разница лишь в том, что большую ось овала АВ располагают перпендикулярно малой оси CD – принадлежащей оси у.
На рис. 4.16 показано упрощенное построение изометрической проекции окружности, расположенной в плоскости, параллельной профильной плоскости проекций. Построение аналогично построению изометрического овала, расположенного в плоскости, параллельной профильной плоскости проекций, разница лишь в том, что большую ось овала АВ располагают перпендикулярно малой оси CD – принадлежащей оси х.
На рис. 4.17 приведен пример построения овалов на изометрии детали с расположением окружностей в плоскостях, параллельных горизонтальной, фронтальной и профильной плоскостям проекций. Построение аксонометрической проекции детали следует начинать с изображения на чертеже аксонометрических осей. Целесообразно за начало координат принимать центр симметрии, а за оси координат – оси симметрии детали.
При построении аксонометрии рекомендуется мысленно разделить деталь на простейшие геометрические тела (цилиндр, конус, призма, пирамида и т. п.). После изображения аксонометрических проекций составных элементов предмета строятся конструктивные скругления в местах их соединения.
Линии, изображающие проекции предмета, параллельны одноименным аксонометрическим осям, поэтому при построении аксонометрических проекций удобно использовать прямые, параллельные аксонометрическим осям.
Как и на комплексном чертеже, полые детали в аксонометрии рекомендуется выполнять с разрезом (рис. 4.18).
Если окружность неполная, то для ее изображения вычерчивают тонкой линией полный овал или эллипс, а затем обводят нужную часть овала (рис. 4,18).
Прямоугольная диметрическая проекция
В прямоугольной диметрии ось z расположена вертикально; ось х – под углом 7° 10′, а ось у – под углом 41°25′ к горизонтальной прямой (рис. 4.19). Все отрезки прямых линий геометрического объекта, которые были параллельны осям х, у и z на комплексном чертеже, останутся параллельными соответствующим осям и в диметрической проекции. Длины рсбер куба на изображении отложенных в направлении осей х и z, сокращаются до 0,94 действительной длины, а в направлении оси у – до 0,47 действительной длины (рис. 4.20).
Построение диметрической проекции точки (рис. 4.21). Сначала строим оси, как показано на рис. 4,19. Откладывая от точки О (начала координат) последовательно отрезки на одной из осей и параллельные двум другим осям, получим точку А.
При построении прямоугольной диметрии координатной ломаной линии следует учитывать, что коэффициент искажения по координатным осям x и z (рис. 4.20) 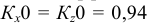
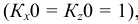
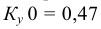
Линии штриховки сечений в прямоугольной диметрической проекции наносят (рис. 4.22) параллельно одной из диагоналей проекции квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям («спроецированная» штриховка).
На рис. 4,23 показано изображение трехгранной призмы в прямоугольной диметрии. Если ребра призмы параллельны оси х или z, то размер высоты не меняется, но искажается форма основания. При расположении ребер параллельно оси у высота призмы сокращается вдвое.
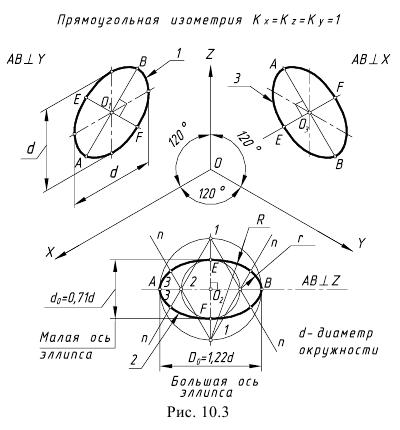
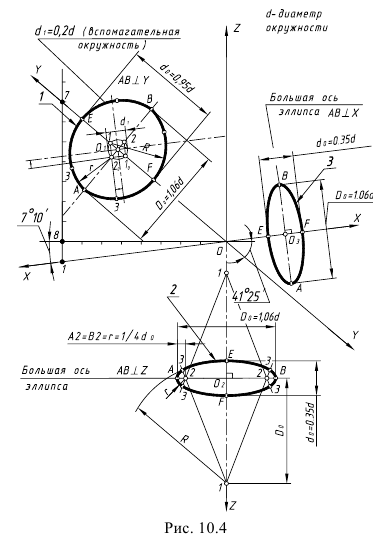
Прямоугольная диметрическая проекция окружности. Если построить диметрическую проекцию куба, в грани которого вписаны окружности диаметра D’ (рис. 4.24, а), то квадратные грани куба будут изображаться в виде параллелограммов, а окружности в виде эллипсов (рис. 4.24, 6). Для построения димстрической проекции окружности (эллипса), расположенной в плоскости, паралельной фронтальной плоскости проекций, надо разделить половину большой диагонали ромба на 10 равных частей. Эллипс должен пройти через точку 3. Проводя через полученную точку 3 две прямые, параллельные осям x и z, на пересечении этих прямых с малой диагональю параллелограмма получим еще две точки 5,принадлежащие эллипсу. Далее, проводя прямые, параллельные осям до пересечения с диагоналями параллелограммов, получаем точки 3 на остальных гранях куба.
Кроме точек 3, имеются еще четыре точки, через которые проходит эллипс. Эти точки расположены на серединах сторон параллелограммов (например, точка n). Найденные точки эллипсов соединяют кривой по лекалу.
Окружности в прямоугольной димстрической проекции изображаются в виде эллипсов. Большая ось эллипсов во всех случаях равна 1,06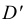
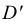
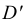
На рис. 4.26, 4.28 и 4.30 показаны поверхности вращения, выполненные в диметрии с овалами, расположенными параллельно горизонтальной плоскости проекций (рис. 4.26), фронтальной плоскости проекций (рис. 4.28), профильной плоскости проекций (рис. 4.30).
В учебных чертежах для упрощения построения диметрических проекций окружности вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения диметрических овалов приведен на рис. 4,27, 4,29, 4,3 1.
Для построения димстрического овала в плоскости, параллельной горизонтальной плоскости проекций (рис. 4.27), через точку О проводим оси x и z, как показано на рис. 4.18, а также большую ось овала АВ проводим перпендикулярно малой оси CD, которая принадлежит оси z. Из центра С, диаметром 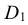
На оси z, вверх и вниз от центра О откладываем отрезки, равные диаметру вспомогательной окружности 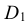
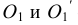
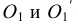
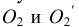
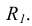
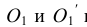
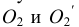
Для построения овала в плоскости, параллельной фронтальной плоскости проекций (рис. 4.29), проводим оси овала х и z так, как показано на рис. 4.17.
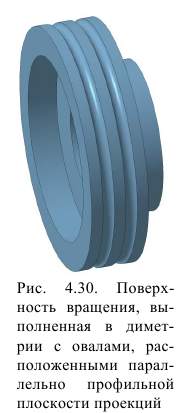
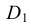
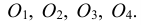
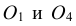
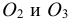
На рис. 4.31 показано упрощенное построение диметрической проекции окружности, расположенного в плоскости, параллельной профильной плоскости проекций. Построение аналогично построению диметрического овала, расположенного в плоскости, параллельной горизонтальной плоскости проекций, разница лишь в том, что большую ось овала AВ проводим перпендикулярно малой оси CD – принадлежащей оси х.
На рис. 4.32 приведен пример построения прямоугольной диметрической проекции детали.
Построение аксонометрических проекций
Построение аксонометрических проекций начинают с проведения аксонометрических осей.
Положение осей
Оси фронтальной ди-метрической проекции располагают, как показано на рис. 85, а: ось х – горизонтально, ось z – вертикально, ось у -под углом 45° к горизонтальной линии.
Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.
Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 85, д).
Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.
При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название “диметрия”, что по-гречески означает “двойное измерение”.
При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название “изометрия”, что по-гречески означает “равные измерения”.
На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток).
Построение фронтальной диметрической и изометрической проекций
Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.
Порядок построения проекций следующий (рис. 87):
- Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты – вдоль оси z, длины – вдоль оси х (рис. 87, а).
- Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной диметрической проекции – сокращенную в 2 раза; для изометрии -действительную (рис. 87, б).
- Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).
- Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).
Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?
Рис. 87. Способ построения аксонометрических проекций
Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.
В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.
Построение аксонометрической проекции квадрата показано на рис. 88, а и б. Вдоль оси х откладывают сторону квадрата а, вдоль оси у – половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.
Построение аксонометрической проекции треугольника показано на рис. 89, а и б.
Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у – его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.
По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и п, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.
Построение плоских фигур в аксонометрических проекциях
Государственный стандарт устанавливает несколько видов аксонометрических проекций. Для построения наиболее наглядных изображений применяется прямоугольная изометрическая проекция (кратко – изометрия, от греч изо – равный, одинаковый). Положение аксонометрических осей этой проекции приведено на рисунке 1, а. Как видно из чертежа, оси проекции в изометрии располагаются под углом 120° друг к другу. При построении фигур размеры отрезков по осям 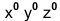
В том случае, когда действительные размеры берут только по двум осям (х°, z°), проекцию называют диметрической (от греч. ди – дважды).
Положение осей диметрической проекции дано на рисунке 1, б.
Аксонометрические проекции многоугольников
Построение аксонометрических проекций начинают с проведения осей. Параллельно им откладывают размеры отрезков.
Рассмотрим построение аксонометрических проекций плоских геометрических фигур, расположенных в горизонтальной плоскости. Построения даны в изометрической проекции.
Треугольник
Симметрично точке 0° по оси х° откладывают отрезки С°А° и 0°Е°, равные половине стороны треугольника, а по оси 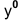
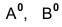
Квадрат
По оси х° от точки 0° откладывают отрезок а, равный стороне квадрата, вдоль оси 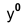
Шестиугольник
По оси х° вправо и влево от точки 0° откладывают отрезки, равные стороне шестиугольника. По оси 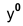
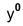
Если контур фигуры сложный, то при построении аксонометрической проекции эту фигуру удобно заключить в квадрат, прямоугольник и пр.
Аксонометрическая проекция окружности
В аксонометрической проекции окружность в общем случае проецируется в кривую, которую называют эллипсом. Эллипс – замкнутая плоская кривая. Ее строят с помощью лекал. Поскольку строить эллипсы трудно, при изображении окружности в аксонометрии их разрешается заменять овалами. Овал – кривая, очерченная дугами окружности.
Рассмотрим построение овала, представляющего изометрическую проекцию окружности. Овал удобно строить, вписывая его в ромб, который является изометрической проекцией квадрата. Построение выполняют в следующем порядке:
- Строят ромб, сторона которого равна диаметру изображаемой окружности. Для этого через точку 0° проводят оси х° и
(рис. 2, а). На них от точки С° откладывают отрезки С°1, С°2 и т. д., равные радиусу изображаемой окружности. Через точки 1,2, 3 и 4 проводят прямые, параллельные осям х° и
, получая на чертеже точки А, Б, С и D.
- Для того чтобы вписать в ромб овал, из вершин тупых углов – точек В и А -проводят дуги. Их радиус R равен расстоянию от вершин тупых углов (точек Б и А) до точек 1, 2 или 3, 4 соответственно (рис. 2, б).
- Через точки В и 1, В и 2 проводят прямые. При пересечении прямых В1 и В2 с большей диагональю ромба CD получают точки
(Рис. 2, в). Эти точки будут центрами малых дуг. Их радиус
равен
(или
Дугами малого радиуса Ri соединяют большие дуги овала.
Изображение в аксонометрических проекциях плоских и объемных тел
Алгоритм построения аксонометрических проекций (первый способ – от передней грани предмета):
Обратите внимание: в аксонометрических проекциях из каждой вершины объекта всегда выходят три луча (видимых или невидимы).
Что такое аксонометрические проекции
Аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства, устанавливает стандарт [14]. Аксонометрические проекции рекомендуется применять для наглядного изображения предметов, выбирая в каждом отдельном случае наиболее подходящую из них.
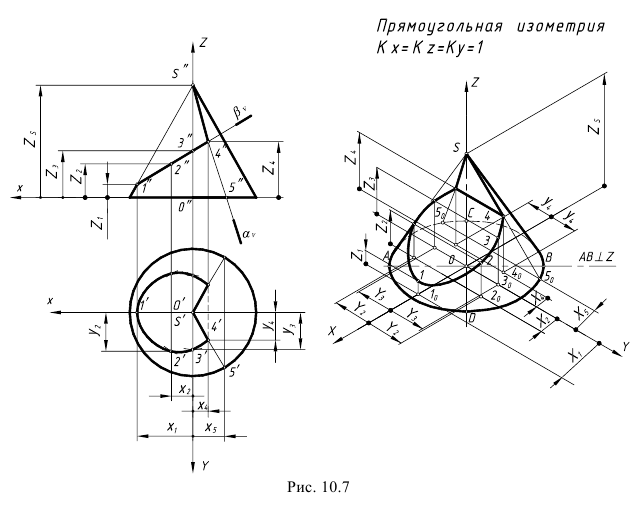
Изометрическая проекция (рис. 120)
Положение аксонометрических осей и основные соотношения для построения изометрических проекций представлены на рис. 117. Все три оси образуют между собой равные углы в 120°, причем ось OZ располагается на изображении вертикально.
Коэффициент искажения по осям X, Y, Z равен 0,82. Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям X, Y, Z, т. е. приняв коэффициент искажения равным единице.
Изометрической проекцией окружности является эллипс (лекальная кривая), но для простоты построения изображают овал (циркульная кривая). Построение овала показано на рис. 118.
При построении точной проекции (с коэффициентом искажения 0,82) большая ось равна диаметру изображаемой окружности, а малая ось равна 0,58 диметра. В данном случае масштаб изображения 1:1. При построении без сокращения размеров по осям OX, OY, OZ большую ось каждого из эллипсов (овалов) следует брать равной 1,22 диаметра изображаемой окружности, а малую ось – равной 0,71 этого диаметра. Тогда масштаб изображения 1,22 : 1.
На рис. 119 показаны направления осей эллипсов (овалов), расположенные в плоскостях, параллельных координатным плоскостям.
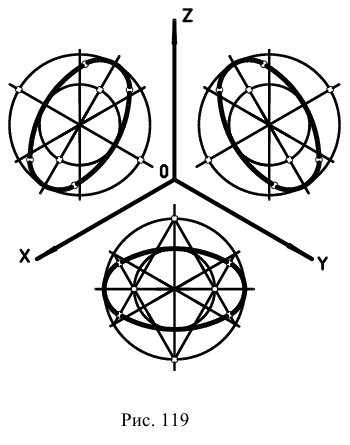
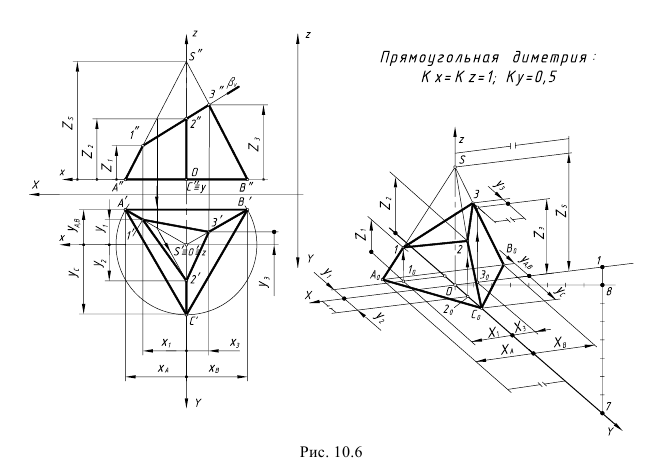
Диметрическая проекция
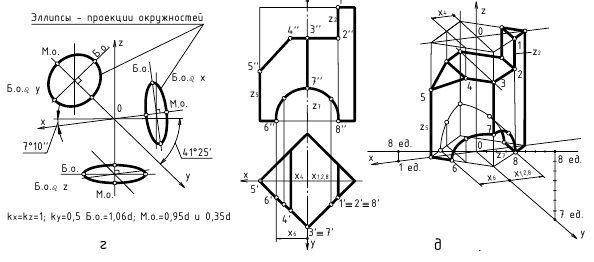
Диметрическая проекция (рис. 126)
Положение осей и основные соотношения для построения диметрических проекций представлены на рис. 121. Для построения угла, приблизительно равного 7°10′, строят прямоугольный треугольник с катетами 1 и 8 единиц; для построения угла, приблизительно равного 41°25′, – с катетами 7 и 8 единиц (рис. 121).
Коэффициент искажения по оси Y равен 0,47, а по осям X и Z – 0,94. Диметрическую проекцию, как правило, выполняют без искажения по осям X и Z и с коэффициентом искажения 0,5 по оси Y.
Диметрической проекцией окружности является эллипс (лекальная кривая), но для простоты построения изображают овал (циркульная кривая), рис. 122. При построении точной проекции с коэффициентами искажения 0,94 и 0,47:
- – в плоскости XOZ большую ось эллипса следует брать равной диаметру изображаемой окружности, а малую ось – равной 0,9 диаметра;
- – в плоскостях XOY и YOZ большую ось эллипса также следует брать равной диаметру, а малую ось – равной 0,33 диаметра.
ГОСТ рекомендует при построении диметрической проекции пользоваться только приведенными коэффициентами. При этом получается изображение, увеличенное в 1,06 раза. При построении по приведенным коэффициентам искажения:
- – в плоскости XOZ большую ось каждого из эллипсов (овалов) следует брать равной 1,06 диаметра изображаемой окружности, а малую ось – равной 0,95 этого диаметра (рис. 122а);
- – в плоскостях XOY и YOZ большую ось следует брать также равной 1,06 диаметра окружности, а малую ось – 0,35 диаметра (рис. 122б).
Направление осей эллипсов (овалов), изображающих окружности, определяют так же, как и в изометрической проекции, т. е. большие оси перпендикулярны к соответствующим аксонометрическим осям, а малые – параллельны им (рис. 123).
Штриховка разрезов в аксонометрии
Линии штриховки разрезов и сечений в аксонометрических проекциях наносят параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рис. 124).
Направление штриховки разрезов в изометрической проекции показано на рис. 124.
Направление штриховки разрезов в диметрической проекции представлено на рис. 125 и 126.
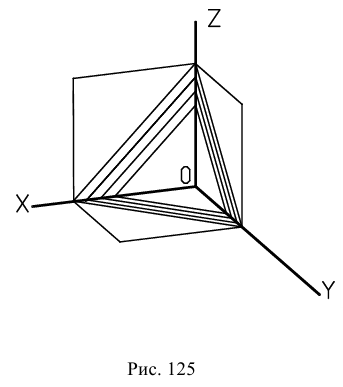
Аксонометрические проекции и комплексный чертеж
Комплексный чертеж является графически простым и удобно измеряемым. Но по нему не всегда легко представить предмет в пространстве. Необходим чертеж, дающий и наглядное представление. Он может быть получен при проецировании предмета вместе с осями координат на одну плоскость. В этом случае на одной проекции можно получить наглядное и метрически определенное изображение. Такие виды изображений называют аксонометрическими проекциями.
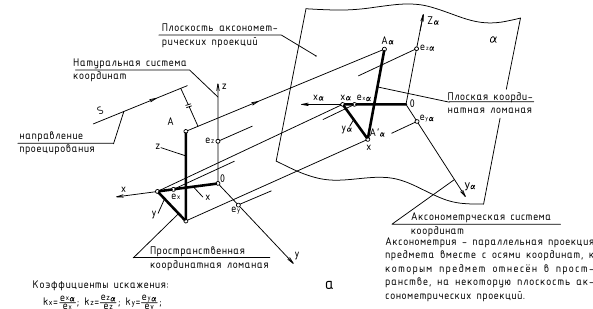
Способ аксонометрического проецирования
Коэффициенты искажения:
Способ аксонометрического проецирования состоит в том, что фигура вместе с осями прямоугольных координат (к которым она отнесена в пространстве) проецируется на некоторую плоскость. Эту плоскость называют плоскостью аксонометрических проекций, или картинной плоскостью. В зависимости от удаления центра проецирования от картинной плоскости аксонометрические проекции разделяют на центральные, когда центр проецирования находится на конечном расстоянии от картинной плоскости, и параллельные, когда центр проецирования находится в бесконечности.
В дальнейшем мы будем рассматривать только параллельное аксонометрическое проецирование.
Слово «аксонометрия» (от гр. 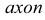
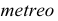
Построим аксонометрическую проекцию точки А, отнесенной к трем взаимно перпендикулярным плоскостям проекций (рис. 6.I).
Оси координат х, у, z называют натуральными осями координат. Возьмем произвольный масштабный отрезок е (натуральный масштаб) и отложим его на осях, обозначив
Спроецируем на картинную плоскость 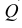
Введем некоторые наименования:
– аксонометрическая проекция точки А;
– вторичные проекции точки А;?
– масштабные отрезки;
– аксонометрические (вторичные) проекции масштабных отрезков.
В зависимости от положения плоскостей проекций Н, V, W, плоскости аксонометрических проекций 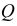
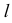
Обозначим эти коэффициенты: по оси 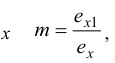
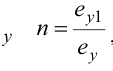
В зависимости от соотношения между коэффициентами искажения по осям различают следующие аксонометрические проекции:
- Изометрические, если
- Димстрические, если
- Триметрическис, если
Наименование проекций произошло от древнегреческих слов: 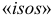
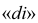
В зависимости от направления проецирования по отношению к плоскости аксонометрических проекций 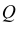
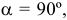
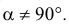
- для косоугольной аксонометрии
- для прямоугольной аксонометрии
В зависимости от положения в пространстве осей координат, плоскости аксонометрических проекций и направления проецирования можно получить множество аксонометрических проекций, отличающихся друг от друга направлением аксонометрических осей и масштабов по ним. Занимаясь теорией аксонометрии, немецкий геометр К. Польке в 1853 году предложил и доказал для частного случая теорему, названную основной теоремой аксонометрии: «Любые три отрезка, выходящие из одной точки на плоскости, могут быть приняты за параллельные проекции трех равных и взаимно перпендикулярных отрезков в пространстве». Доказательство этой теоремы в общем виде было дано в 1864 г. другим немецким геометром Г. Шварцем. С этого времени основная теорема аксонометрии стала называться теоремой Польке – Шварца.
Из рассмотренного выше можно вывести определение аксонометрии: Аксонометрией называется изображение предмета на плоскости, отнесенное к определенной системе координат и выполненное в определенном масштабе с учетом коэффициентов искажения.
Прямоугольная параллельная изометрия
Прямоугольную параллельную изометрию широко применяют в практике технического черчения. В прямоугольной изометрической проекции коэффициенты искажения по всем трем осям одинаковы 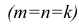
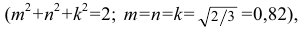
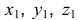
Однако изометрическую проекцию для упрощения, как правило, выполняют приведенной, принимая коэфициенты искажения по осям 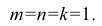
Ось 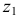
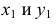
Если, например, даны ортогональные проекции точки А (рис. 6.3), то для построения изометрической проекции этой точки проводим аксонометрические оси (рис. 6.4). Далее от начала координат точки 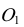
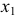
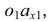
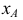
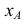
Из точки 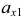
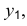
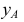
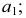
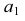
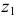
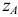
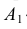
Построение изометрии пятигранной пирамиды по ее чертежу показано на рис. 6.5. Определяем координаты всех точек основания пирамиды. Затем по координатам х и у строим изометрию пяти точек – вершин основания пирамиды. Например, для построения изометрической проекции точки А по оси 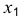
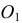
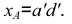
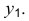
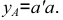
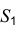
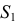
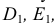
На рис. 6.6 приведен пример построения изометрии шестигранной призмы.
Прямоугольная параллельная диметрия
В прямоугольной диметрии коэффициенты искажения по оси 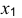
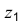
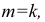
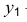
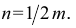
Ось 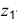
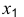
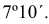
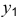
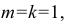
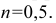
Откладываем по оси 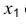
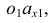
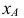
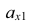
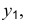
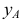
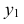
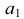
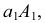
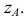
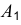
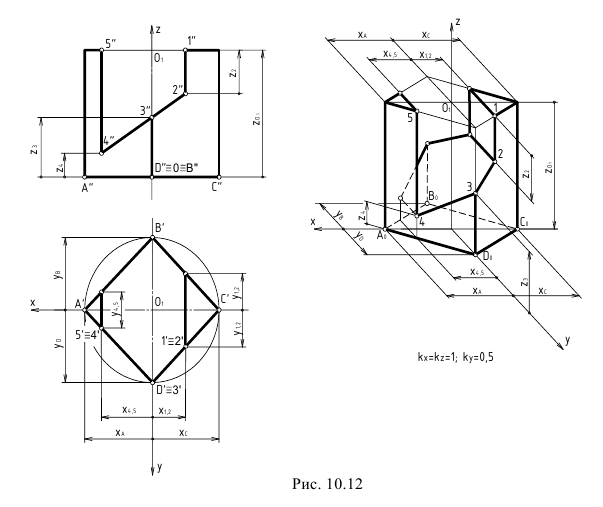
Построение диметрии призмы с призматическим углублением (рис. 6.10) показано на рис. 6.11.
Для выявления внутренней формы детали аксонометрическая проекция выполнена с вырезом 1/4 (угол, образованный секущими плоскостями, выполняется раскрытым). Так как деталь симметрична, начало координат (точку О) выбираем в центре призмы и строим оси х, 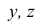
Строим аксонометрические оси и плоские фигуры, полученные при сечении детали плоскостями xOz и yOz (рис. 6.1 1, а).
Обозначим вершины нижнего основания (точки 1,2,3, 4) и строим аксонометрические проекции точек 2, 3, 4.
Строим верхнее основание призмы. Для этого проводим из полученных точек отрезки, параллельные оси 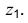
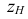
В верхнем основании обозначим вершины призматического отверстия (точки 5, 6, 7, X). Строим аксонометрические проекции точек 6, 7, 8. Из этих точек проводим линии, параллельные оси 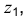
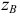
Линии штриховки сечений в аксонометрических проекциях проводят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рис. 6.12 – для изометрии, рис. 6.13 – для диметрии).
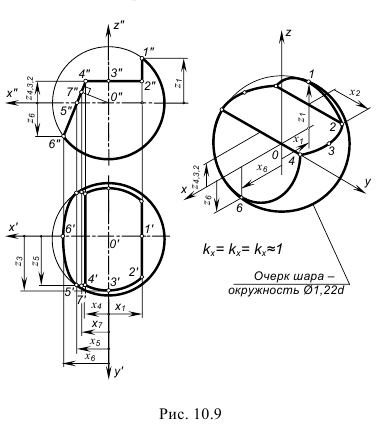
Изображение окружности и шара в прямоугольной аксонометрии
Окружность в аксонометрии в общем случае проецируется в эллипс. При построении эллипса необходимо знать направление его осей и их размеры. Малая ось эллипса всегда должна быть перпендикулярна большой. При построении проекции окружности, лежащей в одной из координатных плоскостей, малая ось эллипса направлена параллельно аксонометрической оси, не участвующей в образовании данной плоскости. Соответственно, большая ось эллипса ей перпендикулярна.
Изометрическая проекция окружности
При построении точной аксонометрии окружности величина большой оси эллипса равна величине диаметра этой окружности. При построении приведенной аксонометрии размеры увеличиваются в 1,22 раза. Поэтому величина большой оси эллипса составляет 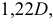
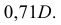
Вычерчиваем окружность диаметра D. хорда АВ = 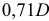
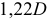
Построим аксонометрические оси 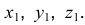
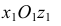
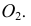
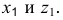
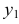
Соединив полученные 8 точек, получим эллипс. Для построения эллипса можно использовать и другие способы.
Построение эллипсов в других плоскостях не отличается по своему характеру, меняется только направление большой и малой осей эллипса.
Диметрическая проекция окружности
В изометрии величины большой и малой осей эллипса остаются одинаковыми независимо от плоскости, в которой расположена окружность. В диметрии постоянной остается только величина большой оси, равная 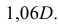
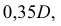
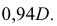
Катеты треугольника равны 100 мм и 35 мм. Гипотенуза при этом равна 106 мм. Отложим по большому катету значение, равное диаметру окружности D (отрезок АВ). Отрезок ВС будет равен 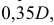
Отрезок АС равен 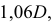
Изображение окружности в прямоугольной диметрической проекции показано на рис. 6.17.
Например, для построения окружности в плоскости V через точку 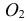
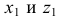
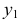
Перпендикулярно малой оси строим большую ось эллипса, равную 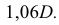
Изображение шара и тора
В прямоугольной параллельной аксонометрии шар изображается окружностью. При построении шара по натуральным показателям искажения его аксонометрической проекцией будет окружность, диаметр которой равен диаметру изображаемого шара.
При построении изображения шара по приведенным показателям диаметр окружности увеличивается в соответствии с увеличением коэффициента приведения: в изометрии – в 1,22 раза (рис. 6.18, а), в диметрии – в 1,06 раза (рис. 6.18, б).
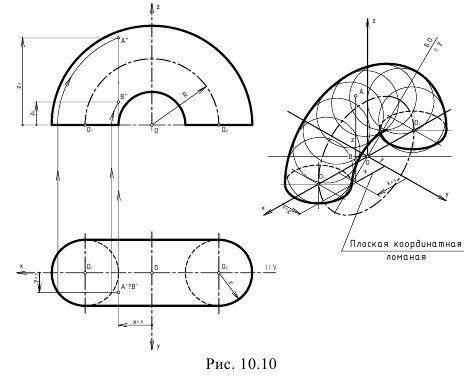
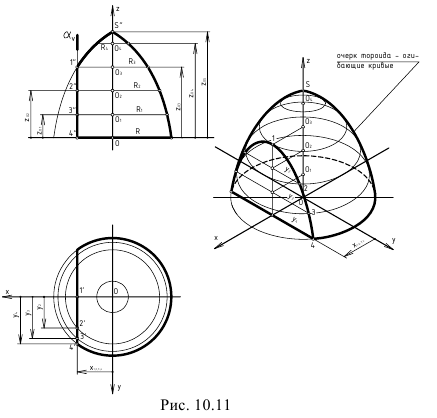
На рис 6.18, в показана изометрическая проекция тора, выполненная с помощью вписанных в него вспомогательных сфер.
Фронтальная изометрическая проекция
В косоугольной фронтальной аксонометрии аксонометрическую плоскость располагают параллельно фронтальной плоскости проекций (рис. 6.19). Направление проецирования выбирают так, чтобы аксонометрические оси располагались, как показано на рис. 6.20.
Допускается применять фронтальные изометрические проекции с углом наклона оси 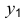
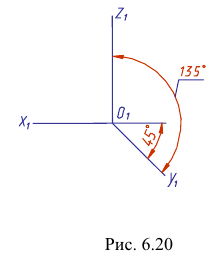
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций V, проецируются па аксонометрическую плоскость в окружности. Окружности, лежащие в плоскостях, параллельных плоскостям Н и W проецируются в эллипсы (рис. 6.2 I).
Большая ось эллипсов 2 и 3 составляет 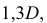
Деталь во фронтальной изометрии нужно располагать по отношению к осям так, чтобы сложные плоские фигуры, окружности, дуги плоских кривых находились в плоскостях, параллельных фронтальной плоскости проекций. Тогда их построение упрощается, так как они изображаются без искажения (рис. 6.22).
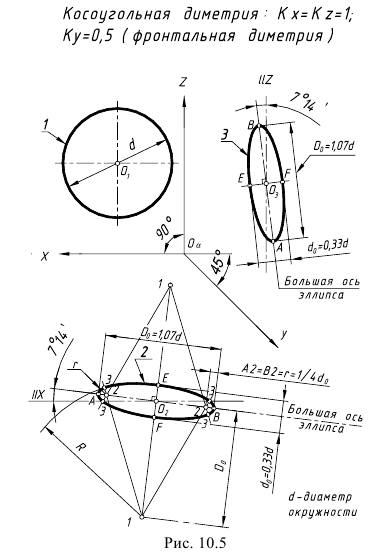
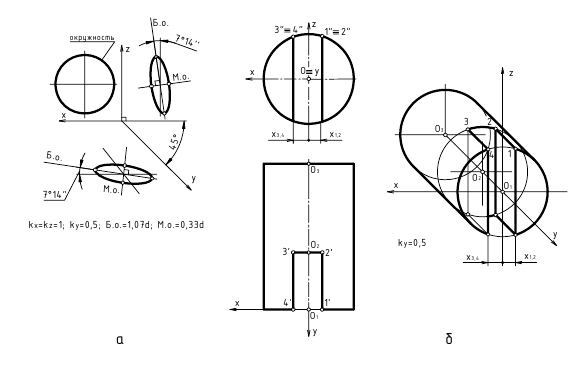
Фронтальная диметрическая проекция
Положение аксонометрических осей такое же, как у фронтальной изометрической проекции (рис. 6.23).
Можно применять фронтальные диметрические проекции с углом наклона оси 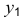
Коэффициент искажения по оси 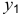
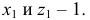
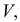
Большая ось эллипсов 2 и 3 АВ = 1,07, а малая ось – CD = 0,33 диаметра окружности. Большая ось эллипса 2 наклонена к горизонтальной оси 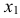
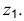
Аксонометрические проекции и их изображения
Аксонометрические проекции наряду с эпюром Монжа являются частным вариантом метода двух изображений, получившим широкое распространение в практике технического черчения. Аксонометрические проекции служат для получения наглядных изображений, дающих более полное представление о конструкции изображаемых объектов (рис. 95).
Аксонометрические проекции как частный случай метода двух изображений
Аксонометрические проекции как частный случай метода двух изображений получаются при использовании следующего аппарата проецирования.
Плоскости 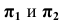
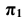
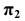
Рассмотрим построение аксонометрической проекции некоторой произвольной точки пространства А. В результате проецирования точки А на плоскости 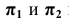
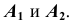
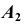
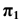
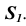
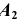
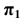
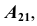
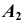
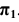
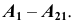
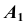
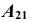
Обратим внимание на построение аксонометрической проекции точки В, принадлежащей плоскости проекций 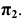
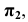
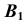
Для решения метрических задач в аксонометрии исходную точку пространства А свяжем с декартовой системой координат 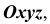
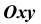
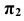
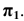
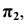
Главной аксонометрической проекцией оси 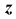
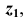
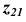
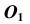
Построение аксонометрической проекции точки А в аксонометрической проекции декартовой системы координат 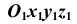
Необходимо отметить, что вторичные проекции могут быть горизонтальными, фронтальными и профильными, и их использование зависит от удобства построения каждого конкретного чертежа. Так, например, на рис. 97 используется горизонтальная вторичная проекция.
В исходной системе координат определим единичные отрезки по каждой оси – 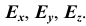
Искажения по аксонометрическим осям определяются коэффициентами искажения, равными отношениям длин аксонометрических единичных отрезков к натуральным масштабным единицам по соответствующим осям:
Теорема Польке
При построении аксонометрических изображений необходимо знать, насколько произвольно могут быть выбраны аксонометрические оси и аксонометрические единичные отрезки. Ответ на этот вопрос дает основная теорема аксонометрии, сформулированная немецким ученым Карлом
Польке и соответственно именуемая теоремой Польке: три отрезка прямых произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на координатных осях от начала.
Таким образом, на основании этой теоремы можно утверждать, что аксонометрические оси и коэффициенты искажения по осям могут выбираться произвольно, т.е. аксонометрий можно построить бесконечно большое количество. Однако доказано, что для любой произвольной аксонометрической проекции коэффициенты искажения связаны между собой со- отношением, называемым основным уравнением аксонометрии: 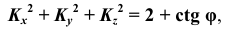
Классификация аксонометрических проекций
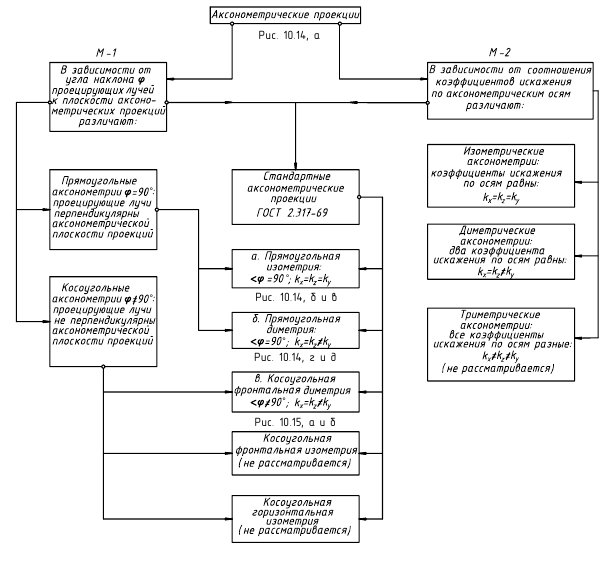
Классифицировать аксонометрические проекции возможно по двум признакам: по виду операции проецирования, используемой при построении аксонометрической проекции, и по показателям искажения. В зависимости от вида операции проецирования аксонометрии могут быть косоугольные (φ ≠ 90°) и прямоугольные (φ = 90°). В зависимости от соотношения показателей искажения аксонометрии могут быть:
- триметрические (все показатели искажения различны);
- диметрические (два показателя искажения равны, но не равны третьему;
- изометрические (все показатели искажения равны друг другу).
Стандартные аксонометрические проекции
В соответствии с теоремой Польке выбор аксонометрических осей и коэффициентов искажения может быть произвольным. Выполнять чертежи, пользуясь произвольным видом аксонометрии, невозможно. Поэтому ГОСТ 2.317–69 устанавливает пять видов стандартных аксонометрических проекций (рис. 98).
Из стандартных аксонометрий наиболее часто используются две прямоугольные (изометрическая и диметрическая) и три вида косоугольных (фронтальная изометрическая, горизонтальная изометрическая, фронтальная диметрическая). При построении стандартных аксонометрических проекций используются приведенные коэффициенты искажения, равные, как правило, 1 или 0,5, т.е. большие, чем коэффициенты искажения, рассчитанные по основному уравнению аксонометрии.
Задача.
Построить стандартные аксонометрические проекции (прямоугольную изометрию и косоугольную фронтальную диметрию) отрезка АВ, заданного на эпюре Монжа координатами точек А (40; 10; 40) и В (10; 50; 20), рис. 99.
Алгоритм решения
- Строим вторичные аксонометрические проекции точек А и В – точки
и
в плоскостях
по соответствующим координатам с учетом коэффициентов искажения по осям.
- По вторичным проекциям точек, строим главные аксонометрические проекции
откладывая значения координат точек А и В по оси
В результате построений получим косоугольную фронтальную диметрию отрезка АВ, представ- ленную на рис. 100, а, и прямоугольную изометрию, представленную на рис. 100, б.
Сравнение изображений геометрических объектов на эпюре Монжа и на аксонометрическом чертеже позволяет сделать следующие выводы:
- изображения геометрических фигур на эпюре Монжа и на аксонометрическом чертеже принципиально ничем не отличаются, так как в основе этих чертежей лежит единая схема метода двух изображений; фигуры на обоих чертежах изображаются двумя проекциями; эпюр Монжа проще и точнее аксонометрического чертежа, так как на эпюре Монжа все единичные отрезки изображаются без искажения, а в аксонометрии – с искажением;
- аксонометрический чертеж нагляднее эпюра Монжа, так как проекции координатных плоскостей в аксонометрии являются невырожденными, а на двухкартинном эпюре Монжа изображение координатной плоскости
в обеих проекциях вырождается в прямую;
- алгоритмы графического решения позиционных задач на эпюре Монжа и на аксонометрическом чертеже одинаковы.
Как построить аксонометрию
Аксонометрические проекции (аксонометрия) служат для наглядного изображения предмета. Название “аксонометрия” образовано из слов древнегреческого языка: “аксон” – ось и “метрео” – измеряю, т.е. измерение по осям.
Аксонометрическая проекция предмета получается параллельным проецированием его вместе с осями прямоугольных координат, к которым этот предмет отнесен, на одну плоскость проекций, называемую аксонометрической плоскостью проекций или картинной плоскостью.
Аксонометрическая проекция – это однокартинный чертеж, на котором получается изображение всех трех измерений предмета. Этим и объясняется его наглядность.
На рис. 249 схематично показано получение аксонометрической проекции точки 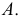
Аксонометрической проекцией точки называется точка пересечения проецирующего луча, проведенного через заданную точку в пространстве, параллельно направлению проецирования, с аксонометрической плоскостью проекций.
Таким образом, чтобы получить аксонометрическую проекцию точки 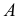
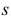
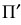
Это построение показывает, что при заданном направлении проецирования каждой точке 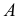
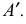
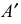
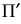
Для устранения этой неопределенности и обеспечения взаимной однозначности между точками пространства и точками аксонометрической (картинной) плоскости проекций на плоскость 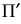
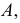
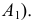
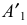
Вторичной проекцией точки называется аксонометрическая проекция одной из ее ортогональных проекций.
Этот термин отражает тот факт, что точка 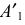
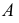
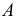
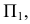
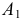
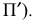
Коэффициенты искажения
В общем случае длина отрезков осей координат в пространстве не равна длине их проекций. Искажение отрезков осей координат при их проецировании на плоскость 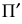
Для определения коэффициентов искажения по аксонометрическим осям 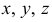
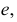
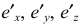
Коэффициентом искажения называется отношение длины аксонометрической проекции отрезка, лежащего на координатной оси или параллельного ей, к истинной длине самого отрезка.
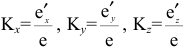
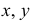
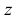
В инженерной практике при построении аксонометрических проекций пользуются не действительными коэффициентами искажения, а приведенными, удобными для построения. Обычно приведенные коэффициенты искажения берут равными единице, что значительно упрощает построение. Изображение при этом несколько увеличивается, однако это не влияет на его наглядность.
При помощи коэффициентов искажения можно перейти от прямоугольных координат к аксонометрическим и наоборот.
Классификация аксонометрических проекций
Аксонометрические проекции классифицируют в основном по двум признакам:
1. По направлению проецирования.
В зависимости от направления проецирования все аксонометрические проекции делятся на две группы:
- – прямоугольные, если направление проецирования перпендикулярно аксонометрической плоскости проекций
- – косоугольные, если направление проецирования не перпендикулярно аксонометрической плоскости проекций
2. По коэффициентам искажения.
В зависимости от коэффициентов искажения все аксонометрические проекции делятся на три группы:
– изометрия – коэффициенты искажения по всем трем осям равны между собой,
– диметрия – коэффициенты искажения по двум осям равны между собой, а третий им не равен,
– триметрия – коэффициенты искажения по всем трем осям не равны между собой,
Между коэффициентами искажения и углом 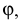
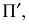
Сумма квадратов коэффициентов искажения по аксонометрическим осям равна двум плюс квадрату котангенса угла проецирования. Котангенс прямого угла равен нулю, следовательно, для прямоугольных аксонометрических проекций справедливо следующее уравнение:
Основная теорема аксонометрии
Всякое изменение положения осей в пространстве и направления проецирования влечет за собой изменение положения аксонометрических осей и коэффициентов искажения по осям.
Вопрос о том, какие положения могут принимать аксонометрические оси и какие величины могут принимать коэффициенты искажения по осям в зависимости от положения осей проекций в пространстве и направления проецирования, был разрешен в прошлом веке геометрами Польке и Шварцем. Они сформулировали основную теорему аксонометрии: любой полный четырехугольник на плоскости всегда является параллельной проекцией некоторого масштабного тетраэдра.
Если на плоскости 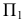
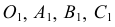
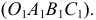
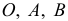
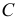
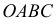
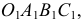
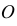
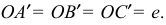
Согласно основной теореме аксонометрии аксономерические оси и коэффициенты искажения по ним могут выбираться произвольно. Задавая разные направления для любой натуральной системы координат, можно получить множество аксонометрических проекций, отличающихся друг от друга как направлением аксонометрических осей, так и величиной коэффициентов искажения вдоль этих осей.
В практике построения наглядных аксонометрических изображений обычно применяют некоторые определенные комбинации направлений аксонометрических осей и коэффициентов искажения, которые дают реальное восприятие предмета и удобны для построения.
Стандартные аксонометрические проекции
Согласно ГОСТ 2.317-69 рекомендуется применять пять стандартных аксонометрических проекций. Из прямоугольных аксонометрических проекций применяют изометрию и диметрию, из косоугольных – фронтальную изометрию, горизонтальную изометрию и фронтальную диметрию.
Прямоугольные проекции
В названии отражается способ получения аксонометрических проекций. Прямоугольная проекция получена прямоугольным проецированием, а слова «изометрия» или «диметрия» говорят о расположении пространственных координатных осей относительно картинной плоскости.
Изометрическая проекция
В изометрии соблюдается равенство коэффициентов искажения 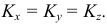
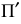
В прямоугольной аксонометрии 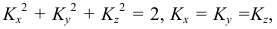
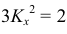
Это действительные коэффициенты искажения по всем осям. Стандарт рекомендует изометрическую проекцию строить без сокращения по осям координат (приведенные коэффициенты искажения по всем осям равны единице), что соответствует увеличению изображения в 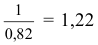
Диметрическая проекция
Эта проекция получается прямоугольным проецированием осей на одну плоскость проекций 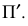
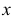
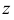
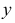
Подставляя эти значения в формулу 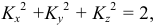
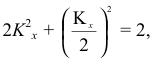
Это действительные коэффициенты искажения. Так как в практике такие дробные числа неудобны, то применяются приведенные коэффициенты искажения:
При этом изображение получается увеличенным в 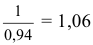
При указанном выше положении осей в пространстве их проекции изображаются так: ось 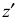
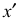
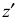
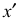
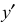
Прямоугольные аксонометрические проекции применяются в машиностроительных чертежах.
Косоугольные проекции
У косоугольных проекций обычно две оси координат 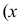
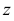
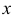
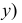
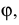
Фронтальная изометрическая проекция
Координатные оси 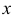
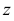
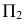
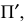
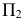
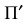
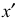
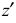
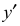
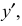
Косоугольная фронтальная изометрическая проекция применяется в сантехнических чертежах при изображении аксонометрических схем трубопроводов.
Горизонтальная изометрическая проекция
Координатные оси 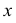
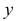
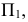
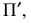
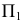
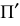
Аксонометрические оси 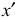
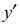
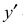
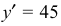
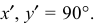
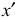
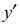
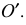
Этот вид аксонометрии удобен при построении наглядного изображения застройки кварталов в инженерно-строительной практике, при решении вопросов пространственной композиции жилых районов и архитектурных ансамблей.
Фронтальная диметрическая проекция
Координатные оси 
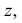
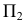
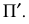
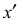
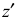
Аксонометрические оси 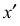
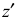
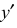
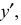
Этот вид аксонометрии применяется в . машиностроительных чертежах при изображении деталей, имеющих большое количество окружностей, расположенных параллельно фронтальной плоскости (детали типа валика).
Построение аксонометрической проекции окружности по восьми точкам
При параллельном проецировании окружности на какую-либо плоскость получаем ее изображение в общем случае в виде эллипса. Отдельные точки окружности строятся как точки пересечения двух прямых, удобных для построения. Обычно в качестве таких прямых берут стороны описанного квадрата и его диагонали. В аксонометрии квадрат в общем случае изображается в виде параллелограмма, т.к. при параллельном проецировании параллельность прямых сохраняется. На рис. 256 показано построение аксонометрической проекции окружности в прямоугольной изометрии, а на рис. 257 – в прямоугольной диметрии.
Четыре точки касания сторон квадрата с окружностью 1, 2, 3, 4 в аксонометрии будут находиться на середине каждой стороны параллелограмма. Еще четыре точки 5, 6, 7, 8 находятся на пересечении диагоналей параллелограмма со вспомогательными прямыми. Они проведены параллельно соответствующим аксонометрическим осям на расстояниях, равных отрезку 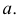
В прямоугольных изометрии и диметрии большие оси эллипсов перпендикулярны отсутствующим в плоскости эллипса осям, а малые оси по направлению совпадают с ними.
Например, эллипс, построенный в плоскости 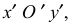
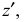
Косоугольные аксонометрические проекции окружности строятся аналогично.
При построении диметрической проекции окружности надо учитывать коэффициент искажения по оси 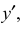
Последовательность построения аксонометрических проекций
Переход от ортогональных проекций предмета к аксонометрическим проекциям рекомендуется осуществлять в такой последовательности:
- на ортогональном чертеже обозначают оси прямоугольной системы координат, к которой и относят данный предмет. Оси ориентируют так, чтобы они допускали удобное измерение координат точек предмета. У поверхностей вращения эти оси целесообразно совмещать с осями симметрии, а у гранных поверхностей – с ребрами;
- строят аксонометрические оси с таким расчетом, чтобы была обеспечена наилучшая наглядность изображения и видимость отдельных элементов предмета;
- по одной из ортогональных проекций предмета чертят вторичную проекцию. Вычерчивать рекомендуется ту вторичную проекцию предмета, которая проще других. Таким образом, используют два измерения предмета;
- создают аксонометрическое изображение, откладывая третье измерение предмета, от соответствующих вторичных проекций.
На рис. 258 показано построение точки 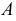
- относят точку
к координатным осям
- проводят аксонометрические оси
углом 120° друг к другу;
- строят вторичную проекцию точки
по ее горизонтальной проекции. Для этого измеряют координаты
и
на координатных осях и откладывают их на аксонометрических осях
и
Через полученные точки проводят прямые, параллельные соответствующим аксонометрическим осям
и
На пересечении этих линий находится точка
– вторичная проекция точки
4. строят аксонометрическую проекцию точки 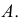
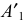
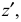
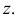
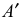
Аксонометрическая и вторичная проекции точки вполне определяют ее положение в пространстве.
Построение конуса в прямоугольной изометрии показано на рис. 259, а, б. По ортогональным проекциям (см. рис. 259, а) строят вторичную проекцию основания – окружность, которая в аксонометрии проецируется в эллипс. Построение эллипса выполняют по 8 точкам (см. рис. 259, б). От центра эллипса откладывают высоту конуса и получают точку 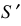
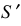
Для определения касательных к эллипсу выполняют следующие геометрические построения:
- – из центра эллипса проводят дугу радиусом равным малой полуоси эллипса;
- – находят точку пересечения этой дуги с окружностью диаметром равным высоте конуса;
- – из полученной точки проводят прямую параллельно большой оси эллипса. Эта прямая пересекает эллипс в искомых точках касания.
В результате указанных построений получают аксонометрическую проекцию прямого кругового конуса.
Тени в аксонометрических проекциях
Ортогональные проекции, обладая рядом достоинств, имеют также и определенные недостатки, главным из которых является отсутствие наглядности полученных изображений.
Более наглядными, достаточно простыми по начертанию и позволяющими выполнять измерения, являются аксонометрические проекции. Аксонометрический проекции, также как и ортогональные, строятся по принципу параллельного проецирования, но на одну плоскость. На рисунке 6.1, показан принцип получения аксонометрии, точки А.
Точка А связана с системой прямоугольных координат OXYZ. На осях отложены единичные отрезки
Это натуральные масштабные единицы.
- S – направление проецирования.
– плоскость аксонометрических проекций (иногда называется картинной плоскостью).
По направлению проецирования, спроецируем единичные отрезки на аксонометрическую плоскость проекций, получим аксонометрическую систему координат O’X’Y’Z’.
Точка 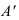
Точка 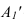
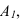
Отрезки 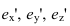
Отношения аксонометрических единиц к натуральным называются показателями искажения по аксонометрическим осям.
– коэффициент искажении по оси X’;
– коэффициент искажения по оси У;
– коэффициент искажения по оси Z’.
Основной теоремой аксонометрии является теорема “Польке-Шварца”:
Всякий не вырождающийся полный четырехугольник можно считать параллельной проекцией тетраэдра наперед заданной формы.
С доказательством теоремы можно познакомиться в учебнике (1,2).
Эта теорема позволяет установить зависимость между углом проецирования и коэффициентами искажения.
В зависимости от угла проецирования 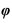
Если направление проецирования является перпендикулярным к плоскости аксонометрических проекций – аксонометрия называется прямоугольной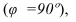
По показателям искажения аксонометрия делится на три типа.
Если все показатели искажения равны, т.е. U = V = W, аксонометрия называется изометрией.
Если два показателя искажения равны, т.е. 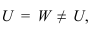
Если все показатели искажения различны, т.е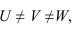
Натуральные показатели искажения по аксонометрическим осям в прямоугольной изометрии одинаковы и равны 0,82. В прямоугольной диметрии U = W = 0,94; V = 0,47.
Однако, при построении аксонометрии натуральные коэффициенты заменяют приведенными, т.е. выраженными целыми числами, что дает увеличение аксонометрического изображения, но на наглядность не влияет.
Cтандартные виды аксонометрических проекций
В таблице 6.1 приведены наиболее применяемые стандартные виды аксонометрических проекций.
Таблица 6.1
Построение аксонометрического изображении
Задача 1. Даны ортогональные проекции схематизированного здания (рисунок 6.2). Построить прямоугольную изометрию.
Прежде всего, выбираем положение ортогональных осей для получения более наглядного изображения (рисунок 6.2).
Строим оси аксонометрических проекций под углом 120° (рисунок 6.3). Построение аксонометрии начинаем с плана, т.е. со вторичной проекции. Так как коэффициенты искажения равны 1, то измеряем, координаты X и У каждой точки плана и откладываем их на аксонометрических осях.
Прямые параллельные в ортогональных проекциях будут оставаться параллельными и в аксонометрии.
После построения плана откладываем все высоты параллельно оси Z, т.е. вертикально.
Соединив полученные точки с учетом видимости, получим аксонометрию здания.
Тени в аксонометрии
Для придания более наглядного и реалистического изображения архитектурным объектам строят тени. Для построения теней задается положение луча света и его вторичной проекции. В принципе направление лучей выбирается произвольным.
На рисунке 6.4 показано построение тени точки А. Через горизонтальную проекцию 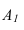
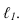
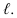
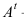
Например.
Тень от прямой перпендикулярной плоскости совпадает с направлением проекции луча на эту плоскость.
Тень от прямой параллельной плоскости ей параллельна и равна но величине.
Тень от прямой на плоскость, которую она пересекает, проходит через эту точку пересечения и т.п.
Задача 2. Построим тени аксонометрии схематизировано здания (рисунок 6.5).
Принимаем направление лучей 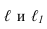
Для высотной части, как и в ортогональных проекциях, контур собственной тени 1,2,3,4,5. Для пристройки – 6,7,8,9. Сначала строим тени падающие на горизонтальную плоскость, т.е. на землю. Затем строим тень, падающую от высотной части на пристройку, используя метод лучевых сечений. Сечение представляет трапецию. Тень от точки 2 падает на наклонную плоскость. По построению мы видим, что тень от ребра 1,2 падает на землю, затем на стену вертикальную и на крышу, т.е. идет но сечению. Далее, чтобы построить тень от прямой 2,3 на наклонной плоскости, находим точку пересечения прямой 2,3 с наклонной плоскостью и соединяет 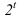
Задача 3. Построить тени козырька на плоскость стены (рисунок 6.6)
Козырек призматический. При заданном направлении лучей определяем контур собственной тени 1,2,3,4,5. Точки 1 и 5 лежит на стене, поэтому строим тени точек 2,3,4. Для построения теней используется метод лучевых секущих плоскостей. Через вторичные проекции точек 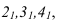
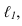
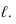
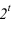
Определение аксонометрической проекции
Аксонометрические изображения обладают большей наглядностью, чем ортогональные проекции, и являются дополнительными к основному проекционному чертежу.
Аксонометрические изображения образуются путем проецирования геометрического объекта вместе с ортогональной системой плоскостей проекций и осей на некую аксонометрическую плоскость, называемую картинной. На рисунке 11.1 изображена схема получения аксонометрических проекций.
Размеры проецируемого тела на аксонометрической проекции искажаются, что учитывается коэффициентами искажения k, m и n. В зависимости от соотношения коэффициентов аксонометрии делятся на изометрию, диметрию и три метрик).
Аксонометрических изображений может быть получено великое множество. Однако, стандартом (ГОСТ 2.317-69) предусмотрены только пять аксонометрических проекций:
- Прямоугольная изометрия;
- Прямоугольная диметрия;
- Косоугольная фронтальная изометрия;
- Косоугольная фронтальная диметрия;
- Косоугольная горизонтальная изометрия.
Самое широкое распространение в конструкторской практике получили прямоугольная изометрия, прямоугольная диметрия и косоугольная фронтальная диметрия.
Рассмотрим прямоугольную изометрию. Она строится в аксонометрических осях OX, OY, OZ, располагаемых под углом 120 градусов. Коэффициенты искажения по осям одинаковы и равны 1:1. Это означает, что размеры детали переносятся с проекционного чертежа на аксонометрию без искажения и пересчета.
В диметрических аксонометрических проекциях (прямоугольная диметрия, косоугольная фронтальная диметрия) оси OX, OY, OZ располагаются под различными углами друг к другу. Коэффициенты искажения по осям OX,OZ одинаковы и равны 1:1. Коэффициент искажения по оси OY равен 1:2. Это означает, что размеры детали по оси OY, взятые с проекционного чертежа, необходимо пересчитать, прежде чем переносить на аксонометрию. На рисунке 11.2 показано направление аксонометрических осей в различных видах аксонометрий и вычерчивание окружностей в аксонометрических плоскостях XOZ, XOY, и ZOY.
На рисунке 11.3 показано направление линий штриховки, если на аксонометрической проекции выполнен разрез (чаще всего на аксонометрической проекции выполняют вырез части детали, например, одной четверти).
На рисунке 11.4 приведены примеры различных аксонометрических проекций детали. На рисунке 11.5 приведен пример чертежа узла в прямоугольной изометрии с вырезом одной четверти.
Подробное объяснение аксонометрической проекции:
Аксонометрическая проекция, или аксонометрия, дает наглядное изображение предмета на одной плоскости. Слово аксонометрия означает осеизмерение.
Способ аксонометрического проецирования состоит в том, что данную фигуру вместе с осями прямоугольных координат, к которым она отнесена в пространстве, параллельно проецируют на некоторую плоскость, принятую за плоскость аксонометрических проекций (ее называют также картинной плоскостью). При различном взаимном расположении осей координат в пространстве и плоскости аксонометрической проекции, а также при разном направлении проецирования можно получить множество аксонометрических проекций, отличающихся одна от другой направлением аксонометрических осей и масштабом по ним.
В конструкторской документации аксонометрические проекции стандартизованы в ГОСТ 2.317-69. Он предусматривает три частных вида аксонометрических проекций:
- – ортогональная изометрия,
- – ортогональная диметрия,
- – фронтальная (косоугольная) диметрия.
Ортогональная изометрическая проекция
Ортогональная (прямоугольная) изометрическая проекция образуется при прямоугольном проецировании предмета и связанных с ним координатных осей на плоскость аксонометрических проекций, одинаково наклоненную к каждой координатной оси [5].
При таком проецировании все три коэффициента искажений будут равны между собой: 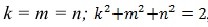
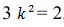
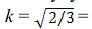
При построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, необходимо умножать на 0,82.
Поскольку такой перерасчет размеров неудобен, изометрическую проекцию для упрощения выполняют без уменьшения размеров (искажения) по осям x, y, z, т.е. принимают приведенный коэффициент искажения равным единице. При этом увеличение изображения предмета составляет 22% (1/0,82 = 1,22). Каждый отрезок, направленный по осям x, y, z или параллельно им, сохраняет свою величину.
Рисунок 5.1 – Расположение Рисунок 5.2 – построение эллипсов осей x, y, z в изометрии в изометрии
На рис. 5.2 показано построение эллипсов, в которые проецируются окружности, лежащие в плоскостях проекций или в плоскостях, параллельным им. Размер большой оси эллипса равен 1,22d, малой – 0,71d, где d – диаметр окружности. В учебных чертежах рекомендуется вместо эллипсов применять овалы, очерченные дугами окружностей. На этом же рисунке показано расположение осей овалов и один из способов построения овалов в прямоугольной изометрической проекции.
Ортогональная диметрическая проекция
Ортогональная диметрическая проекция образуется при прямоугольном проецировании предмета и связанных с ним координатных осей на плоскость аксонометрических проекций, одинаково наклоненную к двум координатным осям [5].
Коэффициенты искажений в диметрической проекции имеют следующие значения: 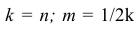
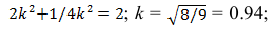
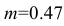
В целях упрощения построений в соответствии с ГОСТ 2.317 – 69, как и в изометрических проекциях, приведенные коэффициенты искажений по осям x и z принимают равным единице; а по оси y коэффициент искажений равен 0,5. Следовательно, по осям x и z или параллельно им все размеры откладывают в натуральную величину, а по оси y размеры уменьшают вдвое. Увеличение в этом случае составляет 6% (выражается числом 1,06 = 1/0,94).
Расположение осей x и y в диметрической проекции, полученное расчетным путем, показано на рис. 5.3. Ось x наклонена по отношению к горизонтальной линии под углом 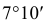
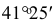
Рисунок 5.3 – Расположение осей
Рисунок 5.4 – построение эллипсов x, y, z в ортогональной диметрии в ортогональной диметрии
С достаточной для практических целей точностью в прямоугольной диметрии оси x и y можно строить по тангенсам углов: 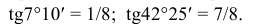
Продолжение оси за центр 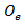
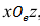
Косоугольная фронтальная диметрия
На практике часто бывает полезным построение такой аксонометрической проекции, в которой хотя бы одна из координат плоскостей не искажается. Очевидно, что для выполнения этого условия плоскость проекций должна быть параллельна одной из координатных плоскостей. При этом нельзя пользоваться ортогональным проецированием, так как координатная ось, перпендикулярная указанной координатной плоскости, изобразится точкой и изображение будет лишено наглядности.
Поэтому пользуются косоугольным проецированием, при котором направление оси y выбирают так, чтобы углы между ней и осями x и z, равнялись бы 135° (рис. 5.5), а показатель искажения 0,5 [5].
Рисунок 5.5 – Расположение
Рисунок 5.6 – построение эллипсов осей x, y, z во фронтальной диметрии во фронтальной диметрии
Такую косоугольную аксонометрическую называют фронтальной диметрией. Коэффициенты искажений по осям x и y равны 1, а по оси y коэффициент искажений равен 0,5.
Напомню:
Аксонометрические проекции представляют собой наглядное изображение предмета на плоскости, при котором изображаются все три измерения.
Аксонометрическое проецирование – это параллельное проецирование предмета вместе с координатной системой на некоторую плоскость.
Если проецирующий луч перпендикулярен плоскости проекций – аксонометрия прямоугольная.
Если не перпендикулярен – косоугольная.
Отношение длины аксонометрической проекции отрезка, // аксонометрической оси, к его истинной длине – коэффициент искажения, к – коэффициент искажения по оси ОХ m – коэффициент искажения по оси ОУ n – коэффициент искажения по оси OZ
Если k = m = n – аксонометрия называется изометрией Если равны только два коэффициента (k = m 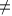
Прямоугольные проекции
Изометрия (к = m 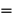
Действительный коэффициент искажения по всем трем осям равен 0,82. Но на практике применяют коэффициент искажения 1. Поэтому в аксонометрии получаем удлинение 1:0,82 = 1,22 МЛ 1,22:1
Диметрия
Действительные коэффициенты искажения по осям X и Z – 0,94, по У – 0,47. Принимаем 1 и 0,5 МЛ 1,06 : 1
Аксонометрическая проекция точки
Все линии, // осям координат в прямоугольной системе, // соответствующим осям в аксонометрии (принцип перпендикулярности не действует)
Построение аксонометрических проекций плоских фигур и геометрических тел
Окружность в аксонометрии
Окружность в изометрии
Окружность в изометрии – эллипс, оси которого перпендикулярны. В учебных чертежах вместо эллипсов применяют овалы.
Для построения овала в плоскости H проводят вертикальную и горизонтальную оси овала. Из точки пересечения осей О проводят вспомогательную окружность диаметром d, равным действительной величине диаметра изображаемой окружности, и находят точки 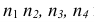
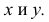
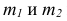
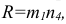
Из центра О радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки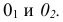
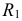
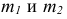
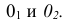
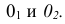
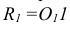
По осям X и У откладываем радиусы окружности от точки О.
БО – большая ось овала МО – меньшая ось овала
Окружность в диметрии
Малая ось овала в аксонометрии по направлению всегда совпадает с отсутствующей осью окружности в прямоугольной системе координат, а большая – ей перпендикулярна.
Аксонометрические изображения
При выполнении технических чертежей наряду с изображением предметов в прямоугольных проекциях часто строят и их аксонометрические изображения. Аксонометрия – греческое слово, составленное из двух слов: аксон – осью и метрео – измеряю, что означает измерение по осям.
При построении прямоугольных проекций проецируемый предмет располагают относительно плоскостей проекций так, чтобы направления основных его измерений (длины, высоты и ширины) были параллельны осям проекций. В результате на каждой плоскости проекций изображаются в натуральную величину два измерения, а третье вырождается в точку. Полученные изображения удобны для нанесения на чертеже размеров, но мало
наглядны.
Если предмет расположить в пространстве так, чтобы ни одно из его измерений не было параллельно какой-либо оси проекций, то при параллельном проецировании на некоторую плоскость все три измерения предмета спроецируются на нее с некоторым искажением. Полученное изображение будет не слишком удобным для нанесения размеров, но весьма наглядным.
Сущность рассматриваемого метода аксонометрического проецирования и заключается в том, что предмет жестко связанный с осями прямоугольных координат параллельно проецируется на аксонометрических проекций (рис. 12.1).
Рис. 12.1. Проецирование предмета и связанных с ним осей координат на плоскость П’
Направление проецирования не должно совпадать ни с одной из координатных осей.
Различным положениям натуральной системы координат по отношению к аксонометрической плоскости проекций и различным направлениям проецирования соответствуют различные положения аксонометрических осей.
Параллелепипед (см. рис. 12.1) связан с прямоугольной системой координат OXYZ и спроецирован вместе с ней и натуральными масштабными отрезками по направлению S на плоскость П’.
- S – направление проецирования;
- П’ – плоскость аксонометрических проекций;
- х, у ,z – натуральные оси (х±уɪz);
- ех, еу, ez – натуральные масштабные отрезки (единица измерения общая для всех трех координатных осей ex=ey=ez);
- х’, у’, z’ – аксонометрические оси;
- ех, еу ez – аксонометрические масштабы.
- А’- аксонометрическая проекция точки А, АВ’ – прямой АВ.
Натуральным масштабным отрезкам ех, еу, ez соответствуют аксонометрические масштабные отрезки ех’, еу’, ez’.
В общем случае прямоугольная система координат Oxyz наклонена под произвольным углом к аксонометрической плоскости проекций. При этом натуральные масштабные отрезки спроецируются на картинную плоскость с различными искажениями.
Показателем искажения называют отношение аксонометрического масштаба к соответствующему натуральному:
- по оси x: u=ex’/ex;
- по оси y: v=еу’/еу;
- по оси z: w=ez’/ez.
Виды аксонометрических проекций
В зависимости от соотношения показателей искажения различают три вида аксонометрических проекций:
- Изометрия – все три показателя искажения равны между собой: u=v=w;
- Диметрия – два показателя искажения одинаковы: u=w≠v;
- Триметрия – все три показателя искажения различны: u≠w≠v.
В зависимости от направления проецирования аксонометрические проекции разделяются на прямоугольные и косоугольные.
Если направление проецирования S перпендикулярно П’, то такая проекция называется прямоугольной или ортогональной аксонометрической проекцией, в остальных случаях – косоугольной аксонометрической проекцией.
Прямоугольные (ортогональные) аксонометрические проекции
Наибольшее распространение в технической практике получили именно ортогональные аксонометрические проекции.
Треугольник X’Y’Z’, по которому плоскость аксонометрических проекций пересекает координатные плоскости натуральной системы координат, называется треугольником следов (рис. 12.2).
Рис. 12.2. Треугольник следов:
П’ – аксонометрическая плоскость проекций;
Ox, Oy, Oz – натуральные координатные оси;
S 
X’ Y’ Z’ – треугольник следов;
O’ x’ ,O’ y’ ,O’ z’ – аксонометрические оси
В ортогональной аксонометрии треугольник следов всегда остроугольный, а аксонометрические оси являются его высотами.
Показатели искажения в ортогональной аксонометрии связаны соотношением:
u2 + v2 + w2 = 2.
Показатели искажения в прямоугольной аксонометрии равны косинусам углов наклона натуральных осей к аксонометрической плоскости проекций:
- по оси x: u — O’ X’/ OX’ — cos α, где а – угол наклона оси x к плоскости П′;
- по оси y: v — O’ Y’ / OY’ — cosβ, где β – угол наклона оси у к плоскости П′;
- по оси z: v — O’ Z’ / Oz’ — cosγ, где γ – угол наклона оси z к плоскости П.
Таким образом, в прямоугольной аксонометрии значения всех трех показателей искажения ограничены крайними значениями то 0 до 1.
Прямоугольная изометрическая и диметрическая проекции
Поскольку в изометрии все три показателя искажения одинаковы, то из соотношения u2 + v2 + w2 = 2 получается, что u — v — w — 0. 82. Треугольник следов в этом случае равносторонний, поэтому аксонометрические оси как высоты равностороннего треугольника образуют углы 1200.
На практике пользуются приведенными показателями: т.е. принимают U=V=W=1. Построение приведенной изометрии значительно проще, нежели построение точной, так как аксонометрические координаты равны соответствующим натуральным. При использовании приведенных показателей искажения изображения получаются увеличенными в 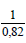
В прямоугольной диметрии два показателя искажения равны u = w, а третий принимают равным u/2, тогда из соотношения u2 + v2 + w2 = 2 следует, что u = w ≈ 0. 94, а v ≈ 0.47. Треугольник следов в этом случае равнобедренный. Если аксонометрическую ось O’z’ расположить на чертеже вертикально, то аксонометрическая ось O’x’ образует с горизонтальной линией угол 7o10’ а ось O’y’ – угол 41025′, тангенсы этих углов равны 1/8 и 1/7 соответственно.
Показатели искажения по аксонометрическим осям O’x’ и O’z’ равны U=V=1, а V=0,5. Изображения в этом случае увеличиваются в 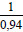
На рис. 12.3. углы между аксонометрическими осями показаны на примере треугольников осей в соответствии с ГОСТ 2.317-68. На чертеже аксонометрические оси наносят штрихпунктирной линией в соответствии с ГОСТ 2.303-68. Треугольники осей всегда изображают рядом с соответствующей аксонометрической проекцией.
Рис. 12.3. Углы между аксонометрическими осями в прямоугольной:
а – изометрии; б – диметрии
Для построения осей прямоугольной изометрии (рис. 12.4,а) строят окружность произвольного радиуса r, затем из нижней точки пересечения ее с вертикальной осью строят дугу того же радиуса. Через центр окружности и полученные точки пересечения проводят оси x и y.
Рис. 12.4. Построение осей графически:
а – прямоугольной изометрии;б -прямоугольной диметрии
Углы между аксонометрическими осями в прямоугольной диметрии можно построить следующим образом (рис.12.4, б): для построения оси O’x’откладывают от начала координат O’ по линии горизонта восемь отрезков и на конце последнего отрезка перпендикулярно к нему – один такой отрезок. Для проведения оси O’y’ – по линии горизонта восемь равных отрезков и от конца последнего отрезка перпендикулярно ему семь таких отрезков.
Для построения приведенной аксонометрической проекции точки A(XA,YA,ZA) следует отложить координаты XA, YA, и ZA в направлении соответствующих аксонометрических осей (рис. 12.5). При построении приведенной диметрии координата Y делится пополам.
Рис. 12.5. Построение аксонометрической проекции точки:
а – трехкартинный комплексный чертеж;
б – прямоугольная изометрия;
в – прямоугольная диметрия
Пример построения приведенной прямоугольной изометрической и диметрической проекций пирамиды и точек на ее поверхности Данная пирамида связывается с натуральной прямоугольной системой координат Oxyz, для чего на комплексном чертеже наносятся проекции координатных осей (рис. 12.6).
Построение приведенной прямоугольной изометрии пирамиды:
1. Построить изометрические оси.
2. Построить изометрические проекции вершин пирамиды:Точка A лежит на оси Ox, поэтому для построения ее проекции достаточно отложить натуральную координату хА =O2A2=O1A1 в положительном направлении изометрической оси x. Для точки C сначала строят вспомогательную точку 1 на оси x, причем расстояние O111 =0’1’ откладывается в отрицательном направлении оси x, затем в положительном направлении оси y откладывают натуральную координату yc=11C1. Остальные вершины строятся аналогично.
3. Соединить построенные вершины и определить видимость ребер пирамиды.
4. Точка М лежит в грани ASB, следовательно, принадлежит прямой l, проходящей через вершину S и пересекающей ребро основания BC в точке 2. Для получения изометрической проекции точки M достаточно построить проекцию прямой l ′ и по координате zM построить M’ ∈ l’.
5. Прямоугольная приведенная диметрия строится аналогично, с учетом коэффициента искажения по оси y 0,5.
Рис. 12.6. Аксонометрические проекции пирамиды:
а – ортогональный чертеж;
б – прямоугольная изометрия;
в – прямоугольная диметрия
Аксонометрические проекции окружности
В общем случае окружность проецируется на аксонометрическую плоскость проекций в виде эллипса, большая ось (БОЭ) которого, в точной аксонометрии, равна диаметру окружности d, а малая (МОЭ) – d cos α, где α – угол наклона плоскости окружности к аксонометрической плоскости проекций.
Если окружность лежит в координатной плоскости или параллельна ей, то на аксонометрическом чертеже большая ось эллипса, изображающего окружность, располагается перпендикулярно той аксонометрической оси, которая отсутствует в наименовании плоскости окружности (рис. 12.7).
Например, если окружность расположена в плоскости П1 (xOy), в аксонометрии большая ось эллипса перпендикулярна оси z.
Размеры осей эллипсов в прямоугольных приведенных изометрии и диметрии даны в табл.1 (d – диаметр окружности).
Таблица 1 Размеры осей эллипсов
Определить размеры осей эллипса можно графически, пользуясь следующими треугольниками:
Изометрия : Строятся два прямоугольных треугольника с общим катетом 100мм и катетами 72мм и 122мм (рис. 12.8,а). На большем (горизонтальном) катете треугольника откладывается значение диаметра (радиуса) окружности и строится подобный треугольник.
- Меньший катет треугольника со сторонами 100 на 122 определяет большую ось эллипса.
- Меньший катет треугольника со сторонами 100 на 72 определяет малую ось эллипса.
Рис. 12.8. Треугольники для определения размеров осей эллипсов:
а – прямоугольная изометрия;
б – прямоугольная диметрия
Диметрия: Строятся три прямоугольных треугольника с общим катетом 100мм, на котором откладывается значение диаметра (радиуса) окружности (рис. 12.8,б).
Меньший катет треугольника со сторонами 100 на 106 определяет большую ось эллипса для всех аксонометрических плоскостей.
Меньший катет треугольника со сторонами 100 на 94 определяет малую ось эллипса для плоскости П2 (xOz).
Меньший катет треугольника со сторонами 100 на 35 определяет малую ось эллипса для плоскости П1 (xOy) и П3(zOy).
Построение эллипсов по восьми точкам
Построение эллипса как аксонометрической проекции окружности начинается с определения положения центра и направления большой и малой осей эллипса. Размеры большой и малой осей рассчитывают или определяют графически и откладывают на чертеже A’B’ большая ось, CD’ – малая. Затем через центр эллипса проводят вспомогательные прямые в направлении аксонометрических осей. В изометрии в направлении осей откладывается натуральный диаметр окружности 1-2 и 3-4.Полученные восемь точек соединяют плавной лекальной кривой. Построение изометрического эллипса по восьми точкам показано на рис. 12.9.
Рис. 12.9. Построение изометрического эллипса по восьми точкам:
А’В’= 1,22d- большая ось эллипса;
CD’=0,7d- малая ось эллипса;
1′-2′ – размер по оси x, равный диаметру окружности d;
3′-4′ – размер по оси y, равный диаметру окружности d
При построении диметрических эллипсов учитывается коэффициент искажения 0,5 направлении оси y. Построение диметрических эллипсов по восьми точкам показано на рис. 12.10.
Рис. 12.10. Построение диметрического эллипса по восьми точкам:
а – для окружностей в плоскостях Π1(xOy) и П3(zOy): БОЭ= 1,06 d-большая ось эллипса; МОЭ= 0,35 d-малая ось эллипса; 1′-2’=d-размер по оси x; 3′-4’=0,5d-размер по оси у;
б – для окружностей в плоскости П2(xOz): БОЭ=1,06 d-большая ось эллипса; МОЭ=0,94 d-малая ось эллипса; 1′-2’=d-размер по оси x; 3′-4’=d-размер по оси z.
Если восьми точек недостаточно, эллипс можно построить по двум осям (рис. 12.11). Этот способ можно применять и для построения эллипсов с произвольными размерами осей, например, для построения проекций окружности, лежащей в проецирующей плоскости.
Рис. 12.11. Построение эллипса по двум осям:
A’B’ – большая ось эллипса;
C’D’ – малая ось эллипса
Строят две окружности с диаметрами, равными большой и малой оси эллипса, и делят их радиальными отрезками нал частей. Затем из каждой точки пересечения большой окружности проводят вертикальные отрезки в сторону большой оси, а из точек пересечения с малой окружностью -горизонтальные отрезки в сторону от малой оси. Точки пересечения отрезков и являются точками эллипса. Полученные точки соединяют плавной лекальной кривой.
Построение овалов
Построение эллипсов требует применения лекал. На практике обычно вместо эллипсов вычерчивают четырехцентровые овалы.
Существует два способа построения четырехцентровых изометрических овалов. Для построения четырехцентрового овала по двум осям (рис. 12.12,а) из центра овала строят две окружности диаметрами равным и большой и малой осям эллипса. Точка пересечения большой окружности с направлением малой оси – центр большой дуги O’, радиус большой дуги R=O’D’. Точка 1′ – центр малой дуги, радиус малой дуги -r=1’A’. Точки 3’4′ – точки сопряжения. Затем строят дуги радиусов R и r между точками сопряжения.
Можно построить четырехцентровой овал используя только диаметр проецируемой окружности (рис. 12.12,б). Из центра овала строят направления большой и малой осей и окружность диаметром, равным диаметру проецируемой окружности. Из точки O’ пересечения окружности с направлением малой оси делят окружность на шесть частей.O’ -центр большой дуги овала. Отрезок O’1’=O’4’=R – радиус большой дуги, Точка O” пересечения отрезка O’4′ с направлением большой оси – центр малой дуги, отрезок O”4’=r- радиус малой дуги. Точки 1’2’3’4′ точки сопряжения. Затем строят дуги соответствующих радиусов между точками сопряжения.
Рис. 12.12. Построение четырехцентровых овалов в изометрии:
а – по двум осям: б- по диаметру окружности:
A B’ -большая ось эллипс AB’ – большая ось эллипса;
CD’-малая ось эллипса; CD’- малая ось эллипса;
O’ -центр большой дуги; O’ – центр большой дуги;
O” -центр малой дуги O” – центр малой дуги;
Диметрические эллипсы также можно заменить четырехцентровыми овалами. Построение диметрических овалов для окружностей в плоскостях, параллельных xOy и zOy показано на рис. 12.13.
Рис. 12.13. Построение диметрического овала в плоскости xOy:
A’B’ – большая ось эллипса;
C’D’ – малая ось эллипса;
O’ – центр большой дуги;
1′ – центр малой дуги;
R=O’D’ – радиус большой дуги;
r=1’A’ – радиус малой дуги;
2′ – точка сопряжения
Для построения овала, изображающего окружность в плоскостях, параллельных xOz,строят большую и малую оси и вспомогательную окружность, диаметром 0,2d (рис. 12.14). Точка 4′ – центр большой дуги, R=O’D’ – радиус большой дуги. Точка 1 ‘ – центр малой дуги, r=1 A’ – радиус малой дуги. Затем строят дуги радиусов R и r между точками сопряжения 5’6’7’8′.
Рис. 12.14. Построение диметрического овала в плоскости xOz:
A’B’ – большая ось эллипса;
C’D’ – малая ось эллипса
Графической работы
Прежде чем приступить к выполнению графической работы, необходимо изучить или повторить теоретическую часть курса.
Студент выполняет тот вариант задания, номер которого соответствует сумме двух последних цифр номера зачетной книжки. Например, если номер зачетной книжки студента 788133, то он во всех контрольных работах выполняет шестой вариант задания.
Каждая контрольная работа представляется на рецензию в полном объеме (необходимое число чертежей с пояснительными записками к ним). На каждую контрольную работу преподаватель кафедры составляет рецензию, в которой кратко отмечает достоинства и недостатки работы. Контрольную работу вместе с рецензией возвращают студенту, и она хранится у него до экзамена. Пометки преподавателя должны быть приняты студентом к исполнению. Если работа не зачтена, преподаватель в рецензии указывает, какую часть контрольной работы надо переделать, или выполнить всю контрольную работу вновь. На повторную рецензию следует высылать всю контрольную работу полностью. К выполнению следующей контрольной работы можно приступать, не ожидая ответа на предыдущую. Контрольные работы представляются на рецензию строго в сроки, указанные в учебном графике или определенные преподавателем.
Графические работы выполняются на листах чертежной бумаги формата А3 или А4(ГОСТ 2.301-68, см. табл.П1, рис. П1). Первая страница должна быть оформлена по образцу (см. рис. П2).
При графическом решении задач точность ответа зависит не только от выбора правильного пути ее решения, но и от точности выполнения геометрических построений, поэтому при выполнении графических работ необходимо пользоваться чертежными инструментами. Все основные и вспомогательные построения должны быть сохранены, все точки и линии на чертеже – обозначены, при этом обозначения следует делать в процессе решения.
Все надписи, буквенные и цифровые обозначения выполняются шрифтом чертежным в соответствии с ГОСТ 2.304-68 (см. рис. П4, П5). Линии видимого контура обводят сплошной толстой основной линией толщиной s=0,8-1mm, линии построений – сплошной тонкой линией толщиной от s/3 до s/2, осевые и центровые линии – штрихпунктирной линией, линии невидимого контура – штриховой в соответствии с ГОСТ 2.303-68 (см. табл. П2). Точки на чертеже вычерчиваются в виде окружностей диаметром 1,5…2мм.
Листы выполненной контрольной работы складывают до формата А4 (см. рис. П3), и высылают в конверте и на рецензию.
Построение линии пересечения треугольных пластин
Задание : Построить линию пересечения треугольных пластинАВСи DEK. Определить натуральную величину треугольника ABC.Данные по вариантам приведены в табл. 14.1.Графическую работу выполнить на листе чертежной бумаги формата А3.
Порядок выполнения работы:
1. Построить в тонких линиях двухкартинный комплексный чертеж треугольных пластин по заданным координатам вершин(рис. 14.1,а).
Рис. 14.1. Двухкартинный комплексный чертеж пластин:
а – наглядное изображение;б – комплексный чертеж
2. Пластины представляют собой ограниченные участки плоскостей общего положения α(ABC) и β(DEK) (рис. 14.1,б), следовательно, задача сводится к определению линии их пересечения. Линией пересечения плоскостей является прямая, для однозначного определения которой достаточно двух точек.
Первая точка – точка N(рис. 14.2), определяется как точка пересечения стороны DK треугольника DEK с плоскостью α(ABC) (первая позиционная задача, см.пп.8.8):
• прямую DK заключить во вспомогательную фронтальнопроецирующую плоскость γ(γ2) (см. рис. 14.2);
Рис. 14.2.Построение первой точки линии пересечения
• определить линию пересечения а вспомогательной плоскости γ(γ2) и плоскости α(ABC). Линия а строится по двум точкам:
точка 1 = γ(γ2) ×AB;
точка 2 = γ(γ2) ×AC.
• определить точку пересечения прямых а (а1, а2)и DK:
N1 =D1K1 × а1;
N2 =N1N2 × D2K2.
Вторую точку линии пересечения – точку M определить аналогично (рис. 14.3).При необходимости полученную линию нужно ограничить в области перекрытия проекций. Соединив полученные точки M и N, получить линию пересечения двух треугольных пластин.
Рис. 14.3.Построение второй точки линии пересечения
3. Определить видимость сторон методом конкурирующих точек (см.пп.7),считая пластины непрозрачными (рис. 14.4).
На горизонтальной плоскости конкурирующие точки находятся в точке наложения проекций сторон A1C1 и D1E1. При этом точка 5 принадлежит стороне AC, а точка 6 – стороне DE. Фронтальная проекция точки 6 лежит выше (ее высота больше, чем высота точки 5).Сторона DE видима полностью, а сторона AC невидима между точками, конкурирующими со сторонами DK и DE.Аналогично определить видимость остальных сторон. Сторона EK невидима между точками, конкурирующими со сторонами AB и BC.Сторона DK невидима от точки N до точки, конкурирующей со стороной BC. Сторона BCвидима полностью, а сторона AB невидима от точки Mдо точки, конкурирующей со стороной DE.
На фронтальной плоскости конкурирующие точки находятся в точке наложения проекций прямых A2B2 и D2K2. При этом точка 1 принадлежит прямой AB, а точка 7 – прямой DK. Горизонтальная проекция точки 7 лежит ниже (ее глубина больше, чем глубина точки 1), следовательно, на П2 видима сторона DK до точки N и за пределами общего объема пластин.
Сторона АВ невидима между точками M и 1.
Рис. 14.4.Определение видимости
Аналогично определить видимость остальных сторон. Стороны DE, AB и ВС видимы полностью. Сторона EK невидима между точками, конкурирующими со сторонами AB и BC.
4. Определить натуральную величину плоскости АВС и показать линию MN – линию его пересечения с плоскостью DEK.
Натуральную величину плоскости АВС определить способом плоскопараллельного движения(см. пп.11.2). Данная задача решается в два этапа: сначала плоскость переводится из общего положения в проецирующее, а затем – в положение плоскости уровня.
Сначала выполняется плоскопараллельное движение плоскости α(ABC) относительно плоскости проекций П1 (рис. 14.5):
• продлить линию MN до пересечения со стороной AC и получить линию ML;
• через точку Cпровести горизонталь h (h1,h2 )в плоскости ABC;
• горизонтальную проекцию h/1 вычертить без изменения на свободном поле чертежа, расположив ее так, как требуется для решения задачи, а именно чтобы она стала проецирующей прямой:
Рис. 14.5.Преобразование плоскости α(ABC) общего положения в положение проецирующей плоскости
• построить новую горизонтальную проекцию плоскости α/1(A/1B/1C/1), конгруэнтную горизонтальной проекции α1(A1B1C1), показав на ней линию пересечения MN:
|A/1B/1| = |A1B1|; |A/1C/1| = |A1C1|; |B/1C/1| = |B1C1|;
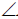
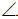
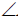
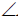
|A/1F /1| = |A1F1|; |A/1F /1| = |A1F1|;
|A/1M /1| = |A1M1|; |A/1B /1| = |A1B1|;
|A/1L /1| = |A1L1|; |A/1C/1| = |A1C1|;
|L/1N /1| = |L1N1|; |N/1M /1| = |N1M1|;
• фронтальные проекции точек A2, B2, C2 перемещаются по прямым -следам плоскостей движения точек σ2, η2 и μ2:
σ2∣∣η2∣∣μ2; σ2
• определить новую фронтальную проекцию плоскости α’2(A/2B /2C/2 ) по линиям связи на основании новой горизонтальной проекции плоскости α’1(A/1B /1C/1);
Вторым плоскопараллельным движением, но уже относительно плоскости проекций П2, плоскость α(ABC) преобразуется в горизонтальную плоскость уровня (рис. 14.6):
• построить новую фронтальную проекцию плоскости α//2(A//2B//2C//2 ) в виде горизонтального отрезка на свободном поле чертежа, для которого |C//2A//2| = |C/2A/2| и |A//2B//2|= |A/2B/2|
Рис. 14.6. Преобразование плоскости α(ABC) общего положения в положение плоскости уровня
• горизонтальные проекции точек A/1, B /1,C/1 перемещаются по прямым – следам плоскостей движения точек λ1, v1 и φ1:
λ1∣∣v1∣∣φ1; λ1
• определить новую горизонтальную проекцию плоскости α//1(A//1B//1C//1 ) по линиям связи на основании новой фронтальной проекции плоскости α//2(A//2B//2C//2 ).
Полученная горизонтальная проекция плоскости α//1(A//1B//1C//1 ) определяет ее натуральную величину: ∆ A//1B//1C//1 = |∆ ABC|.
5. Обвести в соответствии с типами линий, оформить работу. Пример выполнения графической работы приведен на рис. 14.7.
Рис. 14.7. Пример выполнения графической работы 1
Таблица 14.1 Задания для графической работы 1 (координаты и размеры, мм)
|
№ вар. |
Xa |
Уа |
Za |
Xb |
Ув |
Zb |
Xc |
Ус |
Zc |
Xd |
yD |
Zd |
Xe |
Уе |
Ze |
Xk |
Ук |
zκ |
|
1 |
117 |
90 |
9 |
52 |
25 |
79 |
0 |
83 |
48 |
68 |
110 |
85 |
135 |
19 |
36 |
14 |
52 |
0 |
|
2 |
120 |
90 |
10 |
50 |
25 |
80 |
0 |
85 |
50 |
70 |
110 |
85 |
135 |
20 |
35 |
15 |
50 |
0 |
|
3 |
115 |
90 |
10 |
52 |
25 |
80 |
0 |
80 |
45 |
64 |
105 |
80 |
130 |
18 |
35 |
12 |
50 |
0 |
|
4 |
120 |
92 |
10 |
50 |
20 |
75 |
0 |
80 |
46 |
70 |
115 |
85 |
135 |
20 |
32 |
10 |
50 |
0 |
|
5 |
117 |
9 |
90 |
52 |
79 |
25 |
0 |
48 |
83 |
68 |
85 |
110 |
135 |
36 |
19 |
14 |
0 |
52 |
|
6 |
115 |
7 |
85 |
50 |
80 |
25 |
0 |
50 |
85 |
70 |
85 |
110 |
135 |
20 |
20 |
15 |
0 |
50 |
|
7 |
120 |
10 |
90 |
48 |
82 |
20 |
0 |
52 |
82 |
65 |
80 |
110 |
130 |
38 |
20 |
15 |
0 |
52 |
|
8 |
116 |
8 |
88 |
50 |
78 |
25 |
0 |
46 |
80 |
70 |
85 |
108 |
135 |
36 |
20 |
15 |
0 |
52 |
|
9 |
115 |
10 |
92 |
50 |
80 |
25 |
0 |
50 |
85 |
70 |
85 |
110 |
135 |
35 |
20 |
15 |
0 |
50 |
|
10 |
18 |
10 |
90 |
83 |
79 |
25 |
135 |
48 |
82 |
67 |
85 |
110 |
0 |
36 |
19 |
121 |
0 |
52 |
|
11 |
20 |
12 |
92 |
85 |
89 |
25 |
135 |
50 |
85 |
70 |
85 |
110 |
0 |
35 |
20 |
120 |
0 |
52 |
|
12 |
15 |
10 |
85 |
80 |
80 |
20 |
130 |
50 |
80 |
70 |
80 |
108 |
0 |
35 |
20 |
120 |
0 |
50 |
|
13 |
16 |
12 |
88 |
85 |
80 |
25 |
130 |
50 |
80 |
75 |
85 |
110 |
0 |
30 |
15 |
120 |
0 |
50 |
|
14 |
18 |
12 |
85 |
85 |
80 |
25 |
135 |
50 |
80 |
70 |
85 |
110 |
0 |
35 |
20 |
120 |
0 |
50 |
|
15 |
18 |
90 |
10 |
83 |
25 |
79 |
135 |
83 |
48 |
67 |
110 |
85 |
0 |
19 |
36 |
121 |
52 |
0 |
|
16 |
18 |
40 |
75 |
83 |
117 |
6 |
135 |
47 |
38 |
67 |
20 |
0 |
0 |
111 |
48 |
121 |
78 |
86 |
|
17 |
18 |
75 |
40 |
83 |
6 |
107 |
135 |
38 |
47 |
67 |
0 |
20 |
0 |
48 |
111 |
121 |
86 |
78 |
|
18 |
117 |
75 |
40 |
52 |
6 |
107 |
0 |
38 |
47 |
135 |
0 |
20 |
86 |
48 |
111 |
15 |
68 |
78 |
Проекции пирамиды
Задание: Построить проекции пирамиды, основанием которой является треугольник ABC, а ребро SA определяет высоту H пирамиды. Данные по вариантам приведены в табл. 14.2.
Порядок выполнения работы:
6. Построить оси координат. По координатам вершин построить основание пирамиды ABC в тонких линиях (рис. 14.8).
Рис. 14.8. Построение основания пирамиды
7. В плоскости основания построить горизонталь h(h1h2)и фронталь 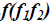
Рис. 14.9. Построение фронтали и горизонтали в плоскости основания
8. Высота пирамиды является перпендикуляром, проведенным из точки A к основанию пирамиды (см. пп. 10.3). Горизонтальную проекцию высоты пирамиды провести из точки A1 перпендикулярно горизонтальной проекции горизонтали плоскости h1, а фронтальную проекцию – из точки A2 перпендикулярно фронтальной проекции фронтали плоскости 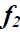
Рис. 14.10 Построение высоты пирамиды
9. Определить натуральную величину высоты пирамиды (рис. 14.11).
Рис. 14.11. Определение натуральной величины высоты пирамиды
Поскольку высота пирамиды является прямой общего положения, то способом вращения вокруг проецирующей прямой поворачиваем ее до положения линии уровня. Для этого на проекции перпендикуляра взять произвольную точку M. Прямую AM повернуть вокруг горизонтально-проецирующей прямой iдо положения фронтали:
A1M1‘ ||х12; M2M2‘
На прямой A2M2‘ отложить натуральную величину высоту пирамиды |A2S2‘|=85мм. Выполнить обратные преобразования и получить вершину пирамиды точку S.
10. Построить ребра пирамиды и определить видимость способом конкурирующих точек (рис. 14.12).
На П1 в качестве конкурирующих точек выбраны точки 1 и 2: 1 ∈(AC), 2∈(SB). Фронтальная проекция точки 2 расположена выше (z2>z1), поэтому ребро SB будет видимо, а ребро AC невидимо. Ребра SA, AB и BC будут также видимы.
Рис. 14.12. Определение видимости
На П2 в качестве конкурирующих точек выбраны точки 3 и 4: 3 ∈ (AB), 4 ∈ (SC) . Горизонтальная проекция точки 4 расположена ниже (y4>y3), поэтому ребро SC будет видимо, а ребро AB невидимо. Ребра SA, SB и BC будут также видимы.
11. Обвести в соответствии с типами линий, оформить работу. Пример выполнения графической работы приведен на рис. 14.13.
Рис. 14.13. Пример выполнения графической работы 2
Таблица 14.2 Задания для графической работы 2 (координаты и размеры, мм)
|
№ варианта |
Xa |
Уа |
Za |
Xb |
Ув |
Zb |
Xc |
Ус |
Zc |
H |
|
1 |
117 |
90 |
9 |
52 |
25 |
79 |
0 |
83 |
48 |
85 |
|
2 |
120 |
90 |
10 |
50 |
25 |
80 |
0 |
85 |
50 |
85 |
|
3 |
115 |
90 |
10 |
52 |
25 |
80 |
0 |
80 |
45 |
85 |
|
4 |
120 |
92 |
10 |
50 |
20 |
75 |
0 |
80 |
46 |
85 |
|
5 |
117 |
9 |
90 |
52 |
79 |
25 |
0 |
48 |
83 |
85 |
|
6 |
115 |
7 |
85 |
50 |
80 |
25 |
0 |
50 |
85 |
85 |
|
7 |
120 |
10 |
90 |
48 |
82 |
20 |
0 |
52 |
82 |
85 |
|
8 |
116 |
8 |
88 |
50 |
78 |
25 |
0 |
46 |
80 |
85 |
|
9 |
115 |
10 |
92 |
50 |
80 |
25 |
0 |
50 |
85 |
85 |
|
10 |
18 |
10 |
90 |
83 |
79 |
25 |
135 |
48 |
83 |
85 |
|
11 |
20 |
12 |
92 |
85 |
80 |
25 |
135 |
50 |
85 |
85 |
|
12 |
15 |
10 |
85 |
80 |
80 |
20 |
130 |
50 |
80 |
85 |
|
13 |
16 |
12 |
88 |
85 |
80 |
25 |
130 |
50 |
80 |
80 |
|
14 |
18 |
12 |
85 |
85 |
80 |
25 |
135 |
50 |
80 |
80 |
|
15 |
18 |
90 |
10 |
83 |
25 |
79 |
135 |
83 |
48 |
80 |
|
16 |
18 |
40 |
75 |
83 |
117 |
6 |
135 |
47 |
38 |
80 |
|
17 |
18 |
75 |
40 |
83 |
6 |
107 |
135 |
38 |
47 |
80 |
|
18 |
117 |
75 |
40 |
52 |
6 |
107 |
0 |
38 |
47 |
80 |
Проекции сферы с отверстием
Задание: Построить три проекции поверхности сферы со сквозным отверстием. Графическая работа выполняется на листе чертежной бумаги формата А3 (см. рис. П1).
Отверстие в поверхности сферы (рис. 14.14) выполнено четырьмя проецирующими плоскостями. Фронтальная проекция отверстия задана, необходимо построить горизонтальную и профильную проекции.
Рис. 14.14. Сфера с отверстием
Порядок выполнения работы:
1. По заданным размерам построить в тонких линиях трехкартинный комплексный чертеж поверхности сферы и фронтальную проекцию отверстия.
2. Определить недостающие проекции точки А и опорные точки 1 и 2 (рис. 14.15).
Рис. 14.15. Определение опорных точек
3. Построить следы секущих плоскостей (см. рис. 14.15). Построить проекции сечений сферы каждой плоскостью. Все сечения представляют собой окружности, которые проецируются на разные плоскости проекций в виде окружностей, отрезков или эллипсов:
Рис. 14.16. Построение сечений
• Сечение поверхности сферы плоскостью α(α2) представляет собой окружность, которая проецируется на фронтальную и профильную плоскости проекций в виде отрезков, а на горизонтальную – в виде окружности l(l1,l2) с центром в точке О(О1,О2) радиусом r. Граница отверстия определится дугой DD’ (рис. 14.16).
• Сечение поверхности сферы плоскостью β(β2) представляет собой окружность, которая проецируется на фронтальную и горизонтальную плоскости проекций в виде отрезков, а напрофильную – в виде окружностиm(m1,m2) с центром в точке О(О1,О2) радиусом r´. Граница отверстия определится дугами CD иC’D’(см. рис. 14.16).
• Построение сечения поверхности сферы плоскостью γ(γ2) аналогично сечению плоскостью α(α2). Граница отверстия определится дугами BC и В’С’ (см. рис. 14.16).
• Сечение поверхности сферы плоскостью δ(δ2) представляет собой окружность, которая проецируется на фронтальную плоскость проекций в виде отрезка, а напрофильнуюи горизонтальную – в виде эллипсов. Граница отверстия определится дугами эллипсов CD иC’D’(рис. 14.17).
Рис. 14.17. Построение эллипса
4. Определить видимость (рис. 14.18).На фронтальной проекции видны все границы отверстия. На горизонтальной проекции видна часть границы отверстия, расположенная выше точек 3 и 4. На профильной – правее точек 5 и 6.
Рис. 14.18. Определение видимости
5. Выполнить обводку. Образец выполнения графической работы представлен на рис. 14.19.
Таблица 14.3 Задания для графической работы 3 (координаты и размеры, мм)
|
№ вар. |
Xo |
yo |
Zo |
Xa |
Уа |
Za |
Xb |
Ув |
Zb |
Xc |
Ус |
Zc |
Xd |
yD |
Zd |
R |
|
1 |
70 |
58 |
62 |
118 |
— |
35 |
56 |
— |
95 |
45 |
— |
95 |
45 |
— |
35 |
46 |
|
2 |
70 |
60 |
60 |
118 |
— |
35 |
56 |
— |
95 |
44 |
— |
95 |
44 |
— |
35 |
46 |
|
3 |
70 |
60 |
58 |
120 |
— |
35 |
58 |
— |
95 |
44 |
— |
95 |
44 |
— |
35 |
18 |
|
4 |
70 |
60 |
58 |
120 |
— |
36 |
56 |
— |
94 |
42 |
— |
94 |
42 |
— |
36 |
48 |
|
5 |
69 |
58 |
60 |
116 |
— |
36 |
58 |
— |
94 |
45 |
— |
94 |
45 |
— |
36 |
47 |
|
6 |
72 |
60 |
58 |
116 |
— |
36 |
60 |
— |
92 |
42 |
— |
92 |
42 |
— |
36 |
47 |
|
7 |
72 |
58 |
60 |
120 |
— |
34 |
60 |
— |
92 |
42 |
— |
92 |
42 |
— |
34 |
48 |
|
8 |
72 |
58 |
58 |
122 |
— |
34 |
60 |
— |
90 |
40 |
— |
90 |
40 |
— |
34 |
45 |
|
9 |
74 |
62 |
60 |
122 |
— |
34 |
55 |
— |
90 |
40 |
— |
90/ |
40 |
— |
34 |
45 |
|
10 |
69 |
58 |
60 |
20 |
— |
36 |
81 |
— |
94 |
94 |
— |
94 |
94 |
— |
36 |
47 |
|
11 |
74 |
62 |
58 |
20 |
— |
36 |
80 |
— |
92 |
94 |
— |
92 |
94 |
— |
36 |
47 |
|
12 |
72 |
62 |
62 |
20 |
— |
35 |
80 |
— |
92 |
92 |
— |
92 |
92 |
— |
36 |
48 |
|
13 |
72 |
60 |
62 |
22 |
— |
35 |
82 |
— |
90 |
92 |
— |
90 |
92 |
— |
35 |
48 |
|
14 |
70 |
60 |
60 |
18 |
— |
35 |
82 |
— |
90 |
90 |
— |
90 |
90 |
— |
35 |
48 |
|
15 |
70 |
60 |
58 |
18 |
— |
34 |
82 |
— |
94 |
92 |
— |
94 |
90 |
— |
34 |
50 |
|
16 |
72 |
62 |
58 |
20 |
— |
34 |
84 |
— |
94 |
96 |
— |
94 |
96 |
— |
34 |
60 |
|
17 |
70 |
62 |
60 |
18 |
— |
32 |
84 |
— |
90 |
96 |
— |
90 |
96 |
— |
32 |
50 |
|
18 |
68 |
60 |
60 |
20 |
— |
32 |
86 |
— |
92 |
95 |
— |
92 |
95 |
— |
32 |
50 |
Рис. 14.19. Пример выполнения графической работы 3
Сечение комбинированной поверхности проецирующей плоскостью
Задание: Построить сечение комбинированной поверхности вращения плоскостью фронтально-проецирующей плоскостью α(α2). Графическая работа выполняется на листе чертежной бумаги формата А4 (см. рис. П1).
Комбинированная поверхность состоит из полусферы и конуса (рис. 14.20). В сечении полусферы получается дуга окружности, а в сечении конуса -часть эллипса (см. пп. 8.16).
Рис. 14.20. Сечение поверхности плоскостью
Порядок выполнения работы:
1. Построить в тонких линиях двухкартинный комплексный чертеж поверхности и след секущей плоскости.
2. Определить опорные точки (рис. 14.21):
Рис. 14.21. Определение опорных точек
• 1 – точка пересечения плоскости α(α2) с очерковой образующей полусферы;
• 2 и 3 – точки пересечения плоскостиα(α2) с плоскостью нижнего основания полусферы;
• 4 и 5 – точки пересечения плоскости α(α2) с плоскостью верхнего основания конуса;
• 6 и 7 – точки пересечения плоскости α(α2) с плоскостью нижнего основания конуса;
• точки 8 и 9, лежащие на образующих, проекции которых совпадают с осью конуса также являются опорными. Эти точки строятся при помощи вспомогательной плоскости уровня γ(γ2), которая рассекает поверхность конуса по линии n,
n = Фк 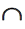
а плоскость α(α2) – по фронтально-проецирующей прямой p:
p = α(α2)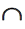
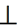
3. Определить промежуточные точки (рис 14.22). Для этого провести вспомогательную плоскость уровня δ(δ2) между опорными точками.
Рис. 14.22. Определение промежуточных точек и видимости
Эта плоскость рассекает поверхность сферы по линии m:
m = Фк 
а плоскость α(α2) – по фронтально-проецирующей прямой q:
q= α(α2) 
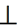
Точки 12 и 13 определить аналогично, с помощью вспомогательной плоскости σ(σ2). Полученные точки соединить плавной лекальной кривой s.
4. Определить видимость линии пересечения s относительно поверхности (см. рис. 14.22). В данном случае видимость определяется только на горизонтальной плоскости проекций. Границей видимости является основание полусферы, таким образом, видимы только точки 1, 2, 3, 10 и 11, лежащие на поверхности полусферы. Точки 2 и 3 – точки смены
видимости.
5. Определить натуральную величину плоскостей проекций (см. пп. 11.1).
Рис. 14.23. Определение натуральной величины сечения
В данном случае выполняется замена горизонтальной плоскости проекций П1 на плоскость П4(рис. 14.23). Плоскость П4 выбирается так, чтобы в системе плоскостей П1/П4 плоскость азаняла положение плоскости уровня:
• Провести ось х 14 параллельно фронтальному следу плоскости;
• Построить вспомогательные точки A, B, C, D и Е на оси симметрии сечения;
• Провести линию связи A2A4 перпендикулярно оси х14 и отложить на ней расстояние yA от оси х14;
• Точки 6 и 7 лежат на линии связи A2A4. Для построения точки 6 отложить по линии связи A2A4 расстояние y6 от оси х14;
• Аналогично построить точки 14, 124, 84, 44,24, 104;
• Точки 74, 134, 94, 54, 44, 114 строятся симметрично относительно оси сечения;
• Соединить полученные точки плавной лекальной кривой.
6. Нанести штриховку сплошными тонкими линиями под углом 45°. Если какие-либо линии сечения наклонены под углом, близким к 45° допускается наносить штриховку под углом 30° или 60°. Пример выполнения графической работы приведен на рис. 14.24.
Рис. 14.24. Пример выполнения графической работы 4
Таблица 14.4 Задания для графической работы 4 (координаты и размеры, мм)
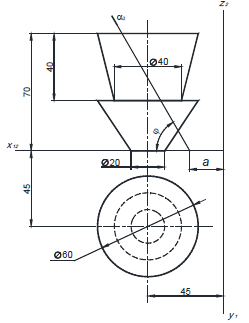 |
Вариант 1: a=20; φ=60° Вариант 2: a=15; φ=45° Вариант 3: a=35; φ=60° |
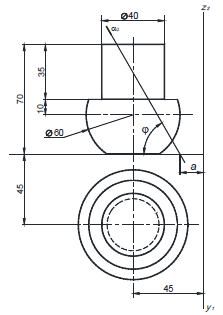 |
Вариант 4: a=15; φ=60° Вариант 5: a=5; φ=45° Вариант 6: a=35; φ=60° |
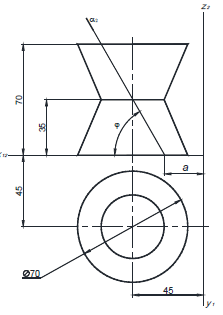 |
Вариант 7: a=20; φ=60° Вариант 8: a=15; φ=45° Вариант 9: a=35; φ=60° |
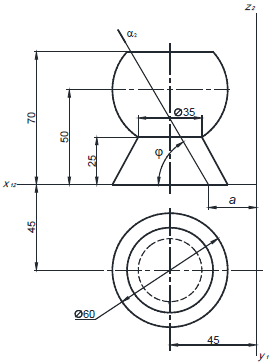 |
Вариант 10: a=25; φ=60° Вариант 11: a=30; φ=75° Вариант 12: a=15; φ=45° |
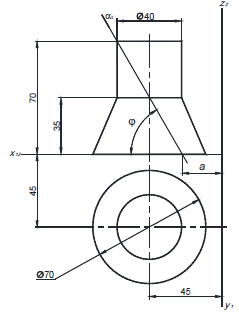 |
Вариант 13: a=25; φ=60° Вариант 14: a=10; φ=60° Вариант 15: a=5; φ=45° |
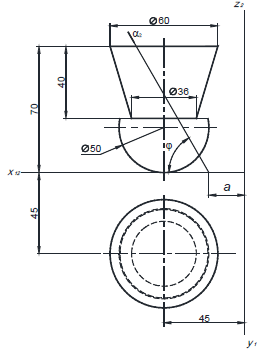 |
Вариант 16: a=20; φ=60° Вариант 17: a=15; φ=45° Вариант 18: a=20; φ=45° |
Пересечение поверхностей
Задание: Построить линию пересечения поверхностей прямого кругового конуса и прямого кругового цилиндра (рис. 14.25).Графическая работа выполняется на листе чертежной бумаги формата А4.
В данном примере линия пересечения поверхностей на плоскости П2 совпадает с очерком цилиндра, поэтому фактически остается построить линию пересечения на плоскости П1.
Рис. 14.25. Пересечение поверхностей:
а – наглядное изображение; б – комплексный чертеж
Порядок выполнения работы:
1. По заданным размерам построить горизонтальную и фронтальную проекции поверхностей в тонких линиях (см. рис. 14.26, б).
2. Определить опорные точки (рис. 14.26).
Конус и цилиндр имеют общую плоскость симметрии μ(μ1), параллельную плоскости П2. Поэтому точки 1, 5,5 ´u 6 линии пересечения получаются как результат пересечения очерковых образующих конуса и цилиндра.
Рис. 14.26. Определение опорных точек линии пересечения поверхностей
Также к опорным точкам относятся точки 3 и 3΄ (рис. 14.27). Они являются точками смены видимости линии пересечения на горизонтальной плоскости проекций.
Рис. 14.27. Определение точек смены видимости линии пересечения поверхностей
Для определения этих точек нужно провести горизонтальную плоскость уровня β(β2). Плоскость β(β2) пересекает цилиндр по образующей – прямойb, а конус – по окружности n, радиусом r:
b(b1 ,b2)=Фц ∩β(β2); n(n1 ,n2)=Фк∩β(β2).
Построив горизонтальные проекции прямой bи окружностиn, определить точки их пересечения 3 и 3′:
31, 3′1=b1×n1;32, 3′2=3132nβ2.
3. Промежуточные точки линии пересечения также определяют с помощью горизонтальных плоскостей уровня.
Фронтальные плоскости уровня пересекают поверхность прямого кругового конуса по гиперболам, следовательно, для решения данной задачи нужно применить горизонтальные плоскости уровня, которые рассекают обе поверхности по простым линиям: конус – по окружностям, а цилиндр – по
прямым линиям.
Более подробно разберем построение точек 2 и 2′ (рис. 14.28).Для их определения надо пересечь обе поверхности вспомогательной горизонтальной плоскостью уровня α(α2). Плоскость α(α2) пересекает конус по окружности m радиусом r´, а цилиндр – по прямой a:
m(m1, m2)Φκ∩α(α2);a(a1, a2)Φц∩α(α2).
Построив горизонтальные проекции прямой а и окружности m, определить точки их пересечения C и C’:
21, 2′1= a1×m1; 21, 2′1=2122∩ α2.
Рис. 14.28. Определение промежуточных точек линии пересечения поверхностей
Аналогичным образом определяют точки 4 и 4/, формирующие линию пересечения (см. рис. 14.28). Они получены с помощью горизонтальной плоскости уровня γ(γ2).
Количество вспомогательных плоскостей должно быть достаточным для определения характера линии пересечения. Пределы этих плоскостей по высоте определяют высшая и низшая опорные точки линии пересечения поверхностей.
4. Последовательно соединить одноименные проекции полученных точек тонкой плавной лекальной кривой, причем полученная линия не должна выходить за пределы области перекрытия проекций данных поверхностей (рис. 14.29).
Рис. 14.29. Получение линии пересечения поверхностей
5. Определить видимость линии пересечения поверхностей и их очерковых образующих (рис. 14.30).
На горизонтальной плоскости проекций видимость линии пересечения определяется по поверхности цилиндра. Видимы будут те точки линии пересечения, которые на П2 расположены выше плоскости β2 – точки 1, 2,2′, 3 и 3‘. Точки 3 и За являются точками смены видимости линии пересечения на П1 Очерковая образующая цилиндра будет невидима между точками 3 и 3′. Поскольку основание конуса расположено ниже цилиндра, оно будет невидимо под проекцией цилиндра.
На фронтальной плоскости проекций видимы будут те точки линии пересечения, которые лежат перед плоскостью симметрии μ(μι) – точки 1,2, 3,4, 5 и 6.Образующая конуса будет невидима между точками 1 и 6, т.к. она находится внутри цилиндра. Очерковая образующая цилиндра видима полностью.
Рис. 14.30. Определение видимости линии пересечения поверхностей
6. Обвести в соответствии с типами линий, оформить работу. Пример выполнения графической работы приведен на рис. 14.31.
Таблица 14.5 Задания для графической работы 5 (координаты и размеры, мм)
|
№вар. |
Xk |
Ук |
Zk |
R |
h |
Xe |
УЕ |
Ze |
Ri |
|
1 |
80 |
70 |
0 |
45 |
100 |
50 |
70 |
32 |
35 |
|
2 |
80 |
70 |
0 |
45 |
100 |
50 |
70 |
32 |
30 |
|
3 |
80 |
72 |
0 |
45 |
100 |
53 |
72 |
32 |
32 |
|
4 |
80 |
72 |
0 |
45 |
100 |
60 |
72 |
35 |
35 |
|
5 |
70 |
70 |
0 |
44 |
102 |
50 |
70 |
32 |
32 |
|
6 |
75 |
70 |
0 |
45 |
98 |
65 |
70 |
35 |
35 |
|
7 |
75 |
70 |
0 |
45 |
98 |
70 |
70 |
35 |
35 |
|
8 |
75 |
72 |
0 |
45 |
98 |
75 |
72 |
35 |
35 |
|
9 |
75 |
72 |
0 |
43 |
98 |
80 |
72 |
35 |
35 |
|
10 |
75 |
75 |
0 |
44 |
102 |
50 |
75 |
35 |
35 |
|
11 |
80 |
75 |
0 |
43 |
102 |
85 |
75 |
36 |
36 |
|
12 |
80 |
75 |
0 |
43 |
102 |
85 |
75 |
40 |
35 |
|
13 |
80 |
75 |
0 |
42 |
102 |
80 |
75 |
40 |
35 |
|
14 |
80 |
70 |
0 |
42 |
102 |
80 |
70 |
40 |
32 |
|
15 |
80 |
70 |
0 |
42 |
100 |
75 |
70 |
40 |
32 |
|
16 |
70 |
72 |
0 |
43 |
100 |
75 |
72 |
42 |
32 |
|
17 |
70 |
72 |
0 |
44 |
100 |
70 |
72 |
40 |
32 |
|
18 |
70 |
74 |
0 |
44 |
100 |
70 |
74 |
36 |
32 |
Рис. 14.30. Пример выполнения графической работы
Аксонометрические чертежи
Аксонометрические чертежи применяют, в основном, для усиления наглядности изображаемого на комплексном чертеже объекта.
Для построения аксонометрического чертежа в пространстве выбирается некоторая ортогональная система Oxyz (натуральная система) и объект Ф, жестко с ней связанный. На каждой из осей координат откладывается единичный отрезок: 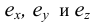
Расстояния каждой точки объекта до координатных плоскостей, измеренные единичным отрезком е, дают три числа (натуральные координаты точки), которые определяют ее положение относительно данной системы координат.
Объект вместе с системой отнесения проецируется параллельно на плоскость П’— аксонометрическую (картинную) плоскость проекций.
Проекции всех геометрических элементов на плоскость П’ получили название аксонометрических.
В зависимости от способа проецирования (центрального, параллельного или прямоугольного) получают различные виды аксонометрических проекций: центральную, параллельную косоугольную или прямоугольную аксонометрии.
Аксонометрические проекции геометрических элементов на координатные плоскости называют вторичными проекциями.
Аксонометрическую координатную ломаную можно построить, если даны аксонометрическая проекция точки и одна из ее вторичных проекций.
В процессе построения аксонометрических чертежей возникает на вопрос: «Каким образом следует задавать на картинной плоскости аксонометрические оси и аксонометрические масштабные единицы? »
Ответ на него дает основная теорема параллельной аксонометрии (теорема Польке), которая утверждает следующее.
В косоугольной аксонометрии аксонометрические оси на плоскости чертежа и единичные отрезки на них могут быть выбраны совершенно произвольно.
Это означает, что, задав на картинной плоскости три проходящие через одну точку несовпадающие прямые 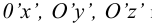
Из теоремы следует, что аксонометрическая система в общем случае определяется пятью независимыми параметрами: тремя аксонометрическими единичными отрезками и двумя углами между аксонометрическими осями.
В зависимости от соотношений между аксонометрическими единичными отрезками параллельные аксонометрические проекции классифицируют как триметрические 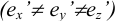
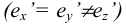
Для большего удобства построений в аксонометрии вводится понятие показателей искажения. Показатель искажения для отрезка данного направления определяют как отношение величины аксонометрической проекции отрезка к его натуральной величине.
Для построения аксонометрической проекции фигуры достаточно знать три показателя искажения вдоль координатных осей. Показатели искажения по осям обозначают буквами 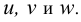
Прямоугольная аксонометрия
Аксонометрическая проекция, полученная при прямоугольном проецировании, называется прямоугольной или ортогональной аксонометрией. В прямоугольной аксонометрии теорема Польке не имеет места.
Для прямоугольной аксонометрии характерно следующее (рисунок 9.2):
- а) в прямоугольной аксонометрии высоты треугольника следов лежат на аксонометрических осях ;
- б) треугольник следов всегда остроугольный;
- в) три выходящие из одной точки (на плоскости) вектора могут быть приняты за оси прямоугольной аксонометрии только в том случае, если они образуют между собой тупые углы;
- г) сумма квадратов показателей искажения равна двум:
В прямоугольной аксонометрии аксонометрические оси являются биссектрисами углов треугольника, cmopоны которого пропорциональны квадратам показателей искажения.
Прямоугольная аксонометрия определяется двумя параметрами: двумя показателями искажения или двумя углами между аксонометрическими осями.
Рисунок 9.2 – Свойства прямоугольной аксонометрии
Практические аксонометрии
При практическом построении аксонометрических чертежей возникает необходимость в определении длины аксонометрических координатных отрезков по их натуральным координатам.
С целью сокращения вычислительной работы путем подбора некоторого множителя т можно один из показателей привести к единице и пересчитать остальные два. В отличие от точных показателей искажения новые показатели называют приведенными, а подобранный множитель — коэффициентом приведения.
Обозначают приведенные __ у. показатели искажения прописными буквами U, V и W} причем
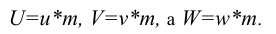
Изображение при этом изменяется подобно в масштабе m: 1. Такая аксонеметрическая проекция называется практической или приведенной.
Для практических аксонометрических систем углы между осями и показатели искажения зафиксированы в общесоюзных государственных стандартах (приложение к ГОСТ 2.317- 69) и эти виды проекций называют стандартными.
Прямоугольная изометрическая проекция. Из равенства углов наклона координатных осей к картинной плоскости следует, что 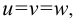
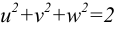
Для упрощения построений пользуются практической (приведенной) изометрией. Приведенные показатели искажения u=V=W = 1. В этом случае на аксонометрических осях откладывают натуральные координатные отрезки. Коэффициент приведения m = 1/0,82 = 1,22. Следовательно, в приведенной прямоугольной изометрии изображение увеличено в 1,22 раза.
В отличие от косоугольных изометрий, прямоугольная изометрия только одна.
В силу свойства прямоугольной изометрии все эллипсы, служащие проекциями окружностей, расположенных в плоскостях, параллельных координатным плоскостям, имеют одинаковую форму. В точной изометрии (для всех эллипсов) большая ось равна диаметру, малая 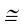
В прямоугольной диметрии две координатные оси (обычно Oz и Оу) наклонены под одинаковыми углами к картинной плоскости, а третья ось направлена так, что показатель искажения вдоль нее вдвое меньше. Например, v=w и u=v/2.
Косоугольных диметрических систем с заданным соотношением показателей искажения существует бесчисленное множество; прямоугольная диметрия — только одна.
Наибольшее распространение получила приведенная диметрия (рисунок 9.4), у нее коэффициенты искажения соответственно равны 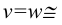
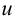
Для получения практической (стандартной) диметрии показатели искажения v и W приравниваются к единице, полагая (m = 1/0,94=1,06) V=W=1 и U=0,5. Масштаб практической диметрии Ml,06:1.
Величина малой оси эллипсов, расположенных в плоскостях Оху и Oxz, равна 1/3 от диаметра окружности, величина большой оси – диаметр. В стандартной диметрии соответственно 0,35 и 1,06 диаметра (рисунок 9.4).
Для эллипса, расположенного в плоскости Oyz, малая ось равна 0,94 диаметра.
Иногда, при решении практических задач, возникает необходимость построения аксонометрического чертежа, в котором одна из координатных плоскостей была бы параллельна картинной плоскости. Это возможно только в случае использования косоугольного проецирования.
Наиболее распространена косоугольная фронтальная диметрия, в которой плоскость xOz параллельна картинной плоскости. На такой проекции аксонометрические оси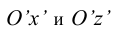
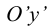
ГОСТ рекомендует направление оси 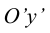
В различных отраслях практической деятельности применяются и другие виды косоугольных проекций, например, кавальерная (косоугольная изометрическая фронтальная проекция), военная перспектива (горизонтальная изометрическая проекция рисунок 9.6) и др.
Объясняю:
Прямоугольные проекции предмета на взаимно перпендикулярные плоскости проекций по методу Г. Монжа позволяют точно передать на чертеже форму предмета и его размеры, просты в построении, но не обладают наглядностью. Создание в уме по комплексному чертежу пространственного образа изображенного предмета требует навыков аналитического мышления и наличия пространственного воображения, т. е. достаточно развитого пространственного мышления.
Для наглядного изображения предмета существуют проекции, которые называют аксонометрическими проекциями, или аксонометриями (в переводе с древнегреческого – осеизмерение).
Аксонометрическая проекция – это параллельная проекция предмета вместе с системой прямоугольных координат, к которым этот предмет отнесен в пространстве, на некоторую плоскость аксонометрических проекций (рис. 10.1).
Чтобы обеспечить наглядность предмета по одному изображению на одной аксонометрической плоскости, направление проецирования (направление проецирующих лучей) не должно быть параллельным координатным плоскостям проекций xOy, xOz и zOy, относительно которых выполняются проекции предмета на чертеже.
Систему прямоугольных координат Oxyz, к которой предмет относят в пространстве для построения его аксонометрии, выбирают обычно так, чтобы оси x, y и z этой системы совпадали с натуральной системой координатных осей чертежа.
Аксонометрические проекции как проекции параллельные имеют некоторые свойства параллельных проекций:
- – аксонометрическая проекция отрезка прямой также является прямой;
- – если отрезки прямых параллельны на предмете, они также параллельны на его аксонометрической проекции;
- – аксонометрической проекцией окружности на аксонометрии в общем случае является эллипс.
На рис. 10.1 показана схема проецирования точки А, построенной на чертеже в системе натуральных прямоугольных координат Оxyz и отнесенную к этим же координатам, на некоторую плоскость аксонометрических проекций α по направлению проецирования S.
Положение точки А определяется в этой системе пространственной координатной ломаной O-Ax-A’-A, отрезки которой соответствуют координатам x, y и z точки А. На взятой произвольно плоскости аксонометрических проекций α получены три прямые xα, yα и zα, выходящие из одной точки Oα, которые называются аксонометрическими осями и являются проекциями пространственных координатных осей x, y и z, к которым отнесена точка А. Полученные углы между аксонометрическими осями зависят от положения аксонометрической плоскости и угла проецирования к этой плоскости. На аксонометрии положение точки Аα определяет плоская координатная ломаная Оα-Аxα-Ao‘-Aα, отрезки которой соответствуют аксонометрическим координатам xα, yα и zα аксонометрической проекции точки А(Аα).
Поскольку направление проецирования S не параллельно ни одной из осей системы прямоугольных пространственных координат, то истинные размеры отрезков пространственной координатной ломаной О-Аx-A’-A на аксонометрической проекции искажаются и, следовательно, искажаются размеры любого предмета на его аксонометрическом изображении.
Для определения степени искажения размеров предмета на аксонометрических проекциях введено понятие коэффициентов искажения по аксонометрическим осям.
Если на осях x, y и z системы натуральных прямоугольных координат отложить от точки О равные масштабные отрезки ex = ey = ez, то в системе аксонометрических координатных осей получаются искаженные проекции этих отрезков еxα, еyα и ezα.
Отношения аксонометрических проекций масштабных отрезков к натуральным величинам масштабных отрезков и называются коэффициентами искажения по аксонометрическим осям:
Расчетные коэффициенты искажения имеют дробные значения, неудобные для выполнения аксонометрических построений (0,82; 0,47 и т. д.).
Для построения на чертежах аксонометрических проекций пользуются так называемыми приведенными коэффициентами искажения, округленными до 1 или 0,5.
Математические (тригонометрические) расчеты величин коэффициентов искажения, углов между аксонометрическими осями, расположение и размеры больших и малых осей эллипсов здесь не рассматриваются (подробнее об этом см. в [12]).
В зависимости от соотношения коэффициентов искажения аксонометрические проекции разделяются на:
- а) изометрические, у которых все коэффициенты искажения равны, т. е. Kx = Ky = Kz (izos – равный);
- б) диметрические, у которых два коэффициента равны, т. е. Kx = Kz, а Ky им не равен (di – двойной);
- в) триметрические, у которых все коэффициенты разные, т. е.
(treis – три).
В зависимости от угла наклона проецирующих лучей к плоскости аксонометрических проекций (угла проецирования), аксонометрические проекции разделяются на:
- а) прямоугольные – проецирующие лучи перпендикулярны аксонометрической плоскости проекций (угол проецирования равен 90°);
- б) косоугольные – проецирующие лучи не перпендикулярны аксонометрической плоскости проекций (угол проецирования не равен 90°).
Аксонометрических проекций можно получить бесконечное множество, как может быть бесконечно количество аксонометрических плоскостей проекций и направлений проецирования к ним.
Основная теорема аксонометрических проекций была сформулирована немецким геометром К. Польке: «Любые три отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельные проекции (то есть аксонометрические проекции) трех равных и взаимно перпендикулярных отрезков (аксонометрических осей) в пространстве».
Г. Шварц, немецкий математик, обобщил теорему К. Польке, доказав, что «любой полный четырехугольник на плоскости всегда является параллельной проекцией некоторого масштабного тетраэдра (пирамиды), имеющего равные и взаимно перпендикулярные ребра» (диагонали четырехугольника можно рассматривать как аксонометрические оси, рис. 10.2). Эту обобщенную теорему и называют теоремой Польке-Шварца.
Стандартные аксонометрии
ГОСТ 2.317–2011 – «Аксонометрические проекции». Математические (тригонометрические) расчеты величин коэффициентов искажения, углов между аксонометрическими осями, расположение и размеры больших и малых осей эллипсов здесь, как указывалось, не рассматриваются (подробнее об этом см. в [12]).
В стандарте даны пять видов аксонометрических проекций:
- Прямоугольная изометрия.
- Прямоугольная диметрия.
- Косоугольная фронтальная диметрия.
- Косоугольная фронтальная изометрия.
- Косоугольная горизонтальная изометрия.
В курсе начертательной геометрии рассматриваются первых три вида аксонометрических проекций.
Окружности на проекциях предметов проецируются на аксонометрическое изображение предмета в виде эллипсов. Различные графические способы построения четырехцентровых овалов, которыми заменяют эллипсы, окружности которых лежат в плоскостях, параллельных плоскостям проекций V, H и W, рассматриваются в учебниках по черчению и инженерной графике. Эллипсы, окружности которых лежат в плоскостях, непараллельных плоскостям проекций, строятся на аксонометриях в основном по точкам, принадлежащих этим окружностям.
Прямоугольная изометрия
В прямоугольной изометрии аксонометрические оси расположены под равными углами друг к другу (120°).
Для прямоугольных аксонометрий получена расчетная формула по коэффициентам искажения:
т. е. сумма квадратов коэффициентов искажения равна двум [12].
В прямоугольной изометрии коэффициенты искажения равны и по приведенной формуле получается, что Kx = Ky = Kz = 0,82. Для построения прямоугольной изометрии пользуются приведенными коэффициентами искажения, округленными до единицы, то есть
Кx = Ky = Kz = 1.
Аксонометрическая плоскость прямоугольной изометрии равнонаклонена ко всем трем плоскостям проекций H, V и W и пересекает эти плоскости проекций по равностороннему треугольнику, который называют треугольником следов. Следовательно, аксонометрические оси прямоугольной изометрии являются высотами, биссектрисами и медианами этого треугольника, а точка Оα их пересечения является точкой начала аксонометрических координат. Как известно из геометрии, углы между высотами равностороннего треугольника равны 120 градусам и соответственно углы между аксонометрическими осями также равны 120°.
На рис. 10.3 показано расположение аксонометрических осей в прямоугольной изометрии (ось «z» всегда располагается вертикально), размеры и расположение больших и малых осей эллипсов и их построение одним из известных способов.
Большие оси АВ всех трех эллипсов равны 1,22d, где d – диаметр окружности, а малые оси EF эллипсов равны 0,71d.
Ориентация больших и малых осей эллипсов относительно аксонометрических осей:
- – эллипс 1 : аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций V: большая ось эллипса перпендикулярна аксонометрической оси y, а малая ось совпадает с осью y;
- – эллипс 2 : аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций H: большая ось эллипса перпендикулярна аксонометрической оси z, а малая ось совпадает с осью z;
- – эллипс 3 : аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций W: большая ось эллипса перпендикулярна аксонометрической оси x, а малая ось совпадает с осью x.
На рис. 10.3 показан один из способов построения четырех центровых овалов, которыми на чертежах заменяют эллипсы в прямоугольной изометрии.
Графические действия для построения овалов следующие:
- – провести две концентрические окружности, диаметры которых равны размерам большой и малой оси эллипса с центром в точке O2;
- – из двух центров в точках 1, лежащих на окружности большой оси, провести две большие дуги радиусами R = 1Е и R = 1F;
- – из точек 1 провести прямые n через точки 2, лежащие на окружности малой оси;
- – на пересечении проведенных дуг и прямых n получить точки 3, которые определяют окончание больших дуг;
- – из двух центров в точках 2 провести две малые дуги радиусами r = 2A и r = 2B до точек 3.
Прямоугольная диметрия
В прямоугольной диметрии коэффициенты искажения по аксонометрическим осям x и z равны между собой, а коэффициент искажения по оси y принят равным их половине. Отсюда по приведенной формуле (1) получены следующие величины коэффициентов искажения по аксонометрическим осям: Kx = Kz = 0,94, а Ky = 0,47. Для построения прямоугольной диметрии пользуются приведенными коэффициентами искажения, округленными и равными: Kx = Kz = 1, а Ky = 0,5.
Аксонометрические оси по математическим расчетам располагаются относительно горизонтальной линии следующим образом: ось z расположена вертикально, ось x – под углом 7°10′, ось y – под углом 41°25′.
На рис. 10.4 показано расположение аксонометрических осей и способ графического построения углов между осями, размеры и расположение больших и малых осей эллипсов и способы построения четырех центровых овалов, заменяющих эллипсы на чертеже.
1. Графический способ построения аксонометрических осей на чертеже:
- – провести горизонтальную линию и вертикальную ось Z и отметить на их пересечении точку O начала координат;
- – отложить на горизонтальной линии от точки O влево (или вправо) 8 размерных единиц (8 раз по 10 мм) и провести вертикальную линию;
- – от конечной точки отложить вниз 1 размерную единицу, а вверх 7 размерных единиц;
- – через конечные точки вертикальных отрезков и точку O провести аксонометрические оси X и Y.
2. Большие оси АВ всех трех эллипсов равны 1,06d, а величины малых осей EF эллипсов следующие:
- – малая ось эллипса 1 равна 0,95d;
- – малые оси эллипсов 2 и 3 равны 0,35d.
Ориентация больших и малых осей эллипсов относительно аксонометрических осей:
- – эллипс 1 : аксонометрическая проекция окружности, лежащей на проекциях предмета в плоскости, параллельной плоскости проекций V: большая ось эллипса перпендикулярна оси y, а малая ось эллипса совпадает с осью y;
- – эллипс 2 : проекция окружности, лежащей в плоскости, параллельной плоскости проекций H: большая ось эллипса перпендикулярна оси z, а малая ось совпадает с осью z;
- – эллипс 3 : проекция окружности, лежащей в плоскости, параллельной плоскости проекций W: большая ось эллипса перпендикулярна оси x, а малая ось совпадает с осью x.
Графические действия для построения овала 1 с центром в точке О1:
- – отложить на прямой, перпендикулярной оси y, отрезок AB, равный размеру большой оси эллипса Do = 1,06d;
- – отложить на оси y отрезок EF, равный размеру малой оси эллипса do = 0,95d;
- – из точки О1 провести окружность d1=0,2d, которая пересечет малую ось эллипса в точках 1 и 1o, а большую ось в точках 2 и 2o;
- – из полученных точек 1 и 1o провести дуги радиусами R от точки 1 до точки F и от точки 1o до точки E; из точек 2 и 2o провести дуги радиусами r от точки 2o до точки A и от точки 2 до точки B;
- – дуги проводить до точек сопряжения 3 (построение показано).
Графические действия для построения овала 2 с центром в точке О2:
- – отложить на горизонтальной прямой, перпендикулярной оси Z, отрезок AB, равный размеру большой оси эллипса 1,06d;
- – отложить на продолжении оси Z отрезок EF, равный размеру малой оси 0,35d;
- – отложить на оси y отрезок EF, равный размеру малой оси эллипса do=0,95d;
- – построить точки 1, отложив от точки О2 вверх и вниз по оси Z отрезки О2-1, равные большой оси эллипса Do = 1,06d;
- – построить точки 2 на большой оси, отложив от точек А и В отрезки А-2 и В-2, равные 1/4 малой оси эллипса do;
- – из полученных точек 1 провести две большие дуги радиусом R = Do + 1/2do, а из точек 2 провести две малые дуги радиусом r = 1/4do;
- – дуги проводить до точек сопряжения “3” (построение показано).
Построение овала 3 выполняется аналогично (большая ось АВ
Косоугольная (фронтальная) диметрия
В качестве аксонометрической плоскости проекций здесь взята плоскость, параллельная плоскости проекций V. Поэтому на аксонометрии сохраняется угол 90° между аксонометрическими осями x и z, а ось y располагают под углом 45° к горизонтальной прямой.
Приведенные коэффициенты искажения по аксонометрическим осям: по осям x и z: Kx = Kz = 1, а по оси y: Ky = 0,5.
На рис. 10.5 показано расположение аксонометрических осей в косоугольной диметрии, размеры и расположение больших и малых осей эллипсов и графический способ построения овалов.
Окружности на проекциях предмета, лежащие в плоскостях, параллельных плоскости проекций V, проецируются на аксонометрическое изображение в виде окружностей, т. е. не искажаются, так как параллельны плоскости аксонометрических проекций.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций H и W, проецируются на аксонометрическое изображение в виде эллипсов, большие оси AB которых равны 1,07d, а малые оси EF равны 0,33d.
Расположение больших и малых осей эллипсов относительно аксонометрических осей:
- – эллипс 2: большая ось AB расположена под углом 7º14′ к горизонтальной линии и наклонена в сторону аксонометрической оси y; малая ось EF перпендикулярна большой оси эллипса;
- – эллипс 3: большая ось AB расположена под углом 7º14′ к вертикальной линии и наклонена в сторону аксонометрической оси y; малая ось EF перпендикулярна большой оси эллипса.
Графическое построение двух одинаковых овалов 2 и 3, заменяющих эллипсы на чертежах, аналогичны построениям овалов для прямоугольной диметрии.
Примеры построения аксонометрических проекций
На рис. 10.6 показан пример построения аксонометрической проекции правильной треугольной пирамиды со срезом фронтально-проецирующей плоскостью β(βV) в прямоугольной диметрии.
Построение аксонометрии пирамиды выполняется по предлагаемому графическому алгоритму.
1-е действие. Отнести пирамиду к системе прямоугольных координат x, y и z, оси которой параллельны осям натуральной системы координат, но проходят через высоту пирамиды (ось z) и ее основание (оси x и y).
2-е действие. Определить в принятой системе координат на проекциях пирамиды координаты x, y и z отмеченных точек 1, 2, 3, лежащих на ребрах пирамиды, и точек ABC – вершин основания пирамиды.
3-е действие. На свободном поле чертежа провести аксонометрические оси прямоугольной диметрии из произвольной точки О: ось z – вертикально, ось x – под углом 7°10′, а ось y – под углом 41°25′ к горизонтальной линии (использовать графический способ построения аксонометрических осей).
4-е действие. Построить тонкими линиями аксонометрическую проекцию пирамиды без среза.
4.1. Построить аксонометрическое изображение основания пирамиды AоBоCо по координатным ломаным этих точек (основание лежит в системе осей xOy и называется вторичной проекцией):
- – точка Aо: координатная ломаная xA – yA;
- – точка Bо: координатная ломаная xB – yB;
- – точка Cо: yC.
!!! Координатные отрезки параллельны соответствующим аксонометрическим осям.
4.2. Построить по координате zS на аксонометрической оси z проекцию вершины пирамиды и соединить вершину S с точками основания AоBоCо ребрами, то есть построить аксонометрию пирамиды.
5-е действие. Достроить срез на аксонометрии пирамиды, построив на ребрах пирамиды по координатам x, y и z аксонометрические проекции отмеченных точек 1, 2 и 3 по соответствующим плоским координатным ломанным:
- – точка 1 на ребре SAо: координатная ломаная – x1-y1-z1;
- – точка 2 на ребре SCо: y2-z2;
- – точка 3 на ребре SBо: x3-z3-y3.
6-е действие. Оформить аксонометрию пирамиды, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полную проекцию пирамиды, невидимые линии и линии построения).
На рис. 10.7 показан пример построения аксонометрической проекции конуса со срезами двумя фронтально-проецирующими плоскостями (в сечении плоскостью α – треугольник со сторонами-образующими, в сечении плоскостью β – эллипс) в прямоугольной изометрии.
Графические действия для построения аксонометрии конуса соответствуют предложенному алгоритму для построения аксонометрии пирамиды:
1-е действие. Отнести конус к такой же системе прямоугольных координат x, y и z (ось z совпадет с высотой конуса, оси x и y проходят по основанию конуса).
2-е действие. Определить координаты x, y и z для точек 1, 2, 3 и 4 на поверхности конуса для построения сечений на его аксонометрии.
3-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести оси прямоугольной изометрии под углами 120° с вертикальной осью z.
4-е действие. Построить аксонометрическую проекцию конуса без срезов:
4.1. Построить эллипс основания конуса с центром в точке О, большая ось которого перпендикулярна аксонометрической оси Z, так как окружность основания конуса лежит в горизонтальной плоскости (см. графическое построение овала 2 на рис. 10.3).
4.2. Построить вершину конуса точку S на оси z по ее координате zs и провести две касательные к эллипсу через вершину S.
5-е действие. Достроить срезы на аксонометрии конуса, построив аксонометрические проекции отмеченных точек 1, 2, 3 и 4 по соответствующим плоским координатным ломаным:
- – точка 1: координатная ломаная x1-z1;
- – точки 2: координатная ломаная x2-y2-z2;
- – точки 3: координатная ломаная y3-z3;
- – точки 4: координатная ломаная x4-y4-z4 (лежат на образующих S-5о).
Соединить построенные точки соответствующими линиям (участок эллипса и треугольник).
6-е действие. Оформить чертеж аксонометрии конуса, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полный контур пирамиды, невидимые линии и линии построения).
На рис. 10.8 показано построение аксонометрической проекции цилиндра с полуцилиндрическим вырезом (их радиусы равны) в прямоугольной изометрии.
В этом частном случае пересечения поверхностей для построения линии пересечения на профильной проекции следует применить теорему Г. Монжа, так как эти две цилиндрические поверхности 2-го порядка равных диаметров описаны вокруг сферы.
Построение аксонометрии выполняется по аналогичному графическому алгоритму:
1-е действие. Отнести цилиндр к системе координатных осей x, y и z: оси x и y провести по нижнему основанию, а ось z – по оси вращения цилиндра.
2-е действие. Обозначить характерные и промежуточные точки 1, 2, 3 и 4 на поверхности цилиндра и определить координаты x, y, z обозначенных точек для построения линии пересечения полуцилиндрического выреза с поверхностью заданного цилиндра (симметричные точки обозначены на одной половине окружности).
3-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии: ось z – вертикально, а оси x и y – под углами 120° к оси z.
4-е действие. Построить аксонометрию цилиндра без выреза.
4.1. Построить эллипс нижнего основания цилиндра в точке О, большая ось которого перпендикулярна оси z, так как окружность основания лежит в горизонтальной плоскости.
4.2. Построить точку О1 верхнего основания по координате zО1 и эллипса верхнего основания; соединить эллипсы двумя очерковыми образующими по конечным точкам больших осей эллипсов.
5-е действие. Достроить вырез на аксонометрии цилиндра, построив проекции обозначенных точек 1, 2, 3 и 4 по координатным ломаным (снизу вверх) x – z:
- точки 1 и 4 → x1(x4) – z1(z4);
- точки 2 → x2 – z2 (четыре точки);
- точки 3 → z3 (две точки);
- точки К (на очерковых образующих; см. построения на горизонтальных проекциях) → xК – zК;
- построенные точки соединить:
- – одна плоская кривая проецируется на аксонометрию в виде эллипса;
- – вторая плоская кривая проецируется в прямую линию (запомните!).
6-е действие. Соедините построенные точки соответствующими линиями – отрезками образующих и участками эллипсов.
7-е действие. Оформить аксонометрию цилиндра, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полный контур цилиндра, невидимые линии и линии построения).
На рис. 10.9 показан пример построения шара со срезами в прямоугольной изометрии.
Напомним, что сечением поверхности шара любой плоскостью является окружность. Но на чертеже окружности проецируются в эллипсы. В примере срезы выполнены профильной плоскостью α(αV), горизонтальной плоскостью β(βV) и фронтально-проецирующей плоскостью γ(γV). Следовательно, на аксонометрическом изображении шара:
- эллипс окружности Øα, лежащий в профильной плоскости;
- эллипс окружности Øβ, лежащий в горизонтальной плоскости;
- эллипс как проекцию окружности, лежащий в плоскости γ, по обозначенным точкам.
Аксонометрическим изображением шара в прямоугольной изометрии является окружность с диаметром, равным 1,22d, где d – диаметр шара.
Графический алгоритм для построения аксонометрии шара следующий:
1-е действие. Отнести шар к системе координат x, y, z, проходящих через его центр (точка О).
2-е действие. Обозначить характерные точки 1, 2, 3, 4, 5 и 6 на поверхности шара и определить координаты обозначенных точек для построения срезов на аксонометрии.
3-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
4-е действие. Построить аксонометрию шара без срезов – провести окружность диаметром 1,22d.
5-е действие. Достроить срезы на аксонометрии шара:
- построить эллипс диаметром Øα, большая ось которого перпендикулярна аксонометрической оси x, с центром в точке О1 с координатой x01;
- построить эллипс диаметром Øβ, большая ось которого перпендикулярна аксонометрической оси z, с центром в точке О2 с координатой x02 (построенные эллипсы пересекаются по линии 2-2);
- построить по координате x4 линию 4-4 на построенном горизонтальном эллипсе;
- построить по координатам точки 5 и 6: точку 5 – по ломаной x5-y5, а точку 6 – по координате z6.
6-е действие. Соединить построенные точки 4-5-6 эллиптической кривой.
7-е действие. Оформить аксонометрию шара, выполнив толстыми линиями его видимый контур, оставив тонкими линиями полный очерк шара, невидимые линии и линии построения.
На рис. 10.10 показан пример построения половины открытого тора в прямоугольной изометрии.
Построение аксонометрии выполняется по следующему графическому алгоритму:
1-е действие. Отнести тор к системе координат x, y, z.
2-е действие. Если тор со срезами, обозначить характерный точки и определить их координаты: например, координаты точек А и В.
3-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
4-е действие. Построить эллипс направляющей окружности радиусом R с центром в точке О, большая ось которого перпендикулярна оси y.
5-е действие. В полученных на оси x точках О1 и О2 построить два эллипса образующих окружностей радиусом r, большие оси которых перпендикулярны оси z.
6-е действие. Построить аксонометрию тора:
- провести достаточное количество образующих окружностей диаметрами, равными 1,22 r с центрами на эллипсе направляющей окружности тора;
- провести две лекальные огибающие касательные кривые.
7-е действие. Достроить аксонометрические проекции заданных точек А и В по их координатным ломаным:
- точка А → xА-yА-zА;
- точка В → xВ-yВ-zВ.
8-е действие. Оформить аксонометрию открытого тора.
На рис. 10.11 показан пример построения тороида (самопересекающегося тора) в прямоугольной изометрии.
Построение аксонометрии выполняется по следующему графическому алгоритму:
1-е действие. Отнести тор к системе координат x, y, z, проходящей по его основанию и ось вращения.
2-е действие. Рассечь тороид достаточным количеством плоскостей, перпендикулярных оси его вращения и определить радиус окружности каждого сечения (измерить линейкой) с центрами в точках О1, О2, О3 и т. д.
3-е действие. Обозначить характерные точки 1, 2, 3 и 4 среза и определить их координаты.
4-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
5-е действие. Построить аксонометрию тороида:
- построить семейство эллипсов в точках О, О1, … , О4 соответствующих радиусов R, R1, R2, … , R4 с координатами z(z1, z2, … , z4), большие оси которых перпендикулярны оси z, так как лежат в горизонтальных плоскостях;
- построить точку S;
- провести две касательные огибающие кривые к эллипсам.
6-е действие. Достроить срез на аксонометрии тороида по координатам отмеченных точек (построения см. рис. 10.11).
7-е действие. Оформить аксонометрию тороида.
!!! Аксонометрическая проекция глобоида в прямоугольной изометрии строится аналогично тем же способом «сечений».
На рис. 10.12 показан пример построения аксонометрической проекции правильной четырехгранной призмы со сквозным пазом, выполненным двумя профильными α1(αV1) и α2(αV2) фронтально-проецирующей плоскостями β(βV) в косоугольной диметрии (коэффициенты искажения kx = kz =1, ky = 0,5).
Построение аксонометрии призмы выполняется по следующему графическому алгоритму:
1-е действие. Отнести («привязать») призму к системе прямоугольных координат x, y, z, оси которой параллельны осям натуральной системы координат, относительно которой построены проекции призмы, но проходят через высоту призмы (ось z) и через центр нижнего основания призмы (оси x и y).
2-е действие. Обозначить характерные точки 1, 2, …, 5 на поверхности призмы.
3-е действие. Определить в отнесенной к призме системе координат на ее проекциях координаты x, y и z обозначенных точек:
- точки 1 и 5, лежащих на верхнем основании и ребрах призмы;
- точек 2 и 4, лежащих на линиях пересечения плоскостей паза, а также обозначенных буквами А, В, С и D вершин нижнего основания призмы.
4-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси косоугольной диметрии: ось z – вертикально; ось x – горизонтально; ось y – под углом 45° к горизонтальной линии (оси x).
5-е действие. Построить тонкими линиями аксонометрическую проекцию призмы без выреза:
5.1. Построить нижнее основание призмы АоВоСоDо по координатам x и y этих точек (основание лежит в горизонтальной плоскости с осями xОy и называется вторичной проекцией):
- точки Ао и Со – симметрично по равным координатам xА и yА на оси x;
- точки Во и Dо – по координатам yВ и yD на оси y (координаты уменьшить в 2 раза!);
- соединить построенные вершины отрезками прямых линий.
5.2. Построить верхнее основание призмы:
- отложить от точки О вверх координату zО1, равную высоте призмы, и через полученную проекцию точки О1 провести аксонометрические оси;
- из точек Ао, Во, Со и Dо нижнего основания провести вертикально ребра призмы параллельно оси z до пересечения с аксонометрическими верхнего основания и достроить верхнее основание призмы.
6-е действие. Достроить на аксонометрии призмы вырез по координатам обозначенных точек (сверху вниз):
- очки 1 и 5 на верхнем основании по координатам x1 и x2;
- точки 2 и 4 – на вертикальных линиях, параллельных оси z, по координатам z2 и z4;
- точки 3 – на ребрах Во и Dо по координате z3;
7-е действие. Соединить построенные точки отрезками прямых линий.
8-е действие. Оформить аксонометрию призмы, выполнив толстыми линиями ее видимый контур; оставить тонкими линиями полную проекцию призмы, невидимые линии и линии построения.
Структуризация материала десятой лекции в рассмотренном объеме схематически представлена на рис. 10.13 (лист 1). На последующих листах 2 и 3 компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 10.14 и 10.15).
Аксонометрические проекции
Аксонометрия – это проекция предмета вместе с осями координат, к которым этот предмет следует отнести в пространстве первого октанта, на некоторую плоскость (плоскость аксонометрических проекций). Направление проецирования на эту плоскость не должно совпадать с направлением натуральных координатных осей первого октанта.
Прямоугольные аксонометрии
Прямоугольная изометрия
Прямоугольная диметрия
Косоугольная фронтальная диметрия
Построение эллипсов на аксонометрических проекциях смотрите также в учебных пособиях [2, 6] или в учебных изданиях по инженерной графике других авторов.
Кстати вы всегда можете заказать чертежи.
Лекции по предметам:
- Инженерная графика
- Начертательная геометрия
- Компас
- Автокад
- Черчение
- Проекционное черчение
- Строительное черчение
- Техническое черчение
- Геометрическое черчение


















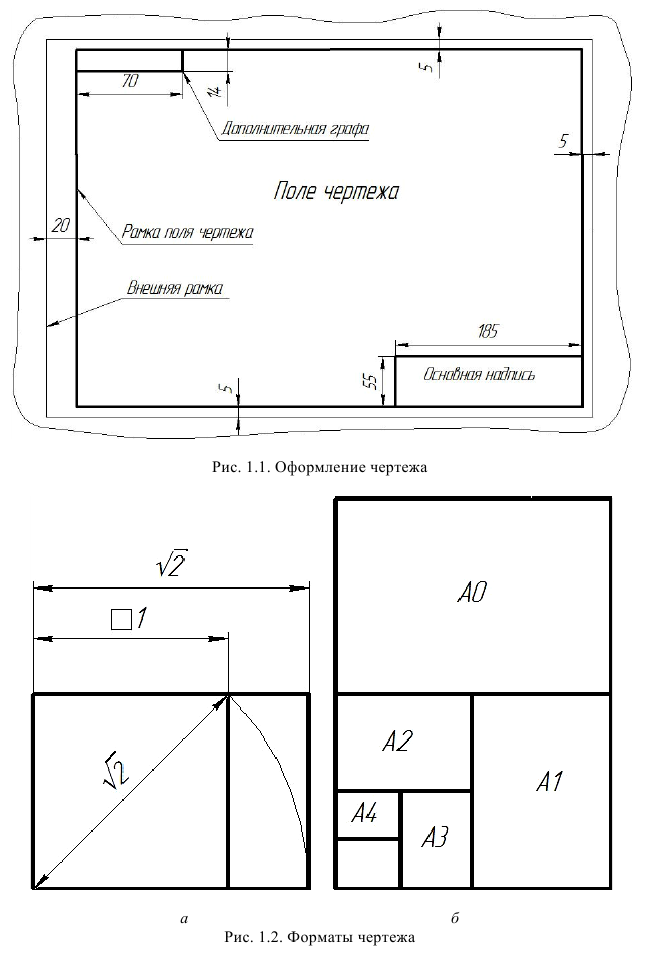
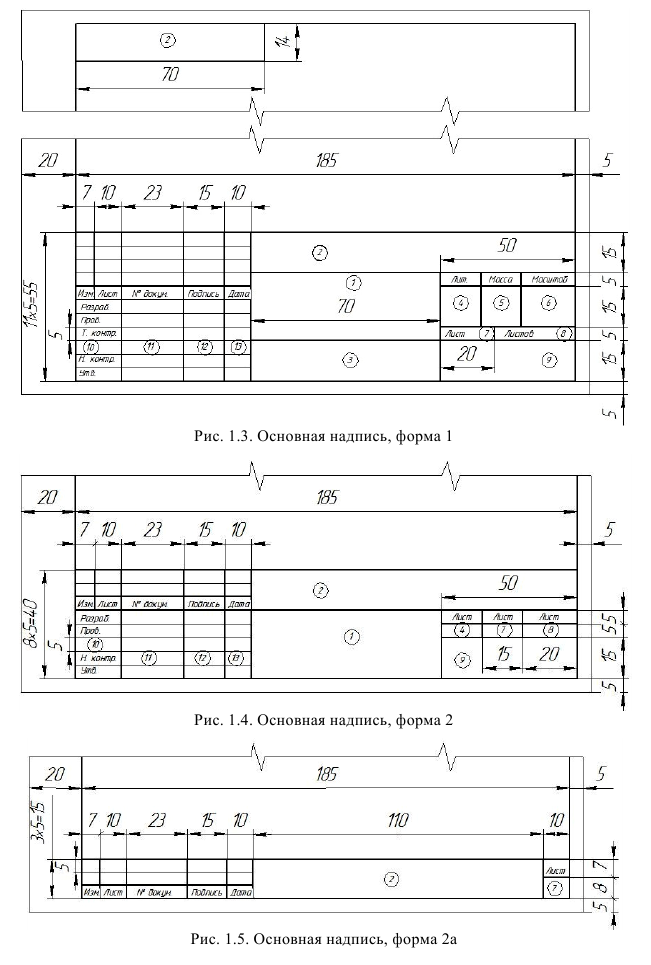
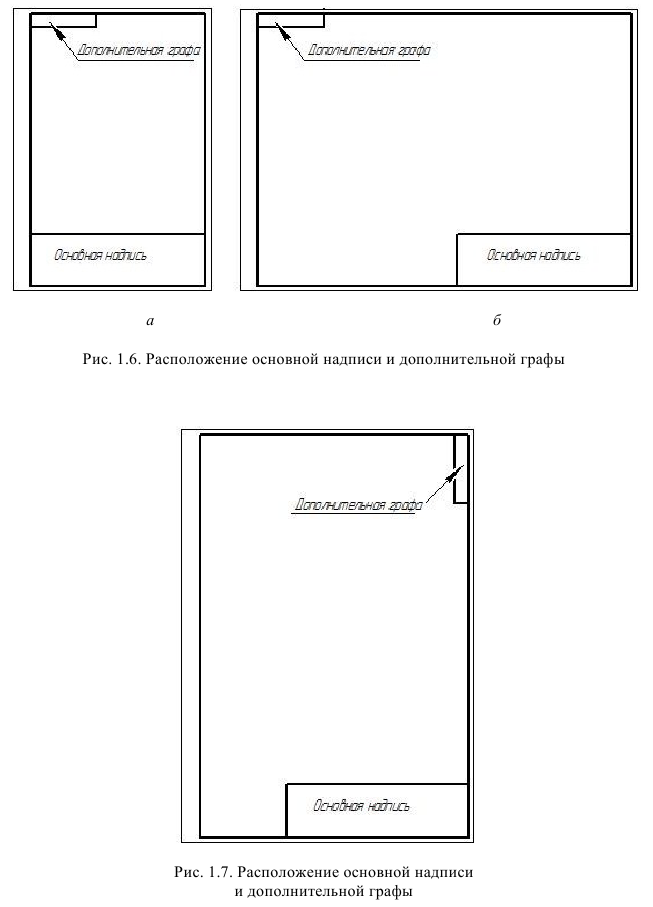
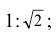
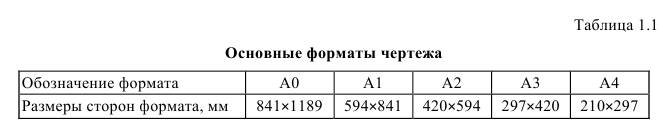
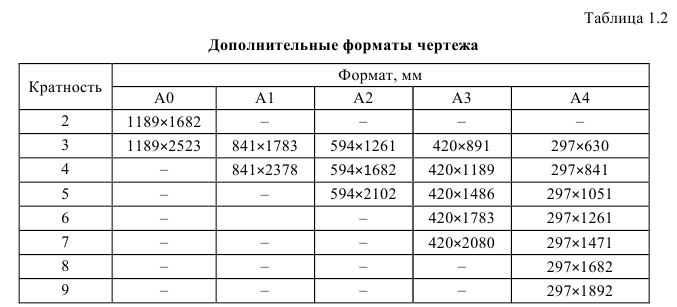

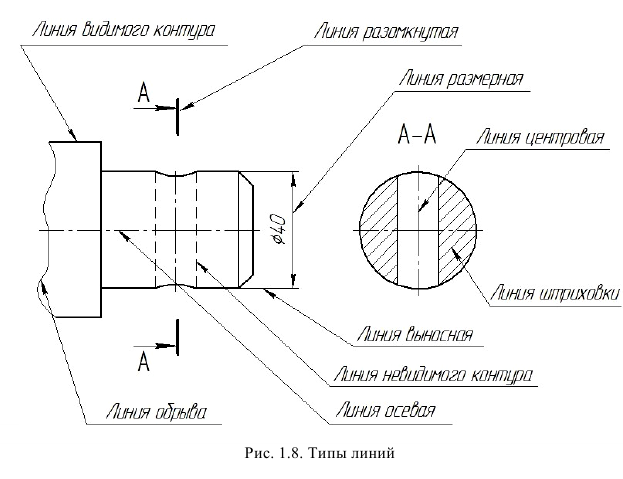
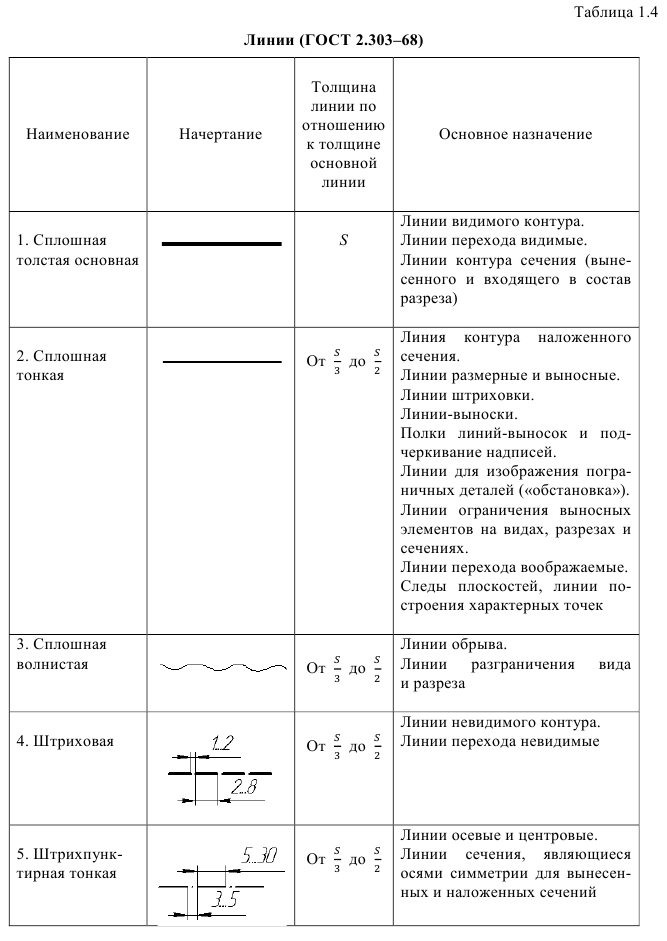
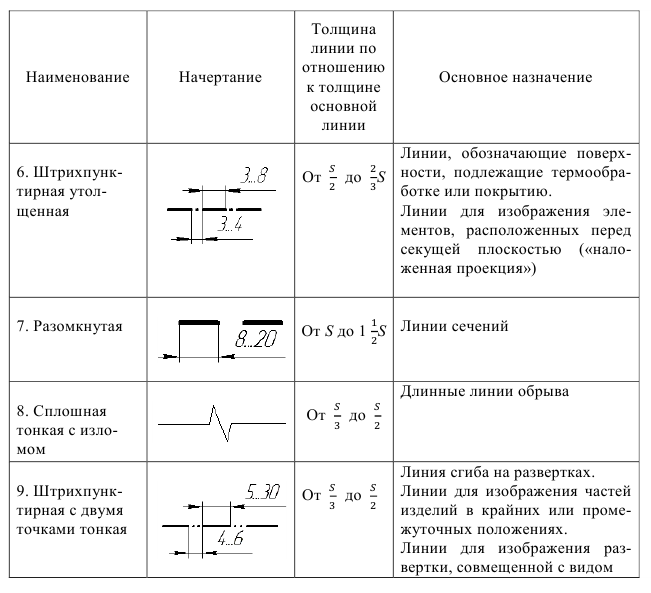


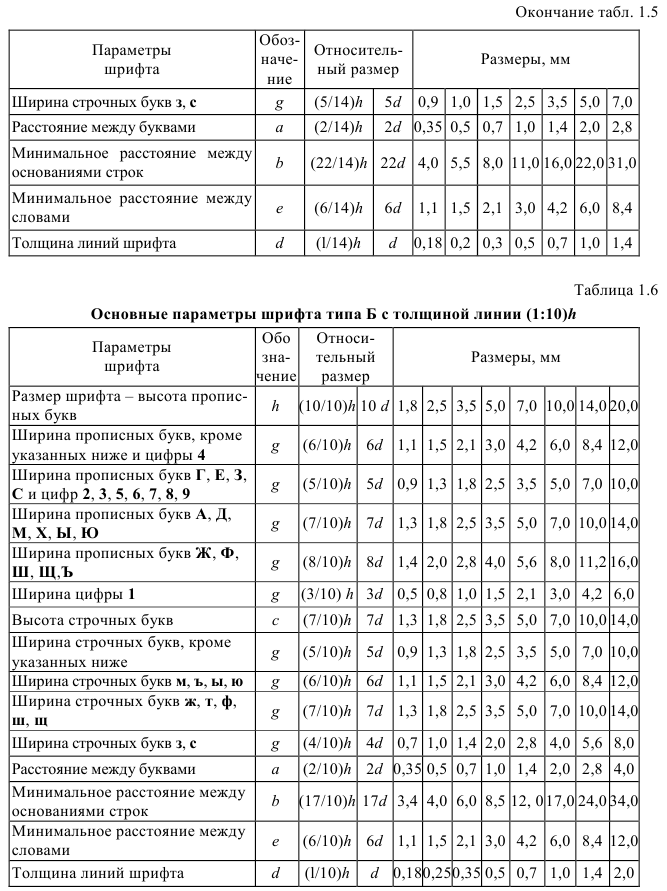
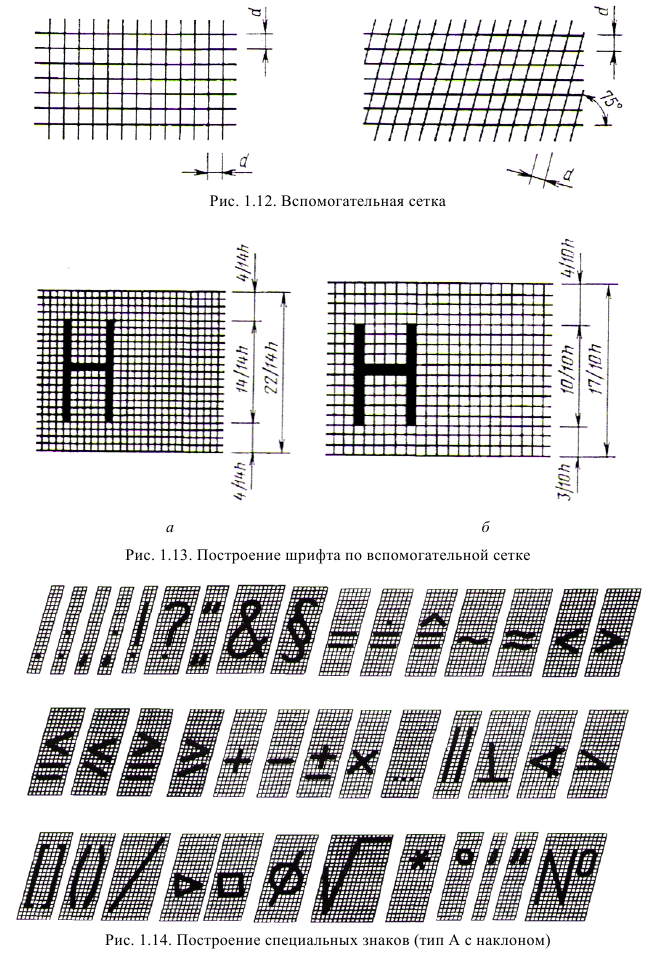


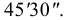
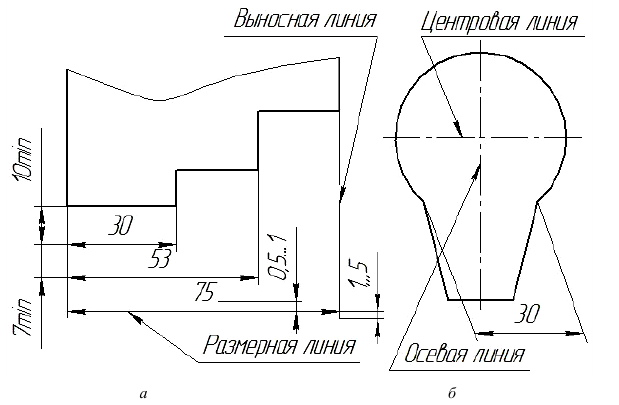
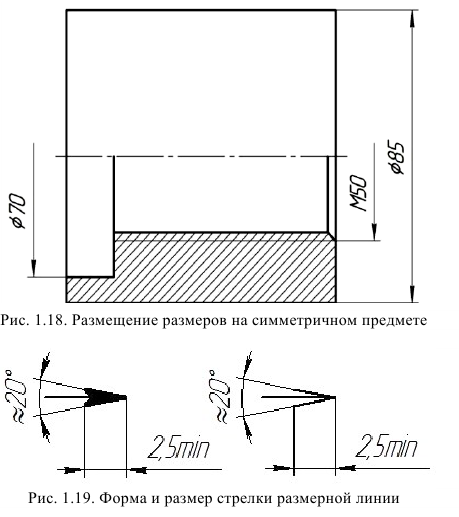
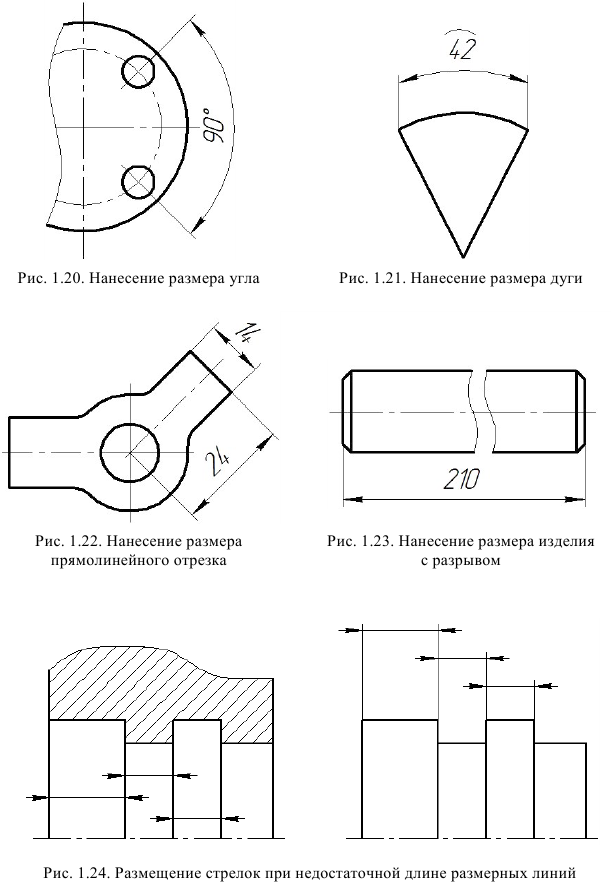
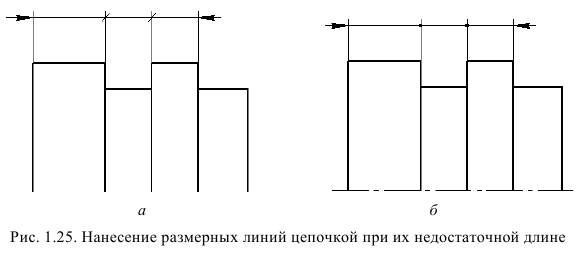
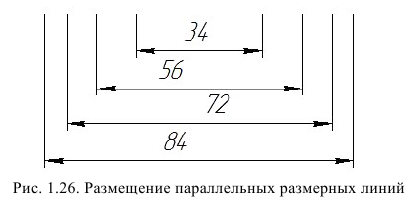
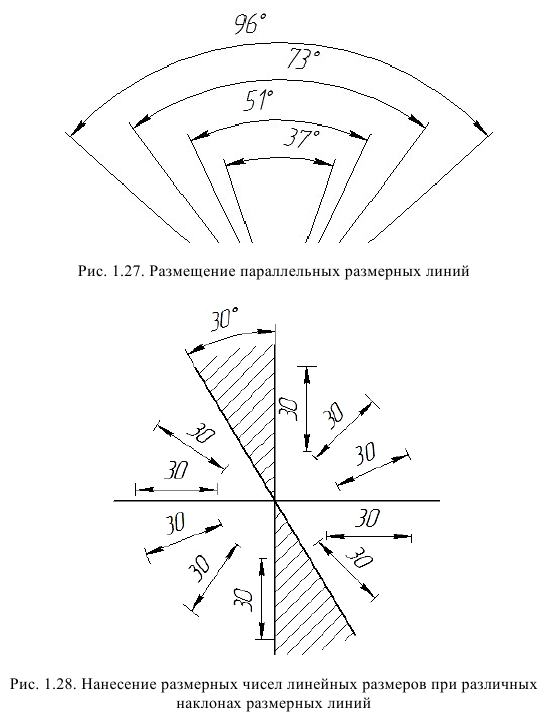
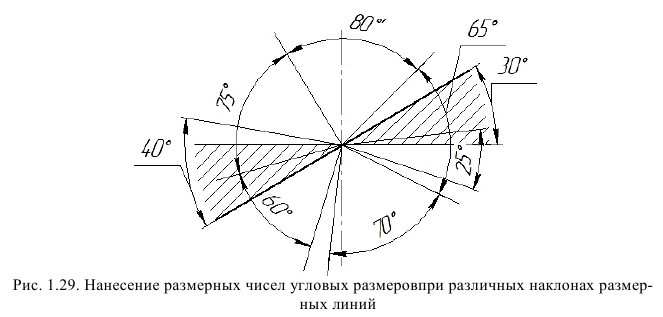
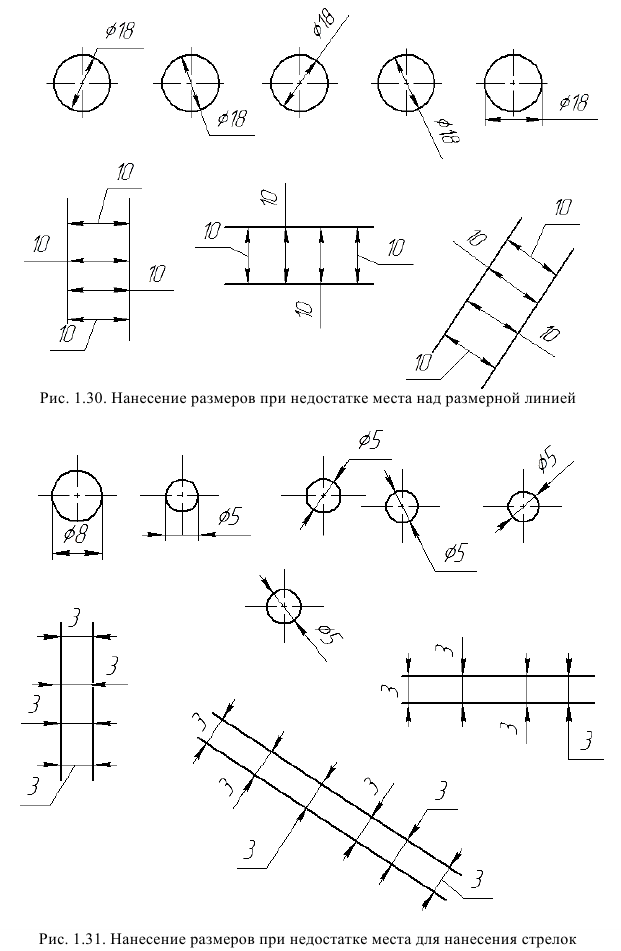
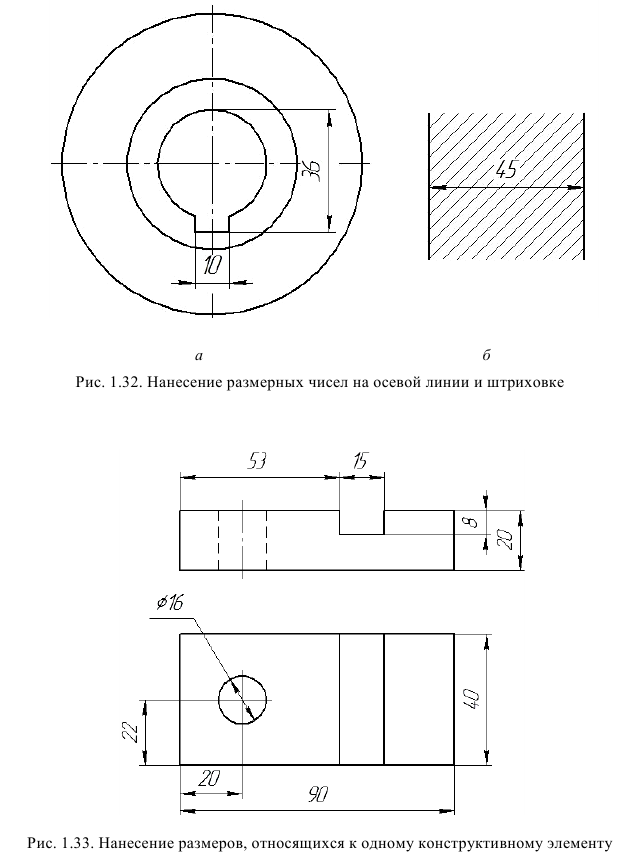
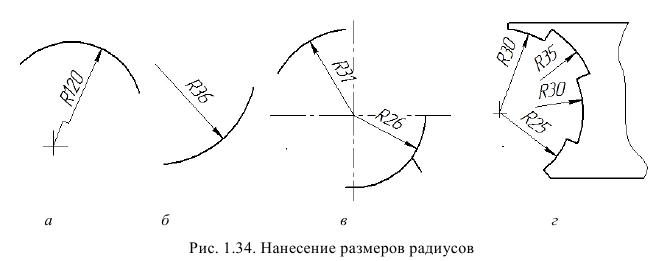
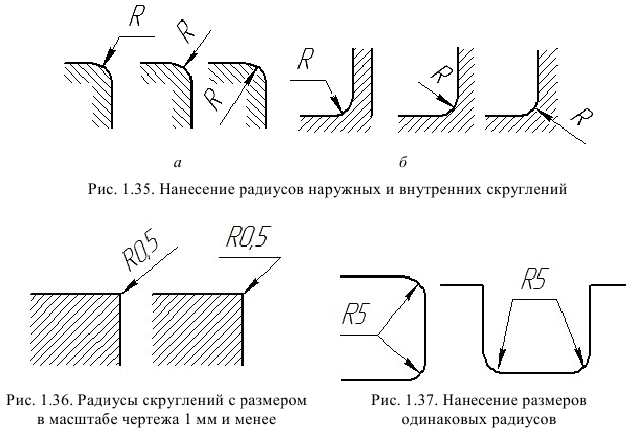
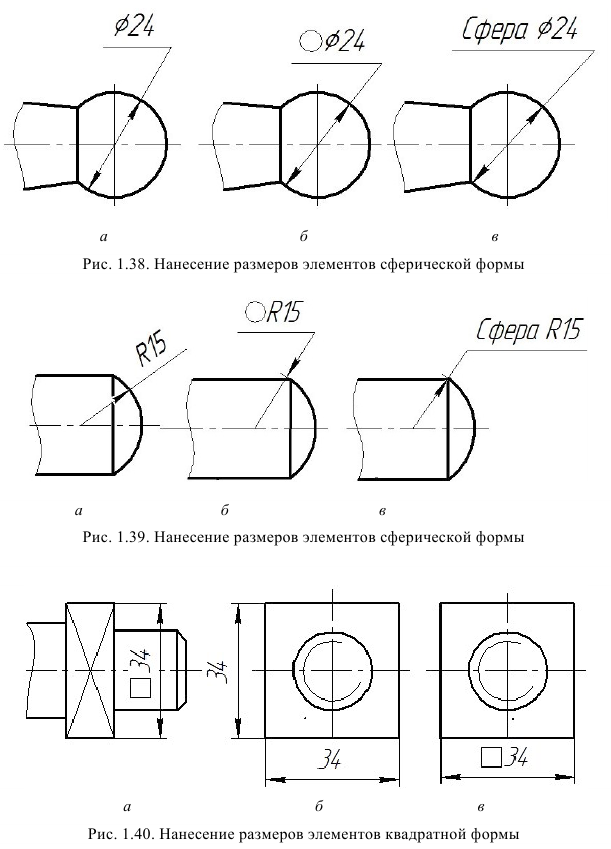
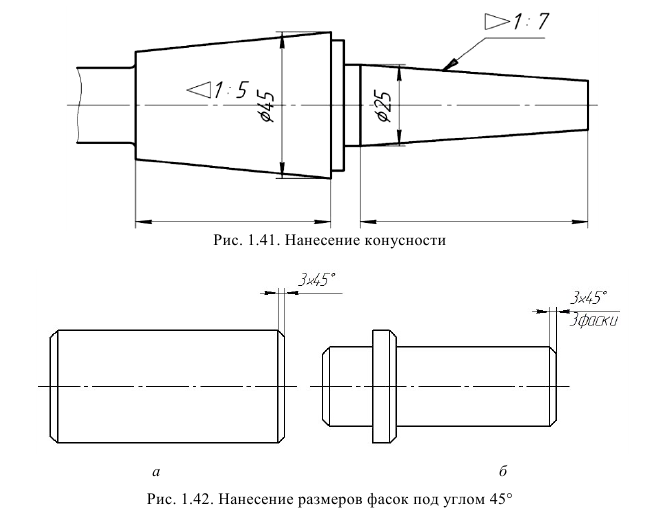
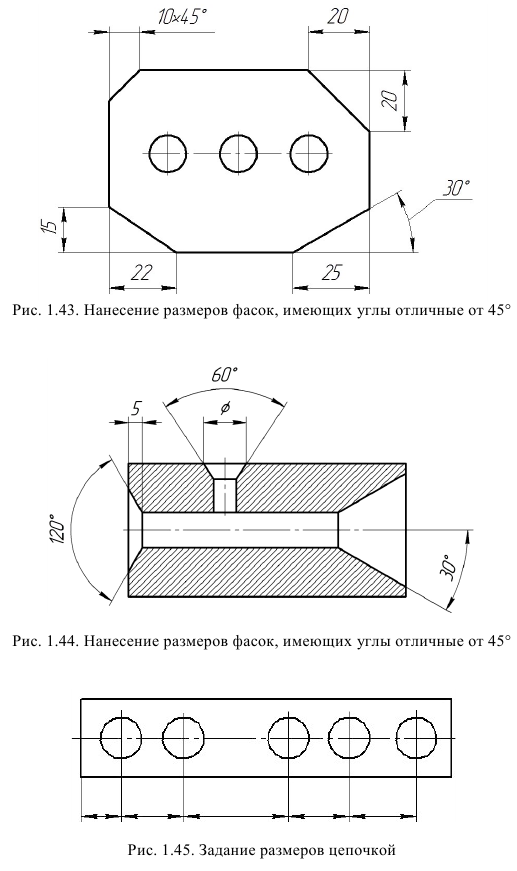
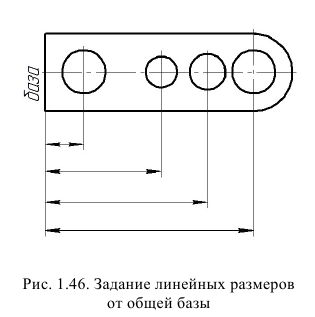
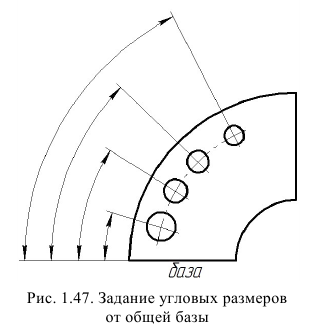
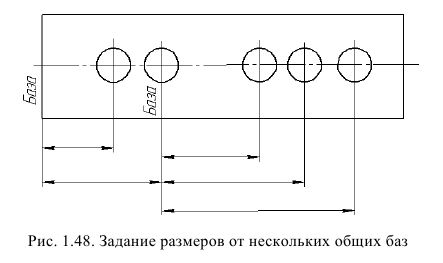
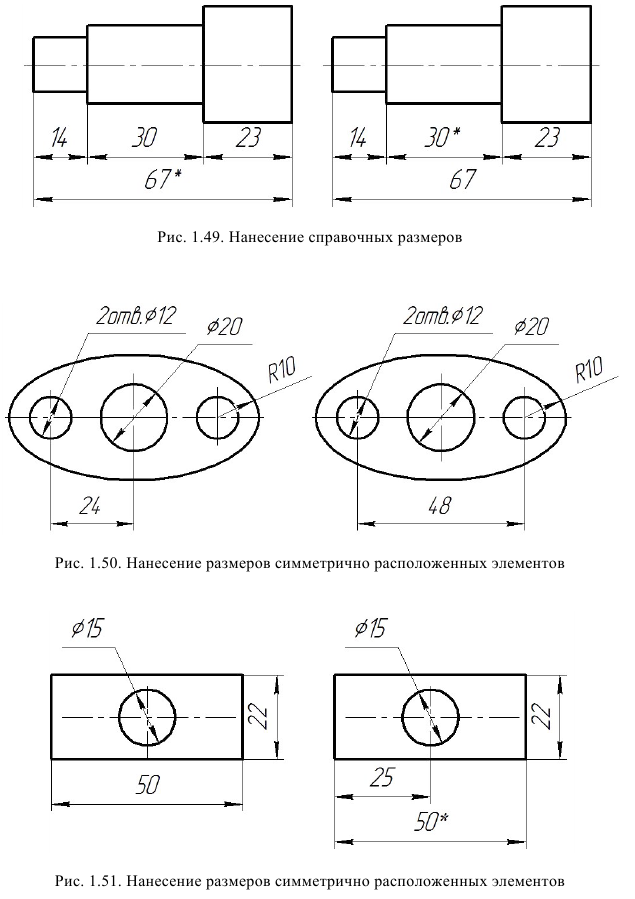
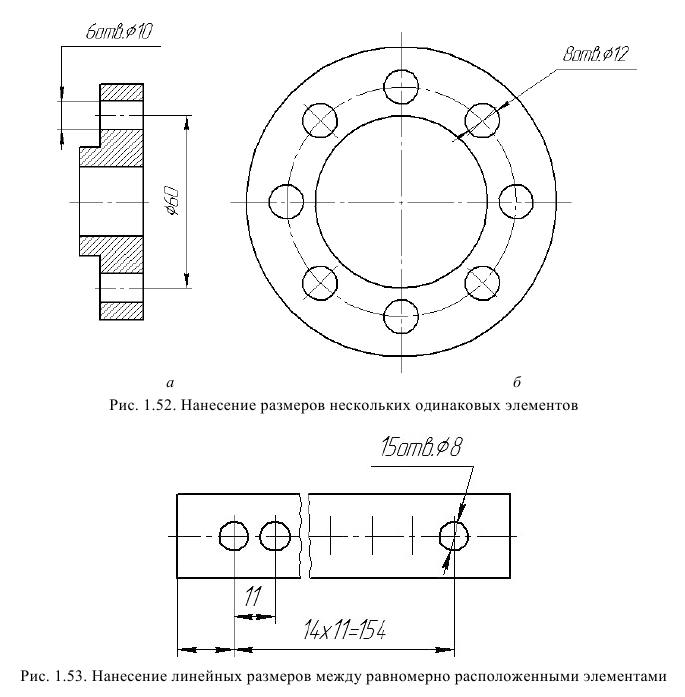
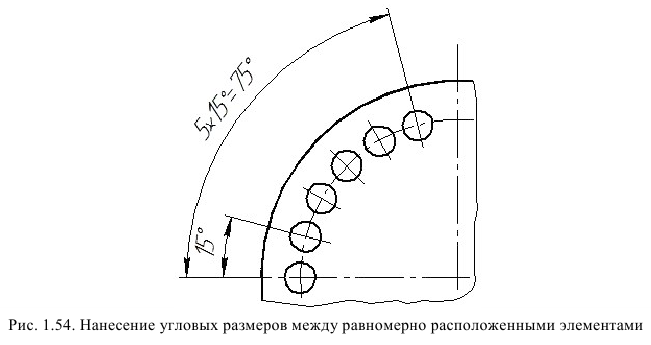
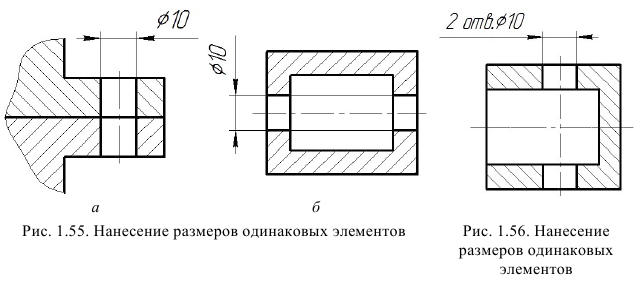
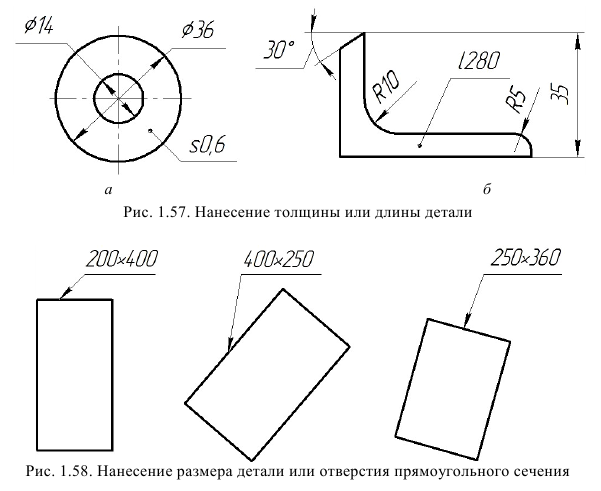
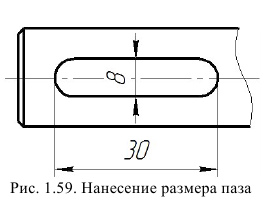
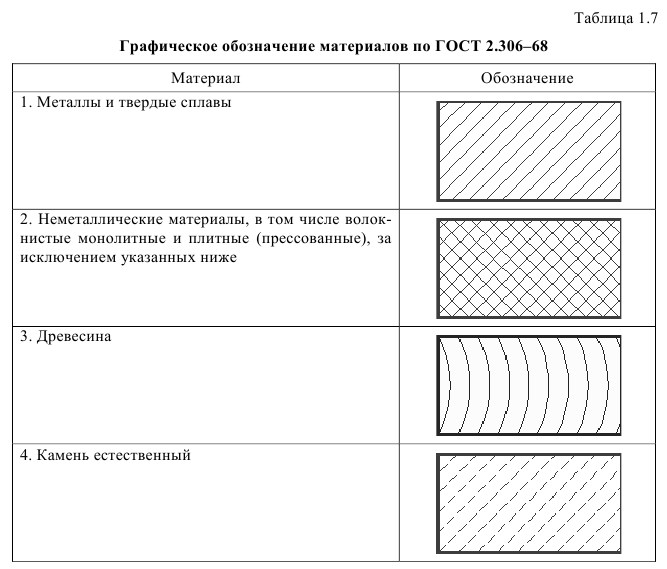

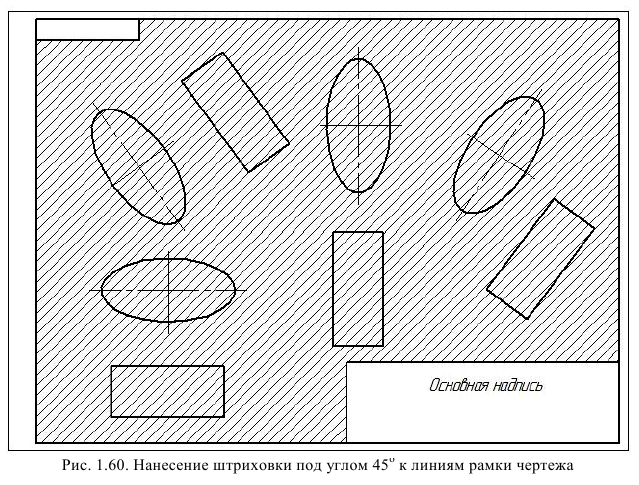
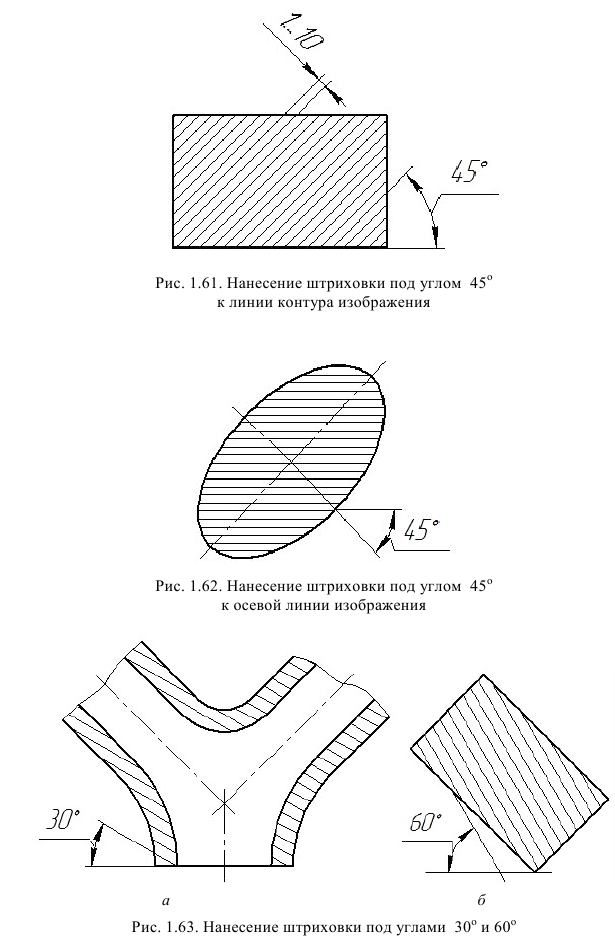
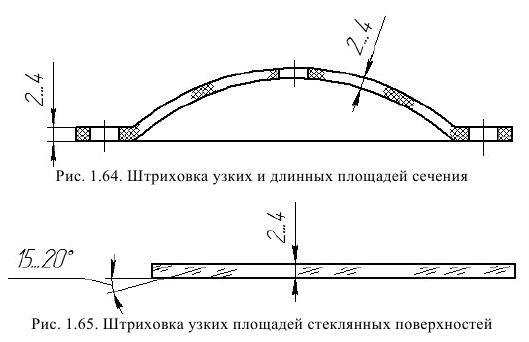
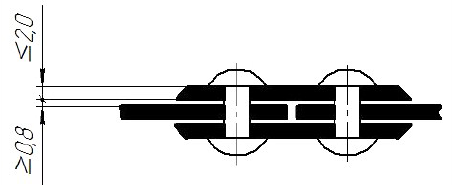
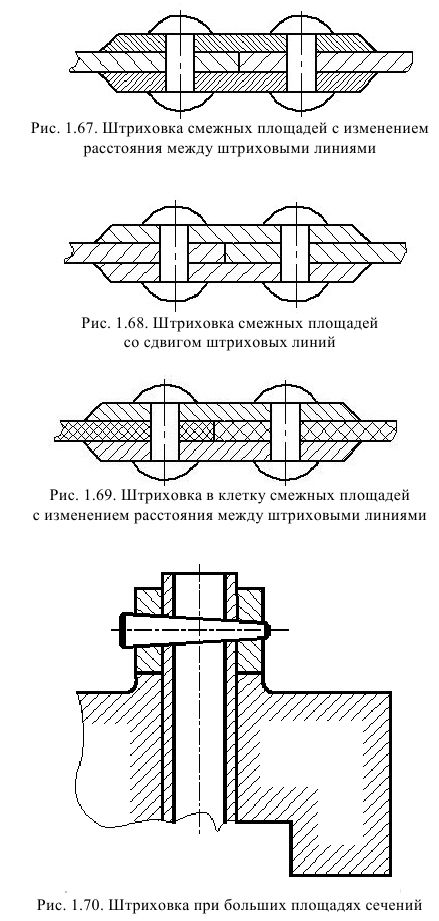
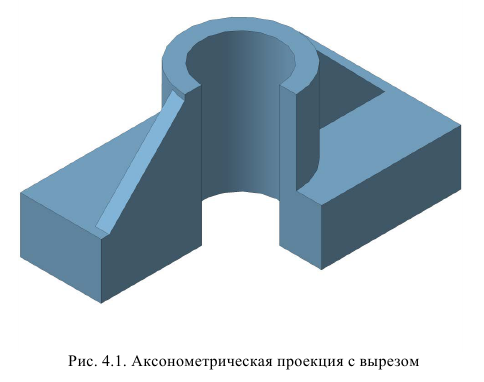
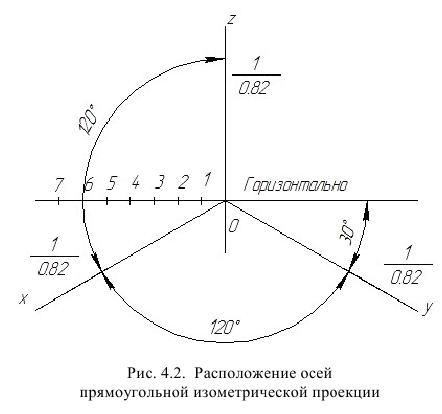
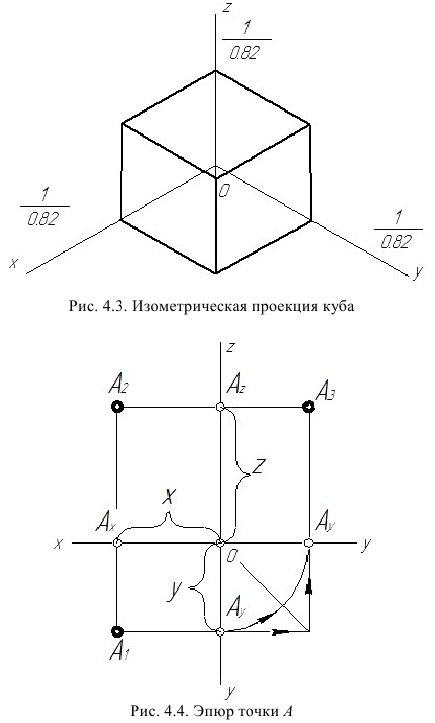
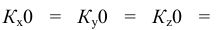
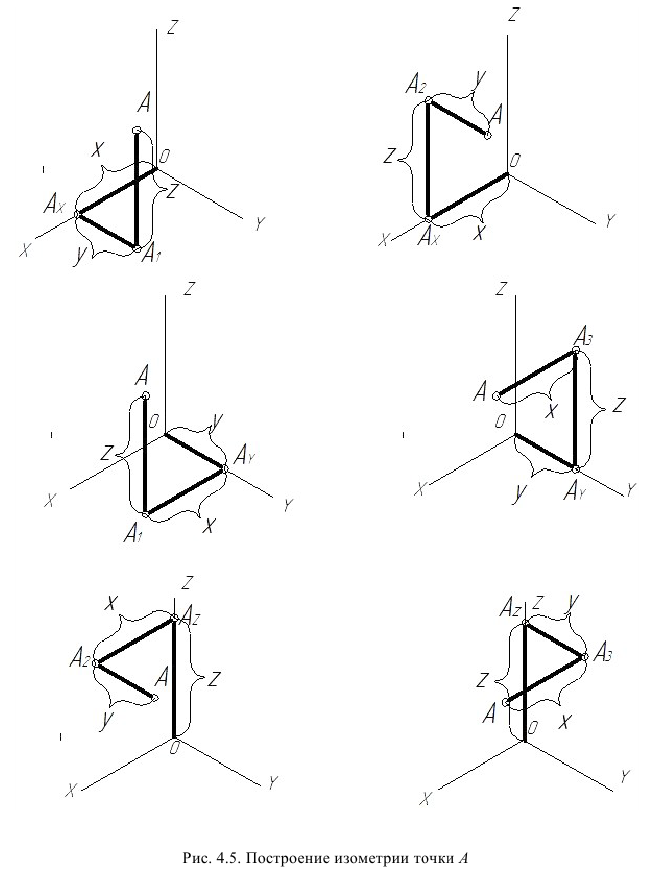
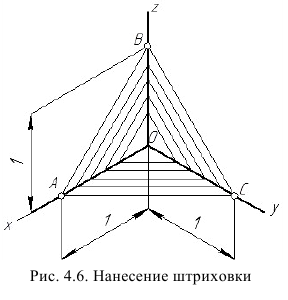
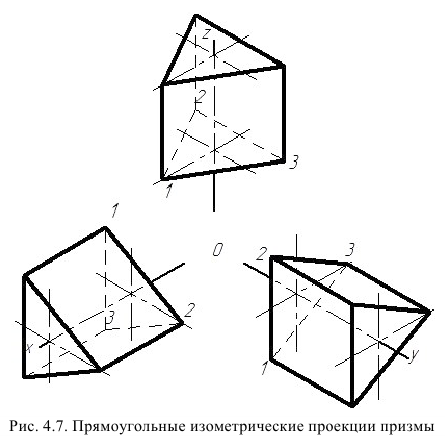
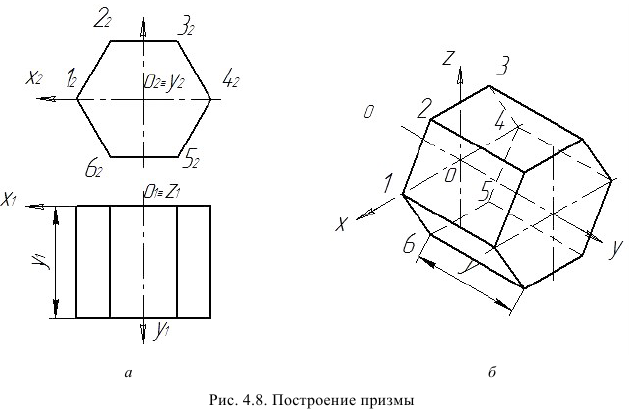
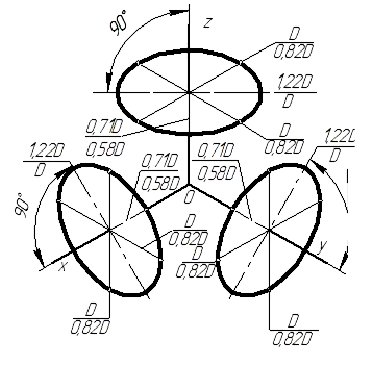

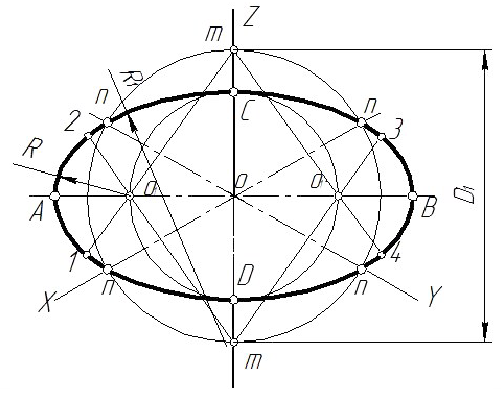
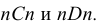
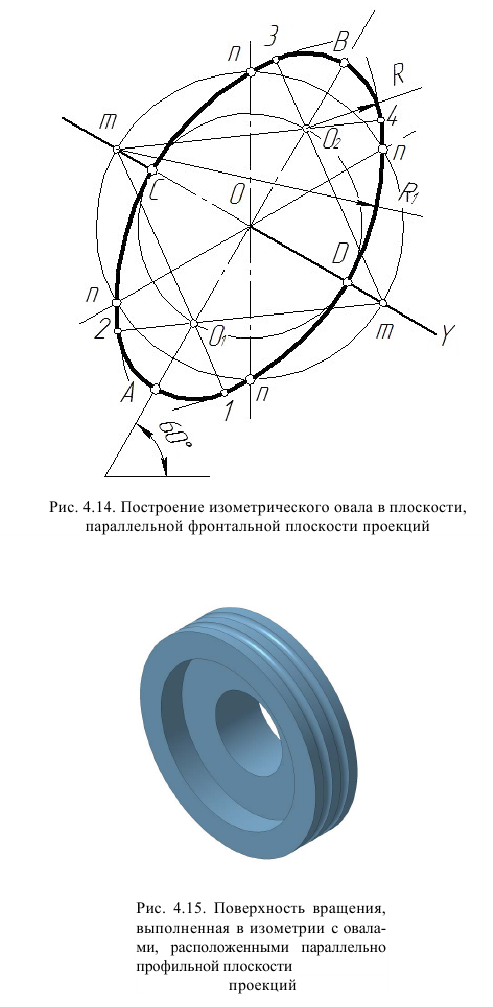
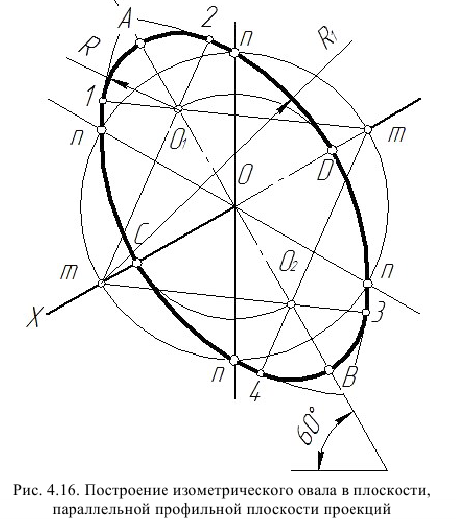
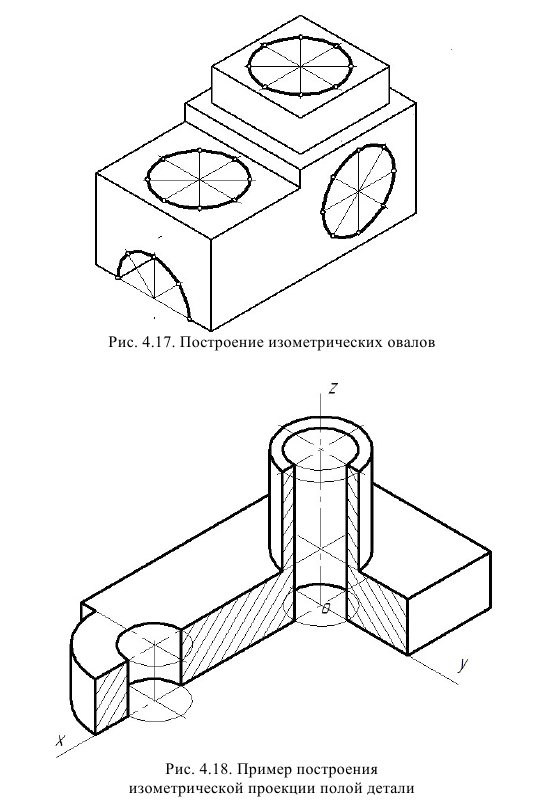
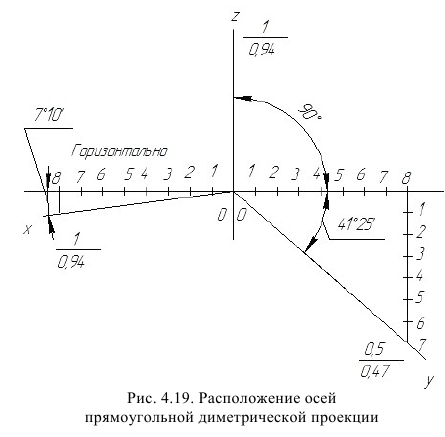
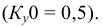
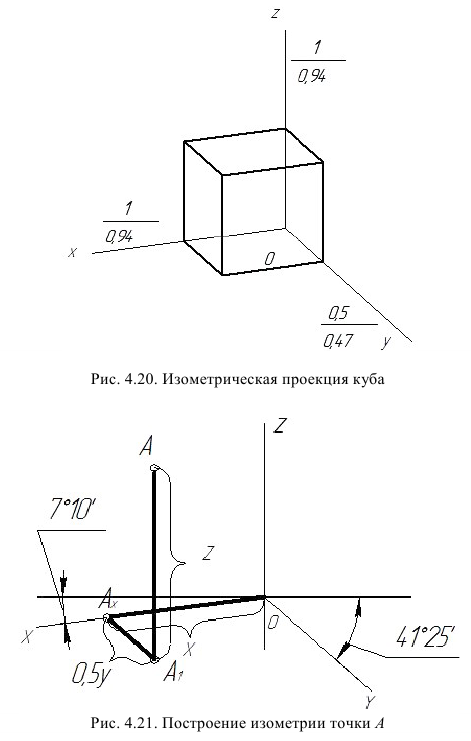
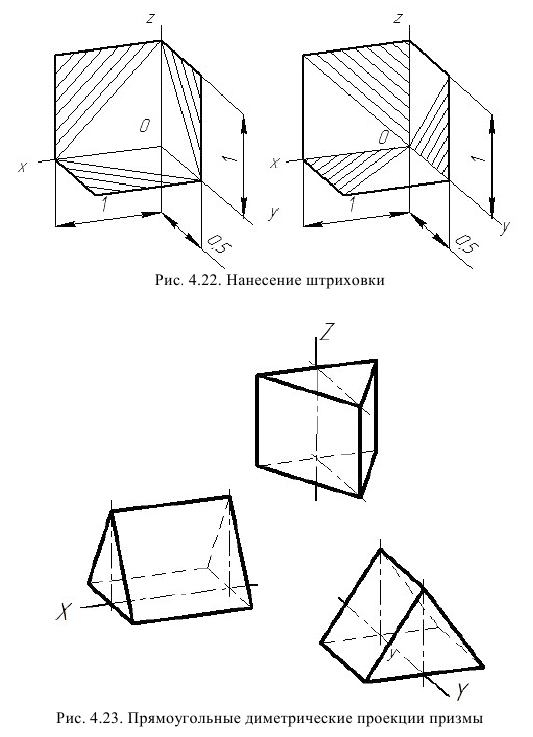
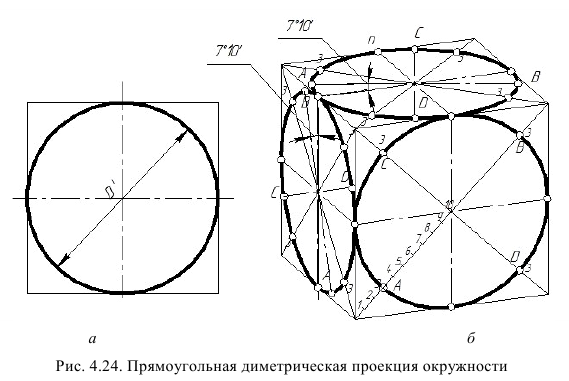
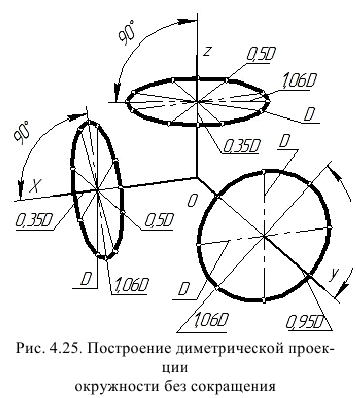

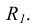
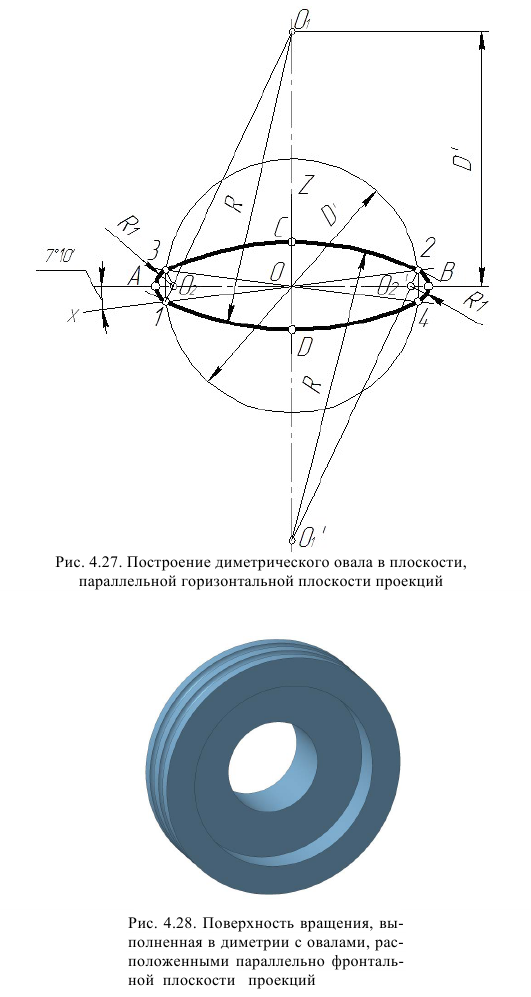
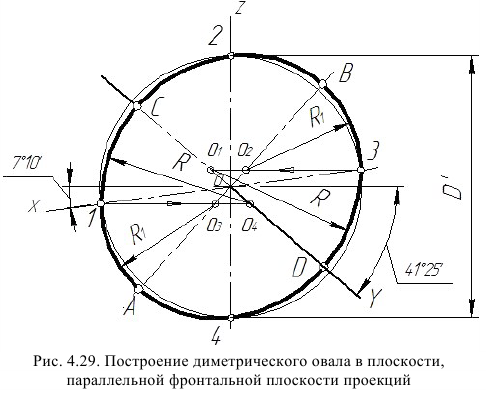
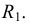
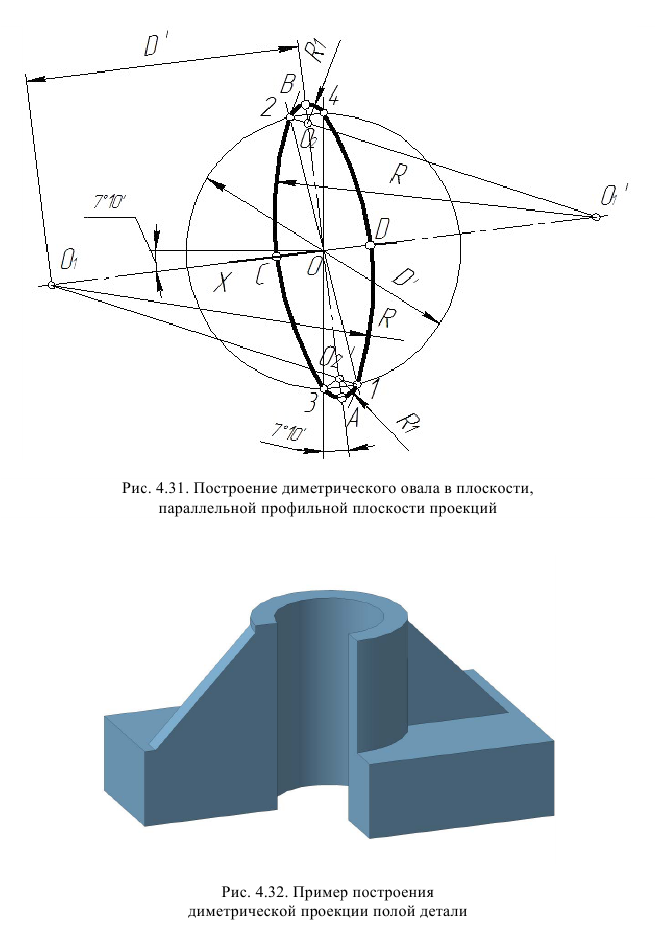
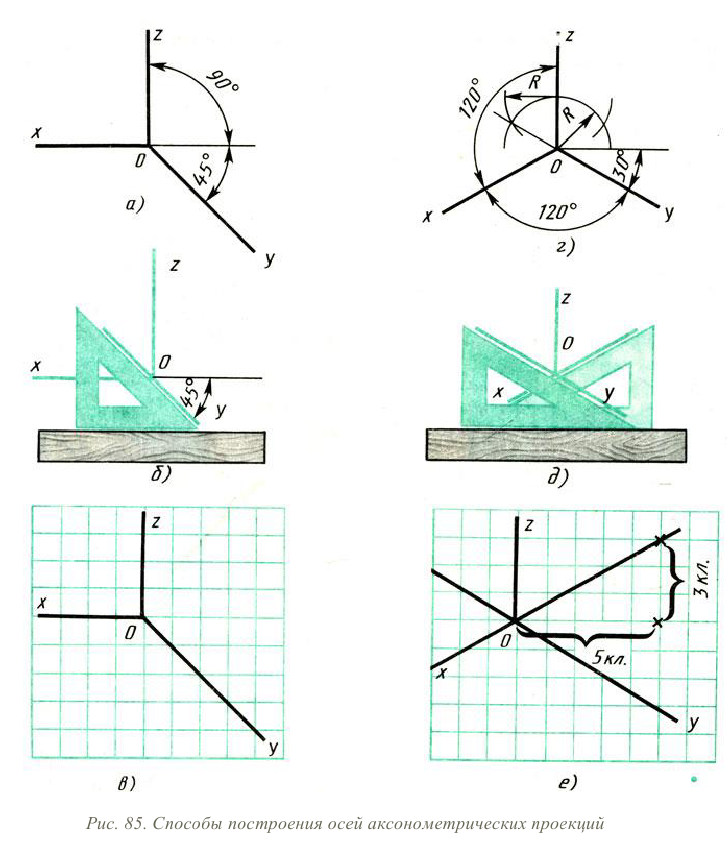
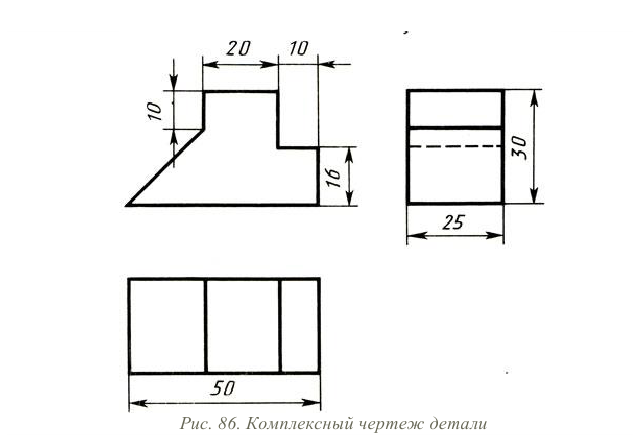
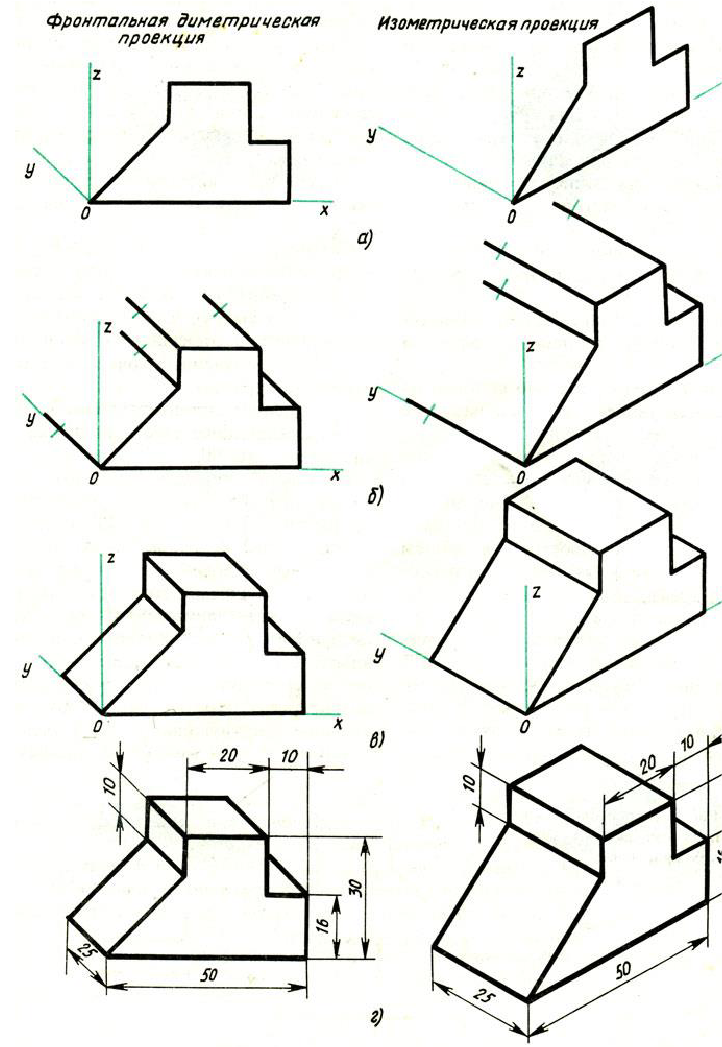
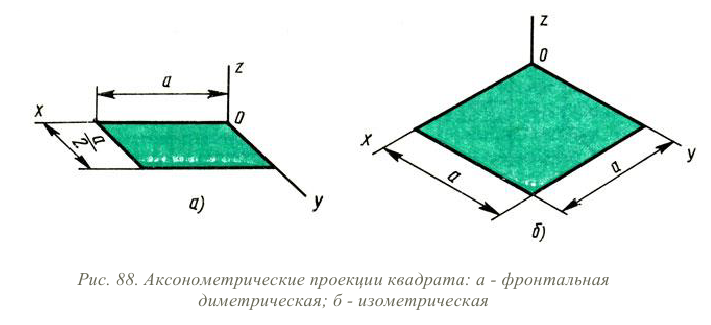
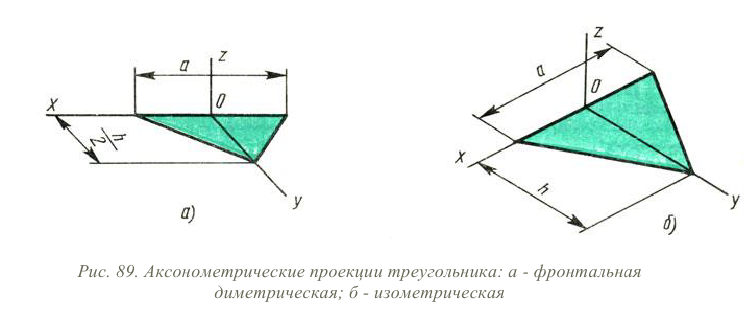
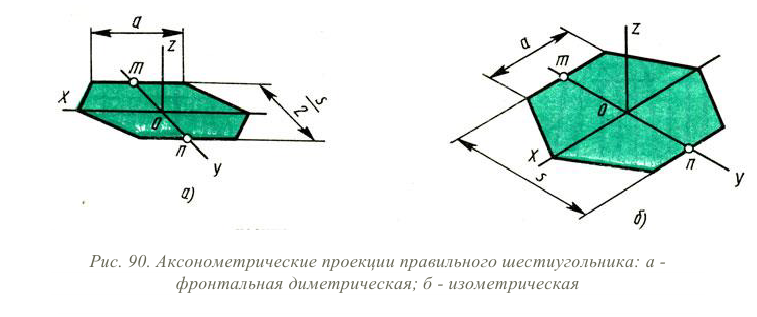
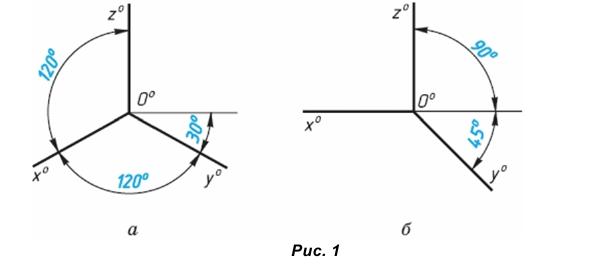
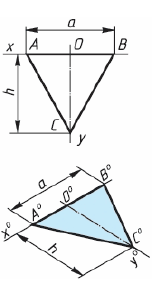
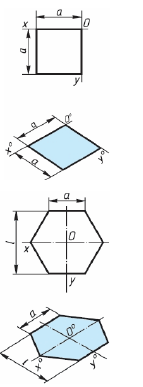
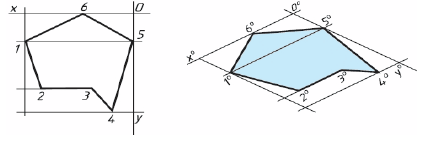
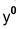 (рис. 2, а). На них от точки С° откладывают отрезки С°1, С°2 и т. д., равные радиусу изображаемой окружности. Через точки 1,2, 3 и 4 проводят прямые, параллельные осям х° и
(рис. 2, а). На них от точки С° откладывают отрезки С°1, С°2 и т. д., равные радиусу изображаемой окружности. Через точки 1,2, 3 и 4 проводят прямые, параллельные осям х° и 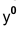 , получая на чертеже точки А, Б, С и D.
, получая на чертеже точки А, Б, С и D.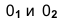 (Рис. 2, в). Эти точки будут центрами малых дуг. Их радиус
(Рис. 2, в). Эти точки будут центрами малых дуг. Их радиус 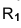 равен
равен 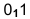 (или
(или 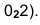 Дугами малого радиуса Ri соединяют большие дуги овала.
Дугами малого радиуса Ri соединяют большие дуги овала.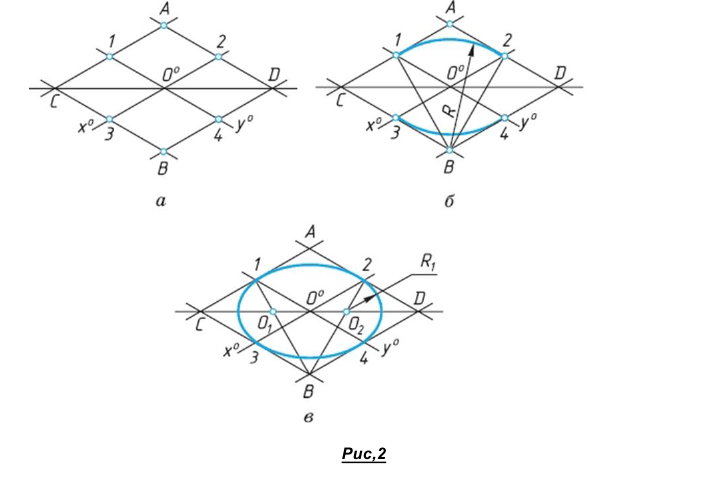
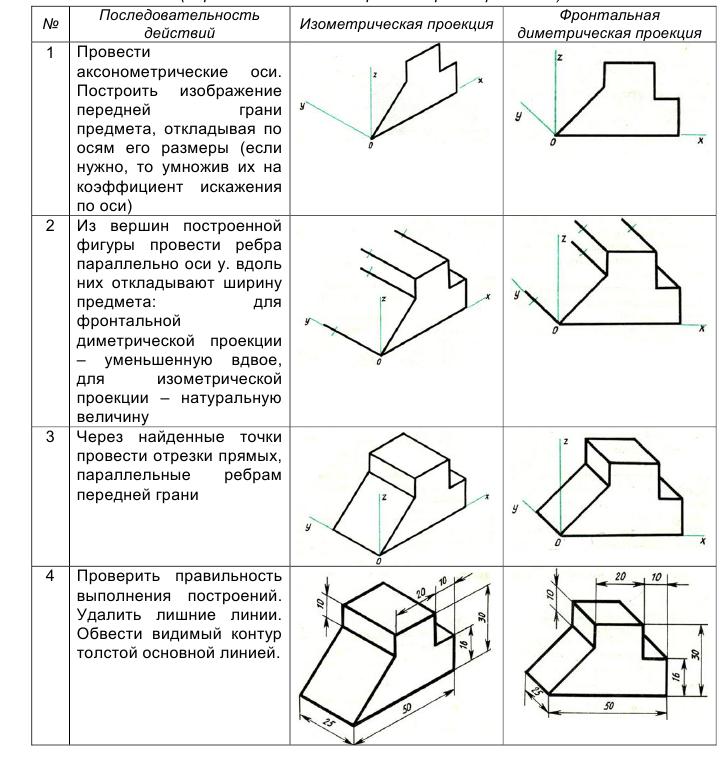
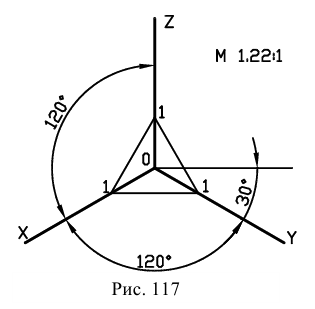
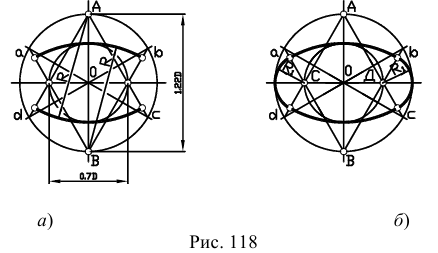
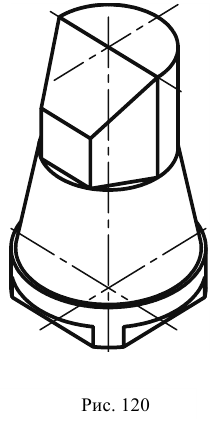
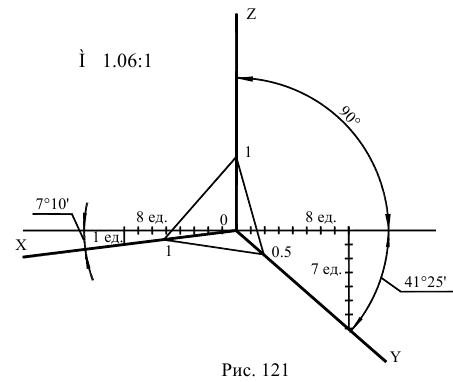
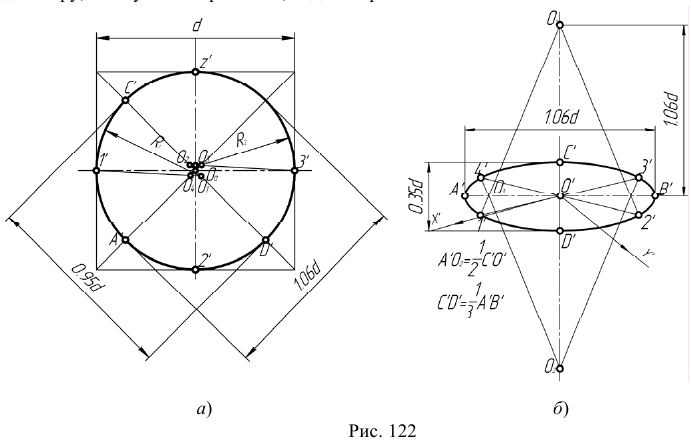
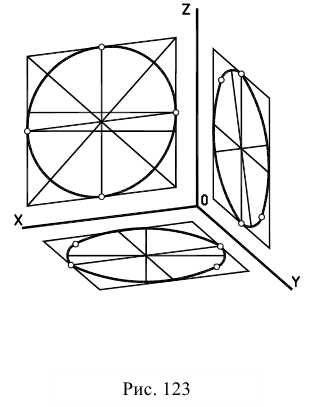
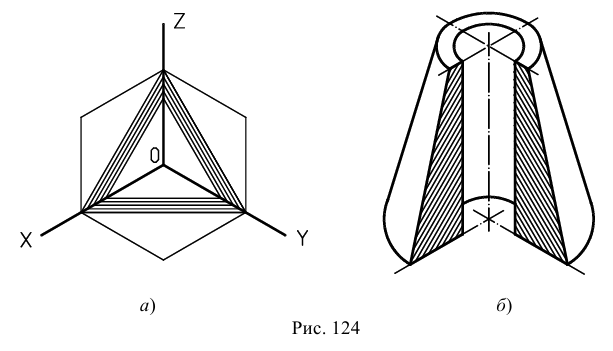
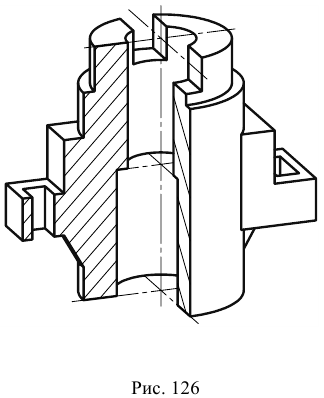
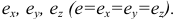
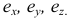
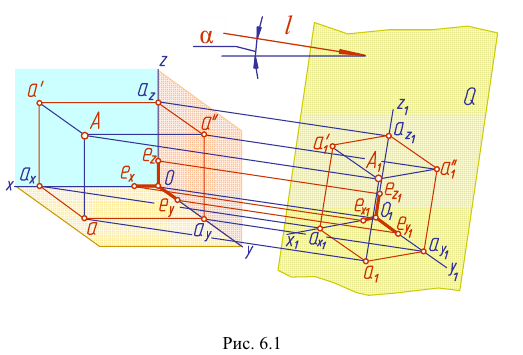
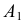 – аксонометрическая проекция точки А;
– аксонометрическая проекция точки А;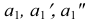 – вторичные проекции точки А;?
– вторичные проекции точки А;?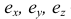 – масштабные отрезки;
– масштабные отрезки;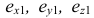 – аксонометрические (вторичные) проекции масштабных отрезков.
– аксонометрические (вторичные) проекции масштабных отрезков.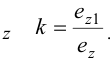
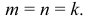
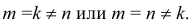
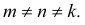
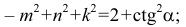
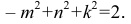
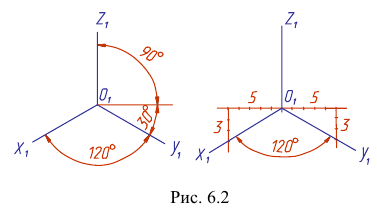
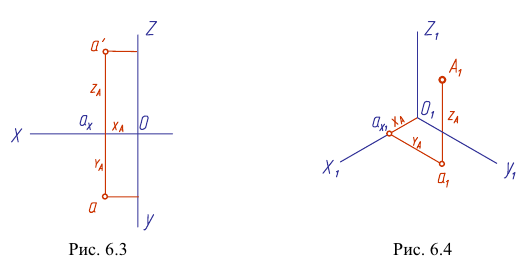
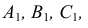
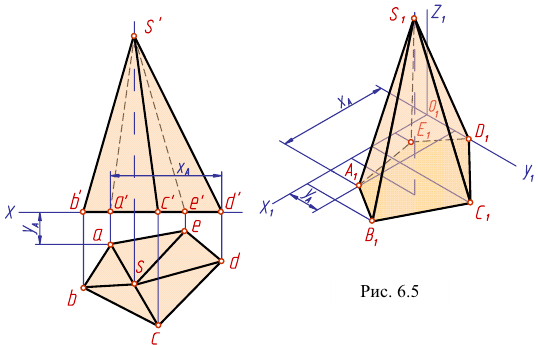
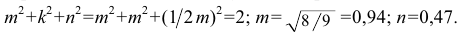
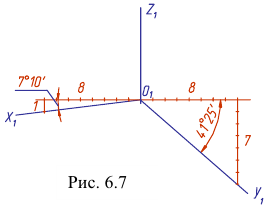
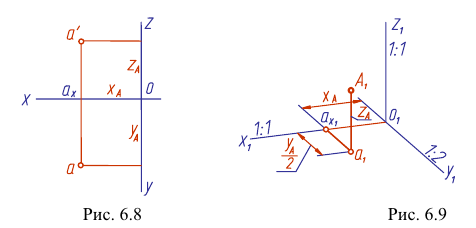
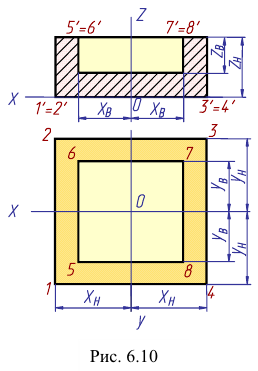
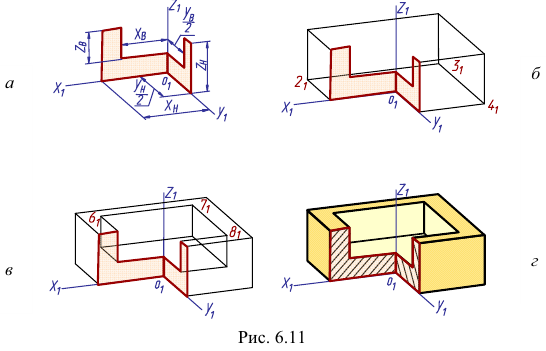
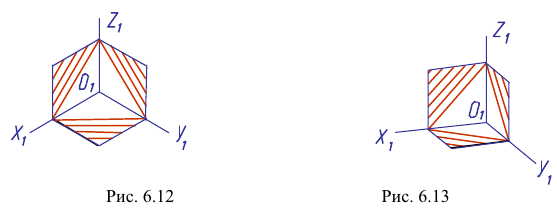
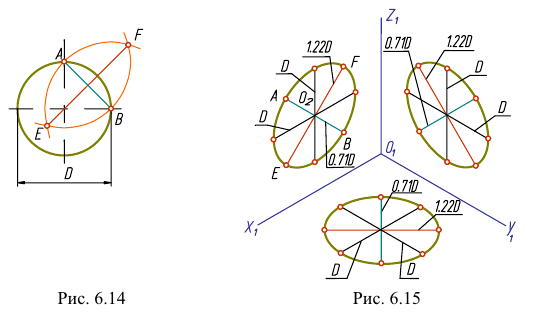
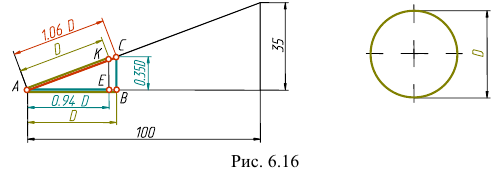
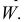
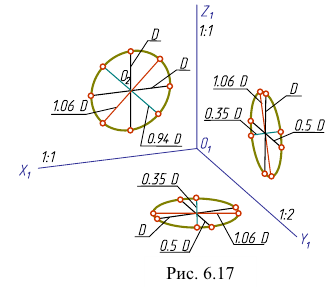
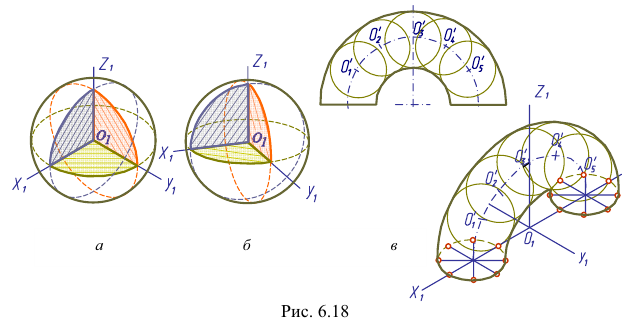
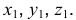
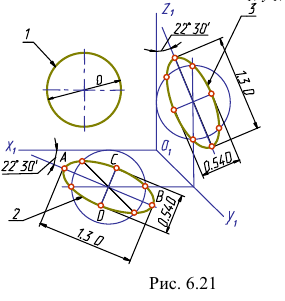
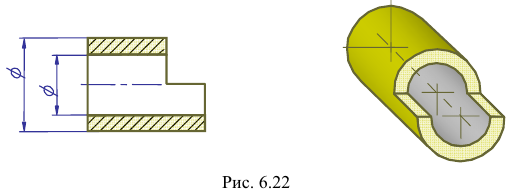
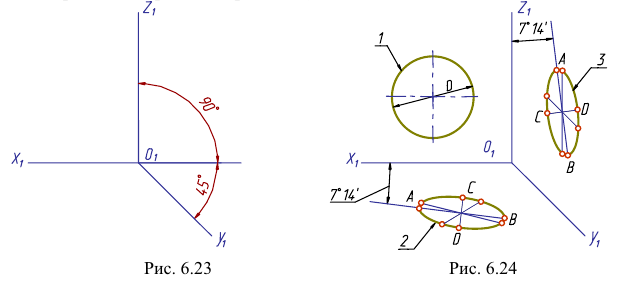
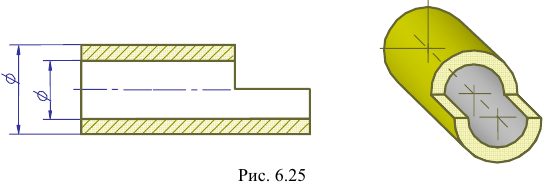
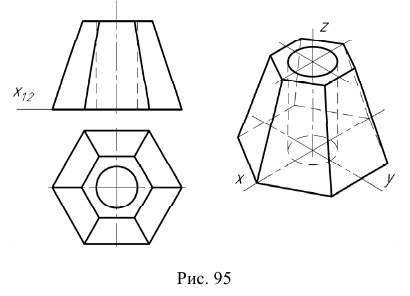
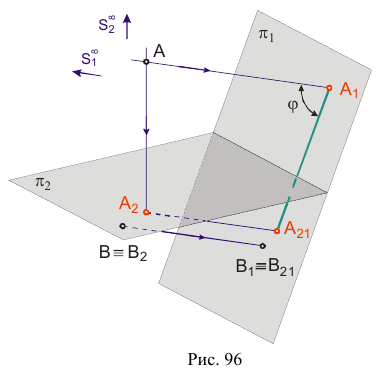
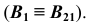
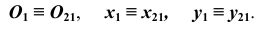
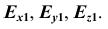
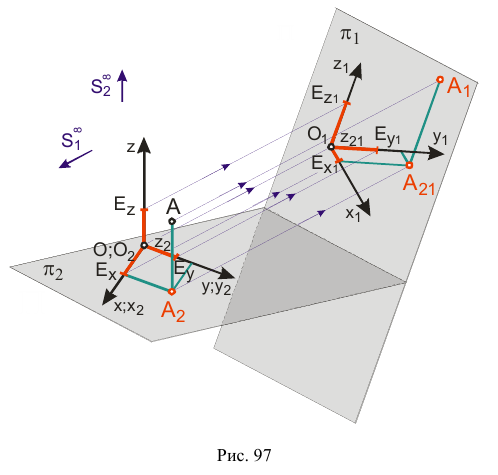
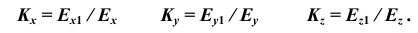
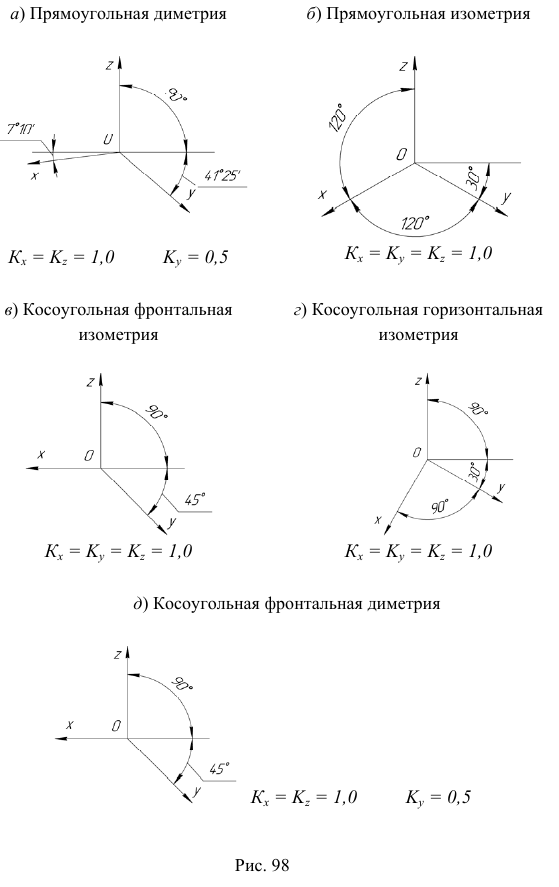
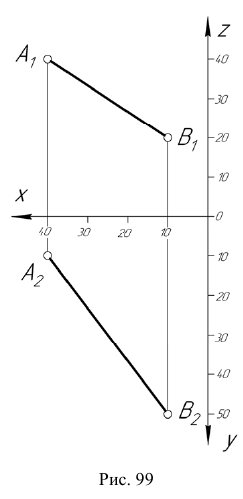
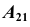 и
и 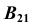 в плоскостях
в плоскостях  по соответствующим координатам с учетом коэффициентов искажения по осям.
по соответствующим координатам с учетом коэффициентов искажения по осям.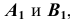 откладывая значения координат точек А и В по оси
откладывая значения координат точек А и В по оси 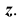 В результате построений получим косоугольную фронтальную диметрию отрезка АВ, представ- ленную на рис. 100, а, и прямоугольную изометрию, представленную на рис. 100, б.
В результате построений получим косоугольную фронтальную диметрию отрезка АВ, представ- ленную на рис. 100, а, и прямоугольную изометрию, представленную на рис. 100, б.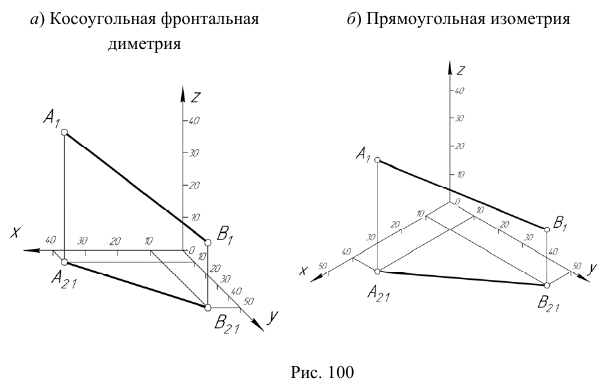
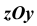 в обеих проекциях вырождается в прямую;
в обеих проекциях вырождается в прямую;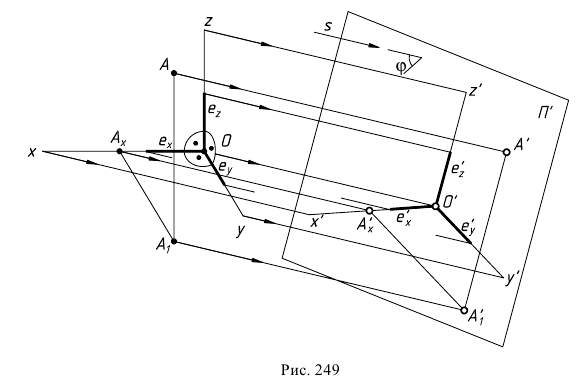
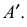
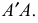
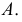
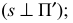
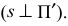
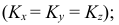
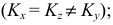
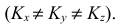
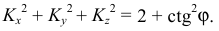
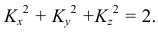
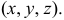
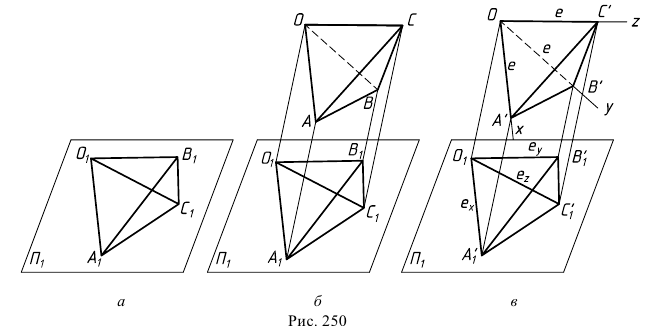
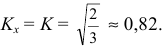
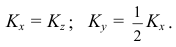
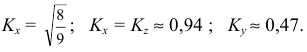
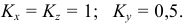
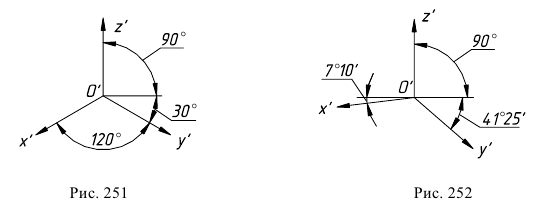
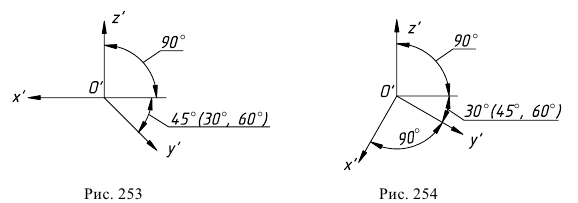
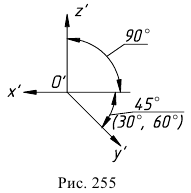
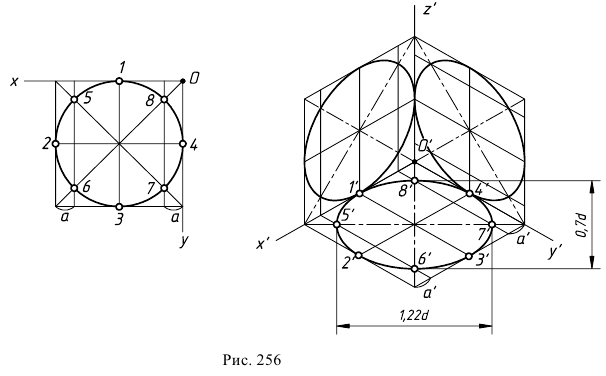
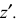
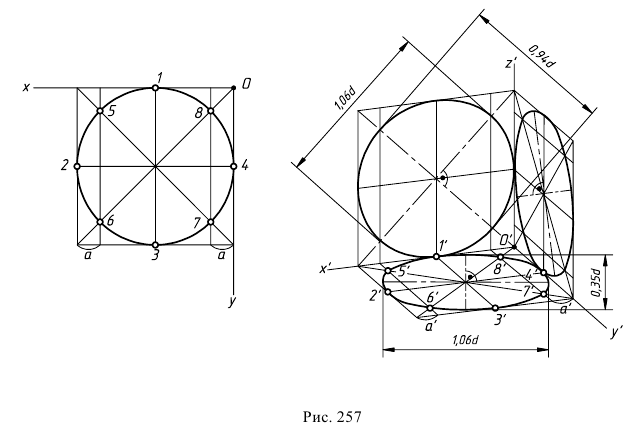
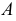 к координатным осям
к координатным осям 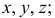
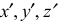 углом 120° друг к другу;
углом 120° друг к другу;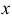 и
и 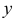 на координатных осях и откладывают их на аксонометрических осях
на координатных осях и откладывают их на аксонометрических осях 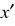 и
и 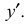 Через полученные точки проводят прямые, параллельные соответствующим аксонометрическим осям
Через полученные точки проводят прямые, параллельные соответствующим аксонометрическим осям 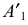 – вторичная проекция точки
– вторичная проекция точки 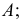
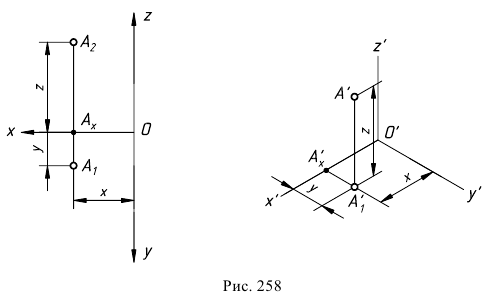
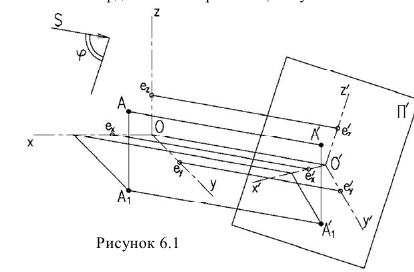
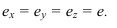
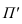 – плоскость аксонометрических проекций (иногда называется картинной плоскостью).
– плоскость аксонометрических проекций (иногда называется картинной плоскостью).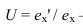 – коэффициент искажении по оси X’;
– коэффициент искажении по оси X’;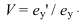 – коэффициент искажения по оси У;
– коэффициент искажения по оси У;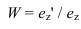 – коэффициент искажения по оси Z’.
– коэффициент искажения по оси Z’.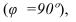
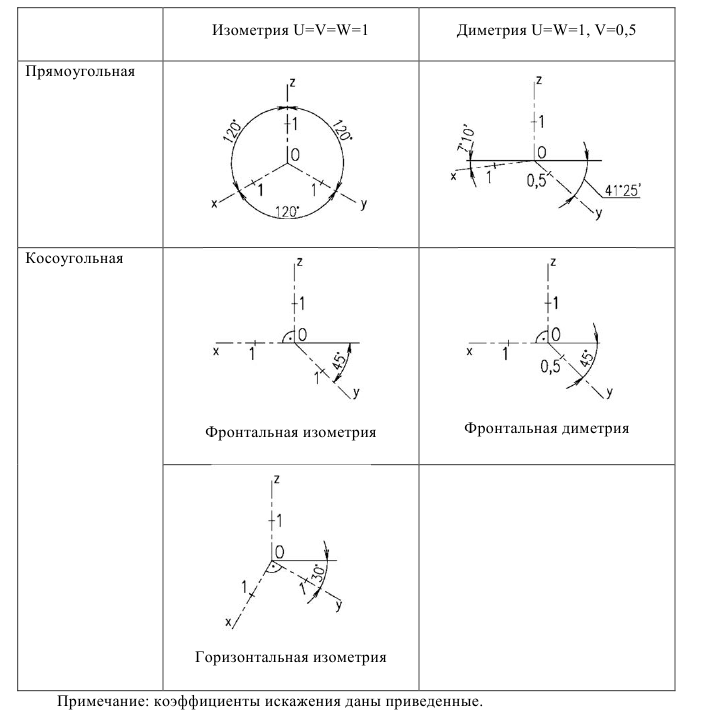
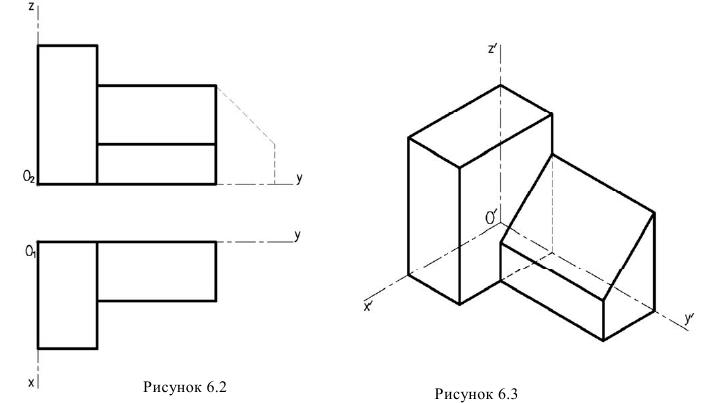
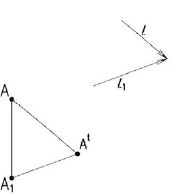
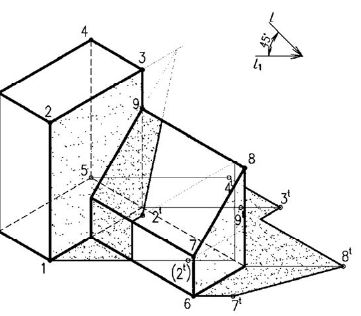
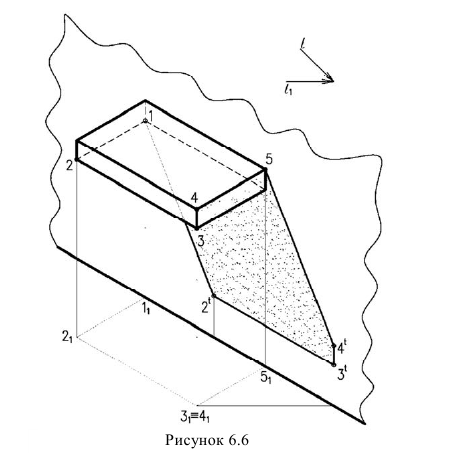
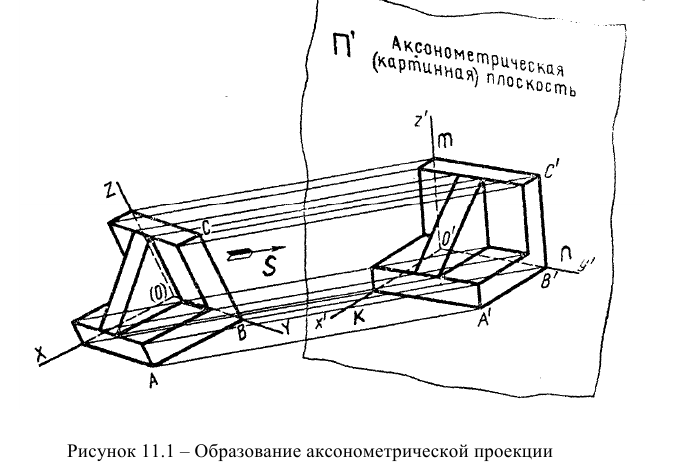
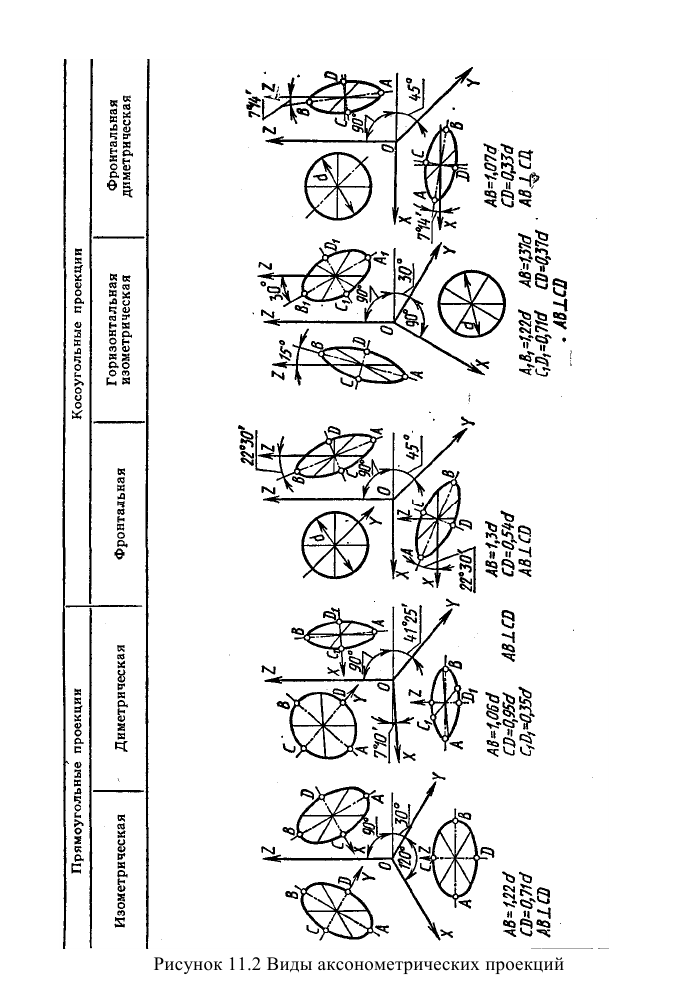
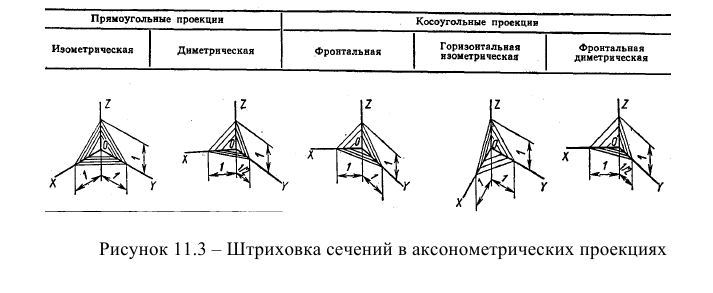
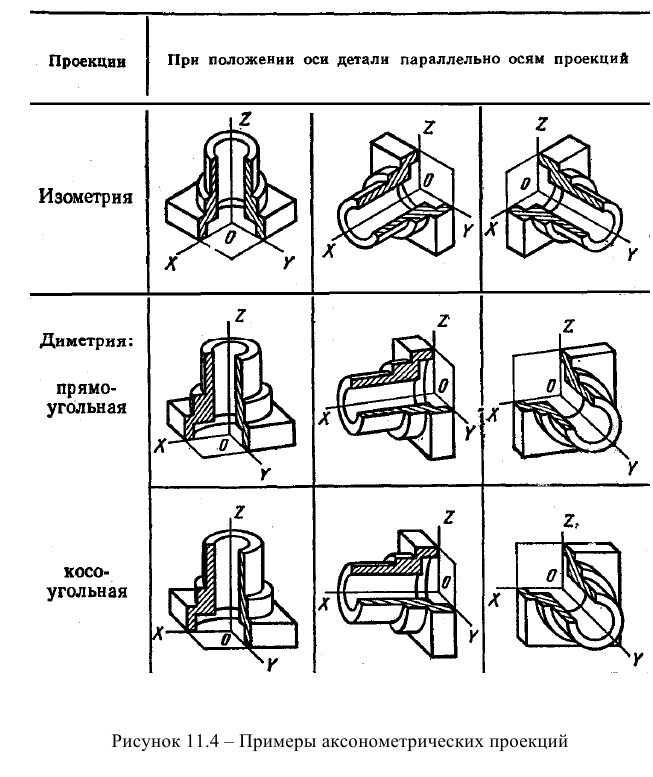
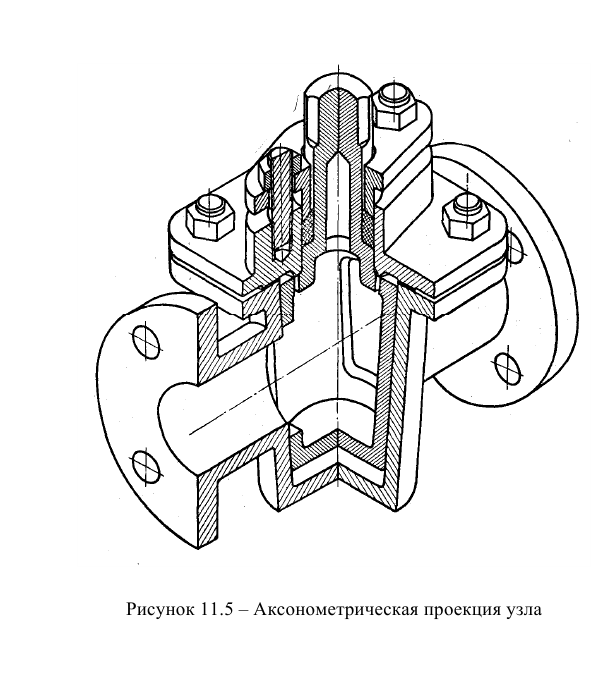
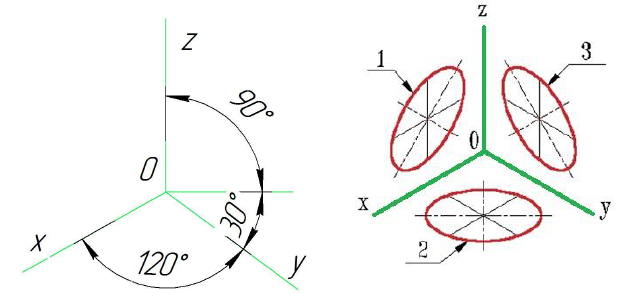
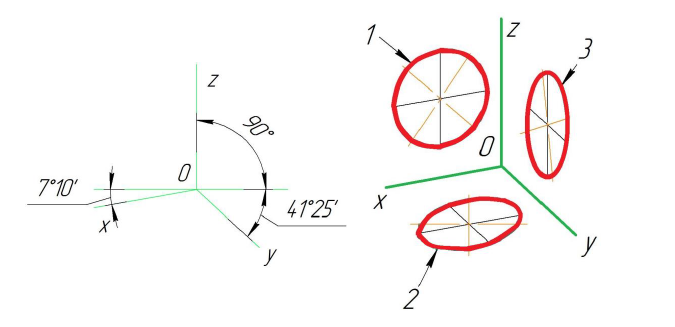
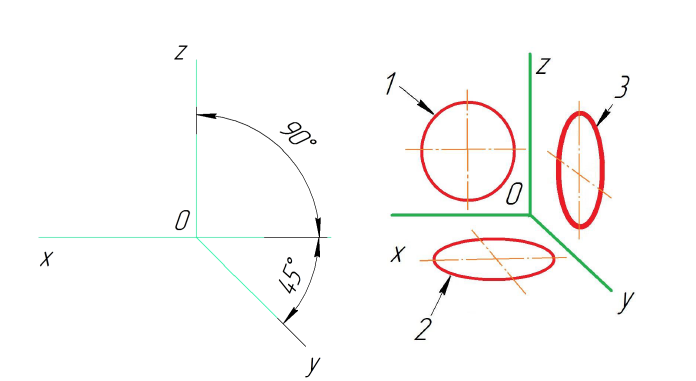
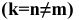
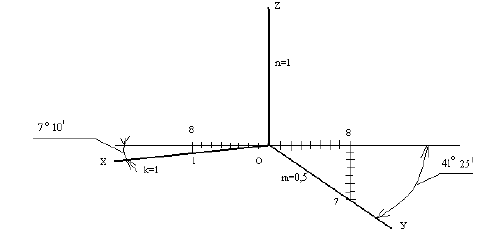
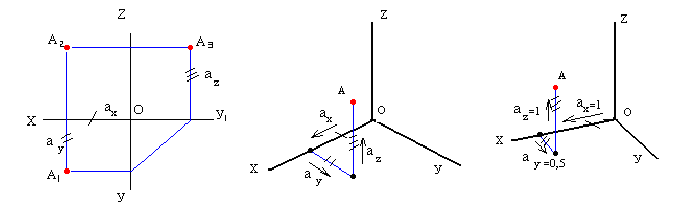
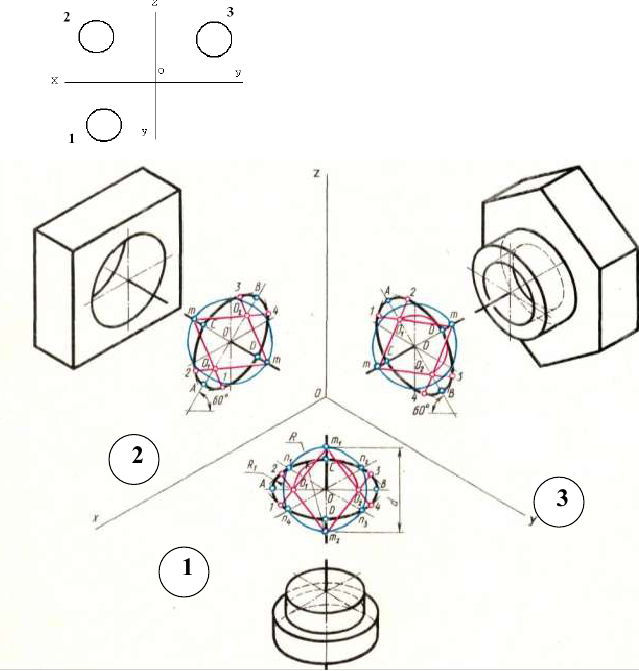
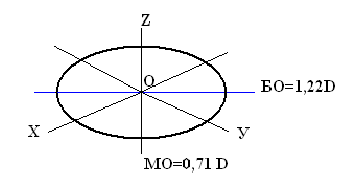
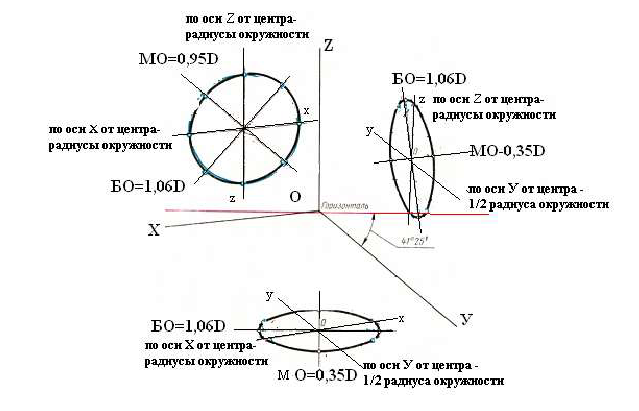
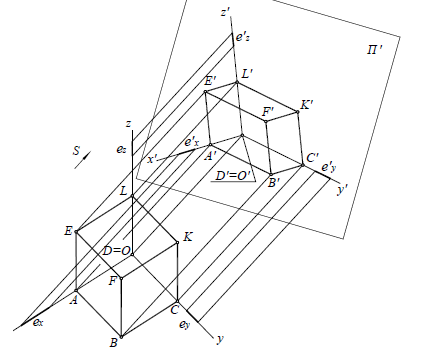
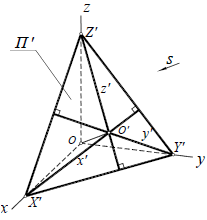
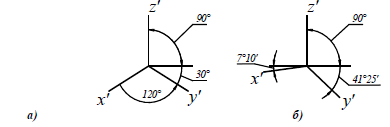
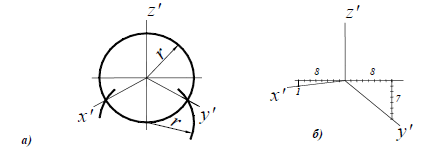
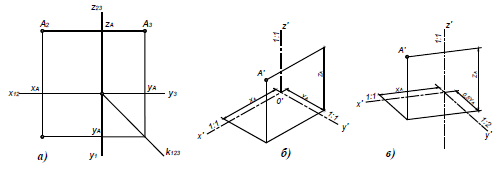
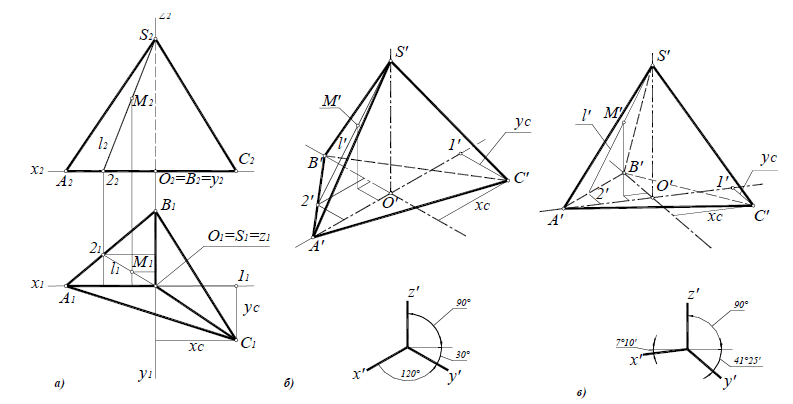
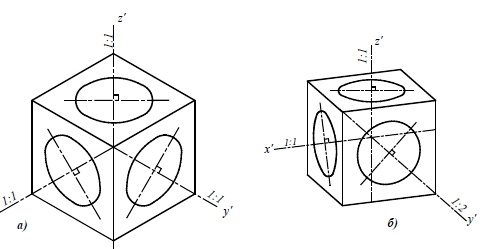
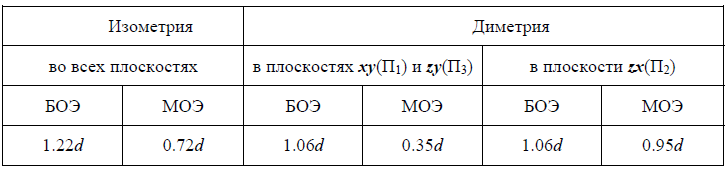
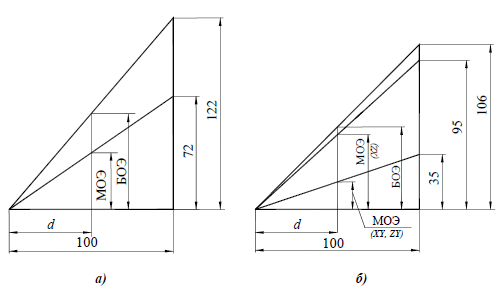
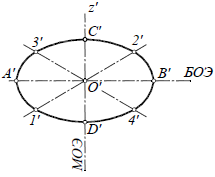
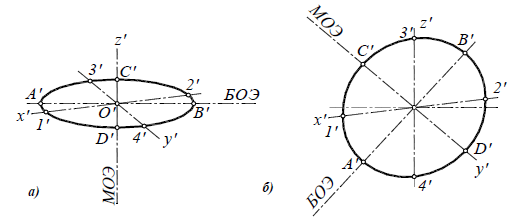
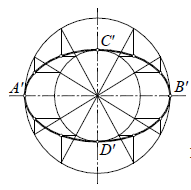
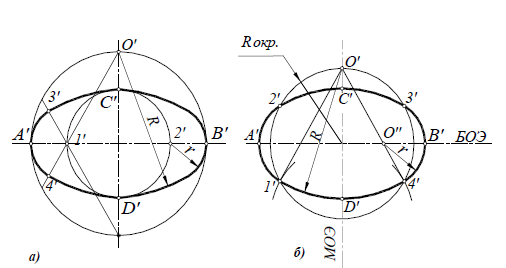
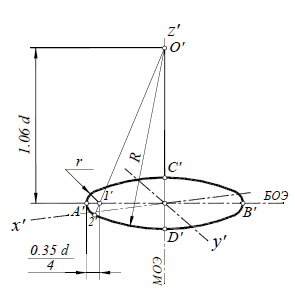
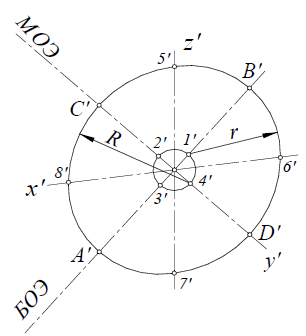
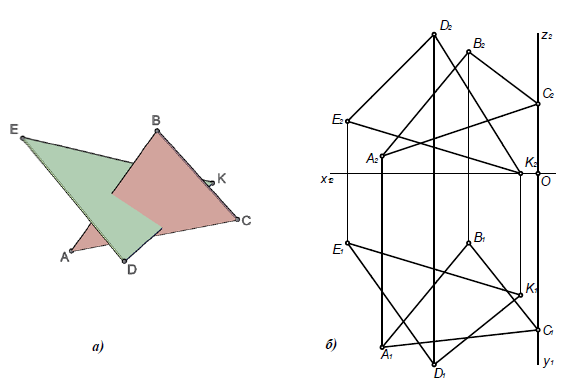
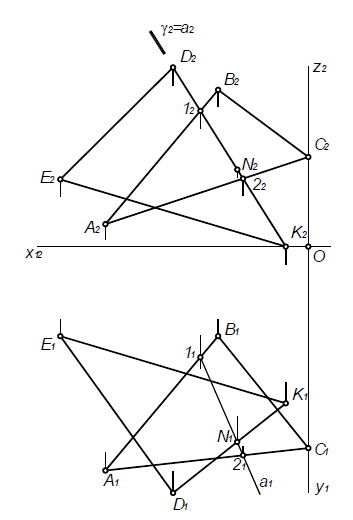
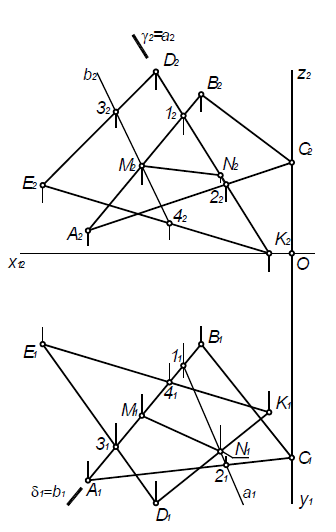
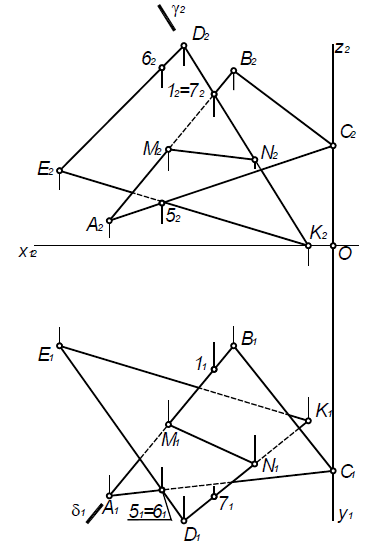
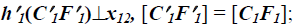
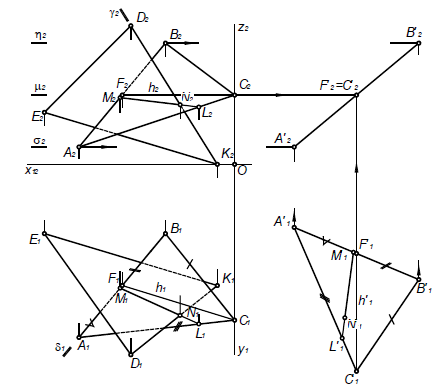
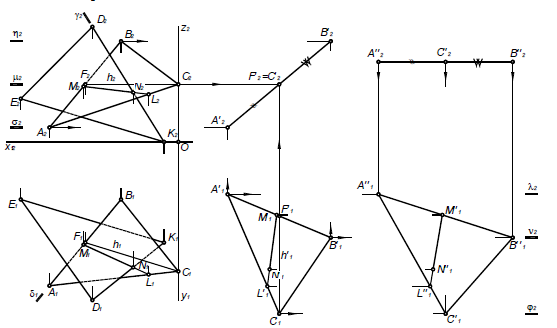
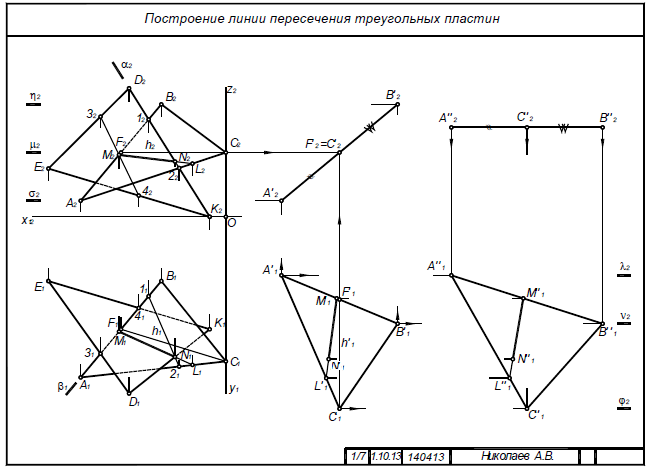
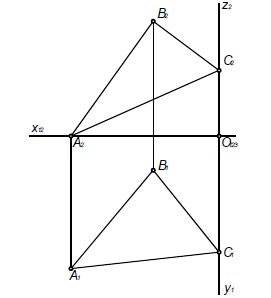
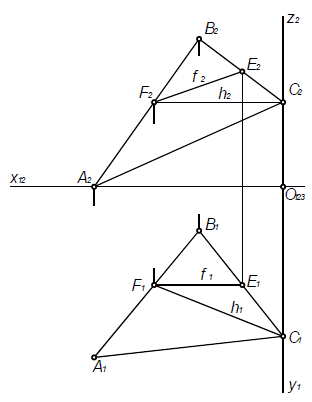
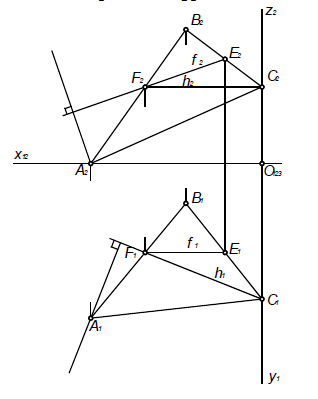
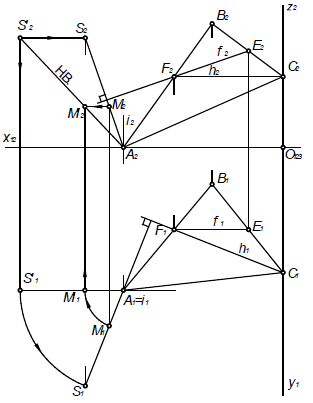
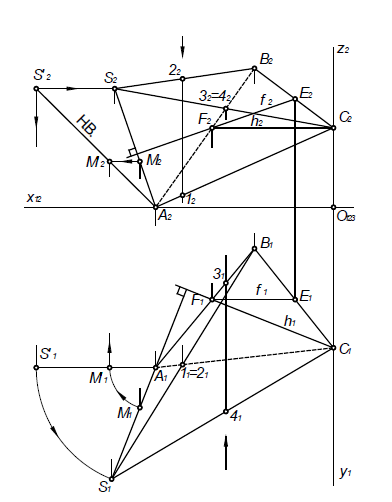
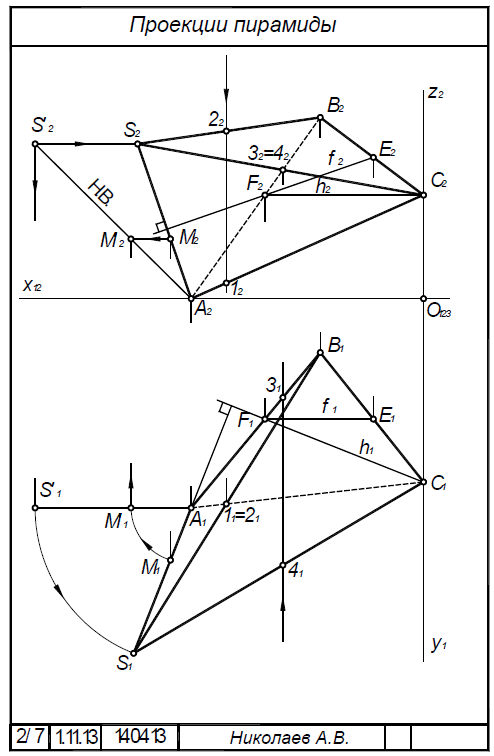
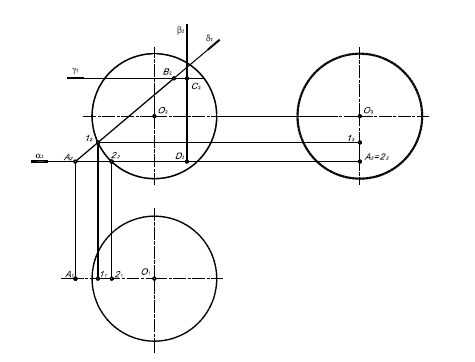
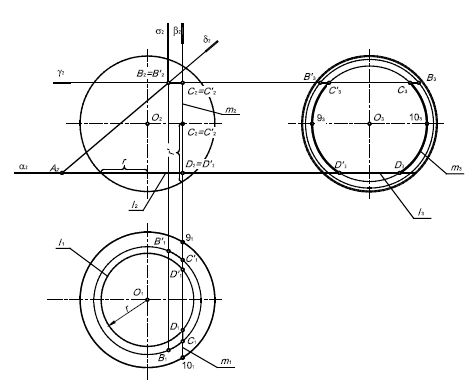
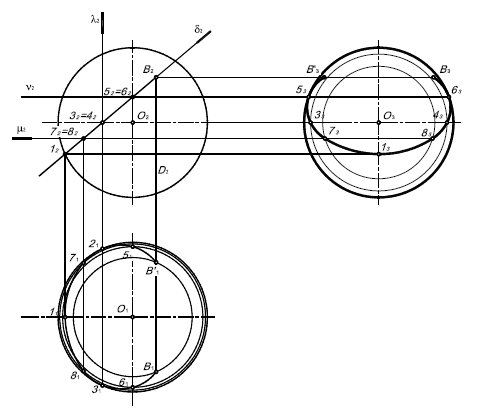
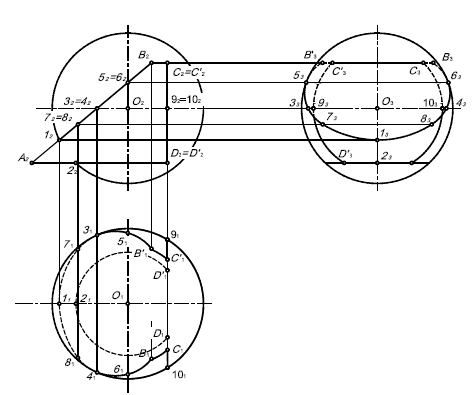
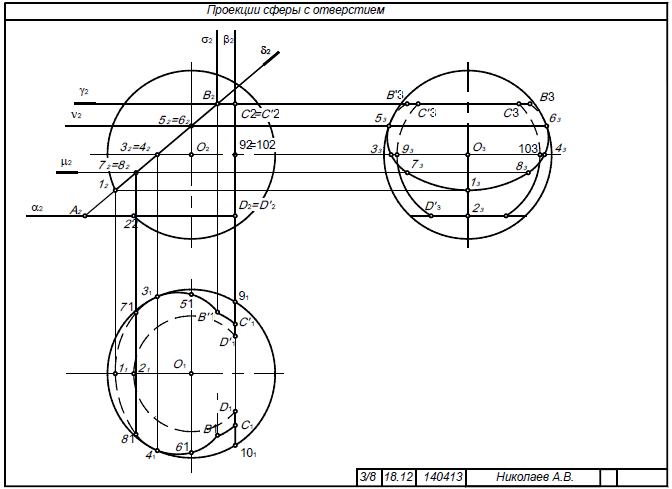
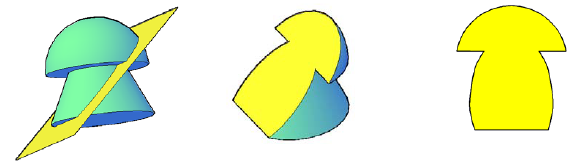
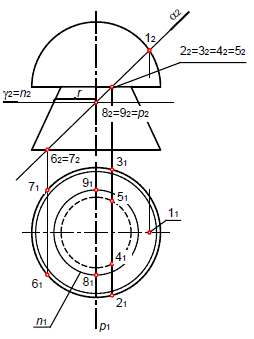
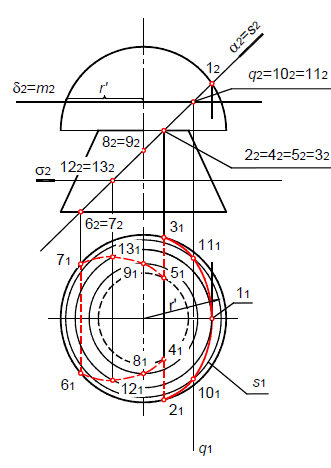
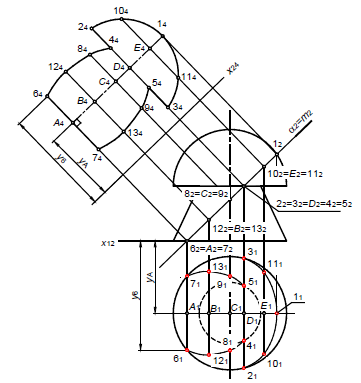
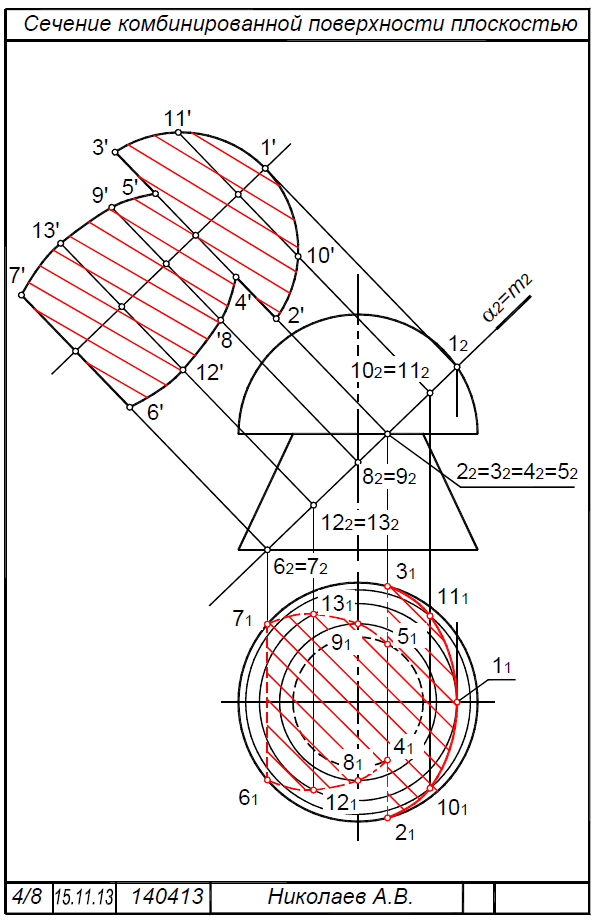
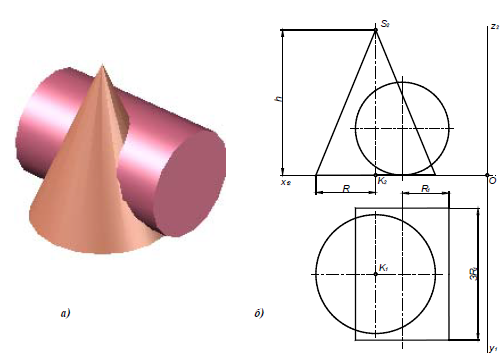
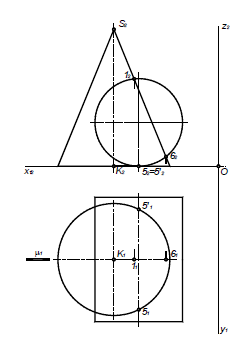
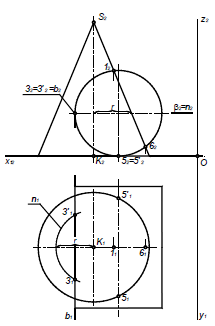
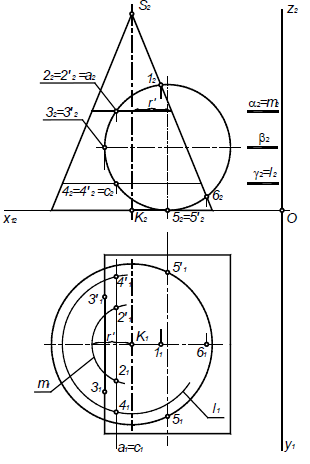
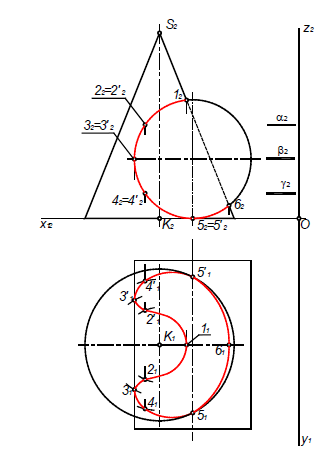
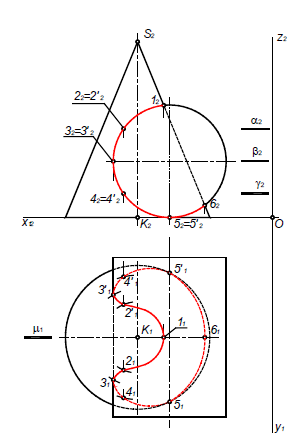
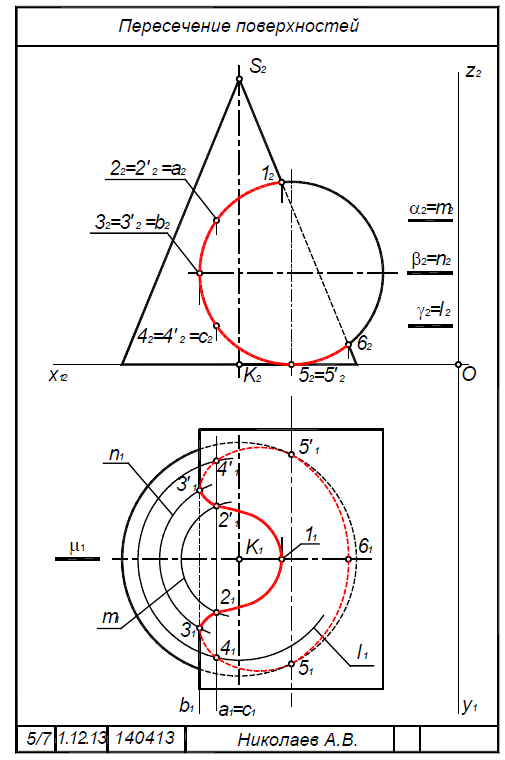
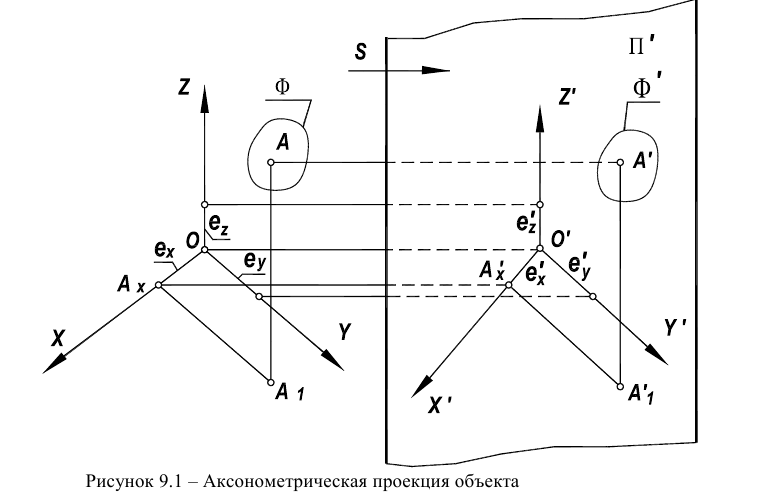
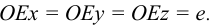
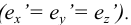
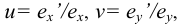
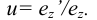
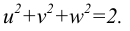
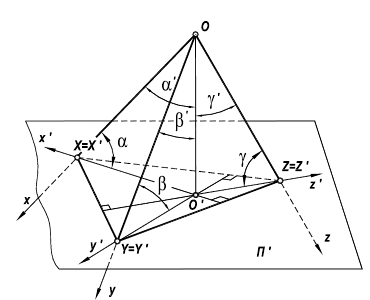
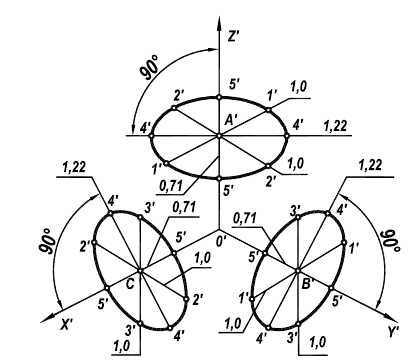
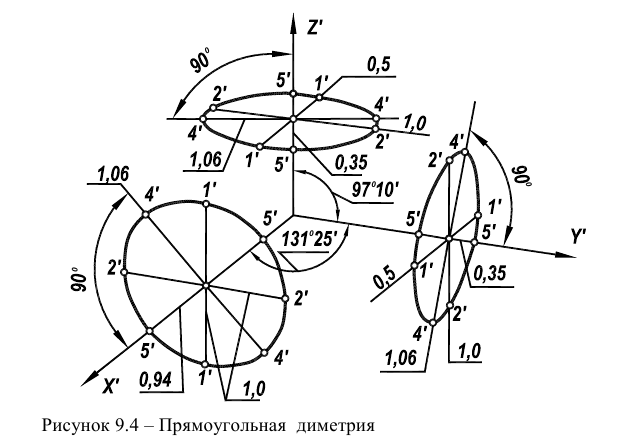
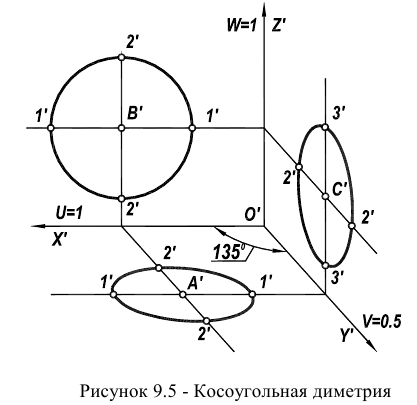
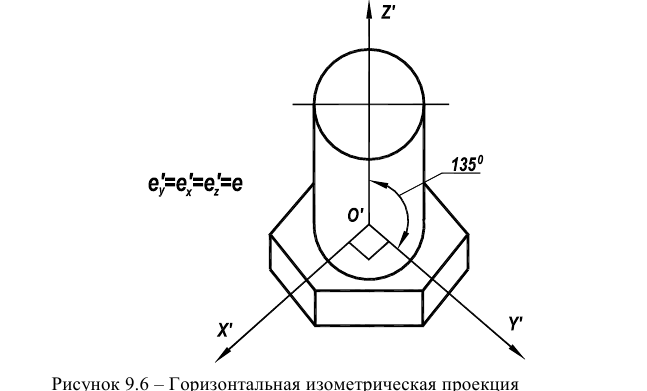
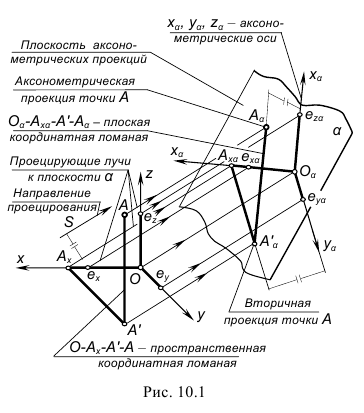
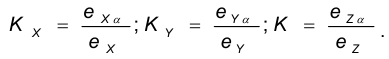
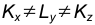 (treis – три).
(treis – три).