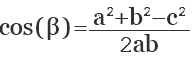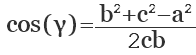Известен один угол как найти остальные углы

Была ли эта статья полезной?

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

Решение:

Из теоремы косинусов имеем:

Откуда

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

Используя онлайн калькулятор для arcsin и arccos находим углы A и B:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Решение:

Найдем сторону c используя теорему косинусов:

Далее, из формулы

найдем cosA:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

Вычисления выше легко производить инженерным онлайн калькулятором.

Из формулы (3) найдем cosA:

Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Решение:

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Откуда

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Ответ:

Исторический термин «решение треугольников» (лат. solutio triangulorum) обозначает решение следующей тригонометрической задачи: найти остальные стороны и/или углы треугольника по уже известным^[1]. Существуют также обобщения этой задачи на случай, когда заданы другие элементы треугольника (например, медианы, биссектрисы, высоты, площадь и т. д.), а также на случай, когда треугольник располагается не на евклидовой плоскости, а на сфере (сферический треугольник), на гиперболической плоскости (гиперболический треугольник) и т. п. Данная задача часто встречается в тригонометрических приложениях — например, в геодезии, астрономии, строительстве, навигации.

Решение плоских треугольников[править | править код]

У треугольника^[2] общего вида имеется 6 основных элементов: 3 линейные (длины сторон ) и 3 угловые (). Сторону, противолежащую углу при вершине, традиционно обозначают той же буквой, что и эта вершина, но не заглавной, а строчной (см. рисунок). В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому далее предполагается, что хотя бы одна из известных величин — линейная^[3].

Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Поскольку вариант «заданы три угла» исключён из рассмотрения, остаются 5 различных вариантов^[4]:

• три стороны;
• две стороны и угол между ними;
• две стороны и угол напротив одной из них;
• сторона и два прилежащих угла;
• сторона, противолежащий угол и один из прилежащих.

Основные теоремы[править | править код]

Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников^[5]:

Теорема косинусов

Теорема синусов

Сумма углов треугольника

Из других иногда полезных на практике универсальных соотношений следует упомянуть теорему тангенсов, теорему котангенсов, теорему о проекциях и формулы Мольвейде.

Замечания[править | править код]

1. Для нахождения неизвестного угла надёжнее использовать теорему косинусов, а не синусов, потому что значение синуса угла при вершине треугольника не определяет однозначно самого угла, поскольку смежные углы имеют один и тот же синус^[6]. Например, если то угол может быть как , так и , потому что синусы этих углов совпадают. Исключением является случай, когда заранее известно, что в данном треугольнике тупых углов быть не может — например, если треугольник прямоугольный. С косинусом такие проблемы не возникают: в интервале от до значение косинуса определяет угол однозначно.
2. При построении треугольников важно помнить, что зеркальное отражение построенного треугольника тоже будет решением задачи. Например, три стороны однозначно определяют треугольник с точностью до отражения.
3. Все треугольники подразумеваются невырожденными, то есть длина стороны не может быть нулевой, а величина угла — положительное число, меньшее, чем .

Три стороны[править | править код]

Пусть заданы длины всех трёх сторон . Условие разрешимости задачи — выполнение неравенства треугольника, то есть каждая длина должна быть меньше, чем сумма двух других длин:

Чтобы найти углы , надо воспользоваться теоремой косинусов^[7]:

Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна

Не рекомендуется второй угол находить по теореме синусов, потому что, как указано в замечании 1, существует опасность спутать тупой угол с острым. Этой опасности не возникнет, если первым определить, по теореме косинусов, наибольший угол (он лежит против наибольшей из сторон) — два других угла точно являются острыми, и применение к ним теоремы синусов безопасно.

Ещё один метод вычисления углов по известным сторонам — использование теоремы котангенсов.

Две стороны и угол между ними[править | править код]

Пусть для определённости известны длины сторон и угол между ними. Этот вариант задачи всегда имеет единственное решение. Для определения длины стороны применяется теорема косинусов^[8]:

Фактически задача сведена к предыдущему случаю. Далее ещё раз применяется теорема косинусов для нахождения второго угла:

Третий угол находится из теоремы о сумме углов треугольника: .

Две стороны и угол напротив одной из них[править | править код]

В этом случае решений может быть два, одно или ни одного. Пусть известны две стороны и угол . Тогда уравнение для угла находится из теоремы синусов^[9]:

Для краткости обозначим (правая часть уравнения). Это число всегда положительно. При решении уравнения возможны 4 случая, во многом зависящие от D^[10][11].

1. Задача не имеет решения (сторона «не достаёт» до линии ) в двух случаях: если или если угол и при этом
2. Если существует единственное решение, причём треугольник прямоугольный:

2. Если то возможны 2 варианта.
   1. Если , то угол имеет два возможных значения: острый угол и тупой угол . На рисунке справа первому значению соответствуют точка , сторона и угол , а второму значению — точка , сторона и угол .
   2. Если , то (большей стороне треугольника соответствует больший противолежащий угол). Поскольку в треугольнике не может быть двух тупых углов, тупой угол для исключён и решение единственно.

Третий угол определяется по формуле . Третью сторону можно найти по теореме синусов:

Сторона и два угла[править | править код]

Пусть задана сторона и два угла. Эта задача имеет единственное решение, если сумма двух углов меньше . В противном случае задача решения не имеет.

Вначале определяется третий угол. Например, если даны углы , то . Далее обе неизвестные стороны находятся по теореме синусов^[12]:

Решение прямоугольных треугольников[править | править код]

В этом случае известен один из углов — он равен 90°. Необходимо знать ещё два элемента, хотя бы один из которых — сторона. Возможны следующие случаи:

• два катета;
• катет и гипотенуза;
• катет и прилежащий острый угол;
• катет и противолежащий острый угол;
• гипотенуза и острый угол.

Вершину прямого угла традиционно обозначают буквой , гипотенузу — . Катеты обозначаются и , а величины противолежащих им углов — и соответственно.

Расчётные формулы существенно упрощаются, так как вместо теорем синусов и косинусов можно использовать более простые соотношения — теорему Пифагора:

и определения основных тригонометрических функций:

Ясно также, что углы и  — острые, так как их сумма равна . Поэтому любой из неизвестных углов однозначно определяется по любой из его тригонометрических функций (синусу, косинусу, тангенсу и др.) путём вычисления соответствующей обратной тригонометрической функции.

При корректной постановке задачи (если заданы гипотенуза и катет, то катет должен быть меньше гипотенузы; если задан один из двух непрямых углов, то он должен быть острый) решение всегда существует и единственно.

Два катета[править | править код]

Гипотенуза находится по теореме Пифагора:

Углы могут быть найдены с использованием функции арктангенса:

или же по только что найденной гипотенузе:

Катет и гипотенуза[править | править код]

Пусть известны катет и гипотенуза — тогда катет находится из теоремы Пифагора:

После этого углы определяются аналогично предыдущему случаю.

Катет и прилежащий острый угол[править | править код]

Пусть известны катет и прилежащий к нему угол .

Гипотенуза находится из соотношения

Катет может быть найден либо по теореме Пифагора аналогично предыдущему случаю, либо из соотношения

Острый угол может быть найден как

Катет и противолежащий острый угол[править | править код]

Пусть известны катет и противолежащий ему угол .

Гипотенуза находится из соотношения

Катет и второй острый угол могут быть найдены аналогично предыдущему случаю.

Гипотенуза и острый угол[править | править код]

Пусть известны гипотенуза и острый угол .

Острый угол может быть найден как

Катеты определяются из соотношений

Решение сферических треугольников[править | править код]

Сферический треугольник общего вида полностью определяется тремя из шести своих характеристик (3 стороны и 3 угла). Стороны сферического треугольника принято измерять не линейными единицами, а величиной опирающихся на них центральных углов.

Решение треугольников в сферической геометрии имеет ряд отличий от плоского случая. Например, сумма трёх углов зависит от треугольника; кроме того, на сфере не существует неравных подобных треугольников, и поэтому задача построения треугольника по трём углам имеет единственное решение. Но основные соотношения: две сферические теоремы косинусов и сферическая теорема синусов, — используемые для решения задачи, аналогичны плоскому случаю.

Из других соотношений могут оказаться полезными формулы аналогии Непера^[13] и формула половины стороны^[14].

Три стороны[править | править код]

Если даны (в угловых единицах) стороны , то углы треугольника определяются из теоремы косинусов^[15]:

,

,

,

Две стороны и угол между ними[править | править код]

Пусть заданы стороны и угол между ними. Сторона находится по теореме косинусов^[15]:

Углы можно найти так же, как в предыдущем случае, можно также использовать формулы аналогии Непера:

Две стороны и угол не между ними[править | править код]

Пусть заданы стороны и угол . Чтобы решение существовало, необходимо выполнение условия:

Угол получается из теоремы синусов:

Здесь, аналогично плоскому случаю, при получаются два решения: и .

Остальные величины можно найти из формул аналогии Непера^[16]:

,

.

Сторона и прилежащие углы[править | править код]

В этом варианте задана сторона и углы . Угол определяется по теореме косинусов^[17]:

Две неизвестные стороны получаются из формул аналогии Непера:

или, если использовать вычисленный угол , по теореме косинусов:

Два угла и сторона не между ними[править | править код]

В отличие от плоского аналога данная задача может иметь несколько решений.

Пусть заданы сторона и углы . Сторона определяется по теореме синусов^[18]:

Если угол для стороны острый и , существует второе решение:

Остальные величины определяются из формул аналогии Непера:

Три угла[править | править код]

Если заданы три угла, стороны находятся по теореме косинусов:

,

,

.

Другой вариант: использование формулы половины угла^[19].

Решение прямоугольных сферических треугольников[править | править код]

Изложенные алгоритмы значительно упрощаются, если известно, что один из углов треугольника (например, угол ) прямой. Прямоугольный сферический треугольник полностью определяется двумя элементами, остальные три находятся при помощи мнемонического правила Непера или из нижеприведённых соотношений^[20]:

Вариации и обобщения[править | править код]

Во многих практически важных задачах вместо сторон треугольника задаются другие его характеристики — например, длина медианы, высоты, биссектрисы, радиус вписанного или описанного круга и т. д. Аналогично вместо углов при вершинах треугольника в задаче могут фигурировать иные углы. Алгоритмы решения подобных задач чаще всего комбинируются из рассмотренных выше теорем тригонометрии.

Примеры:

Примеры практического применения[править | править код]

Триангуляция[править | править код]

Чтобы определить расстояние от берега до недоступной точки — например, до удалённого корабля,— нужно отметить на берегу две точки, расстояние между которыми известно, и измерить углы и между линией, соединяющей эти точки, и направлением на корабль. Из формул варианта «сторона и два угла» можно найти длину высоты треугольника^[23]:

Этот метод используется в каботажном судоходстве. Углы при этом оцениваются наблюдениями с корабля известных ориентиров на земле. Аналогичная схема используется в астрономии, чтобы определить расстояние до близкой звезды: измеряются углы наблюдения этой звезды с противоположных точек земной орбиты (то есть с интервалом в полгода) и по их разности (параллаксу) вычисляют искомое расстояние^[23].

Другой пример: требуется измерить высоту горы или высокого здания. Известны углы наблюдения вершины из двух точек, расположенных на расстоянии . Из формул того же варианта, что и выше, получается^[24]:

Расстояние между двумя точками на поверхности земного шара[править | править код]

Надо вычислить расстояние между двумя точками на земном шаре^[25]:

Точка : широта долгота

Точка : широта долгота

Для сферического треугольника , где  — северный полюс, известны следующие величины:

Это случай «две стороны и угол между ними». Из приведенных выше формул получается:

,

где  — радиус Земли.

История[править | править код]

Зачатки тригонометрических знаний можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.^[26]

Общая постановка задачи решения треугольников (как плоских, так и сферических) появилась в древнегреческой геометрии^[27]. Во второй книге «Начал» Евклида теорема 12 представляет собой словесный аналог теоремы косинусов для тупоугольных треугольников^[28]:

В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.

Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее^[29]: древнейшее из дошедших до нас доказательств теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике», написанной в XIII веке^[30].

Первые тригонометрические таблицы составил, вероятно, Гиппарх в середине II века до н. э. для астрономических расчётов. Позднее астроном II века Клавдий Птолемей в «Альмагесте» дополнил результаты Гиппарха. Первая книга «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные тригонометрические таблицы хорд для острых и тупых углов, с шагом 30 угловых минут. В таблицах Птолемей приводит значение длин хорд с точностью до трех шестидесятиричных знаков^[31]. Такая точность примерно соответствует пятизначной десятичной таблице синусов с шагом 15 угловых минут^[1].

Птолемей явно не формулирует теорему синусов и косинусов для треугольников. Тем не менее он всегда справляется с задачей решения треугольников, разбивая треугольник на два прямоугольных^[32].

Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию^[33]. Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках, аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). По сообщению Паппа, Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов^[34]. Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике.

В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров^[35]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В частности, индийцы первыми ввели в использование косинус^[36]. Кроме того, индийцы знали формулы для кратных углов , для . В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется сферический вариант теоремы синусов, однако общая формулировка этой теоремы в Индии так и не появилась^[37].

В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались «зиджи»; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории^[38]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс^[36].

Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века^[29]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника^[39]. Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения^[40].

Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году^[41]. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам^[42]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для эффективного решения треугольников.

В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10″^[43]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера»^[44]. Алгебраизация тригонометрии, начатая Франсуа Виетом, была завершена Леонардом Эйлером в XVIII веке, после чего алгоритмы решения треугольников приобрели современный вид.

См. также[править | править код]

• Признаки подобия треугольников
• Площадь треугольника
• Сферическая тригонометрия
• Сферический треугольник
• Триангуляция
• Тригонометрические тождества
• Тригонометрические функции
• Формулы Мольвейде

Примечания[править | править код]

Литература[править | править код]

Теория и алгоритмы

• Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия: 7—9 классы. Учебник для общеобразовательных учреждений. — 19-е изд. — М.: Просвещение, 2009. — 384 с. — ISBN 978-5-09-021136-9.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
• Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия, учебник для 10 класса. — М.: МЦНМО, 2002. — ISBN 5-94057-050-X.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Мензел Д. (ред.). Основные формулы физики. Глава 1. Основные математические формулы. — М.: Изд. иностранной литературы, 1957. — 658 с.
• Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1963. — Т. 4. — С. 518—557. — 568 с.
• Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948.

История

• Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.
• Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
• История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
  • Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
  • Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
• Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
• Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
• Цейтен Г. Г. История математики в древности и в средние века. — М.—Л.: ГТТИ, 1932. — 230 с.
• Цейтен Г. Г. История математики в XVI и XVII веках. — М.—Л.: ОНТИ, 1938. — 456 с.

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Углы треугольника

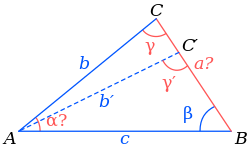
Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.

α = 180°-β-γ

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

a 2 = b 2 + c 2 + 2abc cos (α)

Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:

cos (α) = (b 2 + c 2 — a 2 ) / 2bc

,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.

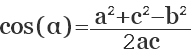
Углы прямоугольного треугольника

Калькулятор расчёта углов прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

• tg α – тангенс угла α
• a – противолежащий катет
• b – прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла – острые.

[spoiler title=”источники:”]

http://kalk.top/sz/corners-pr-triangle

[/spoiler]

Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.

Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).

Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.

Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника

Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co

Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.

Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.

Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.

Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.

Итак,

Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.

Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.

Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.

Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.

Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.

Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.

Как найти углы в прямоугольном треугольнике, если известны стороны?

Дан треугольник АВС, угол С — прямой.

Стороны АВ, АС и ВС известны.

Т.к. угол С — прямой, он равен 90 градусам.

Другие углы можно найти, например, так:

если известен катет и гипотенуза

sinA = BC / AB,

sinB = AC / AB,

если известны два катета

tg A = BC / AC

tg B = AC / BC

Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.

Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.

Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.

sin 15° = 0,259

arcsin0,259 = 15°

Как найти углы в прямоугольном треугольнике, если известен один угол?

Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.

Еединичная окружность (единичный круг)

Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).

Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).

Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.

Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).

Координатные четверти отсчитываются так:

                        y

                       |

                       |

(II четверть)   |   (I четверть)

                       |

________________________ x

                       |0

                       |

(III четверть)  |   (IV четверть)

                       |

                       |

Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).

Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).

Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).

Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).

Например:

• углы первой четверти: 30 градусов, 85 градусов, пи/4;
• углы второй четверти: 120 градусов, 178 градусов;
• углы третьей четверти: 205 градусов, 260 градусов;
• углы четвертой четверти: 272 градуса, 305 градусов.

Тригонометрические функции

К тригонометрическим функциям относятся функции:

y = sin x;

y = cos x;

y = tg x;

y = ctg x;

y = sec x;

y = cosec x.

Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.

Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.

Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.

Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.

Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.

Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.

Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.

Как найти синус угла, если известен косинус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

sin²a = 1 − cos²a

|sin a| = КОРЕНЬ(1 − cos²a)

sin a = ± КОРЕНЬ(1 − cos²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти косинус угла, если известен синус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

cos²a = 1 − sin²a

|cos a| = КОРЕНЬ(1 − sin²a)

cos a = ± КОРЕНЬ(1 − sin²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти синус угла, если известен котангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + ctg² a = 1/sin² a

sin² a = 1 / (1 + ctg² a)

|sin a| = 1/ КОРЕНЬ(1 + ctg² a)

sin a = ±1/ КОРЕНЬ(1 + ctg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)

Как найти косинус угла, если известен тангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + tg² a = 1/cos² a

cos² a = 1 / (1 + tg² a)

|cos a| = 1/ КОРЕНЬ(1 + tg² a)

cos a = ±1/ КОРЕНЬ(1 + tg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)

Тригонометрическое тождество

Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.

Основные тригонометрические тождества:

sin²a + cos²a = 1

tg a = sin a / cos a

ctg a = cos a / sin a

sec a = 1 / cos a

cosec a = 1 / sin a

Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)

• arcsin — читается: арксинус;
• arcos — читается: арккосинус;
• arctg — читается: арктангенс;
• arcctg — читается: арккотангенс.

arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.

Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:

y = arcsin x sin y = x

Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:

y = arccos x cos y = x

Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:

y = arctg x tg y = x

Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:

y = arctg x tg y = x

Например,

sin 30° = 0,5

arcsin0,5 = 30°

Синусоида и косинусоида

График функции y = sin x называется синусоидой.

График функции y = cos x называется косинусоидой.

Источники информации:

• Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
• В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
• docme.ru — зачем нужна тригонометрия?
• ru.wikipedia.org — Википедия — тригонометрия;
• ru.wikihow.com — как изучать тригонометрию?