Как архимед нашел число пи

Активируйте ПРОМОКОД mathematic25 для LITRES.RU до 31.08 и получите скидку 25% на весь каталог электронных книг. 

Подписывайтесь на канал в Яндекс. Дзен или на канал в телеграм “Математика не для всех”, чтобы не пропустить интересующие Вас материалы. Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения!

Добрый день, уважаемые Читатели! Трудно написать что-то новое про число Пи : всё уже десятки раз разжевано не только авторами Дзен, но и на всевозможных других сайтах. С другой стороны, обходить его стороной на блоге, посвященном математике, – чистой воды кощунство. Поехали!

Экскурс в историю

В своём материале, я недавно рассказывал про древнейший сборник математических задач, созданный египетским писарем Ахмесом. В одной из задач требовалось найти площадь круга определенного диаметра, и самое удивительное, египтяне справлялись без числа Пи!

На самом деле, вавилонские, египетские, древнегреческие и древнеиндийские математики были едины в том, что отношение длины окружности к её радиусу – величина постоянная.

В Вавилоне вообще считалось, что это отношение равно 3, что не помешало им построить Вавилонскую башню с использованием этого ошибочного знания. Хотя, все знают, как закончилась её история. Урок на будущее!

Древнеегипетские математики были более точны и определяли его как 3,16, в Индии считали отношение равным √10. Но, без сомнения, самый важный прорыв в изучении числа Пи сделал Архимед.

Как он рассчитал число π ?

Архимед дал оценку числа π, используя “метод исчерпывания”, разработанный еще Евклидом. Для этого Архимед описывал и вписывал в окружность шести-, двенадцати- и так далее до 96-угольника.

Окружность, таким образом, как бы зажималась между многоугольниками, и с увеличением количества углов, их периметр (Архимед умел его вычислять для произвольного многоугольника) всё лучше и лучше приближал длину окружности. Оценка была тем более точной, чем больше сторон у многоугольников. Дойдя до 96-угольника Архимед заключил, что отношение длины окружности к её радиусу примерно равно 3,14, что очень неплохо для почти любых хозяйственных расчетов.

Затем началась настоящая гонка: Птолемей рассматривал 720-угольник, через полторы тысячи лет Франсуа Виет использовал 393216-угольник, получив 10 знаков, а в конце 17 века Людольф Ван Цейлен находит 35 верных знаков числа π , оперируя чудовищным 32515254720 – угольником, потратив на эти расчеты более (!!!) 10 лет.

Отвечая на немой вопрос: все эти математики, конечно, не производили геометрических построений, а пользовались тем фактом, что разница в площади многоугольников формирует геометрическую прогрессию с показателем 4.

Увеличивать количество углов дальше не представлялось рациональным даже самым упорным математикам, ведь все вычисления приходилось проводить вручную. К счастью, наступил 18 век, и пришла эпоха математического анализа, а конкретно её область, изучающая бесконечные ряды. “Первой ласточкой” было установление Яковом Грегори формулы представления арктангенса числа:

Если подставить в эту формулу вместо x единицу, получим слева число π/4, а справа сумму вида (1-1/3)+(1/5-1/7)+(1/9-1/11) + …

Несмотря на то, что для получения лишь 4 верных знаков требовалось вычислить сумму 300 слагаемых, это был шаг вперед. Теперь не требовалось проводить утомительных вычислений квадратных корней, как в случае с “методом исчерпываний”.

Леонард Эйлер, которому, кстати, и приписывают устоявшееся обозначение числа π, использовал следующую доказанную им формулу для нахождения более чем 100 верных знаков:

Еще пару сотен лет, математики продолжали придумывать такого рода формулы и довели количество верных знаков до 519 к середине 19 века. После этого произошел небольшой застой, который, как Вы легко догадаетесь, закончился с изобретением ЭВМ в середине 20 века.

В 1949 году отец информационного века Джон Фон Нейман на компьютере ЭНИАК за 70 часов вычислил более 2000 знаков числа π. Сравните, это время с 10 годами, потраченными Ван Цейленом!

В настоящее время рекорд по вычислению числа π составляет 31,4 триллиона знаков после запятой!

На этом экскурс в историю закончен: в следующем материале я расскажу еще много удивительных фактов про самую великую математическую константу! Например, что будет если принять её равной 3?

Есть, что добавить в историческом плане? Пишите в комментариях!

Читайте мой материал про самые красивую математическую картину

Путеводитель по каналу “Математика не для всех” – здесь собрано больше 100 статей на самые разнообразные темы: как для новичков, так и для более начитанных математиков!

Второй проект – канал “Русский язык не для всех”

Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием. ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.

**************************************************************************

Уже много веков и даже, как ни странно, тысячелетий люди понимают важность и ценность для науки математической постоянной, равной отношению длины окружности к ее же диаметру. Кто открыл число Пи, до сих пор неизвестно, но к нему имели отношение самые лучшие математики на протяжении всей нашей истории. Большинство из них хотели выразить его рациональным числом.

Интересные сведения о числе Пи

1. Исследователи и истинные поклонники числа Пи организовали клуб, для вступления в который требуется знать наизусть достаточно большое количество его знаков.

2. С 1988 года празднуется «День числа Пи», который приходится на 14 марта. Готовят салаты, торты, печенья, пирожные с его изображением.

3. Число Пи уже переложили на музыку, при этом оно весьма неплохо звучит. Ему даже воздвигли памятник в американском Сиэтле перед зданием городского Музея искусств.

Древний период

В то далекое время число Пи старались вычислить при помощи геометрии. То, что это число постоянно для самых разных окружностей, знали еще геометры в Древнем Египте, Вавилоне, Индии и Древней Греции, утверждавшие в своих работах, что оно всего лишь немного больше трех.

В одной из священных книг джайнизма (древняя индийская религия, которая возникла в VI в. до н. э.) упоминается, что тогда число Пи считалось равным корню квадратному из десяти, что в итоге дает 3,162… .

Древнегреческие математики проводили измерение окружности методом построения отрезка, а вот для того, чтобы измерить круг, им приходилось строить равновеликий квадрат, то есть фигуру, равную ему по площади.

Когда еще не знали десятичных дробей, великий Архимед нашел значение числа Пи с точностью 99,9%. Он открыл способ, который стал основой многих последующих вычислений, вписывал в окружность и описывал вокруг нее правильные многоугольники. В результате Архимед рассчитал значение числа Пи как отношение 22 / 7 ≈ 3,142857142857143.

В Китае, математик и придворный астроном, Цзу Чунчжи в V веке до н. э. обозначил более точное значение числа Пи, рассчитав его до семи цифр после запятой и определил его значение между числами 3, 1415926 и 3,1415927. Более 900 лет понадобилось ученым, чтобы продолжить дальше этот цифровой ряд.

Средние века

Известный индийский ученый Мадхава, который жил на рубеже XIV – XV веков, ставший основателем Керальской школы астрономии и математики, впервые в истории стал работать над разложением тригонометрических функций в ряды. Правда, сохранились всего лишь два его труда, а на другие известны лишь ссылки и цитаты его учеников. В научном трактате «Махаджьянаяна», который приписывают Мадхаве, указано, что число Пи равно 3,14159265359. А в трактате «Садратнамала» приведено число с еще большим количеством точных знаков после запятой: 3,14159265358979324. В указанных числах последние цифры не соответствуют правильному значению.

В XV веке самаркандский математик и астроном Ал-Каши вычислил число Пи с шестнадцатью знаками после запятой. Его результат считался наиболее точным в течение последующих 250 лет.

У. Джонсон, математик из Англии, одним из первых смог обозначить отношение длины окружности к ее диаметру буквой π. Пи — это первая буква греческого слова «περιφέρεια» — окружность. Но этому обозначению удалось стать общепринятым лишь после того, как им воспользовался в 1736 году более известный ученый Л. Эйлер.

Заключение

Современные ученые продолжают работать над дальнейшими вычислениями значений числа Пи. Для этого уже используют суперкомпьютеры. В 2011 г. ученый из Японии Сигэру Кондо, сотрудничая с американским студентом Александром Йи, произвели правильный расчет последовательности из 10 триллионов цифр. Но до сих пор так и неясно, кто открыл число Пи, кто впервые задумался над этой проблемой и произвел первые расчеты этого, по-настоящему мистического числа.

Читайте также:

Кто первым создал азбуку для русского языка?

Кто открыл закон инерции: Галилей или Ньютон?

У этого термина существуют и другие значения, см. Пи.

Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π
Система счисления	Оценка числа
Десятичная	3,1415926535897932384626433832795…
Двоичная	11,00100100001111110110…
Шестнадцатеричная	3,243F6A8885A308D31319…
Шестидесятеричная	3; 08 29 44 00 47 25 53 07 …
Рациональные приближения	22⁄7, 179⁄57, 223⁄71, 333⁄106, 355⁄113, 103 993⁄33 102 (перечислено в порядке увеличения точности)
Непрерывная дробь	[3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, … ] (Эта непрерывная дробь не периодическая. Записана в линейной нотации)
Тригонометрия	радиан = 180°

(произносится «пи») — математическая постоянная, равная отношению длины окружности к её диаметру^{[K 1]}. Обозначается буквой греческого алфавита «π». На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой^[2].

Свойства

Трансцендентность и иррациональность

Число  иррационально, то есть его значение не может быть точно выражено в виде дроби , где  — целое число, а  — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа была впервые доказана Иоганном Ламбертом в 1761 году^[3] путём разложения тангенса в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел и . Несколько доказательств подробно приведено в статье Доказательства иррациональности π.

 — трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году^[4]. Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа , то доказательство трансцендентности положило конец попыткам построить квадратуру круга, длившимся более 2,5 тысяч лет.

В 1934 году Гельфонд доказал^[5] трансцендентность числа . В 1996 году Юрий Нестеренко доказал, что для любого натурального числа и алгебраически независимы, откуда, в частности, следует^[6][7] трансцендентность чисел и .

является элементом кольца периодов (а значит, вычислимым и арифметическим числом). Но неизвестно, принадлежит ли к кольцу периодов.

Соотношения

Известно много формул для вычисления числа :

• Формула Виета для приближения числа π:

Это первое известное явное представление с бесконечным числом операций. Доказать его можно следующим образом. Применив тождество рекурсивно и перейдя к пределу, получим

Остаётся подставить и воспользоваться формулой косинуса двойного угла:

• Формула Валлиса:

• Ряд Лейбница:

• Ряд с использованием двойного факториала:

• Формула, найденная Сринивасой Рамануджаном:

• Другие ряды:

(ряд обратных квадратов)

(следует из предыдущих формул)

Следующие ряды позволяют вычислять знаки в шестнадцатеричной записи числа пи без вычисления предыдущих знаков:

• Кратные ряды:

• Пределы:

здесь  — простые числа

где равно числу корней в выражении^[8].

• Тождество Эйлера:

• Другие связи между константами:

Формула, найденная Сринивасой Рамануджаном:

• Т. н. интеграл Пуассона или интеграл Гаусса:

где  — корень Бринга.

• Интегральный синус:

• Выражение через дилогарифм^[9]:

• Через несобственный интеграл:

;

История

Впервые обозначением этого числа греческой буквой воспользовался британский математик Уильям Джонс в 1706 году^[10], а общепринятым оно стало после работ Леонарда Эйлера в 1737 году. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр^[11].

Исследование числа и уточнение его значения шли параллельно с развитием всей математики и занимают несколько тысячелетий. Сначала изучалось с позиции геометрии, затем развитие математического анализа в XVII веке показало универсальность этого числа.

Геометрический период

То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским и древнегреческим геометрам, древнейшие приближения относятся к третьему тысячелетию до н. э.

В Древнем Вавилоне принимали равным трём, что соответствовало замене длины окружности на периметр вписанного в неё шестиугольника. Площадь круга определялась^[12] как квадрат длины окружности, делённый на 12, что также соответствует допущению Самые ранние из известных более точных приближений датируются примерно 1900-ми годами до н. э.: это ²⁵/₈ = 3,125 (глиняная табличка из Суз периода Старовавилонского царства)^[13] и ²⁵⁶/₈₁ ≈ 3,16 (египетский папирус Ахмеса периода Среднего царства); оба значения отличаются от истинного не более, чем на 1 %. Ведийский текст «Шатапатха-брахмана» даёт в качестве приближения дробь ³³⁹/₁₀₈ ≈ 3,139.

Китайский философ и учёный Чжан Хэн во II веке предложил для числа два эквивалента: 92/29 ≈ 3,1724 и ≈ 3,1622. В священных книгах джайнизма, написанных в V—VI веках до н. э., обнаружено, что тогда и в Индии принимали равным ^[14]

Архимед, возможно, первым предложил математический способ вычисления . Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника — как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку и предложил для приближённого вычисления верхнюю из найденных им границ: — 22/7 ≈ 3,142857142857143.

Следующее приближение в европейской культуре связано с астрономом Клавдием Птолемеем (ок. 100 — ок. 170), который создал таблицу хорд с шагом в полградуса, что позволило ему получить для приближение ³⁷⁷/₁₂₀, равное приближённо вычисленной им половине периметра 720-угольника, вписанного в единичную окружность^[15]. Леонардо Пизанский (Фибоначчи) в книге «Practica Geometriae» (около 1220 г.), видимо, принимая приближение Птолемея за нижнюю границу для , приводит своё приближение^[16] — ⁸⁶⁴/₂₇₅. Но оно оказалось хуже, чем у Птолемея, поскольку последний ошибся при определении длины хорды в полградуса в большую сторону, в результате чего приближение ³⁷⁷/₁₂₀ оказалось верхней границей для .

В Индии Ариабхата и Бхаскара I использовали приближение 3,1416. Варахамихира в VI веке пользуется в «Панча-сиддхантике» приближением .

Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм^[en] для вычисления с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для по следующему принципу:

Позднее Лю Хуэй придумал быстрый метод вычисления и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.

В 480-х годах китайский математик Цзу Чунчжи продемонстрировал, что ≈ ³⁵⁵/₁₁₃, и показал, что 3,1415926 < < 3,1415927, используя алгоритм Лю Хуэя применительно к 12288-угольнику. Это значение оставалось самым точным приближением числа в течение последующих 900 лет.

Классический период

До II тысячелетия было известно не более 10 цифр . Дальнейшие крупные достижения в изучении связаны с развитием математического анализа, в особенности с открытием рядов, позволяющих вычислить с любой точностью, суммируя подходящее количество членов ряда.

Ряд Мадхавы — Лейбница

В 1400-х годах Мадхава из Сангамаграмы нашёл первый из таких рядов:

Этот результат известен как ряд Мадхавы — Лейбница, или ряд Грегори — Лейбница (после того, как он был заново обнаружен Джеймсом Грегори и Готфридом Лейбницем в XVII веке). Однако этот ряд сходится к очень медленно, что приводит к сложности вычисления многих цифр числа на практике — необходимо сложить около 4000 членов ряда, чтобы улучшить оценку Архимеда. Однако преобразованием этого ряда в

Мадхава смог вычислить как 3,14159265359, верно определив 11 цифр в записи числа. Этот рекорд был побит в 1424 году персидским математиком Джамшидом ал-Каши, который в своём труде под названием «Трактат об окружности» привёл 17 цифр числа , из которых 16 верные.

Лудольфово число

Первым крупным европейским вкладом со времён Архимеда был вклад голландского математика Людольфа ван Цейлена, затратившего десять лет на вычисление числа с 20 десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n = 60·2²⁹. Изложив свои результаты в сочинении «Об окружности» («Van den Circkel»), Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа . Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число иногда называли «лудольфовым числом» или «константой Лудольфа».

Лудольфово число — приближённое значение для числа с 35 верными десятичными знаками^[17].

Формула Виета для приближения π

Примерно в это же время в Европе начали развиваться методы анализа и определения бесконечных рядов. Первым таким представлением была формула Виета для приближения числа π:

,

найденная Франсуа Виетом в 1593 году.

Формула Валлиса

Другим известным результатом стала формула Валлиса:

,

выведенная Джоном Валлисом в 1655 году.

Аналогичные произведения:

Произведение, доказывающее родственную связь с числом e

Методы, основанные на тождествах

В Новое время для вычисления используются аналитические методы, основанные на тождествах. Перечисленные выше формулы малопригодны для вычислительных целей, поскольку либо используют медленно сходящиеся ряды, либо требуют сложной операции извлечения квадратного корня.

Формулы Мэчина

Первый эффективный и современный способ нахождения числа (а также натуральных логарифмов и других функций), основанный на развитой им теории рядов и математического анализа, дал в 1676 году Исаак Ньютон во втором письме к Ольденбургу^[18], разлагая в ряд . На основе этого метода наиболее эффективную формулу нашёл в 1706 году Джон Мэчин

Разложив арктангенс в ряд Тейлора

,

можно получить быстро сходящийся ряд, пригодный для вычисления числа с большой точностью.

Формулы такого типа, в настоящее время известные как формулы Мэчина^[en], использовались для установки нескольких последовательных рекордов и остались наилучшими из известных методов для быстрого вычисления компьютерами. Выдающийся рекорд был поставлен феноменальным счётчиком Иоганном Дазе, который в 1844 году по распоряжению Гаусса применил формулу Мэчина для вычисления 200 цифр . Наилучший результат к концу XIX века был получен англичанином Уильямом Шенксом, у которого ушло 15 лет для того, чтобы вычислить 707 цифр. Однако он допустил ошибку в 528-й цифре, в результате чего все последующие цифры оказались неверными^[19]. Чтобы избежать подобных ошибок, современные вычисления подобного рода проводятся дважды. Если результаты совпадают, то они с высокой вероятностью верные. Ошибку Шенкса обнаружил один из первых компьютеров в 1948 году; он же за несколько часов подсчитал 808 знаков .

Пи — трансцендентное число

Теоретические достижения в XVIII веке привели к постижению природы числа , чего нельзя было достичь лишь только с помощью одного численного вычисления. Иоганн Ламберт доказал иррациональность в 1761 году, а Адриен Лежандр в 1774 году доказал иррациональность . В 1735 году была установлена связь между простыми числами и , когда Леонард Эйлер решил знаменитую Базельскую проблему — проблему нахождения точного значения

,

которое оказалось равно . И Лежандр, и Эйлер предполагали, что может быть трансцендентным, что было в конечном итоге доказано в 1882 году Фердинандом фон Линдеманом.

В 1945 году Картрайт упростила элементарное доказательство Шарля Эрмита иррациональности числа .

Символ «»

Считается, что книга Уильяма Джонса «Обозрение достижений математики» (Synopsis Palmoriorum Mathesios, 1706 год) первая ввела в использование греческую букву для обозначения этой константы, но эта запись стала общепринятой после того, как Леонард Эйлер принял её (или пришёл к ней независимо) в 1737 году^[11]. Эйлер писал: «Существует множество других способов отыскания длин или площадей соответствующей кривой или плоской фигуры, что может существенно облегчить практику; например, в круге диаметр относится к длине окружности как 1 к ».

Эра компьютерных вычислений

Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр , которое заняло 70 часов. В 1961 году Дэниел Шенкс на IBM 7090 рассчитал 100 000 знаков, а отметка в миллион была пройдена в 1973 году^{[K 2]}. Такой прогресс имел место не только благодаря более быстрому аппаратному обеспечению, но и благодаря новым алгоритмам.

Голландский математик Лёйтзен Брауэр в первой половине XX века привёл в качестве примера бессмысленной задачи поиск в десятичном разложении последовательности  — по его мнению, нужная для этого точность никогда не будет достигнута. В конце XX века эта последовательность была обнаружена, она начинается с 17 387 594 880-го знака после запятой^[20].

В начале XX века индийский математик Сриниваса Рамануджан обнаружил множество новых формул для , некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины. Одна из этих формул — это ряд:

.

Братьями Чудновскими в 1987 году найдена похожая на неё:

,

которая даёт примерно по 14 цифр на каждый член ряда. Чудновские использовали эту формулу для того, чтобы установить несколько рекордов в вычислении в конце 1980-х, включая тот, в результате которого в 1989 году была получена 1 011 196 691 цифра десятичного разложения.

Эта формула используется в программах, вычисляющих на персональных компьютерах, в отличие от суперкомпьютеров, которые устанавливают современные рекорды.

В то время как последовательность обычно повышает точность на фиксированную величину с каждым следующим членом, существуют итеративные алгоритмы, которые на каждом шагу «умножают» количество правильных цифр, однако требуя высоких вычислительных затрат на каждом из таких шагов.

Прорыв в этом отношении был сделан в 1975 году, когда Ричард Брент и Юджин Саламин^[en] независимо друг от друга открыли алгоритм Брента — Саламина^[en], который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков^[21]. Алгоритм состоит из установки начальных значений

и итераций:

,

пока a_n и b_n не станут достаточно близки.
Тогда оценка даётся формулой

При использовании этой схемы 25 итераций достаточно для получения 45 миллионов десятичных знаков. Похожий алгоритм, увеличивающий на каждом шаге точность в четыре раза, был найден Джонатаном Боруэйном^[en] Питером Боруэйном^[en][22]. При помощи этих методов Ясумаса Канада и его группа, начиная с 1980 года, установили большинство рекордов вычисления вплоть до 206 158 430 000 знаков в 1999 году. В 2002 году Канада и его группа установили новый рекорд — 1 241 100 000 000 десятичных знаков. Хотя большинство предыдущих рекордов Канады было установлено при помощи алгоритма Брента — Саламина, вычисление 2002 года использовало две формулы типа мэчиновских, которые работали медленнее, но радикально снижали использование памяти. Вычисление было выполнено на суперкомпьютере Hitachi из 64 узлов с 1 терабайтом оперативной памяти, способном выполнять 2 триллиона операций в секунду.

Важным развитием недавнего времени стала формула Бэйли — Боруэйна — Плаффа, открытая в 1997 году Саймоном Плаффом^[en] и названная по авторам статьи, в которой она впервые была опубликована^[23].
Эта формула,

примечательна тем, что она позволяет извлечь любую конкретную шестнадцатеричную или двоичную цифру числа без вычисления предыдущих^[23]. С 1998 до 2000 года проект распределённых вычислений PiHex^[en] использовал видоизменённую формулу Беллара для вычисления квадриллионного бита числа , который оказался нулём^[24].

В 2006 году Саймон Плафф, используя алгоритм PSLQ, нашёл ряд красивых формул^[25]. Пусть q = e^π, тогда

и другие вида

,

где q = e^π, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:

для рационального p, у которого знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.

В августе 2009 года учёные из японского университета Цукубы рассчитали последовательность из 2 576 980 377 524 десятичных разрядов^[26].

19 октября 2011 года Александр Йи и Сигэру Кондо^[ja] рассчитали последовательность с точностью в 10 триллионов цифр после запятой^[27][28]. 28 декабря 2013 года они же рассчитали последовательность с точностью до 12,1 триллиона цифр после запятой^[29].

14 марта 2019 года, когда отмечался неофициальный праздник числа пи, компания Google представила данное число с 31,4 триллиона знаков после запятой. Вычислить его с такой точностью сумела сотрудница Google в Японии Эмма Харука-Ивао^[30].

В августе 2021 года швейцарские учёные Университета прикладных наук Граубюндена смогли вычислить число с точностью до 62,8 триллиона знаков после запятой, обновив прошлые рекорды. Расчёты производились на суперкомпьютере 108 дней и девять часов. Скорость вычислений в два раза превысила рекорд, установленный Google в 2019 году, и в 3,5 раза — рекорд 2020 года, когда в числе было рассчитано более 50 триллионов цифр после запятой^[31][32].

9 июня 2022 года команда Google под руководством Эммы Харука-Ивао рассчитала первые 100 триллионов знаков числа «пи» после запятой, потратив на это почти 158 дней^[2][33].

Программа «Супер Пи^[en]», фиксирующая время, за которое вычисляется заданное количество знаков (до 32 миллионов) числа Пи, может быть использована для тестирования производительности компьютеров.

Рациональные приближения

Сравнение точности приближений

Число	Округлённое значение	Точность (совпадения разрядов)
	3,14159265…
	3,14285714…	2 разряда после запятой
	3,14166667…	3 разряда после запятой
	3,14159292…	6 разрядов после запятой

Открытые проблемы

Цифра	Сколько раз появляется
0	20 000 030 841
1	19 999 914 711
2	20 000 013 697
3	20 000 069 393
4	19 999 921 691
5	19 999 917 053
6	19 999 881 515
7	19 999 967 594
8	20 000 291 044
9	19 999 869 180

Однако строгое доказательство отсутствует.

• Неизвестно, принадлежит ли к кольцу периодов.

Метод иглы Бюффона

На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к при увеличении числа бросков до бесконечности^[41]. Данный метод иглы базируется на теории вероятностей и лежит в основе метода Монте-Карло^[42].

Мнемонические правила и рекорды запоминания

Стихотворения для запоминания 8—11 знаков числа :

Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Надо только постараться И запомнить всё как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.

Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься, Это каждый должен знать. Можно просто постараться И почаще повторять: «Три, четырнадцать, пятнадцать, Девять, двадцать шесть и пять».

Запоминанию может помогать соблюдение стихотворного размера:

Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один

Существуют стихи, в которых первые цифры числа зашифрованы в виде количества букв в словах:

Это я знаю и помню прекрасно: Пи многие знаки мне лишни, напрасны. Доверимся знаньям громадным Тех, пи кто сосчитал, цифр армаду. Учи и знай в числе известном За цифрой цифру, как удачу примечать.

Раз у Коли и Арины Распороли мы перины. Белый пух летал, кружился, Куражился, замирал, Ублажился, Нам же дал Головную боль старух. Ух, опасен пуха дух! — Георгий Александров

Подобные стихи существовали и в дореформенной орфографии, поэтому во всех словах, заканчивающихся на согласную, в конце стоит «ъ».
Например, следующее стихотворение, сочинённое преподавателем Нижегородской гимназии Шенроком^[43]:

Кто и шутя и скоро пожелаетъ
Пи узнать число, ужъ знаетъ.

Мировой рекорд по запоминанию знаков числа после запятой принадлежит 21-летнему индийскому студенту Раджвиру Мина (Rajveer Meena), который в марте 2015 года воспроизвёл 70 000 знаков после запятой за 9 часов 27 минут^[44]. До этого, на протяжении почти 10 лет, рекорд держался за китайцем Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки^[45][46]. В том же 2006 году японец Акира Харагути заявил, что запомнил число до 100-тысячного знака после запятой^[47], однако проверить это официально не удалось^[48].

В России рекорд по запоминанию был установлен в 2019 году Денисом Бабушкиным (13 202 знака)^[49].

В культуре

• В штате Индиана (США) в 1897 году была предпринята попытка принять Законопроект о числе пи, устанавливающий его значение равным 3,2^[50]. Данный билль не стал законом благодаря своевременному вмешательству профессора Университета Пердью, присутствовавшего в законодательном собрании штата во время рассмотрения данного закона;
• Существует художественный фильм, названный в честь числа Пи;
• Неофициальный праздник «День числа пи» ежегодно отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3,14, что соответствует приближённому значению числа . Считается^[51], что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159;
• Американская прогрессив-метал-группа After The Burial записала песню Pi — The Mercury God of Infinity, в которой партия ритм-гитары и бас-бочки основана на высших разрядах десятичной дроби числа .
• Франсуа Араго в «Общепонятной астрономии» писал^[52]:

Посмотрим, с какою точностью возможно, пользуясь цифрами Пи (числа Пи), вычислить длину окружности, радиус которой равен среднему расстоянию Земли от Солнца (150 000 000 км). Если для Пи взять 18 цифр, то ошибка на одну единицу в последней цифре повлечет за собой в длине вычисляемой окружности погрешность в 0,0003 миллиметра; это гораздо меньше толщины волоса.

Мы взяли 18 цифр Пи. Легко представить себе, какую невообразимо малую погрешность сделали бы, при огромности вычисляемой окружности, если бы воспользовались для Пи всеми известными его цифрами. Из сказанного ясно, как заблуждаются те, которые думают, будто науки изменили бы свой вид, и их применения много выиграли бы от нахождения точного Пи, если бы оно существовало.

Итак, даже для астрономии‚ — науки, прибегающей к наиболее точным вычислениям‚ — не требуется вполне точного решения…

См. также

• Точка Фейнмана
• Число τ
• e (число)

Примечания

Комментарии

Источники

Литература

• Жуков А. В. О числе π. — М.: МЦМНО, 2002. — 32 с. — ISBN 5-94057-030-5.
• Жуков А. В. Вездесущее число «пи». — 2-е изд. — М.: Издательство ЛКИ, 2007. — 216 с. — ISBN 978-5-382-00174-6.
• Кымпан, Флорика. История числа пи. — М.: Наука, 1971. — 217 с.
• Наварро, Хоакин. Секреты числа Почему неразрешима задача о квадратуре круга. — М.: Де Агостини, 2014. — 143 с. — (Мир математики: в 45 томах, том 7). — ISBN 978-5-9774-0629-1.
• Перельман Я. И. Квадратура круга. — Л.: Дом занимательной науки, 1941. Переиздание: ЁЁ Медиа, ISBN 978-5-458-62773-3.
• Шумихин С., Шумихина А. Число Пи. История длиною в 4000 лет. — М.: Эксмо, 2011. — 192 с. — (Тайны мироздания). — ISBN 978-5-699-51331-4. — ISBN 5-4574041-9-6. — ISBN 978-5-4574041-9-9.
• David H. Bailey, Jonathan M. Borwein. Pi: The Next Generation A Sourcebook on the Recent History of Pi and Its Computation. — Springer, 2016. — 507 с. — ISBN 978-3-319-32375-6.
• Arndt, Jörg; Haenel, Christoph. Pi Unleashed (англ.). — Springer-Verlag, 2006. — P. 194–196. — 270 p. — ISBN 978-3-540-66572-4.

Ссылки

• pi.delivery Архивная копия от 10 ноября 2020 на Wayback Machine 50 трлн знаков числа пи (мировой рекорд).
• Weisstein, Eric W. Pi Formulas (англ.) на сайте Wolfram MathWorld.
• Различные представления числа Пи Архивная копия от 12 августа 2011 на Wayback Machine на WolframAlpha (англ.)
• https://functions.wolfram.com/Constants/Pi/ Архивная копия от 12 января 2021 на Wayback Machine
• последовательность A000796 в OEIS
• 22,4 трлн знаков числа пи Архивная копия от 10 ноября 2020 на Wayback Machine (англ.)

Как архимед вычислил длину окружности

Напомним: число π («пи») определяется как отношение длины окружности к ее диаметру . Это кратко выражается формулой для вычисления длины окружности , или . Другая известная формула, в которой встречается π, – формула площади круга , или . В принципе π можно было бы определить как отношение площади круга к квадрату радиуса. За этими формулами скрываются три нетривиальных математических факта:

1)	длина окружности пропорциональна ее диаметру;
2)	площадь круга пропорциональная квадрату радиуса;
3)	коэффициенты пропорциональности в двух последних случаях совпадают.

Десятичная дробь, выражающая число π, бесконечна, хотя можно вычислить различные конечные дроби – десятичные приближения для π. Наиболее популярное приближение – с точностью до сотых: π ≈ 3,14.

Самое простое приближение для π полагает его равным 3 (несмотря на грубость этого приближения, его ошибка менее 5 %). Такое приближение использовалось, например, в Древнем Вавилоне в III–II вв. до н. э.: длину окружности находили по правилу, которое в современных обозначениях можно записать , площадь круга находили по правилу . Значение π = 3 используется и древними иудеями: библейский автор упоминает, что при строительстве храма при царе Соломоне мастер Хирам из Тира в числе других храмовых украшений «сделал литое из меди море, – от края его до края его десять локтей, – совсем круглое. и шнурок в тридцать локтей обнимал его кругом» (3 Цар 7, 23). Позже для более точных вычислений использовалось геометрическое приближение: от площади квадрата, описанного вокруг круга, отнимались площади треугольников с длиной стороны, равной трети стороны квадрата, получалось довольно точное значение

В Древнем Египте для вычисления площади круга использовалось правило , что соответствует значению . Ошибка при этом составляет менее 1 %. Как получали это правило, неизвестно.

У древнегреческих математиков с их превалирующим интересом к геометрическим построениям и доказательствам, а не к вычислениям, вопрос о численном значении π был не столь важным, нежели проблема квадратуры круга, т. е. построения квадрата, равновеликого данному кругу, если удастся, то с помощью циркуля и линейки, а в противном случае – с помощью каких-то других инструментов. Задача о квадратуре круга имела широкую известность не только среди математиков: например, о ней говорится в комедии Аристофана «Птицы».

Изучая задачу о квадратуре круга, Гиппократ Хиосский (V в. до н. э.) нашел некоторые случаи, когда с помощью циркуля и линейки можно найти квадратуру определенных частей круга, ограниченных кривыми линиями (а именно, двумя окружностями). Такие части называются луночками . Самый простой случай – это луночка между окружностью, описанной около равнобедренного прямоугольного треугольника, и другой окружностью, диаметром которой служит катет этого треугольника.

Нетрудно видеть, что, по теореме Пифагора, , а потому площадь круга, построенного на , равна двум площадям круга, построенного на , а значит, площадь полукруга, построенного на , равна площади четверти круга, построенного на . Поэтому, вырезав из этих фигур их общую часть – сегмент – получим равновеликие фигуры: таким образом, площадь луночки равна площади прямоугольного треугольника .

Древнейшие известные попытки собственно квадратуры круга принадлежат Антифонту и Бризону (V в. до н. э.). Антифонт последовательно вписывал в круг правильные многоугольники, каждый раз удваивая количество сторон, и полагал, что в конце концов многоугольник совпадет с окружностью. Бризон строил два квадрата – вписанный в окружность и описанный вокруг нее – и считал, что площадь квадрата, лежащего между ними, равна площади круга. Разумеется, в буквальном понимании и Антифонт, и Бризон заблуждались. Однако их идеи оказались весьма плодотворными: действительно, вписывая в окружность правильные многоугольники со все большим числом сторон, можно сколь угодно близко подойти к площади круга и длине окружности; смысл есть и в том, чтобы рассматривать не только вписанные, но и описанные многоугольники: при этом площадь круга будет лежать между площадями вписанных и описанных многоугольников, а длина окружности – между периметрами тех и других.

В дальнейшем именно вписанные и описанные правильные многоугольники стали активно применяться как для теоретических исследований, так и для конкретного вычисления числа π. Именно с помощью таких многоугольников было сформулировано строгое доказательство того, что площади кругов относятся как квадраты их диаметров, найденное, по-видимому, Евдоксом и приведенное в «Началах» Евклида. Архимед доказал, что площадь круга равна половине произведения длины окружности на ее радиус. Кроме того, с помощью вычисленных им периметров вписанных и описанных правильных многоугольников (от 6-угольника до 96-угольника) Архимед нашел, что:

или, в десятичных дробях, (подлинное значение ).

Таким образом, он не только нашел приближенные значения π, но и оценил точность этих приближений. Уже найденная Архимедом верхняя оценка, равная 22/7, дает приближение π с точностью 0,04 %. Эту дробь часто называют «архимедовым числом». Клавдий Птолемей, использовав правильный 720-угольник, нашел, что , что составляет приблизительно 3,14167 (ошибка меньше 0,003 %).

Как и для удвоения куба, и для трисекции угла, для квадратуры круга были изобретены методы, использующие свойства различных кривых. Общим свойством этих кривых было их образование путем сочетания двух типов движений – равномерного поступательного (вдоль некоторой прямой) и равномерного вращательного (вокруг некоторой точки или оси). При этом имеет место пропорциональность между углом, на который повернулся вращающийся элемент, и длиной отрезка, пройденной при поступательном движении.

Прежде всего, это была уже упомянутая квадратриса (см. урок, посвященный трисекции угла), которую впервые использовал для квадратуры круга Динострат. Оказывается, если – точка, в которой квадратриса пересекает отрезок , то четверть длины окружности, проходящей через точку , с центром в точке , равна длине отрезка .

Из этого следует, что длина дуги равна , а площадь круга радиуса равна площади прямоугольника со сторонами и ; такой прямоугольник легко построить с помощью циркуля и линейки, если известны отрезки и . Построив прямоугольник, можно построить и равновеликий ему квадрат.

Кроме квадратрисы, для квадратуры круга использовались связанные с ней винтовая линия и спираль Архимеда. Винтовая линия получается при движении точки по поверхности цилиндра, складывающемся из двух движений: во-первых, движения с постоянной скоростью вдоль оси цилиндра, а во-вторых, равномерного вращения по окружности основания цилиндра.

Спираль Архимеда – эта кривая, которую заметает точка , равномерно движущаяся вдоль радиуса , который, в свою очередь, равномерно вращается вокруг точки .

Задача, похожая на квадратуру круга, фигурировала и в Древней Индии. В уже упоминавшейся (см. урок по теореме Пифагора) книге «Шулва-сутра», излагавшей правила строительства алтарей, построение круга, равновеликого данному квадрату , производится так. Вокруг квадрата описывается окружность; пусть перпендикуляр к отрезку , проходящий через центр окружности , пересекает прямую и окружность в точках и , а точка делит отрезок в отношении . Тогда – радиус круга, равновеликого данному квадрату. Если – сторона квадрата, то длина полученного радиуса описанный способ соответствует приближенному значению π

В более поздние времена в Индии использовались приближения для π, равные (т. е. ≈ 3,162 – ошибка менее 1 %); 22/7 и даже 3,1416. Интересно наглядное доказательство предложения «площадь круга равна площади прямоугольника, стороны которого равны полуокружности и радиусу» у математика Ганеши (XVI в.). Как и в доказательстве теоремы Пифагора у Бхаскары, здесь все доказательство состоит из чертежа и слова «смотри». Ганеша делит круг на 12 секторов, а затем разворачивает каждый полукруг, состоящий из 6 секторов, в пилообразную фигуру, основание которой равно полуокружности, а высота – радиусу. Прямоугольник, о котором говорится в условии, получится при вставлении зубьев одной «пилы» в зазоры между зубьями другой. По-видимому, читатель должен был представлять себе, что круг разделен не на 12, а на столь большое число секторов, что эти секторы неотличимы от треугольников, составляющих «пилы».

Значение по-видимому, впервые появилось у китайского астронома и философа Чжан Хена (нач. II в. н. э.); вероятно, из Китая оно перешло к индийцам (Брахмагупта, VII в.) и арабам (ал-Хорезми, IX в.); впрочем, метод получения этого значения нам неизвестен. Лю Хуэй (III–IV вв.) с помощью рассмотрения вписанных и описанных многоугольников (в том числе с 3072 вершинами) пришел к приближению , а Цзу Чун-чжи (V в.) доказал, что

Самаркандский математик ал-Каши в «Трактате об окружности» (1424 г.) поставил себе задачу выразить окружность через диаметр с такой точностью, чтобы погрешность в длине окружности, равной 600 000 диаметров Земли, не превосходила толщины волоса. Рассмотрев правильные многоугольники вплоть до фигуры с 805 306 368 (3 ∙ 2 28 ) вершинами, ал-Каши нашел 16 верных знаков (после запятой) числа π, а именно, приближение (в реальности 17-й знак после запятой – 3 или 4, потому что 18-й – 8). Европейские математики достигли такой точности и превзошли ее лишь в конце XVI в.: в 1597 г. голландец вычислил 17-й знак, для чего применил многоугольник с 1 073 741 824 (2 30 ) вершинами.

В начале XVII в. профессор математических и военных наук Лейденского университета Лудольф ван Цейлен довел количество точных знаков (после запятой) числа π до 35. Современники называли найденное им приближение π «числом Лудольфа». Эти знаки он завещал выбить на надгробном камне. Интересно, что, поскольку в то время привычная нам позиционная запись десятичных дробей еще не вполне прижилась, на надгробии было написано не 3,14159265358979323846264338327960288, а

Еще два голландца XVII в. – В. Снеллиус и Х. Гюйгенс – с помощью некоторых тонких геометрических рассуждений смогли достичь большей точности при меньшем числе сторон рассматриваемых многоугольников. Снеллиус воспроизвел результат Архимеда – три верных знака после запятой – рассматривая не более чем а с помощью получил целых 7 верных знаков. Гюйгенс, доказав некоторые геометрические теоремы, смог вычислить 10 верных знаков с помощью 60-угольника.

Далее метод вписанных и описанных многоугольников уступил место новым методам, разработанным с помощью математического анализа – использованию бесконечных сумм, которые дают приближенные значения числа π нужной точности, если оставить в них достаточно большое, но лишь конечное число членов. В результате число верных знаков быстро возросло: вычислители подбирали формулы поудобнее и соревновались друг с другом в том, кто больше получит этих знаков.

Рекорд для XIX в. поставил Уильям Шенкс, нашедший в результате 707 знаков после запятой; в 1-ой половине XX в. эти знаки часто воспроизводили в популярной литературе, а архитекторы даже украшали ими свои сооружения (Дом занимательной науки в Ленинграде, ныне Санкт-Петербург, 1934; Дворец открытий в Париже, 1937). В 1945 г. результаты Шенкса были проверены на компьютере, и оказалось, что из его знаков верны только первые 527. Компьютеры позволили существенно увеличить количество точных цифр в десятичном разложении π, причем, если раньше вычислители тратили на них многие годы, то теперь компьютеры справлялись с этим менее чем за день работы. Этому также способствовало применение более эффективных алгоритмов на основание новых математических формул.

Само обозначение π для отношения окружности к диаметру было введено в 1706 году У. Джонсом.

Что касается принципиальных математических результатов относительно π, то здесь следует упомянуть, во-первых, доказательство иррациональности этого числа, проведенное в 1766 г. И. Г. Ламбертом (некоторый пробел в доказательстве Ламберта был восполнен в 1800 г. А. М. Лежандром), а во-вторых, доказательство трансцендентности π, осуществленное в 1882 г. К. Ф. Линдеманом. Трансцендентность некоторого числа означает, что оно не может быть корнем никакого уравнения вида с целыми коэффициентами . Из этого следует, что оно не может быть представлено в виде конечной комбинации целых чисел, арифметических действий и знака извлечения корня. Поэтому и квадратура круга не может быть решена с помощью циркуля и линейки, которые позволяют строить лишь отрезки, выражаемые через арифметические действия и квадратные корни.

Кто открыл число Пи? История вычислений

Уже много веков и даже, как ни странно, тысячелетий люди понимают важность и ценность для науки математической постоянной, равной отношению длины окружности к ее же диаметру. Кто открыл число Пи, до сих пор неизвестно, но к нему имели отношение самые лучшие математики на протяжении всей нашей истории. Большинство из них хотели выразить его рациональным числом.

Интересные сведения о числе Пи

1. Исследователи и истинные поклонники числа Пи организовали клуб, для вступления в который требуется знать наизусть достаточно большое количество его знаков.

2. С 1988 года празднуется «День числа Пи», который приходится на 14 марта. Готовят салаты, торты, печенья, пирожные с его изображением.

3. Число Пи уже переложили на музыку, при этом оно весьма неплохо звучит. Ему даже воздвигли памятник в американском Сиэтле перед зданием городского Музея искусств.

Древний период

В то далекое время число Пи старались вычислить при помощи геометрии. То, что это число постоянно для самых разных окружностей, знали еще геометры в Древнем Египте, Вавилоне, Индии и Древней Греции, утверждавшие в своих работах, что оно всего лишь немного больше трех.

В одной из священных книг джайнизма (древняя индийская религия, которая возникла в VI в. до н. э.) упоминается, что тогда число Пи считалось равным корню квадратному из десяти, что в итоге дает 3,162. .

Древнегреческие математики проводили измерение окружности методом построения отрезка, а вот для того, чтобы измерить круг, им приходилось строить равновеликий квадрат, то есть фигуру, равную ему по площади.

Когда еще не знали десятичных дробей, великий Архимед нашел значение числа Пи с точностью 99,9%. Он открыл способ, который стал основой многих последующих вычислений, вписывал в окружность и описывал вокруг нее правильные многоугольники. В результате Архимед рассчитал значение числа Пи как отношение 22 / 7 ≈ 3,142857142857143.

В Китае, математик и придворный астроном, Цзу Чунчжи в V веке до н. э. обозначил более точное значение числа Пи, рассчитав его до семи цифр после запятой и определил его значение между числами 3, 1415926 и 3,1415927. Более 900 лет понадобилось ученым, чтобы продолжить дальше этот цифровой ряд.

Средние века

Известный индийский ученый Мадхава, который жил на рубеже XIV – XV веков, ставший основателем Керальской школы астрономии и математики, впервые в истории стал работать над разложением тригонометрических функций в ряды. Правда, сохранились всего лишь два его труда, а на другие известны лишь ссылки и цитаты его учеников. В научном трактате «Махаджьянаяна», который приписывают Мадхаве, указано, что число Пи равно 3,14159265359. А в трактате «Садратнамала» приведено число с еще большим количеством точных знаков после запятой: 3,14159265358979324. В указанных числах последние цифры не соответствуют правильному значению.

В XV веке самаркандский математик и астроном Ал-Каши вычислил число Пи с шестнадцатью знаками после запятой. Его результат считался наиболее точным в течение последующих 250 лет.

У. Джонсон, математик из Англии, одним из первых смог обозначить отношение длины окружности к ее диаметру буквой π. Пи — это первая буква греческого слова «περιφέρεια» — окружность. Но этому обозначению удалось стать общепринятым лишь после того, как им воспользовался в 1736 году более известный ученый Л. Эйлер.

Заключение

Современные ученые продолжают работать над дальнейшими вычислениями значений числа Пи. Для этого уже используют суперкомпьютеры. В 2011 г. ученый из Японии Сигэру Кондо, сотрудничая с американским студентом Александром Йи, произвели правильный расчет последовательности из 10 триллионов цифр. Но до сих пор так и неясно, кто открыл число Пи, кто впервые задумался над этой проблемой и произвел первые расчеты этого, по-настоящему мистического числа.

Как Архимед измерил Вселенную и убивал лазером

Жил, «околдованный сиреною», топил «когтями» корабли и погиб, защищая свои чертежи

Древнегреческий физик, математик и инженер Архимед сделал множество геометрических открытий, заложил основы гидростатики и механики, создал изобретения, послужившие отправной точкой для дальнейшего развития науки. Легенды об Архимеде создавались еще при его жизни.

Математика в стихах

Биография Архимеда известна из трудов Тита, Цицерона, Полибия, Ливия, Витрувия и других авторов, которые жили позже самого ученого. Оценить степень достоверности этих данных сложно.
Известно, что родился Архимед в 287 году до нашей эры в греческой колонии Сиракузы, расположенной на острове Сицилия. Его отцом, предположительно, стал астроном и математик Фидий. Начальное образование ученый, возможно, получил у отца. Плутарх также утверждал, что ученый был близким родственником доброго и искусного правителя Сиракуз Гиерона II.

Вероятно, детские годы Архимед провел в Сиракузах, а в юном возрасте отправился в Александрию, столицу Египта. На протяжении нескольких столетий этот город был культурным и научным центром цивилизованного древнего мира, славился своей библиотекой, где хранилось 700 тысяч книг, и научно-историческим музеем. Учёные, принятые в сотрудники музея, занимались натурфилософией, математикой, астрономией, географией, медициной, теорией музыки, лингвистикой и другими науками. Роль музея — культурная и религиозная — сохранилась и в эпоху римского завоевания.

Достоверно известно, что в музее Архимед встретился с целой группой ученых. Один из них — греческий математик, астроном, географ и филолог Эратосфен — стал его близким другом. Архимед написал сочинение «Для Эратосфена. О методе», в котором объясняет, каким путем приходит к решению задачи. Это было довольно откровенным посланием, ведь в древности математики обычно не разглашали «секретов своего мастерства», а только доказывали правильность полученных результатов. Кроме того, своему другу Архимед посвятил стихотворение, наверное, единственное, написанное в жизни, в котором описал условия сложной математической задачи, а сюжет взял из «Одиссея» Гомера. Прожив в Александрии несколько лет, Архимед вернулся в Сиракузы, где и пребывал до самой смерти.

«Дайте мне точку опоры»

Механика постоянно находилась в круге интересов Архимеда. В одной из своих первых работ он исследует распределение нагрузок между опорами балки. Архимеду принадлежит определение понятия центра тяжести тела. Применяя интеграционные методы, он нашел положение центра тяжести различных фигур и тел. Архимед дал математический вывод законов рычага.

Легенда рассказывает, что построенный царем Гиероном в подарок египетскому царю Птолемею роскошный корабль «Сирокосия» никак не удавалось спустить на воду. Архимед соорудил сложную систему рычагов, с помощью которой он смог проделать эту работу одним движением руки. Этот случай и размышления Архимеда над принципом рычага стали причиной его легендарной фразы: «Дайте мне точку опоры, и я переверну мир!»

В течение многих веков механика рассматривалась как наука о простых статических машинах. Ее основой были теория рычага, изложенная Архимедом в сочинении «О равновесии плоских фигур». В этой книге также содержатся определения центров тяжести треугольника, параллелограмма, трапеции, параболического сегмента, трапеции, боковые стороны которой являются дугами парабол. Не подлежит сомнению, что все законы, постулаты и другие результаты, данные в этой книге, получены Архимедом в результате длительного практического опыта, обобщением которого и явилась механика Архимеда.
Архимед был и одним из крупнейших инженеров-конструкторов своего времени. В сельском хозяйстве и строительстве использовали архимедов винт для перекачки жидкостей и сыпучих веществ, таких как уголь и зерно, и для выкачивания воды изо рвов и шахт. Винт состоял из деревянного валика, на который насажено было червячное колесо. Устройство помещалось в цилиндре, сделанном из деревянных досок. Этот винт применяется до сих пор, особенно в Египте.

Строительная и военная техника была тесно связана с вопросами равновесия и подводила к выработке понятия центра тяжести. В основе этой техники лежал рычаг и другие простые механизмы. Машины, построенные с использованием этих механизмов, и в первую очередь рычага, помогли человеку перехитрить природу и силу тяжести. Отсюда и пошло название «механика». Греческое слово «механе» означало орудие, приспособление, осадную или театральную машину, а также уловку, ухищрение.

Сколько песчинок во Вселенной?

Архимед занимался также астрономией. Он построил небесную сферу – механический прибор, на котором можно было наблюдать движения планет, фазы Луны, солнечные и лунные затмения.

О занятиях Архимеда астрономией свидетельствует и сочинение «Псаммит» — «Исчисление песчинок». Чтобы определить число песчинок, помещающихся во Вселенной, Архимеду нужно было вычислить её размеры. Он сделал предположение, что Вселенная сферическая (заключенная в «сферу удалённых звёзд»), и отношение диаметра Вселенной к диаметру орбиты Земли вокруг Солнца равно отношению диаметра орбиты Земли вокруг Солнца к диаметру Земли.

Для вычисления верхней границы размера Вселенной Архимед специально завышал свои оценки. Он предположил, что длина земной окружности не более 300 мириад стадий (около 500 тысяч км). Для измерения углового диаметра Солнца (то есть, угла, который занимает Солнце на окружности небесной сферы) Архимед проводил эксперимент, выполнявшийся на рассвете, когда свет достаточно слаб, чтобы можно было смотреть прямо на Солнце. Для этого он прикреплял к концу линейки небольшой цилиндр и отдалял его так, чтобы он как раз закрывал собою Солнце. При расчётах Архимед учитывал размер зрачка.
В результате измерений было получено, что угловой диаметр Солнца больше 1/200 части прямого угла. Из этого измерения Архимед показывает, что диаметр Солнца больше стороны вписанного в небесную сферу тысячеугольника. При этом он впервые в истории рассматривает параллакс, замечая различие между наблюдениями Солнца из центра Земли и с её поверхности на восходе.

Из полученных предпосылок Архимед подсчитал, что диаметр Вселенной, если перевести в современную систему исчисления, около двух световых лет. Также он предположил, что в объёме макового зёрнышка помещается не более мириады песчинок, а диаметр макового зёрнышка не менее сороковой части дюйма. В итоге Архимед показал, что Вселенная может содержать в себе не более дециллиарда песчинок – это 10 в 63-й степени, число в котором 63 нуля. Таким образом, Архимед принимает мир, хотя и очень большим, но конечным, что позволяет ему довести свой расчет до конца.

Голым побежал к царю

Рассмотрим теперь знаменитый закон Архимеда, изложенный в его сочинении «О плавающих телах». Он определил, что на всякое тело, погруженное в жидкость, оказывает давление выталкивающая сила. Она направлена вверх, а по величине равна весу жидкости, которая была вытеснена при помещении тела в жидкость, вне зависимости от того, какова плотность этой жидкости. Существует легенда, что Архимед пришел к своему закону, решая задачу: содержит ли золотая корона, заказанная царем Гиероном мастеру, посторонние примеси или нет? Не добавил ли туда хитрый ювелир серебро или же другие металлы?
Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объём короны: ведь она имела неправильную форму! Архимед всё время размышлял над этой задачей. Как-то он принимал ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить её объём, измерив объём вытесненной ею воды. Согласно легенде, Архимед выскочил голый на улицу с криком: «Эврика!» Т. е, «Нашёл!» И в таком виде побежал к царю. В этот момент был открыт основной закон гидростатики. Сравнив объёмы воды, вытесненные короной и слитком золота равного с ней веса, учёный доказал обман ювелира.

Однако, вероятно, мотивация работы Архимеда была все же более серьезной. Ведь Сиракузы были портовым и судостроительным городом. Вопросы плавания тел здесь решались ежедневно, и поэтому перед Архимедом стояла задача выяснения научной основы этих вопросов. В своей книге он разбирает не только условия плавания тел, но и вопрос об устойчивости равновесия плавающих тел различной геометрической формы. Научный гений Архимеда в этом сочинении, оставшемся, по-видимому, незаконченным, проявился с огромной силой.

Головоломки из Древней Греции

И все же любимым делом его жизни была математика. По словам Плутарха, Архимед был просто одержим ею. Он забывал о пище, совершенно не заботился о себе. Его работы относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Ряд работ имеет вид посланий к друзьям и коллегам. Иногда Архимед предварительно сообщал им без доказательств свои открытия, с тонкой иронией добавляя несколько неверных гипотез.

Центральной темой математических работ Архимеда являются задачи на нахождение площадей поверхностей и объемов. Архимед вычислил площади эллипса, параболического сегмента, нашел площади поверхности конуса и шара, объемы шара и сферического сегмента, а также различных тел вращения и их сегментов. Он нашёл общий метод, позволяющий найти любую площадь или объём. Трудно переоценить значение этого метода, без которого была бы немыслима ни физика, ни астрономия. Идеи Архимеда легли в основу интегрального исчисления.

А как вам такая головоломка — дана кривая линия, как определить касательную в любой её точке? В школе учат, как проводить касательную к окружности. Древние греки умели, кроме того, находить касательные к эллипсу, гиперболе и параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот метод впоследствии лёг в основу дифференциального исчисления.

В математике, физике и астрономии очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин — их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объём? Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления.

Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру. Архимед исследовал свойства т. н. архимедовой спирали, дал построение касательной к этой спирали, нашел площадь ее витка. Архимеду принадлежит формула для определения площади треугольника через три его стороны. Он дал теорию полуправильных выпуклых многогранников, которые стали называться архимедовы тела.

Солнечный лазер и «когти» Архимеда

В 212 году до нашей эры римский флот подошел под стены Сиракуз. Это стало завершающим этапом осады. Город, блокированный с суши, теперь был заперт и со стороны моря. Тяжелые корабли с веслами в пять рядов подошли под самые стены и метатели с их палуб забрасывали войска оборонявшихся стрелами и камнями. Архимед до сих пор использовал свой гений только в мирных целях, но когда война пришла в его дом, он не оставил исследований, но начал работу, которая могла бы помочь родному городу.

Одна за другой у жителей Сиракуз стали появляться чудодейственные машины. Одни метали в нападавших копья и камни. Другие захватывали корабли за нос, поднимали над водой и с высоты бросали вниз – эти устройства получили название «когти Архимеда». Неожиданно возникшие водовороты как скорлупки швыряли тяжелые боевые суда по морской глади и выбрасывали их на прибрежные скалы. Плутарх писал: «Вдруг с высоты стен бревна опускались, вследствие своего веса и приданной скорости, на суда и топили их. То железные когти и клювы захватывали суда, поднимали их в воздух носом вверх, кормою вниз и потом погружали в воду. А то суда приводились во вращение и, кружась, попадали на подводные камни и утесы у подножия стен. Большая часть, находящихся на судах, погибала под ударом. Всякую минуту видели какое-нибудь судно поднятым в воздухе над морем. Страшное зрелище!»

Но и это еще не все. Нежданно на стене появилось огромное зеркало. Оно отразило лучи Солнца, направило их на один из вражеских кораблей, и тот вспыхнул, как факел. Огонь быстро распространялся, и вот под угрозой оказались соседние суда. Римляне решили отвести флот дальше от города. Архимед хорошо знал зажигательные свойства вогнутых зеркал, проводил опыты по преломлению света, знал свойства изображений в плоских, выпуклых и вогнутых зеркалах.

Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело… римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузцев одного старца». Только вследствие измены Сиракузы были взяты римлянами. При этом Архимед был убит.

«Не наступай на мои чертежи!»

Рассказывали несколько разных историй о гибели великого ученого.

Например, говорили, что в разгар боя он сидел на пороге своего дома, углубленно размышляя над чертежами, сделанными им прямо на дорожном песке. В это время пробегавший мимо римский воин наступил на технический рисунок. И возмущенный изобретатель бросился на римлянина с криком: «Не наступай на мои чертежи!» Эта фраза стоила Архимеду жизни. Солдат остановился и хладнокровно зарубил старика мечом.

В другом повествовании военачальник римлян Марцелл специально послал солдата на поиски знаменитого Архимеда. Воин разыскал ученого и сказал: «Иди со мной, тебя зовет Марцелл». — «Какой еще Марцелл?! Я должен решить задачу!» – отвечал Архимед. Разгневанный неповиновением римлянин грубо потащил ученого, приставив меч к его горлу. Архимед сопротивлялся, как мог, но силы были не равны. К тому же рука легионера дрогнула, и меч пронзил 75-летнего старика.

То, что истина и наука были для Архимеда дороже, чем жизнь, рассказывается и в еще одной легенде. Когда солдат ворвался в дом Архимеда для грабежа и занес меч на хозяина, тот не убегал, а успел крикнуть: «Остановись, подожди хотя бы немного. Я хочу закончить решение задачи, а потом делай, что хочешь!»

И, наконец, в древних летописях есть упоминание о том, что Архимед сам отправился к Марцеллу, чтобы отнести ему свои приборы для измерения величины Солнца. По дороге его ноша привлекла внимание римских солдат. Они решили, что ученый несет в ларце золото или драгоценности и, недолго думая, перерезали ему горло.

Однако многие историки полагают, что Архимед был убит неслучайно — ведь его ум стоил в те времена целой армии. Захватчики, во-первых, хотели отмстить ему за неудачный штурм, а во-вторых, всерьез опасались, что неугомонный изобретатель может вновь огорошить их какой-нибудь дьявольской выдумкой.

Учитель гениев

Современникам Архимеда было трудно самостоятельно пользоваться плодами его трудов, слишком сложными и новаторскими были его идеи – они на века опередили время. Работы Архимеда позже изучали и преподавали математики Анфимий из Тралл и Исидор из Милета, архитекторы собора св. Софии, возведенного в Константинополе в VI веке. А реформа преподавания математики, которую проводил в Константинополе в IX веке Лев Фессалоникийский, по-видимому, способствовала собиранию работ Архимеда.

Человечество вновь и вновь «открывало» Архимеда. В Средние века часть трактатов Архимеда перевели на арабский язык. Достижения античного учёного оказали влияние на развитие математики исламского Средневековья, в частности, на определение объёмов тел вращения, центров тяжести сложных геометрических конструкций. Несмотря на то, что учёные их даже вычислили несколько новых интегралов, далеко они не продвинулись. Их достижения лишь несколько дополнили открытия Архимеда.

Средневековые латиноязычные ученые впервые услышали об Архимеде в XII веке, когда появились два перевода с арабского на латынь его сочинения «Об измерении круга». Но наибольшее влияние работы Архимеда оказали на математиков Европы в XVI—XVII веках. Результаты его работ использовали в своих сочинениях такие всемирно известные математики и физики, как Иоганн Кеплер, Галилео Галилей, Рене Декарт, Пьер Ферма, Исаак Ньютон, Готфрид Лейбниц.

А недавно были найдены неизвестные ранее труды Архимеда. Американские учёные из Музея искусств имени Уолтерса в Балтиморе обнаружили несколько неизвестных ранее текстов, написанных древнегреческим математиком. Уникальные записи были скрыты под картинами, нанесёнными поверх текста. Специалисты сумели прочесть трактаты Архимеда, не разрушая поверхностный слой. Тексты были написаны на пергаменте из козлиной шкуры в X веке. Тремя веками позднее свитки попали в иерусалимский монастырь. Монахи превратили пергамент в палимпсест — счистили тексты Архимеда, нанесли поверх них греческие православные молитвы, разрезали листы пополам и сделали из них 174-страничную книгу. Поскольку страницы сшивались в произвольном порядке, некоторые фрагменты трудов Архимеда могут быть безвозвратно утеряны.

В XX веке какие-то умельцы, желая увеличить ценность этой сенсационной находки и продать её подороже, дорисовали золотой краской на пергаменте иллюстрации религиозного содержания. В результате оригинальный текст был почти полностью уничтожен и расшифровать его учёные смогли только с помощью рентгеновской аппаратуры, которую обычно применяют геологи и биологи. Пергамент был пропущен через синхротрон (ускоритель электронов), и, благодаря тому, что древний писец использовал чернила с железосодержащим пигментом, текст стал различим. Работа эта была очень кропотливой — на восстановление текста одной страницы уходило около 12 часов.

«Околдованный домашнею сиреною»

Среди чудом обнаруженных произведений Архимеда – «Метод механических теорем» и «Стомахион», ранее известные лишь по одной копии, а также уникальный трактат «О плавающих телах». В настоящее время специалисты занимаются изучением трудов великого математика и философа.

Плутарх пишет: «Архимед был настолько горд наукой, что именно о тех своих открытиях, благодаря которым он приобрел славу, он не оставил ни одного сочинения». Многих работ Архимеда современные ученые действительно не читали. Мы не знаем, например, конструкций его боевых машин, нам неизвестно, как он мог вычислять квадратные корни из больших чисел, и многое другое.

Плутарх писал: «Нет оснований не верить написанному об Архимеде, что он жил как бы околдованный какою-то домашнею сиреною, постоянной его спутницей, заставляющей его забывать пищу, питье, всякие заботы о своем теле. Иногда, приведенный в баню, он чертил пальцем на золе очага геометрические фигуры, или проводил линии на умащенном маслом своем теле. Автор прекрасных открытий, он просил своих родственников поставить на его могиле цилиндр, включающий в себя конус и шар, и подписать отношение их объемов (3:2:1)». И в память об этом гении древности потомки Архимеда через века пронесут его радостный возглас, боевой клич науки: «Эврика!» — «Я нашел!»

Подготовил Иоанн Микрюков по материалам «История» , «Планета» , «Люди» , «24 СМИ»

[spoiler title=”источники:”]

http://vseonauke.com/1164165224217709154/kto-otkryl-chislo-pi-istoriya-vychislenij/

http://yagazeta.com/lichnost/kak-arhimed-izmeril-vselennuyu-i-ubival-lazerom/

[/spoiler]

Создатель ресурса Better Explained Калид Азад предлагает посмотреть на математику не с точки зрения сложных формул, которые сейчас используются для описания той или иной проблемы, а с точки зрения того, как эту проблему решали тогда, когда она впервые возникла. Таким образом мы сможем последовательно воссоздать шаги человечества на пути понимания математической задачи, в данном случае — поиска числа π.

Источник: Better Explained.

Помочь человеку понять сложные концепции — нехитрая и нелёгкая цель сервиса. Помните знаменитое высказывание Эйнштейна: «Если вы не можете объяснить это просто, значит, вы сами не понимаете этого достаточно хорошо»? Нужно выходить за пределы механических описаний, считает Калид Азад, и находить способы объяснения, которые будут вдохновлять и удивлять людей, которые позволят любому человеку воскликнуть «Эврика!». По мнению автора проекта Better Explained, трудно начинать рассказывать о какой-то идее, но легко заканчивать этот рассказ. Умножение, чтение и даже способ завязывать шнурки поначалу кажутся трудными, а после воспринимаются как нечто само собой разумеющееся.

Калид говорит:

Ищите карту, а не инструкцию, куда идти. Запоминание — это не понимание, это заучивание последовательности действий, использование формул без главного вопроса «почему они такие, а не другие?». Советы и инструкции — это легко, но что будет, если следуя им, вы не там повернёте? Новое направление? Этот сайт — о создании карты, о понимании и глубокой интуиции, которые могут привести вас куда угодно. Оставим сухие теории для энциклопедий.

Итак, мы отправляемся вместе с Better Explained в те далёкие времена, когда человечество ещё не знало всех загадок числа π, но уже было заинтриговано тем, что за ним скрывалось.

Источник: Flickr.com.

π — это загадка. Конечно, вы «знаете», что оно примерно равно 3,14159, потому что вы читали об этом в какой-то книге.  А если бы у вас не было ни учебников, ни компьютеров, ни даже исчисления (ужас!), а только ваш собственный мозг и листок бумаги. Смогли бы вы найти число π?

Ещё 2 000 лет назад Архимед нашёл число π с точностью 99,9%, когда ещё не были известны десятичные дроби и даже ноль! Более того, он разработал методы, которые легли в основу всего исчисления. «Жаль, что я не узнал об истории открытия числа π в школе, — говорит Калид, — это помогло бы мне понять, что такое исчисление».

Как мы находим π?

Число π — это длина окружности с диаметром 1. Как мы можем получить такое число?

• Можно сказать, что π = 3 и успокоиться на этом.
• Можно твёрдой рукой нарисовать круг, приложить к нему по контуру нитку и измерить её длину точнейшей линейкой.
• И, наконец, можно использовать вариант № 3. Что это за вариант? Математика!

Источник: Flickr.com.

Как это сделал Архимед?

Архимед не знал ничего о длине окружности. Но он не волновался и начал с того, что он знает: с периметра квадрата. (На самом деле он использовал шестиугольники, но с квадратами легче работать и рисовать их, так что пойдём этим путём).

Мы не знаем длины окружности, но ради смеха давайте возьмём окружность с диаметром 1 и нарисуем её между двух квадратов.

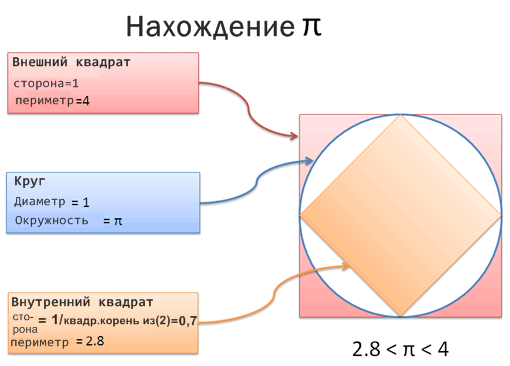
Какой бы ни была длина окружности, она находится где-то между периметрами этих квадратов: эта длина меньше, чем периметр внешнего квадрата, но больше, чем у внутреннего.

А так как квадраты — это квадраты, то их периметры можно легко найти:

• Внешний квадрат (это легко): его стороны равны 1 (так его стороны равны диаметру нашей окружности, который как раз и есть 1), поэтому его периметр равен 4.
• Внутренний квадрат (уже не так легко): его диагональ (сверху вниз) равна диаметру окружности, т.е., 1. Мы знаем теорему Пифагора для сторон прямоугольного треугольника: сумма квадратов катетов равна квадрату гипотенузы. Согласно этой теореме сторона₁² + сторона₂² = 1. Так как стороны квадрата равны между собой, получается, что сторона² = ½, значит, сторона внутреннего квадрата равна 1/2 или примерно 0,7. Таким образом, периметр внутреннего квадрата равен 0,7 x 4 = 2,8.

Мы можем не знать, где находится Пи, но эта тварь точно снуёт между 2,8 и 4. Можно сказать, что π находится где-то на полпути между ними, то есть π = 3,4.

Квадраты отдыхают, восьмиугольники правят миром

Мы оценили число π как 3,4, но, честно говоря, мы бы добились большего с линейкой и нитью. Что же делает нашу оценку настолько плохой?

Квадраты неэффективны. Они не очень хорошо аппроксимируют круг, а в ошибках нашего вычисления виноваты зазоры между ними. Однако увеличение числа сторон (например, до восьмиугольника) даст нам более точную подгонку и, таким образом, более верное значение числа π.

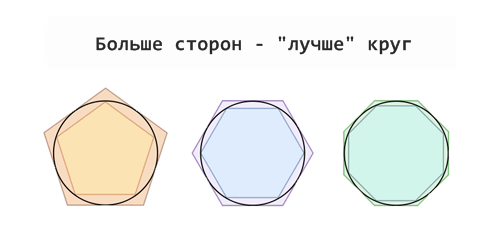
Отлично! По мере увеличения количества сторон многоугольником мы всё больше приближаемся к форме круга.

Итак, как нам теперь найти периметр восьмиугольника? Калид говорит: «Я не уверен, что я помню формулу для нахождения его периметра». Конечно, можно использовать 16-угольники или 32-угольники для улучшения нашей оценки длины окружности. Однако вопрос тот же: чему равны их периметры?

О да, вот они, те самые трудные вопросы. К счастью, Архимед использовал своего рода креативный подход к тригонометрии, в рамках которого он приближал круг двумя многоугольниками с числом сторон 2ⁿ (например, 2³ = 8, 2⁴ = 16 и т.д.), одним внешним и одним внутренним. На каждом шаге производится оценка длины окружности, которая находится между периметром внешнего и периметром внутреннего многоугольника. Если p_n — это периметр внутреннего многоугольника с числом сторон 2ⁿ, а P_n — периметр внешнего многоугольника с числом сторон 2ⁿ, между которыми заключён наш круг, длина окружности которого l, то p_n ≤ l ≤ P_n. На каждом шаге увеличивается число сторон многоугольников (8, 16, 32 и т.д.), и таким образом достигается всё более точная оценка.

Таким образом, Архимед проводил приближенную оценку длин различных окружностей и уже на их основе установил величину числа π. Мы же, зная, что длина окружности равна πd, где d — диаметр окружности, и взяв окружность единичного диаметра, можем тем же самым способом оценить число π.

• Периметр внутреннего многоугольника. Одна сторона внутреннего многоугольника a (например, квадрата) равна sin(x/2), где x — это угол, дополняющий угол нашего многоугольника до π.

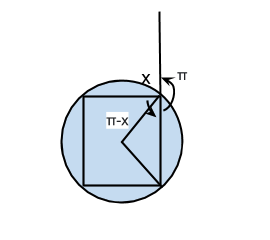
Это легко понять на примере квадрата. Из центра круга (который совпадает с центром квадрата) проведём два радиуса в вершины нашего многоугольника (квадрата в данном случае). Это будут радиусы, так как вершины вписанного многоугольника лежат на окружности. Эти радиусы являются биссектрисами соответствующих углов многоугольника, т.е., делят угол пополам. Таким образом, в получившемся треугольнике угол, прилегающий к основанию (величину которого мы и хотим найти), равен (π—x)/2.

Из вершины треугольника опустим перпендикуляр к основанию. Получится прямоугольный треугольник, у которого один из катетов равен a/2, а гипотенуза равна радиусу нашей окружности, и, как следствие, ½ (так как диаметр окружности 1).

       

В случае квадрата, например, получится, что одна сторона внутреннего квадрата равна sin (90/2) = sin (45) ~ 0,7. Затем измеряем полный периметр: 4 * 0,7 = 2,8. Получаем тот же результат, что у нас был. Аналогичные вычисления можно провести и для вписанного восьмиугольника с учётом того, что угол там равен 45.

• Периметр внешнего многоугольника. Точно таким же образом узнаём, что один наружный сегмент равен tg(х/2), где х представляет собой угол между сторонами. Таким образом, одна часть внешнего периметра tg(45) = 1, а общий периметр = 4.

Изящно — у нас есть простая формула! Добавление большего количества сторон делает угол меньше:

• Квадраты имеют внутренний периметр 4 * sin(90/2).
• Восьмиугольники имеют восемь углов по 45 градусов с внутренним периметром 8 * sin(45/2).

Попробуйте это! С квадратом (4 стороны) мы имеем 91% точности, а с восьмиугольником (8 сторон) мы достигаем 98%!

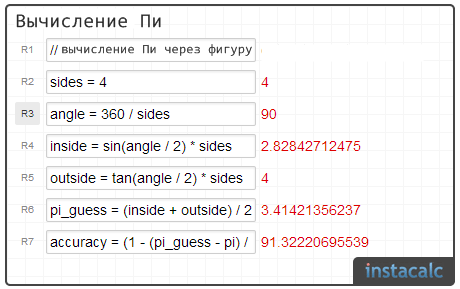
Источник: InstaCalc.com. 

Но есть одна проблема: у Архимеда не было калькулятора с волшебной кнопкой «sin». Вместо этого он использовал тождества, чтобы выразить sin и tan, а также связать между собой периметры вписанных и описанных вокруг нашей окружности многоугольников с числом сторон 2ⁿ и 2ⁿ⁺¹.

Для этого нужно сделать следующее. Так как мы используем 2ⁿ—многоугольники, то при переходе к каждому следующему соответствующий угол у многоугольника уменьшается вдвое.

Если для n стороны соответственно внутреннего и внешнего многоугольников равны s_n=sin(x/2), T_n=tg(x/2), то для n+1 будет s_n+1=sin(x/4), T_n+1=tg(x/4).

Выразим формулы для (n+1) через формулы для n.

Если перейти к периметрам (помня, что у нас 2ⁿ-угольники), то получим:

 

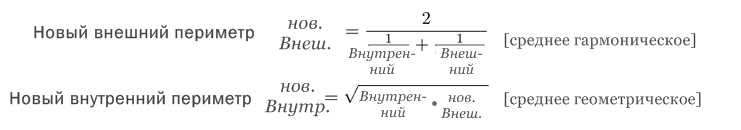
Эти формулы используют только арифметику, тригонометрия здесь не требуется. Так как мы начали с такими известными числами как √2 и √1, мы можем повторно применить эту формулу, чтобы увеличить количество сторон и ещё ближе подойти к значению π.

Запускаем формулу

Начав с четырёх сторон квадрата, мы постепенно приближаемся к π.

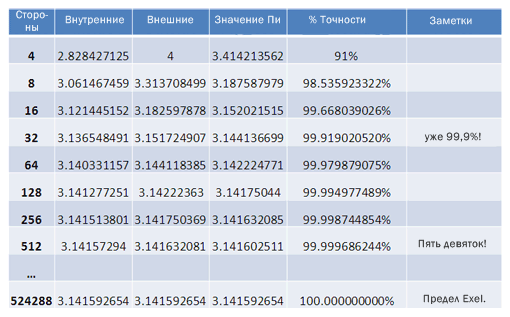
В каждом раунде мы удваиваем количество сторон (4, 8, 16, 32, 64) и уменьшаем диапазон, в котором π может скрываться. Давайте предположим, что π находится на полпути между внутренней и наружной границами.

После 3-го этапа (32 стороны) у нас уже есть 99,9% точности. После 7 шагов (512 сторон) мы получим пять девяток. А после 17 шагов и полмиллиона сторон наше определение π достигнет предельной точности в Excel. «Неплохая техника, Архимед!», говорит Калид.

К сожалению, десятичные дроби не были изобретены в 250-м году до н.э., не говоря уже о таблицах. Поэтому Архимед должен был трудиться в поте лица с этими формулами, используя дроби. Он начал с шестиугольников (6 сторон) и продолжил до 12, 24, 48, 96 и далее. А вы пробовали когда-нибудь найти квадратный корень, используя только дроби?. Его окончательная оценка числа π, которая основывалась на многоугольнике с 96-ю сторонами, была:

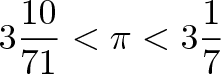
Среднее число π равняется 3,14185, что является более чем на 99,9% точным. Неплохо!

Если вы любите дроби, то знаете, что загадочная симметрия 355/113 является чрезвычайно точной (99,99999%) оценкой π и была лучшей на протяжении тысячелетий.

Некоторые люди используют симметрию 22/7 для π, но теперь вы можете поправить свой монокль и усмехнуться: «Боже, 22/7 является лишь верхней границей, найденной Архимедом 2000 лет назад!».

Где исчисление?

Архимед не занимался исчислением, но он заложил основу для его развития: начал с грубой модели (квадрат, имитирующий круг) и уточнил её.

Источник: Flickr.com.

Исчисление вращается вокруг таких задач:

• Мы не знаем ответа, но у нас есть предположение. У нас было предположение для π: это число находится где-то между 2,8 и 4. Есть много специальных средств, вроде рядов Тейлора, когда необходимо делать предположительные подсчёты с разной степенью точности.
• Давайте усовершенствуем наши подсчёты. Архимед открыл, что добавление сторон даёт более точный результат. Существуют численные методы, позволяющие уточнять формулы. Например, компьютер может начать с грубой догадки относительно квадратного корня и на основе этого прийти к правильному результату (быстрее, чем если бы он начал поиск правильного ответа с самого начала).
• Можно убегать, но не прятаться. Мы не знали точно, на каком отрезке находилось π, но искали его в ловушке между двумя границами. Когда мы уменьшили внешние пределы, мы знали, что π прячется где-то внутри. Это явление официально известно как лемма о двух милиционерах (в русской версии).
• π является недостижимым идеалом. Поиск π — это процесс, который никогда не заканчивается. Когда мы видим π, мы сталкиваемся с дилеммой: «Вы хотите совершенства? Хотеть не вредно. Просто начните искать и сумейте остановиться, когда π станет достаточно точным».

Я скажу это снова: достаточно хорошо — это достаточно хорошо. Фигура с 96-ю сторонами была достаточна хороша для того, чего Архимед хотел добиться. Идея «близкого подсчёта» кажется странной: разве математика не должна быть точной? Но математика является моделью для описания мира. Наши уравнения не должны быть остры как бритва, если вселенная и наши инструменты и так достаточно нежны», заключает Калид Азад и приводит в конце своей статьи несколько уроков, которые можем извлечь из поиска числа π.

Уроки жизни

Даже математика может заключать в себе скрытые уроки жизни. Иногда лучшее — враг хорошего. Перфекционизм («Мне нужно точное значение π!») может помешать найти хорошие и удобные результаты.

Будь то создание оценки или написание программного обеспечения, возможно, вам стоит начать с грубой версии и улучшать её в течение какого-то времени без мучительных раздумий о какой-то совершенной модели (ведь это работало у Архимеда!). Большая точность может зависеть от начальных шагов, а будущие подсчёты могут сделать необходимые уточнения (Принцип Парето в действии).

По иронии судьбы, «грубые» методы, представленные здесь, привели к появлению систем исчисления, что, в свою очередь, привело к улучшению формулы для нахождения π.

Источник: Flickr.com.

Уроки математики

Исчислению часто не хватает определённой приземлённости: мы можем считать яблоки, изучая арифметику, но слишком трудно думать об абстрактных уравнениях, которые неоднократно совершенствовались.

Открытие Архимедом π является ярким конкретным примером для нашего инструментария. Так же, как геометрия уточняет наши знания о линиях и углах, исчисление определяет правила уравнений, которые могут становиться совершеннее со временем. Это пример того, когда интуиция используется в качестве отправной точки, оставляя позади изучение новых идей в вакууме.

Позже мы обсудим, что это значит для числа – «быть достаточно близко». Просто помните, что 96 сторон были достаточно хороши для Архимеда, а полмиллиона сторон достаточно хороши для Excel. У каждого из нас есть свои пределы.

Трудно с этим не согласиться. Но пока есть возможность, мы будем эти пределы расширять, погружаясь в загадки математики с Better Explained. 

По материалам Better Explained.