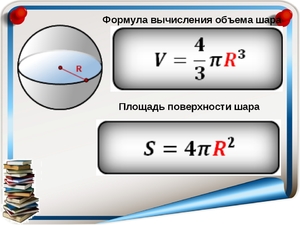
Имея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара. Формула будет иметь вид S =4πR2, где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» – это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
- Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Рождение формулы
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара, был Архимед. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи» и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.
Видео
На примере этого видео вам будет легко понять, как найти площадь поверхности шара.
Содержание:
- Площадь поверхности шара. Доказательство Архимеда
- Площадь сегмента шара
- Площадь шарового пояса
- Задача пример №81
Площадь поверхности шара находится по формуле 
. Здесь 
радиус шара. В окружность радиусом 
впишем правильный многоугольник.
Поверхность шара, полученного при вращении относительно диаметра соответствующих кругов, можно рассматривать как сумму пределов боковых поверхностей фигур – конуса, усеченного конуса и цилиндра, образующие которых являются сторонами данного многоугольника. Покажем, что при вращении сторон многоугольника вокруг оси получается тело (конус, усеченный конус, цилиндр), площадь боковой поверхности которого равна площади боковой поверхности цилиндра, высота которого равна высоте данного тела, радиус основания равен апофеме многоугольника. Обозначим апофему многоугольника через 
.
– площадь боковой поверхности конуса с образующей 
. Так как 
, то 
.
Умножим на 2 обе части равенства 
. Учитывая, что 
, 
, получим 
.
Значит, 
– площадь боковой поверхности усеченного конуса. Зная, что
, получим что 
. Так как 
, то 
Умножим на 2 обе части равенства 
. Учитывая,что 
, получим 
.
Значит, 
.
Понятно, что площадь боковой поверхности цилиндра с образующей 
равна 
. Аналогично получаем, что площадь боковых поверхностей усеченного конуса с образующей 
и конуса с образующей 
можно найти по формулам 
. Таким образом, поверхность тела, полученного вращением многоугольника вокруг диаметра, равна :
При бесконечном увеличении количества сторон многоугольника значение 
стремится к радиусу, а площадь поверхности полученного тела к площади поверхности шара, т.е. 
.
Площадь поверхности шара. Доказательство Архимеда
Найдя сумму поверхностей усеченных конусов и цилиндра, можно найти площадь поверхности шара. Рассмотрим осевое сечение одного из усеченных конусов. Пусть радиус средней окружности равен 
, а высота 
, радиус шара 
сторона многоугольника, описанного вокруг большего круга равна 
. Площадь боковой поверхности усеченного конуса будет 
, а также 
, т.е. боковая поверхность усеченного конуса равна боковой поверхности цилиндра, радиус основания которого равен и высота . Значит, фигуру, описанную вокруг шара, можно принять за цилиндр. Отсюда получается, что площадь поверхности шара равна площади боковой поверхности цилиндра с радиусом основания и высотой 
Т.е., 
Площадь сегмента шара
Часть шара, отсекаемая плоскостью сечения называется сегментом. Круг, полученный при сечении плоскостью, называется основанием сегмента. Часть диаметра шара, перпендикулярного основанию сегмента, расположенная внутри него, называется высотой сегмента. Из доказательства формулы поверхности шара, аналогично, можно показать, что для шара радиуса 
площадь сферической поверхности сегмента высотой 
, вычисляется по формуле 
.
Площадь шарового пояса
Часть поверхности шара, расположенная между двумя параллельными плоскостями, называется шаровым поясом. Расстояние между параллельными плоскостями называется высотой шарового пояса. Площадь поверхности шарового пояса можно найти, как разность площадей сегментов, отсекаемых параллельными плоскостями.
Площадь поверхности шарового пояса высотой 
отсекаемого от шара радиуса 
вычисляется по формуле 
Задача пример №81
Радиус шара разбит на три равные части и через эти точки проведены перпендикулярные к радиусу плоскости. Зная, что радиус шара 
, найдите площадь поверхности шарового пояса.
Решение:
если 
и 
, то площадь поверхности шарового пояса будет 
.
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Производная сложной функции примеры решений
- Определение предела функции
- Вычисление пределов
- Формулы сокращенного умножения
- Прямоугольная система координат в пространстве
- Действия со степенями
- Найти три первых отличных от нуля
- Предел логарифма: пример решения
- Исследовать сходимость ряда по признаку Даламбера
- Линейная комбинация векторов
III век до н.э. на острове Сицилия жил математик исключительной одарённости. И сейчас, более чем через две тысячи лет после его кончины, его имя известно любому школьнику. Это Архимед. Замечательный геометр, механик, физик и военный инженер.
«Он заложил первоосновы почти всех открытий, развитием которых гордится наш век», — так говорит об Архимеде английский математик Джон Валлис (1616 – 1703). Здесь я расскажу лишь о некоторых важных открытиях Архимеда.
ИЗМЕРЕНИЕ КРУГА
В своей работе «Измерение круга» Архимед определил, что число π (отношение длины окружности к диаметру круга) лежит в пределах:
Подробнее о числе π можно прочитать в моей статье:
Архимед изучал новые для науки того времени методы вычисления площадей криволинейных фигур (например, параболического сегмента) и объёмов тел, ограниченных кривыми поверхностями (например, шара, вписанного в цилиндр).
В письме-трактате «О шаре и цилиндре» Архимед изложил свой метод вычисления объёма шара и поверхности шара:
объём шара, вписанного в цилиндр, в 1,5 раза меньше объёма цилиндра и также относятся поверхности этих тел.
Сейчас это утверждение Архимеда легко доказать, пользуясь готовыми формулами:
Но в то далёкое время эти формулы ещё не были открыты, не было такой удобной алгебраической символики, как не было привычной десятичной позиционной формы записи чисел.
Известно, что Архимед завещал высечь на его будущем надгробии фигуру цилиндра с вписанным в него шаром, что и было сделано впоследствии.
ПЕРВЫЙ В МИРЕ ПЛАНЕТАРИЙ
Изумительное изобретение Архимеда — механический небесный глобус — своеобразный планетарий, демонстрирующий все видимые движения небесных тел и даже фазы Луны. На поверхности глобуса нанесены звёзды и 12 зодиакальных созвездий, через которые движется Солнце, проходя одно созвездие в месяц.
Это был первый на Земле планетарий, много столетий бывший непревзойдённым творением практической механики.
«ВИНТ-УЛИТКА» (Архимедов винт)
Этот водяной винт похож на штопор, размещённый в трубе. С его помощью можно поднимать воду из водоёмов (рек, озёр или колодца).
Учёный изобрёл эту машину, когда был в Александрии (Египте) для поливки полей. Архимедов винт долгое время имел большое хозяйственное значение в Египте, где дожди бывают очень редко, и всё сельское хозяйство основано на искусственном орошении.
ИСТОРИЯ О ЗОЛОТОЙ КОРОНЕ
Наверно это самый интересный факт в биографии Архимеда. Король Гиерон II заказал у ремесленника золотую корону. Когда корона была готова, то оказалось, что она весила столько же, сколько и золото.
Решить проблему было поручено Архимеду.
Было известно, что золото плотнее серебра, поэтому 1 кубический см золота будет весить больше, чем 1 кубический см серебра. Поскольку корона была неправильной формы, её объём был неизвестен.
По легенде Архимед измерил уровень воды в чашке, сравнив измерения при погружении 1 кг золота и столько серебра, и обнаружил, что корона была смесью золота и серебра. Считается, что Архимед решил эту проблему, когда принимал ванну, заметив при этом, как меняется уровень воды. Именно тогда он вскочил из ванны и выбежал голым на улицу, выкрикивая своё знаменитое: «ЭВРИКА» (Нашёл!).
НЕ ТРОНЬ МОИХ КРУГОВ!
Как я уже писала выше, Архимед был ещё и гениальным военным изобретателем. Он сыграл важную роль в защите Сиракуз от осады римских легионеров в 213 году до н.э.
Город держался долгое время, благодаря гениальным инженерным изобретениям Архимеда. При помощи нескольких десятков хорошо отполированных щитов воинов, собирающих в одну точку солнечные зайчики (такое своеобразное вогнутое зеркало), он поджигал галеры римлян, подступавших с моря, или схватывали галеры железными челюстями-клювами и разбивали их о скалы.
Архимед изобрёл также высокоточные катапульты, которые обрушивали на римлян град камней массой почти в четверть тонны. Он мог сделать это на основании математических расчётов и понимания траектории снаряда.
Но город всё-таки пал. По одной версии предания первым знаком того, что город пал, была для Архимеда тень римского солдата, упавшего на чертёж, который Архимед построил на пыльной земле. Солдат наступил на чертёж, а рассердившийся учёный воскликнул: «Не трогай моих чертежей!». Разъярённый солдат поднял меч и убил 75-летнего старца.
По другой версии, солдат убил Архимеда за его отказ подчиниться приказу идти с солдатами к командиру римлян. Так или иначе восклицание: «Не порти мои круги!» стало афоризмом — заповедью высокой морали на все последующие эпохи.
В Сиракузах воздвигли памятник Архимеду с моделью вогнутого зеркала в руке. Зеркало имеет вид сферического сегмента, радиус кривизны которого равен примерно одному метру. Как вы думаете, с какого расстояния при помощи такого зеркала Архимед мог поджечь корабли римлян?
В заключение приведу задачу-легенду.
Однажды царь приказал Архимеду установить, сколько потребуется золота, чтобы оно по массе равнялось бы массе слона. Но таких весов, чтобы взвесить этот громадный груз, нигде не оказалось. Каким способом решил эту непростую задачу Архимед?
Архимед решил задачу, поместив слона на большой плот и отметив уровень, до которого плот погрузился в воду. Потом слона сняли с плота и стали нагружать плот слитками золота до тех пор, пока плот не погрузился до отмеченного уровня. В этом положении вес плота с золотом сравнялся с весом плота со слоном, и, значит, золото весило столько же, сколько слон.
Конечно, это не все открытия великого учёного, но надеюсь, что в этой статье вы узнали что-то новое об Архимеде.
Автор: #ирина_чудневцева главный редактор и соавтор канала Хакнем Школа, 44 года, город Ярославль
#хакнем_математика 👈 подпишись на рубрику, содержащую интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Другие статьи рубрики:
Пусть это изобразят на моем надгробии!
В утверждении 34 трактата «О шаре и цилиндре» содержится результат, которым, как нам точно известно, более всего гордился Архимед:
Соотношение объемов цилиндра и вписанного в него шара равно 3/2. Соотношение площадей поверхности цилиндра и вписанного в него шара также равно 3/2 (см. рисунок):
Vцилиндра 3/2 Vшара
Sцилиндра = 3/2 Sшара
Он смог найти абсолютно точное отношение между объемами шара и цилиндра, в который тот вписан. Речь идет о случае, когда диаметр шара равен как диаметру основания цилиндра, так и его высоте. Объем цилиндра получается в полтора раза (3/2) больше объема шара. Такое же соотношение и у площадей их поверхностей. Как мы уже говорили, Архимед даже завещал выбить изображение шара, вписанного в цилиндр, на своем надгробном памятнике вместо эпитафии. В I веке до н. э. Цицерону, по его словам, удалось увидеть это надгробие. До нашего времени оно, к сожалению, не дошло.
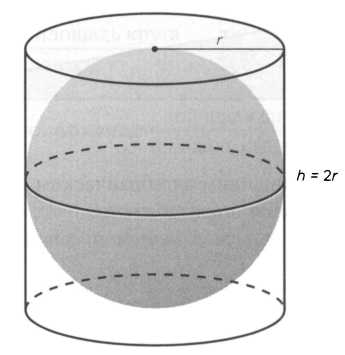
РИС.З
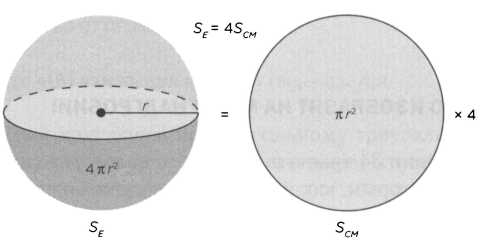
РИС. 4
Чтобы получить нужный результат, Архимед использовал различные определения, постулаты и утверждения, попутно найдя важные соотношения площадей других фигур. «О шаре и цилиндре» — это трактат, состоящий из двух книг, написанных в разные годы его жизни. Первая книга служит теоретической основой для второй, представляющей собой ответы на вопросы Досифея, которому она и посвящена. Первая книга заключает в себе 44 утверждения, шесть определений и пять постулатов. Кроме того, некоторые утверждения содержат важные следствия: например, рассматриваемое соотношение между шаром и цилиндром представлено в форме следствия из двух утверждений. Речь идет об утверждениях 33 и 34.
«Утверждение 33. Поверхность любого шара в четыре раза больше площади его большого круга» (рисунок 4).
Большой круг — это круг, который делит шар на две равные половины. Данное утверждение (рисунок 4) можно пояснить следующим умозрительным образом. Если мы сложим четыре раза площадь SCM большого круга (SCM= ?r?), то сумма будет равна площади поверхности всего шара SE (SE = 4?r?). Это означает, что потребовалось бы равное количество краски, чтобы покрасить поверхность шара и четыре больших круга.
«Утверждение 34. Любой шар [по объему] в четыре раза больше конуса, база которого равна большому кругу, а высота — радиусу шара».
В алгебраической записи показать данное соотношение объемов можно так (рисунок 5). Объем Vc конуса с радиусом r и высотой r равен
Vc = 1/3?r?
а объем шара VE с радиусом r равен
VE=4/3?r?.
Таким образом: VE = 4 Vc. То есть объем шара с радиусом r равен объему четырех конусов с радиусом основания r и высотой r. Другими словами, чтобы наполнить весь шар с радиусом r 4 л воды, потребуются 4 конуса с радиусом r и высотой r, вмещающие по 1 л каждый.
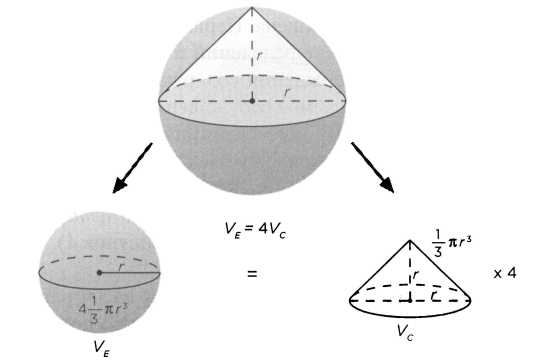
РИС. 5
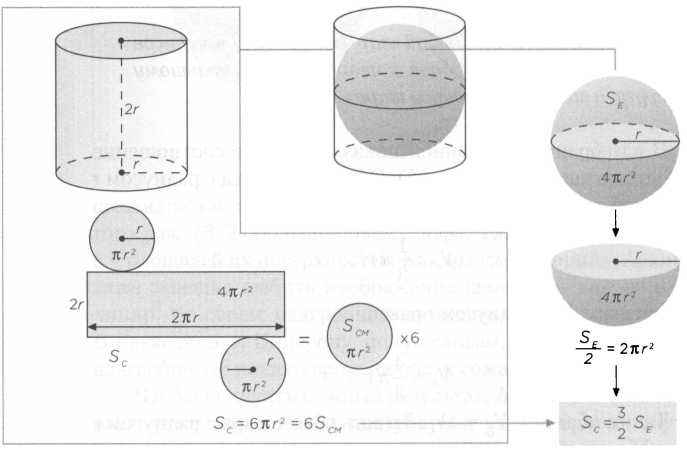
РИС. 6
В качестве следствия из утверждения 34 Архимед выводит заключение, упомянутое в начале главы и действительное для объемов и площадей:
«Поверхность шара составляет 3/2 поверхности цилиндра с основанием, равным большому кругу шара, и высотой, равной его диаметру» (рисунок 6).
Чтобы вычислить площадь поверхности цилиндра, надо сложить площади его боковой поверхности и двух оснований. Боковая поверхность равна по площади прямоугольнику с основанием 2кг и высотой 2r. Следовательно, ее площадь будет составлять 4?r?.
С другой стороны, два основания представляют собой круги с радиусом г, так что площадь каждого равна ?r?. Сложив площади боковой поверхности и удвоенную площадь основания, получаем площадь поверхности цилиндра: Sc = 6?r?.
Итак, из расчетов следует, что площадь цилиндра равна шести площадям круга с таким же радиусом. И значит, один шар равен четырем кругам, а шесть кругов — полутора шарам. Нам понадобится одинаковое количество краски, чтобы покрасить шесть кругов радиусом r, полтора шара радиусом r или один цилиндр с радиусом основания r и высотой 2r. Надо прибавить, что полученные отношения действительны также и для объемов, то есть объем цилиндра составляет 3/2 объема вписанного в него шара (рисунок 7).
Легче и нагляднее представить себе это соотношение следующим образом: если один шар вмещает 2 л воды, то в описанный вокруг него цилиндр войдет 3 л.
Вот почему часто говорят, что отношение цилиндра к шару — три к двум.
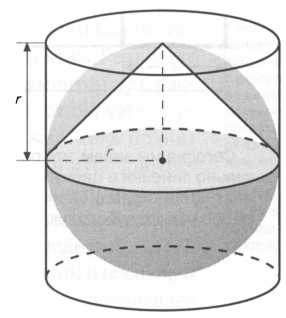
РИС. 7
ДЕЛОССКАЯ ЗАДАЧА
В V веке до н. э. Афины опустошила эпидемия чумы, одной из жертв которой стал знаменитый Перикл (495-429 гг. до н. э.), афинский политический деятель, которому удалось собрать в Афинах множество талантливых людей со всех концов греческого мира. Тогда группа афинян решила идти к оракулу Аполлона в Дельфах, чтобы узнать, как можно остановить чуму. По преданию, полученный ответ был таков: надо сделать новый кубический алтарь взамен старого так, чтобы по объему он был ровно в два раза больше. В этой легенде — в одном из двух ее вариантов — ставится знаменитая задача удвоения куба, известная как «делосская задача»: как построить куб объемом в два раза больше заданного, используя только линейку и циркуль. Из книги Архимеда «О шаре и цилиндре» понятно: он вполне осознавал, что для удвоения куба невозможно идти по интуитивно напрашивающемуся пути — просто удвоить его ребро. Ведь если ребро куба I1 = а, его объем будет составлять V1 = а?; удвоив же ребро I2 =2а, мы получим объем нового куба V2 = (2а)? = 8а?, а это значит, что V2 = 8V1. Объем куба не удвоился, а «увосьмерился», как показано на рисунке.
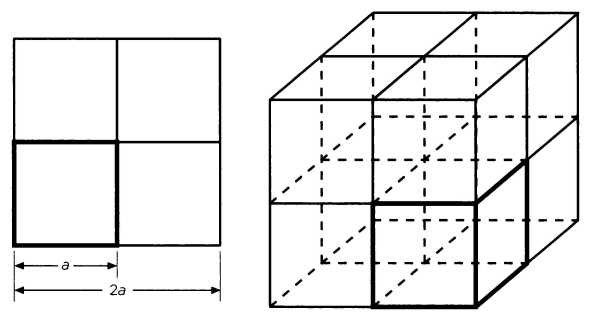
Сегодня мы знаем, что решить «делосскую задачу» с помощью исключительно линейки и циркуля невозможно, потому что ее решение представляет собой иррациональное число. Так, чтобы удвоить куб с ребром а, ребро нового куба должно равняться
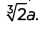
Yes, the mapping preserves area of any shape. You can convince yourself of this by taking by small patches on the sphere, between two constant latitude lines and two longitude lines, which I believe is what they did with the state of Colorado and the sate of Wyoming. Anyway, any nice enough shape is made up, to sufficient accuracy, by a large number of these curved rectangles, and these quite definitely are mapped in an area-preserving manner. This is the oldest example of a “symplectic” map.
I do not know that much about the history of this exact example, but I do know that a book of Archimedes called The Method was thought to be lost until about 1900, and translations are available. See EUDOXUS and METHOD and SPHERE_AND_CYLINDER finally MOOSE_AND_SQUIRREL
Alright, somebody at Wikipedia is not paying attention. The equal area MAP projection is due to Archimedes.
