Как быстрее найти степень числа

Как быстрее найти степень числа

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 ноября 2022 года; проверки требуют 2 правки.

Алгоритмы быстрого возведения в степень (дихотомический алгоритм возведения в степень, бинарный алгоритм возведения в степень) — алгоритмы, предназначенные для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении степени[1]. Многие из этих алгоритмов основаны на том, что для возведения числа x в степень n не обязательно перемножать число x на само себя n раз, а можно перемножать уже вычисленные степени. В частности, если n=2^k степень двойки, то для возведения в степень n достаточно число возвести в квадрат k раз, затратив при этом k умножений вместо 2^k. Например, чтобы возвести число x в восьмую степень, вместо выполнения семи умножений {displaystyle xcdot xcdot xcdot xcdot xcdot xcdot xcdot x} можно возвести число в квадрат ({displaystyle x^{2}=xcdot x}), потом результат возвести ещё раз в квадрат и получить четвёртую степень ({displaystyle x^{4}=x^{2}cdot x^{2}}), и наконец результат ещё раз возвести в квадрат и получить ответ ({displaystyle x^{8}=x^{4}cdot x^{4}}).

Кроме того, некоторые алгоритмы для дальнейшей оптимизации используют тот факт, что операция возведения в квадрат быстрее операции умножения за счёт того, что при возведении в квадрат цифры в сомножителе повторяются[2].

Бинарный алгоритм возведения в степень был впервые предложен в XV веке персидским математиком Аль-Каши[3].

Данные алгоритмы не всегда оптимальны. Например, при использовании схемы «слева направо» быстрое возведение в степень n = 15 потребует выполнения трёх операций умножения и трёх операций возведения в квадрат, хотя возведение в 15-ю степень можно выполнить и за 3 умножения и 2 возведения в квадрат[4]. Оптимальное возведение в степень соответствует построению кратчайшей аддитивной цепочки.

Описание[править | править код]

Основным алгоритмом быстрого возведения в степень является схема «слева направо». Она получила своё название вследствие того, что биты показателя степени просматриваются слева направо, то есть от старшего к младшему[5].

Пусть

n=(overline {m_{{k}}m_{{k-1}}...m_{{1}}m_{{0}}})_{2} — двоичное представление степени n, то есть,
n=m_{{k}}cdot 2^{{k}}+m_{{k-1}}cdot 2^{{k-1}}+dots +m_{{1}}cdot 2+m_{{0}},

где m_{{k}}=1,m_{{i}}in {0,1}. Тогда

x^{n}=x^{((dots((m_{k} cdot 2+m_{k-1}) cdot 2+m_{k-2}) cdot 2+dots) cdot 2+m_{1}) cdot 2 + m_{0}}=((dots(((x^{m_{k}})^{2} cdot x^{m_{k-1}})^{2}dots)^{2} cdot x^{m_{1}})^2 cdot x^{m_{0}}[5].

Последовательность действий при использовании данной схемы можно описать так:

  1. Представить показатель степени n в двоичном виде
  2. Если m_i = 1, то текущий результат возводится в квадрат и затем умножается на x. Если m_i = 0, то текущий результат просто возводится в квадрат[6]. Индекс i изменяется от k-1 до 0[7].

Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера[6]:

{begin{Bmatrix}s_{1}=x\s_{{i+1}}=s_{i}^{2}cdot x^{{m_{{k-i}}}}\i=1,2,dots ,kend{Bmatrix}}.

Обобщения[править | править код]

Пусть пара (S, *) — полугруппа, тогда мы можем назвать операцию * умножением и определить операцию возведения в натуральную степень:

a^{n}=left{{begin{array}{ll}a&n=1\a*left(a^{{n-1}}right)&n>1end{array}}right.

Тогда для вычисления значений an в любой полугруппе (в абелевой группе в частности) можно использовать алгоритмы быстрого возведения в степень[8].

Примеры решения задач[править | править код]

Применяя алгоритм, вычислим 2113:

{displaystyle 13_{10}=1101_{2}}
{displaystyle m_{3}=1,m_{2}=1,m_{1}=0,m_{0}=1}
{displaystyle {begin{aligned}21^{13}&=(((1cdot 21^{m_{3}})^{2}cdot 21^{m_{2}})^{2}cdot 21^{m_{1}})^{2}cdot 21^{m_{0}}\&=(((1cdot 21^{1})^{2}cdot 21^{1})^{2}cdot 21^{0})^{2}cdot 21^{1}\&=(((1cdot 21)^{2}cdot 21)^{2}cdot 1)^{2}cdot 21\&=((21^{2}cdot 21)^{2})^{2}cdot 21\&=((441cdot 21)^{2})^{2}cdot 21\&=85766121^{2}cdot 21\&=154472377739119461end{aligned}}}

Схема «справа налево»[править | править код]

В данной схеме, в отличие от схемы «слева направо», биты показателя степени просматриваются от младшего к старшему[5].

Последовательность действий при реализации данного алгоритма.

  1. Представить показатель степени n в двоичном виде.
  2. Положить вспомогательную переменную z равной числу x.
    1. Если {displaystyle m_{i}=1}, то текущий результат умножается на z, а само число z возводится в квадрат. Если m_i = 0, то требуется только возвести z в квадрат[6]. При этом индекс i, в отличие от схемы слева направо, изменяется от 0 до k-1 включительно[7].

Данная схема содержит столько же умножений и возведений в квадрат, сколько и схема «слева направо». Однако несмотря на это, схема «слева направо» выгоднее схемы «справа налево», особенно в случае, если показатель степени содержит много единиц. Дело в том, что в схеме слева направо в операции result = result · x содержится постоянный множитель x. А для небольших x (что нередко бывает в тестах простоты) умножение будет быстрым. К примеру, для x = 2 мы можем операцию умножения заменить операцией сложения[7].

Математическое обоснование работы данного алгоритма можно представить следующей формулой:

d=a^{n}=
= a^{sum_{i=0}^k m_icdot 2^i} =
= a^{m_0}cdot a^{2m_1}cdot a^{2^2*m_2}cdot ... cdot a^{2^k*m_k}=
= a^{m_0}cdot (a^2)^{m_1}cdot (a^{2^2})^{m_2}cdot ... cdot (a^{2^k})^{m_k}=
=prod _{{i=0}}^{k}{(a^{{2^{{i}}}})^{{m_{i}}}}[9].

Пример. Посчитаем с помощью схемы возведения в степень «справа налево» значение 2113.

i 0 1 2 3
a^{2^{i}} 21 441 194 481 37 822 859 361
m_i 1 0 1 1
  1. 21 · 194 481 = 4084 101
  2. 4084 101 · 37 822 859 361 = 154 472 377 739 119 461

Вычислительная сложность[править | править код]

И для схемы «слева направо», и для схемы «справа налево» количество операций возведения в квадрат одинаково и равно k, где k — длина показателя степени n в битах, k sim ln{n}. Количество же требуемых операций умножения равно весу Хэмминга, то есть количеству ненулевых элементов в двоичной записи числа n. В среднем требуется frac{1}{2}cdotln{n} операций умножения[6].

Например, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 операций умножения и возведения в квадрат[5].

Для сравнения, при стандартном способе возведения в степень требуется n-1 операция умножения, то есть количество операций может быть оценено как O(n) [10].

Оптимизация алгоритма[править | править код]

Как правило, операция возведения в квадрат выполняется быстрее операции умножения. Метод окон позволяет сократить количество операций умножения и, следовательно, сделать алгоритм возведения в степень более оптимальным[8].

Окно фактически представляет собой основание системы счисления[7]. Пусть w — ширина окна, то есть за один раз учитывается w знаков показателя.

Рассмотрим метод окна.

  1. Для i = overline {0, 2^w-1} заранее вычисляется xi
  2. Показатель степени представляется в следующем виде: n = sum_{i=0}^{k/w}{n_icdot2^{icdot w}}, где n_i in {(0, 1, ..., 2^w-1)}
  3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y=x^{n_{k/w}}.
  4. Для всех i = k/w — 1, k/w — 2, …, 0 выполнить следующие действия:
    1. y = y^{2^w}
    2. y = ycdot x^{n_i}[8].

В данном алгоритме требуется k возведений в квадрат, но число умножений в среднем сокращается до k/w[8].

Ещё более эффективным является метод скользящего окна. Он заключается в том, что ширина окна во время выполнения процесса может изменяться:

  1. Показатель степени представляется в виде n = sum_{i=0}^{l}{n_icdot2^{e_i}}, где n_i in {(1, 3, 5, ..., 2^w-1)}, а ei+1 — ei ≥ w.
  2. Для i = (1, 3, 5, ..., 2^w-1) вычисляется xi. Далее будем обозначать xi как xi.
  3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y=x^{n_{l}}.
  4. Для всех i = l — 1, l — 2, …, 0 выполнить следующие действия:
    1. Для всех j от 0 до ei+1 — ei — 1 y возвести в квадрат
    2. j = m_i
    3. y = ycdot x_j
  5. Для всех j от 0 до e0 — 1 y возвести в квадрат[8].

Количество операций возведения в степень в данном алгоритме такое же, как и в методе окна, а вот количество операций умножений сократилось до l, то есть до frac{k}{w+1} в среднем[8].

Для примера возведём методом скользящего окна число x в степень 215. Ширина окна w = 3.

  1. 215 = 27 + 5 · 24 + 7
  2. y = 1
  3. y = y · x = x
  4. y 3 раза возводится в квадрат, так как на данном шаге e2 — e1 −1 = 7 — 4 — 1 = 2, а отсчёт ведётся с нуля, то есть y = y8 = x8
  5. y = y · x5 = x13
  6. y 4 раза возводится в квадрат, так как на данном шаге e1 — e0 −1 = 4 — 0 — 1 = 3, то есть y = y16= x208
  7. y = y · x7 = x215

Применение[править | править код]

Алгоритм быстрого возведения в степень получил широкое распространение в криптосистемах с открытым ключом. В частности, алгоритм применяется в протоколе RSA, схеме Эль-Гамаля и других криптографических алгоритмах[11].

См. также[править | править код]

  • Возведение в степень по модулю
  • Алгоритмы быстрого возведения в степень по модулю

Примечания[править | править код]

  1. ↑ Швец А. Н. Быстрое возведение в степень. Дата обращения: 13 ноября 2015. Архивировано 17 ноября 2015 года.
  2. ↑ Панкратова, 2009, с. 7.
  3. ↑ Панкратова, 2009, с. 11.
  4. ↑ Панкратова, 2009, с. 10.
  5. ↑ 1 2 3 4 Рябко, Фионов, 2004.
  6. ↑ 1 2 3 4 Handbook, 2006.
  7. ↑ 1 2 3 4 Крэндалл, Померанс, 2011.
  8. ↑ 1 2 3 4 5 6 Криптография, 2005.
  9. ↑ Габидулин, Кшевецкий, Колыбельников, 2011.
  10. ↑ Маховенко, 2006.
  11. ↑ Прикладная криптография, 2002.

Литература[править | править код]

  • Шнайер Б. Алгоритмы с открытыми ключами // Прикладная криптография. — Триумф, 2002. — ISBN 5-89392-055-4.
  • Рябко Б. Я., Фионов А. Н. Основы современной криптографии для специалистов в информационных технологиях — Научный мир, 2004. — С. 15. — 173 с. — ISBN 978-5-89176-233-6
  • Смарт Н. Алгоритмы возведения в степень // Криптография. — Москва: Техносфера, 2005. — С. 287—292. — 528 с. — ISBN 5-94836-043-1.
  • Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006. — С. 154—155. — ISBN 978-5-85438-143-7
  • Cohen H., Frey G. Handbook of Elliptic and Hyperelliptic Curve Cryptography. — Chapman & Hall/CRC, 2006. — С. 145—150. — 808 с. — ISBN 1-58488-518-1.
  • Панкратова И. А. Теоретико-числовые методы криптографии — Томск: ТГУ, 2009. — 120 с.
  • Габидулин Э. М., Кшевецкий А. С., Колыбельников А. И. Защита информации: учебное пособие — М.: МФТИ, 2011. — С. 230—231. — 225 с. — ISBN 978-5-7417-0377-9
  • Крэндалл Р., Померанс К. Алгоритмы с открытыми ключами // Простые числа: Криптографические и вычислительные аспекты — М.: URSS, 2011. — С. 514—520. — 663 с. — ISBN 978-5-453-00016-6, 978-5-397-02060-2
Источник

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Возведение в степень — это вычисление значения степени некоторого числа.

То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0 , 5 в пятую степень”, это следует понимать как “вычислите значение степени ( 0 , 5 ) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Условие: возведите — 2 в степень 4 .

Решение

Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Выполните возведение в квадрат числа π .

Решение

Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

5 0 = 1 , ( — 2 , 56 ) 0 = 1 2 3 0 = 1

0 0 — не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Возведите 2 в степень — 3 .

Решение

Используя определение выше, запишем: 2 — 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8

Возведите 1 , 43 в степень — 2 .

Решение

Переформулируем: 1 , 43 — 2 = 1 ( 1 , 43 ) 2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: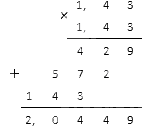

В итоге у нас вышло ( 1 , 43 ) — 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: ( 1 , 43 ) — 2 = 10000 20449

Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .

Пример: 3 − 1 = 1 / 3

9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Вычислите 8 — 2 3 .

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2

После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Возведите 44 , 89 в степень 2 , 5 .

Решение

Преобразуем значение показателя в обыкновенную дробь — 44 , 89 2 , 5 = 49 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 .

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную — значения не имеет: 0 — 4 3 .

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Вычислите приближенное значение 21 , 174367 .

Решение

Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .

Ещё Ричард Фейнман в книге «Вы конечно шутите, мистер Фейнман!» поведал несколько приёмов устного счёта. Хотя это очень простые трюки, они не всегда входят в школьную программу.

Например, чтобы быстро возвести в квадрат число X около 50 (50 2 = 2500), нужно вычитать/прибавлять по сотне на каждую единицы разницы между 50 и X, а потом добавить разницу в квадрате. Описание звучит гораздо сложнее, чем реальное вычисление.

52 2 = 2500 + 200 + 4
47 2 = 2500 – 300 + 9
58 2 = 2500 + 800 + 64

Молодого Фейнмана научил этому трюку коллега-физик Ханс Бете, тоже работавший в то время в Лос-Аламосе над Манхэттенским проектом.

Ханс показал ещё несколько приёмов, которые использовал для быстрых вычислений. Например, для вычисления кубических корней и возведения в степень удобно помнить таблицу логарифмов. Это знание очень упрощает сложные арифметические операции. Например, вычислить в уме примерное значение кубического корня из 2,5. Фактически, при таких вычислениях в голове у вас работает своеобразная логарифмическая линейка, в которой сложение и деление чисел заменяется сложением и вычитанием их логарифмов. Удобнейшая вещь.


Логарифмическая линейка

До появления компьютеров и калькуляторов логарифмическую линейку использовали повсеместно. Это своеобразный аналоговый «компьютер», позволяющий выполнить несколько математических операций, в том числе умножение и деление чисел, возведение в квадрат и куб, вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени. Точность расчётов — около 3 значащих цифр.

Чтобы быстро проводить в уме сложные расчёты даже без логарифмической линейки, неплохо запомнить квадраты всех чисел, хотя бы до 25, просто потому что они часто используются в расчётах. И таблицу степеней — самых распространённых. Проще запомнить, чем вычислять каждый раз заново, что 5 4 = 625, 3 5 = 243, 2 20 = 1 048 576, а √3 ≈ 1,732.

Ричард Фейнман совершенствовал свои навыки и постепенно замечал всё новые интересные закономерности и связи между числами. Он приводит такой пример: «Если кто-то начинал делить 1 на 1,73, можно было незамедлительно
ответить, что это будет 0,577, потому что 1,73 — это число, близкое к квадратному корню из трёх. Таким образом, 1/1,73 — это около одной трети квадратного корня из 3».

Настолько продвинутый устный счёт мог бы удивить коллег в те времена, когда не было компьютеров и калькуляторов. В те времена абсолютно все учёные умели хорошо считать в уме, поэтому для достижения мастерства требовалось достаточно глубоко погрузиться в мир цифр.

В наше время люди достают калькулятор, чтобы просто поделить 76 на 3. Удивить окружающих стало гораздо проще. Во времена Фейнмана вместо калькулятора были деревянные счёты, на которых тоже можно было производить сложные операции, в том числе брать кубические корни. Великий физик уже тогда заметил, что использование таких инструментов, людям вообще не нужно запоминать множество арифметический комбинаций, а достаточно просто научиться правильно катать шарики. То есть люди с «расширителями» мозга не знают чисел. Они хуже справляются с задачами в «автономном» режиме.

Вот пять очень простых советов устного счёта, которые рекомендует Яков Перельман в методичке «Быстрый счёт» 1941 года издательства.

1. Если одно из умножаемых чисел разлагается на множители, удобно бывает последовательно умножать на них.

225 × 6 = 225 × 2 × 3 = 450 × 3
147 × 8 = 147 × 2 × 2 × 2, то есть трижды удвоить результат

2. При умножении на 4 достаточно дважды удвоить результат. Аналогично, при делении на 4 и 8, число делится пополам дважды или трижды.

3. При умножении на 5 или 25 число можно разделить на 2 или 4, а затем приписать к результату один или два нуля.

74 × 5 = 37 × 10
72 × 25 = 18 × 100

Здесь лучше сразу оценивать, как проще. Например, 31 × 25 удобнее умножать как 25 × 31 стандартным способом, то есть как 750+25, а не как 31 × 25, то есть 7,75 × 100.

При умножении на число, близкое к круглому (98, 103), удобно сразу умножить на круглое число (100), а затем вычесть/прибавить произведение разницы.

37 × 98 = 3700 – 74
37 × 104 = 3700 + 148

4. Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 85), умножают число десятков (8) на него же плюс единица (9), и приписывают 25.

8 × 9 = 72, приписываем 25, так что 85 2 = 7225

Почему действует это правило, видно из формулы:

(10Х + 5) 2 = 100Х 2 + 100Х + 25 = 100Х (X+1) + 25

Приём применяется и к десятичным дробям, которые оканчиваются на 5:

8,5 2 = 72,25
14,5 2 = 210,25
0,35 2 = 0,1225

5. При возведении в квадрат не забываем об удобной формуле

(a + b) 2 = a 2 + b 2 + 2ab
44 2 = 1600 + 16 + 320

Конечно же, все способы можно сочетать между собой, создавая более удобные и эффективные приёмы для конкретных ситуаций.

Алгоритмы быстрого возведения в степень (дихотомический алгоритм возведения в степень, бинарный алгоритм возведения в степень) — алгоритмы, предназначенные для возведения числа x <displaystyle x> в натуральную степень n <displaystyle n> за меньшее число умножений, чем это требуется в определении степени [1] . Алгоритмы основаны на том, что для возведения числа x <displaystyle x> в степень n <displaystyle n> не обязательно перемножать число x <displaystyle x> на само себя n <displaystyle n> раз, а можно перемножать уже вычисленные степени. В частности, если n = 2 k <displaystyle n=2^> степень двойки, то для возведения в степень n <displaystyle n> достаточно число возвести в квадрат k <displaystyle k> раз, затратив при этом k <displaystyle k> умножений вместо 2 k <displaystyle 2^> . Например, чтобы возвести число x <displaystyle x> в восьмую степень, вместо выполнения семи умножений x ⋅ x ⋅ x ⋅ x ⋅ x ⋅ x ⋅ x ⋅ x <displaystyle xcdot xcdot xcdot xcdot xcdot xcdot xcdot x> можно возвести число в квадрат ( x 2 = x ⋅ x <displaystyle x^<2>=xcdot x> ), потом результат возвести ещё раз в квадрат и получить четвёртую степень ( x 4 = x 2 ⋅ x 2 <displaystyle x^<4>=x^<2>cdot x^<2>> ), и наконец результат ещё раз возвести в квадрат и получить ответ ( x 8 = x 4 ⋅ x 4 <displaystyle x^<8>=x^<4>cdot x^<4>> ).

Кроме того, некоторые алгоритмы для дальнейшей оптимизации используют тот факт, что операция возведения в квадрат быстрее операции умножения за счёт того, что при возведении в квадрат цифры в сомножителе повторяются [2] .

Бинарный алгоритм возведения в степень был впервые предложен в XV веке персидским математиком Аль-Каши [3] .

Данные алгоритмы не всегда оптимальны. Например, при использовании схемы «слева направо» быстрое возведение в степень n = 15 потребует выполнения трёх операций умножения и трёх операций возведения в квадрат, хотя возведение в 15-ю степень можно выполнить и за 3 умножения и 2 возведения в квадрат [4] .

Содержание

Описание [ править | править код ]

Основным алгоритмом быстрого возведения в степень является схема «слева направо». Она получила своё название вследствие того, что биты показателя степени просматриваются слева направо, то есть от старшего к младшему [5] .

n = ( m k m k − 1 . . . m 1 m 0 ¯ ) 2 <displaystyle n=(<overline m_. m_<1>m_<0>>>)_<2>> — двоичное представление степени n, то есть, n = m k ⋅ 2 k + m k − 1 ⋅ 2 k − 1 + ⋯ + m 1 ⋅ 2 + m 0 , <displaystyle n=m_cdot 2^+m_cdot 2^+dots +m_<1>cdot 2+m_<0>,>

где m k = 1 , m i ∈ < 0 , 1 ><displaystyle m_=1,m_in <0,1>> . Тогда

x n = x ( ( … ( ( m k ⋅ 2 + m k − 1 ) ⋅ 2 + m k − 2 ) ⋅ 2 + … ) ⋅ 2 + m 1 ) ⋅ 2 + m 0 = ( ( … ( ( ( x m k ) 2 ⋅ x m k − 1 ) 2 … ) 2 ⋅ x m 1 ) 2 ⋅ x m 0 <displaystyle x^=x^<((dots ((m_cdot 2+m_)cdot 2+m_)cdot 2+dots )cdot 2+m_<1>)cdot 2+m_<0>>=((dots (((x^>)^<2>cdot x^>)^<2>dots )^<2>cdot x^<1>>)^<2>cdot x^<0>>> [5] .

Последовательность действий при использовании данной схемы можно описать так:

  1. Представить показатель степени n в двоичном виде
  2. Если m i <displaystyle m_>= 1, то текущий результат возводится в квадрат и затем умножается на x. Если m i <displaystyle m_>= 0, то текущий результат просто возводится в квадрат [6] . Индекс i изменяется от k-1 до 0 [7] .

Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера [6] :

Обобщения [ править | править код ]

Пусть пара (S, *) — полугруппа, тогда мы можем назвать операцию * умножением и определить операцию возведения в натуральную степень:

1end>
ight.>”> a n = < a n = 1 a ∗ ( a n − 1 ) n >1 <displaystyle a^=left<<egina&n=1a*left(a^
ight)&n>1end>
ight.> 1end>
ight.”/>

Тогда для вычисления значений a n в любой полугруппе (в абелевой группе в частности) можно использовать алгоритмы быстрого возведения в степень [8] .

Примеры решения задач [ править | править код ]

Применяя алгоритм, вычислим 21 13 :

13 10 = 1101 2 <displaystyle 13_<10>=1101_<2>> m 3 = 1 , m 2 = 1 , m 1 = 0 , m 0 = 1 <displaystyle m_<3>=1,m_<2>=1,m_<1>=0,m_<0>=1> 21 13 = ( ( ( 1 ⋅ 21 m 3 ) 2 ⋅ 21 m 2 ) 2 ⋅ 21 m 1 ) 2 ⋅ 21 m 0 = ( ( ( 1 ⋅ 21 1 ) 2 ⋅ 21 1 ) 2 ⋅ 21 0 ) 2 ⋅ 21 1 = ( ( ( 1 ⋅ 21 ) 2 ⋅ 21 ) 2 ⋅ 1 ) 2 ⋅ 21 = ( ( 21 2 ⋅ 21 ) 2 ) 2 ⋅ 21 = ( ( 441 ⋅ 21 ) 2 ) 2 ⋅ 21 = 85766121 2 ⋅ 21 = 154472377739119461 <displaystyle <egin21^<13>&=(((1cdot 21^<3>>)^<2>cdot 21^<2>>)^<2>cdot 21^<1>>)^<2>cdot 21^<0>>&=(((1cdot 21^<1>)^<2>cdot 21^<1>)^<2>cdot 21^<0>)^<2>cdot 21^<1>&=(((1cdot 21)^<2>cdot 21)^<2>cdot 1)^<2>cdot 21&=((21^<2>cdot 21)^<2>)^<2>cdot 21&=((441cdot 21)^<2>)^<2>cdot 21&=85766121^<2>cdot 21&=154472377739119461end>>

Схема «справа налево» [ править | править код ]

В данной схеме, в отличие от схемы «слева направо», биты показателя степени просматриваются от младшего к старшему [5] .

Последовательность действий при реализации данного алгоритма.

  1. Представить показатель степени n в двоичном виде.
  2. Положить вспомогательную переменную z равной числу x.
  1. Если m i = 1 <displaystyle m_=1>, то текущий результат умножается на z, а само число z возводится в квадрат. Если m i <displaystyle m_>= 0, то требуется только возвести z в квадрат [6] . При этом индекс i, в отличие от схемы слева направо, изменяется от 0 до k-1 включительно [7] .

Данная схема содержит столько же умножений и возведений в квадрат, сколько и схема «слева направо». Однако несмотря на это, схема «слева направо» выгоднее схемы «справа налево», особенно в случае, если показатель степени содержит много единиц. Дело в том, что в схеме слева направо в операции result = result · x содержится постоянный множитель x. А для небольших x (что нередко бывает в тестах простоты) умножение будет быстрым. К примеру, для x = 2 мы можем операцию умножения заменить операцией сложения [7] .

Математическое обоснование работы данного алгоритма можно представить следующей формулой:

d = a n = <displaystyle d=a^=> = a ∑ i = 0 k m i ⋅ 2 i = <displaystyle =a^<sum _^m_cdot 2^>=> = a m 0 ⋅ a 2 m 1 ⋅ a 2 2 ∗ m 2 ⋅ . . . ⋅ a 2 k ∗ m k = <displaystyle =a^<0>>cdot a^<2m_<1>>cdot a^<2^<2>*m_<2>>cdot . cdot a^<2^*m_>=> = a m 0 ⋅ ( a 2 ) m 1 ⋅ ( a 2 2 ) m 2 ⋅ . . . ⋅ ( a 2 k ) m k = <displaystyle =a^<0>>cdot (a^<2>)^<1>>cdot (a^<2^<2>>)^<2>>cdot . cdot (a^<2^>)^>=> = ∏ i = 0 k ( a 2 i ) m i <displaystyle =prod _^<(a^<2^>)^>>> [9] .

Пример. Посчитаем с помощью схемы возведения в степень «справа налево» значение 21 13 .

i 1 2 3
a 2 i <displaystyle a^<2^>> 21 441 194 481 37 822 859 361
m 1 <displaystyle m_<1>> 1 1 1
  1. 21 · 194 481 = 4084 101
  2. 4084 101 · 37 822 859 361 = 154 472 377 739 119 461

Вычислительная сложность [ править | править код ]

И для схемы «слева направо», и для схемы «справа налево» количество операций возведения в квадрат одинаково и равно k, где k — длина показателя степени n в битах, k ∼ ln ⁡ n <displaystyle ksim ln > . Количество же требуемых операций умножения равно весу Хэмминга, то есть количеству ненулевых элементов в двоичной записи числа n. В среднем требуется 1 2 ⋅ ln ⁡ n <displaystyle <frac <1><2>>cdot ln > операций умножения [6] .

Например, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 операций умножения и возведения в квадрат [5] .

Для сравнения, при стандартном способе возведения в степень требуется n − 1 <displaystyle n-1> операция умножения, то есть количество операций может быть оценено как O ( n ) <displaystyle O(n)> [10] .

Оптимизация алгоритма [ править | править код ]

Как правило, операция возведения в квадрат выполняется быстрее операции умножения. Метод окон позволяет сократить количество операций умножения и, следовательно, сделать алгоритм возведения в степень более оптимальным [8] .

Окно фактически представляет собой основание системы счисления [7] . Пусть w — ширина окна, то есть за один раз учитывается w знаков показателя.

Рассмотрим метод окна.

  1. Для i = 0 , 2 w − 1 ¯ <displaystyle i=<overline <0,2^-1>>>заранее вычисляется x i
  2. Показатель степени представляется в следующем виде: n = ∑ i = 0 k / w n i ⋅ 2 i ⋅ w <displaystyle n=sum _^cdot 2^>>, где n i ∈ ( 0 , 1 , . . . , 2 w − 1 ) <displaystyle n_in <(0,1. 2^-1)>>
  3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y = x n k / w <displaystyle y=x^>>.
  4. Для всех i = k/w — 1, k/w — 2, …, 0 выполнить следующие действия:
  1. y = y 2 w <displaystyle y=y^<2^>>
  2. y = y ⋅ x n i <displaystyle y=ycdot x^>>[8] .

В данном алгоритме требуется k возведений в квадрат, но число умножений в среднем сокращается до k/w [8] .

Ещё более эффективным является метод скользящего окна. Он заключается в том, что ширина окна во время выполнения процесса может изменяться:

  1. Показатель степени представляется в виде n = ∑ i = 0 l n i ⋅ 2 e i <displaystyle n=sum _^cdot 2^>>>, где n i ∈ ( 1 , 3 , 5 , . . . , 2 w − 1 ) <displaystyle n_in <(1,3,5. 2^-1)>>, а ei+1 — ei ≥ w.
  2. Для i = ( 1 , 3 , 5 , . . . , 2 w − 1 ) <displaystyle i=(1,3,5. 2^-1)>вычисляется x i . Далее будем обозначать x i как xi.
  3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y = x n l <displaystyle y=x^>>.
  4. Для всех i = l — 1, l — 2, …, 0 выполнить следующие действия:
  1. Для всех j от 0 до ei+1 — ei — 1 y возвести в квадрат
  2. j = m i <displaystyle j=m_>
  3. y = y ⋅ x j <displaystyle y=ycdot x_>
  • Для всех j от 0 до e — 1 y возвести в квадрат [8] .

    • Количество операций возведения в степень в данном алгоритме такое же, как и в методе окна, а вот количество операций умножений сократилось до l, то есть до k w + 1 <displaystyle <frac >> в среднем [8] .

    Для примера возведём методом скользящего окна число x в степень 215. Ширина окна w = 3.

    1. 215 = 2 7 + 5 · 2 4 + 7
    2. y = 1
    3. y = y · x = x
    4. y 3 раза возводится в квадрат, так как на данном шаге e2 — e1 −1 = 7 — 4 — 1 = 2, а отсчёт ведётся с нуля, то есть y = y 8 = x 8
    5. y = y · x 5 = x 13
    6. y 4 раза возводится в квадрат, так как на данном шаге e1 — e −1 = 4 — 0 — 1 = 3, то есть y = y 16 = x 208
    7. y = y · x 7 = x 215

    Применение [ править | править код ]

    Алгоритм быстрого возведения в степень получил широкое распространение в криптосистемах с открытым ключом. В частности, алгоритм применяется в протоколе RSA, схеме Эль-Гамаля и других криптографических алгоритмах [11] .

    Источник

    Для возведения числа x в степень n, как правило, используют стандартный метод, т. е. число x умножают n раз само на себя. В задачах математического толка, решаемых при помощи бумаги и ручки, такой метод вполне приемлем, ведь степенная функция быстро растет и поэтому сомнительно, что придется производить затруднительные операции вручную.

    Другое дело программирование, где важно не только решить поставленную задачу, но и составить оптимальное решение, удовлетворяющее предусмотренному диапазону входных данных. Так, в частности, для операции возведения числа в степень имеется алгоритм, позволяющий значительно сократить число требуемых операций. Он достаточно прост и основывается на математических свойствах степеней.

    Пусть имеется некоторая степень xn, где x – действительное число, а n – натуральное. Тогда для xn справедливо равенство:

    xn = (xm)k

    При этом m*k=n. Например: 36=(33)2, 57=(57)1. Это свойство является одним из основных степенных свойств, и именно на нем основывается рассматриваемый метод. Далее, заметим, что в случае, если n является четным числом, то верно следующее равенство:

    xn = (xn/2)2 = xn/2 * xn/2

    Так, если x=3, а n=6, то имеем 36 = (36/2)2 = 36/2 * 36/2. Используя это свойство, удастся существенно уменьшить число операций необходимых для возведения x в степень n. Теперь адаптируем формулу для случая с нечетным n. Для этого понадобиться просто перейти к степени на единицу меньшей. Например: 57 = 56*5, 125 = 124*12. Общая форма равенства перехода:

    xn = xn-1*x

    В программе, реализующей алгоритм быстрого возведения в степень, используются указанные свойства: если степень n четная, то переходим к степени вдвое меньшей, иначе заменяем по имеющимся правилам нечетную степень на четную.

    Код программы на C++:

    #include "stdafx.h"
#include <iostream>
using namespace std;
//быстрое возведение в степень
float bpow(float x, int n)
{
float count=1;
if (!n) return 1;
while (n)
{
if (n%2==0)
{
n/=2;
x*=x;
}
else
{
n--;
count*=x;
}
}
return count;
}
//главная функция
void main()
{
setlocale(LC_ALL,"Rus");
float x; int n;
cout<<"Основание > "; cin>>x;
cout<<"Степень > "; cin>>n;
cout<<x<<"^"<<n<<"="<<bpow(x, n);
system("pause>>void");
}

    Код программы на Pascal:

    program Exponentiation;
uses crt;
var x: real; n: integer;
{быстрое возведение в степень}
function bpow(x: real; n: integer): real;
var count: real;
begin
if n=0 then
begin
bpow:=1; exit;
end;
count:=1;
while n>0 do
begin
if n mod 2=0 then
begin
n:=n div 2;
x:=x*x;
end
else
begin
n:=n-1;
count:=count*x;
end;
end;
bpow:=count;
end;
{основной блок программы}
begin
write('Основание > '); read(x);
write('Степень > '); read(n);
write(x, '^', n, '=', bpow(x, n));
end.

    Источник

    Как посчитать степень?

    Как посчитать степень?

    В математике n степенью числа a называется число b, полученное в результате перемножения числа a на само себя n раз. Обозначается данное определение так:

    • b = a n или b = a^n, где a – основание степени; n – показатель степени.

    Как посчитать число в степени, изучают на школьных уроках алгебры. Поэтому каждый ученик способен выполнить данную операцию. Однако некоторым детям довольно сложно понять технологию вычисления. Однако все очень просто.

    • Например, пусть a = 25, n = 4, тогда b = 25^4 = 25*25*25*25 = 390 625

    Для быстрого подсчета степеней чисел с заданной точностью можно также воспользоваться онлайн-калькулятором. Его обычно применяют для вычисления степеней крупных чисел, поскольку при увеличении числа и степени вычисление становится трудоемким.

    Вместе с тем, при возведении числа в степень следует всегда помнить о следующих моментах.

    Нулевая степень абсолютно любого числа всегда равна единице.

    • 7^0=1
    • (-10)^0=1
    • (1/7)^0=1

    Возведение отрицательного числа в четную степень (n) дает знак плюс, в нечетную степень (-n) – знак минус.

    • (-3)^2 = (-3)*(-3) = 9
    • (-3)^3 = (-3)*(-3)*(-3) = -27

    Когда n=2, степень называется квадратом, когда n=3 – кубом.

    Дополнительную информацию вы можете найти в нашей статье Как возводить в дробную степень.

    Как посчитать степень числа

    Как посчитать степень числа

    разбирают в школе на уроках алгебры. В жизни такая операция выполняется редко. Например, при расчете площади квадрата или объёма куба используются степени, потому что длина, ширина, а для куба и высота – равные величины. В остальном возведение в степень чаще всего носит прикладной производственный характер.Вам понадобится

    Посчитать степень числа на математическом языке означает возвести любое число в какую-нибудь степень. Предположим, необходимо число Х возвести в степень n.
    Для этого число Х умножается само на себя n раз.

    Пусть Х = 125, а степень числа, т. е. n = 3. Это означает, что число 125 нужно умножить само на себя 3 раза.
    125^3 = 125*125*125 = 1 953 125
    Ещё пример.
    3^4 = 3*3*3*3 = 81

    При работе с отрицательным числом нужно быть аккуратным со знаками. Следует помнить, что четная степень (n) даст знак плюс, нечетная – знак минус.
    Например
    (-7)^2 = (-7)*(-7) = 49
    (-7)^3 = (-7)*(-7)*(-7) = 343

    Нулевая степень (n = 0) от любого числа всегда будет равна единице.
    15^0 = 1
    (-6)^0 = 1
    (1/3)^0 = 1Если n = 1, число умножать само на себя не надо.
    Будет
    7^1 = 7
    329^1 = 329

    Операция, обратная возведению числа в степень, называется извлечение корня.
    Если 5^2 = 25, то квадратный корень из 25 будет равен 5.
    Если 5^3 = 125, то корень третей степени равен 5.
    Если 8^4= 4 096, то корень четвертой степени из 4 096 будет равен 8.

    Если n = 2, тогда степень называют квадратом, если n = 3, степень называют кубом. Вычисление квадрата и куба из чисел первого десятка производить достаточно легко. Но с увеличением числа, возводимого в степень, и с увеличением самой степени, вычисления становятся трудоемкими. Для таких вычислении были разработаны специальные таблицы. Также существуют специальные инженерные и online калькуляторы, программные продукты. В качестве простейшего программного продукта для операций со степенями можно использовать табличный редактор Excel.

    Калькулятор степеней

    Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.

    Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».

    Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.

    Как возвести число в степень.

    Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:

    Возведение в степень

    А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.

    5 3 = 5 x 5 x 5 = 125

    Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.

    Как возводить в отрицательную степень.

    При возведении в отрицательную степень необходимо использовать простое правило:

    как возводить в отрицательную степень

    Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
    2 -3

    Источник

    Материал из Викиконспекты

    Перейти к: навигация, поиск

    Алгоритм быстрого возведения в степень — алгоритм, предназначенный для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении.

    Пусть  — двоичное представление степени n. Тогда , где и .

    Функция быстрого возведения в степень

    function Power(value, pow: int): int
  int result = 1
  while (pow > 0)
    if pow mod 2 == 1
      result *= value
    value *= value
    pow /= 2;
  return result;

    Ссылки

    • BinPow and 2^k-ary pow
    • Montgomerry Ladder
    Источник

    Добавить комментарий