Маленькая интродукция
Задача поиска элемента в массиве стоит перед всеми достаточно часто и хорошо бы расписать, как это можно сделать.
Ищут обычно в массиве элементы типа Number, String или Object. Естественно, самый быстрый способ поиска – по элементам типа Number, сравнение числа, даже очень большого, происходит очень быстро, гораздо проще проверить один элемент, чем лексиграфически сравнивать строки, а с объектами вообще другая история. Если мы ищем именно тот объект, который мы добавили в массив, то есть сравниваем ссылки – это так же быстро, как и сравнивать числа, а вот если же надо искать по свойствам объекта, то это может весьма и весьма затянуться. В особо сложных случаях, советую составлять какой-нибудь хэш объекта и строить отдельным массив-карту, в которой уже спокойно искать всё, что надо найти.
Разберем 6 способов сделать это на нативном JS разной новизны и 3 способа с их разбором на популярных фреймворках: jQuery, underscore и lodash.
Часть первая, нативная, в стиле аллегро
Для начала надо пройтись по родным возможностям языка и посмотреть, что можно сделать самим.
Поиск в лоб
Попробуем просто идти по элементам массива, пока мы не встретим то, что нам нужно. Как всегда самое простое решение является в среднем самым быстрым.
function contains(arr, elem) {
for (var i = 0; i < arr.length; i++) {
if (arr[i] === elem) {
return true;
}
}
return false;
}
Работает везде. Сравнивает строго, с помощью ===. Легко можно заменить на ==, бывает полезно, когда элементы массива разных типов, но может замедлить поиск. Его можно и модифицировать, добавив возможность начинать поиск элемента с конца. Шикарно ищет цифры, строки. Немного расширив, можно добавить возможность поиска элемента по своему условию (это поможет нам искать по свойствам объекта или, например, первый элемент, который больше 100500):
function contains(arr, pred) {
for (var i = 0; i < arr.length; i++) {
if (typeof pred == 'function' && pred(arr[i], i, arr) || arr[i] === elem) {
return true;
}
}
return false;
}
Array.prototype.indexOf()
Array.prototype.indexOf(searchElement[, fromIndex = 0]) – старый добрый метод, заставляющий всех мучиться со своей -1 в случае, когда элемента нет.
function contains(arr, elem) {
return arr.indexOf(elem) != -1;
}
Поддерживается он везде, кроме IE <= 7, но это уже давно забытая шутка. Данный метод выполняет поиск элемента строго от меньшего индекса к большему, применяя при сравнении ===. Увы, по свойствам объекта мы так искать не сможем. arr.indexOf(searchElement, fromIndex) принимает два аргумента, первый searchElement – это элемент который ищем, а второй, fromIndex, индекс с которого начнем искать (отрицательный говорит интерпретатору начинать поиск с arr.length + fromIndex индекса). Аккуратней, если вы укажете fromIndex больше длины массива, метод нераздумывая вернёт -1.
function contains(arr, elem, from) {
return arr.indexOf(elem, from) != -1;
}
Array.prototype.lastIndexOf()
Array.prototype.lastIndexOf(searchElement[, fromIndex = arr.length - 1]) – справедливости ради надо рассказать и про него. Работает полностью аналогично Array.prototype.indexOf(), но только полностью наоборот (поиск идет в обратном порядке и fromIndex изначально отсчитывается с конца). Заменил конструкцию ret != -1 на !!~ret ради забавы.
function contains(arr, elem, from) {
return !!~arr.lastIndexOf(elem, from);
}
Array.prototype.find()
Array.prototype.find(callback[, thisArg]) – модный стильный и молодежный ES6, со всеми вытекающими:
function contains(arr, elem) {
return arr.find((i) => i === elem) != -1;
}
Возвращает элемент или -1, если ничего не найдено. Ищет с помощью callback(elem, index, arr), то есть, если эта функция вернет true, то это именно тот самый, искомый элемент. Конечно, эту функцию можно задавать самому, поэтому метод универсален.
Array.prototype.findIndex()
Array.prototype.findIndex(callback[, thisArg]) – полностью аналогичный предыдущему метод, за исключением того, что функция возвращает не элемент, а индекс. Забавы ради сделаю её с возможностью передать свою функцию:
function contains(arr, pred) {
var f = typeof pred == 'function' ? pred : ( i => i === pred );
return arr.findIndex(f) != -1;
}
Array.prototype.includes()
Array.prototype.includes(searchElement[, fromIndex]) – а это уже ES7, с ещё пока оочень сырой поддержкой. Наконец-то у нас будет специальный метод, чтобы узнать, есть ли элемент в массиве! Поздравляю!
arr.includes(elem);
Это всё, что нужно, чтобы найти элемент. Аргументы у этой функции полностью аналогичны Array.prototype.indexOf(). А вот вернет он true в случае успеха и false в обратном. Естественно искать по свойствам объектов нельзя, для этого есть Array.prototype.find(). Должен быть самым быстрым, но… Возможно, что он и станет со временем самым быстрым.
Часть вторая, со вниманием, но чужая и в стиле сонаты
Теперь, наконец, можно поговорить об этой же теме, но в контексте парочки фреймворков! Говорят, что всегда хорошо посмотреть сначала, как делают другие, перед тем, как начнешь делать это сам. Может это откроет нам глаза на что-нибудь интересное!
jQuery
jQuery.inArray(value, array [, fromIndex ]) – между прочим весьма быстрый метод, по тестам.
Использует внутри строгое равенство === и возвращает -1, если ничего не нашел, а если все таки нашёл, то вернет его индекс. Для удобства и одинаковости обернем её в функцию:
function contains(arr, elem) {
return jQuery.inArray( elem, arr) != -1;
}
А теперь поговорим, как она работает. Вот, что она представляет из себя в версии 2.1.3:
inArray: function( elem, arr, i ) {
return arr == null ? -1 : indexOf.call( arr, elem, i );
}
Где indexOf это вот это:
// Use a stripped-down indexOf as it's faster than native
// http://jsperf.com/thor-indexof-vs-for/5
indexOf = function( list, elem ) {
var i = 0,
len = list.length;
for ( ; i < len; i++ ) {
if ( list[i] === elem ) {
return i;
}
}
return -1;
}
Забавный комментарий говорит, что так быстрее, чем родной Array.prototype.indexOf() (могу предположить, что из-за отсутствия всех проверок) и предлагает посмотреть тесты производительности.
По сути – это самый первый способ из первой части.
Underscore
_.contains(list, value) – вот такой метод предлагает нам популярная библиотека для работы с коллекциями. То же самое, что и _.include(list, value).
Использует === для сравнения. Вернёт true, если в list содержится элемент, который мы ищем. Если list является массивом, будет вызван метод indexOf.
_.contains = _.include = function(obj, target) {
if (obj == null) return false;
if (nativeIndexOf && obj.indexOf === nativeIndexOf) return obj.indexOf(target) != -1;
return any(obj, function(value) {
return value === target;
});
};
Где nativeIndexOf – штука, которая говорит, что Array.prototype.indexOf() существует, а obj.indexOf === nativeIndexOf говорит, что list – массив. Теперь понятно, почему этот метод медленнее, чем jQuery.inArray(), просто обертка над Array.prototype.indexOf(). Ничего интересного.
Lodash
_.includes(collection, target, [fromIndex=0]) – вот последняя надежда на новые мысли, от второй знаменитейшей библиотеки для работы с коллекциями. То же самое, что _.contains() и _.include().
Возвращает true, если содержит и false если нет. fromIndex индекс элемента, с которого начинаем поиск.
function includes(collection, target, fromIndex, guard) {
var length = collection ? getLength(collection) : 0;
if (!isLength(length)) {
collection = values(collection);
length = collection.length;
}
if (typeof fromIndex != 'number' || (guard && isIterateeCall(target, fromIndex, guard))) {
fromIndex = 0;
} else {
fromIndex = fromIndex < 0 ? nativeMax(length + fromIndex, 0) : (fromIndex || 0);
}
return (typeof collection == 'string' || !isArray(collection) && isString(collection))
? (fromIndex <= length && collection.indexOf(target, fromIndex) > -1)
: (!!length && getIndexOf(collection, target, fromIndex) > -1);
}
guard – служебный аргумент. Сначала находится длина коллекции, выбирается fromIndex, а потом… нет, не Array.prototype.indexOf()! Для поиска в строке используется String.prototype.indexOf(), а мы идем дальше в _.getIndexOf() и в результате попадём в ло-дашскую имплементацию indexOf():
function indexOf(array, value, fromIndex) {
var length = array ? array.length : 0;
if (!length) {
return -1;
}
if (typeof fromIndex == 'number') {
fromIndex = fromIndex < 0 ? nativeMax(length + fromIndex, 0) : fromIndex;
} else if (fromIndex) {
var index = binaryIndex(array, value);
if (index < length &&
(value === value ? (value === array[index]) : (array[index] !== array[index]))) {
return index;
}
return -1;
}
return baseIndexOf(array, value, fromIndex || 0);
}
Она интересна тем, что fromIndex может принимать значения как Number, так и Boolean и если это всё таки значение булевого типа и оно равно true, то функция будет использовать бинарный поиск по массиву! Прикольно. Иначе же выполнится indexOf() попроще:
function baseIndexOf(array, value, fromIndex) {
if (value !== value) {
return indexOfNaN(array, fromIndex);
}
var index = fromIndex - 1,
length = array.length;
while (++index < length) {
if (array[index] === value) {
return index;
}
}
return -1;
}
Интересный ход для случая, когда мы ищем NaN (напомню, что из-за досадной ошибки он не равен сам себе). Выполнится indexOfNaN(), и действительно ни один из всех способов описанных ранее не смог бы найти NaN, кроме тех, естественно, где мы могли сами указать функцию для отбора элементов.
Можно предложить просто обернуть _.indexOf() для поиска элемента:
function contains(arr, elem, fromIndex) {
return _.indexOf(arr, elem, fromIndex) != -1;
}
Где fromIndex будет либо индексом откуда начинаем искать, либо true, если мы знаем, что arr отсортирован.
Заключение, хотя и в стиле интермеццо
И да, все эти варианты имеют смысл, только если момент с поиском данных част в вашем алгоритме или поиск происходит на очень больших данных. Вот приведу ниже несколько тестов на поиск элементов типа Number и String в массивах длинной 1000000 (миллион) элементов для трех случаев, когда элемент находится вначале массива, в середине (можно считать за среднюю по палете ситуацию) и в конце (можно считать за время поиска отсутствующего элемента, кроме метода с Array.prototype.lastIndexOf()).
Number, 1000000 элементов, искомый элемент в начале;Number, 1000000 элементов, искомый элемент в середине;Number, 1000000 элементов, искомый элемент в конце;String, 1000000 элементов, искомый элемент в начале;String, 1000000 элементов, искомый элемент в середине;String, 1000000 элементов, искомый элемент в конце.
Результаты тестов могут сильно зависеть от версии браузера, да и от самих браузеров, как этого избежать не знаю, но рекомендую протестить на нескольких.
Видно, что в среднем везде выигрывает первый способ из первой части (написанный собственноручно), а второе место обычно делят lоdash и Array.prototype.includes().
Да, прошу заметить, что если взбредёт в голову искать NaN, то это может не получиться почти во всех методах, так как NaN !== NaN.
-
Главная
-
Инструкции
-
JavaScript
-
Методы поиска в массивах JavaScript
Поиск в массиве — довольно несложная задача для программиста. На ум сразу приходит перебор через цикл for или бинарный поиск в отсортированном массиве, для элементов которого определены операции «больше» и «меньше». Но, как и любой высокоуровневый язык программирования, JavaScript предлагает разработчику встроенные функции для решения различных задач. В этой статье мы рассмотрим четыре метода поиска в массивах JavaScript: find, includes, indexOf и filter.
indexOf
indexOf — это функция поиска элемента в массиве. Этот метод с помощью перебора ищет искомый объект и возвращает его индекс или “-1”, если не находит подходящий.
Синтаксис
Функция имеет такой синтаксис:
Array.indexOf (search element, starting index)где:
- Array — массив;
- search element — элемент, который мы ищем;
- starting index — индекс, с которого начинаем перебор. Необязательный аргумент, по умолчанию работа функции начинается с индекса “0”, т.е. метод проверяет весь Array. Если starting index больше или равен Array.length, то метод сразу возвращает “-1” и завершает работу.
Если starting index отрицательный, то JS трактует это как смещение с конца массива: при starting index = “-1” будет проверен только последний элемент, при “-2” последние два и т.д.
Практика
Опробуем метод на практике. Запустим такой код и проверим результаты его работы:
let ExampleArray = [1,2,3,1,'5', null, false, NaN,3];console.log("Позиция единицы", ExampleArray.indexOf(1) );
console.log("Позиция следующей единицы", ExampleArray.indexOf(1,2) );
console.log("Позиция тройки", ExampleArray.indexOf(3) );
console.log("Позиция тройки, если starting index отрицательный", ExampleArray.indexOf(3,-2) );
console.log("Позиция false", ExampleArray.indexOf(false) );
console.log("Позиция 5", ExampleArray.indexOf("5") );
console.log("Позиция NaN", ExampleArray.indexOf(NaN));
В результате работы этого кода мы получили такой вывод:
Позиция единицы 0
Позиция следующей единицы 3
Позиция тройки 2
Позиция тройки, если starting index отрицательный 8
Позиция false 6
Позиция 5 -1
Позиция NaN -1indexOf осуществляет поиск элемента в массиве слева направо и останавливает свою работу на первом совпавшем. Отчетливо это проявляется в примере с единицей. Для того, чтобы идти справа налево, используйте метод LastIndexOf с аналогичным синтаксисом.
Для сравнения искомого и очередного объекта применяется строгое сравнение (===). При использовании строгого сравнения для разных типов данных, но с одинаковым значение, например 5, ‘5’ и “5” JavaScript даёт отрицательный результат, поэтому IndexOf не нашел 5.
Также стоит помнить, что indexOf некорректно обрабатывает NaN. Так что для работы с этим значением нужно применять остальные методы.
includes
includes не совсем проводит поиск заданного элемента в массиве, а проверяет, есть ли он там вообще. Работает он примерно также как и indexOf. В конце работы includes возвращает «True», если нашел искомый объект, и «False», если нет. Также includes правильно обрабатывает NaN
Синтаксис
includes имеет следующий синтаксис:
Array.includes (search element, starting index)где:
- Array — массив;
- search element — элемент, который мы ищем;
- starting index — индекс, с которого начинаем перебор. Необязательный аргумент, по умолчанию работа функции начинается с индекса “0”, т.е. метод проверяет весь Array. Если starting index больше или равен Array.length, то метод сразу возвращает «False» и завершает работу.
Если starting index отрицательный, то JS трактует это как смещение с конца массива: при starting index = “-1” будет проверен только последний элемент, при “-2” последние два и т.д.
Практика
Немного изменим код из предыдущего примера и запустим его:
let Example = [1,2,3,1,'5', null, false,NaN, 3];console.log("Наличие единицы", Example.includes(1) );
console.log("Наличие следующей единицы", Example.includes(1,2) );
console.log("Наличие тройки", Example.includes(3) );
console.log("Наличие тройки, если starting index отрицательный", Example.includes(3,-1) );
console.log("Наличие false", Example.includes(false) );
console.log("Наличие 5", Example.includes(5) );
console.log("Наличие NaN", Example.includes(NaN));
Вывод:
Наличие единицы true
Наличие следующей единицы true
Наличие тройки true
Наличие тройки, если starting index отрицательный true
Наличие false true
Наличие 5 false
Наличие NaN trueДля includes отсутствует альтернативная функция, которая проводит поиск по массиву js справа налево, которая, в общем-то, и не очень актуальна.
find
Предположим, что нам нужно найти в массиве некий объект. Но мы хотим найти его не по значению, а по его свойству. Например, поиск числа в массиве со значением между 15 и 20. Как и прежде, мы можем воспользоваться перебором с помощью for, но это не слишком удобно. Для поиска с определенным условием в JavaScript существует метод find.
Синтаксис
Array.find(function(...){
//если элемент соответствует условиям (true), то функция возвращает его и прекращает работу;
//если ничего не найдено, то возвращает undefined
})- Array — массив;
- function(…) — функция, которая задает условия.
Практика
Как и в прошлых примерах, напишем небольшой код и опробуем метод:
let ExampleArray = ["Timeweb", 55555, "Cloud", "облачный провайдер", "буквы"];console.log(ExampleArray.find(element => element.length == 5))
Вывод:
CloudВ этом примере мы искали строки с длиной в 5 символов. Для числовых типов данных длина не определена, поэтому 55555 не подходит. find находит первый элемент и возвращает его, поэтому «буквы» также не попали в результат работы нашей функции. Для того, чтобы найти несколько элементов, соответствующих некоторому условию, нужно использовать метод filter.
Также не стоит забывать о методе findIndex. Он возвращает индекс подходящего элемента. Или -1, если его нет. В остальном он работает точно также, как и find.
filter
find ищет и возвращает первый попавшийся элемент, соответствующий условиям поиска. Для того, чтобы найти все такие элементы, необходимо использовать метод filter. Результат этой функции — массив (если ничего не найдено, то он будет пустым).
Синтаксис
Array.find(function(...){
//если элемент соответствует условиям (true), то добавляем его к конечному результату и продолжаем перебор;
})- Array — массив;
- function(…) — функция, которая задает условия.
Практика
Представим следующую задачу: у нас есть список кубоидов (прямоугольных параллелепипедов) с длинами их граней и нам нужно вывести все кубоиды с определенным объемом. Напишем код, реализующий решение данной задачи:
let ExampleArray = [
[10, 15, 8],
[11, 12, 6],
[5, 20, 1],
[10, 10, 2],
[16,2, 4]
];console.log(ExampleArray.filter(element=> element[0]*element[1]*element[2]>300))
Вывод:
[ [ 10, 15, 8 ],
[ 11, 12, 6 ] ]В этом примере мы нашли прямоугольные параллелепипеды с объемом больше 300. В целом, метод filter в JS позволяет реализовывать всевозможные условия для поиска.
Заключение
В этой статье узнали о методах поиска в JavaScript и научились ими пользоваться. Все перечисленные методы — универсальные инструменты для разработчиков. Но, как и любые универсальные инструменты, они не всегда являются самыми производительными. Так, например, бинарный поиск будет куда эффективнее, чем find и filter.
Содержание
- 1 Array.includes() — есть ли элемент в массиве
- 2 Array.indexOf() — индекс элемента в массиве
- 3 Array.find() — найти элемент по условию
- 4 Array.findIndex() — найти индекс элемента в массиве
- 5 Поиск всех совпадений в массиве
- 6 Поиск в массиве объектов
- 7 Заключение
Для поиска по массиву в JavaScript существует несколько методов прототипа Array, не считая что поиск можно выполнить и методами для перебора массива и в обычном цикле.
Итак, мы сегодня рассмотрим следующие варианты:
- Array.includes()
- Array.indexOf()
- Array.find()
- Array.findIndex()
- Array.filter()
- Array.forEach()
Array.includes() — есть ли элемент в массиве
Данный метод ищет заданный элемент и возвращает true или false, в зависимости от результата поиска. Принимает два параметра:
element— то, что мы будем искатьfromIndex(необязательный) — с какого индекса начинать поиск. По умолчанию с 0.
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry'];
console.log(arr.includes('Apple')); // true
console.log(arr.includes('Apple', 1)); // falseКак видно из примера выше, в первом случае мы получим true, т.к. начали с нулевого элемента массива. Во втором случае мы передали второй параметр — индекс, с которого нужно начать поиск — и получили false, т.к. дальше элемент не был найден.
Array.indexOf() — индекс элемента в массиве
Данный метод, в отличие от предыдущего, возвращает индекс первого найденного совпадения. В случае если элемент не найден, будет возвращено число -1
Также принимает два параметра:
element— элемент, который мы будем искатьfromIndex(необязательный) — с какого индекса начинать поиск. По умолчанию с 0.
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
console.log(arr.indexOf('Apple')); // 0
console.log(arr.indexOf('Apple', 1)); // 4
console.log(arr.indexOf('Orange', 2)); // -1Как видно из примера выше, в первом случае мы получаем 0, т.к. сразу нашли первый элемент массива (первое совпадение, дальше поиск уже не выполняется). Во втором случае 4, т.к. начали поиск с индекса 1 и нашли следующее совпадение. В третьем примере мы получили результат -1, т.к. поиск начали с индекса 2, а элемент Orange в нашем массиве под индексом 1.
Так как данный метод возвращает индекс или -1, мы можем присвоить результат в переменную для дальнейшего использования:
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
const index = arr.indexOf('Lemon');
if (index !== -1) {
// сделать что-то
}Чтобы произвести какие-то действия над найденным элементом массива, мы можем использовать следующий синтаксис:
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
const index = arr.indexOf('Lemon');
arr[index] = 'Lime'; // заменяем найденный элемент
console.log(arr)ж // ['Apple', 'Orange', 'Lime', 'Cherry', 'Apple']Примеры использования данного метода вы можете также найти в посте про удаление элемента из массива
Array.find() — найти элемент по условию
Данный метод callback и thisArg в качестве аргументов и возвращает первое найденное значение.
Callback принимает несколько аргументов:
item — текущий элемент массива
index — индекс текущего элемента
currentArray — итерируемый массив
Пример использования:
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
const apple = arr.find(item => item === 'Apple');
console.log(apple); // AppleДанный метод полезен тем, что мы можем найти и получить сразу и искомый элемент, и его index
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
let indexOfEl;
const apple = arr.find((item, index) => {
if (item === 'Apple') {
indexOfEl = index;
return item;
}
});
console.log(apple, indexOfEl); // Apple 0Также работа кода прекратиться как только будет найден нужный элемент и второй элемент (дубликат) не будет найден.
В случае если ничего не найдено будет возвращен undefined.
Array.findIndex() — найти индекс элемента в массиве
Этот метод похож на метод find(), но возвращать будет только индекс элемента, который соответствует требованию. В случае, если ничего не найдено, вернет -1
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
const index = arr.findIndex(item => item === 'Apple');
console.log(index); // 0Ну и по аналогии с предыдущим методом, поиск завершается после первого совпадения.
Поиск всех совпадений в массиве
Метод filter() кроме всего остального также можно использовать для поиска по массиву. Предыдущие методы останавливаются при первом соответствии поиска, а данный метод пройдется по массиву до конца и найдет все элементы. Но данный метод вернет новый массив, в который войдут все элементы соответствующие условию.
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
const filteredArr = arr.filter(item => item === 'Apple');
console.log(filteredArr); // ['Apple', 'Apple']
console.log(arr); // ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];Как видите из примера выше, первоначальный массив не будет изменен.
Подробнее про метод JS filter() можете прочитать в этом посте.
Для этих же целей можно использовать метод forEach(), который предназначен для перебора по массиву:
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
let indexes = [];
arr.forEach((item, index) => {
if (item === 'Apple') indexes.push(index)
});
console.log(indexes); // [0, 4]В массив indexes мы получили индексы найденных элементов, это 0 и 4 элементы. Также в зависимости от вашей необходимости, можно создать объект, где ключом будет индекс, а значением сам элемент:
const arr = ['Apple', 'Orange', 'Lemon', 'Cherry', 'Apple'];
let arrObjMap = {};
arr.forEach((item, index) => {
if (item === 'Apple') {
arrObjMap[index] = item;
}
});
console.log(arrObjMap); // {0: 'Apple', 4: 'Apple'}Поиск в массиве объектов
Если у вас массив состоит не из примитивных типов данных, а к примеру, каждый элемент это объект со своими свойствами и значениями, тогда можно использовать следующие варианты для получения индекса элемента.
Первый способ. С использованием метода map для массива
const arr = [
{ name: 'Ben', age: 21 },
{ name: 'Clif', age: 22 },
{ name: 'Eric', age: 18 },
{ name: 'Anna', age: 27 },
];
const index = arr.map(item => item.name).indexOf('Anna');
console.log(index); //3
console.log(arr[index]); // {name: 'Anna', age: 27}В данном случае по массиву arr мы проходим и на каждой итерации из текущего элемента (а это объект со свойствами name и age) возвращаем имя человека в новый массив и сразу же выполняем поиск по новому массиву на имя Anna. При совпадении нам будет возвращен индекс искомого элемента в массиве.
Второй способ. Данный вариант будет немного проще, т.к. мы можем сразу получить индекс при совпадении:
const index = arr.findIndex(item => item.name === 'Anna');
console.log(index); //3
console.log(arr[index]); // {name: 'Anna', age: 27}Заключение
Как видите любой из вышеприведенных методов можно использовать для поиска по массиву. Какой из них использовать зависит от вашей задачи и того, что вам нужно получить — сам элемент или его индекс в массиве, найти только первое совпадение или все совпадения при поиске.
Ваши вопросы и комментарии:
Поиск – распространённое действие, выполняемое в бизнес-приложениях. Под катом лежат реализации известных алгоритмов поиска на Java.

Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Интересно, хочу попробовать
Программирование на Java – всегда интересный экспириенс. Но куда интереснее работать, применяя правильные для конкретных ситуаций алгоритмы.
Реализуем алгоритмы на Java и проанализируем производительность с помощью параметров временной и пространственной сложности.
Линейный поиск
Линейный или последовательный поиск – простейший алгоритм поиска. Он редко используется из-за своей неэффективности. По сути, это метод полного перебора, и он уступает другим алгоритмам.
У линейного поиска нет предварительных условий к состоянию структуры данных.
Объяснение
Алгоритм ищет элемент в заданной структуре данных, пока не достигнет конца структуры.
При нахождении элемента возвращается его позиция в структуре данных. Если элемент не найден, возвращаем -1.
Реализация
Теперь посмотрим, как реализовать линейный поиск в Java:
public static int linearSearch(int arr[], int elementToSearch) {
for (int index = 0; index < arr.length; index++) {
if (arr[index] == elementToSearch)
return index;
}
return -1;
}
Для проверки используем целочисленный массив:
int index = linearSearch(new int[]{89, 57, 91, 47, 95, 3, 27, 22, 67, 99}, 67);
print(67, index);
Простой метод для вывода результата:
public static void print(int elementToSearch, int index) {
if (index == -1){
System.out.println(elementToSearch + " not found.");
}
else {
System.out.println(elementToSearch + " found at index: " + index);
}
}
Вывод:
67 found at index: 8
Временная сложность
Для получения позиции искомого элемента перебирается набор из N элементов. В худшем сценарии для этого алгоритма искомый элемент оказывается последним в массиве.
В этом случае потребуется N итераций для нахождения элемента.
Следовательно, временная сложность линейного поиска равна O(N).
Пространственная сложность
Этот поиск требует всего одну единицу памяти для хранения искомого элемента. Это не относится к размеру входного массива.
Следовательно, пространственная сложность линейного поиска равна O(1).
Применение
Линейный поиск можно использовать для малого, несортированного набора данных, который не увеличивается в размерах.
Несмотря на простоту, алгоритм не находит применения в проектах из-за линейного увеличения временной сложности.
Двоичный поиск
Двоичный или логарифмический поиск часто используется из-за быстрого времени поиска.
Объяснение
Этот вид поиска использует подход «Разделяй и властвуй», требует предварительной сортировки набора данных.
Алгоритм делит входную коллекцию на равные половины, и с каждой итерацией сравнивает целевой элемент с элементом в середине. Поиск заканчивается при нахождении элемента. Иначе продолжаем искать элемент, разделяя и выбирая соответствующий раздел массива. Целевой элемент сравнивается со средним.
Вот почему важно иметь отсортированную коллекцию при использовании двоичного поиска.
Поиск заканчивается, когда firstIndex (указатель) достигает lastIndex (последнего элемента). Значит мы проверили весь массив Java и не нашли элемента.
Есть два способа реализации этого алгоритма: итеративный и рекурсивный.
Временная и пространственная сложности одинаковы для обоих способов в реализации на Java.
Реализация
Итеративный подход
Посмотрим:
public static int binarySearch(int arr[], int elementToSearch) {
int firstIndex = 0;
int lastIndex = arr.length - 1;
// условие прекращения (элемент не представлен)
while(firstIndex <= lastIndex) {
int middleIndex = (firstIndex + lastIndex) / 2;
// если средний элемент - целевой элемент, вернуть его индекс
if (arr[middleIndex] == elementToSearch) {
return middleIndex;
}
// если средний элемент меньше
// направляем наш индекс в middle+1, убирая первую часть из рассмотрения
else if (arr[middleIndex] < elementToSearch)
firstIndex = middleIndex + 1;
// если средний элемент больше
// направляем наш индекс в middle-1, убирая вторую часть из рассмотрения
else if (arr[middleIndex] > elementToSearch)
lastIndex = middleIndex - 1;
}
return -1;
}
Используем алгоритм:
int index = binarySearch(new int[]{89, 57, 91, 47, 95, 3, 27, 22, 67, 99}, 67);
print(67, index);
Вывод:
67 found at index: 5
Рекурсивный подход
Теперь посмотрим на рекурсивную реализацию:
public static int recursiveBinarySearch(int arr[], int firstElement, int lastElement, int elementToSearch) {
// условие прекращения
if (lastElement >= firstElement) {
int mid = firstElement + (lastElement - firstElement) / 2;
// если средний элемент - целевой элемент, вернуть его индекс
if (arr[mid] == elementToSearch)
return mid;
// если средний элемент больше целевого
// вызываем метод рекурсивно по суженным данным
if (arr[mid] > elementToSearch)
return recursiveBinarySearch(arr, firstElement, mid - 1, elementToSearch);
// также, вызываем метод рекурсивно по суженным данным
return recursiveBinarySearch(arr, mid + 1, lastElement, elementToSearch);
}
return -1;
}
Рекурсивный подход отличается вызовом самого метода при получении нового раздела. В итеративном подходе всякий раз, когда мы определяли новый раздел, мы изменяли первый и последний элементы, повторяя процесс в том же цикле.
Другое отличие – рекурсивные вызовы помещаются в стек и занимают одну единицу пространства за вызов.
Используем алгоритм следующим способом:
int index = binarySearch(new int[]{3, 22, 27, 47, 57, 67, 89, 91, 95, 99}, 0, 10, 67);
print(67, index);
Вывод:
67 found at index: 5
Временная сложность
Временная сложность алгоритма двоичного поиска равна O(log (N)) из-за деления массива пополам. Она превосходит O(N) линейного алгоритма.
Пространственная сложность
Одна единица пространства требуется для хранения искомого элемента. Следовательно, пространственная сложность равна O(1).
Рекурсивный двоичный поиск хранит вызов метода в стеке. В худшем случае пространственная сложность потребует O(log (N)).
Применение
Этот алгоритм используется в большинстве библиотек и используется с отсортированными структурами данных.
Двоичный поиск реализован в методе Arrays.binarySearch Java API.
Алгоритм Кнута – Морриса – Пратта
Алгоритм КМП осуществляет поиск текста по заданному шаблону. Он разработан Дональдом Кнутом, Воном Праттом и Джеймсом Моррисом: отсюда и название.
Объяснение
В этом поиске сначала компилируется заданный шаблон. Компилируя шаблон, мы пытаемся найти префикс и суффикс строки шаблона. Это поможет в случае несоответствия – не придётся искать следующее совпадение с начального индекса.
Вместо этого мы пропускаем часть текстовой строки, которую уже сравнили, и начинаем сравнивать следующую. Необходимая часть определяется по префиксу и суффиксу, поэтому известно, какая часть уже прошла проверку и может быть безопасно пропущена.
КМП работает быстрее алгоритма перебора благодаря пропускам.
Реализация
Итак, пишем метод compilePatternArray(), который позже будет использоваться алгоритмом поиска КМП:
public static int[] compilePatternArray(String pattern) {
int patternLength = pattern.length();
int len = 0;
int i = 1;
int[] compliedPatternArray = new int[patternLength];
compliedPatternArray[0] = 0;
while (i < patternLength) {
if (pattern.charAt(i) == pattern.charAt(len)) {
len++;
compliedPatternArray[i] = len;
i++;
} else {
if (len != 0) {
len = compliedPatternArray[len - 1];
} else {
compliedPatternArray[i] = len;
i++;
}
}
}
System.out.println("Compiled Pattern Array " + Arrays.toString(compliedPatternArray));
return compliedPatternArray;
}
Скомпилированный массив Java можно рассматривать как массив, хранящий шаблон символов. Цель – найти префикс и суффикс в шаблоне. Зная эти элементы, можно избежать сравнения с начала текста после несоответствия и приступать к сравнению следующего символа.
Скомпилированный массив сохраняет позицию предыдущего местонахождения текущего символа в массив шаблонов.
Давайте реализуем сам алгоритм:
public static List<Integer> performKMPSearch(String text, String pattern) {
int[] compliedPatternArray = compilePatternArray(pattern);
int textIndex = 0;
int patternIndex = 0;
List<Integer> foundIndexes = new ArrayList<>();
while (textIndex < text.length()) {
if (pattern.charAt(patternIndex) == text.charAt(textIndex)) {
patternIndex++;
textIndex++;
}
if (patternIndex == pattern.length()) {
foundIndexes.add(textIndex - patternIndex);
patternIndex = compliedPatternArray[patternIndex - 1];
}
else if (textIndex < text.length() && pattern.charAt(patternIndex) != text.charAt(textIndex)) {
if (patternIndex != 0)
patternIndex = compliedPatternArray[patternIndex - 1];
else
textIndex = textIndex + 1;
}
}
return foundIndexes;
}
Здесь мы последовательно сравниваем символы в шаблоне и текстовом массиве. Мы продолжаем двигаться вперёд, пока не получим совпадение. Достижение конца массива при сопоставлении означает нахождение шаблона в тексте.
Но! Есть один момент.
Если обнаружено несоответствие при сравнении двух массивов, индекс символьного массива перемещается в значение compiledPatternArray(). Затем мы переходим к следующему символу в текстовом массиве. КМП превосходит метод грубой силы однократным сравнением текстовых символов при несоответствии.
Запустите алгоритм:
String pattern = "AAABAAA";
String text = "ASBNSAAAAAABAAAAABAAAAAGAHUHDJKDDKSHAAJF";
List<Integer> foundIndexes = KnuthMorrisPrathPatternSearch.performKMPSearch(text, pattern);
if (foundIndexes.isEmpty()) {
System.out.println("Pattern not found in the given text String");
} else {
System.out.println("Pattern found in the given text String at positions: " + .stream().map(Object::toString).collect(Collectors.joining(", ")));
}
В текстовом шаблоне AAABAAA наблюдается и кодируется в массив шаблонов следующий шаблон:
- Шаблон
A(Одиночная A) повторяется в 1 и 4 индексах. - Паттерн
AA(Двойная A) повторяется во 2 и 5 индексах. - Шаблон
AAA(Тройная A) повторяется в индексе 6.
В подтверждение наших расчётов:
Compiled Pattern Array [0, 1, 2, 0, 1, 2, 3] Pattern found in the given text String at positions: 8, 14
Описанный выше шаблон ясно показан в скомпилированном массиве.
С помощью этого массива КМП ищет заданный шаблон в тексте, не возвращаясь в начало текстового массива.
Временная сложность
Для поиска шаблона алгоритму нужно сравнить все элементы в заданном тексте. Необходимое для этого время составляет O(N). Для составления строки шаблона нам нужно проверить каждый символ в шаблоне – это еще одна итерация O(M).
O (M + N) – общее время алгоритма.
Пространственная сложность
O(M) пространства необходимо для хранения скомпилированного шаблона для заданного шаблона размера M.
Применение
Этот алгоритм используется в текстовых инструментах для поиска шаблонов в текстовых файлах.
Поиск прыжками
От двоичного поиска этот алгоритм отличает движение исключительно вперёд. Имейте в виду, что такой поиск требует отсортированной коллекции.
Мы прыгаем вперёд на интервал sqrt(arraylength), пока не достигнем элемента большего, чем текущий элемент или конца массива. При каждом прыжке записывается предыдущий шаг.
Прыжки прекращаются, когда найден элемент больше искомого. Затем запускаем линейный поиск между предыдущим и текущим шагами.
Это уменьшает поле поиска и делает линейный поиск жизнеспособным вариантом.
Реализация
public static int jumpSearch(int[] integers, int elementToSearch) {
int arrayLength = integers.length;
int jumpStep = (int) Math.sqrt(integers.length);
int previousStep = 0;
while (integers[Math.min(jumpStep, arrayLength) - 1] < elementToSearch) {
previousStep = jumpStep;
jumpStep += (int)(Math.sqrt(arrayLength));
if (previousStep >= arrayLength)
return -1;
}
while (integers[previousStep] < elementToSearch) {
previousStep++;
if (previousStep == Math.min(jumpStep, arrayLength))
return -1;
}
if (integers[previousStep] == elementToSearch)
return previousStep;
return -1;
}
Мы начинаем с jumpstep размером с корень квадратный от длины массива и продолжаем прыгать вперёд с тем же размером, пока не найдём элемент, который будет таким же или больше искомого элемента.
Сначала проверяется элемент integers[jumpStep], затем integers[2jumpStep], integers[3jumpStep] и так далее. Проверенный элемент сохраняется в переменной previousStep.
Когда найдено значение, при котором integers[previousStep] < elementToSearch < integers[jumpStep], производится линейный поиск между integers[previousStep] и integers[jumpStep] или элементом большим, чем elementToSearch.
Вот так используется алгоритм:
int index = jumpSearch(new int[]{3, 22, 27, 47, 57, 67, 89, 91, 95, 99}, 67);
print(67, index);
Вывод:
67 found at Index 5
Временная сложность
Поскольку в каждой итерации мы перепрыгиваем на шаг, равный sqrt(arraylength), временная сложность этого поиска составляет O(sqrt (N)).
Пространственная сложность
Искомый элемент занимает одну единицу пространства, поэтому пространственная сложность алгоритма составляет O(1).
Применение
Этот поиск используется поверх бинарного поиска, когда прыжки в обратную сторону затратны.
С ограничением сталкиваются при работе с вращающейся средой. Когда при легком поиске по направлению вперёд многократные прыжки в разных направлениях становятся затратными.
Интерполяционный поиск
Интерполяционный поиск используется для поиска элементов в отсортированном массиве. Он полезен для равномерно распределенных в структуре данных.
При равномерно распределенных данных местонахождение элемента определяется точнее. Тут и вскрывается отличие алгоритма от бинарного поиска, где мы пытаемся найти элемент в середине массива.
Для поиска элементов в массиве алгоритм использует формулы интерполяции. Эффективнее применять эти формула для больших массивов. В противном случае алгоритм работает как линейный поиск.
Реализация
public static int interpolationSearch(int[] integers, int elementToSearch) {
int startIndex = 0;
int lastIndex = (integers.length - 1);
while ((startIndex <= lastIndex) && (elementToSearch >= integers[startIndex]) &&
(elementToSearch <= integers[lastIndex])) {
// используем формулу интерполяции для поиска возможной лучшей позиции для существующего элемента
int pos = startIndex + (((lastIndex-startIndex) /
(integers[lastIndex]-integers[startIndex]))*
(elementToSearch - integers[startIndex]));
if (integers[pos] == elementToSearch)
return pos;
if (integers[pos] < elementToSearch)
startIndex = pos + 1;
else
lastIndex = pos - 1;
}
return -1;
}
Используем алгоритм так:
int index = interpolationSearch(new int[]{1,2,3,4,5,6,7,8}, 6);
print(67, index);
Вывод:
6 found at Index 5
Смотрите, как работают формулы интерполяции, чтобы найти 6:
startIndex = 0 lastIndex = 7 integers[lastIndex] = 8 integers[startIndex] = 1 elementToSearch = 6
Теперь давайте применим эти значения к формулам для оценки индекса элемента поиска:
index=0+(7−0)/(8−1)∗(6−1)=5
Элемент integers[5] равен 6 — это элемент, который мы искали. Индекс для элемента рассчитывается за один шаг из-за равномерной распределенности данных.
Временная сложность
В лучшем случае временная сложность такого алгоритма – O(log log N). При неравномерном распределении элементов сложность сопоставима с временной сложностью линейного алгоритма, которая = O(N).
Пространственная сложность
Алгоритм требует одну единицу пространства для хранения элемента для поиска. Его пространственная сложность = O(1).
Применение
Алгоритм полезно применять для равномерно распределенных данных вроде телефонной книги.
Экспоненциальный поиск
Экспоненциальный поиск используется для поиска элементов путём перехода в экспоненциальные позиции, то есть во вторую степень.
В этом поиске мы пытаемся найти сравнительно меньший диапазон и применяем на нем двоичный алгоритм для поиска элемента.
Для работы алгоритма коллекция должна быть отсортирована.
Реализация
public static int exponentialSearch(int[] integers, int elementToSearch) {
if (integers[0] == elementToSearch)
return 0;
if (integers[integers.length - 1] == elementToSearch)
return integers.length;
int range = 1;
while (range < integers.length && integers[range] <= elementToSearch) {
range = range * 2;
}
return Arrays.binarySearch(integers, range / 2, Math.min(range, integers.length), elementToSearch);
}
Применяем алгоритм Java:
int index = exponentialSearch(new int[]{3, 22, 27, 47, 57, 67, 89, 91, 95, 99}, 67);
print(67, index);
Мы пытаемся найти элемент больше искомого. Зачем? Для минимизации диапазона поиска. Увеличиваем диапазон, умножая его на 2, и снова проверяем, достигли ли мы элемента больше искомого или конца массива. При нахождении элемента мы выходим из цикла. Затем выполняем бинарный поиск с startIndex в качестве range/2 и lastIndex в качестве range.
В нашем случае значение диапазона достигается в элементе 8, а элемент в integers[8] равен 95. Таким образом, диапазон, в котором выполняется бинарный поиск:
startIndex = range/2 = 4 lastIndex = range = 8
При этом вызываем бинарный поиск:
Arrays.binarySearch(integers, 4, 8, 6);
Вывод:
67 found at Index 5
Здесь важно отметить, что можно ускорить умножение на 2, используя оператор левого сдвига range << 1 вместо *.
Временная сложность
В худшем случае временная сложность этого поиска составит O(log (N)).
Пространственная сложность
Итеративный алгоритм двоичного поиска требует O(1) места для хранения искомого элемента.
Для рекурсивного двоичного поиска пространственная сложность становится равной O(log (N)).
Применение
Экспоненциальный поиск используется с большими массивами, когда бинарный поиск затратен. Экспоненциальный поиск разделяет данные на более доступные для поиска разделы.
Заключение
Каждая система содержит набор ограничений и требований. Правильно подобранный алгоритм поиска, учитывающий эти ограничениях, играет определяющую роль в производительности системы.
В этой статье мы рассмотрели работу алгоритмов поиска Java и случаи их применения.
Описанные алгоритмы доступны на Github.
Источник
- 25 самых используемых регулярных выражений в Java
- Создаём приложение с чистой архитектурой на Java 11
- ТОП-10 лучших книг по Java для программистов
Пробуйте сами и делитесь своими впечатлениями!
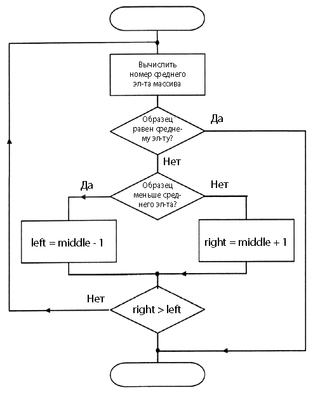
Целочисленный двоичный поиск (бинарный поиск) (англ. binary search) — алгоритм поиска объекта по заданному признаку в множестве объектов, упорядоченных по тому же самому признаку, работающий за логарифмическое время.
| Задача: |
| Пусть нам дан упорядоченный массив, состоящий только из целочисленных элементов. Требуется найти позицию, на которой находится заданный элемент. |
Содержание
- 1 Принцип работы
- 2 Правосторонний/левосторонний целочисленный двоичный поиск
- 2.1 Пример:
- 3 Алгоритм двоичного поиска
- 4 Код
- 5 Несколько слов об эвристиках
- 6 Применение двоичного поиска на некоторых неотсортированных массивах
- 7 Переполнение индекса середины
- 8 См. также
- 9 Источники информации
- 10 Примечания
Принцип работы
Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остаётся та часть множества, где находится искомый объект. Или же, в зависимости от постановки задачи, мы можем остановить процесс, когда мы получим первый или же последний индекс вхождения элемента. Последнее условие — это левосторонний/правосторонний двоичный поиск.
Правосторонний/левосторонний целочисленный двоичный поиск
Для простоты дальнейших определений будем считать, что и что (массив нумеруется с ).
| Определение: |
| Правосторонний бинарный поиск (англ. rightside binary search) — бинарный поиск, с помощью которого мы ищем , где — массив, а — искомый ключ |
| Определение: |
| Левосторонний бинарный поиск (англ. leftside binary search) — бинарный поиск, с помощью которого мы ищем , где — массив, а — искомый ключ |
Использовав эти два вида двоичного поиска, мы можем найти отрезок позиций таких, что и
Пример:
Задан отсортированный массив .
Правосторонний поиск двойки выдаст в результате , в то время как левосторонний выдаст (нумерация с нуля).
Отсюда следует, что количество подряд идущих двоек равно длине отрезка , то есть .
Если искомого элемента в массиве нет, то правосторонний поиск выдаст максимальный элемент, меньший искомого, а левосторонний наоборот, минимальный элемент, больший искомого.
Алгоритм двоичного поиска
Идея поиска заключается в том, чтобы брать элемент посередине, между границами, и сравнивать его с искомым.
Если искомое больше(в случае правостороннего — не меньше), чем элемент сравнения,
то сужаем область поиска так, чтобы новая левая граница была равна индексу середины предыдущей области. В противном случае присваиваем это значение правой границе. Проделываем эту процедуру до тех пор, пока правая граница больше левой более чем на .
Код
int binSearch(int[] a, int key): // Запускаем бинарный поиск int l = -1 // l, r — левая и правая границы int r = len(a) while l < r - 1 // Запускаем цикл m = (l + r) / 2 // m — середина области поиска if a[m] < key l = m else r = m // Сужение границ return r
Инвариант цикла: правый индекс не меньше искомого элемента, а левый — строго меньше (т.к значение присваевается левой границе , только тогда, когда строго меньше искомого элемента ), тогда если (что эквивалентно ), то понятно, что — самое левое вхождение искомого элемента (так как предыдущие элементы уже меньше искомого элемента)
В случае правостороннего поиска изменится знак сравнения при сужении границ на , а возвращаемой переменной станет .
Несколько слов об эвристиках
Эвристика с завершением поиска, при досрочном нахождении искомого элемента
Заметим, что если нам необходимо просто проверить наличие элемента в упорядоченном множестве, то можно использовать любой из правостороннего и левостороннего поиска.
При этом будем на каждой итерации проверять “не попали ли мы в элемент, равный искомому”, и в случае попадания заканчивать поиск.
Эвристика с запоминанием ответа на предыдущий запрос
Пусть дан отсортированный массив чисел, упорядоченных по неубыванию.
Также пусть запросы приходят в таком порядке, что каждый следующий не меньше, чем предыдущий.
Для ответа на запрос будем использовать левосторонний двоичный поиск.
При этом после того как обработался первый запрос, запомним чему равно , запишем его в переменную .
Когда будем обрабатывать следующий запрос, то проинициализируем левую границу как .
Заметим, что все элементы, которые лежат не правее , строго меньше текущего искомого элемента, так как они меньше предыдущего запроса, а значит и меньше текущего. Значит инвариант цикла выполнен.
Применение двоичного поиска на некоторых неотсортированных массивах
| Задача: |
| Пусть отсортированный по возрастанию массив из элементов , все элементы которого различны, был циклически сдвинут, требуется максимально быстро найти элемент в таком массиве. |
Если массив, отсортированный по возрастанию, был циклически сдвинут, тогда полученный массив состоит из двух отсортированных частей. Используем двоичный поиск, чтобы найти индекс последнего элемента левой части массива. Для этого в реализации двоичного поиска заменим условие в if на , тогда в будет содержаться искомый индекс:
int l = -1 int r = len(a) while l < r - 1 // С помощью бинарного поиска найдем максимум на массиве m = (l + r) / 2 // m — середина области поиска if a[m] > a[n - 1] // Сужение границ l = m else r = m int x = l // x — искомый индекс.
Затем воспользуемся двоичным поиском искомого элемента , запустив его на той части массива, в которой он находится: на или на . Для определения нужной части массива сравним с первым и с последним элементами массива:
if key > a[0] // Если key в левой части l = -1 r = x + 1 if key < a[n] // Если key в правой части l = x r = n
Время выполнения данного алгоритма — .
| Задача: |
| Массив образован путем приписывания в конец массива, отсортированного по возрастанию, массива, отсортированного по убыванию. Требуется максимально быстро найти элемент в таком массиве. |
Найдем индекс последнего элемента массива, отсортированного по возрастанию, воспользовавшись троичным поиском, затем запустим левосторонний двоичный поиск для каждого массива отдельно: для элементов и для элементов , где в качестве мы возьмем индекс максимума, найденный троичным поиском. Для массива, отсортированного по убыванию используем двоичный поиск, изменив условие в if на .
Время выполнения алгоритма — (так как и бинарный поиск, и тернарный поиск работают за логарифмическое время с точностью до константы).
| Задача: |
| Два отсортированных по возрастанию массива записаны один в конец другого. Требуется максимально быстро найти элемент в таком массиве. |
Мы имеем массив, образованный из двух отсортированных подмассивов, записанных один в конец другого. Запустить сразу бинарный или тернарный поиски на таком массиве нельзя, так как массив не будет обязательно отсортированным и он не будет иметь точку экстремума. Поэтому попробуем найти индекс последнего элемента левого массива, чтобы потом запустить бинарный поиск два раза на отсортированных массивах.
Докажем, что найти этот индекс невозможно быстрее, чем за . Возьмем возрастающий массив целых чисел, начиная с . Он удовлетворяет условию задачи. Вставим в него на любую позицию. Такой массив по-прежнему будет удовлетворять условию задачи. Следовательно, из-за того, что может находиться на любой позиции, мы можем его найти лишь за .
| Задача: |
| Массив образован путем циклического сдвига массива, образованного приписыванием отсортированного по убыванию массива в конец отсортированного по возрастанию. Требуется максимально быстро найти элемент в таком массиве. |
После циклического сдвига мы получим массив , образованный из трех частей: отсортированных по возрастанию-убыванию-возрастанию () или по убыванию-возрастанию-убыванию (). С помощью двоичного поиска найдем индексы максимального и минимального элементов массива, заменив условие в if на (ответ будет записан в ) или на (ответ будет записан в ) соответственно.
Фактически, при поиске индексов минимума и максимума мы проверяем, возрастает или убывает массив на промежутке , а затем, в зависимости от того, что мы ищем, мы либо поднимаемся, либо опускаемся по этому промежутку возрастания (убывания). Однако при таком решении могут быть неправильно найдены значения минимума или максимума. Рассмотрим случаи, когда они будут неправильно найдены. Определить, какого вида наш массив возможно, сравнив первые два элемента массива.
Рассмотрим отдельно ситуацию, если наш массив вида возрастание-убывание-возрастание (). В таком случае может быть неправильно найдено значение максимума, если последний промежуток возрастания занимает больше половины массива (мы будем подниматься по последнему промежутку возрастания вплоть до конца массива и за максимум будет принят последний элемент массива, что не всегда верно). Тогда, если последний элемент массива меньше первого, нужно еще раз запустить поиск максимума, но уже на промежутке от до , потому что истинный максимум будет находиться в первой точке экстремума, которую мы таким образом и найдем.
В случае же убывание-возрастание-убывание () может быть, что будет неправильно найден минимум. Найдем правильный минимум аналогично поиску максимума в предыдущем абзаце.
Затем, в зависимости от типа нашего массива, запустим бинарный поиск три раза на каждом промежутке.
Время выполнения данного алгоритма — .
Переполнение индекса середины
В некоторых языках программирования присвоение m = (l + r) / 2 приводит к переполнению. Вместо этого рекомендуется использовать m = l + (r - l) / 2; или эквивалентные выражения.[1]
См. также
- Вещественный двоичный поиск
- Троичный поиск
- Поиск с помощью золотого сечения
- Интерполяционный поиск
Источники информации
- Д. Кнут — Искусство программирования (Том 3, 2-е издание)
- Википедия — двоичный поиск
- Типичные ошибки при написании бинарного поиска
- Бинарный поиск на algolist
Примечания
- ↑ https://ai.googleblog.com/2006/06/extra-extra-read-all-about-it-nearly.html
