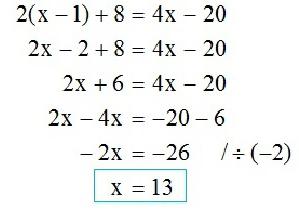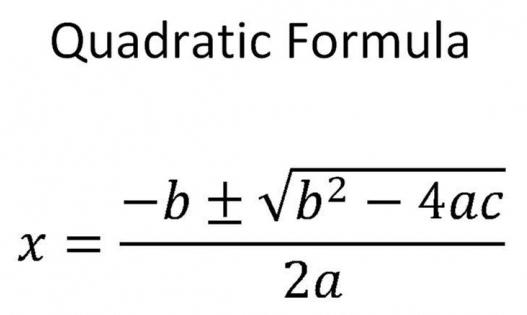- Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
- Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax 2 + c = 0, при b = 0;
- ax 2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
- Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
- перенесем c в правую часть: ax 2 = — c,
- разделим обе части на a: x 2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
- не имеет корней при — c/а 0.
| В двух словах |
|---|
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
- Перенесем свободный член в правую часть:
Разделим обе части на 8:
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
0,5x = 0,125,
х = 0,125/0,5
Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b 2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b 2 −4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
- Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x 2 = 0.
- Произведем равносильные преобразования. Умножим обе части на −1
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x 2 — х = 0.
- Преобразуем уравнение так, чтобы появились множители
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x 2 — 10 = 39.
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
- Найдем дискриминант по формуле
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения 
Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:
2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>
Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n 2 — ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n 2 — ac;
- если D1 0, значит можно найти два действительных корня по формуле
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>
Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
Найти корень уравнения? Это просто!
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
- перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
- разделить обе части получившегося равенства на коэффициент «а».
х = -в/а.
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с. После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:
х = (-в) / (2 * а).
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.
Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
Нужно вернуться к введенному обозначению. х1,2 = ± 1, х3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.
Если х = -1, то получается такой же результат. Корень тоже подходящий.
Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
источники:
http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya
http://www.syl.ru/article/199384/new_nayti-koren-uravneniya-eto-prosto
Почему я сейчас пишу эту статью?
Потому, что, наблюдая за детьми, когда они сражаются сами с собой, вычисляя дискриминант с многозначными числовыми коэффициентами, мне становится их жалко. Они знают лишь один способ решения квадратного уравнения – по формулам (см. картинку 1 ниже). В своей статье я расскажу ещё о девяти способах нахождения его корней.
Хитом среди способов решения квадратного уравнения (и он занимает первое место в нашем списке) становится способ решения квадратного уравнения по готовым формулам.
Но сможете ли Вы с лёгкостью решить этим способом, например, такие уравнения, как на картинке 2 (см. ниже)?
Удивительное рядом: применяя формулы для отыскания корней квадратного уравнения, ученики не могут объяснить, откуда они берутся. Я не стану в этой статье их выводить, а для пытливых посоветую обратиться к учебникам и хотя бы один раз прочитать теоретический материал. Но если всё же кому-то понадобится моя помощь, то вывод формул могу прикрепить в комментариях.
Итак, какой же способ решения квадратного уравнения стоит на втором месте по частоте его применения? Нет, не так, по остаточным воспоминаниям о нём?
Второе место присуждается способу отыскания корней квадратного уравнения по обратной теореме Виета (см. картинку 3).
Замечу, что большинству школьников он кажется слишком “мудрёным”, поэтому его используют реже, чем первый (см. картинку 4).
Третьим по популярности способом решения квадратного уравнения является метод разложения на множители. Он успешно применяется в неполных квадратных уравнениях, когда b=0 или с=0 (картинки 5,6). Интересен следующий факт: в “решебниках” из интернета часто используется именно третий способ, причём даже тогда, когда уравнение содержит полный набор слагаемых.
Следующий способ решения квадратного уравнения, занимающий четвёртую позицию в списке, – это метод извлечения квадратного корня из обеих частей уравнения. К сожалению, применяя его, ученики часто допускают ошибки. Думаю, это происходит потому, что они не знают свойств квадратного корня, модуля и свойств неравенств. На картинках 7 и 8 я покажу, для каких квадратных уравнений его стоит применять, и как это делать правильно.
Пятая строчка нашего списка отдаётся способу решения квадратного уравнения, имеющего чётное значение коэффициента b (картинка 9). Я считаю этот способ решения весьма эффективным, особенно в тех случаях, когда нельзя применить способы 6 и 7 (о них будет рассказано ниже), а значения коэффициентов уравнения представляются многозначными числами . При нахождении корней этим способом мы извлекаем двойную выгоду: 1) находим дискриминант в 4 раза меньший, чем “обычный”, 2) нам не приходится сначала выносить из-под корня числа, затем раскладывать на множители числитель и “сокращать” дробь.
Шестой и седьмой способы решения квадратного уравнения опираются на следствия к обратной теореме Виета.
Назову шестым способ решения квадратного уравнения с нулевым значением суммы всех его коэффициентов (картинка 11).
На седьмом месте находится способ решения квадратного уравнения с коэффициентом b, равным сумме a и с (картинка 12).
Восьмое место отдаётся способу решения квадратного уравнения методом подбора. Этот не очень популярный метод оказывается весьма полезным, если ученик может делить многочлены “уголком” на линейные многочлены. Метод решения опирается на следствие к теореме Безу (см. картинку 13). Первый корень находится подбором, затем многочлен делится “уголком” на разность (х-найденный корень).
В каких задачах можно применять восьмой способ решения? Показываю на картинке 14.
Отдадим девятое место одному из самых трудных для понимания способов решения квадратного уравнения – методу выделения полного квадрата. Как он работает, покажу на картинке 15.
Топ-10 способов решения квадратного уравнения завершает самый не популярный способ его решения – графический. Я не могла не упомянуть о нём, так как он часто используется при решении задач с параметрами на экзаменах и в 9-ом и в 11-ом классе. Рассмотрим его на примере.
Надеюсь, что статья оказалась Вам полезной.
С уважением, автор.
Квадратное уравнение. Дискриминант. Теорема Виета.
теория по математике 📈 уравнения
Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.
Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.
Дискриминант
Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).
Нахождение корней квадратного уравнения
Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:
D=b 2 –4ac
-
Если D>0, то уравнение имеет два различных
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Теорема Виета
Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.
Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.
Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.
Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:
Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.
Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:
Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:
Данное уравнение является квадратным. Но в его условии присутствует квадратный
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х 2 − 2 х − 24 = 0
Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .
pазбирался: Даниил Романович | обсудить разбор | оценить
Теорема Виета для квадратного уравнения
О чем эта статья:
Основные понятия
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Существует три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:
- если D 0, есть два различных корня.
В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .
В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=”215″ src=”https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE” width=”393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=”52″ src=”https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG” width=”125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=”52″ src=”https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo” width=”112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.
Доказательство теоремы Виета
Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что следующие равенства верны
- x₁ + x₂ = −b,
- x₁ * x₂ = c.
Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.
-
Объединим числитель и знаменатель в правой части.
Раскроем скобки и приведем подобные члены:
Сократим дробь полученную дробь на 2, остается −b:
Мы доказали: x₁ + x₂ = −b.
Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.
-
Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:
Перемножаем числители и знаменатели между собой:
Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:
Далее произведем трансформации в числителе:
Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.
Далее раскроем скобки и приведем подобные члены:
Сократим:
Мы доказали: x₁ * x₂ = c.
Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.
Обратная теорема Виета
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:
Обратная теорема Виета
Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.
Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.
Докажем теорему, обратную теореме Виета
Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.
Зафиксируем, что сумма m и n равна −b, а произведение равно c.
Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.
-
Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:
Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:
При x = m получается верное равенство. Значит число m является искомым корнем.
- Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.
При x = n получается верное равенство. Значит число n является искомым корнем.
Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.
Примеры
Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.
Дано: x 2 − 6x + 8 = 0.
Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=”59″ src=”https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv” width=”99″>
Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.
Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=”57″ src=”https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=”64″>
Неприведенное квадратное уравнение
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:
ax 2 + bx + c = 0, где а = 1.
Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .
- Получилось следующее приведенное уравнение:
-
Получается, второй коэффициент при x равен, свободный член —. Значит сумма и произведение корней будут иметь вид:
Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.
Теорема Виета
Теорема Виета:
Сумма корней приведённого квадратного уравнения
равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену
Если приведённое квадратное уравнение имеет вид
то его корни равны:

где D = p 2 – 4q. Чтобы доказать теорему, сначала найдём сумму корней:

а теперь найдём их произведение:
Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:
называются формулами Виета.
Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.
Обратная теорема
Теорема:
Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:
Это доказывает, что число x1 является корнем уравнения x 2 + px + q = 0. Точно так же можно доказать, что и число x2 является корнем для этого уравнения.
Решение примеров
Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.
Пример 1. Найти корни уравнения:
Решение: Так как
очевидно, что корни равны 1 и 2:
Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:
1 2 – 3 · 1 + 2 = 0
2 2 – 3 · 2 + 2 = 0.
Пример 2. Найти корни уравнения:
Методом подбора находим, что корни равны -3 и -5:
С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.
Пример 1. Составить квадратное уравнение по его корням:
Решение: Так как x1 = -3, x2 = 6 корни уравнения x 2 + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения:
Следовательно, искомое уравнение:
Пример 2. Записать приведённое квадратное уравнение, имеющее корни:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/teorema-vieta-formula
http://izamorfix.ru/matematika/algebra/teorema_vieta.html
[/spoiler]
Решение квадратных уравнений
6 июля 2011
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
[x=frac{-12+sqrt{0}}{2cdot 1}=-6]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Метод коэффициентов, часть 1
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: строительные бригады
Способы решения квадратных уравнений
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ: Разложение левой части уравнения на множители.
х 2 + 10х — 24 = 0.
Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х 2 + 6х — 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2* х * 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2* х * 3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
х 2 + 6х — 7 = 0,
прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х — 7 = х 2 + 2* х * 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 — 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 — 4 = 0, х1= 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах 2 + bх + с = 0, а ? 0
на 4а и последовательно имеем:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах * b + b 2 ) — b 2 + 4ac = 0,
(2ax + b) 2 = b 2 — 4ac,
2ax + b = ± v b 2 — 4ac,
2ax = — b ± v b 2 — 4ac,
Примеры.
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 * 4 * 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b 2 — 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 * 4 * 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах 2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 * 2 * 4 = 9 — 32 = — 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b 2 — 4ac < 0,
уравнение ах 2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2= q,
x1 + x2= — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
x 2 — 3x + 2 = 0; x1= 2 и x2= 1, так как q = 2 > 0 и p = — 3 < 0;
x 2 + 8x + 7 = 0; x1 = — 7 и x2= — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
x 2 + 4x — 5 = 0; x1= — 5 и x2= 1, так как q= — 5 < 0 и p = 4 > 0;
x 2 — 8x — 9 = 0; x1 = 9 и x2= — 1, так как q = — 9 < 0 и p = — 8 < 0.
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, где а ? 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у 2 + by + ас = 0,
равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
х1= у1/а и х1= у2/а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 — 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 — 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1= 5/2 x1= 2,5
у2= 6 x2= 6/2 x2= 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах 2 + bх + с = 0, где а ? 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
Доказательство. Разделим обе части уравнения на а ? 0, получим приведенное квадратное уравнение
x 2 + b/a * x + c/a = 0.
Согласно теореме Виета
x1+ x2= — b/a,
x1x2= 1* c/a.
По условию а — b + с = 0, откуда b = а + с. Таким образом,
x1+ x2= — а + b/a= -1 — c/a,
x1x2= — 1* ( — c/a),
т.е. х1= -1 и х2= c/a, что м требовалось доказать.
1) Решим уравнение 345х 2 — 137х — 208 = 0.
Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то
х1= 1, х2= c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х 2 — 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 — 247 + 115 = 0), то
х1= 1, х2= c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k — четное число, то формулу корней
Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k 2 — ac = (- 7) 2 — 3 * 16 = 49 — 48 = 1, D > 0, два различных корня;
В. Приведенное уравнение
х 2 + рх + q= 0
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Формулу (3) особенно удобно использовать, когда р — четное число.
Пример. Решим уравнение х 2 — 14х — 15 = 0.
Решение. Имеем: х1,2=7±
Ответ: х1= 15; х2= -1.
7. СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении
х 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х 2 = — px — q.
Построим графики зависимости у = х 2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —
прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квад- ратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
1) Решим графически уравнение х 2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х 2 = 3х + 4.
Построим параболу у = х 2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1= — 1 и х2 = 4. Ответ: х1= — 1;
2) Решим графически уравнение (рис. 3) х 2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х 2 = 2х — 1.
Построим параболу у = х 2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х 2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х 2 = 5х — 5. Построим параболу у = х 2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х 2 — 2х + 5 = 0 корней не имеет.
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах 2 + bх + с = 0, и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB * OD = OA * OC, откуда OC = OB * OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах 2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Решим уравнение х 2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1= — 1; х2= 3.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение
z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни
z1= 8,0 и z2= 1,0 (рис.12).
2) Решим с помощью номограммы уравнение
2z 2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z 2 — 4,5z + 1 = 0.
Номограмма дает корни z1= 4 и z2= 0,5.
3) Для уравнения
z 2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение
t 2 — 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1= 0,6 и t2= 4,4, откуда z1= 5t1= 3,0 и z2= 5t2= 22,0.
10. СПОСОБ: Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4* 2,5х = 10х ) и четырех пристроенных квадратов (6,25* 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0.
Решение представлено на рис. 16, где
у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.
Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1= 2, у2= — 8 (рис.16).
3) Решить геометрически уравнение у 2 — 6у — 16 = 0.
Преобразуя уравнение, получаем
у 2 — 6у = 16.
На рис. 17 находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,
получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± v25, или у — 3 = ± 5, где у1= 8 и у2= — 2.
Квадратное уравнение
Квадратное уравнение — важное уравнение не только в школьном курсе алгебры. Квадратное уравнение часто используется в геометрии при расчете. Поэтому знать формулы корней квадратного уравнения, чтобы решать его быстрее, нужно всем.
Определение квадратного уравнения
Квадратное уравнение — это уравнение вида , где
— переменная,
,
,
— некоторые числа, причем
. В квадратном уравнении
коэффициент
называют первым коэффициентом,
— вторым коэффициентом,
— свободным членом.
Формула корней
Формула корней квадратного уравнения имеет вид:
Выражение
называется дискриминантом квадратного уравнения и обозначается буквой
.
Влияние дискриминанта на корни квадратного уравнения
Максимальное количество корней квадратного уравнения равно степени уравнения. Квадратное уравнение имеет вторую степень переменной, поэтому и должно иметь два корня. Однако возможны случаи совпадения корней, тогда формально говорят, что «уравнение имеет один корень», хотя правильнее говорить — «уравнение имеет одно значение переменной», или «корни уравнения совпадают и равны…» Есть еще вариант, что уравнение не имеет действительных корней или не имеет действительных решений. Узнать о том — решается квадратное уравнение и сколько имеет корней можно вычислив дискриминант.
- Если
, то существует только одно значение переменной, удовлетворяющее уравнению
. Однако условились говорить, что в этом случае квадратное уравнение имеет два равных действительных корня, а само число
называют корнем кратности два.
- Если
, то квадратное уравнение не имеет действительных корней.
- Если
, то квадратное уравнение имеет два различных действительных корня.
Приведенное квадратное уравнение
Пусть дано квадратное уравнение . Так как
, то, разделив обе части уравнения на
, получим уравнение
. Считая, что
и
, получим уравнение
, в котором первый коэффициент равен 1. Это уравнение называется приведенным.
Формула корней приведенного квадратного уравнения имеет вид:
Неполные квадратные уравнения
Уравнения вида ,
и
называются квадратными уравнениями.
Биквадратное уравнение
Уравнение вида называется биквадратным уравнением. Оно решается с помощью замены переменной по формуле
и приводится к квадратному уравнению
.
Примеры решения квадратного уравнения
Уравнение 1
Решите уравнение
Решение:Найдем дискриминант ,
.
Найдем корни уравнения по формуле корней квадратного уравнения: .
,
.
Ответ: ,
.
Уравнение 2
Решите уравнение .
Решение: находим дискриминант ,
. Применим формулу корней квадратного уравнения:
. Тогда
,
.
Ответ: ,
.
Уравнение 3
Решите уравнение .
Решение: найдем дискриминант ,
. Так как дискриминант отрицателен, то уравнение не имеет корней.
Ответ: нет корней.
Уравнение 4
Решите уравнение
Решение: находим дискриминант ,
. Применим формулу корней квадратного уравнения
.
,
Таким образом, уравнение имеет единственный корень .
Ответ:
Уравнение 5
Решите квадратное уравнение
Решение: Применим формулу корней для приведенного квадратного уравнения: . Отсюда
,
.
Ответ: ,
.
Квадратные уравнения
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Пример 3 . Решить уравнение
Пример 4 . Решить уравнение
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D < 0 , квадратный трехчлен нельзя разложить на линейные множители.
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D < 0 , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D < 0 , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . |
(16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . |
(17) |
Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.