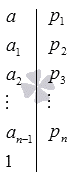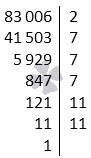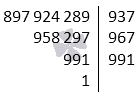Загрузить PDF
Загрузить PDF
Множители – числа, которые при перемножении дают исходное число. То есть любое число есть результат произведения его множителей. Умение раскладывать числа на множители – один из основных математических навыков, который необходим не только в математике, но и в других науках.
-
1
Запишите целое число. Это число, не являющееся обыкновенной или десятичной дробью.
- Рассмотрим число 12.
-
2
Найти два числа, которые при перемножении дадут данное число. Любое целое число можно записать в виде произведения двух других чисел. Даже простое число можно записать как произведение 1 и самого числа.
- В нашем примере у числа 12 есть несколько множителей: 12*1; 6*2; 3*4. Таким образом, вы можем заявить, что множителями числа 12 являются числа 1, 2, 3, 4, 6, 12. Рассмотрим пару множителей 6 и 2.
- Четные числа легко разложить на множители, так как множителем любого четного числа является 2. 4 = 2*2, 26 = 13*2 и т.д.
-
3
Если возможно, разложите на множители найденные множители. Когда вы нашли все множители числа, определите, можно ли разложить их на множители.
- В нашем примере мы разложили 12 на 2*6. Обратите внимание, что 6 можно разложить на множители: 3*2 = 6. Таким образом, вы можете заявить, что 12 = 2*(3*2).
-
4
Если множителями являются простые числа, то дальше можете не продолжать. Простые числа – это числа, которые делятся только на себя или на 1. Например, 2, 3, 5, 7, 11, 13 или 17 – простые числа.
- В нашем примере вы разложили 12 на 2*(2*3). 2, 2, 3 – это простые числа. Их можно разложить на множители, например, 2=2*1 и 3=3*1, но это не имеет смысла (по крайней мере в большинстве задач).
-
5
Отрицательные числа раскладываются на множители аналогичным образом. Единственным отличием является необходимость учесть знаки множителей, чтобы при их перемножении получить отрицательное число.
- Например, разложим на множители число -60.
- -60 = -10*6
- -60 = (-5*2)*6
- -60 = (-5*2)*(3*2)
- -60 = -5*2*3*2. Обратите внимание, что при разложении на множители отрицательного числа количество отрицательных множителей должно быть нечетным. Например, вы можете разложить число -60 и так: -5*2*-3*-2.
Реклама
- Например, разложим на множители число -60.
-
1
Разложить на множители большое число – нелегкая задача. Большинство людей затрудняются раскладывать четырех- или пятизначные числа. Для упрощения процесса запишите число над двумя колонками.
- Разложим на множители число 6552.
-
2
Разделите данное число на наименьший простой делитель (кроме 1), на который данное число делится без остатка. Запишите этот делитель в левой колонке, а в правой колонке запишите результат деления. Как отмечалось выше, четные числа легко раскладывать на множители, так как их наименьшим простым множителем всегда будет число 2 (у нечетных чисел наименьшие простые множители различны).
- В нашем примере число 6552 – четное, поэтому 2 является его наименьшим простым множителем. 6552 ÷ 2 = 3276. В левой колонке запишите 2, а в правой – 3276.
-
3
Далее разделите число в правой колонке на наименьший простой делитель (кроме 1), на который данное число делится без остатка. Запишите этот делитель в левой колонке, а в правой колонке запишите результат деления (продолжите этот процесс до тех пор, пока в правой колонке не останется 1).
- В нашем примере: 3276 ÷ 2 = 1638. В левой колонке запишите 2, а в правой – 1638. Далее: 1638 ÷ 2 = 819. В левой колонке запишите 2, а в правой – 819.
-
4
Вы получили нечетное число; для таких чисел найти наименьший простой делитель сложнее. Если вы получили нечетное число, попробуйте разделить его на наименьшие простые нечетные числа: 3, 5, 7, 11.
- В нашем примере вы получили нечетное число 819. Разделите его на 3: 819 ÷ 3 = 273. В левой колонке запишите 3, а в правой – 273.
- При подборе делителей опробуйте все простые числа вплоть до квадратного корня из наибольшего делителя, который вы нашли. Если ни один делитель не делит число нацело, то вы, скорее всего, получили простое число и можете прекратить вычисления.
-
5
Продолжите процесс деления чисел на простые делители до тех пор, пока в правой колонке не останется 1 (если в правой колонке вы получили простое число, разделите его само на себя, чтобы получить 1).
- Продолжим вычисления в нашем примере:
- Разделите на 3: 273 ÷ 3 = 91. Остатка нет. В левой колонке запишите 3, а в правой – 91.
- Разделите на 3. 91 делится на 3 с остатком, поэтому разделите на 5. 91 делится на 5 с остатком, поэтому разделите на 7: 91 ÷ 7 = 13. Остатка нет. В левой колонке запишите 7, а в правой – 13.
- Разделите на 7. 13 делится на 7 с остатком, поэтому разделите на 11. 13 делится на 11 с остатком, поэтому разделите на 13: 13 ÷ 13 = 1. Остатка нет. В левой колонке запишите 13, а в правой – 1. Ваши вычисления закончены.
- Продолжим вычисления в нашем примере:
-
6
В левой колонке представлены простые множители исходного числа. Другими словами, при перемножении всех чисел из левой колонки вы получите число, записанное над колонками. Если один множитель появляется в списке множителей несколько раз, используйте показатели степени для его обозначения. В нашем примере в списке множителей 2 появляется 4 раза; запишите эти множители как 24, а не как 2*2*2*2.
- В нашем примере 6552 = 23× 32 × 7 × 13. Вы разложили число 6552 на простые множители (порядок множителей в этой записи не имеет значения).
Реклама
Советы
- Также важным является понятие простого числа – это число, которое имеет только два множителя: 1 и само себя. 3 – простое число, потому что его простые множители 1 и 3. С другой стороны, 4 имеет 2 в качестве простого множителя. Число, которое не является простым, называется составным . (1 – число, которое считается ни простым, ни составным – это особый случай.)
- Наименьшие простые числа: 2, 3, 5, 7, 11, 13, 17, 19 и 23.
- Поймите, что одно число является множителем другого, большего числа, если оно “делит его полностью”, то есть без остатка. Например, 6 является множителем 24, потому что 24 ÷ 6 = 4 (без остатка). С другой стороны , 6 не является множителем 25.
- Если цифры в числе при их сложении делятся на 3 , то 3 является множителем этого числа. (819 = 8 +1 +9 = 18, 1 +8 = 9. Три – множитель девяти, так что 3 является множителем и 819.)
- Помните, что мы рассматривали только “натуральные числа” – 1, 2, 3, 4, 5 … Мы не рассматривали отрицательные числа или дроби, которые могут быть описаны в других статьях.
- Некоторые числа могут быть разложены более быстрыми способами, но этот метод работает каждый раз и, как дополнительный бонус, в ответе дает простые множители в порядке их возрастания.
Реклама
Предупреждения
- Не делайте лишней работы. После того, как вы убрали неподходящий множитель, вы не должны рассматривать его далее. После того, как мы решили, что 2 не является множителем 819, нам не надо рассматривать 2 дальше в процессе вычисления.
Реклама
Что вам понадобится
- Бумага
- Карандаш и ластик
- Калькулятор (по желанию)
Об этой статье
Эту страницу просматривали 71 089 раз.
Была ли эта статья полезной?
Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.
Что значит разложить число на простые множители?
Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.
Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30, тогда получим 2,3,5. Запись примет вид 30=2·3·5. Не исключено, что множители могут повторяться. Такое число как 144 имеет 144=2·2·2·2·3·3.
Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.
При z, относящемуся к целым числам, представляется в виде произведения а и b, где z делится на а и на b. Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1, то его разложение на множители p1, p2, …, pn принимает вид a=p1, p2, …, pn. Разложение предполагается в единственном варианте.
Каноническое разложение числа на простые множители
При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p1s1·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.
При разложении числа 609840 получим, что 609 840=2·2·2·2·3·3·5·7·11·11,его канонический вид будет 609 840=24·32·5·7·112. При помощи канонического разложения можно найти все делители числа и их количество.
Алгоритм разложения числа на простые множители
Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p1, p2, …,pn чисел a, a1, a2, …, an-1, это дает возможность получить a=p1·a1, где a1=a:p1, a=p1·a1=p1·p2·a2, где a2=a1:p2, …, a=p1·p2·…·pn·an, где an=an-1:pn. При получении an=1, то равенство a=p1·p2·…·pn получим искомое разложение числа а на простые множители. Заметим, что p1≤p2≤p3≤…≤pn.
Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z. При взятии простых чисел 2,3,5,11 и так далее, причем на них делим число z. Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z. Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
Рассмотрим на примере числа 87. При его делении на 2 имеем, что 87:2=43 с остатком равным 1. Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87:3=29. Отсюда вывод – 3 является наименьшим простым делителем числа 87.
При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a. При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000.
Рассмотрим алгоритм разложения на простые множители:
- нахождение наименьшего множителя при делителе p1 числа a по формуле a1=a:p1, когда a1=1, тогда а является простым числом и включено в разложение на множители, когда не равняется 1, тогда a=p1·a1 и следуем к пункту, находящемуся ниже;
- нахождение простого делителя p2 числа a1 при помощи последовательного перебора простых чисел, используя a2=a1:p2, когда a2=1, тогда разложение примет вид a=p1·p2, когда a2=1, тогда a=p1·p2·a2, причем производим переход к следующему шагу;
- перебор простых чисел и нахождение простого делителя p3 числа a2 по формуле a3=a2:p3, когда a3=1, тогда получим, что a=p1·p2·p3, когда не равняется 1, тогда a=p1·p2·p3·a3 и производим переход к следующему шагу;
- производится нахождение простого делителя pn числа an-1 при помощи перебора простых чисел с pn-1, а также an=an-1:pn, где an=1, шаг является завершающим, в итоге получаем, что a=p1·p2·…·pn.
Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.
Полученный алгоритм можно применять при помощи разложения чисел на простые множители.
Примеры разложения на простые множители
Во время разложения на простые множители следует придерживаться основного алгоритма.
Произвести разложение числа 78 на простые множители.
Решение
Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78. То есть 78:2=39. Деление без остатка, значит это первый простой делитель, который обозначим как p1. Получаем, что a1=a:p1=78:2=39. Пришли к равенству вида a=p1·a1, где 78=2·39. Тогда a1=39, то есть следует перейти к следующему шагу.
Остановимся на нахождении простого делителя p2 числа a1=39. Следует перебрать простые числа, то есть 39:2=19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
Наименьший простой делитель числа a2=13 ищется при помощи перебора чисел, начиная с 3. Получим, что 13:3=4 (ост. 1). Отсюда видно, что 13 не делится на 5,7,11, потому как 13:5=2 (ост. 3), 13:7=1 (ост. 6) и 13:11=1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a3=a2:p3=13:13=1. Получили, что a3=1, что означает завершение алгоритма. Теперь множители записываются в виде 78=2·3·13(a=p1·p2·p3).
Ответ: 78=2·3·13.
Разложить число 83 006 на простые множители.
Решение
Первый шаг предусматривает разложение на простые множители p1=2 и a1=a:p1=83 006:2=41 503, где 83 006=2·41 503.
Второй шаг предполагает, что 2, 3 и 5 не простые делители для числа a1=41 503, а 7 простой делитель, потому как 41 503:7=5 929. Получаем, что p2=7, a2=a1:p2=41 503:7=5 929. Очевидно, что 83 006=2·7·5 929.
Нахождение наименьшего простого делителя p4 к числу a3=847 равняется 7. Видно, что a4=a3:p4=847:7=121, поэтому 83 006=2·7·7·7·121.
Для нахождения простого делителя числа a4=121 используем число 11, то есть p5=11. Тогда получим выражение вида a5=a4:p5=121:11=11, и 83 006=2·7·7·7·11·11.
Для числа a5=11 число p6=11 является наименьшим простым делителем. Отсюда a6=a5:p6=11:11=1. Тогда a6=1. Это указывает на завершение алгоритма. Множители запишутся в виде 83 006=2·7·7·7·11·11.
Каноническая запись ответа примет вид 83 006=2·73·112.
Ответ: 83 006=2·7·7·7·11·11=2·73·112.
Произвести разложение числа 897 924 289 на множители.
Решение
Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2. Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297.
Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа 937. Число 967 можно считать простым, потому как оно является простым делителем числа a1=958 297. Отсюда получаем, что p2=967, то a2=a1:p1=958 297:967=991 и 897 924 289=937·967·991.
Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991. Примерное значение подкоренного выражения имеет вид 991<402. Иначе запишем как 991<402. Отсюда видно, что p3=991 и a3=a2:p3=991:991=1. Получим, что разложение числа 897 924 289 на простые множители получается как 897 924 289=937·967·991.
Ответ: 897 924 289=937·967·991.
Использование признаков делимости для разложения на простые множители
Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Если необходимо произвести разложение на множители 10, то по таблице видно: 2·5=10. Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10.
Если необходимо произвести разложение числа 48, то по таблице видно: 48=6·8. Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6=2·3 и 8=2·4. Тогда полное разложение отсюда получается как 48=6·8=2·3·2·4. Каноническая запись примет вид 48=24·3.
При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100. Отсюда получаем, что 3 400=34·100, где 100 можно разделить на 10, то есть записать в виде 100=10·10, а значит, что 3 400=34·10·10. Основываясь на признаке делимости получаем, что 3 400=34·10·10=2·17·2·5·2·5. Все множители простые. Каноническое разложение принимает вид 3 400=23·52·17.
Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5. Получим, что 75=5·15, причем 15=3·5. То есть искомое разложение пример вид произведения 75=5·3·5.
Формат:
Кратко
Подробно
В столбик
Онлайн калькулятор раскладывает число в произведение простых множителей.
Для вычислений используется длинная арифметика, поэтому можно легко
разложить на множители даже большие числа.
Что такое разложение числа на множители?
Любое натуральное число можно представить в виде
произведения простых чисел. Это представление называется разложением
числа на простые множители.
Натуральное число называется делителем целого числа
если для подходящего целого числа
верно
равенство . В этом случае говорят, что
делится на
или что число
кратно
числу .
Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным
числом называют число, имеющее больше двух различных делителей (любое натуральное число не равное
имеет как минимум два делителя: и
). Например, числа
– простые, а числа
– составные.
Основная теорема арифметики. Любое натуральное число большее единицы, можно
разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования
сомножителей.
Как разложить число на множители?
В школе на уроках математики разложение числа на множители обычно записывают столбиком в две колонки. Делается это
так: в левую колонку выписываем исходное число, затем
- Берём самое маленькое простое число — 2 и по признакам
делимости или обычным делением проверяем, делится ли исходное число на 2. - Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую
колонку под исходным числом. - Если не делится, то берём следующее простое число — 3.
Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение
заканчивается, когда в левой колонке будет записано число 1.
Чтобы лучше понять алгоритм, разберём несколько примеров.
Пример. Разложить на множители число 84.
Решение. Записываем число 84 в левую колонку:
Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2,
то и 84 делится на 2 по признаку делимости. Записываем 2 в
правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:
Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число
21 записываем в левую колонку.
Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3,
21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили
Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:
Всё, число разложено!
В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.
Онлайн калькулятор для разложения числа на множители
Программа раскладывает числа на множители методом
перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие
числа. Однако если число простое или имеет большие простые делители, разложение его на множители занимает
продолжительное время.
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Теория чисел
- Простые числа
- Разложение на простые множители
- Решето Эратосфена
- Линейное решето Эратосфена*
- НОД и НОК
- Алгоритм Евклида
- Расширенный алгоритм Евклида*
- Операции по модулю
- Быстрое возведение в степень
- Деление по простому модулю*
Простые числа
Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.
Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).
Примеры составных чисел: (4), (15), (2^{30}).
Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).
Проверка на простоту за линию
С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) – нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.
def is_prime(n):
if n == 1:
return False
for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
if n % i == 0:
return False
return True
for i in range(1, 10):
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)Проверка на простоту за корень
Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).
Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).
Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).
Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).
Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.
def is_prime(n):
if n == 1:
return False
# Удобно вместо for i in range(2, n ** 0.5) писать так:
i = 2
while i * i <= n:
if n % i == 0:
return False
i += 1
return True
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)Разложение на простые множители
Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.
[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]
Рассмотрим, например, такую задачу:
Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.
Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:
[N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]
Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).
Алгоритм разложения на простые множители
Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.
Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.
Напишем алгоритм факторизации:
def factorize(n):
factors = []
i = 2
while i * i <= n: # перебираем простой делитель
while n % i == 0: # пока N на него делится
n //= i # делим N на этот делитель
factors.append(i)
i += 1
# возможно, в конце N стало большим простым числом,
# у которого мы дошли до корня и поняли, что оно простое
# его тоже нужно добавить в разложение
if n > 1:
factors.append(n)
return factors
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, '=', ' x '.join(str(x) for x in factorize(i)))1 =
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007Задание
За сколько работает этот алгоритм?
.
.
.
.
Решение
За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) – простое.
А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).
Задание
Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.
Разные свойства простых чисел*
Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:
- Простых чисел, меньших (N), примерно (frac{N}{ln N}).
- N-ое простое число равно примерно (Nln N).
- Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
- Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
- Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить – это начать с (N! + 2).
- Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
- Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
- Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
- Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
- Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
- Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
- Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.
Решето Эратосфена
Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).
Но древний грек Эратосфен предложил делать так:
Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.
Красивая визуализация
Задание
Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:
N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
if prime[i]:
for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
prime[j] = 0
for i in range(1, N + 1):
if prime[i]:
print(i)2
3
5
7
11
13
17
19
23
29
31
37
41
43
47У этого алгоритма можно сразу заметить несколько ускорений.
Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.
Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).
Асимптотика
Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.
Гармонический ряд
Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.
Возьмем (N) равное (2^i – 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i – 1}} + ldots + frac{1}{2^i – 1}right)]
Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} – 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]
Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i – 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).
Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).
Попытка объяснения асимптотики** (для старших классов)
Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]
А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.
Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда
[sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} – lnln 2) sim N(lnln N – lnlnln N) sim N lnln N]
Но вообще-то решето можно сделать и линейным.
Задание
Решите 5 первых задач из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Линейное решето Эратосфена*
Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes – это ровно те числа (x), у которых (min_d[x] = x).
Основное утверждение такое:
Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).
Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое – добавим в primes и сделаем (min_d[i] = i).
Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) – это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).
Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).
N = 30
primes = []
min_d = [0] * (N + 1)
for i in range(2, N + 1):
if min_d[i] == 0:
min_d[i] = i
primes.append(i)
for p in primes:
if p > min_d[i] or i * p > N:
break
min_d[i * p] = p
print(i, min_d)
print(min_d)
print(primes)2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти – ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.
Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.
НОД и НОК
Введем два определения.
Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).
Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).
Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)
Зачем они нужны? Например, они часто возникают в задачах.
Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?
Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).
Еще пример задачи на применение НОД и НОК:
Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?
Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.
Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.
Пусть (t = НОД(n, m)), тогда (n = at, m = bt).
Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))
Значит, итоговый ответ: ((n-1) + (m-1) – (t-1)).
Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.
Алгоритм Евклида
Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.
Давайте для начала научимся искать (НОД(a, b)).
Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b – a), b > a]
Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b – a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.
Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]
(так как (НОД(a, b) = НОД(a, b – a) = НОД(a, b – 2a) = НОД(a, b – 3a) = ldots = НОД(a, b operatorname{%} a)))
Это равенство дает идею следующего рекурсивного алгоритма:
[НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]
Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]
Задание:
Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250
По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))1
10
6
1
50
6Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.
А за сколько оно вообще работает?
Задание
Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).
Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.
Как выразить НОК через НОД
(НОК(a, b) = frac{ab}{НОД(a, b)})
По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?
Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).
[ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]
Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]
Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]
Формула доказана.
Как посчитать НОД/НОК от более чем 2 чисел
Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:
(НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))
(НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))
Почему это верно?
Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.
С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.
Задание
Решите задачи F, G, H, I из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Расширенный алгоритм Евклида*
Очень важным для математики свойством наибольшего общего делителя является следующий факт:
Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).
Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x – 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)
Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.
Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).
Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]
Теперь сделаем в этом выражении замену (r = a – bq):
[bx_0 + ry_0 = bx_0 + (a – bq)y_0 = ay_0 + b(x_0 – qy_0)]
Tаким образом, можно взять (x = y_0), а (y = (x_0 – qy_0) = (x_0 – (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).
В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x – (a / b)y)) (решение для чисел (a) и (b)).
Это удобно реализовывать рекурсивно:
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
d, x, y = extended_gcd(b, a % b)
return d, y, x - (a // b) * y
a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))3 * 2 + 5 * -1 = 1Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 – 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 – 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 – y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 – y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 – y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 – 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]
Действительно, (116times(-3) + 44times8 = 4)
Задание
Решите задачу J из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Операции по модулю
Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».
Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a – b)) делится на (m).
Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).
Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.
С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.
a = 30
b = 50
mod = 71
print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)Задание
Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 – 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)
Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).
intвмещает до (2^{31} – 1 approx 2 cdot 10^9).long longвмещает до (2^{63} – 1 approx 8 cdot 10^{18}).long long longв плюсах нет, при попытке заиспользовать выдает ошибкуlong long long is too long.- Под некоторыми компиляторами и архитектурами доступен
int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).
Зачем нужно считать ответ по модулю
Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)
Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)
int mod = 1e9 + 7; # В C++
cout << mod;1000000007N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))1000000007.0
1000000007Быстрое возведение в степень
Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).
Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.
Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):
- (3^2)
- (3^4)
- (3^8)
- (3^{16})
- (3^{32})
- (3^{33})
- (3^{66})
- (3^{132})
- (3^{133})
- (3^{266})
- (3^{532})
- (3^{533})
- (3^{1066})
Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:
- (a^0 = 1)
- (a^{2k}=(a^{k})^2)
- (a^{2k+1}=a^{2k}times a)
Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)
Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)
Асимптотика этого алгоритма, очевидно, (O(log c)) – за каждые две итерации число уменьшается хотя бы в 2 раза.
Задание
Решите задачу K из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Задание
Решите как можно больше задач из практического контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
(a / b) = (a times b^{-1}), где (b^{-1}) – это обратный элемент к (b).
Определение: (b^{-1}) – это такое число, что (bb^{-1} = 1)
Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))
Задание
Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) – и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x – y) a) делится на (p), (a) – ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) – простое, (a neq 0 pmod p)).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).
((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число – значит умножить на обратный к нему, который существует).
А значит, (a^{p – 1} = 1 pmod p).
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) – это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).
Обобщение У малой теоремы Ферма есть обобщение для составных (p):
Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) – взаимно просто с (p), а (varphi(p)) – это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).
Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) – 1}).
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
[ax + py = 1]
Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.
Тогда если взять остаток по модулю (p):
[ax = 1 pmod p]
А значит, найденный (x) и будет обратным элементом к (a).
То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.
Как разложить число на простые множители?
МатематикаАлгебраУравнения
Анонимный вопрос
12 августа 2018 · 120,5 K
Главный редактор издания «Популярный университет», научный журналист, химик · 28 авг 2018 · popuni.ru
Очень просто:
1) Сначала нужно убедиться, что раскладываемое число делится не только на 1 и на само себя. В противном случае это будет простое число, которое само же и является своим множителем.
2) После того, как мы поняли, что число делится не только на 1 и на само себя, нужно разделить его на самое маленькое простое число, которое является его делителем. Например, если взять число 12, то самым маленьким простым числом для него будет 2. Смотрим остаток их деления: 12/2=6. Продолжаем те же действия, но уже с цифрой 6 – для 6 наименьшим простым числом будет тоже 2: 6/2=3. Продолжать такие действия нужно, пока в конце мы не получим простое число (в нашем случае – 3). Таким образом, разложение будет выглядеть так: 12=2*2*3.
67,2 K
Спасибо вы мне очень помогли
Комментировать ответ…Комментировать…
ЕГЭ и поступление в вуз – новости и законы. Веду ютуб-канал и паблик в ВК · 31 янв 2019 ·
Разложить число на простые множители – значит представить его в виде произведения простых чисел.
Например, 15=5*3, 30=5*3*2 и т.п
Простые числа приведены ниже: Читать далее
11,4 K
Комментировать ответ…Комментировать…
Учитель математики в средней школе И ВУЗе. Не учу жизни, учу решать задачи. Готовлю к ОГЭ… · 10 авг 2019
Сначала четко представляем, что числа бывают простые (те, которые делятся только на себя и на 1. Числа 5, 11, 13 и т.д.) и составные ( они делятся и на другие числа кроме самого себя и 1. Допустим число 15 делится ещё на 5 и на 3).
Теперь берём число и делим на самый маленький простой делитель (кроме 1). Получаем частное от деления, его опять делим и т.д., пока не… Читать далее
5,3 K
Комментировать ответ…Комментировать…
Для того чтобы разложить число на простые множители нужно, для начала, поделить его на 2. Если число разделится на 2 без остатка, то 2 – это первый множитель. Далее полученный результат опять делим на 2, если число разделится на 2 без остатка, то второй множитель тоже 2. Если же при делении получается остаток, то пробуем делим на 3, 4, … n, до тех пор число не… Читать далее
3,0 K
Комментировать ответ…Комментировать…
Давайте разложим 756 на простые множители. Оно делиться на 2, так как оно чётное. Имеем 756:2=378. Проведём вертикальную линию и слева от неё запишем делимое (756), а справа делитель- 2. Частное запишем под числом 756. Число 378 тоже делится на 2, так как оно чётное. При делении получили в частном 189. Число 189 не делится на 2, но делится на 3, так как сумма цифр… Читать далее
3,6 K
Комментировать ответ…Комментировать…
Skysmart – онлайн-школа для учеников 1–11 классов и тех, кто только готовится к учебе
· 21 янв 2020 · skysmart.ru
Проверьте, не является ли ваше число простым — тогда оно делится только на себя и на единицу. Используйте базовые признаки делимости:
— четные числа делятся на 2;
— числа, сумма всех цифр которого делится на 3, тоже делится на 3.
— числа, где последняя цифра 5, делятся на 5, где 0 — на 5 и 2.
Если число большое, например 3209, лучше проверить его по списку простых… Читать далее
1,7 K
Комментировать ответ…Комментировать…
Нужно сразу убедиться, что число не простое, а составное, то есь если это число не присутствует в списке простых чисел. Далее:
-
Проверяем на чётность, выбрав все числа 2.
-
В оставшемся числе смотрим признак деления на 3.
-
Проверяем признак деления на 5, 7, 11 до того момента, пока не останется какое-то простое число.
-
Записываем все множители.
3,3 K
в каком списке? ряд чисел бесконечен, не слышал про списки 20-значных чисел, например. Если число сколь-нибудь… Читать дальше
Комментировать ответ…Комментировать…
Всякое составное число можно разложить на простые множители .При любом способе получается одно и то же разложение .если не учитавать порядка записи множителей.
6,6 K
Комментировать ответ…Комментировать…