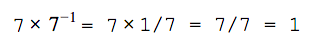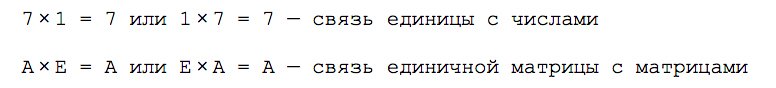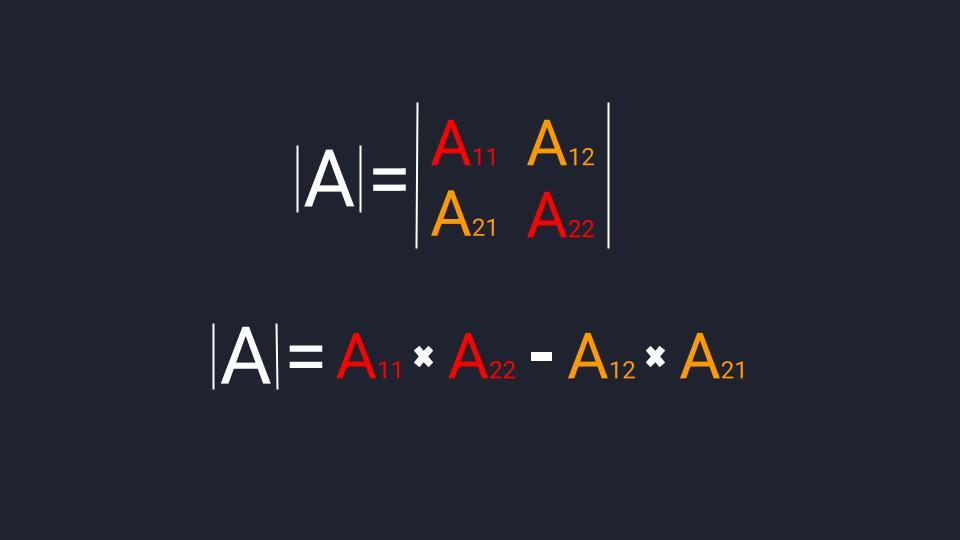Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} – (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 – 4cdot5 = 27 – 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) – 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 – 0 – 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 – 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 – 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 – 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 – 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 – 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 – 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |
Обратная матрица и её свойства
15 февраля 2018
- Домашняя работа
- Ответы
Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.
Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.
Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.
Повторение: умножение матриц
Прежде всего договоримся об обозначениях. Матрицей $A$ размера $left[ mtimes n right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:
[A=left[ mtimes n right]=underbrace{left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \end{matrix} right]}_{n}]
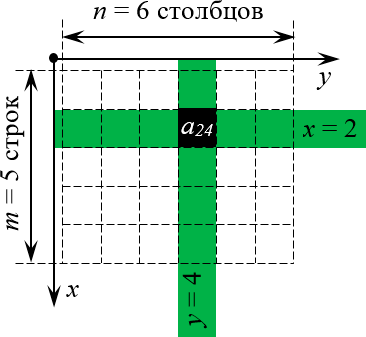
Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:
Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $left( x;y right)$ — это и будет номер строки и номер столбца.
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.
А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.
В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.
Определение. Матрицы $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.
Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $left( A;B right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $left( B;A right)$ — тоже согласована.
Умножать можно только согласованные матрицы.
Определение. Произведение согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:
[{{c}_{ij}}=sumlimits_{k=1}^{n}{{{a}_{ik}}}cdot {{b}_{kj}}]
Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=Acdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.
Да, вот такое суровое определение. Из него сразу следует несколько фактов:
- Умножение матриц, вообще говоря, некоммутативно: $Acdot Bne Bcdot A$;
- Однако умножение ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$;
- И даже дистрибутивно: $left( A+B right)cdot C=Acdot C+Bcdot C$;
- И ещё раз дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$.
Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.
Если всё же получается так, что $Acdot B=Bcdot A$, такие матрицы называются перестановочными.
Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:
Определение. Матрица $E$ называется единичной, если $Acdot E=A$ или $Ecdot A=A$. В случае с квадратной матрицей $A$ можем записать:
[Acdot E=Ecdot A=A]
Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)
А ещё из-за этой $E$ кое-кто придумал всю ту дичь, которая будет написана дальше.
Что такое обратная матрица
Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.
Ключевое определение
Что ж, пора познать истину.
Определение. Матрица $B$ называется обратной к матрице $A$, если
[Acdot B=Bcdot A=E]
Обратная матрица обозначается через ${{A}^{-1}}$ (не путать со степенью!), поэтому определение можно переписать так:
[Acdot {{A}^{-1}}={{A}^{-1}}cdot A=E]
Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:
- Всегда ли существует обратная матрица? И если не всегда, то как определить: когда она существует, а когда — нет?
- А кто сказал, что такая матрица ровно одна? Вдруг для некоторой исходной матрицы $A$ найдётся целая толпа обратных?
- Как выглядят все эти «обратные»? И как, собственно, их считать?
Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.
Основные свойства
Начнём с того, как в принципе должна выглядеть матрица $A$, чтобы для неё существовала ${{A}^{-1}}$. Сейчас мы убедимся в том, что обе эти матрицы должны быть квадратными, причём одного размера: $left[ ntimes n right]$.
Лемма 1. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда обе эти матрицы — квадратные, причём одинакового порядка $n$.
Доказательство. Всё просто. Пусть матрица $A=left[ mtimes n right]$, ${{A}^{-1}}=left[ atimes b right]$. Поскольку произведение $Acdot {{A}^{-1}}=E$ по определению существует, матрицы $A$ и ${{A}^{-1}}$ согласованы в указанном порядке:
[begin{align} & left[ mtimes n right]cdot left[ atimes b right]=left[ mtimes b right] \ & n=a end{align}]
Это прямое следствие из алгоритма перемножения матриц: коэффициенты $n$ и $a$ являются «транзитными» и должны быть равны.
Вместе с тем определено и обратное умножение: ${{A}^{-1}}cdot A=E$, поэтому матрицы ${{A}^{-1}}$ и $A$ тоже согласованы в указанном порядке:
[begin{align} & left[ atimes b right]cdot left[ mtimes n right]=left[ atimes n right] \ & b=m end{align}]
Таким образом, без ограничения общности можем считать, что $A=left[ mtimes n right]$, ${{A}^{-1}}=left[ ntimes m right]$. Однако согласно определению $Acdot {{A}^{-1}}={{A}^{-1}}cdot A$, поэтому размеры матриц строго совпадают:
[begin{align} & left[ mtimes n right]=left[ ntimes m right] \ & m=n end{align}]
Вот и получается, что все три матрицы — $A$, ${{A}^{-1}}$ и $E$ — являются квадратными размером $left[ ntimes n right]$. Лемма доказана.
Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.
Лемма 2. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда эта обратная матрица — единственная.
Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:
[begin{align} & Acdot B=Bcdot A=E; \ & Acdot C=Ccdot A=E. \ end{align}]
Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $left[ ntimes n right]$. Следовательно, определено произведение:
[Bcdot Acdot C]
Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:
[begin{align} & Bcdot Acdot C=left( Bcdot A right)cdot C=Ecdot C=C; \ & Bcdot Acdot C=Bcdot left( Acdot C right)=Bcdot E=B; \ & Bcdot Acdot C=C=BRightarrow B=C. \ end{align}]
Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.
Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $bne 0$. Единственное существенное дополнение — учёт размерности матриц.
Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.
Лемма 3. Дана матрица $A$. Если обратная к ней матрица ${{A}^{-1}}$ существует, то определитель исходной матрицы отличен от нуля:
[left| A right|ne 0]
Доказательство. Мы уже знаем, что $A$ и ${{A}^{-1}}$ — квадратные матрицы размера $left[ ntimes n right]$. Следовательно, для каждой из них можно вычислить определитель: $left| A right|$ и $left| {{A}^{-1}} right|$. Однако определитель произведения равен произведению определителей:
[left| Acdot B right|=left| A right|cdot left| B right|Rightarrow left| Acdot {{A}^{-1}} right|=left| A right|cdot left| {{A}^{-1}} right|]
Но согласно определению $Acdot {{A}^{-1}}=E$, а определитель $E$ всегда равен 1, поэтому
[begin{align} & Acdot {{A}^{-1}}=E; \ & left| Acdot {{A}^{-1}} right|=left| E right|; \ & left| A right|cdot left| {{A}^{-1}} right|=1. \ end{align}]
Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:
[left| A right|ne 0;quad left| {{A}^{-1}} right|ne 0.]
Вот и получается, что $left| A right|ne 0$. Лемма доказана.
На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.
Но для начала сформулируем «вспомогательное» определение:
Определение. Вырожденная матрица — это квадратная матрица размера $left[ ntimes n right]$, чей определитель равен нулю.
Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.
Как найти обратную матрицу
Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.
Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $left[ 2times 2 right]$ и — частично — размера $left[ 3times 3 right]$. А вот начиная с размера $left[ 4times 4 right]$ его лучше не применять. Почему — сейчас сами всё поймёте.
Алгебраические дополнения
Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».
Начнём с главного. Пусть имеется квадратная матрица размера $A=left[ ntimes n right]$, элементы которой именуются ${{a}_{ij}}$. Тогда для каждого такого элемента можно определить алгебраическое дополнение:
Определение. Алгебраическое дополнение ${{A}_{ij}}$ к элементу ${{a}_{ij}}$, стоящего в $i$-й строке и $j$-м столбце матрицы $A=left[ ntimes n right]$ — это конструкция вида
[{{A}_{ij}}={{left( -1 right)}^{i+j}}cdot M_{ij}^{*}]
Где $M_{ij}^{*}$ — определитель матрицы, полученной из исходной $A$ вычёркиванием той самой $i$-й строки и $j$-го столбца.
Ещё раз. Алгебраическое дополнение к элементу матрицы с координатами $left( i;j right)$ обозначается как ${{A}_{ij}}$ и считается по схеме:
- Сначала вычёркиваем из исходной матрицы $i$-строчку и $j$-й столбец. Получим новую квадратную матрицу, и её определитель мы обозначаем как $M_{ij}^{*}$.
- Затем умножаем этот определитель на ${{left( -1 right)}^{i+j}}$ — поначалу это выражение может показаться мозговыносящим, но по сути мы просто выясняем знак перед $M_{ij}^{*}$.
- Считаем — получаем конкретное число. Т.е. алгебраическое дополнение — это именно число, а не какая-то новая матрица и т.д.
Саму матрицу $M_{ij}^{*}$ называют дополнительным минором к элементу ${{a}_{ij}}$. И в этом смысле приведённое выше определение алгебраического дополнения является частным случаем более сложного определения — того, что мы рассматривали в уроке про определитель.
Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:
- Берём в квадратной матрице $k$ строчек и $k$ столбцов. На их пересечении получится матрица размера $left[ ktimes k right]$ — её определитель называется минором порядка $k$ и обозначается ${{M}_{k}}$.
- Затем вычёркиваем эти «избранные» $k$ строчек и $k$ столбцов. Снова получится квадратная матрица — её определитель называется дополнительным минором и обозначается $M_{k}^{*}$.
- Умножаем $M_{k}^{*}$ на ${{left( -1 right)}^{t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.
Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.
Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:
Определение. Союзная матрица $S$ к квадратной матрице $A=left[ ntimes n right]$ — это новая матрица размера $left[ ntimes n right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:
[A=left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} \end{matrix} right]Rightarrow S=left[ begin{matrix} {{A}_{11}} & {{A}_{12}} & … & {{A}_{1n}} \ {{A}_{21}} & {{A}_{22}} & … & {{A}_{2n}} \ … & … & … & … \ {{A}_{n1}} & {{A}_{n2}} & … & {{A}_{nn}} \end{matrix} right]]
Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)
Что ж, всё это очень мило, но зачем это нужно? А вот зачем.
Основная теорема
Вернёмся немного назад. Помните, в Лемме 3 утверждалось, что обратимая матрица $A$ всегда не вырождена (т.е. её определитель отличен от нуля: $left| A right|ne 0$).
Так вот, верно и обратное: если матрица $A$ не вырождена, то она всегда обратима. И даже существует схема поиска ${{A}^{-1}}$. Зацените:
Теорема об обратной матрице. Пусть дана квадратная матрица $A=left[ ntimes n right]$, причём её определитель отличен от нуля: $left| A right|ne 0$. Тогда обратная матрица ${{A}^{-1}}$ существует и считается по формуле:
[{{A}^{-1}}=frac{1}{left| A right|}cdot {{S}^{T}}]
А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:
- Посчитать определитель $left| A right|$ и убедиться, что он отличен от нуля.
- Составить союзную матрицу $S$, т.е. посчитать 100500 алгебраических дополнений ${{A}_{ij}}$ и расставить их на месте ${{a}_{ij}}$.
- Транспонировать эту матрицу $S$, а затем умножить её на некое число $q={1}/{left| A right|};$.
И всё! Обратная матрица ${{A}^{-1}}$ найдена. Давайте посмотрим на примеры:
Задача. Найдите обратную матрицу:
[left[ begin{matrix} 3 & 1 \ 5 & 2 \end{matrix} right]]
Решение. Проверим обратимость. Посчитаем определитель:
[left| A right|=left| begin{matrix} 3 & 1 \ 5 & 2 \end{matrix} right|=3cdot 2-1cdot 5=6-5=1]
Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:
[S=left[ begin{matrix} {{A}_{11}} & {{A}_{12}} \ {{A}_{21}} & {{A}_{22}} \end{matrix} right]]
Посчитаем алгебраические дополнения:
[begin{align} & {{A}_{11}}={{left( -1 right)}^{1+1}}cdot left| 2 right|=2; \ & {{A}_{12}}={{left( -1 right)}^{1+2}}cdot left| 5 right|=-5; \ & {{A}_{21}}={{left( -1 right)}^{2+1}}cdot left| 1 right|=-1; \ & {{A}_{22}}={{left( -1 right)}^{2+2}}cdot left| 3 right|=3. \ end{align}]
Обратите внимание: определители |2|, |5|, |1| и |3| — это именно определители матриц размера $left[ 1times 1 right]$, а не модули. Т.е. если в определителях стояли отрицательные числа, убирать «минус» не надо.
Итого наша союзная матрица выглядит так:
[S=left[ begin{array}{*{35}{r}}2 & -5 \ -1 & 3 \end{array} right]]
Осталось посчитать обратную:
[{{A}^{-1}}=frac{1}{left| A right|}cdot {{S}^{T}}=frac{1}{1}cdot {{left[ begin{array}{*{35}{r}} 2 & -5 \ -1 & 3 \end{array} right]}^{T}}=left[ begin{array}{*{35}{r}} 2 & -1 \ -5 & 3 \end{array} right]]
Ну вот и всё. Задача решена.
Ответ. $left[ begin{array}{*{35}{r}} 2 & -1 \ -5 & 3 \end{array} right]$
Задача. Найдите обратную матрицу:
[left[ begin{array}{*{35}{r}} 1 & -1 & 2 \ 0 & 2 & -1 \ 1 & 0 & 1 \end{array} right]]
Решение. Опять считаем определитель:
[begin{align} & left| begin{array}{*{35}{r}} 1 & -1 & 2 \ 0 & 2 & -1 \ 1 & 0 & 1 \end{array} right|=begin{matrix} left( 1cdot 2cdot 1+left( -1 right)cdot left( -1 right)cdot 1+2cdot 0cdot 0 right)- \ -left( 2cdot 2cdot 1+left( -1 right)cdot 0cdot 1+1cdot left( -1 right)cdot 0 right) \end{matrix}= \ & =left( 2+1+0 right)-left( 4+0+0 right)=-1ne 0. \ end{align}]
Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. И каждое из них будет содержать определитель $left[ 2times 2 right]$. Полетели:
[begin{matrix} {{A}_{11}}={{left( -1 right)}^{1+1}}cdot left| begin{matrix} 2 & -1 \ 0 & 1 \end{matrix} right|=2; \ {{A}_{12}}={{left( -1 right)}^{1+2}}cdot left| begin{matrix} 0 & -1 \ 1 & 1 \end{matrix} right|=-1; \ {{A}_{13}}={{left( -1 right)}^{1+3}}cdot left| begin{matrix} 0 & 2 \ 1 & 0 \end{matrix} right|=-2; \ … \ {{A}_{33}}={{left( -1 right)}^{3+3}}cdot left| begin{matrix} 1 & -1 \ 0 & 2 \end{matrix} right|=2; \ end{matrix}]
Короче, союзная матрица будет выглядеть так:
[S=left[ begin{matrix} 2 & -1 & -2 \ 1 & -1 & -1 \ -3 & 1 & 2 \end{matrix} right]]
Следовательно, обратная матрица будет такой:
[{{A}^{-1}}=frac{1}{-1}cdot left[ begin{matrix} 2 & -1 & -2 \ 1 & -1 & -1 \ -3 & 1 & 2 \end{matrix} right]=left[ begin{array}{*{35}{r}}-2 & -1 & 3 \ 1 & 1 & -1 \ 2 & 1 & -2 \end{array} right]]
Ну и всё. Вот и ответ.
Ответ. $left[ begin{array}{*{35}{r}} -2 & -1 & 3 \ 1 & 1 & -1 \ 2 & 1 & -2 \end{array} right]$
Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:
Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.
Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.
Альтернативный способ
Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $left[ 2times 2 right]$ и $left[ 3times 3 right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.
Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $left[ 10times 10 right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.
Элементарные преобразования
Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:
- Умножение. Можно взять $i$-ю строку (столбец) и умножить её на любое число $kne 0$;
- Сложение. Прибавить к $i$-й строке (столбцу) любую другую $j$-ю строку (столбец), умноженную на любое число $kne 0$ (можно, конечно, и $k=0$, но какой в этом смысл? Ничего не изменится же).
- Перестановка. Взять $i$-ю и $j$-ю строки (столбцы) и поменять местами.
Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.
Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.
Присоединённая матрица
Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.
Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?
Определение. Пусть дана матрица $A=left[ ntimes n right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $left[ Aleft| E right. right]$ — это новая матрица размера $left[ ntimes 2n right]$, которая выглядит так:
[left[ Aleft| E right. right]=left[ begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} & 1 & 0 & … & 0 \{{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} & 0 & 1 & … & 0 \… & … & … & … & … & … & … & … \{{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} & 0 & 0 & … & 1 \end{array} right]]
Короче говоря, берём матрицу $A$, справа приписываем к ней единичную матрицу $E$ нужного размера, разделяем их вертикальной чертой для красоты — вот вам и присоединённая.:)
В чём прикол? А вот в чём:
Теорема. Пусть матрица $A$ обратима. Рассмотрим присоединённую матрицу $left[ Aleft| E right. right]$. Если с помощью элементарных преобразований строк привести её к виду $left[ Eleft| B right. right]$, т.е. путём умножения, вычитания и перестановки строк получить из $A$ матрицу $E$ справа, то полученная слева матрица $B$ — это обратная к $A$:
[left[ Aleft| E right. right]to left[ Eleft| B right. right]Rightarrow B={{A}^{-1}}]
Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:
- Записать присоединённую матрицу $left[ Aleft| E right. right]$;
- Выполнять элементарные преобразования строк до тех пор, пока права вместо $A$ не появится $E$;
- Разумеется, слева тоже что-то появится — некая матрица $B$. Это и будет обратная;
- PROFIT!:)
Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $left[ 3times 3 right]$ и $left[ 4times 4 right]$.
Задача. Найдите обратную матрицу:
[left[ begin{array}{*{35}{r}} 1 & 5 & 1 \ 3 & 2 & 1 \ 6 & -2 & 1 \end{array} right]]
Решение. Составляем присоединённую матрицу:
[left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 3 & 2 & 1 & 0 & 1 & 0 \ 6 & -2 & 1 & 0 & 0 & 1 \end{array} right]]
Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 3 & 2 & 1 & 0 & 1 & 0 \ 6 & -2 & 1 & 0 & 0 & 1 \end{array} right]begin{matrix} downarrow \ -1 \ -1 \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 5 & -7 & 0 & -1 & 0 & 1 \end{array} right] \ end{align}]
Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 5 & -7 & 0 & -1 & 0 & 1 \end{array} right]begin{matrix} \ downarrow \ -2 \end{matrix}to \ & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right] \ end{align}]
Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} -1 \ -2 \ uparrow \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & -1 & 0 & -3 & 5 & -2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right] \ end{align}]
Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:
[begin{align} & left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & -1 & 0 & -3 & 5 & -2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} \ left| cdot left( -1 right) right. \ \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & 1 & 0 & 3 & -5 & 2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} -6 \ updownarrow \ +1 \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \ 0 & 1 & 0 & 3 & -5 & 2 \ 1 & 0 & 0 & 4 & -7 & 3 \end{array} right] \ end{align}]
Осталось лишь поменять местами строки 1 и 3:
[left[ begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \ 0 & 1 & 0 & 3 & -5 & 2 \ 0 & 0 & 1 & -18 & 32 & -13 \end{array} right]]
Готово! Справа — искомая обратная матрица.
Ответ. $left[ begin{array}{*{35}{r}}4 & -7 & 3 \ 3 & -5 & 2 \ -18 & 32 & -13 \end{array} right]$
Задача. Найдите обратную матрицу:
[left[ begin{matrix} 1 & 4 & 2 & 3 \ 1 & -2 & 1 & -2 \ 1 & -1 & 1 & 1 \ 0 & -10 & -2 & -5 \end{matrix} right]]
Решение. Снова составляем присоединённую:
[left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]]
Немного позалимаем, попечалимся от того, сколько сейчас придётся считать… и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]begin{matrix} downarrow \ -1 \ -1 \ \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right] \ end{align}]
Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]begin{matrix} \ left| cdot left( -1 right) right. \ left| cdot left( -1 right) right. \ left| cdot left( -1 right) right. \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \end{array} right]begin{matrix} -2 \ -1 \ updownarrow \ -2 \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right]begin{matrix} +1 \ -3 \ -2 \ uparrow \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right]begin{matrix} 6 \ updownarrow \ -5 \ \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
И снова слева единичная матрица, значит справа — обратная.:)
Ответ. $left[ begin{matrix} 33 & -6 & -26 & 17 \ 6 & -1 & -5 & 3 \ -25 & 5 & 20 & -13 \ -2 & 0 & 2 & -1 \end{matrix} right]$
Ну вот и всё. Проверку сделайте сами — мне в лом.:)
Смотрите также:
- Определитель
- Дополнительные соображения
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Четырехугольная пирамида в задаче C2
- Задача B5: площадь кольца
- Случай четырехугольной пирамиды
Обра́тная ма́трица — такая матрица 


Обратную матрицу можно определить как:
- где
— соответствующая присоединённая матрица,
— определитель матрицы
.
Из этого определения следует критерий обратимости: матрица обратима тогда и только тогда, когда она невырождена, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы[править | править код]
Пусть квадратные матрицы 
Способы нахождения обратной матрицы[править | править код]
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы[править | править код]
Метод Жордана—Гаусса[править | править код]
Возьмём две матрицы: саму 



При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц 
Вторая матрица после применения всех операций станет равна 

С помощью матрицы алгебраических дополнений[править | править код]
Матрица, обратная матрице 
- где
— присоединенная матрица (матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы).
Сложность алгоритма зависит от сложности 

Использование LU- или LUP-разложения[править | править код]
Матричное уравнение 

















Матрицу, обратную к заданной невырожденной матрице 
Результатом LUP-разложения матрицы 

















В случае использования LU-разложения (


Сложность обоих алгоритмов — 
Итерационные методы[править | править код]
Матрицу 
Последовательность матриц 


Выбор начального приближения[править | править код]
Проблема выбора начального приближения 

















Для метода Ньютона в качестве начального приближения можно выбрать 






Примеры[править | править код]
Матрица 2 × 2[править | править код]
[4]
Обращение матрицы 2 × 2 возможно только при условии, что 
Примечания[править | править код]
- ↑ Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, — М.: Вильямс, 2006 (с. 700).
- ↑ Petković, M. D. Generalized Schultz iterative methods for the computation of outer inverses (англ.) // Computers & Mathematics with Applications. — 2014. — June (vol. 67, iss. 10). — P. 1837—1847. — doi:10.1016/j.camwa.2014.03.019.
- ↑ Pan, V., Reif, J. Fast and efficient parallel solution of dense linear systems (англ.) // Computers & Mathematics with Applications. — 1989. — Vol. 17, iss. 11. — P. 1481—1491. — doi:10.1016/0898-1221(89)90081-3.
- ↑ Как найти обратную матрицу? mathprofi.ru. Дата обращения: 18 октября 2017. Архивировано 17 октября 2017 года.
Ссылки[править | править код]
- Реализация с полным выбором ведущего элемента на C++
Что такое обратная матрица
Сложная тема из линейной алгебры.
Что такое обратная матрица
Сложная тема из линейной алгебры.
Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:
- Познакомились с вектором
- Поделали с ними операции
- Научились определять их параллельность
- Познакомились с матрицами
Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.
С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.
Читать ли эту статью?
❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.
✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.
Обратное — это как?
В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:
Обратные числа при умножении друг на друга всегда дают единицу:
Обратная матрица
В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.
Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:
Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.
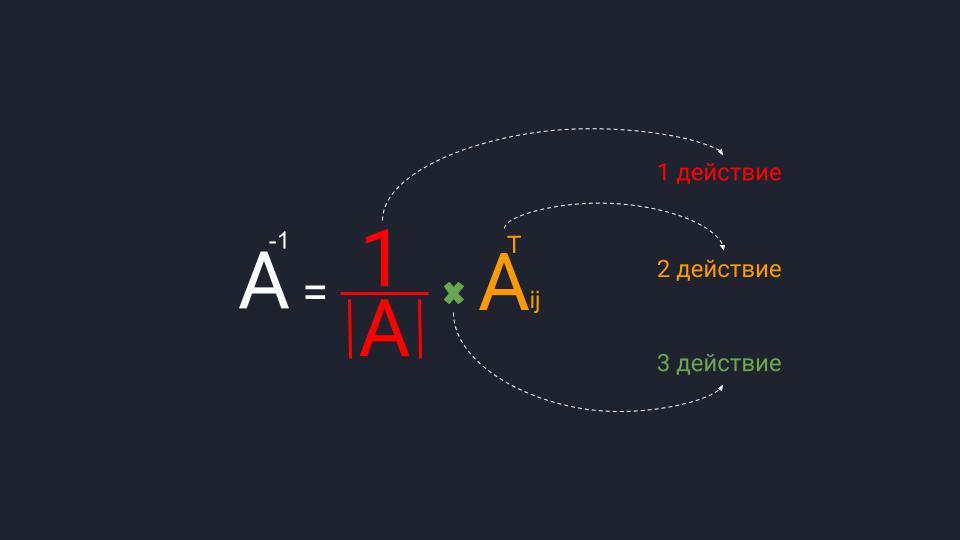
Как рассчитать обратную матрицу
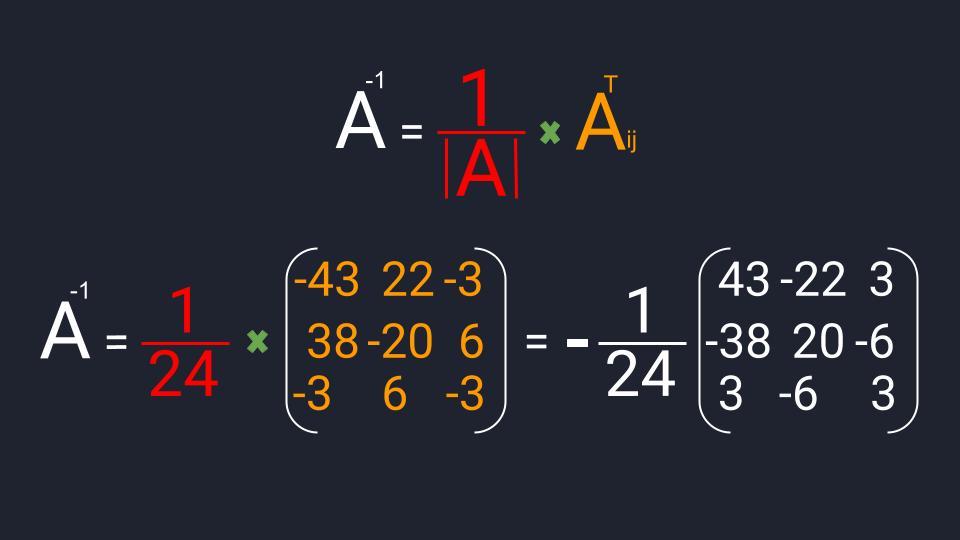
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:
- Разделить единицу на матричный определитель.
- Найти транспонированную матрицу алгебраических дополнений.
- Перемножить полученные значения.
Далее мы по порядку во всём разберёмся.
Определитель — это особое число, которое «определяет» свойства матрицы.
Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.
Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.
Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.
Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.
Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.
Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.
Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.
Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.
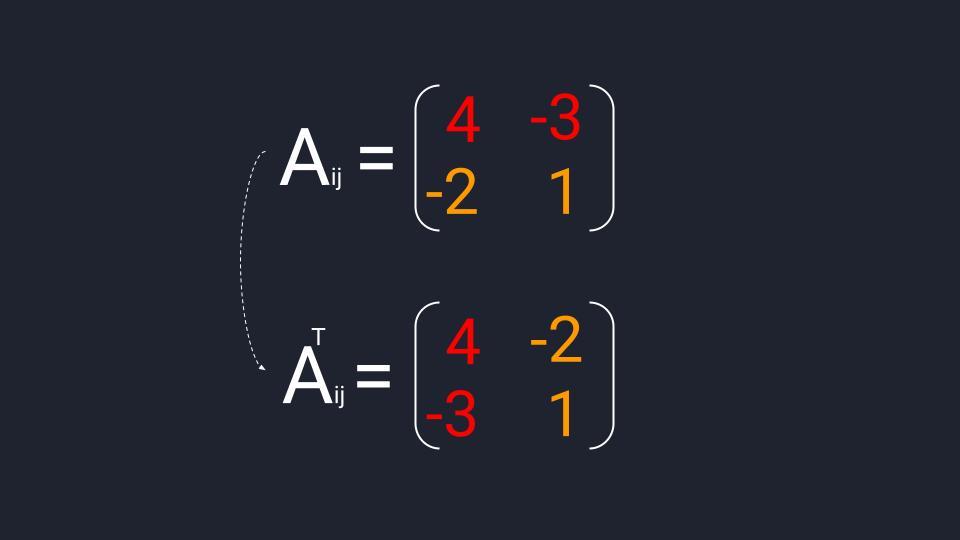
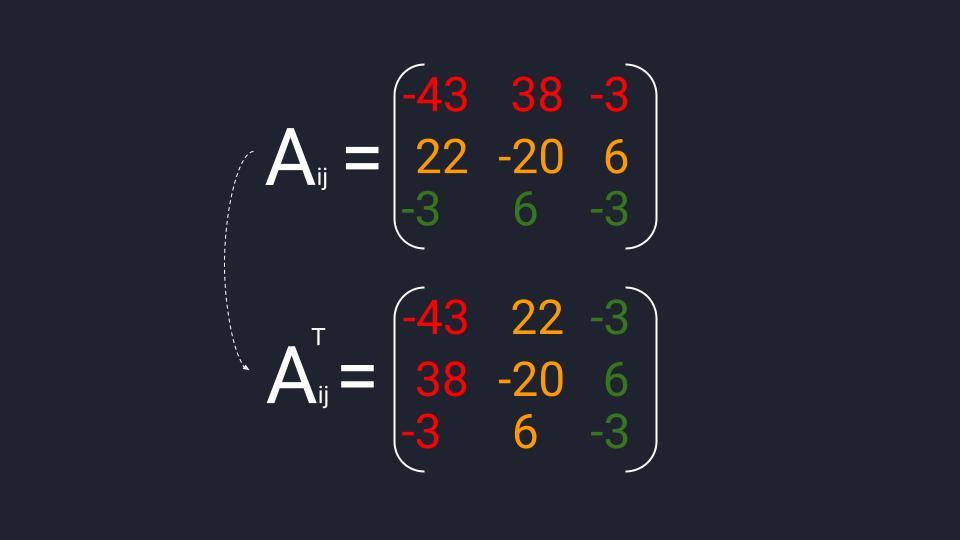
Транспонированная матрица алгебраических дополнений вычисляется в три шага:
- Мы из исходной матрицы находим матрицу миноров.
- Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.
- Находим транспонированную матрицу из матрицы алгебраических дополнений.
Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.
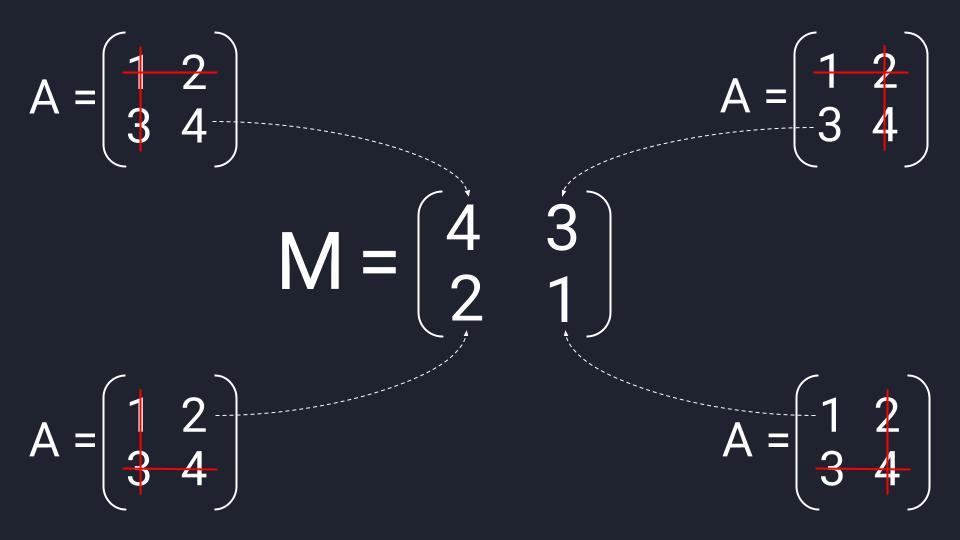
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:
- Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.
- Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
- Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
- Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.
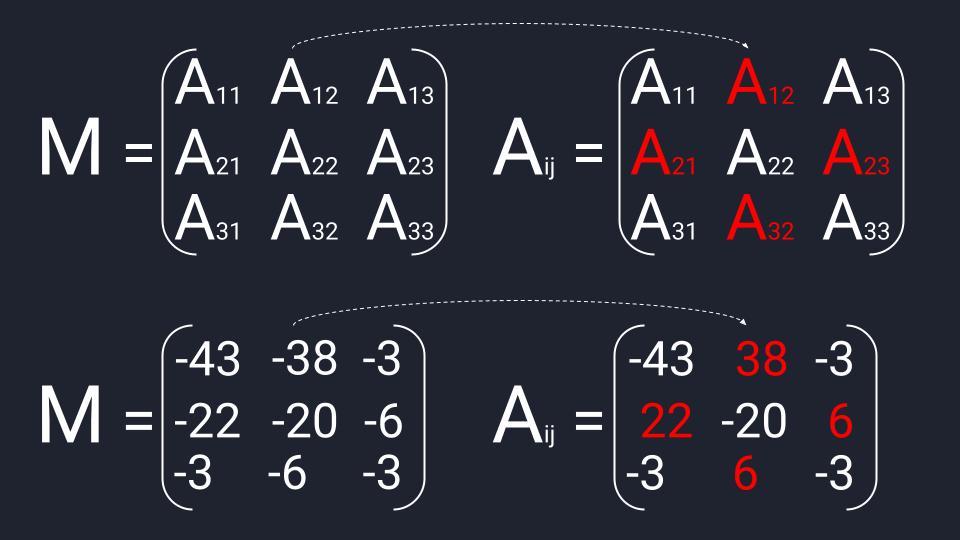
Матрица миноров третьего порядка рассчитывается по следующему принципу:
- Последовательно вычёркиваем строки и столбцы.
- Получаем четыре элемента и считаем определитель.
- Записываем результат в матрицу миноров третьего порядка.
Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:
- Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
- Найдите этот же элемент в исходной матрице и отметьте его точкой.
- Проведите от этой точки две линии: вдоль строки и вдоль столбца.
После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.
Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.
1-я строка 1-й элемент:
Δ = 5×1 – 8×6 = -43
1-я строка 2-й элемент:
Δ = 4×1 – 7×6 = -38
1-я строка 3-й элемент:
Δ = 4×8 – 7×5 = -3
2-я строка 1-й элемент:
Δ = 2×1 – 8×3 = -22
2-я строка 2-й элемент:
Δ = 1×1 – 7×3 = -20
2-я строка 3-й элемент:
Δ = 1×8 – 7×2 = -6
3-я строка 1-й элемент:
Δ = 2×6 – 5×3 = -3
3-я строка 2-й элемент:
Δ = 1×6 – 4×3 = -6
3-я строка 3-й элемент:
Δ = 1×5 – 4×2 = -3
Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:
Господи, зачем всё это?
Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?
Смотрите:
- Вам не нужно уметь решать все эти уравнения самостоятельно. Для этого давно есть мощные алгоритмы.
- Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда.
- В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
- И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия.
Спокойствие, всё будет хорошо.
Получите ИТ-профессию
В «Яндекс Практикуме» можно стать разработчиком, тестировщиком, аналитиком и менеджером цифровых продуктов. Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.
Начать карьеру в ИТ