Для того, чтобы выразить косинус через синус, вспомним основное тригонометрическое тождество:
sin²α + cos²α = 1.
Таким образом, если известен синус, то косинус найти можно так:
cos²α = 1 – sin²α.
Возможны 2 варианта:
1) cosα = √(1 – sin²α), если угол α находится в 1 четверти (0 < α < 90) или в 4 четверти (270 < α < 360).
2) cosα = – √(1 – sin²α), если угол α находится во 2 четверти (90 < α < 180) или в 3 четверти (180 < α < 270).
Пример
1) Синус угла α = 0,3 и 90 < α < 180. Нужно найти, чему равен косинус угла α.
Так как угол α находится во второй четверти, то косинус будет отрицательным. Выразим его по формуле:
cosα = – √ (1 – 0,09) = -√0,91 = – 0,95.
2) Синус угла α = 0,7 и 270 < α < 360. Выразим косинус.
Так как угол α находится в 4 четверти, то косинус будет положительным.
cosα = √ (1 – 0,49) = √0,51 = 0,71.

Примеры:
(sin(-π)=-sin,π)
(cos(-225^° )=cos, 225^°)
(tg(-frac{π}{2}-x)=-tg(frac{π}{2}+x))
И сразу два важных замечания.
Замечание №1
Многие ученики думают, что если можно вынести минус из тригонометрической функции, то можно вынести и число, но это не так:
(sin,2x≠2 sin,x)
(cos,3x≠3cos,x)
(tg,4x≠4tg,x)
Замечание №2
(sin^2(-x)=sin^2x)
(cos^2(-x)=cos^2x)
(tg^2 (-x)=tg^2 x)
(ctg^2 (-x)=ctg^2 x)
Квадрат меняет ситуацию. Всё дело в том, что (sin^2(-x)=(sin(-x) )^2=(-sin,x )^2=sin^2x), т.е. минус все равно выносится, но так как синуса два и они перемножаются, то в итоге получается плюс.
Примеры из ЕГЭ
Пример (ЕГЭ). Найдите значение выражения (24sqrt{2},cos(-frac{π}{3}),sin(-frac{π}{4})).
Решение. (24sqrt{2},cos(-frac{π}{3}),sin(-frac{π}{4})=-24sqrt{2},cosfrac{π}{3},sinfrac{π}{4}).

Из рисунка видно, что и косинус, и синус положителен. Косинус из трех стандартных значений (frac{1}{2}), (frac{sqrt{2}}{2}), (frac{sqrt{3}}{2}) принимает наименьшее т.е. (cos,frac{π}{3}=frac{1}{2}). Синус из трех стандартных значений будет равен среднему т.е. (sin,frac{π}{4}=frac{sqrt{2}}{2}). Получается:
(-24sqrt{2},cosfrac{π}{3},sinfrac{π}{4}=-24sqrt{2}cdot)(frac{1}{2})(cdot)(frac{sqrt{2}}{2})(=)(frac{-24sqrt{2}cdotsqrt{2}}{4})(=)(frac{-24cdot 2}{4})(=-6cdot2=-12)
Ответ: (-12).
Если вы не поняли почему (frac{π}{3}) и (frac{π}{4}) находятся на круге там, где мы из обозначили, то читайте статью «Как обозначать числа с пи на числовой окружности?». А если не поняли, как мы нашли синус и косинус, то читайте статью «Как найти синус и косинус без тригонометрической таблицы».
Пример (ЕГЭ). Найдите значение выражения (44sqrt{3},tg,(-480^° )).
Решение. (44sqrt{3},tg(-480^° )=-44sqrt{3},tg(480^° )=-44sqrt{3},tg(360^°+120^° )=-44sqrt{3},tg(360^°+90^°+30^°)).
Находим (480^°) на окружности:

Соединяем точку, соответствующую (480^°) и центр окружности, и продляем до оси тангенсов:

Мы попадаем в самое маленькое (из стандартных) значение тангенса.
Значит, (tg(480^° )=-sqrt{3}).
В итоге имеем: (44sqrt{3} tg(-480^° )=-44sqrt{3}cdot(-sqrt{3})=44cdot 3=132).
Ответ: (132).
Если вам не понятно, как мы нашли значение тангенса, то читайте статью «Как найти тангенс и котангенс без тригонометрической таблицы?».
Доказательства формул с минусом в аргументе:
| tg(2α) = | 2tg(α)
1 – tg2(α) |
| ctg(2α) = | ctg2(α) – 1
2ctg(α) |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021
Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.
- Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$ - Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$ - Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$ - Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$ - Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$ - Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$ - Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$ - Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$ - Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$ - Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$ - Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$ - Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$ - Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$ - Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$ - Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$ - Формулы приведения можно найти в отдельной статье
Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Основное тригонометрическое тождество
$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)
Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус – это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$
Ответ: (4.)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.
Основные связи тригонометрических функций
А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:
$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$
Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.
Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).
Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$
Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)
Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$
Вывод связи тангенса с косинусом и котангенса с синусом
Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство – формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).
Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$
Формулы суммы и разности тригонометрических функций
- Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$ - Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$ - Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$ - Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$
Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.
Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:
Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).
Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$
Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:
Пример 4
Найдите значение (sin(15^o)=?)
(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.
Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Пример 5
Найдите значение (cos(75^o)=?)
(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.
Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Мы не будем выводить эти формулы – это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.
Формулы двойного угла
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)
Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)
Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$
Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)
Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$
Формулы тройного угла
Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$
Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$
Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$
Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.
Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.
Формулы половинного угла (двойного аргумента)
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$
Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$
Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$
Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$
Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$
Формулы понижения степени
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Формулы понижения второй степени на самом деле дублируют формулы половинного угла.
Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.
Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.
Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:
$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$
Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.
Аналогично выводятся все остальные формулы.
Пример 10
Вычислить (sin(165)+sin(75)=?)
(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$
Преобразование произведения тригонометрических функций
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.
Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:
$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.
Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.
Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)
Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция – arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
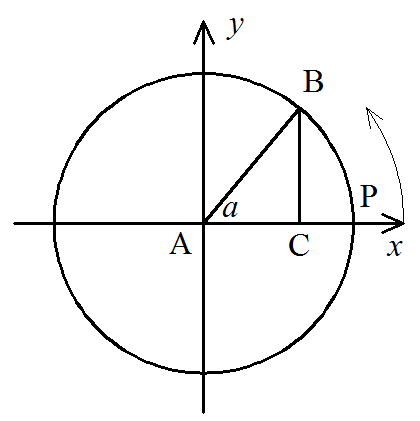
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы